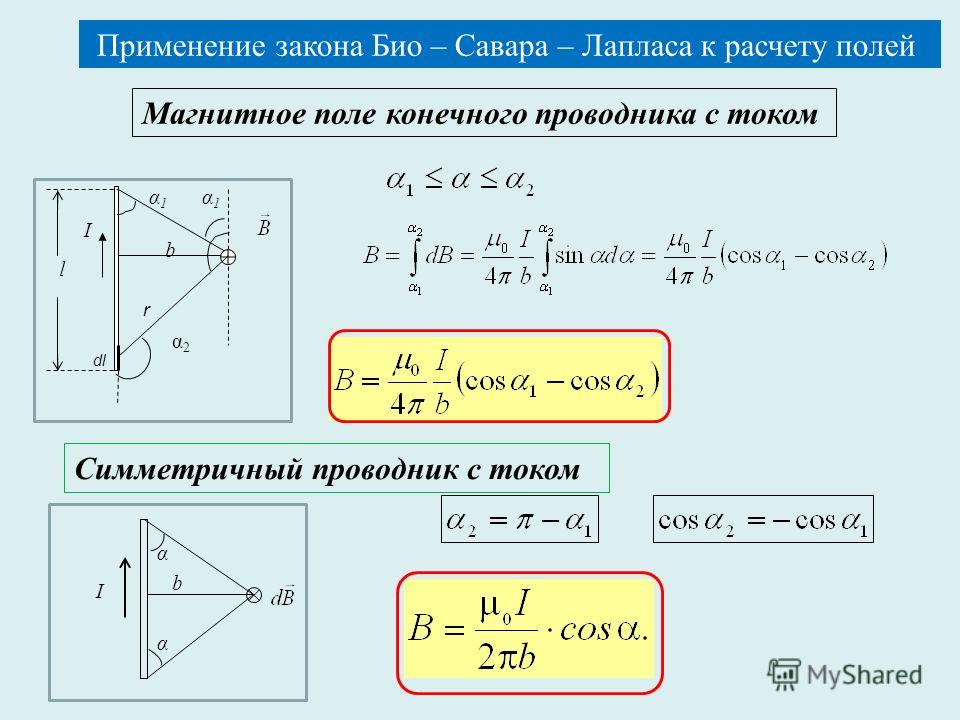
§ 2. Закон Био – Савара – Лапласа

Французские физики Ж.Био (1774 – 1862) и Ф.Савар (1791 – 1841) провели в 1820 году экспериментальное исследование магнитных полей, создаваемых токами, проходящими по проводам различной формы. Их соотечественник знаменитый физик и математик П.Лаплас (1749 – 1827) проанализировал эти экспериментальный данные и установил, что наблюдаемое многообразие магнитных полей для различных проводников с током может быть сведено к магнитному полю элементарного проводника с током, которое описывается выражением универсального вида. При этом Лаплас предположил, что для магнитного поля, так же, как и для электрического поля, справедлив принцип суперпозиции:

магнитная индукция, создаваемая произвольным проводником с током равна геометрической сумме магнитных индукций, создаваемых фрагментами этого проводника:

(2)

М агнитное поле элементарного проводника с током, согласно Лапласу, описывается выражением

(3)

г

Рис. 4 Магнитная индукция, создаваемая элементарным проводником с током в т. А (а). Правило буравчика (б).

де dB –магнитная индукция, создаваемая элементарным проводником длиной dl, по которому течет ток I, в точке А (см. рис.4а). В формуле (3)  – угол между направлением тока в проводнике и радиусом вектором , соединяющим элемент тока с точкой А ( r – модуль радиуса-вектора ).

Формула (3) описывает закон Био – Савара –Лапласа.

Коэффициент пропорциональности в выражении (3) зависит от выбора системы единиц и от магнитных свойств среды, окружающей проводник с током. Если проводник находится в вакууме, то этот коэффициент определяется только выбором системы единиц и в СИ равен

,

где ₀ = 410^-7 – магнитная постоянная.

Если проводник с током окружен веществом, то коэффициент k в законе Био – Савара – Лапласа записывается в виде:

,

где  – магнитная проницаемость среды, которая показывает, во сколько раз индукция вещества больше, чем в вакууме при прочих равных условиях.

Выражение (3) может быть переписано в векторной форме

, (4)

которая отражает закон Био – Савара – Лапласа в наиболее общем виде.

Рис.5 Магнитная индукция в центре кругового тока (а). Применение правила буравчика для определения направления вектора магнитной индукции (б)

В соответствии с правилом векторного произведения вектор оказывается перпендикулярным плоскости, в которой лежат вектора и . Направление вектора задается уже упоминавшимся правилом буравчика: если рукоятку буравчика сначала совместить с первым вектором векторного произведения ( ), а затем путем кратчайшего поворота совместить со вторым вектором произведения ( ), то направление, куда будет завинчиваться при этом буравчик, укажет направление векторного произведения, то есть вектора (рис.4б).

Как уже отмечалось, магнитная индукция, создаваемая проводником с током, зависит от окружающего этот проводник вещества и отличается в  раз от магнитной индукции, создаваемой тем же проводником с током в вакууме. Если несущие ток провода находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является

магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле В’, которое накладывается на обусловленное токами поле В_о. Оба поля в сумме дают результирующее поле В = В₀ + В’

Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. Под В подразумевается усредненное (макроскопическое) поле.

Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток, обусловленный движением заряженных частиц внутри самих атомов и молекул, обладает магнитным моментом и создает в окружающем пространстве магнитное поле.

Согласно теории выдающегося датского физика Н.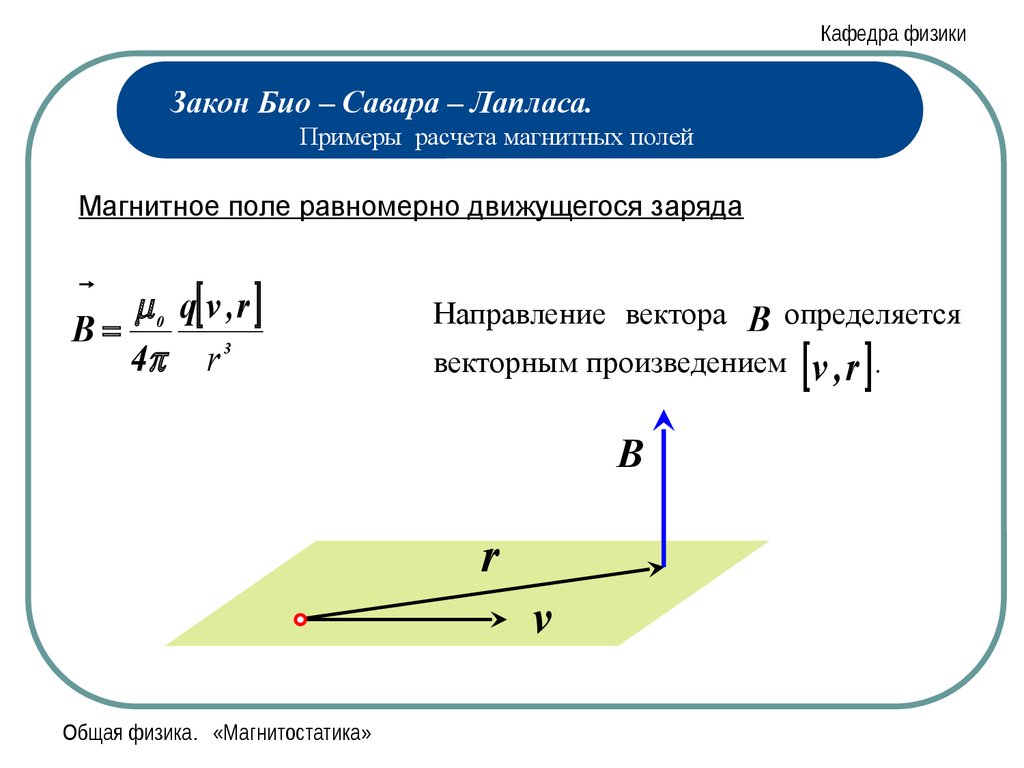 Бора (1885 — 1962), электроны вращаются вокруг атомных ядер по замкнутым орбитам. Кроме того, электронам присущ собственный механический момент (момент импульса), который получил название спина электрона. Спином обладают не только электроны, но и атомные ядра. Орбитальные и спиновые движения заряженных частиц порождают так называемые микроскопические токи, которые также возбуждают магнитные поля. Виток с током создает вокруг себя магнитное поле. Поэтому можно ожидать, что микроскопические кольцевые токи также будут возбуждать магнитные поля.

По современным представлениям магнитные свойства вещества обусловлены тремя факторами:

– орбитальным движением электронов;

– спиновым движением электронов;

– спиновым движением атомных ядер.

Тяжелые атомные ядра движутся значительно медленнее легких электронов, поэтому их спиновое движение можно не учитывать.

В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю.

В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается — его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В‘.

Намагничение магнетика естественно характеризовать магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают буквой

J.

Итак, магнитное поле в веществе, описываемое вектором магнитной индукции , определяется как макроскопическими токами (токами проводимости в проводниках), так и микроскопическими токами (обусловленными орбитальным и спиновым движением электронов, входящих в состав атомов вещества). По аналогии с электростатикой, в магнитостатике вводят физическую величину – напряженность магнитного поля , которая характеризует магнитное поле макроскопических токов и не зависит от магнитных свойств окружающей среды.

В однородной и изотропной среде напряженность магнитного поля определяется следующим соотношением:

(5)

Из формул (5) и (4) следует, что напряженность магнитного поля, создаваемого элементом тока , определяется выражением

, (6)

то есть действительно не зависит от свойств среды. Выражение (6) описывает закон Био – Савара – Лапласа для напряженности магнитного поля.

Единицей измерения Н в СИ является .

Намагниченность принято связывать не с магнитной индукцией, а с напряженностью поля. Полагают, что в каждой точке магнетика

J = H,

где — характерная для данного магнетика величина, называемая магнитной восприимчивостью^. Опыт показывает, что для слабомагнитных (неферромагнитных) веществ при не слишком сильных полях  не зависит от Н. Размерность Н совпадает с размерностью J. Следовательно,  — безразмерная величина.

Безразмерная величина называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества.

Диамагнетики, парамагнетики, ферромагнетики. Магнитная индукция В и напряженность магнитного поля макроскопических токов

Н связаны соотношением В = ₀Н. Магнитная проницаемость  показывает, во сколько раз магнитное поле макроскопических токов усиливается вследствие намагничивания среды

По значению магнитной проницаемости  все вещества делятся на три группы: диамагнетики ( < 1), парамагнетики ( > 1) и ферромагнетики ( > 1) и меняется в зависимости от напряженности поля макроскопических токов)

Магнитные свойства тел определяются магнитными свойствами составляющих их атомов и молекул, движением электрических зарядов в последних.

Для диамагнетиков полный магнитный момент атома в отсутствие поля равен нулю, поэтому в поле вследствие изменения магнитного момента каждого электрона на отрицательную величину магнитный момент атома становится отрицательным. Все вещество в целом приобретает магнитный момент, направленный против поля.

Для парамагнетиков магнитный момент каждого атома в отсутствие внешнего магнитного поля отличен от нуля, но вследствие хаотического расположения атомов вещество в целом магнитным моментом не обладает.

При внесении парамагнетика в магнитное поле атомы стремятся установиться так, чтобы их магнитные моменты были ориентированы по полю, в результате чего парамагнетик намагничивается по полю.

При помещении парамагнетика между полюсами магнита на его концах возникают полюсы, разноименные с близлежащими полюсами магнита. Парамагнетик втягивается в магнитное поле

Ферромагнетик обладает отдельными микроскопическими (линейные размеры ~10^-4см) областями (доменами), которые намагничены до насыщения и в отсутствие внешнего поля.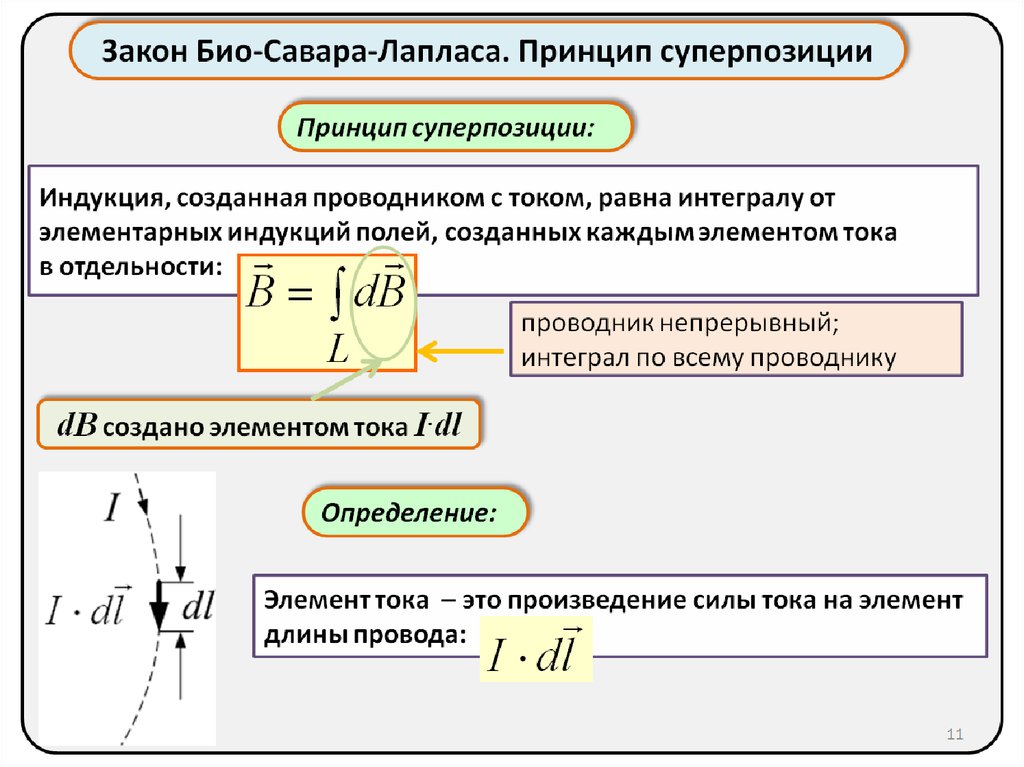 Однако магнитные моменты всех этих областей ориентированы хаотически, и магнитный момент макроскопического объема равен нулю.

При внесении ферромагнетика во внешнее магнитное поле по полю ориентируются не магнитные моменты отдельных атомов, а целые области спонтанного (самопроизвольного) намагничивания.

| Закон Био-Савара-Лапласа | Fiziku5

Если частицы будут двигаться антипараллельно, то при остальных равных условиях разноимённые частицы будут притягиваться, а одноимённые будут отталкиваться также в соответствие с III-им законом Ньютона.

Но в общем случае III-й закон Ньютона выполняться не будет:

Рис.19.7

, но линии действия этих сил не совпадают. Есть пример ещё более красноречивый:

Рис.19.8

В этом случае .

Дело в том, что III-й закон Ньютона является частным случаем закона сохранения импульса замкнутой системы. Импульс системы двух движущихся зарядов не сохраняется, поскольку она не является замкнутой. Таковой является система «заряды+электромагнитное поле». Импульс электромагнитного поля компенсирует несохранение импульса частиц.

§19.7. Закон Био-Савара-Лапласа

По принципу суперпозиции магнитные поля движущихся частиц векторно складываются, причём каждый заряд возбуждает поле, не зависящее от наличия других источников. Следовательно, магнитное поле, созданное элементом объёма dV проводника с током, равно сумме магнитных полей каждого носителя, находящегося в этом объёме. Поскольку, все носители одинаковы, имеют общую скорость и находятся в одной точке, то общее поле

,

где — общее количество носителей, — поле одного носителя. То есть,

Рис.19.9

Полученная формула и есть закон Био-Савара-Лапласа, то есть соотношение, описывающее магнитную индукцию, созданную элементом проводника с током I (рис.19.9):

§19.8. Простейшие примеры применения закона Био-Савара-Лапласа

19.8.1. Магнитное поле прямолинейного проводника с током.

Рис.19.10

Для всех элементов рассматриваемого на рисунке 19.10 участка прямолинейного проводника с током направление элементарного вклада в общий вектор магнитной индукции – одинаково (перпендикулярно плоскости рисунка от нас). Следовательно, для подсчёта модуля вектора в точке А В(А) достаточно учитывать только модули элементарных вкладов

Из дополнительного рисунка видно, что

.

Следовательно,

Окончательно:

В случае бесконечно длинного проводника

Þ

Силовая линия представляет собой окружность, концентрическую с проводником, направление вектора магнитной индукции будет соответствовать правилу правого винта:

Рис.19.11

19.8.2. Взаимодействие двух бесконечно длинных прямых параллельных токов

Рис.19.12

Этими формулами пользуются для определения единицы измерения тока.

19.8.3. Магнитное поле кругового витка с током в центре витка

; Þ

Þ .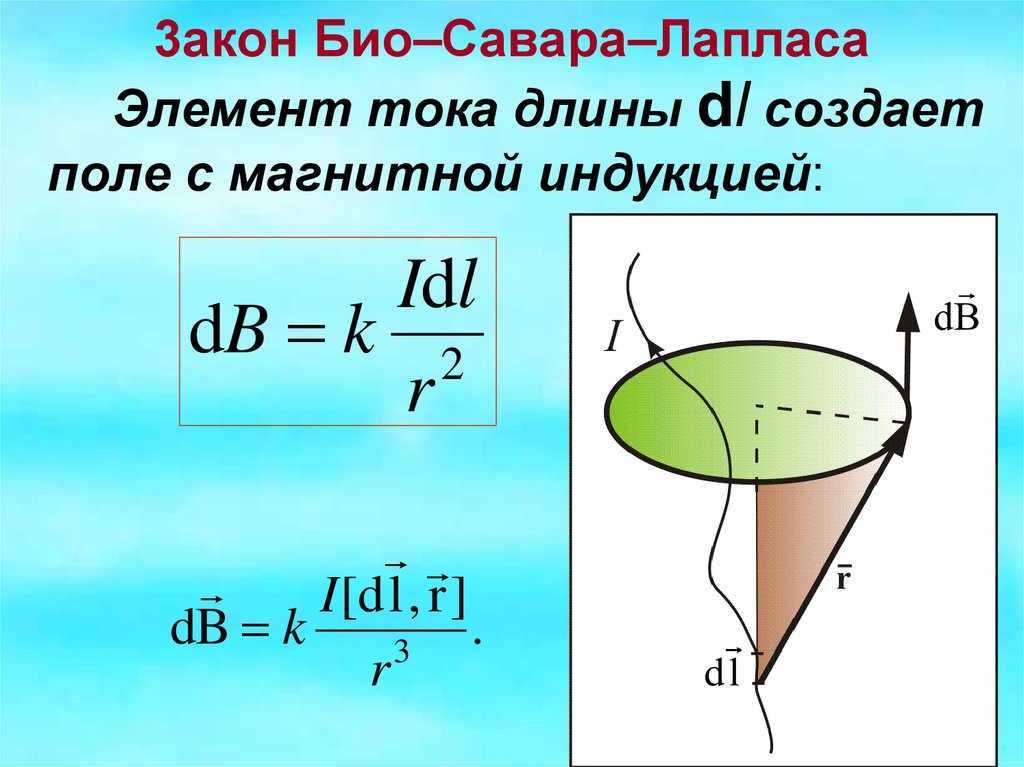

, следовательно,

.

19.8.4. Магнитное поле кругового витка с током на произвольной точке оси, перпендикулярной витку и проходящей через его центр

; ; ; Þ

Þ .

Рис.19.14

Поскольку dB создан двумя диаметрально противоположными элементами dl, то интегрирование нужно производить по половине окружности. Следовательно,

.

С учётом направления:

;

при .

19.8.5. Магнитное поле кругового витка с током в произвольной точке плоскости витка, удалённой от витка

Рис.19.15

При векторы параллельны друг другу, следовательно, линии диаметрально противоположных элементарных участков витка пересекают их под одинаковым углом a. По закону БСЛ:

Они направлены антипараллельно, то есть

После подстановки получаем:

.

Точно так же, как и в предыдущем пункте, интегрировать нужно по половине окружности, следовательно,

.

Из рисунка видно, что

Значение, формула, правило правой руки, применение

Дом »Физика

Гурприт Сингх | Обновлено: 6 октября 2021 г. 13:34 IST

0

Сохранить

Скачать публикацию в формате PDF

Закон Био-Савара — это специфический электромагнетизм в физике, это математическое выражение, объясняющее магнитное поле, создаваемое постоянным электрическим током. Этот закон является центральным для магнитостатики и играет существенную роль в электростатике, связанной с законом Кулона.

Внимательно прочтите эту статью, чтобы понять формулу закона Био-Савара и ее применение.

Что такое закон Био-Савара?

Закон Био-Савара — это уравнение, которое описывает магнитное поле, создаваемое постоянным электрическим током, и связывает магнитное поле с величиной, направлением, длиной и близостью электрического тока. Он дает соотношение напряженности магнитного поля, создаваемого компонентом источника тока.

Жан Батиль Био и Феликс Савар провозгласили правило в 1820 году. Направление магнитного поля подчиняется законам правой руки для прямого провода. Правило Био Савара также считается законом Лапласа или законом Ампера. Эти два ученых предположили, глядя на отклонение стрелки магнитного компаса, что любой существующий компонент излучает магнитное поле в окружающее его пространство.

Формула закона Био-Савара

Рассмотрим провод, по которому течет электрический ток I, на расстоянии x от точки A и провод бесконечно малой длины dl.

Закон Био Савара гласит, что: в точке A напряженность магнитного поля dH связана с током I, протекающим через небольшой элемент dl:

1. Прямо пропорциональна току (I), длине элемента ( dl), синус угла θ между направлением тока и линией, соединяющей элемент dl из точки A.
2. Обратно пропорционален квадрату расстояния (x) точки A от элемента dl.

Здесь k постоянно и зависит от магнитных свойств среды.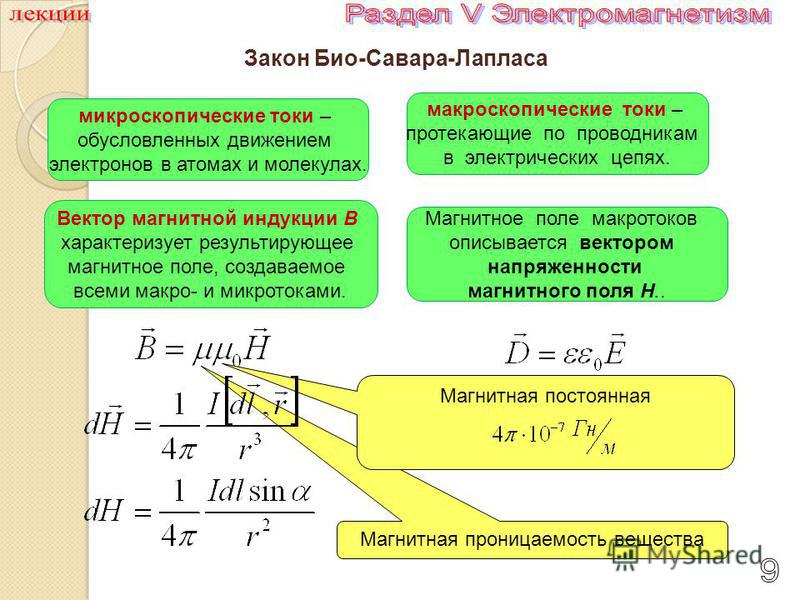

Здесь µ0 – абсолютная проницаемость воздуха или вакуума, и ее значение составляет 4 x 10-7 Вб/А·м, а µr – относительная проницаемость среды.

Направление магнитного поля всегда перпендикулярно линии элемента и вектору положения на плоскости. Это дается правилом большого пальца правой руки, где большой палец указывает на обычное направление тока, а остальные пальцы показывают направление магнитного поля.

Применение закона Био-Савара

Это правило можно использовать даже на химической или ядерной стадии для расчета магнитных реакций. Его можно использовать для оценки желаемой скорости вихревых линий в аэродинамической теории. Правило Био-Савара идентично электростатическому закону Кулона. Этот закон часто применяется к очень маленьким проводникам, по которым течет ток. Закон распространяется на распределение симметричного тока.

Заключение

Наконец, из приведенной выше информации мы можем сделать вывод, что этот закон можно использовать для расчета магнитного поля, создаваемого элементом тока. Однако это правило используется для оценки магнитного поля из-за некоторых условий, таких как вращающийся провод, диск, участок линии.

Итак, все дело в законе Био-Савара. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

Скачать публикацию в формате PDF

Подробнее от Testbook.com

9007 9007 4007 400749007 40074.ship. Определение, компоненты, уравнение мощности

Скорость побега: определение, вывод, формулы и решаемые примеры
Геостационные спутники: обучение, использование, условия и разница с геосинхронным Satellite
Простое гармоническое движение (SHM): определение, типы, родственные уравнения, примеры решений

электромагнетизм — Закон Био-Савара получен эмпирически или его можно вывести?

Возможно, в былые времена люди измерили силу, возникающую в результате нитевидного тока, открыли закон Био-Савара, а затем, в свою очередь, использовали его как вдохновение для построения уравнений Максвелла. Если так исторически сложилось, то хорошо.

Но это аналогично тому, как какой-нибудь инопланетный археолог через 10 миллионов лет найдет в Земле скелет руки и ноги. По руке археолог приходит к пониманию того, что любило делать с ней животное, имевшее эту руку: что оно могло хватать и использовать инструменты и так далее. Из ноги археолог приходит к выводу, что животное, которому он принадлежал, ходило на двух ногах и обычно весило в зрелом возрасте около 100-300 фунтов.

Только позже археолог догадается, что рука и нога принадлежат одному и тому же животному — человеку. Но характер работы означает, что загадка того, чем был человек, должна быть разбита на куски, которые можно понять по отдельности, прежде чем вся картина может сложиться воедино. Тем не менее, было бы обратным предположением, что рука и нога более фундаментальны, чем сам человек.

Уравнения Максвелла были построены таким образом, чтобы они соответствовали закону Био-Савара и другим элементам информации, таким как закон Кулона.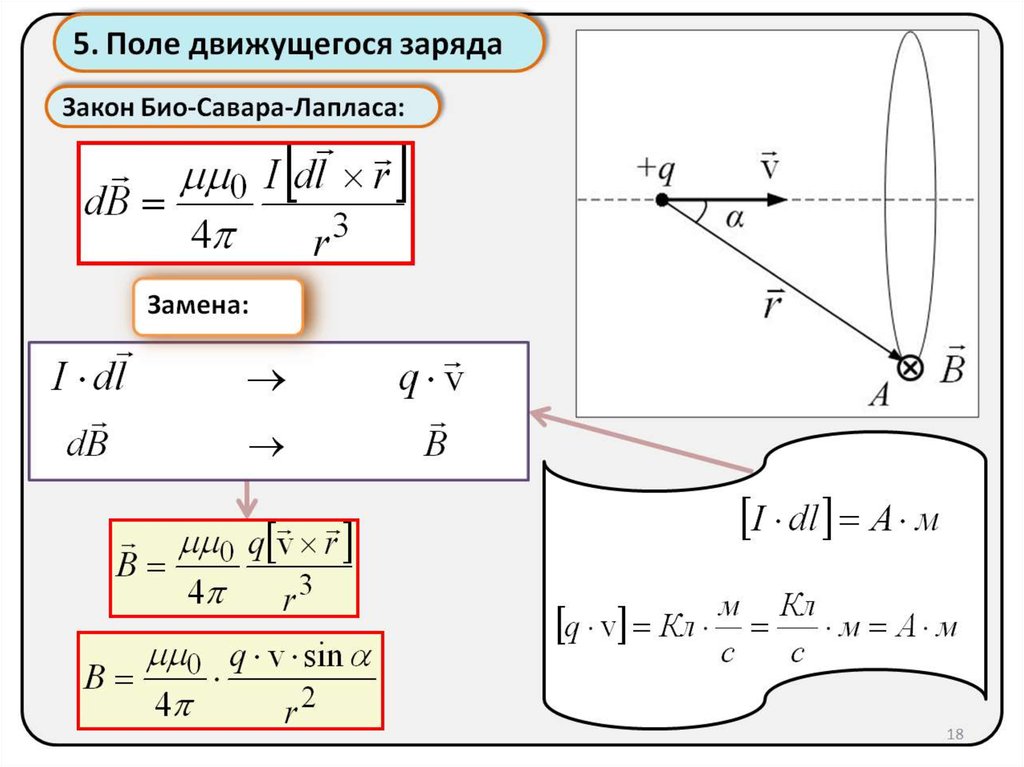 Таким образом, вы можете вывести Био-Савара из Максвелла, но не наоборот, ибо Максвелл более общий и всеобъемлющий.

Если вы уже знаете закон силы Лоренца, вы можете определить силу магнитного поля по проводу, просто стреляя заряженными тестовыми частицами вблизи провода и наблюдая за их движением. Но это ставит под вопрос, откуда вы уже знаете закон силы Лоренца и так далее.

Вы можете целый день ходить кругами над тем, что является или не является фундаментальным, над тем, что должно быть основано на экспериментальных наблюдениях и что просто построено, чтобы согласовываться с этими наблюдениями, но часто предпочтение отдается рассмотрению «простых» экспериментальных наблюдений. фундаментальные и теоретические конструкции, которые включают в себя многие такие наблюдения — см. комментарий Криса Уайта о том, что уравнения Максвелла могут быть получены из закона Кулона и некоторых других вещей.

Для меня это глупо. Уравнения Максвелла включают в себя сумму наших наблюдений (по крайней мере, тех, которые соответствуют классическому режиму). Для меня это — это того, что мы знаем о классическом электромагнетизме. Сказать, что вы можете вывести уравнение Максвелла только с одним результатом плюс несколько предположений… ну, это упускает из виду тот факт, что эти предположения и должны были быть проверены и проверены в первую очередь. На мой взгляд, очень и очень отстало выделять частные случаи (чистые электрические, чисто магнитные, статические или динамические поля) и рассматривать их как «фундаментальные».

---

Редактировать: но на самом деле физик должен работать в обоих направлениях. Чтобы создать новую теорию, у нас часто есть частные случаи, о которых мы не знаем, что они связаны, и мы должны соединить их вместе. Это построение уравнений Максвелла из закона Кулона и закона Био-Савара. Чтобы наиболее легко проанализировать конкретную проблему, для которой мы не уверены, что существует формула для особого случая, мы должны прибегнуть к наиболее общему описанию (Максвелл) и попытаться свести его к чему-то более простому и легко решаемому (в в случае отсутствия тока и зависимости от времени можно вернуться к закону Кулона).