ГДЗ по физике за 10-11 класс к задачнику «Физика. 10-11 класс. Пособие для учебных заведений» Рымкевич А.П.ГЛАВА IX. МАГНИТНОЕ ПОЛЕ. 39. Магнитное поле тока. Магнитная индукция. Магнитный поток. Закон Ампера. Сила Лоренца. Магнитные свойства веществ
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
ГЛАВА IX. МАГНИТНОЕ ПОЛЕ. 39. Магнитное поле тока. Магнитная индукция. Магнитный поток. Закон Ампера. Сила Лоренца. Магнитные свойства веществ
- № 821. В каком направлении повернется магнитная стрелка в контуре с током, как показано на рисунке 89?
- № 822. Обозначить полюсы источника тока, питающего соленоид, чтобы наблюдалось указанное на рисунке 90 взаимодействие.
- № 823. Максимальный вращающий момент, действующий на рамку площадью 1 см2, находящуюся в магнитном поле, равен 2 мкН ⋅ м. Сила тока в рамке 0,5 А. Найти индукцию магнитного поля.
- № 824.
 Рамка площадью 400 см2 помещена в однородное магнитное поле индукцией 0,1 Тл так, что нормаль к рамке перпендикулярна линиям индукции. При какой силе тока на рамку будет действовать вращающий момент 20 мН ⋅ м?
Рамка площадью 400 см2 помещена в однородное магнитное поле индукцией 0,1 Тл так, что нормаль к рамке перпендикулярна линиям индукции. При какой силе тока на рамку будет действовать вращающий момент 20 мН ⋅ м? - № 825. Плоская прямоугольная катушка из 200 витков со сторонами 10 и 5 см находится в однородном магнитном поле индукцией 0,05 Тл. Какой максимальный вращающий момент может действовать на катушку в этом поле, если сила тока в катушке 2 А?
- № 826. Из проволоки длиной 8 см сделаны контуры: а) квадратный; б) круговой. Найти максимальный вращающий момент, действующий на каждый контур, помещенный в магнитное поле индукцией 0,2 Тл при силе тока в контуре 4 А.
- № 827. Магнитный поток внутри контура, площадь поперечного сечения которого 60 см2, равен 0,3 мВб. Найти индукцию поля внутри контура. Поле считать однородным и перпендикулярным плоскости проводника.
- № 828. Какой магнитный поток пронизывает плоскую поверхность площадью 50 см2 при индукции поля 0,4 Тл, если эта поверхность: а) перпендикулярна вектору индукции поля; б) расположена под углом 45° к вектору индукции; в) расположена под углом 30° к вектору
- № 829.
 На рисунке 91 представлены различные случаи взаимодействия магнитного поля с током. Сформулировать задачу для каждого из приведенных случаев и решить ее.
На рисунке 91 представлены различные случаи взаимодействия магнитного поля с током. Сформулировать задачу для каждого из приведенных случаев и решить ее. - № 830. Какова индукция магнитного поля, в котором на проводник с длиной активной части 5 см действует сила 50 мН? Сила тока в проводнике 25 А. Проводник расположен перпендикулярно вектору индукции магнитного поля.
- № 831. С какой силой действует магнитное поле индукцией 10 мТл на проводник, в котором сила тока 50 А, если длина активной части проводника 0,1 м? Линии индукции поля и ток взаимно перпендикулярны.
- № 832. Сила тока в горизонтально расположенном проводнике длиной 20 см и массой 4 г равна 10 А. Найти индукцию (модуль и направление) магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
- № 833. Проводник ab, длина которого l и масса m, подвешен на тонких проволочках. При прохождении по нему тока I он отклонился в однородном магнитном поле (рис.
 92) так, что нити образовали угол α с вертикалью. Какова индукция магнитного поля?
92) так, что нити образовали угол α с вертикалью. Какова индукция магнитного поля? - № 834. В проводнике с длиной активной части 8 см сила тока равна 50 А. Он находится в однородном магнитном поле индукцией 20 мТл. Какую работу совершил источник тока, если проводник переместился на 10 см перпендикулярно линиям индукции?
- № 835. В какую сторону сместится под действием магнитного поля электронный луч в вакуумной трубке, изображенной на рисунке 93?
- № 836. Если к точкам С и D (рис. 94) тонкого металлического листа, по которому проходит электрический ток, подключить чувствительный гальванометр, то в случае наличия магнитного поля (направление линий магнитной индукции показано на рисунке) он покажет во
- № 837. Какая сила действует на протон, движущийся со скоростью 10 Мм/с в магнитном поле индукцией 0,2 Тл перпендикулярно линиям индукции?
- № 838. В направлении, перпендикулярном линиям индукции, влетает в магнитное поле электрон со скоростью 10 Мм/с.
 Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см.
Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см. - № 839. Протон в магнитном поле индукцией 0,01 Тл описал окружность радиусом 10 см. Найти скорость протона.
- № 840. В однородное магнитное поле индукцией В = 10 мТл перпендикулярно линиям индукции влетает электрон с кинетической энергией WK = 30 кэВ. Каков радиус кривизны траектории движения электрона в поле?
- № 841. Протон и α-частица1 влетают в однородное магнитное поле перпендикулярно линиям индукции. Сравнить радиусы окружностей, которые описывают частицы, если у них одинаковы: а) скорости; б) энергии.
- № 842. Электрон движется в однородном магнитном поле индукцией В = 4 мТл. Найти период Т обращения электрона.
- № 843. Линии напряженности однородного электрического поля и линии индукции однородного магнитного поля взаимно перпендикулярны. Напряженность электрического поля 1 кВ/м, а индукция магнитного поля 1 мТл. Какими должны быть направление и модуль скорости э
- № 844*.
 В масс-спектрографе (рис. 95) заряженные частицы ускоряются на участке KL электрическим полем и, попав в магнитное поле индукцией Б, описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряже
В масс-спектрографе (рис. 95) заряженные частицы ускоряются на участке KL электрическим полем и, попав в магнитное поле индукцией Б, описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряже - № 845
- № 846. По графику (рис. 96) определить магнитную проницаемость стали при индукции В0 намагничивающего поля 0,4 и 1,2 мТл.
- № 847. Во сколько раз изменится магнитный поток, если чугунный сердечник в соленоиде заменить стальным таких же размеров? Индукция намагничивающего поля В0 = 2,2 мТл. Использовать рисунок 96.
- № 848. Внутри соленоида без сердечника индукция поля B0 = 2мТл. Каким станет магнитный поток, если в соленоид ввести чугунный сердечник площадью поперечного сечения 100 см
- № 855(н). Электрон, влетающий в однородное магнитное поле под углом 60° к направлению поля, движется по винтовой линии радиусом 5 см с периодом обращения 60 мкс. Какова скорость электрона, индукция магнитного поля и шаг винтовой линии?
- № 858(н).
 {2}}\right)\) — Гравитационная постоянная
{2}}\right)\) — Гравитационная постоянная\({m}_{1}\,(\text{кг})\) — Масса первого тела
\({m}_{2}\,(\text{кг})\) — Масса второго тела
\(r\,(м)\) — Расстояние между центрами тяжести тел
• Сила трения \((\text{Н})\):
• Сила поверхностного натяжения \((\text{Н})\):
$$F=\sigma \cdot l$$
\(\mu\,\) — Коэффициент трения
\(N\,(\text{Н})\) — Сила нормальной реакции
\(\sigma\,(\text{Н/м})\) — Коэффициент поверхностного натяжения
\(l\,(\text{м})\) — Длина границы поверхностного натяжения
• Сила \((\text{Н})\):
$$F={E}\cdot{q}$$
• Сила Лоренца \((\text{Н})\):
$${F}_{Л}=|q| \cdot \upsilon \cdot B \cdot \sin{\alpha}$$
\(E\,(\text{Н/Кл})\) — Напряжённость электрического поля
\(q\,(\text{Кл})\) — Электрический заряд
\(\upsilon \,(\text{м/с})\) — Скорость
\(B \,(\text{Тл})\) — Магнитная индукция
\(\alpha\,(^{\circ})\) — Угол между вектором магнитной индукции и вектором скорости заряженной частицы
• Сила Ампера \((\text{Н})\):
$${F}_{А}=B \cdot I \cdot l \cdot \sin{\alpha}$$
• Максимальная действующая сила Ампера \((\text{Н})\):
$${F}_{А\:\text{max}}=B \cdot I \cdot l$$
\(B \,(\text{Тл})\) — Магнитная индукция
\(I\,(\text{А})\) — Сила тока
\(l\,(\text{м})\) — Длина отрезка проводника
\(\alpha\,(^{\circ})\) — Угол между вектором магнитной индукции и направлением тока в проводнике
• Сила \((\text{Н})\):
$$F={p}\cdot{S}$$
• Сила первого поршня \((\text{Н})\):
$$\frac{{F}_{2}}{{F}_{1}}=\frac{{S}_{2}}{{S}_{1}} \Rightarrow {F}_{1}=\frac{{F}_{2}\cdot{S}_{1}}{{S}_{2}}$$
• Сила второго поршня \((\text{Н})\):
$$\frac{{F}_{2}}{{F}_{1}}=\frac{{S}_{2}}{{S}_{1}} \Rightarrow {F}_{2}=\frac{{F}_{1}\cdot{S}_{2}}{{S}_{1}}$$
\(p\,(\text{Па})\) — Давление
\(S\,({м}^{2})\) — Площадь
\({F}_{1}\,(\text{Н})\) — Сила первого поршня
\({F}_{2}\,(\text{Н})\) — Сила второго поршня
\({S}_{1}\,({м}^{2})\) — Площадь первого поршня
\({S}_{2}\,({м}^{2})\) — Площадь второго поршня
• Сила гидравлического давления, действующая на дно сосуда \((\text{Н})\):
$${F}_{д}=\rho \cdot g \cdot h \cdot {S}_{д}$$
• Сила гидравлического давления, действующая на боковую поверхность сосуда\((\text{Н})\):
$${F}_{б}=\frac{1}{2} \cdot \rho \cdot g \cdot h \cdot {S}_{б}$$
\(g=9.
 {2})\) — Площадь боковой поверхности сосуда
{2})\) — Площадь боковой поверхности сосуда• Сила \((\text{Н})\):
$$M={F}\cdot{l} \Rightarrow F=\frac{M}{l}$$
• Сила первого рычага \((\text{Н})\):
$${F}_{1}\cdot{l}_{1}={F}_{2}\cdot{l}_{2} \Rightarrow {F}_{1}=\frac{{F}_{2}\cdot{l}_{2}}{{l}_{1}}$$
• Сила второго рычага \((\text{Н})\):
$${F}_{1}\cdot{l}_{1}={F}_{2}\cdot{l}_{2} \Rightarrow {F}_{2}=\frac{{F}_{1}\cdot{l}_{1}}{{l}_{2}}$$
\(M\,(\text{Н·м})\) — Момент силы
\(l\,(м)\) — Плечо силы
\({F}_{1}\,(\text{Н})\) — Сила первого рычага
\({F}_{2}\,(\text{Н})\) — Сила второго рычага
\({l}_{1}\,(м)\) — Плечо первого рычага
\({l}_{2}\,(м)\) — Плечо второго рычага
• Фокусное расстояние линзы \((\text{м})\):
$${F}=\frac{1}{D}$$
\(D\,(\text{дптр})\) — Оптическая сила линзы
2.
 9 Индукция магнитного поля. Сила Ампера
9 Индукция магнитного поля. Сила АмпераЗадача 1. Магнитное поле создано двумя параллельными проводниками с одинаковой силой тока (см. рис.). Результирующий вектор магнитной индукции в точке A направлен:
Ответ: вниз
Задача 2. Круговой виток радиусом r с током I расположен таким образом, что его плоскость перпендикулярна линиям магнитной индукции однородного магнитного поля. Момент сил, действующий на виток, равен:
Ответ: 0
Задача 3. Круглый проводящий виток с током, направленным против часовой стрелки, свободно висит на подводящих проводах (рис.). Если перед витком поместить полосовой магнит, северный полюс которого обращен к витку, то виток:
Ответ: оттолкнется от магнита
Задача 4.
 На изолированный проводник с током в
магнитном поле действует сила Ампера,
равная 0,3 Н. Если проводник сложить втрое
при той же силе тока, то сила Ампера,
действующая на проводник, будет равна:
На изолированный проводник с током в
магнитном поле действует сила Ампера,
равная 0,3 Н. Если проводник сложить втрое
при той же силе тока, то сила Ампера,
действующая на проводник, будет равна:Ответ: 0,1 Н
Задача 5. Два электрона движутся параллельно в одном направлении с одинаковыми скоростями, векторы которых v перпендикулярны плоскости рисунка (рис. а). Какое из указанных направлений соответствует направлению вектора силы, действующей на один электрон со стороны магнитного поля другого электрона?
Ответ: а)
Задача 6. Два прямолинейных проводника с противоположно направленными токами по 20 А находятся на расстоянии 10 см друг от друга. Индукция магнитного поля в точке, лежащей посередине между проводниками, равна:
Ответ: 1,6*10^-4 Тл
Задача 7.
 -5 А
-5 АЗадача 10. В вертикальном однородном магнитном поле с индукцией 0,75 Тл на двух невесомых нитях подвешен горизонтальный проводник массой 18 г и длиной 30 см. Если по проводнику пропустить ток силой 1,0 А, то угол отклонения нитей от вертикали равен:
Ответ: 52*
Задача 11. Горизонтальные рельсы, расстояние между которыми 0,5 м, находятся в вертикальном магнитном поле индукцией 2 Тл. На рельсах лежит стержень массой 1 кг. Коэффициент трения стержня о рельсы 0,1. Минимальная сила тока, необходимая для того чтобы стержень двигался с ускорением 1 м/с2, равна:
Ответ: 2 А
Задача 1. Две частицы с одинаковыми зарядами, ускоренные одинаковой разностью потенциалов, попадают в однородное магнитное поле и движутся в нем по круговым траекториям. Если отношение масс этих частиц = 4, то отношение радиусов их траекторий равно:
Ответ: 2
Задача 2.
 2)
2)Задача 5. Протон, имеющий скорость 1 * 104 м/с, влетает в однородное магнитное поле индукцией 10 мТл под углом 60° к линиям магнитной индукции. Через 13 мкс протон сместится вдоль поля на расстояние и совершит за это время число оборотов:
Ответ: 6cм; 2;
Задача 6. Электрон влетает в слой магнитного поля толщиной l скорость электрона перпендикулярна как индукции поля , так и границами слоя. Пролетев слой, электрон вылетает из магнитного поля под углом, равным:
Ответ: arcSIN(qBl/mv)
Задача 7. В однородное магнитное поле индукцией 0,50 Тл перпендикулярно линиям магнитной индукции влетает электрон. Сила тока, созданного движущимся электроном, равна:
Ответ:2,2*10^-9 A
Задача 8.
 2)
2)Задача 10. Через плоский незаряженный конденсатор, помещенный в магнитное поле индукцией , пропускают поток электронов, прошедших ускоряющую разность потенциалов U. Пластины конденсатора площадью S параллельны линиям индукции. Направление движения электронов перпендикулярно вектору магнитной индукции (рис.). Заряд, который накопится на пластинах конденсатора, равен:
Ответ: EBS*корень из (2eU/m)
22.7 Магнитное воздействие на проводник с током – Колледж физики: OpenStax
Глава 22 Магнетизм
Резюме
- Описать действие магнитной силы на проводник с током.
- Рассчитайте магнитную силу, действующую на проводник с током.
Поскольку обычно заряды не могут покинуть проводник, магнитная сила, действующая на заряды, движущиеся в проводнике, передается самому проводнику.
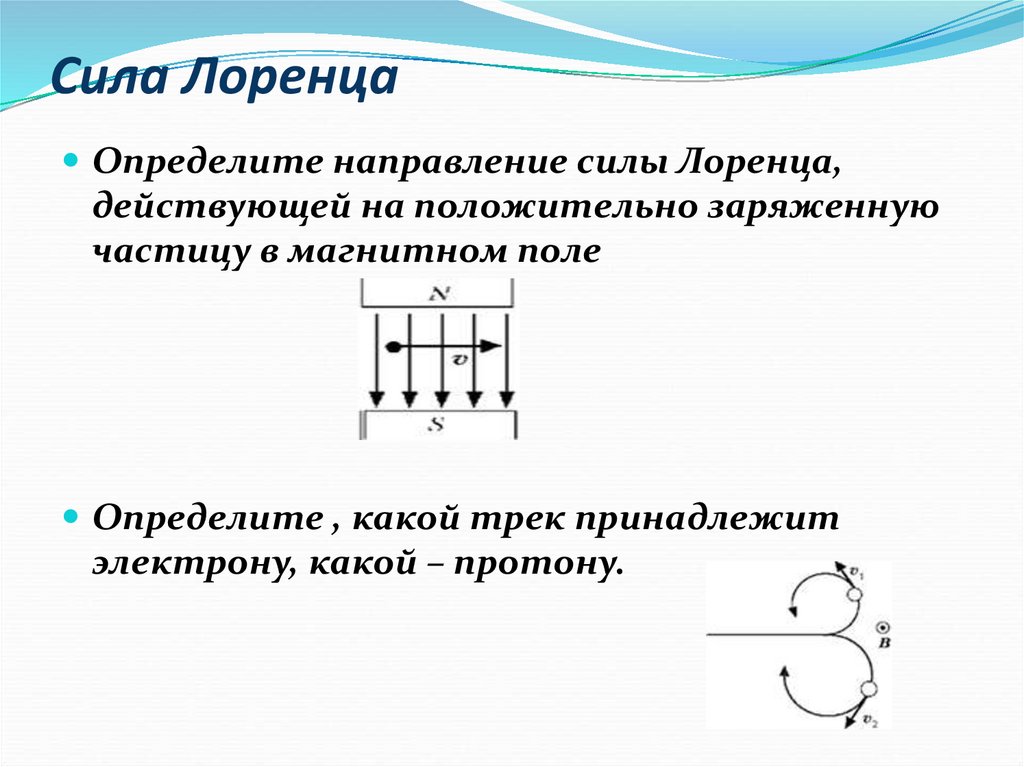
Рис. 1. Магнитное поле действует на проводник с током в направлении, определяемом правилом правой руки 1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, поскольку типичные токи состоят из очень большого количества движущихся зарядов.
Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, потому что они имеют одинаковое направление.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется как [латекс]\boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}[ /латекс]. Принимая [латекс]\boldsymbol{B}[/латекс] равномерным по всей длине провода [латекс]\boldsymbol{l}[/латекс] и равным нулю в других местах, общая магнитная сила, действующая на провод, равна [латекс]\ boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}[/latex], где [latex]\boldsymbol{N}[/latex] – количество носителей заряда в сечении проволока длиной [латекс]\boldsymbol{l}[/латекс].
 Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Учитывая, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,
Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Учитывая, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,[латекс]\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.[/latex]
Поскольку [латекс]\boldsymbol{nqAv_d = I}[/латекс] (см. Главу 20.1 Текущая версия),
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta}[/latex]
представляет собой уравнение для магнитной силы, действующей на отрезок [латекс]\boldsymbol{l}[/латекс] провода, по которому течет ток [латекс]\boldsymbol{I}[/латекс] в однородном магнитном поле [латекс]\boldsymbol {B}[/latex] , как показано на рисунке 2. Если мы разделим обе части этого выражения на [latex]\boldsymbol{l}[/latex], мы обнаружим, что магнитная сила на единицу длины провода в однородное поле равно [латекс]\boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}[/latex].
Рис. 2. Сила, действующая на проводник с током в магнитном поле, равна F = IlB sin θ . Его направление задает RHR-1. Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2.
Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2.Расчет магнитной силы на проводе с током: сильное магнитное поле
Рассчитайте силу, действующую на провод, показанную на рис. 1, при [латексе]\boldsymbol{B = 1,50 \;\textbf{T}}[/latex] , [латекс]\boldsymbol{l = 5,00 \;\textbf{см}}[/латекс] и [латекс]\boldsymbol{I = 20,0 \;\textbf{A}}[/латекс].
9{\circ}}[/latex], так что [латекс]\boldsymbol{\textbf{sin} \;\theta = 1}[/latex].Решение
Ввод заданных значений в [латекс]\boldsymbol{F = IlB \;\textbf{sin} \theta}[/latex] дает
[латекс]\boldsymbol{F = IlB \;\ textbf{sin} \theta = (20.
 0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/latex]
0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/latex]Единицы тесла: [латекс]\boldsymbol{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{м}}}[/латекс]; таким образом,
[латекс]\boldsymbol{F = 1,50 \;\textbf{N}}.[/latex]
Обсуждение
Это большое магнитное поле создает значительную силу на проводе небольшой длины.
Магнитная сила на проводниках с током используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. рис. 3.)
Рис. 3. Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса.Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке.
Рис. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок. 4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».
4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».- Магнитная сила, действующая на проводники с током, определяется выражением
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta},[/latex]
, где [латекс]\boldsymbol{I}[/латекс] – сила тока, [латекс]\boldsymbol{l}[/латекс] – длина прямого проводника в однородном магнитном поле [латекс]\boldsymbol{B} [/latex], а [latex]\boldsymbol{\theta}[/latex] — это угол между [latex]\boldsymbol{I}[/latex] и [latex]\boldsymbol{B}[/latex]. Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Задачи и упражнения
1: Каково направление действия магнитной силы на ток в каждом из шести случаев на рис.
Рисунок 5. 5?
5?2: Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 6, если предположить, что ток течет перпендикулярно [латексу]\boldsymbol{B}[/ латекс]?
Рисунок 63: Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев на рисунке 7, при условии, что [latex]\boldsymbol{B}[/latex] перпендикулярно [латексу]\boldsymbol{I}[/латекс]? 9{-5}- \textbf{T}}[/latex]. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.
6: Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Т, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для практических МГД-приводов.
 )
)7:9{\circ}}[/latex] с полем?
10: Сила, действующая на прямоугольную проволочную петлю в магнитном поле на рисунке 8, может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю. (b) Если используется ток 5,00 А, какова сила на тесла на петле шириной 20,0 см?
Рисунок 8.Инженер — Искусственные звезды: оценка структурной целостности в высокопроизводительных установках ядерного синтеза для производства электроэнергии
Исследователи Центра плазменной науки и термоядерного синтеза Массачусетского технологического института используют численное моделирование для оценки и оптимизации предложенной конструкции эксперимента Advanced Divertor — компактной установки для ядерного синтеза, которая вмещает полномасштабную мощность реактора в исследовательский испытательный стенд.

Ядерный синтез происходит естественным образом в ядре Солнца, высвобождая огромное количество лучистой энергии по мере потери массы, когда ядра водорода сливаются вместе, образуя более крупные атомы гелия. Мы наблюдаем эту энергию здесь, на Земле, как солнечный свет, несмотря на то, что в среднем она составляет около 93 миллиона миль.
Демонстрация возможности синтеза водорода как чистого, безопасного и практически безграничного источника энергии была основной целью более 50 лет международных исследований. В Массачусетском технологическом институте концепция подхода к термоядерному синтезу с очень сильным магнитным полем была в центре внимания исследований. В Центре плазменной науки и термоядерного синтеза Массачусетского технологического института (PSFC) эксперимент, передовая теория и численное моделирование объединяются для выявления и понимания науки и технологий, которые могут сделать термоядерную энергию более доступной.
Advanced Divertor eXperiment (ADX) представляет собой эксперимент по ядерному синтезу, а точнее токамак, предложенный исследователями из PSFC для обеспечения тепловых потоков, плотностей и температур, подобных тем, которые мы ожидаем получить в термоядерном реакторе, хотя только с короткие плазменные разряды (см.

В токамаке при температуре свыше 150 миллионов градусов Цельсия электроны отделяются от ядер, образуя полностью ионизированную перегретую плазму из газообразного водородного топлива. Плазма активной зоны содержится в вакуумном сосуде в форме тороида или пончика и поддерживается под высоким давлением для получения плотной плазмы с высокой вероятностью столкновения. Внешние магнитные поля удерживают и контролируют плазму аналогично интенсивным гравитационным полям в солнечном ядре, вызывая таким образом ядерный синтез.
«Недавние достижения в области высокотемпературных сверхпроводников могут позволить нам спроектировать токамак, работающий в более сильных магнитных полях, увеличив производительность плазмы до уровня реактора», — объясняет Джеффри Дуди, инженер-механик PSFC. «Затем фокус исследований переключается с улучшения характеристик плазмы на вспомогательные системы в токамаке».

Используя численное моделирование, Дуди и его коллеги проектируют структуру ADX для поддержания тепловых потоков и магнитных полей на уровне реактора, что делает ее подходящим испытательным стендом для систем выхлопа энергии и взаимодействия плазмы с материалом для поддержки разработки термоядерных машин следующего этапа. .
Сохранившиеся распределения плазмы
Предлагаемая конструкция вакуумной камеры ADX является инновационной, поскольку она состоит из пяти отдельных осесимметричных оболочек, как показано на рис. 2, вместо одного цилиндра. Модульная конструкция позволяет заменять магнитные катушки и тестировать различные конфигурации дивертора, где дивертор представляет собой компонент, служащий системой отвода мощности для удаления пепла термоядерного синтеза из токамака. Когда ионы выходят из-под контроля магнитных полей, управляющих плазмой, дивертор собирает их и выводит из сосуда.Модульный сосуд должен не только выдерживать высокие тепловые потоки и магнитные поля, необходимые для осуществления ядерного синтеза, но и выдерживать разрывы плазмы, которые являются еще одним источником напряжения в оболочке вакуумного сосуда, возникающего при коллапсе плазмы.
[Рис. 2] Вакуумный сосуд ADX имеет уникальную конструкцию с пятью отдельными корпусами, скрепленными болтами. — Массачусетский технологический институт / COMSOL [Рисунок 3] Геометрия модели (слева), используемая для определения вихревых токов в стенках вакуумной камеры ADX, справа. — MIT/COMSOL
«Для оценки предлагаемой конструкции сосуда ADX мы выполнили численное моделирование в программном обеспечении COMSOL Multiphysics®, чтобы предсказать магнитные поля, вихревые токи и силы Лоренца, возникающие в результате разрушения плазмы», — объясняет Дуди. «Рассчитанные нагрузки затем применяются к отдельной структурной модели судна, чтобы предсказать напряжение и смещение». На рисунке 3 показана геометрия магнитной модели ADX с циклической симметрией, включая корпус, плазму и полоидальные магнитные катушки, которые необходимы для удержания плазмы в ее равновесном положении.
Наихудший сценарий существует для разрывов плазмы в событиях вертикального смещения (VDE), когда плазма дрейфует вверх, неся ток 1,5 миллиона ампер, останавливается через 10 миллисекунд и теряет весь свой ток за одну миллисекунду.
 Быстро меняющиеся магнитные поля, окружающие разрушающую плазму, создают вихревые токи в оболочке вакуумного сосуда. Силы Лоренца действуют на сосуд, когда вихревые токи пересекают как полоидальные магнитные поля, так и более сильные тороидальные магнитные поля токамака, удерживающие плазму.
Быстро меняющиеся магнитные поля, окружающие разрушающую плазму, создают вихревые токи в оболочке вакуумного сосуда. Силы Лоренца действуют на сосуд, когда вихревые токи пересекают как полоидальные магнитные поля, так и более сильные тороидальные магнитные поля токамака, удерживающие плазму.Во время VDE вихревые токи больше по величине из-за того, насколько близко плазма подходит к стенке сосуда, и поэтому VDE является предпочтительным тестовым случаем в вычислительной модели ADX. На рис. 3 показано распределение вихревых токов, рассчитанное по численной модели. Вторая модель была разработана для определения сил Лоренца, обусловленных тороидальными магнитными полями токамака, где в первую модель ADX были включены только полоидальные поля.
Усиление вакуумного сосуда ADX
[Рисунок 4] Вверху геометрия структурной модели ADX показывает фиолетовые границы, где структура зафиксирована. Результаты моделирования напряжения и смещения показывают, что конструкция требует усиления. Внизу геометрия модели показывает дополнительную фиксированную границу, соответствующую опорному блоку, добавленному в проект ADX. — MIT/COMSOL
Плазменные нарушения приводят к сильным силам Лоренца, которые действуют на стенки ADX, особенно в верхнем и нижнем карманах вакуумного сосуда во время VDE. В структурной модели сосуда ADX, показанной на рисунке 4, верхняя и нижняя границы прикреплены к крышке сосуда и не могут быть смещены во время моделирования. К соответствующим границам приложены нагрузки, соответствующие силе Лоренца, действующей на сосуд. В этом испытательном примере сила Лоренца была определена для токамака, работающего с током плазмы 1,5 миллиона ампер и напряженностью тороидального поля 6,5 тесла.
К соответствующим границам приложены нагрузки, соответствующие силе Лоренца, действующей на сосуд. В этом испытательном примере сила Лоренца была определена для токамака, работающего с током плазмы 1,5 миллиона ампер и напряженностью тороидального поля 6,5 тесла.Компоненты модульного сосуда изготовлены из Inconel 625, прочного сплава на основе никеля, который также обладает высоким сопротивлением току, сводя к минимуму вихревые токи. Предел текучести материала составляет 460 МПа, однако критерии проектирования АДС предусматривают, что стенки сосуда не должны испытывать напряжения, превышающие 306 МПа, что составляет две трети значения предела текучести.

Численное моделирование показывает, что без каких-либо конструктивных изменений сила Лоренца из-за VDE приводит к большим напряжениям в сосуде, приближающимся к пределу текучести, и вызывает прогиб конструкции в 1 сантиметр. Чтобы стабилизировать стенку вакуумного сосуда, добавляется опорный блок для фиксации дополнительной границы, как показано в нижнем ряду на рисунке 4. Результаты моделирования, полученные для случая с установленным опорным блоком, демонстрируют значительное снижение напряжения и смещения сосуда. стены, что указывает на то, что стабилизированный вакуумный сосуд может выдержать разрушение плазмы и поддерживать работу ADX.
Следующий этап ядерного синтеза и последующие этапы
Проектирование ADX на основе моделирования поможет обеспечить его безопасную и успешную работу в PSFC, где он станет новейшей термоядерной машиной, которая будет служить научно-исследовательской платформой для проверки концепций дивертора требуется для термоядерного реактора.
Джеффри Дуди — инженер-механик из Центра плазменной науки и синтеза Массачусетского технологического института. На фото он изображен на конференции COMSOL 2015 в Бостоне, где он получил награду за свою работу по моделированию. — MIT
Решения Бальбхарати для физики 12-й стандарт Совета штата Махараштра HSC, глава 10 — Магнитные поля, вызванные электрическим током [Последнее издание]
Решения Бальбхарати для физики 12-й стандарт Совета штата Махараштра HSC, глава 10 Магнитные поля, вызванные электрическим током Упражнения [ Страницы 248 — 250]
Упражнения | Вопрос 1.1 | Страница 248
Проводник имеет 3 сегмента; две прямые длиной L каждая и полукруглая радиуса R. По ней течет ток I. Чему равно магнитное поле B в точке P? 92)`
`(μ_0I)/(4R)`
`(μ_0I)/(4π)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 1.2 |
Выберите правильный вариант:
На рисунках (a) и (b) показаны две петли Ампера, связанные с проводниками, по которым течет ток I, в указанном направлении.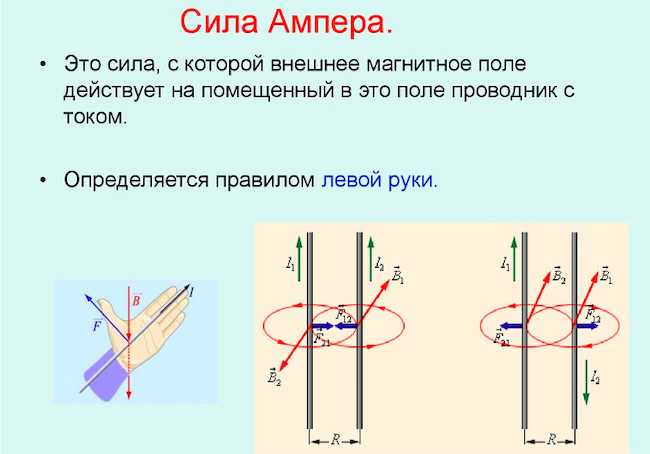 `точка vecB * vecdl` в случаях (а) и (б) равна соответственно.
`точка vecB * vecdl` в случаях (а) и (б) равна соответственно.
– мк 0 I, 0
µ 0 I, 0
0, µ 0 I
0, — µ 0 I
. Вопрос 1.3 | Страница 248
Выберите правильный вариант:
Протон входит в перпендикулярное однородное магнитное поле B в начале координат вдоль положительной оси x со скоростью v, как показано на рисунке. Затем он пойдет по следующему пути. [Магнитное поле направлено в бумагу].
Он будет продолжать двигаться вдоль положительной оси x.
Он будет двигаться по криволинейной траектории, изгибаясь в сторону положительной оси y
Он будет двигаться по криволинейной траектории, изгибаясь в сторону отрицательной оси y
положительная ось x
ПРОСМОТР РЕШЕНИЯ
Упражнения | Вопрос 1.4 | Страница 249
Выберите правильный вариант.
Проводящий толстый медный стержень длиной 1 м несет ток силой 15 А и расположен на экваторе Земли. Здесь силовые линии магнитного поля Земли горизонтальны, с полем 1,3 x 10 90 293 -4 90 294 Тл, с юга на север. Величина и направление силы, действующей на стержень, когда он ориентирован так, что ток течет с запада на восток, равны ______.
14 × 10 -4 С, вниз
20 × 10 -4 С, вниз
14 × 10 -4 С, вверх
20 × 10 -4 С, вверх
ПРОСМОТР РЕШЕНИЕ 9 с 00502 90 РЕШЕНИЕ | Вопрос 1,5 |
Выберите правильный вариант ответа:
Заряженная частица движется с начальной скоростью vecv, когда входит в область однородного магнитного поля, перпендикулярного vecv. Из-за магнитной силы кинетическая энергия частицы будет
Оставить без изменений
Уменьшить
Увеличить
Уменьшить до нуля
ПОСМОТРЕТЬ РЕШЕНИЕ
5 90 | вопрос 2 | Страница 249
Кусок прямой проволоки массой 20 г и длиной 1 м. Он должен левитировать с помощью протекающего через него тока силой 1 А и перпендикулярного магнитного поля В в горизонтальном направлении. Какой должна быть величина В магнитного поля?
Он должен левитировать с помощью протекающего через него тока силой 1 А и перпендикулярного магнитного поля В в горизонтальном направлении. Какой должна быть величина В магнитного поля?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 3 |
Рассчитайте значение магнитного поля на расстоянии 2 см от очень длинного прямого провода с током 5 А (Дано: μ 0 = 4π × 10 -7 Вб/Ам).
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 4 |
Электрон движется со скоростью 3 × 10 -7 м/с в магнитном поле напряженностью 6 × 10 -4 Тл перпендикулярно его пути. Каков будет радиус пути? Какова будет частота и энергия в кэВ?
[ Дано: масса электрона = 9 × 10 −31 кг, заряд e = 1,6 × 10 −19 Кл, 1 эВ = 1,6 × 10 −19 Дж]
ПРОСМОТР РЕШЕНИЯ
25 | Вопрос 5 | Страница 249
Альфа-частица (ядро атома гелия) (с зарядом +2) ускоряется и движется в вакуумной трубе с кинетической энергией = 10 МэВ. Он проходит через однородное магнитное поле с напряженностью 1,88 Тл и описывает круговой путь радиусом 24,6 см. Получите массу альфа-частицы. [л эВ = 1,6 × 10 -19 Дж, заряд электрона = 1,6 × 10 -19 Кл]
Он проходит через однородное магнитное поле с напряженностью 1,88 Тл и описывает круговой путь радиусом 24,6 см. Получите массу альфа-частицы. [л эВ = 1,6 × 10 -19 Дж, заряд электрона = 1,6 × 10 -19 Кл]
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 6 | Страница 249
Два провода, показанные на рисунке, соединены в последовательную цепь, и через них протекает одинаковый ток 10 А, но в противоположных направлениях. Расстояние между двумя проводами составляет 8 мм. Длина АВ равна 22 см. Получите направление и величину магнитного поля, обусловленного током в проводе 2, на следующем рисунке сегменте AB провода 1. Кроме того, получите величину и направление силы, действующей на провод 1. [μ 0 = 4π × 10 -7 T.m/A]
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | вопрос 7 | Страница 249
По очень длинному прямому проводу течет ток силой 5,2 А. Какова величина магнитного поля на расстоянии 3,1 см от провода?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 8 | Страница 249
Токи одинаковой величины проходят через два длинных параллельных провода, расстояние между которыми составляет 1,35 см. Если сила на единицу длины, действующая на каждую из проволок, равна 4,76 х 10 -2 N, какой я должен быть?
Если сила на единицу длины, действующая на каждую из проволок, равна 4,76 х 10 -2 N, какой я должен быть?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 9 | Стр. 249
Магнитное поле на расстоянии 2,4 см от длинного прямого [токонесущего] провода составляет 16 мкТл. Какова сила тока в проводе?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 10 |
Магнитное поле в центре круглого контура с током радиусом 12,3 см составляет 6,4 × 10 -6 Тл. Каков магнитный момент контура?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 11 | Страница 250
По круговой петле радиусом 9,7 см протекает ток 2,3 А. Получите величину магнитного поля
(а) в центре петли
(б) на расстоянии 9,7 см от центра петли а на оси.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 12 | Страница 250
Круглая катушка провода, состоящая из 100 витков радиусом 8,0 см каждый, по которой течет ток силой 0,40 А. Какова величина магнитного поля B в центре катушки?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 13 | Страница 250
Для ускорения протонов используется циклотрон, в котором приложено магнитное поле 1,4 Вб/м 2 . Найдите период времени, в течение которого электрическое поле между двумя D меняется на противоположное.
Найдите период времени, в течение которого электрическое поле между двумя D меняется на противоположное.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 14 | Страница 250
Гальванометр с подвижной катушкой снабжен прямоугольной катушкой, имеющей 50 витков и размерами 5 см × 3 см. Радиальное магнитное поле, в котором подвешена катушка, составляет 0,05 Вб/м 2 . Постоянная кручения пружины составляет 1,5 × 10 −9 Нм/градус. Получите ток, который необходимо пропустить через гальванометр так, чтобы получить отклонение на 30°.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 15 | Страница 250
Соленоид длиной π м и диаметром 5 см имеет обмотку из 1000 витков и течет ток 5 А. Рассчитайте магнитное поле в его центре вдоль оси.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 16 | Страница 250
Тороид с центральным радиусом 10 см имеет обмотки из 1000 витков. Какой ток необходимо пропустить через его обмотки при напряженности магнитного поля 5·10 -2 Тл вдоль его центральной оси?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 17 | Страница 250
В циклотроне нужно ускорять протоны. Радиус его D равен 60 см. и частота его генератора 10 МГц. Какова будет кинетическая энергия ускоренного таким образом протона?
Радиус его D равен 60 см. и частота его генератора 10 МГц. Какова будет кинетическая энергия ускоренного таким образом протона?
(масса протона = 1,67 × 10 −27 кг, e = 1,60 × 10 −19 Кл, эВ = 1,6 × 10 −19 Дж)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 18 | Страница 250
Проволочная петля формы, показанной на следующем рисунке, несет ток I. Получите величину и направление магнитного поля в точке P. Вопрос 19 | Страница 250
Два длинных параллельных провода, по которым течет ток I, направленный в плоскость страницы, разделены расстоянием R. Покажите, что в точке P, равноудаленной от проводов и образующей угол θ с плоскостью, содержащей провода, величина магнитного поля равна B = `(mu_0)/pi «I»/»R»` sin 2θ. Каково направление магнитного поля?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 20 | Страница 250
На рисунке показан цилиндрический провод диаметром а, по которому течет ток I. Плотность тока в проводе направлена в направлении оси и изменяется линейно с радиальным расстоянием r от оси согласно соотношению J = `» J»_0 «р»/»а»`.


 Рамка площадью 400 см2 помещена в однородное магнитное поле индукцией 0,1 Тл так, что нормаль к рамке перпендикулярна линиям индукции. При какой силе тока на рамку будет действовать вращающий момент 20 мН ⋅ м?
Рамка площадью 400 см2 помещена в однородное магнитное поле индукцией 0,1 Тл так, что нормаль к рамке перпендикулярна линиям индукции. При какой силе тока на рамку будет действовать вращающий момент 20 мН ⋅ м? На рисунке 91 представлены различные случаи взаимодействия магнитного поля с током. Сформулировать задачу для каждого из приведенных случаев и решить ее.
На рисунке 91 представлены различные случаи взаимодействия магнитного поля с током. Сформулировать задачу для каждого из приведенных случаев и решить ее. 92) так, что нити образовали угол α с вертикалью. Какова индукция магнитного поля?
92) так, что нити образовали угол α с вертикалью. Какова индукция магнитного поля? Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см.
Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см. В масс-спектрографе (рис. 95) заряженные частицы ускоряются на участке KL электрическим полем и, попав в магнитное поле индукцией Б, описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряже
В масс-спектрографе (рис. 95) заряженные частицы ускоряются на участке KL электрическим полем и, попав в магнитное поле индукцией Б, описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряже {2}}\right)\) — Гравитационная постоянная
{2}}\right)\) — Гравитационная постоянная {2})\) — Площадь боковой поверхности сосуда
{2})\) — Площадь боковой поверхности сосуда 9 Индукция магнитного поля. Сила Ампера
9 Индукция магнитного поля. Сила Ампера На изолированный проводник с током в
магнитном поле действует сила Ампера,
равная 0,3 Н. Если проводник сложить втрое
при той же силе тока, то сила Ампера,
действующая на проводник, будет равна:
На изолированный проводник с током в
магнитном поле действует сила Ампера,
равная 0,3 Н. Если проводник сложить втрое
при той же силе тока, то сила Ампера,
действующая на проводник, будет равна: -5 А
-5 А 2)
2) 2)
2)
 Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Учитывая, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,
Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Учитывая, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора, Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2.
Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2. 0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/latex]
0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/latex] Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.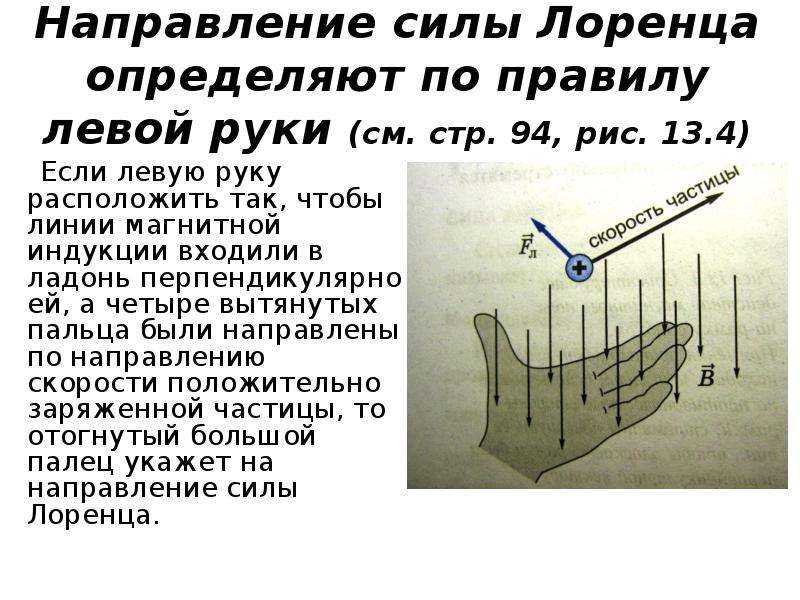 4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».
4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ». 5?
5? )
)



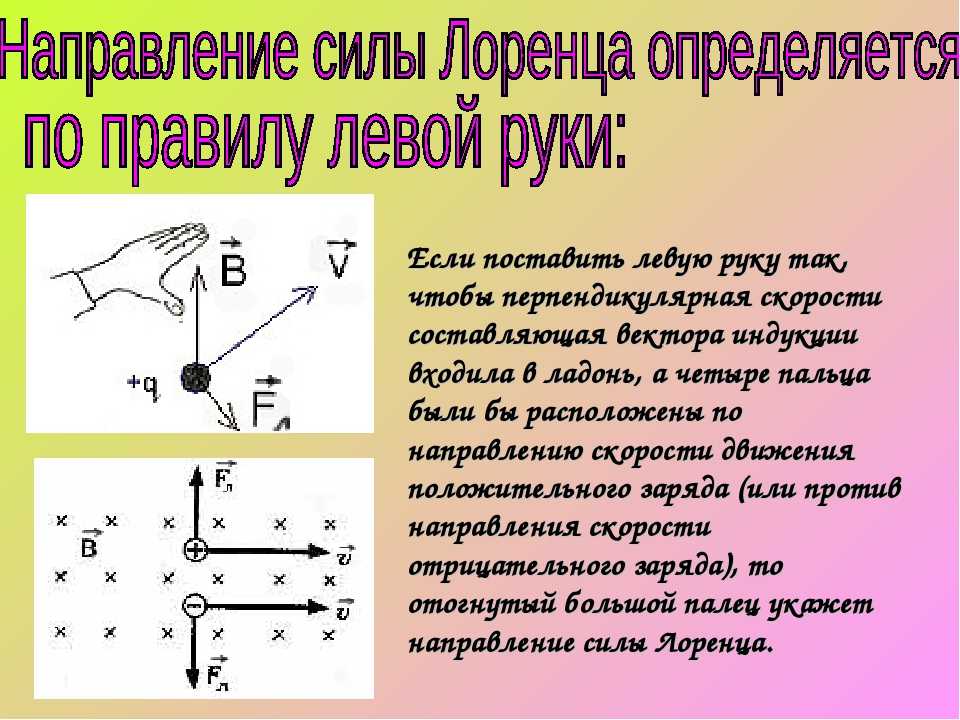 Быстро меняющиеся магнитные поля, окружающие разрушающую плазму, создают вихревые токи в оболочке вакуумного сосуда. Силы Лоренца действуют на сосуд, когда вихревые токи пересекают как полоидальные магнитные поля, так и более сильные тороидальные магнитные поля токамака, удерживающие плазму.
Быстро меняющиеся магнитные поля, окружающие разрушающую плазму, создают вихревые токи в оболочке вакуумного сосуда. Силы Лоренца действуют на сосуд, когда вихревые токи пересекают как полоидальные магнитные поля, так и более сильные тороидальные магнитные поля токамака, удерживающие плазму. К соответствующим границам приложены нагрузки, соответствующие силе Лоренца, действующей на сосуд. В этом испытательном примере сила Лоренца была определена для токамака, работающего с током плазмы 1,5 миллиона ампер и напряженностью тороидального поля 6,5 тесла.
К соответствующим границам приложены нагрузки, соответствующие силе Лоренца, действующей на сосуд. В этом испытательном примере сила Лоренца была определена для токамака, работающего с током плазмы 1,5 миллиона ампер и напряженностью тороидального поля 6,5 тесла.
