Задачи на силу лоренца и силу ампера с решением: Решение задач по физике в 11 классе «Сила Ампера. Сила Лоренца» — RC74 — интернет-магазин радиоуправляемых моделей

{2})\) — Площадь боковой поверхности сосуда

• Сила $(\text{Н})$:

$$M={F}\cdot{l} \Rightarrow F=\frac{M}{l}$$

• Сила первого рычага $(\text{Н})$:

$${F}_{1}\cdot{l}_{1}={F}_{2}\cdot{l}_{2} \Rightarrow {F}_{1}=\frac{{F}_{2}\cdot{l}_{2}}{{l}_{1}}$$

• Сила второго рычага $(\text{Н})$:

$${F}_{1}\cdot{l}_{1}={F}_{2}\cdot{l}_{2} \Rightarrow {F}_{2}=\frac{{F}_{1}\cdot{l}_{1}}{{l}_{2}}$$

$M\,(\text{Н·м})$ — Момент силы

$l\,(м)$ — Плечо силы

${F}_{1}\,(\text{Н})$ — Сила первого рычага

${F}_{2}\,(\text{Н})$ — Сила второго рычага

${l}_{1}\,(м)$ — Плечо первого рычага

${l}_{2}\,(м)$ — Плечо второго рычага

• Фокусное расстояние линзы $(\text{м})$:

$${F}=\frac{1}{D}$$

$D\,(\text{дптр})$ — Оптическая сила линзы

Содержание

3. Сила Ампера. Сила Лоренца. Эффект Холла.

Протон влетел в однородное магнитное поле под углом 60⁰ к направлению линий поля и движется по спирали, радиус которой 25 мм.

Индукция магнитного поля 0.05 Тл. Найти кинетическую энергию протона.

На протон, движущийся в магнитном поле, действует сила Лоренца, равная , направленная перпендикулярно скорости и индукции поля. Величина силы равна . Скорость v протона можно разложить на две составляющие: одна перпендикулярна направлению поля, другая параллельна: ; (рис.7). Тогда можно представить силу Лоренца как . Движение частицы является суперпозицией двух: вращение по окружности радиуса R со скоростью в плоскости, перпендикулярной полю, и равномерное поступательное движение вдоль линий поля со скоростью ; в результате получается движение по винтовой линии с шагом (расстоянием между соседними витками), равным , где – период вращения. По второму закону Ньютона , или . Отсюда ; ; . Для решения нашей задачи достаточно из второго закона Ньютона выразить скорость и затем найти кинетическую энергию: ; ; ; . Подставим численные значения:., или .

Провод в виде тонкого полукольца радиусом 10 см находится в однородном магнитном поле с индукцией 50 мТл. По проводу течет ток силой 10 А. Найти силу, действующую на провод, если плоскость полукольца перпендикулярна линиям индукции, а подводящие провода находятся вне поля.

Выделим элемент тока (рис.8). Пусть индукция магнитного поля направлена из-за рисунка к нам. Угол между элементом тока и вектором индукции равен 90⁰, тогда величина силы Ампера, действующей на этот элемент, , а направление её, найденное по правилу левой руки, указано на рисунке. Проекции силы Ампера на оси OX и OY равны соответственно: и . Элемент длины проводника можно выразить через приращение угла : . Тогда

Полученные выражения проинтегрируем по всей длине полуокружности, то есть по углу в пределах :

. Аналогично, . Таким образом, результирующая сила направлена по оси

OX и равна . Подставим численные значения: .

По двум параллельным проводам длиной 1 м каждый текут токи одинаковой силы. Расстояние между проводами равно 0.01 м. Токи взаимодействуют с силой 110^-3 Н. Найти силу тока в проводах.

По двум параллельным проводникам длиной 3 м каждый текут одинаковые токи силой 500 А. Расстояние между ними 0.1 м. Определить силу взаимодействия проводников.

По трем прямым параллельным длинным проводам, находящимся на одинаковом расстоянии 0.2 м друг от друга, текут токи одинаковой силы 400 А. В двух проводах направления токов совпадают. Вычислить силу, действующую на единицу длины каждого провода.

По трем параллельным длинным прямым проводам, находящимся на одинаковом расстоянии 10 см друг от друга, в одном направлении текут одинаковые токи силой 100 А. Определить силу, действующую на отрезок 1 м каждого провода.

По двум длинным параллельным проводникам, расстояние между которыми 7.5 см, текут в одном направлении токи 10 А и 5 А. Где следует поместить параллельный им третий проводник с током, чтобы он находился в равновесии?

Прямой проводник длиной 20 см и весом 50 мН подвешен горизонтально на двух легких нитях в однородном горизонтальном магнитном поле, перпендикулярном проводнику. Какой силы ток надо пропустить через проводник, чтобы одна из нитей разорвалась? Напряженность магнитного поля 31.8 кА/м. Каждая нить разрывается при нагрузке, превышающей 40 мН.

По двум длинным параллельным проводникам в одном направлении текут токи силой по 2 кА. В одной плоскости с проводниками параллельно им закреплен отрезок прямого провода длиной 50 см. Определить силу тока в проводе, если после снятия закрепления он начинает двигаться с ускорением 1 м/с

2. Масса провода 100 г, он расположен на расстоянии 20 см от одного и 40 см от другого проводника. Расстояние между проводниками 20 см.

Медный провод, площадь сечения которого 2 мм², согнут в виде трех сторон квадрата и подвешен за концы к горизонтальной оси в вертикальном магнитном поле. Когда по проводу пропускают ток силой 10 А, он отклоняется от вертикали на угол 15⁰. Определить магнитную индукцию.

Прямой провод длиной 40 см, по которому течет ток 100 А, движется в однородном магнитном поле, индукция которого перпендикулярна проводу и равна 0.5 Тл. Какую работу совершают силы, действующие на провод со стороны поля, при перемещении провода на расстояние 40 см, если направление перемещения перпендикулярно линиям индукции и проводу?

Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две стороны ее параллельны проводу. По рамке и проводу текут одинаковые токи силой 110³ А. Определить силу, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.

По кольцу диаметром 10 см из свинцовой проволоки площадью сечения 0.7 мм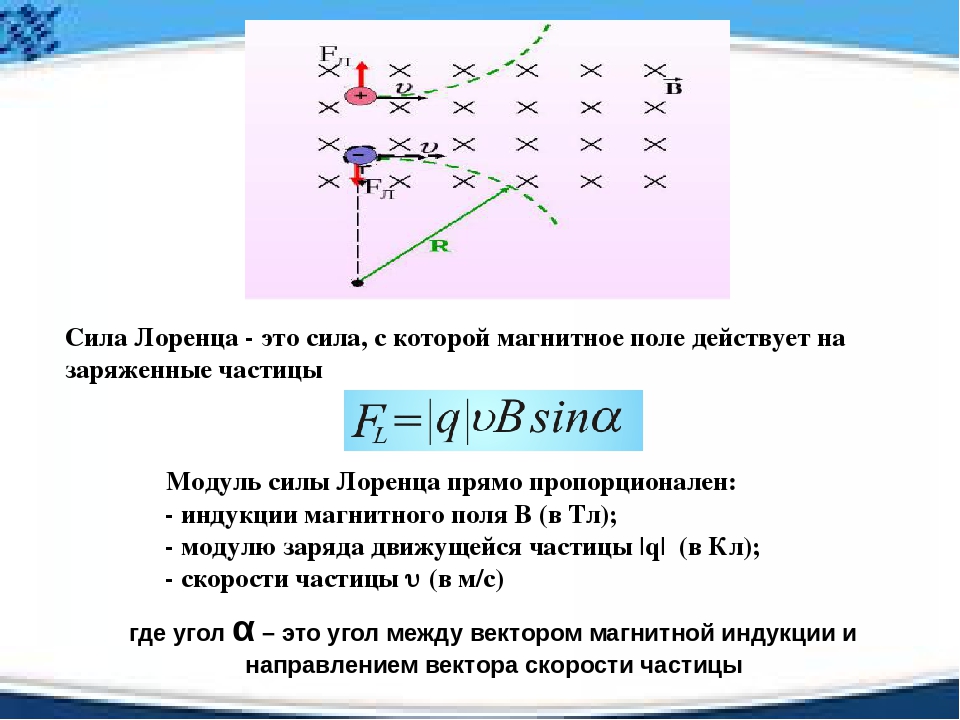

2 идет ток силой 7 А, при этом температура проволоки повышается.

Прочность свинца на разрыв при этой температуре равна 2 Н/мм². Разорвется ли такое кольцо, если поместить его в магнитное поле с индукцией 1 Тл, перпендикулярное плоскости кольца?

Ток течет по длинному однослойному соленоиду, радиус сечения которого 5.5 см. Число витков на единицу длины соленоида 15 см^-1. Найти предельную силу тока, при которой проволока не разорвется, если проволока выдерживает максимальную нагрузку 100 Н.

По двум тонким проводам, изогнутым в виде кольца радиусом 0.1 м, текут одинаковые токи по 10 А. Найти силу взаимодействия колец, если плоскости, в которых лежат кольца, параллельны, а расстояние между центрами колец равно 0.001 м.

По двум одинаковым квадратным плоским контурам со стороной 20 см текут токи силой 10 А каждый. Определить силу взаимодействия контуров, если плоскости, в которых лежат контуры, параллельны, а расстояние между соответственными сторонами контуров равно 2 мм.

Вычислить радиус дуги окружности, которую описывает протон в магнитном поле с индукцией 1.510^-2 Тл, если скорость протона равна 210⁶ м/с.

Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией 0.015 Тл по окружности радиусом 0.1 м. Определить импульс иона.

Частица, несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией 0.5 Тл. Определить момент импульса, которым обладала частица при движении в магнитном поле, если ее траектория представляла дугу окружности радиусом 0.001 м.

Заряженная частица влетела перпендикулярно линиям индукции в однородное магнитное поле, созданное в среде. В результате взаимодействия с веществом частица, находясь в поле, потеряла половину своей первоначальной энергии. Во сколько раз будут отличаться радиусы кривизны траектории начала и конца пути?

Заряженная частица, двигаясь в магнитном поле по дуге окружности радиусом 0. 02 м, прошла через свинцовую пластинку, расположенную на пути частицы. Вследствие потери энергии частицей радиус кривизны траектории изменился и стал равным 0.01 м. Определить относительное изменение энергии частицы.

Протон, прошедший ускоряющую разность потенциалов 600 В, влетел в однородное магнитное поле с индукцией 0.3 Тл и начал двигаться по окружности. Вычислить ее радиус.

Электрон движется в однородном магнитном поле перпендикулярно линиям индукции. Определить силу, действующую на него со стороны поля, если индукция равна 0.2 Тл, а радиус кривизны траектории 2 мм.

Протон и α-частица, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле перпендикулярно линиям индукции. Во сколько раз радиус кривизны траектории протона меньше радиуса кривизны траектории α-частицы?

Два иона с одинаковыми зарядами, пройдя одну и ту же разность потенциалов, влетели в однородное магнитное поле перпендикулярно линиям индукции. Один ион с массой 12 а.е.м. описал дугу окружности радиусом 0.02 м. Определить массу (в а.е.м.) другого иона, который описал дугу окружности радиуса 2.31 см.

Заряженная частица, имеющая скорость 210⁶ м/с, влетела в однородное магнитное поле с индукцией 0.52 Тл. Найти отношение заряда частицы к ее массе, если она в поле описала дугу окружности радиусом 0.04 м. По этому отношению определить, какая это частица.

Заряженная частица, прошедшая ускоряющую разность потенциалов 210³ В, движется в однородном магнитном поле с индукцией 0.015 Тл по окружности радиусом 0.01 м. Определить отношение заряда частицы к ее массе и скорость частицы.

# Между полюсами магнита на двух тонких непроводящих нитях подвешен горизонтально линейный проводник весом 0.1 Н и длиной 20 см. Напряженность однородного магнитного вертикального поля равна 200 кА/м. На какой угол от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток 2 А? Весом нитей пренебречь.

# С какой силой действует постоянный ток 10 А, проходящий по прямолинейному бесконечно длинному проводнику, на контур из провода, изогнутого в виде квадрата? Проводник расположен в плоскости контура параллельно двум его сторонам. Длина стороны контура 40 см, сила тока в нем 2.5 А. Расстояние от прямолинейного тока до ближайшей стороны контура 2 см.

# Провод в виде тонкого полукольца радиусом 10 см находится в однородном магнитном поле с индукцией 50 мТл. По проводу течет ток силой 10 А. Найти силу, действующую на провод, если плоскость полукольца перпендикулярна линиям индукции, а подводящие провода находятся вне поля.

# По тонкому проводу в виде кольца радиусом 20 см течет ток силой 100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией 20 мТл. Найти силу, растягивающую кольцо.

# Протон влетел в однородное магнитное поле под углом 60⁰ к направлению линий поля и движется по спирали, радиус которой 25 мм. Индукция магнитного поля 0.05 Тл. Найти кинетическую энергию протона.

Протон с кинетической энергией 6 эВ влетел в однородное магнитное поле перпендикулярно линиям индукции 1 Тл. Какова должна быть минимальная протяженность поля в направлении, по которому летел протон, когда он находился вне поля, чтобы оно изменило направление движения протона на противоположное?

Протон с кинетической энергией 110⁶ эВ влетел в однородное магнитное поле перпендикулярно линиям индукции (В=1 Тл). Какова должна быть минимальная протяженность поля в направлении, по которому летел протон, когда он находился вне поля, чтобы оно изменило направление движения протона на противоположное?

Электрон движется по окружности в однородном магнитном поле напряженностью 110⁴ А/м. Вычислить период вращения электрона.

Электрон в однородном магнитном поле с индукцией 0. 1 Тл движется по окружности. Найти силу эквивалентного кругового тока, создаваемого движением электрона.

Электрон, влетев в однородное магнитное поле с индукцией 0.2 Тл, стал двигаться по окружности радиусом 0.05 м. Определить магнитный момент эквивалентного кругового тока.

Протон движется по окружности в однородном магнитном поле с индукцией 2 Тл. Определить силу эквивалентного кругового тока, создаваемого движением протона.

В однородном магнитном поле с индукцией 2 Тл движется α-частица. Траектория ее движения представляет собой винтовую линию с радиусом 0.01 м и шагом 0.06 м. Определить кинетическую энергию α-частицы.

Заряженная частица прошла ускоряющую разность потенциалов 52 В и влетела в скрещенные под прямым углом электрическое с напряженностью 10⁴ В/м и магнитное с индукцией 0.1 Тл поля. Найти отношение заряда частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. Определить, какая это частица.

Два иона, имеющие одинаковые заряды, но различные массы, влетели в однородное магнитное поле. Первый ион начал двигаться по окружности радиусом 0.05 м, второй ион по окружности радиусом 0.025 м. Найти отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.

В однородном магнитном поле с индукцией 10^-4 Тл движется электрон по винтовой линии. Определить скорость электрона, если шаг винтовой линии равен 0.20 м, а радиус 0.05 м.

Электрон движется в однородном магнитном поле с индукцией 0.009 Тл по винтовой линии, радиус которой 0.01 м и шаг 0.078 м. Определить период вращения электрона и его скорость.

В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 0.10 м и шагом 0.60 м. Определить кинетическую энергию протона.

Электрон влетает в однородное магнитное поле напряженностью 1610³ А/м со скоростью 810⁶ м/с. Вектор скорости составляет угол 60⁰ с направлением линии индукции. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон в магнитном поле. Определить шаг винтовой линии для электрона, летящего под малым углом к линиям индукции.

Вычислить скорость и кинетическую энергию α-частицы, выходящей из циклотрона, если, подходя к выходному окну, ионы движутся по окружности радиусом 0.50 м. Индукция магнитного поля циклотрона 1.7 Тл.

Электрон, прошедший ускоряющую разность потенциалов 10 кВ, влетает в вакууме в однородное магнитное поле с напряженностью 79600 А/м под углом 53⁰ к направлению линий магнитной индукции. Найти радиус и шаг спирали, по которой электрон будет двигаться в магнитном поле.

Параллельно длинному прямолинейному проводнику с током 10 А на расстоянии 2 мм от проводника движется электрон со скоростью 10 Мм/с. С какой силой будет действовать магнитное поле тока на электрон?

Положительный заряд влетает с постоянной скоростью в однородное магнитное поле перпендикулярно линиям индукции. Индукция поля 1 Тл. В течение 100 мкс параллельно индукции магнитного поля действует электрическое поле напряженностью 100 В/м. Вычислить постоянный (при установившемся движении) шаг спиральной траектории заряда.

Пучок однозарядных ионов неона, пройдя в электрическом поле ускоряющую разность потенциалов 1 кВ, влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, численно равной 0.14 Тл. В магнитном поле ионы движутся по двум дугам окружностей, радиусы которых 14.5 см и 15.5 см. Найти массовые числа изотопов неона.

Электрон, пройдя ускоряющую разность потенциалов 400 В, влетел в однородное магнитное поле с напряженностью 1000 А/м перпендикулярно силовым линиям поля. Определить радиус кривизны траектории и частоту обращения электрона в магнитном поле.

Электрон, прошедший в ускоряющем электрическом поле разность потенциалов 10 кВ, движется в однородном магнитном поле с индукцией 0.5 Вб/м², перпендикулярной его скорости. Определить момент импульса электрона.

Электрон, влетевший в однородное магнитное поле с напряженностью 32 кА/м перпендикулярно направлению силовых линий поля, движется в нем по окружности радиусом 2 см. Найти разность потенциалов, которую прошел электрон перед тем, как влететь в магнитное поле.

Определить число оборотов, которые должен сделать протон в магнитном поле циклотрона, чтобы приобрести кинетическую энергию 1010⁶ эВ, если при каждом обороте протон проходит между дуантами разность потенциалов 3010³ В.

Через сечение S=ab медной пластинки толщиной a=0. 5 мм и высотой b=10 мм идет ток силой 20 А. При помещении пластинки в магнитное поле, перпендикулярное ребру b и направлению тока, возникает поперечная разность потенциалов 3.1 мкВ. Индукция магнитного поля 1 Тл. Определить: 1) концентрацию электронов проводимости в меди; 2) их среднюю скорость при этих условиях.

Через сечение S=ab алюминиевой пластинки (a=0.1 мм — толщина, b — высота пластинки) пропускается ток силой 5 А. Пластинка помещена в магнитное поле, перпендикулярное ребру b и направлению тока. Определить возникающую при этом поперечную разность потенциалов, если индукция магнитного поля равна 0.5 Тл. Концентрацию электронов проводимости считать равной концентрации атомов.

При измерении эффекта Холла в натриевом проводнике напряженность поперечного поля оказалась 5 мкВ/см при плотности тока 200 А/см² и индукции магнитного поля 1 Тл. Найти концентрацию электронов проводимости и ее отношение к концентрации атомов в проводнике.

Найти подвижность электронов проводимости в медном проводнике, если при измерении эффекта Холла в магнитном поле с индукцией 0.1 Тл напряженность поперечного электрического поля у данного проводника оказалась в 3100 раз меньше напряженности продольного электрического поля.

# Перпендикулярно однородному магнитному полю с индукцией 10^-3 Тл возбуждено однородное электрическое поле напряженностью 10³ В/м. Перпендикулярно обоим полям влетает α-частица со скоростью 10⁶ м/с. Определить нормальное и тангенциальное ускорения ее в момент вхождения в поле.

# Циклотрон предназначен для ускорения протонов до энергии 8^.10^-15 Дж. Каков должен быть радиус дуантов циклотрона, если индукция магнитного поля равна 1 Тл? Какова наименьшая продолжительность одного цикла работы этого ускорителя, если начальная энергия протонов мала, а амплитуда напряжения между дуантами 16 кВ?

# В циклотроне требуется ускорить ионы гелия Не⁺⁺. Частота переменной разности потенциалов, приложенной к дуантам, равна 1010⁶ Гц. Какова должна быть индукция магнитного поля, чтобы период вращения ионов совпадал с периодом изменения разности потенциалов?

# Пластинка полупроводника толщиной a=0.2 мм помещена в магнитное поле, направленное вдоль a. Удельное сопротивление полупроводника 10^-5 Ом^.м. Индукция магнитного поля 1 Тл. Перпендикулярно полю вдоль пластинки пропускается ток силой 0.1 А, при этом возникает поперечная разность потенциалов 3.25 мВ. Определить подвижность носителей тока в полупроводнике.

Задачи на силу Лоренца и их решение

Международный журнал физики . 2014 , 2(6), 211-216
DOI: 10.12691/ijp-2-6-5

Открытый доступСтатья

Задачи о силе Лоренца и их решение

Ф. Ф. Менде ^1,

¹ Б.И. Веркина НАН Украины, пр. Ленина, 47, г. Харьков, Украина

Опубл. Дата: 12 ноября 2014 г.

Просмотр полного текста Полный текст PDF Полнотекстовый ePUB

Процитируйте эту статью:
Ф.Ф. Менде. Проблемы силы Лоренца и их решение. Международный журнал физики . 2014; 2(6):211-216. doi: 10.12691/ijp-2-6-5

Аннотация

В статье доказано, что сила Лоренца является следствием зависимости скалярного потенциала заряда от скорости. Показано, что зависимость силы Лоренца от скорости носит нелинейный характер, как предполагалось ранее. Показано также, что силы взаимодействия проводников, по которым течет ток, несимметричны. При совпадении направления движения зарядов в проводниках сила их взаимодействия возникает меньше, чем при различном направлении движения.

Ключевые слова:
уравнения максвелла сила Лоренца закон ампера закон фарадея законы индукции

Эта работа размещена под лицензией Creative Commons Attribution 4.0 International License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/

Ссылки:

[1]	В.В.Никольский, Т.И. Никольская, Электродинамика и распространение радиоволн, Москва, Наука, 1989.

[2]	Р. Фейнман, Р. Лейтон, М. Сендс, Фейнмановские лекции по физике, –М. Мир, Том. 6 (1977).

[3]	Дж. Джексон, Классическая электродинамика, Мир, Москва, 1965, 702.
9 0058
[4]	Ф. Ф. Менде, Об уточнении уравнений электромагнитной индукции, — Харьков, депонировано в ВИНИТИ, № 774-В88 Деп. (1988).

[5]	Ф. Ф. Менде, Есть ли ошибки в современной физике. Харьков, Константа, 2003.

[6]	Ф.Ф. Менде. Об уточнении некоторых законов классической электродинамики. Харьков, НТМТ, 2012.

Вопросы о силе Лоренца — практические вопросы с ответами и пояснениями

В физике сила Лоренца представляет собой пару электрических сил и магнитных сил, действующих на заряженную точечную частицу и вызываемых электромагнитными полями. Другими словами, сила Лоренца — это сила, приложенная к заряженной частице со скоростью вдоль электрического поля и магнитного поля.

Сила Лоренца

Суммарная электромагнитная сила, действующая на данную частицу, известна как сила Лоренца. Он назван в честь физика Хендрика А. Лоренца.

Сила Лоренца определяется выражением

F = qE + qv × B

Где,

F — сила Лоренца

q — заряд данной частицы

E электрическое поле

B — это магнитное поле

v это скорость

Магнитная сила пропорциональна значению векторного векторного произведения v × B и q. В случае угла ϕ между B и v значение силы эквивалентно qvB sin ϕ. В однородном магнитном поле сила Лоренца вызывает движение заряженных частиц. Если скорость v перпендикулярна магнитному полю B, заряженная частица будет двигаться по круговой траектории с радиусом (r), равным mv/qB. Если угол ϕ равен нулю, то на заряженную частицу не действует магнитная сила (она будет продолжать двигаться неотклоняясь через силовые линии).

Ускорители частиц, такие как циклотроны, используют тот факт, что заряженные частицы движутся по круговым орбитам, когда B и v перпендикулярны друг другу. При каждом обороте точно управляемое электрическое поле сообщает заряженным частицам дополнительную кинетическую энергию. Это позволяет им двигаться по большим орбитам. Когда эти частицы обладают идеальной энергией, они используются по-разному. Он применяется при изучении субатомных частиц для различных медицинских процедур.

Ключевые точки силы Лоренца

Уравнения Максвелла показывают, как электрически заряженные частицы и движущиеся заряженные частицы или токи генерируют магнитные и электрические поля. С другой стороны, закон силы Лоренца дополняет общую картину, показывая силу, действующую на движущийся заряд q в электромагнитном поле. Сила Лоренца описывает воздействие В и Е на точечный электрический заряд. Однако такие ЭМ силы не дают полной картины. Электрически заряженные частицы, скорее всего, связаны с другими силами, такими как ядерное взаимодействие и гравитация. Итак, уравнения Максвелла существуют независимо от других физических законов, но связаны с ними через плотности тока и заряд. Влияние заряженной частицы на силу Лоренца — один из аспектов. Другой аспект — создание В и Е зарядами и токами. В реальных веществах силы Лоренца недостаточно для объяснения общего поведения точечных частиц, как в расчете, так и в принципе. В материальных средах эти частицы не только реагируют на поля В и Е, но и создают эти поля. Необходимо ответить на сложные уравнения, чтобы найти пространственный отклик и время заряда. Например, проанализируйте гидродинамику, электрогидродинамику, магнитогидродинамику и сверхпроводимость.

Видео описывает основы магнитного поля и линий магнитного поля

Магнитное поле и силовые линии магнитного поля: что такое магнитное поле?

Применение силы Лоренца

Важные применения силы Лоренца приведены ниже.

Ускорители частиц, такие как циклотроны, используют силу Лоренца. Пузырьковая камера использует силу Лоренца для создания графика траекторий движения заряженных частиц. В электронно-лучевых телевизорах используется концепция силы Лоренца, позволяющая двигать электроны по прямой линии, чтобы они попадали в определенные точки на экране.

Сила Лоренца существует во многих электрических устройствах, таких как ускорители частиц, масс-спектрометры, магнетроны, скоростные фильтры и силовая калориметрия Лоренца.

В своем проявлении в виде силы Лапласа, действующей на ток в проводнике, эта сила возникает во многих электрических устройствах, включая электродвигатели, рельсотроны, линейные двигатели, громкоговорители, магнитоплазмодинамические двигатели, громкоговорители, униполярные генераторы, электрические генераторы и линейные генераторы переменного тока.

Важные вопросы о силе Лоренца с ответами

1) Что такое сила Лоренца?

Сила Лоренца представляет собой пару электрической и магнитной сил, действующих на заряженную точечную частицу, вызванную электромагнитными полями. Другими словами, сила Лоренца — это сила, приложенная к заряженной частице со скоростью вдоль электрического поля и магнитного поля.

2) По какой формуле рассчитать силу Лоренца?

Сила Лоренца определяется выражением

F = qE + qv × B

Где,

F — сила Лоренца

q — заряд данной частицы

E электрическое поле

B — это магнитное поле

v это скорость

3) Как ускорители частиц используют силу Лоренца?

4) Сила Лоренца названа в честь физика _____.

Ответ: Хендрик Лоренц

Пояснение: Сила Лоренца названа в честь физика Хендрика Лоренца.

5) Сколько Гаусс равно одному Тесла?

Один Тесла равен 10000 Гаусс.

6) Какие известные устройства используют силу Лоренца?

Циклотроны и другие ускорители частиц с круговым движением, масс-спектрометры, скоростные фильтры, магнетроны и лоренцевские велосиметры используют силу Лоренца.

7) Какова роль силы Лоренца в электронно-лучевых телевизорах?

В электронно-лучевых телевизорах используется концепция силы Лоренца, которая заставляет электроны двигаться по прямой линии, чтобы они попадали в определенные точки на экране.

8) В чем главный недостаток концепции силы Лоренца?

Сила Лоренца описывает воздействие В и Е на точечный электрический заряд. Однако такие ЭМ силы не дают полной картины. Электрически заряженные частицы, скорее всего, связаны с другими силами, такими как ядерное взаимодействие и гравитация. Итак, уравнения Максвелла существуют независимо от других физических законов, но связаны с ними через плотности тока и заряд. В реальных веществах силы Лоренца недостаточно для объяснения общего поведения точечных частиц, как в расчете, так и в принципе. В материальных средах эти частицы не только реагируют на поля В и Е, но и создают эти поля.

9) ______ пропорционально значению векторного векторного произведения v × B и q.

Ответ: Магнитная сила

Объяснение: Магнитная сила пропорциональна значению векторного векторного произведения v × B и q.

10) ______ показывают, как электрически заряженные частицы и движущиеся заряженные частицы или токи создают магнитные и электрические поля.

Ответ: уравнения Максвелла

Пояснение: Уравнения Максвелла показывают, как электрически заряженные частицы и движущиеся заряженные частицы или токи создают магнитные и электрические поля.