16 системы счисления сложение

Вы искали 16 системы счисления сложение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и в сложение чисел в системах счисления, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «16 системы счисления сложение».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 16 системы счисления сложение,в сложение чисел в системах счисления,вычитание и сложение в системах счисления,вычитание и сложение систем счисления,как складывать в системе счисления,как складывать в шестнадцатиричной системе счисления,как складывать системы счисления,как складывать числа в десятичной системе счисления,как складывать числа в разных системах счисления,как складывать числа в шестнадцатеричной системе счисления,как складывать шестнадцатиричные числа,как сложить шестнадцатеричные числа,онлайн сложение чисел в восьмеричной системе счисления,онлайн сложение чисел в разных системах счисления,онлайн сложение чисел в шестнадцатеричной системе счисления,онлайн сложение шестнадцатиричных чисел,систем счисления сложение,система счисления вычитание и сложение,система счисления сложение,системы счисления 16 сложение,системы счисления как складывать,системы счисления сложение,сложение 16 ричных чисел,сложение 16 ричных чисел онлайн,сложение 16 системы счисления,сложение 2 системы счисления,сложение в 16 системе счисления,сложение в 2 системе счисления,сложение в 8 системе счисления,сложение в разных системах счисления,сложение в системах счисления,сложение в системе счисления,сложение в шестнадцатеричной системе,сложение в шестнадцатеричной системе счисления,сложение восьмеричных чисел калькулятор,сложение и вычитание в разных системах счисления,сложение и вычитание в системах счисления,сложение и вычитание в шестнадцатеричной системе счисления,сложение и вычитание систем счисления,сложение и вычитание чисел в разных системах счисления,сложение и вычитание шестнадцатеричных чисел,сложение разных систем счисления,сложение систем счисления,сложение систем счисления с решением онлайн сложение,сложение система счисления,сложение системы счисления,сложение системы счисления 16,сложение сс,сложение чисел в восьмеричной системе счисления онлайн,сложение чисел в разных системах счисления,сложение чисел в разных системах счисления онлайн,сложение чисел в системах счисления,сложение чисел в шестнадцатеричной системе,сложение чисел в шестнадцатеричной системе счисления,сложение чисел в шестнадцатеричной системе счисления онлайн,сложение шестнадцатеричной системы счисления,сложение шестнадцатеричных чисел,сложение шестнадцатиричной системы,сложение шестнадцатиричной системы счисления,сложение шестнадцатиричных чисел онлайн,сложения в шестнадцатеричной в системе счисления,сложения систем счисления,сложить числа в восьмеричной системе счисления онлайн,сложить шестнадцатеричные числа,таблица сложения 16 ричной системы счисления.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 16 системы счисления сложение. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычитание и сложение в системах счисления).

Решить задачу 16 системы счисления сложение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Позиционные системы счисления — что это, определение и ответ

Системы счисления – одна из самых базовых тем в информатике, поэтому разберемся в этой теме по порядку.

Допустим, необходимо посчитать количество цветов на поляне. Можно загибать пальцы, делать зарубки на дереве, как это делали древние люди, и так далее. Можно сделать вывод, что форма счета может быть любой, также, как и форма записи. Для способа записи чисел ввели такое понятие, как система счисления.

Существует два типа систем счисления:

• Непозиционная

• Позиционная

В непозиционной системе счисления величина, которая обозначает цифру, не зависит от положения в числе.

К таким системам счисления можно отнести египетскую и римскую системы счисления.

Пример. Число в римской системе счисления – это набор стоящих подряд заглавных латинских букв, таких как I, V, X, L, C, В и M, которые обозначают числа 1, 5, 10, 50, 100, 500 и 1000 соответственно.

Тогда число 67 в римской системе счисления можно записать, как LXVII.

Непозиционные системы счисления годны для записи числа, но при сложных вычислениях вызывают массу неудобств хотя бы потому, что в них отсутствуют единые правила формирования больших чисел.

Позиционные системы счисления основаны на том, что «вес» цифры зависит от её положения – или позиции – в числе, отсюда и такое название.

Самые популярные в информатике позиционные системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.

Десятичная система счисления

Исторически сложилось, что это самая распространенная система счисления. Именно её мы используем, когда мы делаем покупки в магазине, набираем номер телефона или открываем страницу в книге. На каждой позиции может стоять только одна цифра из диапазона от 0 до 9.

Основанием (то есть, количество цифр) является число 10. Это значит, что «вес» любой цифры в числе будет кратен 10 в степени, равной позиции этой цифры. При этом позиции (их называют разрядами) отсчитываются с правого конца числа, начиная с нуля.

Пример. Чтобы разобраться подробнее, возьмем число 123. Давайте «разложим» это число по разрядам. Для этого каждую цифру числа умножим на основание системы, в данном случае число 10, возведенное в степень, равную номеру разряда. Цифра 3 стоит в нулевом разряде, цифра 2 – в первом, а цифра 1 – во втором. Получается, значение равно:

1∙10² + 2∙10¹ + 3∙10⁰ = 100 + 20 + 3 = 123.

При работе с разными системами счисления, чтобы избежать путаницы, справа от числа приписывают нижний индекс с основанием: 123₁₀.

Двоичная система счисления

Эта система счисления используется в вычислительной технике. Десятичную систему счисления в компьютерах не стали использовать, потому что требовалось производство устройств, способных работать в десяти состояниях, а это сильно увеличило бы цену и размер таких устройств.

Пример. Возьмем число 1001 – это число 9 в десятичной системе счисления. Для того, чтобы перевести число из двоичной в десятичную систему счисления, необходимо точно так же «разложить» число на разряды, т.е. каждую цифру двоичного числа умножить на основание 2, возведенное в степень, равную разряду:

1001₂ = 1∙2³ + 0∙2² + 0∙2¹ + 1∙2⁰ = 8 + 0 + 0 + 1 = 9.

Точно так же выполняется перевод из любой n-ричной системы счисления в десятичную. Для этого надо:

1. Определить количество разрядов;

2. Умножить каждую цифру n-ричной системы счисления на основание «n», возведенное в степень, равную разряду.

Пример. Посмотрим, как переводить число из десятичной системы счисления в двоичную. Пусть нужно перевести число 240₁₀ в двоичную систему счисления. Для этого надо последовательно делить число 240 на 2, фиксируя получающиеся остатки (удобнее всего делать это «лесенкой»), пока не дойдем до последнего частного, которое на 2 уже не делится. Это будет первая цифра числа в двоичной системе. А остальные цифры – это получившиеся остатки, записанные в обратном порядке:

Осталось записать обведенные кружком цифры в обратном порядке, начиная с самой правой (выделена жирным). Получаем, что число

240₁₀ = 11110000_2.

Точно так же выполняется перевод из десятичной системы счисления в любую n-ричную.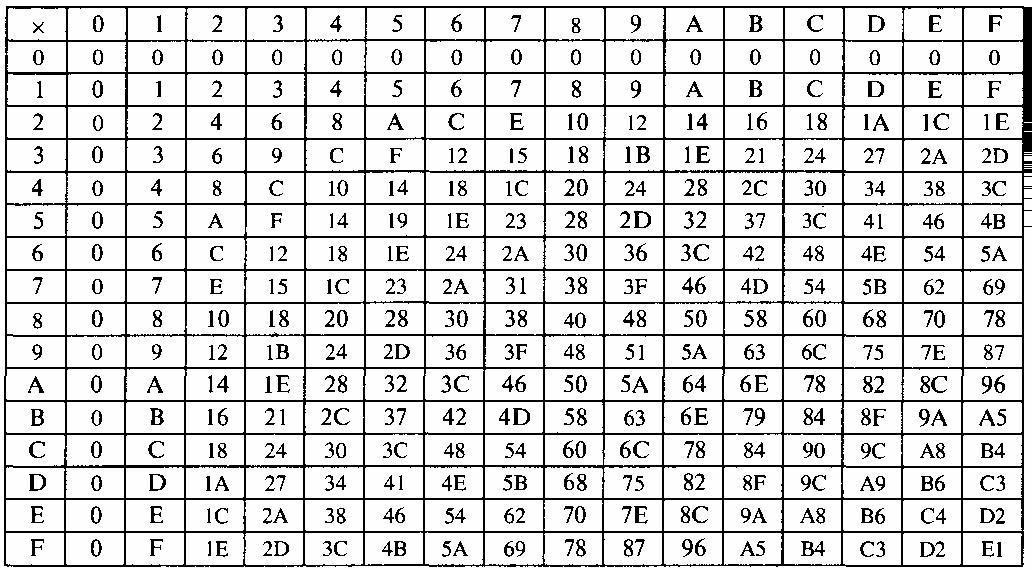 Для этого надо:

1. Целую часть числа последовательно делить на основание новой системы счисления, пока не останется число или цифра, которая уже делиться не будет;

2. Эта оставшаяся цифра (частное) будет первой цифрой нового числа. Остальные цифры – это остатки от всех делений, записанные в обратном порядке.

Восьмеричная система счисления

Имеет основание 8, использует цифры от 0 до 7.

Для того, чтобы перевести из восьмеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 8, возведенное в степень, равную разряду.

Пример.

671₈ = 6∙8² + 7∙8¹ + 1∙8⁰ = 384 + 56 + 1 = 441_10.

Перевод из десятичной системы счисления в восьмеричную осуществляется аналогично

переводу в двоичную, только делителем в данном случае является 8.

Пример. Пусть надо перевести число 163₁₀ в восьмеричную систему:

Получаем, что:

163₁₀ = 243_8.

Шестнадцатеричная система счисления

Имеет основание 16, использует цифры от 0 до 9 и буква A, B, C, D, E, F, где буква А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.

Для того, чтобы перевести из шестнадцатеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 16, возведенное в степень, равную разряду.

Пример.

127₁₆ = 1∙16² + 2∙16¹ + 7∙16⁰ = 256 + 32 + 7 = 295_10.

Для того, чтобы перевести из десятичной системы счисления в шестнадцатеричную, нужно целую часть числа находить делением на основание новой.

Пример. 191₁₀ переведем в шестнадцатеричную систему:

При этом 11 = B, 15 = F. Получаем, что:

191₁₀ = BF_16.

Метод триад и тетрад

Для перевода чисел, записанных в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов.

Триады – числа, состоящие из трех цифр, вообще говоря, это перевод восьмеричных чисел от 0 до 7 в двоичную систему счисления. Тетрады состоят из четырех, и являются переводом шестнадцатеричных чисел от 0 до F в двоичную систему счисления.

Триады и тетрады переводятся, начиная с конца числа (т.е. с младших разрядов). Если крайние триады (тетрады) оказались неполными, они дополняются нулями. Если при переводе в двоичную систему в начале числа (слева) возникают нули, их следует отбросить (они незначащие).

Пример.

12345667₈ = 001 010 011 100 101 110 110 111₂ = 1 010 011 100 101 110 110 111₂.

Таблица с триадами и тетрадами, которую надо знать наизусть.

Число	Триада	Тетрада
0	000	0000
1	001	0001
2	010	0010
3	011	0011
4	100	0100
5	101	0101
6	110	0110
7	111	0111
8		1000
9		1001
A (10)		1010
B (11)		1011
С (12)		1100
D (13)		1101
E (14)		1110
F (15)		1111

Перевод из десятичной системы счисления в двоичную с помощью степенной таблицы

Рассмотрим еще один альтернативный метод перевода из десятичной системы счисления в двоичную, который заключается в использовании таблицы степеней двоек.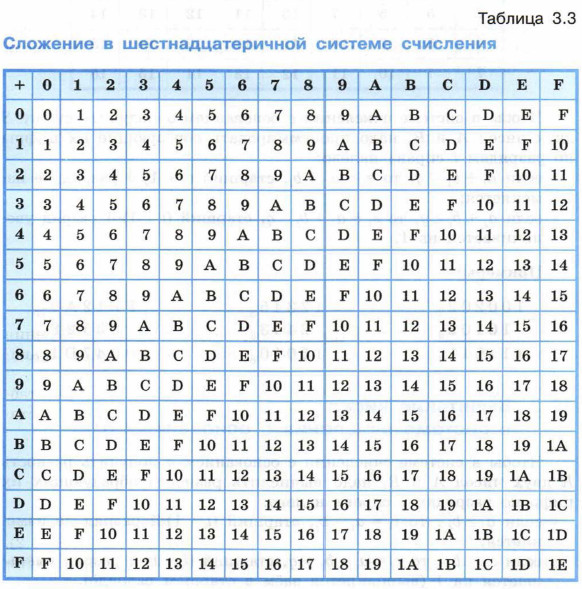 Рассмотрим данный алгоритм подробнее:

1. Записываем таблицу степеней двойки в обратном порядке.

2. Выбираем самое большое значение степени, помещающееся в число, которое переводим в двоичную систему. Эту степень обводим.

3. Переходим к следующей степени двойки.

4. Вычитаем каждое следующее помещающееся число. Вмещающиеся степени обводим.

5. Продолжаем вычитать, пока не дойдем до конца таблицы.

6. Под обведенными степенями пишем «1», под не обведенными «0».

7. Записываем получившееся число.

Пример. С помощью этого метода переведем число 79₁₀ из десятичной системы счисления в двоичную.

79 = 64 + 8 + 4 + 2 + 1

Получаем:

79₁₀ = 1001111_{2 .}

Арифметика в позиционных системах счисления

С первого класса вас учили производить расчеты в десятичной системе счисления, далее мы рассмотрим, как производить расчеты в произвольной позиционной системе счисления.

Все позиционные системы счисления «одинаковы», и выполнение арифметических вычислений во всех них производятся по общим правилам сложения, вычитания, умножения и деления столбиком, аналогичным правилам в десятичной системе счисления.

Сложение в позиционных системах счисления

Сложение многозначных чисел в n-ричной системе счисления производится поразрядно, начиная с младшего разряда. Если при суммировании цифр одного разряда сумма оказывается больше n – 1, то в данном разряде записывается младшая цифра суммы, а старшая цифра прибавляется к ближайшему слева разряду. При этом таблица сложения в двоичной системе счисления выглядит следующим образом:

Пример. Рассмотрим сложение чисел в двоичной системе счисления, опираясь на таблицу сложения. Маленькими цифрами сверху обозначены значения, переносимые при сложении в соседний слева разряд.

Вычитание в позиционных системах счисления

Вычитание многозначных чисел в n-ричной системе производится также столбиком. Если в очередном разряде уменьшаемого стоит цифра, меньшая чем у вычитаемого, то занимается единица у ближайшего слева ненулевого разряда. В результате к вычисляемому разряду уменьшаемого добавляется n. Если единица занималась не у соседнего слева разряда, то к промежуточным разрядам добавляется n – 1.

Пример. Рассмотрим вычитание чисел в восьмеричной системе счисления.

Умножение и деление в позиционных системах счисления

Наконец, умножение сводится к многократному сложению со сдвигом разрядов, а деление – к многократному вычитанию. Для данных операций удобно использовать таблицу умножения в двоичной системе счисления:

Пример. Рассмотрим, как умножать и делить числа в двоичной системе счисления.

Пример. Закрепим операции умножения и деления чисел в пятеричной системе счисления.

Числа Фибонначи и Фибоначчиевая система счисления

Итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи, открыл удивительную последовательность чисел:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Именно такие числа называются «числами Фибоначчи», а сама последовательность – последовательностью Фибоначчи.

В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел:

1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.

Пример. Запомнить правило последовательности Фибоначчи просто с помощью задачи про кроликов. Пусть пару кроликов поместили в некое место, огражденное со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару кроликов, а рождаются кролики у пары со второго месяца.

Решая эту задачу, получаем таблицу с данными, которые являются членами последовательности Фибоначчи:

Числа Фибоначчи используются в так называемой Фибоначчиевой системе счисления.

Принцип разложения любого числа в Фибоначчиевой системе счисления основывается на вышеупомянутым переводе десятичного числа в двоичное с помощью степенной таблицы, но данном случае верхнюю строку таблицы заполняем числами Фибоначи в порядке убывания вместо степеней двоек. При этом нижний индекс для обозначения системы счисления выглядит следующим образом: _Fib.

Пример. Рассмотрим прямое и обратное разложение числа в Фибоначчиевой системе счисления.

25₁₀ = X_Fib

25 = 21 + 3 + 1

Таким образом, получаем:

25₁₀ = 1000101_Fib.

10010101_Fib = X₁₀

Тогда:

10010101_Fib = 34 + 8 + 3 + 1 = 46_10.

Шестнадцатеричное сложение/вычитание и дополнение до 2 | Penji

В этой статье рассматриваются сложение и вычитание без знака, а также сложение и вычитание в дополнении до 2 по основанию 16 (шестнадцатеричное). В этой статье также будет затронута тема переполнения в связи с этими операциями.

Что такое шестнадцатеричный формат?

Шестнадцатеричная система — это система счисления с основанием 16. Она имеет 16 различных символов, 0–9 для представления соответствующих двоичных значений и A, B, C, D, E и F для представления 10–15 соответственно. .

Для полноты давайте начнем с преобразования шестнадцатеричного числа в его десятичный эквивалент. Каждая позиция в шестнадцатеричном числе представляет степень 16, очень похожую на двоичную, за исключением того, что вместо этого мы используем основание 16. Возьмем, к примеру, 19FDE_16. Десятичный эквивалент рассчитывается следующим образом:

1) Запишите, на что будет умножаться каждый символ, исходя из его позиции

2) Теперь преобразуйте буквы в их десятичные значения

3) Теперь умножьте и сложите, и вы есть ответ! Помните, что базы поднимаются справа налево, а не слева направо!

Сложение в шестнадцатеричном формате

Вы вводите шестнадцатеричное сложение только в том случае, если ваше число превышает 15. В остальном это почти то же самое, что и десятичное сложение. Начнем с небольшого примера.

Начните справа и добавьте.

1) 6 + 3 = 9 без переноса

2) A + B = 10 + 11 = 21 (> 15), значит перенос есть! Вычтите 16 из 21 и перенесите 1 (это похоже на обычное сложение, но вместо вычитания 10 просто вычтите 16, так как мы находимся в базе 16).

3) 4 + 1 + 1 (перенос) = 6

И вы получите ответ:

= 659_16 = 1190_10 + 435_10 = 1625_10

90 002 Эта практическая задача взята из предыдущего курса ECS 50. :

Теперь давайте сделаем часть а.

Переполнение — это когда у вас недостаточно места для хранения всего ответа, поэтому, если номер крайнего левого столбца больше 15, для этого расчета возникает переполнение. Для этой конкретной части нет переполнения.

Вычитание в шестнадцатеричном формате

Это похоже на обычное десятичное вычитание, но заимствованное число отличается. В десятичной системе вы заимствуете группу 10_10, а в шестнадцатеричной системе вы заимствуете группу 16_10.

Вычтем наш предыдущий пример:

Теперь давайте сделаем часть b.

Опять же, здесь тоже нет переполнения!

Дополнение до 2

Чтобы получить отрицательное представление числа в дополнении до 2, запишите число в двоичной форме, инвертируйте биты и добавьте 1.

Предположим, мы хотим узнать, как выглядит -14, используя для простоты 7 бит.

1) Сначала запишем 14 в двоичном виде: 0 0 0 1 1 1 0

2) Затем инвертируем биты, 0 станет 1, а 1 станет 0: 1 1 1 0 0 0 1

3) Теперь мы добавляем 1:

Это -14 в записи дополнения до 2. ПРИМЕЧАНИЕ. Чтобы узнать, является ли число отрицательным в дополнении до 2, первый бит известен как «знак», но 0 означает, что число положительное, а 1 означает, что число отрицательное.

Теперь, чтобы преобразовать шестнадцатеричное число в дополнение до 2, вам нужно преобразовать шестнадцатеричное число в двоичное, а затем двоичное в дополнение до 2 (если вы хотите отрицание числа, которое вы конвертируете).

Чтобы преобразовать шестнадцатеричный код в двоичный, используйте следующую таблицу:

Каждая шестнадцатеричная цифра преобразуется в 4 двоичных: Возьмем, например, (4E)_16

4_16 = 0100_2

E_16 = 1110_2 900 03

Со (4Э)_16 =(01001110)_2

Дополнение до 2 полезно для вычитания, но сложение с дополнением до 2 такое же, как обычное сложение, но переполнение отличается.

Давайте сделаем часть c .

Но для этого есть переполнение!

2 Complement Overflow

Переполнение происходит при добавлении двух подписанных 2 дополнительных чисел и 1) если оба операнда положительные, но результат отрицательный или 2) когда оба операнда отрицательные, но результат положительный. Итак, вернемся к части c.

Теперь часть d , вычитание дополнения до 2.

Сначала запишите двоичные формы обоих чисел.

Теперь получите дополнение до 2 для B8FDE3.

Инвертируйте цифры: 010001110000001000011100

Добавьте 1: 010001110000001000011101 (отрицательное значение B8FDE3).

Теперь «добавить» A689BE+(-B8FDE3).

Итак, ваш окончательный ответ: ED8BD8_16. Переполнения нет, так как это операнды с разными знаками!

‍

Добавление шестнадцатеричных чисел | Изучение и решение вопросов

Обзор шестнадцатеричных чисел

Буквы «Hexa» и «deci» во фразе «шестнадцатеричный» обозначают числа «6» и «10» соответственно.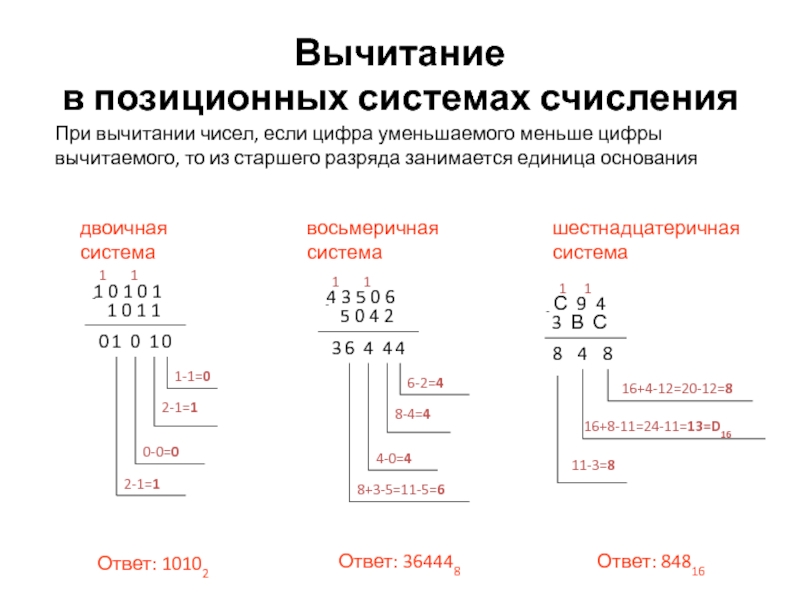 16-значное шестнадцатеричное представление цифр от 0 до 9 и букв от A до F известно как шестнадцатеричная система счисления. Иными словами, первые девять чисел или цифр представлены как числа, а следующие шесть цифр представлены буквами от A до F. Десятичная система счисления, имеющая основание 9, и шестнадцатеричная очень похожи. Поэтому после 9цифр, 10-я цифра представлена ​​в виде символа — 10 как A, 11 как B, 12 как C, 13 как D, 14 как E и 15 как F.

Что такое шестнадцатеричные числа?

Поскольку каждая цифра имеет вес в степени 16, шестнадцатеричная система счисления также известна как позиционная система счисления. Каждая последующая цифра в 16 раз важнее предыдущей. Например: \[7B{3_{16}}\] ,\[4B2{A_{16}},67{F_{16}}{\rm{ \;и }}{76_{16}}\]

Шестнадцатеричное сложение чисел

Единственная разница между шестнадцатеричным сложением и десятичным сложением заключается в добавлении букв A, B, C, D, E и F. Вот иллюстрация шестнадцатеричного сложения. Проверьте приведенный ниже пример, а для получения дополнительной информации см. абзац под ним.

Пример шестнадцатеричного сложения

При наличии чисел выше 9 (буквы от A до F) шестнадцатеричное сложение включает в себя вычисление основного десятичного сложения при преобразовании между шестнадцатеричным и десятичным числом. В примере B + 8 равно 11 + 8 или 19..

Шестнадцатеричная таблица

Шестнадцатеричное сложение станет намного проще, если вы воспользуетесь приведенной ниже таблицей.

Шестнадцатеричная таблица

Как складывать шестнадцатеричные числа

Десятичная система счисления, имеющая основание 9, и шестнадцатеричная очень похожи. Мы можем очень легко складывать шестнадцатеричные числа, понимая шестнадцатеричную таблицу и следуя простому сложению.

Давайте разберемся на примере:

Сложение шестнадцатеричных чисел

Здесь будем прибавлять с разряда единиц:

Итак, 3 + 1 = 4

Теперь прибавим разряд десятков с помощью шестнадцатеричной таблицы

b + 2 = d

Прибавим теперь сотый разряд.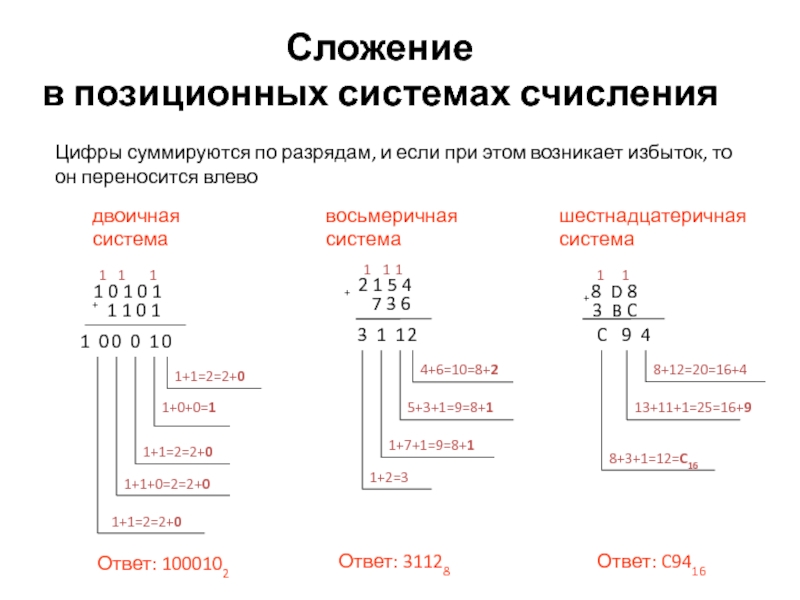

f + 6 = 15 (1 будет переноситься)

7 + b = 12

И так как 1 был переносом, то 12 + 1 = 13

Теперь, наконец, 1 + 1 = 2

Таким образом , окончательный ответ 235d4.

Решенные примеры

Пример 1: Добавьте следующее шестнадцатеричное число.

8AB + B78

Ответ: 8AB + B78

Мы знаем:

8 + B = 13

A + 7 = 11

8 + B = 13

8AB + B78 = 1423

Таким образом, ответ 1423.

Пример 2: Добавьте следующие шестнадцатеричные числа.

D6E + 8C6

Ответ: Мы знаем, что

E + 6 = 14

6 + C = 12

D + 8 = 15

Таким образом,

901 40 D6E + 8C6

= 1634

Следовательно, его сумма будет 1634.

Пример 3: Какая польза от шестнадцатеричной системы счисления?

Ответ: Применение шестнадцатеричной системы счисления:

Существует способ записи чисел в шестнадцатеричном формате.