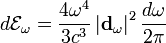диполь — это… Что такое диполь?
ДИПОЛЬ — (от греч. di приставка, означающая дважды, двойной, и polos полюс) электрический, совокупность двух равных по абс. величине разноимённых точечных зарядов (+е, е), находящихся на нек ром расстоянии l друг от друга. Осн. хар кой электрич. Д. явл.… … Физическая энциклопедия
ДИПОЛЬ — (от ди… и греч. polos полюс) 1) электрический диполь совокупность двух точечных электрических зарядов, равных по величине и противоположных по знаку, находящихся на некотором расстоянии друг от друга;2) магнитный диполь совокупность двух равных … Большой Энциклопедический словарь
диполь — антенна Словарь русских синонимов. диполь сущ., кол во синонимов: 1 • антенна (17) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
диполь — я, м. dipôle < di(s) + polos полюс. 1. физ. Совокупность двух равных по ведичине электрических зарядов, расположенных на некотором расстонии друг от друга. Крысин 1998. 2. техн. Один из типов антенн для коротких волн. Крысин 1998. Антенна… … Исторический словарь галлицизмов русского языка
диполь — Совокупность двух частиц, находящихся одна от другой на расстоянии, много большем размера частиц и много меньшем расстояния от частиц до точек наблюдения, и обладающих электрическими зарядами, равными по абсолютному значению, но противоположными… … Справочник технического переводчика
ДИПОЛЬ — ДИПОЛЬ, молекула с разделенным электрическим зарядом. В КОВАЛЕНТНОЙ СВЯЗИ между двумя атомами пары электронов не обязательно равномерно распределены между атомами. В хлориде водорода (НСl) электроны притягиваются к атому хлора, имеющему больший… … Научно-технический энциклопедический словарь
Диполь — (от греческого di приставка, означающая дважды, двойной, polos полюс) гидродинамический точечная особенность в поле безвихревого течения идеальной несжимаемой жидкости, которая представляет собой предельное состояние источников и стоков равной… … Энциклопедия техники
ДИПОЛЬ — антенна, представляющая собой короткий горизонтальный или вертикальный провод, в середине к рого подводится энергия от радиопередатчика или отбирается энергия для радиоприемника. Д. применяется при работе на коротких и ультракоротких волнах и… … Технический железнодорожный словарь
ДИПОЛЬ — система двух разноименных равных по величине зарядов (электрических или магнитных), находящихся в непосредственной близости друг от друга. Д. характеризуется своим моментом, представляющим собой вектор, направленный от отрицательного заряда к… … Геологическая энциклопедия
диполь — dipole Dipol – 1) Двополюсник. Розрізняють Д. електричний і магнітний. Електричний Д. – сукупність двох рівних за абсолютною величиною різнойменних зарядів, які знаходяться на певній відстані один від одного. Характеристикою Д. електричного є… … Гірничий енциклопедичний словник
2.3. Полярность связи. Дипольный момент молекулы
l
µ = δ l
Рис. 2.23. Схема образования диполя в гетероядерной молекуле АВ
При образовании ковалентной химической связи между разными атомами (гетероядерные молекулы) электронная плотность распределяется не симметрично относительно ядер. В молекуле она сдвинута в сторону ато-
ма, имеющего большее значение электро- | Атом А | Атом В | |||
отрицательности. Вследствие | |||||
χА<χВ | |||||
двухатомной молекуле | центры | тяжести | |||
δ+ | δ− | ||||
положительных зарядов | ядер и | отрица- | |||
тельных зарядов электронов не совпадают. Возникает система разных по знаку, но одинаковых по величине электриче-
ских зарядов (δ+ и δ−) – электрический диполь (рис. 2.23).
Мерой полярности связи (характеристикой диполя) является диполь-
ный момент µ – произведение величины заряда δ на расстояние между центрами тяжести положительных и отрицательных зарядов (длина диполя l).
Единицей измерения дипольного момента в системе СИ [Кл м] чаще
используется внесистемная единица Дебай (D): 1 D = 3,33 10-30 Кл м.
В гетероядерных молекулах связь всегда полярна, но если число атомов в молекуле три и более, то возникающая при этом система распределения зарядов может привести к тому, что молекула в целом не будет являться диполем – центры тяжести положительных и отрицательных зарядов совпадают. Как правило, это связано с симметричным строением молекулы.
Если молекулу, даже если она не является диполем, поместить в электрическое поле напряженностью Е, происходит разделение центров тяжести зарядов в результате смещения электронов относительно ядер, и смещения атомов относительно друг друга в молекуле. При этом молекула приобретает наведенный (индуцированный) дипольный момент. Способность молекул приобретать в электрическом поле дипольный момент на-
зывается поляризуемостью.
Дипольный момент наведенного диполя пропорционален напряженности электрического поля: µи = α ε0 E , где α – коэффициент поляризуе-
мости (поляризуемость) атома или молекулы, ε0 – электрическая постоянная.
Пример.
Молекула | Дипольный мо- | Дипольный момент | Строение | ||
| мент связи, D | молекулы, D | молекулы | ||
O3 | 0 | 0 | О |
| |
О | О | ||||
|
|
| |||
h3O | 1,5 | 1,84 | Н |
| |
О | Н | ||||
|
|
| |||
CO2 | 2,7 | 0 | С | O | |
|
| О | |||
3 . ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ
ИЖИДКОСТЯХ
3.1.Агрегатные состояния
Вещества в зависимости от внешних условий (температура и давление) и их химического состава могут существовать в трех основных агрегатных состояниях: газообразном, жидком и твердом. При достаточно низких температурах вещества находятся в твердом состоянии, а при относительно высоких – в жидком и газообразном.
При нагревании происходит, как правило, последовательный переход веществ из твердого в жидкое и газообразное состояние (плавление и испарение), а при охлаждении протекают обратные процессы (конденсация и кристаллизация). Эти переходы осуществляются при определенной температуре (температуре фазового перехода), при этом скачкообразно изменяется молярный объем вещества и энтропия (энергетическая характеристика степени разупорядоченности системы), поглощается или выделяется тепловая энергия (энтальпия фазового перехода). Температура перехода из одного состояния в другое зависит от химической природы вещества и давления. Конкретные значения температур фазовых переходов для различных веществ лежат в широких пределах (табл. 3.1). Необходимо отметить, что при определенных условиях возможен фазовый переход твердое состояние – газ (сублимация-кристаллизация).
|
|
|
|
|
|
|
|
| Таблица 3 . 1 | ||
Температуры (°С), энтальпия (∆Н0, кДж/моль) и энтропии (∆S0, Дж/моль К) фазо- | |||||||||||
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ве- | Тип кристалла |
|
|
|
| Фазовый переход |
|
|
|
| |
щест- |
|
| Плавление — |
|
|
| Кипение – |
| |||
во |
| кристаллизация |
| конденсация |
| ||||||
|
| tпл, °С |
| ∆Н0пл, |
| ∆S0 пл, | tкип, °С |
| ∆Н0исп, |
| ∆ S0исп, |
N2 | Молекулярный | -210 |
| 0,721 |
| 11,4 | -195,8 |
| 5,59 |
| 72,4 |
Ch5 | -//- | -182,5 |
| 0,938 |
| 10,4 | -164 |
| 8,18 |
| 75,0 |
h3O | -//- | 0 |
| 6,013 |
| 22,0 | 100 |
| 40,683 |
| 109,07 |
C6Н6 | -//- | 5,5 |
| 9,837 |
| 35,3 | 80,1 |
| 30,76 |
| 87,1 |
S(β) | -//- | 119,3 |
| 1,72 |
| 4,4 | 445 |
| 9,2 |
| 12,8 |
Si | Ковалентный | 1415 |
| 49,8 |
| 29,5 | 3300 |
| 356 |
| 99,6 |
AgCl | Ионный | 455 |
| 13,2 |
| 18,1 | 1557 |
| 184 |
| 100,5 |
NaCl | -//- | 801 |
| 28,2 |
| 26,3 | 1490 |
| 138 |
| 78,3 |
MgF2 | -//- | 1263 |
| 58 |
| 37,8 | 2270 |
| 274 |
| 107,7 |
Na | Металлический | 97,9 |
| 2,60 |
| 7,01 | 886 |
| 90.1 |
| 77,7 |
Ag | -//- | 960,5 |
| 11,3 |
| 9,2 | 2167 |
| 251 |
| 102,9 |
W | -//- | 3420 |
| 35,1 |
| 9,5 | 5680 |
| 770 |
| 129,3 |
Жидкое и твердое агрегатные состояния относят к конденсированному состоянию вещества. Оно отличается от газообразного тем, что энергия взаимодействия между частицами, образующими вещество, сравнима по величине или превышает энергию их теплового движения. Это приводит к тому, что среднее расстояние между частицами (между центрами частиц) в газе при нормальных условиях составляет величину ~ 10 их диаметров, тогда как в конденсированном состоянии оно сравнимо с их диаметром. Молярный объем любого газа при нормальных условиях равен 22,4 л/моль, тогда как молярные объемы твердых веществ и жидкостей примерно в 103 раз меньше (0,01–0,05 л/моль).
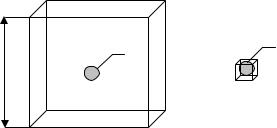
Пример. Расчет средних размеров пространства, занимаемого одной частицей при атмосферном давлении.
Газ Жидкость, кристалл
V = a3 – объем пространства a – ребро куба
d – средний диаметр частицы
Газ. | 1 | моль | газа при нормальных | условиях | занимает | объем | |||||
Vν = 22,4 л/моль и содержит 6,02 1023 молекул (число Авогадро). |
| ||||||||||
Средний размер пространства, занимаемого одной частицей: |
| ||||||||||
V = | 22,4 10 | -3 |
|
|
|
|
| 0 | |||
| = 3,7 10-26 м3 , a = 3 V = 3 3,7 10−26 = 3,3 10-9 м = 33А. | ||||||||||
|
| 6,02 1023 |
|
|
|
|
|
| |||
Размер молекулы азота (две длины связи) d N2 3 Ǻ. |
|
| |||||||||
Жидкость. |
| 1 | моль | жидкого брома | (Br2) | занимает | объем | ||||
V = | M | = | 160 | = 51,2 cм3 . | М=160 г/моль | – | молярная масса | брома, | |||
ν | ρ |
| 3,12 |
|
|
|
|
|
|
|
|
ρ=3,12 г/см3 – плотность жидкого брома, Vν – молярный объем жидкого брома.
Средний размер пространства, занимаемого одной частицей:
V = | 51,2 | 10 | -6 | = 8,5 10-29 м3 | , a = 3 V = 3 | 8,5 10−29 = 4,4 10-10 | 0 | |||
| м = 4,4 А . | |||||||||
| 1023 | |||||||||
6,02 |
|
|
|
|
|
|
| |||
Размер молекулы брома (две длины связи) d Br2 4,56 Ǻ. |
| |||||||||
Кристалл. 1 | моль металлического серебра занимает объем |
| ||||||||
|
|
|
| V = | M = |
| 108 | = | 10,3 cм3. |
|
|
|
|
| 10,50 |
| |||||
|
|
|
| ν | ρ |
|
|
| ||
М=108 г/моль – молярная масса серебра, ρ=10,50 г/см3 – плотность серебра, Vν – молярный объем серебра.
Средний размер пространства, занимаемого одной частицей:
V = | 10,3 | 10 | -6 | =1,7 10-29 м3 , a = 3 V = 3 1,7 10−29 | = 2,6 10-10 | 0 |
| м = 2,6 А. | |||||
| 6,02 | 1023 |
|
|
| |
Размер атома серебра (два металлических радиуса) d Ag 2,68 Ǻ.
В газах частицы находятся в броуновском движении, при этом отсутствуют ближний и дальний порядок в положении частиц. Газ не имеет собственного объема и, соответственно, формы. В жидкостях броуновское движение осложнено наличием более или менее устойчивого ближнего порядка в положении частиц относительно друг друга за счет возникновения химических связей между отдельными частицами. Жидкость имеет собственный объем, но из-за слабого межмолекулярного взаимодействия под действием силы тяжести принимает форму сосуда, в котором она находится. В твердом состоянии вещества энергия взаимодействия между частицами намного превышает энергию теплового движения, что приводит к фиксированию положений частиц в пространстве, вокруг которых они совершают колебательные и вращательные движения. Это определяет наличие у твердых тел собственной формы и объема и большое сопротивление сдвигу.
Сравнение энергетических характеристик фазовых переходов свидетельствует о существенно меньшей перестройке вещества при плавлении, чем при испарении. Как видно из табл. 3.1, для всех кристаллов с различным типом химической связи теплота (энтальпия) плавления много меньше теплоты испарения. Энтропия фазового перехода, характеризующая изменение степени упорядоченности системы, также для плавления много меньше, чем для испарения.
В газообразном состоянии, где присутствуют слабо или совсем не взаимодействующие между собой молекулы вещества, химическая связь внутри них рассматривается с использованием моделей «классической» ковалентной связи.
При рассмотрении конденсированного состояния вещества химическая связь описывается с использованием моделей ковалентной, ионной и металлической связи. При этом необходимо принимать во внимание близкое расположение частиц, образующих систему. Это обстоятельство в ряде случаев (жидкости, молекулярные кристаллы) обусловливает необходимость учитывать существенный вклад межмолекулярного взаимодействия в энергию химических связей.
Необходимо отметить, что целый ряд веществ может не иметь одного из агрегатных состояний. Чаще всего это относится к жидкому и газообразному состояниям. Данное обстоятельство связано с соотношением между энергией, необходимой для перевода вещества из одного агрегатного состояния в другое, и энергией, достаточной для разрыва внутримолекулярных химических связей. Например, во многих нерастворимых в воде гидроксидах металлов при нагревании раньше протекает реакция дегидратации (Cu(OH)2→ CuO + h3O), а затем происходит плавление вещества.
3.2.Межмолекулярное взаимодействие
Как было отмечено выше, в конденсированном состоянии вещества на величину энергии химической связи существенно влияют межмолекулярные взаимодействия. Они связаны с электростатическим взаимодействием зарядов, возникающих в результате нарушения симметрии распределения электронной плотности в молекулах.
3.2.1.Межмолекулярные взаимодействия (силы Ван-дер-Ваальса)
В конденсированных фазах (жидкость, твердое тело) расстояние между молекулами соизмеримо с размерами самих молекул. На таких малых расстояниях проявляют себя силы электростатического взаимодействия диполей, как постоянных, так и наведенных. При этом энергия системы понижается.
Межмолекулярные взаимодействия характеризуются отсутствием обмена электронами между частицами, отсутствием специфичности и насыщаемости. Энергия межмолекулярного взаимодействия сравнительно невелика, однако она вносит существенный вклад в энергетическое состояние системы, определяя в значительной степени физические и химические свойства вещества.
На сравнительно больших расстояниях r между молекулами, когда электронные оболочки не перекрываются, действуют только силы притяжения. При этом возможны три механизма возникновения сил притяжения.
1. Ориентационный эффект (диполь – дипольное взаимодействие). Если молекулы полярны, то проявляется электростатическое взаимодействие двух постоянных диполей. Полярные молекулы ориентируются относительно друг друга противоположно заряженными частями, энергия притяжения прямо пропорциональна дипольным моментам (µi2) и обратно пропорциональна расстоянию между ними (r6). Повышение температуры ослабляет это взаимодействие, так как тепловое взаимодействие стремится
нарушить взаимную ориентацию молекул.
2. Индукционный эффект (взаимодействие диполь – наведенный диполь).
Неполярные молекулы под действием поля полярной молекулы поляризуются, возникает индуцированный диполь. Индуцированный дипольный момент прямо пропорционален поляризуемости молекул (µи α µд). Энергия притяжения таких молекул прямо пропорциональна дипольным моментам (α µд2) и обратно пропорциональна расстоянию между ними (r6). Так как наведение диполей происходит при любом пространственном расположении молекул, индукционный эффект от температуры не зависит.
3. Дисперсионный эффект (взаимодействие мгновенных диполей).
В отличие от ориентационного и индукционного взаимодействия дисперсионный эффект имеет объяснение только в рамках квантовой механики. Его возникновение можно представить следующим образом: в процессе движения электронов распределение зарядов внутри атомов может стать несимметричным, что приводит к образованию «мгновенных диполей», которые притягиваются друг к другу. Более того, при сближении молекул движение электронов перестает быть независимым и возникает «самосогласованная» система взаимодействующих мгновенных диполей. Энергия притяжения прямо пропорциональна поляризуемостям молекул (αi) и обратно пропорциональна расстоянию между ними (r6).
Дисперсионный эффект, как наиболее универсальный, проявляется при взаимодействии как полярных, так и неполярных молекул. Причем для неполярных молекул и молекул с небольшим дипольным моментом он является основным.
Индукционный и ориентационный эффекты играют существенную роль при взаимодействии полярных молекул. Для молекул с большим значением дипольного момента основным является ориентационный эффект. Индукционный эффект обычно невелик и становится значительным лишь тогда, когда полярные молекулы сосуществуют с сильно поляризующимися молекулами (табл. 3.2).
На малых расстояниях между молекулами, когда их электронные оболочки сильно перекрываются, электростатическое отталкивание ядер и электронов становится больше их взаимного притяжения. Энергия отталкивания гораздо сильнее зависит от расстояния (r12), чем энергия притяжения. На больших расстояниях межмолекулярное взаимодействие определяется силами притяжения, а на малых силами отталкивания.
Таблица 3 . 2
Относительный вклад каждой составляющей в энергию межмолекулярного взаимодействия для различных молекул
| Ориентацион- | Индукционное | Дисперсион- | µ, Кл м |
| α, м3 |
Молекула | ное |
| ное | Диполь- |
| Поляри- |
|
|
|
| |||
| % |
| ный |
| зуемость | |
|
|
| момент |
|
| |
|
|
|
|
| ×1030 | |
CO | < 0,01 | 0,1 | 99,9 | 0,33 |
| 1,926 |
HCl | 14,4 | 4,2 | 81,4 | 3,47 |
| 2,561 |
Nh4 | 44,9 | 5,3 | 49,7 | 4,94 |
| 2,145 |
h3O | 76,9 | 4,0 | 19,0 | 6,10 |
| 1,444 |
3.2.2.Водородная связь
Особым типом межмолекулярного взаимодействия является водородная связь. Она возникает между молекулами, которые содержат в своей структуре атом водорода и малый по размерам атом элемента с большим значением электроотрицательности (кислород, фтор, азот и др.). Поскольку разница в электроотрицательностях водорода и этих элементов велика, то связь сильно поляризована, на атомах возникают сравнительно большие отрицательные и положительные заряды. В то же время небольшой размер этих атомов позволяет им близко подходить друг к другу при ди- поль-дипольном взаимодействии. Поэтому энергия ориентационного взаимодействия значительно больше (примерно на порядок), чем в других случаях. Кроме того, энергия связи существенно увеличивается за счет частичного образования ковалентной составляющей связи между взаимодействующими атомами соседних молекул по донорно-акцепторному механизму. 1s-орбиталь водорода частично оголена благодаря сильной поляризации связи (это еще не Н+, но уже и не Н0), а на электроотрицательном атоме имеются неподеленные электронные пары.
79
Оба эти фактора приводят к увеличению энергии связи по сравнению с энергией межмолекулярного взаимодействия. Энергия водородной связи составляет величину порядка 100 кДж/моль, энергия межмолекулярного взаимодействия (силы Ван-дер-Ваальса) – 10-20 кДж/моль.
При конденсации молекул, способных к образованию водородных связей, их взаимное расположение будет определяться как направлением в пространстве атомов водорода внутри молекулы, так и направлением в пространстве электронных орбиталей электроотрицательного атома, связанного с атомом водорода соседней молекулы.
Водородная связь определяет многие физические и химические свойства веществ, в частности увеличивается температура плавления и кипения, изменяется плотность вещества. Особую роль водородная связь играет в биохимии, органические молекулы (в том числе и полимеры), содержащие H-O, H-N связи, образуют большое число водородных связей.
Примеры. Вода h3O.
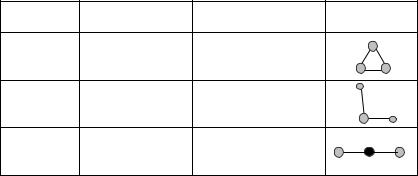
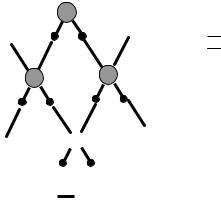
В конденсированном состоянии каждая молекула воды может иметь четыре водородные связи: две между атомом кислорода (функции донора) и атомами водорода двух соседних молекул воды; еще две – за счет двух атомов водорода (функция акцептора). В кристаллическом состоянии образуется правильная алмазоподобная структура. В узлах располагаются большие атомы кислорода, которые связаны между собою через атом водорода. В жидком состоянии часть водородных связей разорвана (рис.3.1).
Нδ+ | Нδ+ Длина связи О | Н | 0,99 Ǻ |
| Длина связи О | Н | 1,77 Ǻ |
Оδ− | Угол связи 104,5о |
| |
Оδ− |
|
| |
Нδ+ | Нδ+ Нδ+ Нδ+ |
|
|
 Оδ−
Оδ−
Рис. 3.1. Схема образования тетраэдрической пространственной структуры воды вкристаллическом и жидком состояниях: — ковалентная связь, — водородная связь
— водородная связь
Фтористый водород HF.
В газообразном состоянии при невысоких температурах, за счет образования водородных связей, образуются ассоциаты (HF)2, (HF)6.. В конденсированном состоянии, в частности в твердом, HF образует зигзагообразные цепи (рис. 3.2).
ДИПОЛЬНЫЙ МОМЕНТ — это… Что такое ДИПОЛЬНЫЙ МОМЕНТ?
- ДИПОЛЬНЫЙ МОМЕНТ
- электрический, векторная величина, характеризующая асимметрию распределения положит. и отрицат. зарядов в электрически нейтральной системе. Два одинаковых по величине заряда +q и Чq образуют электрич. диполь с Д. м. m = q l, где l- расстояние между зарядами. Для системы из пзарядов
i
радиусы-векторы к-рых i, В молекулах и мол. системах центры положит. зарядов q А совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом случае Д. м.
В молекулах и мол. системах центры положит. зарядов q А совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом случае Д. м.  Вектор Д. м. направлен от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе Д. м. молекулы иногда приписывают противоположное направление. Часто вводят представление о Д. м. отдельных хим. связей, векторная сумма к-рых дает Д. м. молекулы. При этом Д. м. связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда. Д. м. хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий Д. м. существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный Д. м. молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО 2 и CCl4). Если же Д. м. молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н 2 О полярна; суммирование Д. м. двух полярных связей ОН также дает отличный от нуля Д. м., направленный по биссектрисе валентного угла НОН. Порядок величины Д. м. молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим.
связи (порядка 10—10 м), т. е. составляет 10—29 Кл. м. В справочной литературе Д. м. молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл. м. Спектроскопич. методы определения Д. м. молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие Д. м. со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины Д. м. (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора Д. м. Важно, что точность определения Д. м. почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых Д. м. ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, Д. м. пропана равен 0,085 b0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов. Направление вектора Д. м. молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка. Др. группа методов определения Д. м. основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены Д. м. молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине Д. м. основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний Д. м. единицы объема) складывается из наведенной, или индуцированной, поляризации Р м и ориентационной поляризации Р ор и связана с m ур-нием Ланжевена — Дебая:
Вектор Д. м. направлен от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе Д. м. молекулы иногда приписывают противоположное направление. Часто вводят представление о Д. м. отдельных хим. связей, векторная сумма к-рых дает Д. м. молекулы. При этом Д. м. связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда. Д. м. хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий Д. м. существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный Д. м. молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО 2 и CCl4). Если же Д. м. молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н 2 О полярна; суммирование Д. м. двух полярных связей ОН также дает отличный от нуля Д. м., направленный по биссектрисе валентного угла НОН. Порядок величины Д. м. молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим.
связи (порядка 10—10 м), т. е. составляет 10—29 Кл. м. В справочной литературе Д. м. молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл. м. Спектроскопич. методы определения Д. м. молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие Д. м. со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины Д. м. (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора Д. м. Важно, что точность определения Д. м. почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых Д. м. ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, Д. м. пропана равен 0,085 b0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов. Направление вектора Д. м. молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка. Др. группа методов определения Д. м. основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены Д. м. молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине Д. м. основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний Д. м. единицы объема) складывается из наведенной, или индуцированной, поляризации Р м и ориентационной поляризации Р ор и связана с m ур-нием Ланжевена — Дебая: 
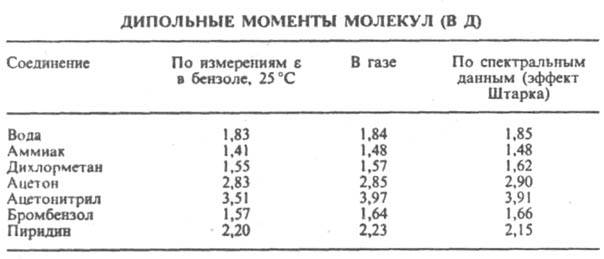
где М — мол. масса, d — плотность, a — поляризуемость молекулы, NA — число Авогадро, k — постоянная Больцмана, Т — абс. т-ра. Измерения диэлектрич. проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. При наиб. распространенном варианте метода — измерениях в разбавл. р-рах неполярных р-рителей — предполагается аддитивность поляризаций растворенного в-ва и р-рителя. Сопоставление Д. м. полярных молекул нек-рых орг. соед., полученных разными методами, показано в таблице.
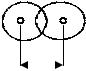
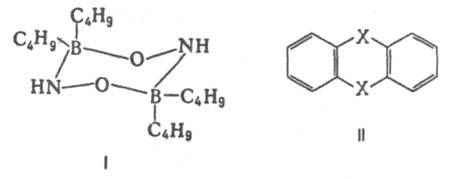
Важнейшая область применения данных о Д. м. молекул -структурные исследования, установление конформации молекул, конформационного и изомерного состава в-ва, его зависимости от т-ры. Величины Д. м. молекул позволяют судить о распределении электронной плотности в молекулах и зависимости этого распределения от характера отдельных заместителей. В общем случае структурная интерпретация Д. м. требует сравнения эксперим. величин со значениями, полученными квантовомех. расчетом либо при помощи аддитивной векторной схемы с использованием Д. м. отдельных связей и атомных групп. Последние находят либо по интенсивностям колебат. полос поглощения, либо путем векторного разложения Д. м. нек-рых симметричных молекул. Расчеты с использованием векторной аддитивной схемы могут учитывать разл. проявления стереохим. нежесткости, напр., затрудненное или своб. внутр. вращение молекулы. Высокосимметричные мол. структуры, обладающие центром инверсии, двумя взаимно перпендикулярными осями вращения или осями, перпендикулярными плоскости симметрии, не должны иметь Д. м. По наличию или отсутствию Д. м. молекулы можно в отдельных случаях выбрать для нее ту или иную структуру без к.-л. теоретич. расчетов. Так, равенство нулю эксперим. Д. м. димера аминооксидибутилборана (ф-ла I) служит доказательством того, что он существует в виде устойчивой кресловидной конформации, обладающей центром инверсии. Наоборот, наличие Д. м. у тиантрена (ф-ла II, X = S) и селенантрена (II, X = Se), равных 1,57 Д и 1,41 Д соотв., исключает для них центросимметричную структуру, в частности плоскую.
Лит.: Минкин В. И., Осипов О. А., Жданов Ю. А., Дипольные моменты в органической химии. Л., 1968; Осипов О. А., Минкин В. И., Гарновский А. Д., Справочник по дипольным моментам, 3 изд.. М., 1971; Exner О., Dipole moments in organic chemistry, Stuttg., 1975. В. И. Muнкин.
Химическая энциклопедия. — М.: Советская энциклопедия. Под ред. И. Л. Кнунянца. 1988.
- ДИПOЛЬ-ДИПOЛЬНОЕ ВЗАИМОДЕЙСТВИЕ
- ДИРАКА УРАВНЕНИЕ
Смотреть что такое «ДИПОЛЬНЫЙ МОМЕНТ» в других словарях:
ДИПОЛЬНЫЙ МОМЕНТ — физическая величина, характеризующая свойства диполя. Электрический дипольный момент равен произведению положительного заряда электрического диполя на расстояние между зарядами и направлен от отрицательного заряда к положительному. Магнитный… … Большой Энциклопедический словарь
ДИПОЛЬНЫЙ МОМЕНТ — электрический, величина, характеризующая электрич. св ва системы заряж. ч ц. Д. м. р электронейтральной системы, состоящей из n заряж. ч ц, равен: ,где ei заряд i той ч цы, ri; её радиус вектор. Д. м. не зависит от выбора начала координат и… … Физическая энциклопедия
Дипольный момент — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
дипольный момент — физическая величина, характеризующая свойства диполя. Электрический дипольный момент равен произведению положительного заряда электрического диполя на расстояние между зарядами и направлен от отрицательного заряда к положительному. Магнитный… … Энциклопедический словарь
дипольный момент — постоянный электрический момент частицы; дипольный момент; отрасл. постоянный дипольный момент Электрический момент частицы (молекулы или комплекса молекул) при отсутствии внешнего электрического поля … Политехнический терминологический толковый словарь
дипольный момент — dipolinis momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. dipole moment vok. Dipolmoment, n rus. дипольный момент, m pranc. moment de dipôle, m; moment… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
дипольный момент — dipolinis momentas statusas T sritis chemija apibrėžtis Vektorinis dydis, lygus bet kurio dipolio elektros krūvio ir atstumo tarp polių sandaugai. atitikmenys: angl. dipole moment rus. дипольный момент ryšiai: sinonimas – elektrinio dipolio… … Chemijos terminų aiškinamasis žodynas
дипольный момент — dipolinis momentas statusas T sritis fizika atitikmenys: angl. dipole moment vok. Dipolmoment, n rus. дипольный момент, m pranc. moment dipolaire, m … Fizikos terminų žodynas
Дипольный момент — электрический, физическая величина, характеризующая электрические свойства системы заряженных частиц. Д. м. системы из N заряженных частиц равен где ei заряд частицы номера i, а ri её радиус вектор. Д. м. нейтральной в… … Большая советская энциклопедия
ДИПОЛЬНЫЙ МОМЕНТ — физ. величина, характеризующая свойства диполя. Электрич. Д. м. равен произведению положит. заряда электрич. диполя на расстояние между зарядами и направлен от отрицат. заряда к положительному. Магн. Д. м. контура с током пропорционален… … Естествознание. Энциклопедический словарь
|
|
ДИПОЛЬНЫЙ МОМЕНТ электрический, векторная величина, характеризующая асимметрию распределения положит. и отрицат. зарядов в электрически нейтральной системе. Два одинаковых по величине заряда +q и —q образуют электрич. диполь с дипольным моментом m = q l, где l — расстояние между зарядами. Для системы из n зарядов qi радиусы-векторы к-рых ri, В молекулах и мол. системах
центры положит. зарядов qА совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом
случае дипольный момент Вектор дипольного момента направлен
от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе дипольному моменту молекулы иногда приписывают противоположное направление. Часто вводят представление о дипольных моментах отдельных хим. связей, векторная сумма к-рых дает дипольный момент молекулы. При этом дипольный момент связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда.
Дипольный момент хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий дипольный момент существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный дипольный момент молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО2 и
CCl4). Если же дипольный момент молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н2О полярна; суммирование дипольных моментов двух полярных связей ОН также дает отличный от нуля дипольный момент, направленный по биссектрисе валентного угла НОН.
Порядок величины дипольного момента молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим. связи (порядка 10—10 м), т. е. составляет 10—29 Кл.м. В справочной литературе дипольные моменты молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл.м.
Спектроскопич. методы определения дипольных моментов молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие дипольный момент со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины дипольного момента (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора дипольного момента. Важно, что точность определения дипольного момента почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых дипольных моментов ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, дипольный момент пропана равен 0,085 b 0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов.
Направление вектора дипольного момента молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка.
Др. группа методов определения дипольного момента основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены дипольные моменты молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине дипольного момента основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний дипольный момент единицы объема) складывается из наведенной, или индуцированной, поляризации Рм и ориентационной поляризации Рор и связана с m ур-нием Ланжевена — Дебая:
где М — мол. масса, d — плотность, a — поляризуемость молекулы, NA — число Авогадро, k — постоянная Больцмана, Т — абс. т-ра. Измерения диэлектрич. проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. При наиб. распространенном варианте метода — измерениях в разбавл. р-рах неполярных р-рителей — предполагается аддитивность поляризаций растворенного в-ва и р-рителя. Сопоставление дипольных моментов полярных молекул нек-рых орг. соед., полученных разными методами, показано в таблице. Важнейшая область применения данных о дипольных моментах молекул -структурные исследования, установление конформации молекул, конформационного и изомерного состава в-ва, его зависимости от т-ры. Величины дипольных моментов молекул позволяют судить о распределении электронной плотности в молекулах и зависимости этого распределения от характера отдельных заместителей. В общем случае структурная интерпретация дипольных моментов требует сравнения эксперим. величин со значениями, полученными квантовомех. расчетом либо при помощи аддитивной векторной схемы с использованием дипольных моментов отдельных связей и атомных групп. Последние находят либо по интенсивностям колебат. полос поглощения, либо путем векторного разложения дипольных моментов нек-рых симметричных молекул. Расчеты с использованием векторной аддитивной схемы могут учитывать разл. проявления стереохим. нежесткости, напр., затрудненное или своб. внутр. вращение молекулы. Высокосимметричные мол. структуры, обладающие центром инверсии, двумя взаимно перпендикулярными осями вращения или осями, перпендикулярными плоскости симметрии, не должны иметь дипольных моментов. По наличию или отсутствию дипольного момента молекулы можно в отдельных случаях выбрать для нее ту или иную структуру без к.-л. теоретич. расчетов. Так, равенство нулю эксперим. дипольного момента димера аминооксидибутилборана (ф-ла I) служит доказательством того, что он существует в виде устойчивой кресловидной конформации, обладающей центром инверсии. Наоборот, наличие дипольного момента у тиантрена (ф-ла II, X = S) и селенантрена (II, X = Se), равных 1,57 Д и 1,41 Д соотв., исключает для них центросимметричную структуру, в частности плоскую. === Исп. литература для статьи «ДИПОЛЬНЫЙ МОМЕНТ»: Минкин В. И., Осипов О. А., Жданов Ю. А., Дипольные моменты в органической химии. Л., 1968; Осипов О. А., Минкин В. И., Гарновский А. Д., Справочник по дипольным моментам, 3 изд.. М., 1971; Exner О., Dipole moments in organic chemistry, Stuttg., 1975. В. И. Muнкин. Страница «ДИПОЛЬНЫЙ МОМЕНТ» подготовлена по материалам химической энциклопедии. |
Электрический диполь — это… Что такое Электрический диполь?
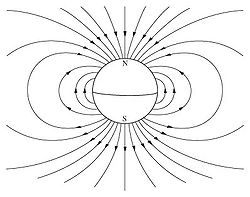
Магнитное поле Земли примерно совпадает с полем диполя. Однако «N» и «S» (северный и южный) полюса отмечены «географически», то есть противоположно принятому обозначению для полюсов магнитного диполя.
Диполь — идеализированная система, служащая для приближенного описания распространения поля. Дипольное приближение основано на разложении потенциалов поля в ряд по степеням радиус-вектора и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно описывать поле в случае если
- Размеры излучающей поле системы малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд.
- Член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности.
- В уравнениях рассматриваются градиенты потенциалов не выше первого порядка.
Типичный пример диполя — два бесконечно близких заряда, равных по величине и противоположных по знаку. Поле такой системы полностью описывается дипольным приближением.
Дипольный момент системы
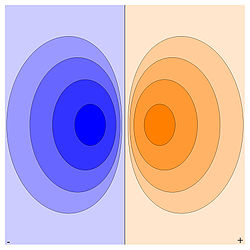
Эквипотенциальные поверхности электрического диполя
Электрический диполь
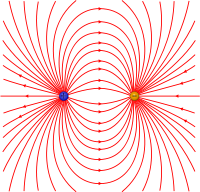
Силовые линии электрического диполя
Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.
Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга
Произведение вектора 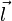 , проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов
, проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов 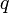 , называется дипольным моментом:
, называется дипольным моментом: 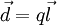 .
.
Во внешнем электрическом поле 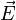 на диполь действует момент сил
на диполь действует момент сил 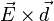 , который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля. Потенциальная энергия диполя в электрическом поле равна
, который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля. Потенциальная энергия диполя в электрическом поле равна 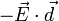 .
.
Вдали от диполя напряжённость его электрического поля убывает с расстоянием R как 1 / R3, то есть быстрее, чем у точечного заряда.
Любая электронейтральная система в некотором приближении может рассматриваться как электрический диполь с моментом 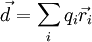 , где
, где 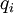 — заряд i-го элемента,
— заряд i-го элемента, 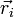 — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.
— его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.
Магнитный диполь
Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» (эта аналогия условна, так как магнитных зарядов, с точки зрения современной электродинамики, не существует). В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых изучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади 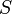 , по которой течёт ток
, по которой течёт ток 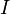 . При этом магнитным моментом диполя (в системе СГСМ) называют величину
. При этом магнитным моментом диполя (в системе СГСМ) называют величину 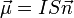 , где
, где 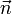 — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, с которого ток в рамке течёт против часовой стрелки.
— единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, с которого ток в рамке течёт против часовой стрелки.
Поле колеблющегося диполя
В этом разделе рассматривается поле, создаваемое точечным электрическим диполем  находящимся в заданной точке пространства.
находящимся в заданной точке пространства.
Поле на близких расстояниях
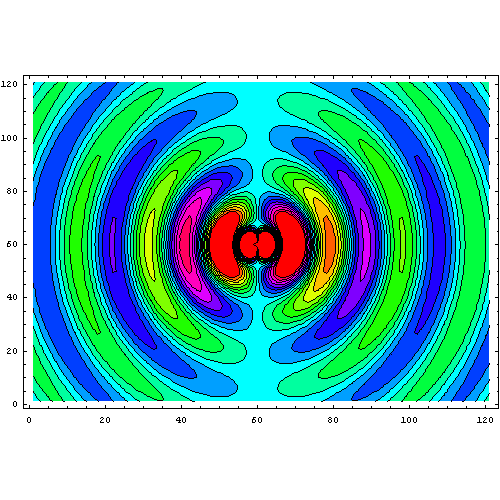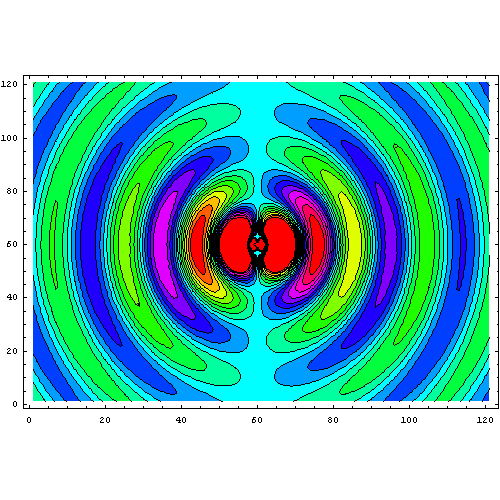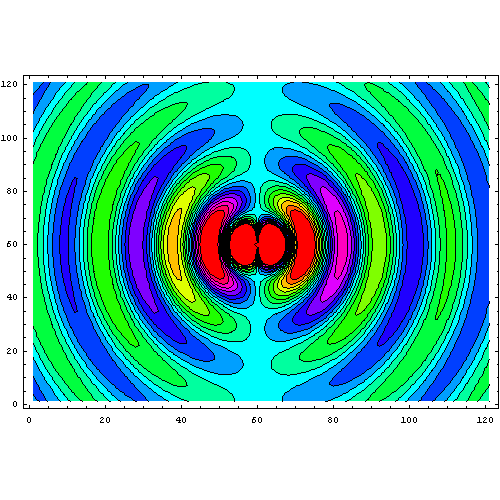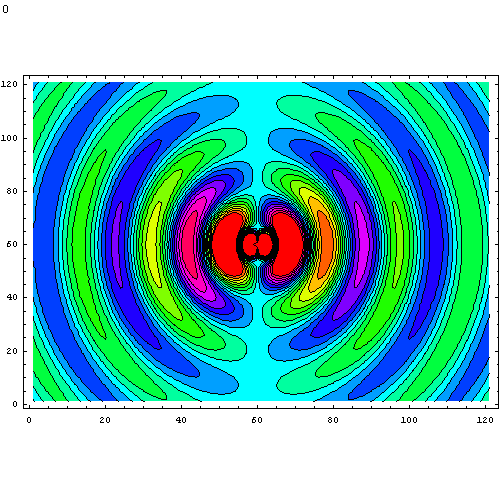
Эволюция поля колеблющегося электрического диполя в реальном времени. Диполь находится в точке (60,60) и колеблется по вертикали с частотой 1 рад/с (~0.16 Гц)
Поле точечного диполя, колеблющегося в вакууме, имеет вид

![\mathbf{B} = \left[\frac{\dot \mathbf{d}}{c R^2} + \frac{\ddot \mathbf{d}}{R c^2} , \mathbf{n} \right] =
\left[\mathbf{n} , \mathbf{E} + \frac{\mathbf{d}}{R^3}\right]](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) ,
,
где 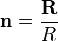 — единичный вектор в рассматриваемом направлении, c — скорость света.
— единичный вектор в рассматриваемом направлении, c — скорость света.
Этим выражениям можно придать несколько другую форму, если ввести вектор Герца
Напомним, что диполь покоится в начале координат, так что 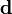 является функцией одной переменной. Тогда
является функцией одной переменной. Тогда
При этом потенциалы поля можно выбрать в виде
Указанные формулы можно применять всегда, когда применимо дипольное приближение.
Дипольное излучение (излучение в волновой зоне)
Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для 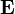 и
и 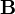 существенными оказываются только члены, содержащие вторые производные от
существенными оказываются только члены, содержащие вторые производные от 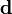 , так как
, так как
Выражения для полей принимают вид
В плоской волне интенсивность излучения в телесный угол do равна
 ,
,
поэтому для дипольного излучения
где θ — угол между векторами 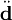 и
и 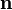 . Найдём полную излучаемую энергию. Учитывая, что
. Найдём полную излучаемую энергию. Учитывая, что 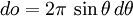 , проинтегрируем выражение по dθ от 0 до π. Полное излучение равно
, проинтегрируем выражение по dθ от 0 до π. Полное излучение равно
Укажем спектральный состав излучения. Он получается заменой вектора 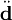 на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом:
на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом:
Литература
См. также
Wikimedia Foundation. 2010.
Диполь — Справочник химика 21
Длина. диполя имеет значение порядка диаметра атома, т. е. 10 , а заряд электрона 1,6-10″ Кл, поэтому электрический момент диполя выражается величиной порядка 10 Кл-м (кулон-метр) [c.83]
Исследование электрического момента диполя [c.156]
Индукционное взаимодействие молекул осуществляется за счет их индуцированных диполей. Допустим, что встречаются полярная и неполярная молекулы. Под действием полярной молекулы неполярная молекула деформируется и-в ней возникает (индуцируется) диполь. Индуцированный диполь притягивается к постоянному диполю полярной молекулы. Индуцированный диполь в свою очередь усиливает электрический момент диполя полярной молекулы. [c.90]
Значения электрических моментов диполя некоторых молекул приведены в табл. 9. [c.85]
Электрические моменты диполей ( х) некоторых молекул [c.85]
Неполярные и полярные молекулы. В зависимости от характера распределения электронной плотности молекулы могут быть неполярными и полярными. В неполярных молекулах центры тяжести положительных и отрицательных зарядов совпадают. Полярные молекулы являются диполями, т. е. системами, состоящими из двух равных по величине и противоположных по знаку зарядов — -q и —q), находящихся на некотором расстоянии I друг от друга. Расстояние между центрами тяжести положительного и отрицательного зарядов назывгется длиной диполя. Полярность молекулы, как и полярность связи, оценивают величиной ее электрического момента диполя х, представляющего собой произведение длины диполя I на величину электрического заряда х = Iq. [c.83]
Электрический момент диполя молекулы представляет собой векторную сумму моментов всех связей и несвязывающих электронных пар в молекуле. Результат сложения зависит от структуры молекулы. Например, молекула СО г имеет симметричное линейное строение [c.83]
Эта формула дает лучшую сходимость с опытом, чем формула Борна. Метод Ван-Аркеля и де-Бура отличается от борновского тем, что в нем процесс гидратации разделяется на два этапа. Энергия образования первого гидратного слоя вычисляется на основе взаимодействия между газообразным ионом и полярными молекулами воды, т. е. взаимодействия, происходящего вне сферы жидкой фазы. Такой способ расчета позволяет учесть свойства отдельных молекул воды (их дипольные моменты, поляризуемость и т. п.). Поэтому при рассмотрении процесса образования первого гидратного слоя, где эти свойства особенно важны, появляется возможность отказаться от представления о воде лишь как о среде с определенной диэлектрической пропицаемостью. Поскольку на второй стадии цикла в воду вносится ион, уже частично гидратированный, с радиусом, зиачителглю большим, чем радиус исходного иона, то одна и та же ошибка в его определении здесь будет иметь меньи ее значение. Возмуихения, вызванные введением такого гидратированного иоиа в воду, будут меньшими, и представление о воде как о непрерывной среде с определенной диэлектрической проницаемостью, а следовательно, и применение формулы (2.14) оказываются более оправданными, чем в методе Борна. Молекулу воды Ван-Аркель и де-Бур представляют себе в виде с([)еры с радиусом 0,125 нм и электрическим моментом диполя, равкым 6,17-10 ° Кл.м (1,85 0). [c.59]
Электрическим моментом диполя обладают также угловая молекула SOa, пирамидальные молекулы h4N, NP3 и т. д. Отсутствие такого момента свидетельствует о высоко симметричной структуре молекулы, наличие электрического момента диполя — о несимметричности структуры молекулы (табл. 8). [c.84]
Зная экспериментальные значения электрического момента диполя, можно рассчитать полярность связей и эффективные заряды атомов. В простейшем случае двухатомных молекул можно приближенно считать, что центры тяжести зарядов совпадают с ядрами, т. е. I равно межъядерному расстоянию или длине связи. Так, в молекуле НС1 НС1 = 0,127 нм. Если бы хлорид водорода был чисто ионным соединением q равно заряду электрона), то его электрический момент диполя был бы равен [c.85]
Электрический момент диполя определяется как произведение любого из его зарядов q па расстояние между нх центрами тяжести I [c.55]
Под действием внешнего электрического поля молекула поляризуется, т. е. в ней происходит перераспределение зарядов, и молекула приобретает новое значение электрического момента диполя. При этом неполярные молекулы могут превратиться в полярные, а полярные становятся еще более полярными. Иначе говоря, под действием внешнего электрического поля в молекулах индуцируется
ДИПОЛЬ ЭЛЕКТРИЧЕСКИЙ • Большая российская энциклопедия
-

-

-

В книжной версии
Том 9. Москва, 2007, стр. 46
-

Скопировать библиографическую ссылку:
Авторы: В. И. Денисов

Электрическое поле диполя.
ДИПО́ЛЬ ЭЛЕКТРИ́ЧЕСКИЙ, в простейшем случае система из двух равных по величине и противоположных по знаку точечных электрич. зарядов, находящихся на некотором расстоянии $l$ друг от друга. Осн. характеристикой Д. э. является дипольный момент $p$ – вектор, направленный от отрицательного заряда $–q$ к положительному $+q$ и численно равный произведению $ql$. В случае произвольной системы точечных зарядов дипольный момент получается суммированием по всем зарядам произведений заряда на его радиус-вектор. Если система электронейтральна, т. е. её суммарный электрич. заряд равен нулю, то дипольный момент не зависит от того, в какой точке пространства помещено начало отсчёта системы координат. В этом случае отличие дипольного момента от нуля указывает на то, что заряды в системе распределены несферически-симметрично: есть области пространства с преобладанием отрицат. зарядов и области пространства с преобладанием положит. зарядов. Когда система зарядов не электронейтральна, электрич. дипольный момент зависит от выбора начала отсчёта системы координат и уже не служит показателем меры отклонения распределения зарядов от сферически-симметричного. В этом случае существует точка пространства, поместив в которую начало отсчёта системы координат, можно обратить в нуль электрич. дипольный момент, это т. н. центр заряда.
Поле Д. э. на расстояниях, бо́льших по сравнению с линейными размерами занятой зарядами области, с ростом расстояния $R$ убывает обратно пропорционально $R^3$. В специально выбранных координатах компоненты напряжённости поля $\mathbf\it{E}$ вдоль оси Д. э. $(E_p)$ и в перпендикулярном направлении $(E_⊥)$ (рис.) пропорциональны $p$ и в гауссовой системе единиц равны: $$E_p=\frac{p}{R^3}(3cos^2\vartheta-1),$$ $$E_⊥=\frac{p}{R^3}(3cos\vartheta{sin\vartheta})$$где ϑ – угол между $p$ и радиус-вектором $R$.
Во внешнем электрич. поле на Д. э. действует вращательный момент сил, стремящийся повернуть вектор дипольного момента вдоль вектора внешнего поля. Если внешнее поле неоднородно, т. е. его напряжённость различна в разных точках системы зарядов, то на диполь действует ещё и сила, стремящаяся переместить его в область более сильного поля. Действие внешнего электрич. поля на диполь также пропорционально $p$. Многие молекулы имеют отличный от нуля электрич. дипольный момент. Именно в результате взаимодействия дипольных моментов молекул вещества и образуются молекулярные кристаллы.
Во многих случаях Д. э. является хорошим приближением для описания любой электронейтральной в целом системы на расстояниях, значительно превышающих размеры системы. Напр., полярные молекулы можно приближённо рассматривать как Д. э. Атомы, неполярные молекулы и ионы в электрич. поле приобретают дипольный момент, т. к. составляющие их частицы несколько смещаются под действием внешнего поля.
Д. э. с изменяющимся во времени дипольным моментом излучает электромагнитные волны (см. Дипольное излучение).


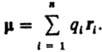 В молекулах и мол. системах центры положит. зарядов q А совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом случае Д. м.
В молекулах и мол. системах центры положит. зарядов q А совпадают с положениями атомных ядер (радиусы-векторы rA), а электронное распределение описывается плотностью вероятности r(r). В этом случае Д. м. 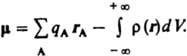 Вектор Д. м. направлен от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе Д. м. молекулы иногда приписывают противоположное направление. Часто вводят представление о Д. м. отдельных хим. связей, векторная сумма к-рых дает Д. м. молекулы. При этом Д. м. связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда. Д. м. хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий Д. м. существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный Д. м. молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО 2 и CCl4). Если же Д. м. молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н 2 О полярна; суммирование Д. м. двух полярных связей ОН также дает отличный от нуля Д. м., направленный по биссектрисе валентного угла НОН. Порядок величины Д. м. молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим.
связи (порядка 10—10 м), т. е. составляет 10—29 Кл. м. В справочной литературе Д. м. молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл. м. Спектроскопич. методы определения Д. м. молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие Д. м. со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины Д. м. (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора Д. м. Важно, что точность определения Д. м. почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых Д. м. ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, Д. м. пропана равен 0,085 b0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов. Направление вектора Д. м. молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка. Др. группа методов определения Д. м. основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены Д. м. молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине Д. м. основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний Д. м. единицы объема) складывается из наведенной, или индуцированной, поляризации Р м и ориентационной поляризации Р ор и связана с m ур-нием Ланжевена — Дебая:
Вектор Д. м. направлен от центра тяжести отрицат. зарядов к центру тяжести положительных. В хим. литературе Д. м. молекулы иногда приписывают противоположное направление. Часто вводят представление о Д. м. отдельных хим. связей, векторная сумма к-рых дает Д. м. молекулы. При этом Д. м. связи определяют двумя положит. зарядами ядер атомов, образующих связь, и распределением отрицат. (электронного) заряда. Д. м. хим. связи обусловлен смещением электронного облака в сторону одного из атомов. Связь наз. полярной, если соответствующий Д. м. существенно отличается от нуля. Возможны случаи, когда отдельные связи в молекуле полярны, а суммарный Д. м. молекулы равен нулю; такие молекулы наз. неполярными (напр., молекулы СО 2 и CCl4). Если же Д. м. молекулы отличен от нуля, молекула наз. полярной. Напр., молекула Н 2 О полярна; суммирование Д. м. двух полярных связей ОН также дает отличный от нуля Д. м., направленный по биссектрисе валентного угла НОН. Порядок величины Д. м. молекулы определяется произведением заряда электрона (1,6.10—19 Кл) на длину хим.
связи (порядка 10—10 м), т. е. составляет 10—29 Кл. м. В справочной литературе Д. м. молекул приводят в дебаях (Д или D), по имени П. Дебая; 1 Д = 3,33564.10—30 Кл. м. Спектроскопич. методы определения Д. м. молекул основаны на эффектах расщепления и сдвига спектральных линий в электрич. поле (эффект Штарка). Для линейных молекул и молекул типа симметричного волчка известны точные выражения, связывающие Д. м. со штарковским расщеплением линий вращательных спектров. Этот метод дает наиб. точные значения величины Д. м. (до 10—4 Д), причем экспериментально определяется не только величина, но и направление вектора Д. м. Важно, что точность определения Д. м. почти не зависит от его абс. величины. Это позволило получить весьма точные значения очень малых Д. м. ряда молекул углеводородов, к-рые нельзя надежно определить др. методами. Так, Д. м. пропана равен 0,085 b0,001 Д, пропилена 0,364 b 0,002 Д, пропина 0,780 b 0,001 Д, толуола 0,375 b 0,01 Д, азулена 0,796 b 0,01 Д. Область применения метода микроволновой спектроскопии ограничена, однако, небольшими молекулами, не содержащими атомов тяжелых элементов. Направление вектора Д. м. молекулы м. б. определено экспериментально и по Зеемана эффекту второго порядка. Др. группа методов определения Д. м. основана на измерениях диэлектрич. проницаемости е в-ва. Этими методами измерены Д. м. молекул более 10 тыс. в-в. Переход от измеряемого значения e газа, чистой жидкости или разбавл. р-ра, т. е. макроскопич. характеристики диэлектрика, к величине Д. м. основан на теории поляризации диэлектриков. Считается, что при наложении электрич. поля на диэлектрик его полная поляризация Р (средний Д. м. единицы объема) складывается из наведенной, или индуцированной, поляризации Р м и ориентационной поляризации Р ор и связана с m ур-нием Ланжевена — Дебая: 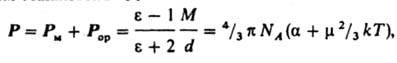
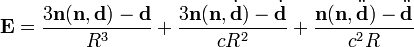
![\mathbf{B} = \left[\frac{\dot \mathbf{d}}{c R^2} + \frac{\ddot \mathbf{d}}{R c^2} , \mathbf{n} \right] =
\left[\mathbf{n} , \mathbf{E} + \frac{\mathbf{d}}{R^3}\right]](/800/600/https/dic.academic.ru/pictures/wiki/files/54/635b5333913a247b016e637bf3d14265.png) ,
,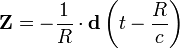

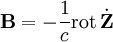

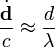
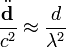
![\mathbf{B} = \frac{1}{c^2 R}[\ddot \mathbf{d},\mathbf{n}], ~~ \mathbf{B} = [\mathbf{n} , \mathbf{E}]](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2f581493f584683037b692d09b2a8928.png)
![\mathbf{E} = \frac{1}{c^2 R}\left[ [\ddot \mathbf{d},\mathbf{n}] , \mathbf{n} \right], ~~ \mathbf{E} = [\mathbf{B} , \mathbf{n}]](/800/600/https/dic.academic.ru/pictures/wiki/files/101/ee8c127945423b770e8bdd993be8375a.png)
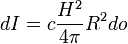 ,
,![dI = \frac{1}{4 \pi c^3}[\ddot \mathbf{d}, \mathbf{n}]^2 do
= \frac{\ddot d^2}{4\pi c^3}\sin^2{\theta} do](/800/600/https/dic.academic.ru/pictures/wiki/files/102/fd5e5428406be3ca2ace3836f800718a.png)