1. Векторы. Действия над векторами.

Вектором наз. упорядоченная совокупность чисел Х={X₁,X₂,…X_n} вектор дан в n-мерном пространстве. Т(X₁,X₂,X₃). n=1,2,3. Геометрический вектор — направленный отрезок. |AB|=|a| — длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.

1.умножение на число: произведение вектора А на число наз. такой вектор В, который обладает след. св-ми: а) А||В. б) >0, то АВ, <0, то АВ. в)>1, то А<В, )<1, то А>В. 2. Разделить вектор на число n значит умножить его на число, обратное n:

а/n=a*(1/n).

3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.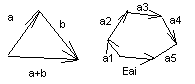

2.3. Декартова прямоугольная система координат. Базис.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.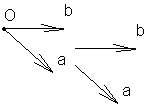

Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.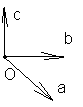

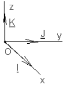
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе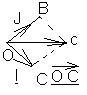

4. Действия над векторами.

а=х₁i+y₁j+z₁k; b=х₂i+y₂j+z₂k

*a=(х₁i+y₁j+z₁k)= (х₁)i+ (y₁)j+(z1)k

ab=(x₁x₂)i+(y₁y₂)j+(z₁z₂)k

ab=x₁x₂ii+y₁x₂ij+x₂z₁ki+x₁y₂

ij+y₁y₂jj+ z₁y₂kj+x₁z₁ik+y₁z₂jk+z₁z₂kk=x₁x₂+y₁y₂+z₁z₂

ii=1; ij=0; и т.д.

скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.

аа=x²+y²+z²=|a|² a{x,y,z}, aa=|a|*|a|, то a²=|a|²

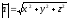
ab=|a|*|b|*cos

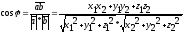
а)ав=0,<=>ав, x₁x₂+y₁y₂+z₁z₂=0

б)а||в — коллинеарны, если , x₁/x₂=y₁/y₂=z₁/z₂

5. Скалярное произведение векторов и его свойства.

-(“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а,в)- скалярное произведение.

а*в=|а|*|в|*cos, =/2, cos/2=0, ab=>ab=0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).

6. Векторное произведение 2х векторов.

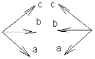
левая —— правая

Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки — левая. Векторным произведением 2х векторов а и в наз. такой вектор с

, который удовлетворяет условиям: 1. |c|=|a|*|b|*sin. 2. ca и cb. 3. тройка а,в,с-правая.

7. Смешанное произведение векторов и его свойства.

Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где

a={a_x,a_y,a_z}

b={b_x,b_y,b_z}

c={c_x,c_y,c_z}

Св-ва:1. При перестановке 2х сомножителей:

a*b*

c=-b*c*a

2. не меняется при перестановке циклических сомножителей:

a*b*c=c*a*b=b*c*a

3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0

б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах

если a*b*c>0, то тройка a,b,c — правая

если a*b*c<0, то тройка a,b,c — левая

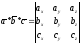
Нормальный вектор прямой, координаты нормального вектора прямой

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами.  Для начала ознакомимся с понятием вектора прямой.

Определение 1

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1.  Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·

Направляющий вектор прямой, координаты направляющего вектора прямой

С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.

В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.

Что такое направляющий вектор прямой

Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.

Сформулируем, что такое направляющий вектор.

Определение 1

Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a→ является направляющий вектором прямой a, то другой направляющий вектор мы можем обозначить как t·a→ при любом значении t, соответствующем действительному числу.

Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a1 являются параллельными, то вектор a→ будет направляющим и для a, и для a

Вектор в системе координат — урок. Геометрия, 9 класс.

Вспомним, что при умножении вектора на число k≠0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k>0, или противоположно направлены, если k<0. Длины векторов различаются \(k\) раз.

Справедливо и обратное суждение.

Если ненулевые векторы коллинеарны, то обязательно можно найти число k≠0 так, что b→=k⋅a→.

Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c→=k⋅a→+m⋅b→. Говорят, что вектор c→ разложен по векторам a→ и b→, а числа \(k\) и \(m\) называют коэффициентами разложения.

Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.

Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i→ и j→.

 

 

Если от начала координат отложить вектор a→, то его можно разложить по векторам i→ и j→ следующим образом: a→=3⋅i→&plus;2⋅j→.

В этом разложении коэффициенты координатных векторов называют координатами вектора a→.

Это записывают как a→3;2.

 

Любой вектор, который равен с вектором a→, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.

Равные векторы имеют равные координаты.

Но в то же время в координатной системе можно переместить векторы i→ и j→, таким образом определить координаты векторов независимо от их места расположения в координатной системе.

 

Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.

 

Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.

У противоположных векторов противоположные координаты.

Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.

 

Вектор – Уикипедия

В математиката и физиката вектори се наричат елементите на линейните пространства. Най-често те се отъждествяват с координатните си представяния като наредени n{\displaystyle n}-орки от съответното числово поле. Така евклидовите пространства  R2{\displaystyle \ \mathbb {R} ^{2}} и  R3{\displaystyle \ \mathbb {R} ^{3}} се отъждествяват със съответно евклидовите равнина — (x,y){\displaystyle (x,y)}, и пространство — (x,y,z){\displaystyle (x,y,z)}, където x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z} са реални числа.

В математиката, физиката и инженерството, евклидов вектор (понякога наричан геометричен или пространствен вектор) или просто вектор е геометричен обект, който има величина (или дължина) и посока и може да бъде добавен към други вектори, съгласно с векторната алгебра. В евклидовата геометрия векторът често се представя от част от линия с определена посока.

В аналитичната геометрия се използват следните определения за вектор в равнината и пространството. — Отсечка, на която единият край е избран за първи (начало), а другият за втори (край) наричаме насочена отсечка (свързан вектор). Множеството от всички насочени отсечки, равни на дадена насочена отсечка AB→{\displaystyle {\overrightarrow {AB}}} наричаме вектор (свободен вектор), породен от насочената отсечка AB→{\displaystyle {\overrightarrow {AB}}}. Всяка от тези насочени отсечки AB→=a→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {a}}} наричаме представител на вектора a→{\displaystyle {\overrightarrow {a}}}.

Във всяка точка всеки вектор има точно един представител. Посока и дължина на вектор наричаме посоката и дължината на кой да е негов представител. Нулев вектор 0→{\displaystyle {\overrightarrow {0}}} – има за представител коя да е нулева насочена отсечка, т.е. той няма посока и има дължина 0. За краткост, ако a→=AB→{\displaystyle {\overrightarrow {a}}={\overrightarrow {AB}}} или AB→=a→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {a}}} разбираме, че е даден вектор с представител насочената отсечка AB→{\displaystyle {\overrightarrow {AB}}}, т.е. AB→∈a→{\displaystyle {\overrightarrow {AB}}\in {\overrightarrow {a}}}

• Нулева насочена отсечка – началната точка А съвпада с крайната точка В
• Ненулева насочена отсечка – началната точка А не съвпада с крайната точка В
• Дължина – на насочената отсечка AB→{\displaystyle {\overrightarrow {AB}}} наричаме дължината на отсечката АВ, т.е разстоянието

от А до В.

• начало – точка А
• край – точка В
• посока – посоката на лъча AB→{\displaystyle {\overrightarrow {AB}}}
• директриса – правата АВ
• дължина – дължината на АВ

Еднопосочни и противопосочни вектори[редактиране | редактиране на кода]

Свойства на ненулевите вектори[редактиране | редактиране на кода]

Насочена права[редактиране | редактиране на кода]

Ос (насочена права) х наричаме права, на която едната от двете ѝ посоки е избрана за положителна, а другата – за отрицателна.

Алгебрична мярка[редактиране | редактиране на кода]

Алгебрична мярка (относителна стойност) АВ^— на ненулевата насочена отсечка АВ^→ върху ос наричаме дължина на вектор, взета със знак плюс (+) или минус(-) в зависимост от това дали посоката ѝ съвпада с положителната или отрицателната посока на оста, т.е алгебричната мярка е реално число, като AB→=+∣AB→∣{\displaystyle {\overrightarrow {AB}}=+\mid {\overrightarrow {AB}}\mid } или AB→=−∣AB→∣{\displaystyle {\overrightarrow {AB}}=-\mid {\overrightarrow {AB}}\mid }

множеството от всички насочени отсечки, равни на дадена насочена отсечка АВ^→

Видове вектори[редактиране | редактиране на кода]

• Векторът −a→{\displaystyle -{\overrightarrow {a}}} с представител BA→{\displaystyle {\overrightarrow {BA}}} наричаме противоположен на вектора a→{\displaystyle {\overrightarrow {a}}} с представител AB→{\displaystyle {\overrightarrow {AB}}}.
• Колинеарни са група вектори, които лежат на една права или на успоредни прави.
• Компланарни са група вектори, които лежат в една равнина или в успоредни равнини. Всяка двойка вектори е компланарна.

Действия с вектори в равнината[редактиране | редактиране на кода]

Равенство[редактиране | редактиране на кода]

a→=b→⇔∣a→∣=∣b→∣⇔a→⇈b→{\displaystyle {\overrightarrow {a}}={\overrightarrow {b}}\Leftrightarrow \mid {\overrightarrow {a}}\mid =\mid {\overrightarrow {b}}\mid \Leftrightarrow {\overrightarrow {a}}\upuparrows {\overrightarrow {b}}}

Сума[редактиране | редактиране на кода]

• Правило на триъгълника:

AB→+BC→=AC→{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {BC}}={\overrightarrow {AC}}}

• Правило на успоредника:

AB→+AD→=AC→{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {AD}}={\overrightarrow {AC}}}

• Правило на многоъгълника:

AB→+BC→+CD→+DE→+EF→=AF→{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {BC}}+{\overrightarrow {CD}}+{\overrightarrow {DE}}+{\overrightarrow {EF}}={\overrightarrow {AF}}}

a→+b→=b→+a→{\displaystyle {\overrightarrow {a}}+{\overrightarrow {b}}={\overrightarrow {b}}+{\overrightarrow {a}}}

(a→+b→)+c→=a→+(b→+c→){\displaystyle ({\overrightarrow {a}}+{\overrightarrow {b}})+{\overrightarrow {c}}={\overrightarrow {a}}+({\overrightarrow {b}}+{\overrightarrow {c}})}

a→+0→=a→{\displaystyle {\overrightarrow {a}}+{\overrightarrow {0}}={\overrightarrow {a}}}

0→+(−a→)=−a→{\displaystyle {\overrightarrow {0}}+(-{\overrightarrow {a}})=-{\overrightarrow {a}}}

a→+(−a→)=a→−a→=0→{\displaystyle {\overrightarrow {a}}+(-{\overrightarrow {a}})={\overrightarrow {a}}-{\overrightarrow {a}}={\overrightarrow {0}}}

Разлика[редактиране | редактиране на кода]

• От правилото на триъгълника и правилото на успоредника следва:

a→−b→=a→+(−b→){\displaystyle {\overrightarrow {a}}-{\overrightarrow {b}}={\overrightarrow {a}}+(-{\overrightarrow {b}})}

Произведение[редактиране | редактиране на кода]

Произведение с реално число[редактиране | редактиране на кода]

Произведение на вектор a→≠0→{\displaystyle {\overrightarrow {a}}\neq {\overrightarrow {0}}} с число λ ∈ R наричаме вектора λa→{\displaystyle \lambda {\overrightarrow {a}}} с дължината ∣λa→∣=∣λ∣∗∣a→∣{\displaystyle \mid \lambda {\overrightarrow {a}}\mid =\mid \lambda \mid *\mid {\overrightarrow {a}}\mid } и с посока:

λa→⇈a→{\displaystyle \lambda {\overrightarrow {a}}\upuparrows {\overrightarrow {a}}}, ако λ>0 и

λa→↑↓a→{\displaystyle \lambda {\overrightarrow {a}}\uparrow \downarrow {\overrightarrow {a}}}, ако λ<0

Ако λ=0{\displaystyle \lambda =0} или a→=0→{\displaystyle {\overrightarrow {a}}={\overrightarrow {0}}}, то λ∗a→=0→{\displaystyle \lambda *{\overrightarrow {a}}={\overrightarrow {0}}}.

Свойства на произведението[редактиране | редактиране на кода]

λ∗(μa→)=(λμ)∗a→{\displaystyle \lambda *(\mu {\overrightarrow {a}})=(\lambda \mu )*{\overrightarrow {a}}}

(λ+μ)∗a→=λa→+μa→{\displaystyle (\lambda +\mu )*{\overrightarrow {a}}=\lambda {\overrightarrow {a}}+\mu {\overrightarrow {a}}}

λ∗(a→+b→)=λa→+λb→{\displaystyle \lambda *({\overrightarrow {a}}+{\overrightarrow {b}})=\lambda {\overrightarrow {a}}+\lambda {\overrightarrow {b}}}

Вектори в пространството[редактиране | редактиране на кода]

Векторна база в пространството[редактиране | редактиране на кода]

Определение[редактиране | редактиране на кода]

Нека a→, b→, {\displaystyle {\overrightarrow {a}}{,~}{\overrightarrow {b}}{,~}} и c→{\displaystyle {\overrightarrow {c}}} са ненулеви вектори в пространството и точка О е произволна точка. Нека OA→=a→, OB→=b→, OC→=c→.{\displaystyle {\overrightarrow {OA}}={\overrightarrow {a}}{,~}{\overrightarrow {OB}}={\overrightarrow {b}}{,~}{\overrightarrow {OC}}={\overrightarrow {c}}{.}}

Векторите a→, b→, c→.{\displaystyle {\overrightarrow {a}}{,~}{\overrightarrow {b}}{,~}{\overrightarrow {c}}{.}} се наричат компланарни, ако точките О, А, В и С лежат в една или в успоредни равнини.

Ако лежат в различни равнини, те се наричат некомпланарни. Прието е нулевият вектор да е компланарен с произволна двойка вектори.

Тройка некомпланарни вектори в пространството се наричат векторна база в пространството.

Теореми[редактиране | редактиране на кода]

Ако векторите a→, b→, c→{\displaystyle {\overrightarrow {a}}{,~}{\overrightarrow {b}}{,~}{\overrightarrow {c}}} образуват база {a→; b→; c→}{\displaystyle \{{\overrightarrow {a}}{;~}{\overrightarrow {b}}{;~}{\overrightarrow {c}}\}} в пространството, то за всеки вектор съществува единствено базисно представяне в тази база.

Следствие: Ако {a→; b→; c→}{\displaystyle \{{\overrightarrow {a}}{;~}{\overrightarrow {b}}{;~}{\overrightarrow {c}}\}} е векторна база в пространството, то равенство от вида αa→+βb→+γc→=ma→+nb→+pc→{\displaystyle \alpha {\overrightarrow {a}}+\beta {\overrightarrow {b}}+\gamma {\overrightarrow {c}}={m}{\overrightarrow {a}}+{n}{\overrightarrow {b}}+{p}{\overrightarrow {c}}} е възможно тогава и само тогава, когато α=m, β=n, γ=p{\displaystyle \alpha ={m}{,~}\beta ={n}{,~}\gamma ={p}}

Скаларно произведение на вектори в пространството[редактиране | редактиране на кода]

Скаларно произведение на два ненулеви вектора a→, b→{\displaystyle {\overrightarrow {a}}{,~}{\overrightarrow {b}}} е числото ∣a→∣∗∣b→∣∗cos⁡∠(a→;b→) ,{\displaystyle \mid {\overrightarrow {a}}\mid *\mid {\overrightarrow {b}}\mid *\cos {\angle {({\overrightarrow {a}}{;}{\overrightarrow {b}})}}{~,}}

където cos⁡∠(a→;b→){\displaystyle \cos {\angle {({\overrightarrow {a}}{;}{\overrightarrow {b}})}}} е косинусът на ъгъла между двата вектора, a ∣a→∣{\displaystyle \mid {\overrightarrow {a}}\mid } и ∣b→∣{\displaystyle \mid {\overrightarrow {b}}\mid } са дължините на векторите. Ъгълът може да приема стойности в интервала [0o;180o]{\displaystyle \left[{0^{o};180^{o}}\right]}.