Трение покоя: определение, формула расчета, пример

Каждый из нас знаком с проявлением силы трения. Действительно, любое движение в повседневной жизни, будь то ходьба человека или перемещение транспортного средства, невозможно без участия этой силы. В физике принято изучать три вида сил трения. В данной статье рассмотрим один из них, разберемся, что собой представляет трение покоя.

Брусок на горизонтальной поверхности

Прежде чем переходить к ответам на вопросы, что такое сила трения покоя и чему равна она, рассмотрим простой случай с бруском, который лежит на горизонтальной поверхности.

Проанализируем, какие силы действуют на брусок. Во-первых, это вес самого предмета. Обозначим его буквой P. Он направлен вертикально вниз. Во-вторых, это реакция опоры N. Она направлена вертикально вверх. Второй закон Ньютона для рассматриваемого случая запишется в таком виде:

m*a = P — N.

Знак минус здесь отражает противоположные направления векторов веса и реакции опоры. Поскольку брусок покоится, то величина a равна нулю. Последнее означает, что:

P — N = 0 =>

P = N.

Реакция опоры уравновешивает вес тела и равна ему по абсолютной величине.

Действующая внешняя сила на брусок на горизонтальной поверхности

Теперь к описанной выше ситуации добавим еще одну действующую силу. Предположим, что человек начал толкать брусок вдоль горизонтальной поверхности. Обозначим эту силу буквой F. Можно заметить удивительную ситуацию: если сила F невелика, то несмотря на ее действие, брусок продолжает покоиться на поверхности. Вес тела и реакция опоры направлены перпендикулярно поверхности, поэтому их горизонтальные проекции равны нулю. Иными словами, силы P и N не могут оказать никакого противодействия величине F. В таком случае, почему брусок остается в состоянии покоя и не движется?

Очевидно, что должна существовать сила, которая направлена против силы F. Этой силой является трение покоя. Она направлена против F вдоль горизонтальной поверхности. Действует она в области контакта нижней грани бруска и поверхности. Обозначим ее символом F_t. Закон Ньютона для горизонтальной проекции запишется в виде:

F = F_t.

Таким образом, модуль силы трения покоя всегда равен абсолютной величине внешних сил, действующих вдоль горизонтальной поверхности.

Начало движения бруска

Чтобы записать формулу трения покоя, продолжим начатый в предыдущих пунктах статьи эксперимент. Будем увеличивать абсолютное значение внешней силы F. Брусок какое-то время еще будет оставаться в покое, но наступит момент, когда он начнет двигаться. В этот момент сила трения покоя приобретет максимальное значение.

Чтобы найти это максимальное значение, возьмем еще один точно такой же брусок, как и первый, и положим его сверху. Площадь контакта бруска с поверхностью не изменилась, однако его вес увеличился вдвое. Экспериментально было установлено, что сила F отрыва бруска от поверхности также увеличилась вдвое. Этот факт позволил записать следующую формулу трения покоя:

F_t = µ_s*P.

То есть максимальная величина силы трения оказывается пропорциональной весу тела P, где в качестве коэффициента пропорциональности выступает параметр µ_s. Величина µ_s называется коэффициентом трения покоя.

Поскольку вес тела в проведенном эксперименте равен силе реакции опоры N, то формулу для F_t можно переписать так:

F_t = µ_s*N.

В отличие от предыдущего, это выражение можно использовать всегда, даже когда тело находится на наклонной плоскости. Модуль силы трения покоя прямо пропорционален силе реакции опоры, с которой поверхность действует на тело.

Физические причины возникновения силы Ft

Вопрос, почему появляется трение покоя, является сложным и требует рассмотрения контакта между телами на микроскопическом и атомарном уровне.

В общем случае можно назвать две физические причины возникновения силы F_t:

1. Механическое взаимодействие между пиками и впадинами.
2. Физико-химическое взаимодействие между атомами и молекулами тел.

Насколько бы гладкой ни была любая поверхность, она обладает неровностями и неоднородностями. Грубо эти неоднородности можно представить в виде микроскопических пиков и впадин. Когда пик одного тела попадает во впадину другого тела, то происходит механическое сцепление между этими телами. Огромное число микроскопических сцепок является одной из причин появления трения покоя.

Вторая причина заключается в физико-химическом взаимодействии между молекулами или атомами, из которых состоят тела. Известно, когда два нейтральных атома приближаются друг к другу, то между ними могут возникать некоторые электрохимические взаимодействия, например, диполь-дипольные или ван-дер-ваальсовые. В момент начала движения брусок вынужден преодолевать эти взаимодействия, чтобы оторваться от поверхности.

Особенности силы Ft

Выше уже было отмечено, чему равна сила трения покоя максимальная, а также указано ее направление действия. Здесь перечислим другие характеристики величины F_t.

Трение покоя не зависит от площади контакта. Она определяется исключительно реакцией опоры. Чем больше площадь контакта, тем меньше деформация микроскопических пиков и впадин, однако тем больше их количество. Этот интуитивный факт объясняет, почему максимальная величина F_t не изменится, если брусок перевернуть на грань с меньшей площадью.

Трение покоя и трение скольжения имеют одну и ту же природу, описываются одинаковыми формулами, однако вторая всегда меньше, чем первая. Трение скольжения появляется, когда брусок начинает движение по поверхности.

Сила F_t в большинстве случаев является неизвестной величиной. Формула, которая приведена выше для нее, соответствует максимальному значению F_t в момент начала движения бруска. Чтобы яснее понять названный факт, ниже приведен график зависимости силы F_t от внешнего воздействия F.

Видно, что с возрастанием F трение покоя растет линейно, достигает максимума, а затем уменьшается, когда тело начинает движение. Во время движения говорить о силе F_t уже нельзя, поскольку ее заменяет трение скольжения.

Наконец, последней важной особенностью силы F_t является то, что она не зависит от скорости перемещения (при относительных больших скоростях F_t уменьшается).

Коэффициент трения µs

Так как в формуле для модуля силы трения фигурирует величина µ_s, следует сказать о ней несколько слов.

Коэффициент трения µ_s является уникальной характеристикой двух поверхностей. Он не зависит от веса тела, его определяют экспериментально. Например, для пары дерево-дерево он изменяется от 0,25 до 0,5 в зависимости от типа дерева и качества обработки поверхности трущихся тел. Для смазанной воском деревянной поверхности на мокром снегу µ_s = 0,14, а для человеческих суставов этот коэффициент принимает весьма низкие значения (≈0,01).

Какое бы значение ни имел µ_s для рассматриваемой пары материалов, аналогичный коэффициент трения скольжения µ_k будет всегда меньше.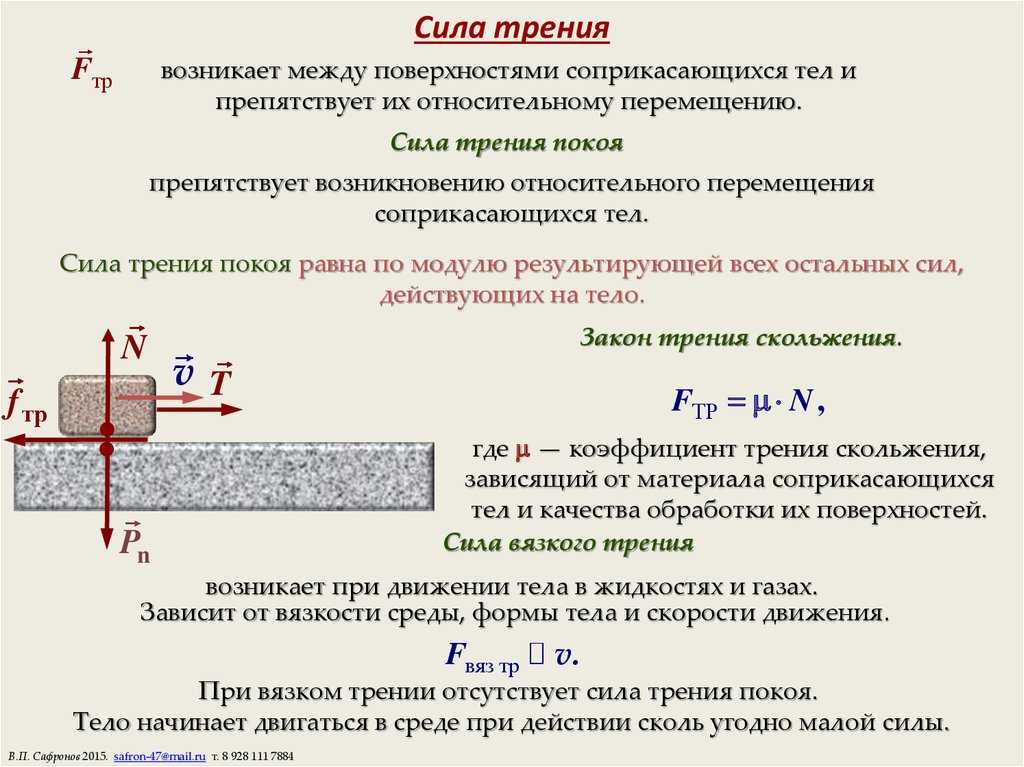 Например, при скольжении дерева по дереву он равен 0,2, а для суставов человека не превышает величины 0,003.

Далее рассмотрим решение двух физических задач, в которых применим полученные знания.

Брусок на наклонной поверхности: расчет силы Ft

Первая задача является достаточно простой. Предположим, что на деревянной поверхности лежит брусок из дерева. Его масса равна 1,5 кг. Поверхность наклонена под углом 15^o к горизонту. Необходимо определить силу трения покоя, если известно, что брусок не движется.

Подвох этой задачи заключается в том, что многие начинают вычислять реакцию опоры, а затем, используя справочные данные для коэффициента трения µ_s, пользуются приведенной выше формулой для определения максимального значения F_t. Однако в данном случае F_t не является максимальной. Ее модуль равен лишь внешней силе, которая стремится сдвинуть брусок с места вниз по плоскости. Эта сила равна:

F = m*g*sin(α).

Тогда сила трения F_t будет равна величине F. Подставляя данные в равенство, получаем ответ: сила трения покоя на наклонной плоскости F_t = 3,81 ньютона.

Брусок на наклонной поверхности: расчет максимального угла наклона

Теперь решим такую задачу: деревянный брусок находится на деревянной наклонной плоскости. Полагая коэффициент трения равным 0,4, необходимо найти максимальный угол наклона α плоскости к горизонту, при котором брусок начнет скользить.

Скольжение начнется, когда проекция веса тела на плоскость станет равной максимальной силе трения покоя. Запишем соответствующее условие:

F = F_t =>

m*g*sin(α) = µ_s*m*g*cos(α) =>

tg(α) = µ_s =>

α = arctg(µ_s).

Подставляя в последнее уравнение значение µ_s = 0,4, получаем α = 21,8^o.

формула движения, скорость и давление

Сила трения покоя

На тело, лежащее на наклонной плоскости действуют сила тяжести и сила нормальной реакции опоры.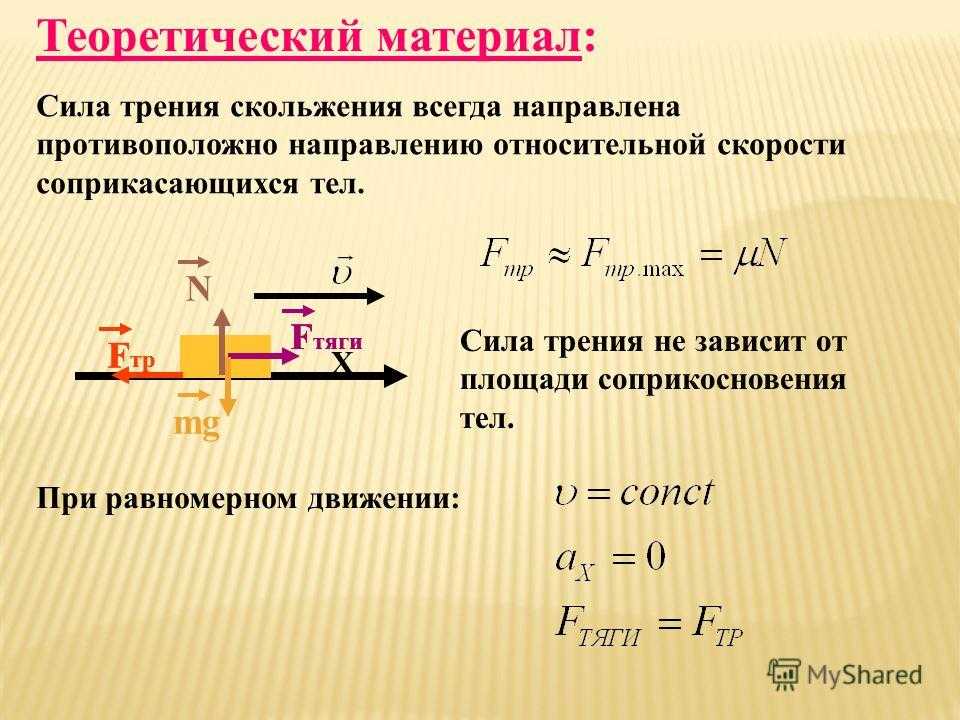 Но если бы на него действовали только две эти силы, то тело обязательно соскальзывало бы вниз. Существует сила, которая мешает лежащему на наклонной поверхности телу двигаться, ее называют силой трения.

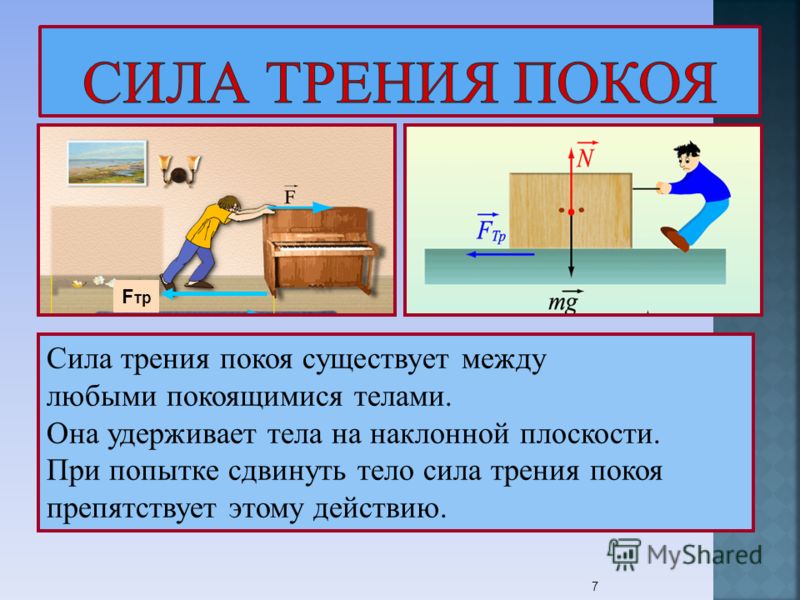
Когда тело находится в покое на наклонной плоскости, оно удерживается силой трения. Если тело, лежащее на горизонтальной поверхности, пытаться сдвинуть, то сила трения создаст сопротивление этому движению.

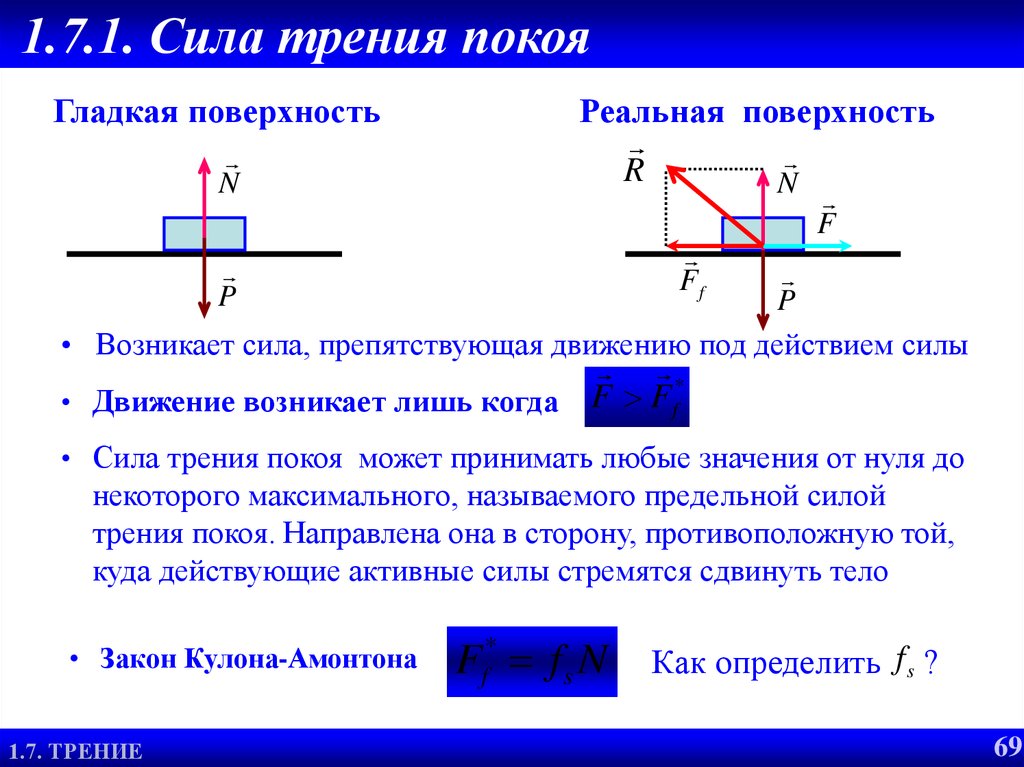
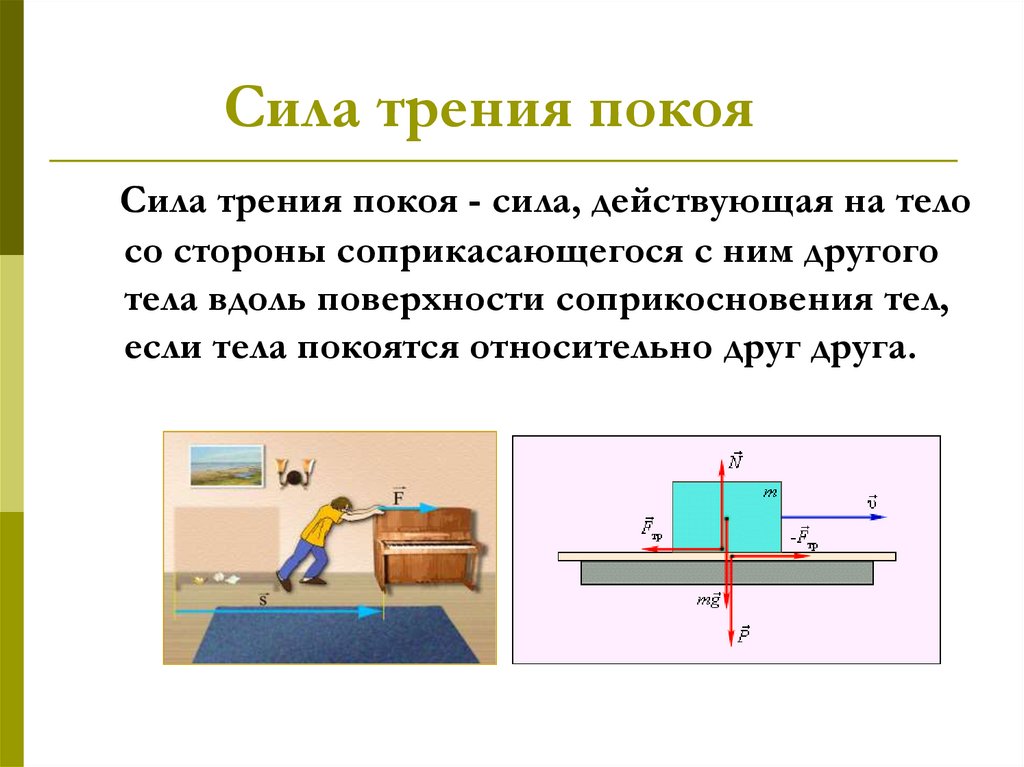
Определение 1

Сила трения покоя — сила, возникающая между двумя контактирующими телами и препятствующая относительному движению.

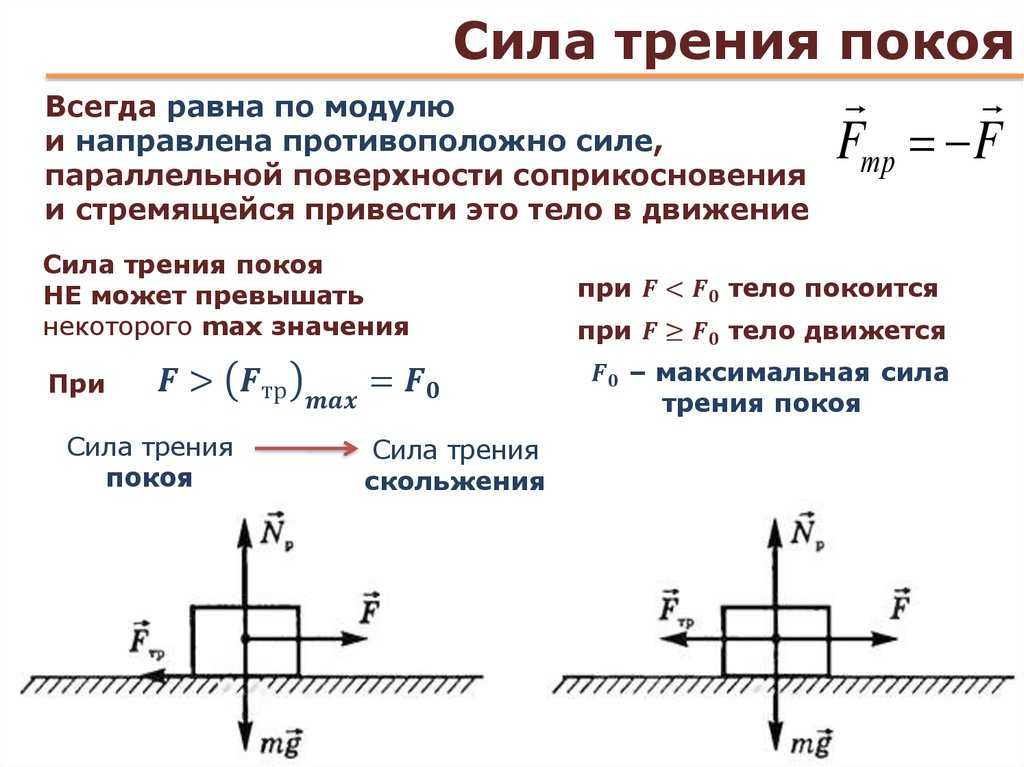
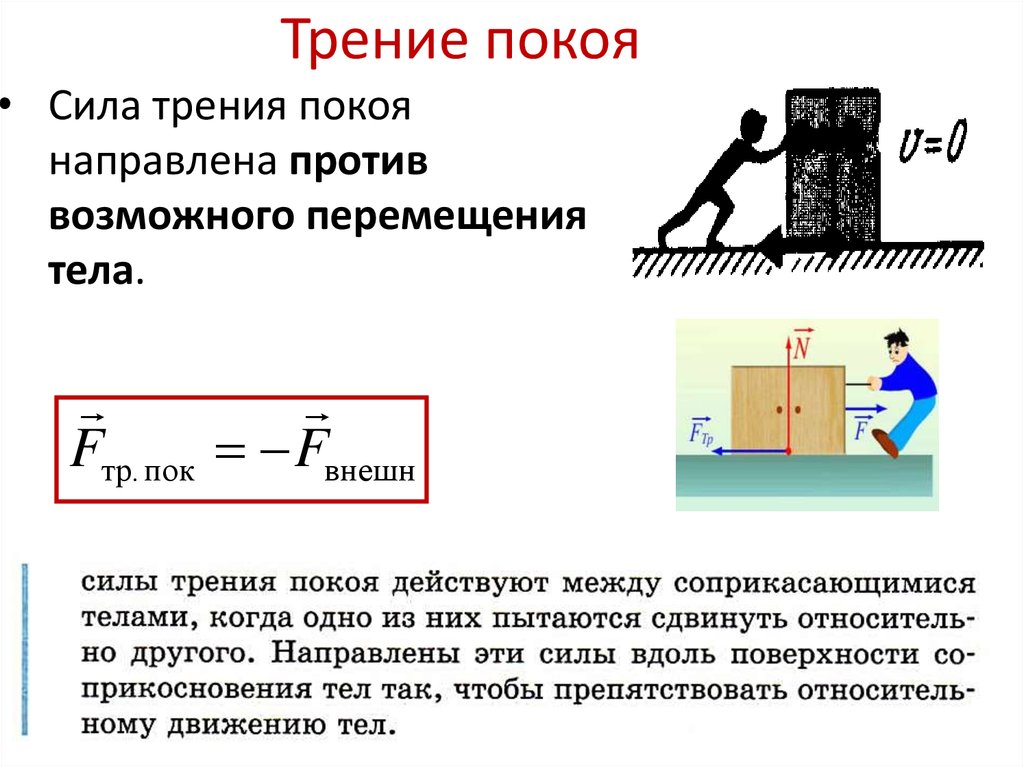
Сила трения покоя возникает при попытке вывести тело из состояния покоя, и приложена к этому телу. Направление силы трения покоя — против того движения, которое должно было бы возникнуть (вдоль поверхности соприкосновения).

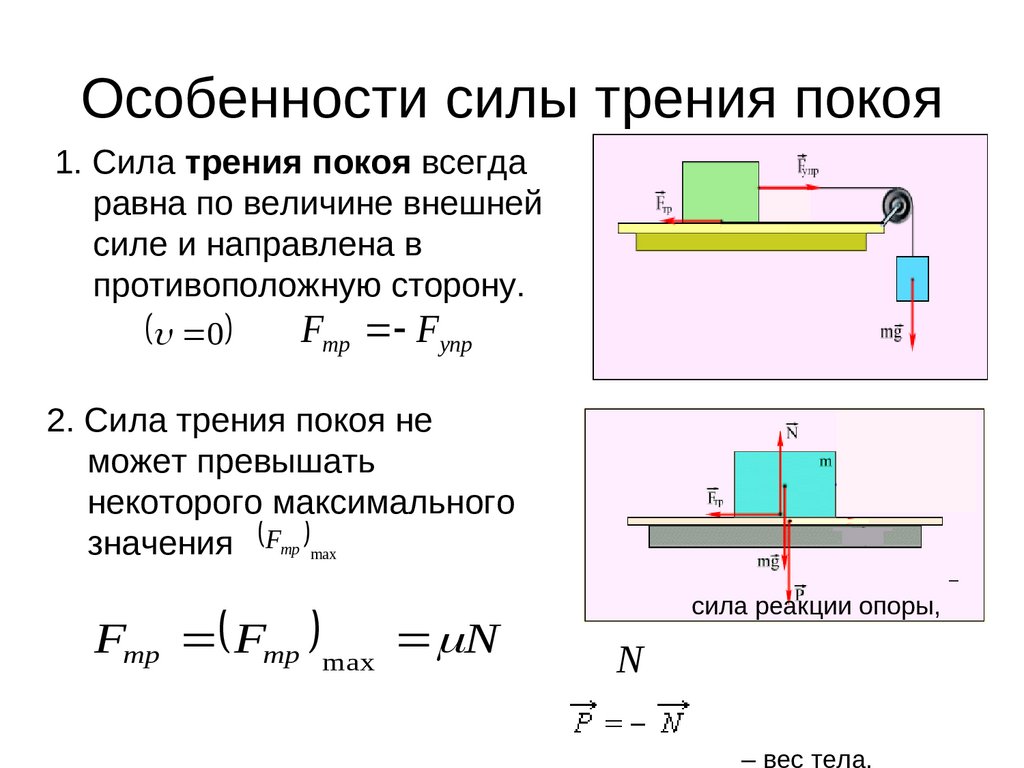
Сила трения покоя всегда по модулю равна приложенной внешней силе и увеличивается по мере увеличения этой силы.

Формула 1

Fтр=F

где Fтр — сила трения покоя,

F — приложенная внешняя сила.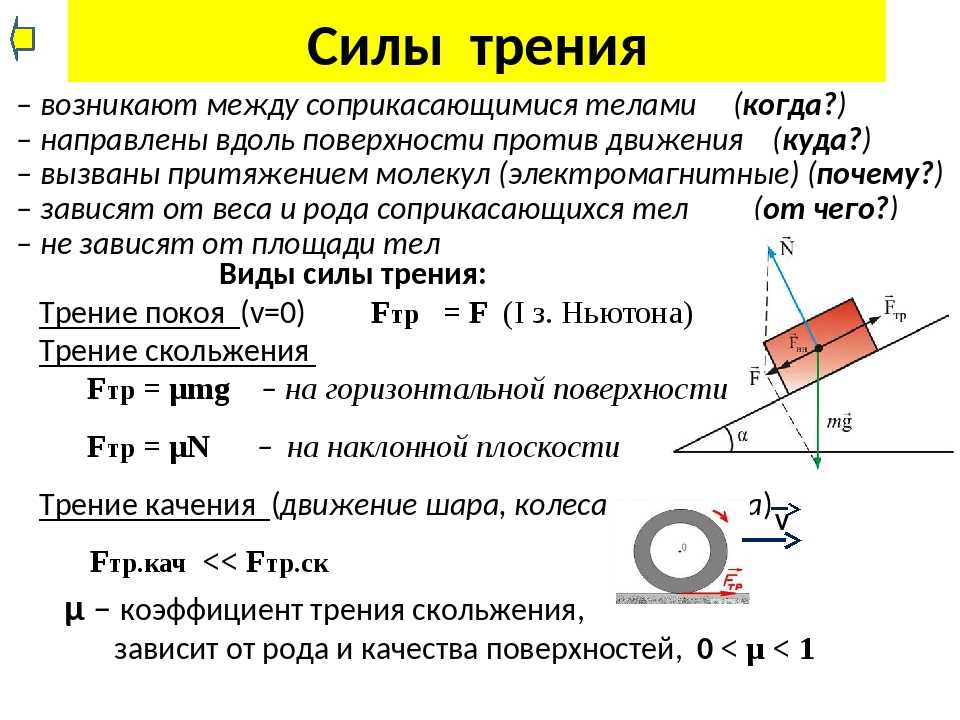

На рисунке ниже изображено направление и место приложения силы трения покоя.

Причины возникновения силы трения

Возникновение силы трения связано с двумя причинами.

1. Неровная поверхность соприкасающихся тел. Даже ровные на вид поверхности имеют шероховатости, которыми они цепляются друг за друга, что создает силу, препятствующую движению.
2. Если поверхности тел идеально гладкие и имеют минимум неровностей, то контакт между такими поверхностями очень тесный. При соприкосновении часть молекул располагается настолько близко друг от друга, что становится заметным притяжение между молекулами соприкасающихся тел.

Предельная сила трения покоя

Существует предельная или максимальная величина силы трения покоя, равная величине силы, необходимой, чтобы вывести тело из состояния покоя. Если приложить к телу силу меньше предельной силы трения покоя, то тело не сдвинется. Если приложить силу больше предельной силы трения покоя, то тело придет в движение.

Величина модуля максимальной силы трения покоя прямо пропорциональна модулю силы нормальной реакции опоры. Максимальная сила трения покоя зависит от массы покоящегося тела и характеристик соприкасающихся поверхностей, и не зависит от площади соприкосновения тел.

 

Fтр. макс=μN

где Fтр. макс — максимальная сила трения покоя,

N — сила нормальной реакции опоры (для покоящегося на горизонтальной поверхности тела равна силе тяжести, действующей на тело, или силе давления тела на плоскость, N=Р=mтелаg),

μ — коэффициент пропорциональности или коэффициент трения.

Коэффициент трения покоя μ характеризует две соприкасающиеся поверхности и зависит от материалов, из которых они изготовлены, и качества обработки поверхности. 0<μ<1.

Сила трения скольжения

Если на покоящееся на плоскости тело действует сила, большая чем предельная сила трения покоя, то тело начинает скользить по поверхности, и на него начинает действовать сила трения скольжения.

Определение 2

Сила трения скольжения — сила, возникающая между контактирующими телами, движущимися относительно друг друга.

При равномерном скольжении сила трения скольжения лишь немного меньше предельной силы трения покоя. Приближенно можно считать, что они равны. Также при равномерном прямолинейном скольжении по горизонтальной поверхности модуль силы трения скольжения равен модулю силы, своим действием вызывающей движение тела.

Fтр.ск=Fтр. макс

Формула 3

Fтр.ск=Fтяги

где Fтр.ск — сила трения скольжения,

Fтр. макс — предельная сила трения покоя,

Fтяги — сила, своим действием вызывающая движение тела.

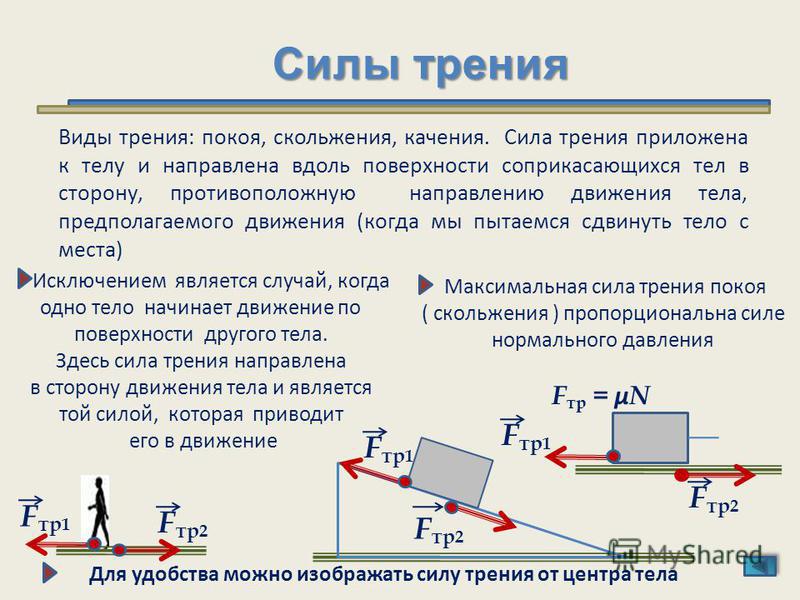
При скольжении на каждое из соприкасающихся тел действует своя сила трения. Сила трения скольжения параллельна плоскости соприкосновения тел и направлена противоположно скорости относительного движения тела.

Сила трения на наклонной плоскости

Для силы трения на наклонной плоскости также справедлива формула Fтр=μN.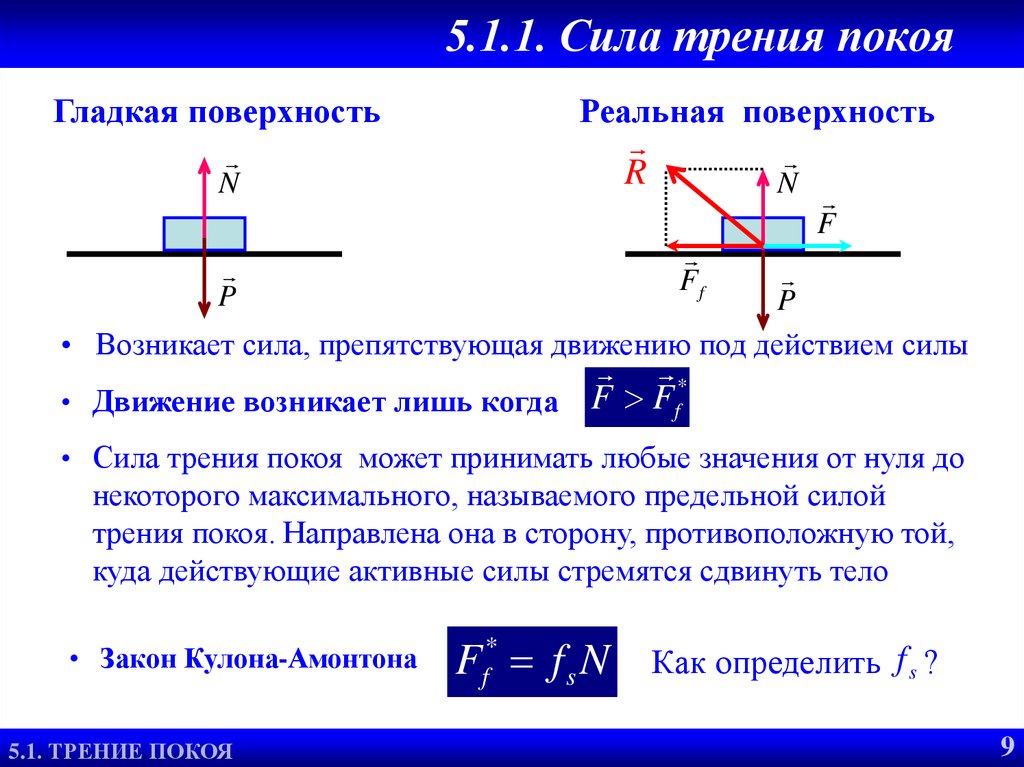

На тело, находящееся на наклонной плоскости или самопроизвольно скользящее по ней, действуют три силы: сила тяжести G, равная mg, нормальная сила реакции опоры N и сила трения Fтр. 

Уравнение движения тела, находящегося на наклонной плоскости

Формула 4

ma→=mg→+N→+Fтр→

Сложив силы mg→ и N→ получим равнодействующую силу F→, стремящуюся привести тело в движение и направленную вниз, вдоль наклонной плоскости, F→=mg→+N→. При этом F=mg·sinα, а N=mg·cosα, где α — угол наклона плоскости. Следовательно,

Формула 5

Fтр=μN=μmg·cosα

Уравнение движения принимает следующий вид:

Формула 6

ma=F-Fтр

Тогда силу трения можно найти по формуле:

Формула 7

Fтр=mg·sinα-ma.

Кроме того на тело может действовать Fвн — приложенная внешняя сила.

В этом случае F — равнодействующая силы тяжести, силы нормальной реакции опоры и приложенной силы F→=mg→+N→+Fвн→. Тогда

Формула 8

Fтр=mg·sinα+Fвн-ma, если направления движения и приложенной силы совпадают.

Формула 9

Fтр=mg·sinα-Fвн-ma, если направления движения и приложенной силы противоположны.

Сила трения на графике

На графике ось абсцисс — приложенная сила, ось ординат — сила трения. На первом этапе с увеличением приложенной силы растет сила трения покоя, в этот период тело еще не движется. Точка максимума — предельное значение силы трения покоя, за которой наступает скольжение.

Если и дальше увеличивать приложенную силу, то на тело будет действовать уже не сила трения покоя, а сила трения скольжения, при этом она будет иметь постоянное значение (горизонталь на графике).

Задачи на силы трения покоя и скольжения с решениями

Задача

Дано: деревянный брусок покоится на наклонной плоскости, расположенной под углом 20°, величина силы трения покоя — 0,68 Н.

Найти: величину силы тяжести, действующей на брусок.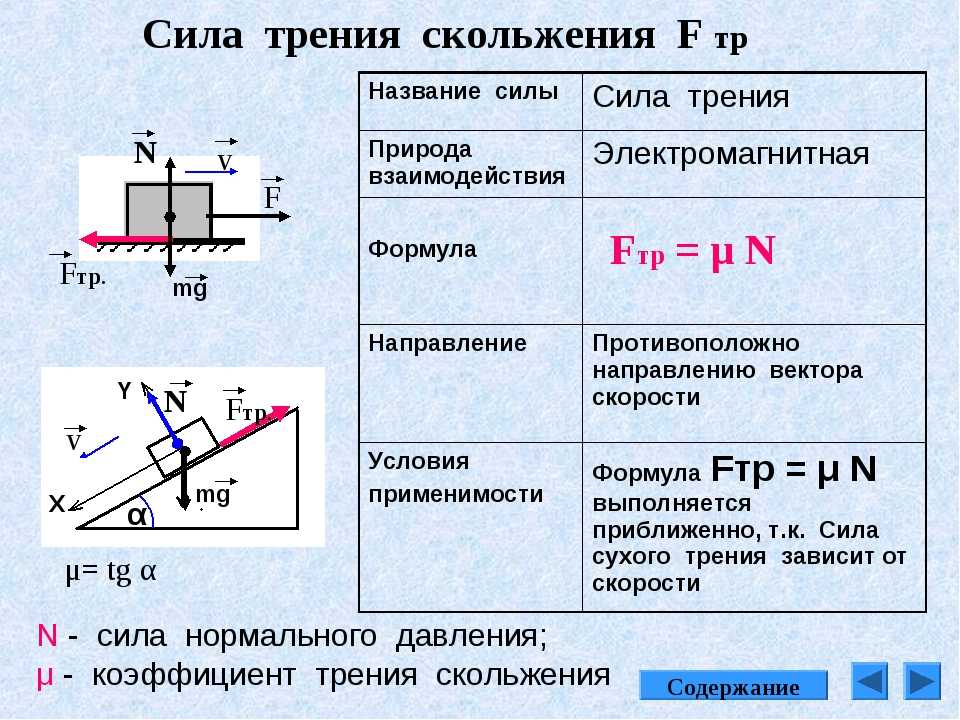

Решение:

Так как брусок покоится, сумма всех действующих на него сил равна нулю: mg·sinα-Fтр=0. Откуда mg=Fтрsinα.sin20°≈0,34.

mg=Fтрsin20°=0,68 Н0,34=2 Н.

Ответ: на брусок действует сила тяжести 2 Н.

Задача 2

Дано: брусок медленно и равномерно движется по горизонтальной поверхности и при этом давит на поверхность с силой, равной 30 Н, сила трения равна 6 Н.

Найти: коэффициент трения скольжения.

Решение:

Выразим коэффициент трения из формулы Fтр=μP и подставим известные величины:

μ=FтрР=6 Н30 Н=0,2.

Ответ: коэффициент трения скольжения равен 0,2.

Задача 3

Дано: на верстаке лежат металлическая четырехкилограммовая шайба и пластиковый предмет с весом 2 кг. Чтобы подвинуть шайбу, нужно приложить силу 20 Н. Коэффициент трения между предметом из пластика и верстаком в два раза меньше, чем коэффициент трения между шайбой и верстаком.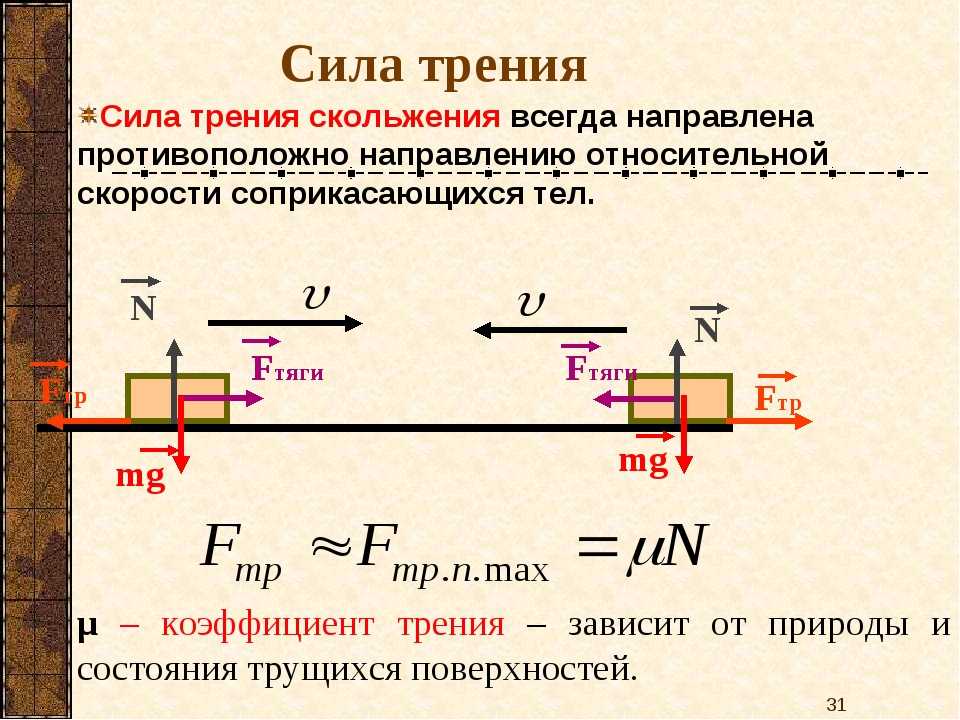

Найти: максимальные силы трения покоя для шайбы и пластикового предмета.

Решение:

1. Максимальная сила трения покоя для шайбы равна силе, которую нужно приложить, чтобы сдвинуть шайбу с места. Fmax1=20 Н.
2. Сила трения скольжения равна максимальной силе трения покоя, поэтому сила трения скольжения для шайбы Fскольж1=Fmax1=20 Н.
3. Из формулы Fтрения=μ·m·g выразим коэффициент μ. μ=Fтренияm·g.
4. Коэффициент трения для шайбы μ1=Fскольж1m1·g.
5. Коэффициент трения для пластикового предмета μ2=Fскольж2m2·g.
6. μ2=½μ1, следовательно, Fскольж2m2·g=Fскольж1m1·g·12.
7. 2Fскольж2m2·g=Fскольж1m1·g.
8. 2Fскольж2m2=Fскольж1m1.
9. 2Fскольж2=Fскольж1·m2m1.
10. Fскольж2=Fскольж1·m22m1=20 ·22·4=5(Н).

Ответ: максимальная сила трения покоя для шайбы 20 Н, для пластикового предмета — 5 Н.

Коэффициент статического трения Формула

Трение — это сила, противодействующая движению двух тел навстречу друг другу. Это контактная сила, когда два объекта соприкасаются, они испытывают трение.

Трение определяется как противодействие соприкасающихся поверхностей, когда они находились в относительном движении.

Существуют различные виды трения в зависимости от типа объектов, противодействующие движению скользящих объектов или противодействующие движению двух объектов, когда они находятся в относительном движении друг к другу. Виды трения как,

1. Статическое трение
2. Трение скольжения
3. Трение качения
4. Кинетическое трение
5. Жидкостное трение.

Статическое трение

Статическое трение, как следует из названия, означает статическое состояние в состоянии покоя, поэтому статическое трение действует на объекты, когда они находятся в состоянии покоя. Когда оба объекта находятся в состоянии покоя или один из объектов немного наклонен или наклонен, тогда трение, противодействующее движению объекта, известно как статическое трение.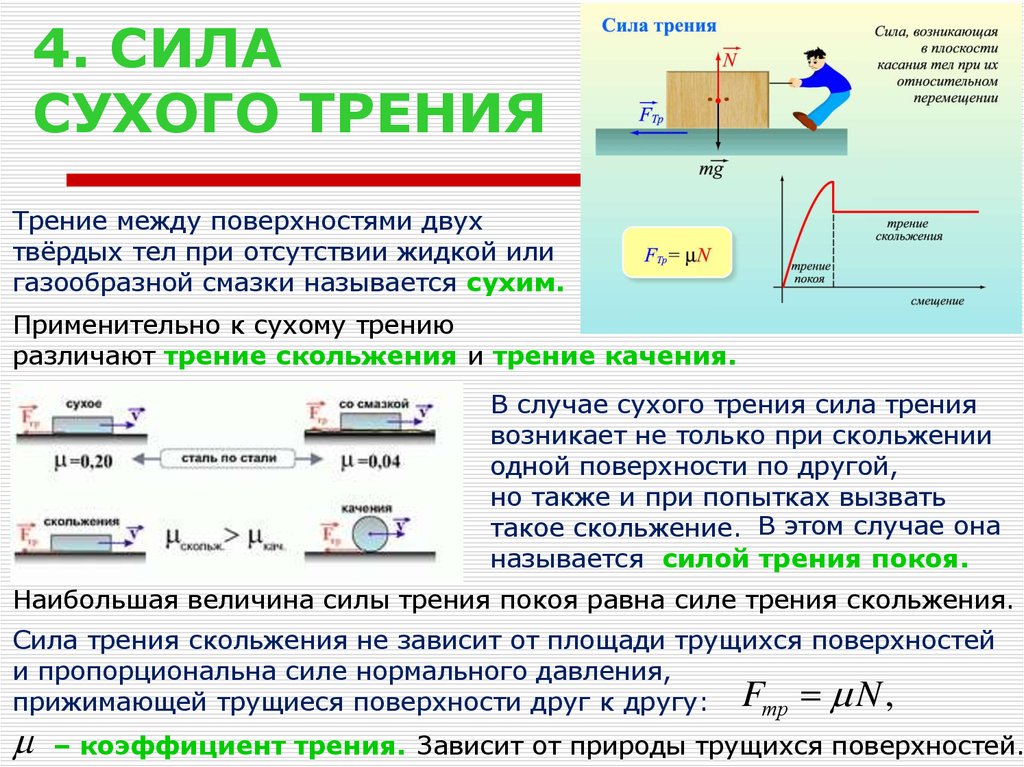

Формула коэффициента статического трения

Коэффициент статического трения можно рассчитать по формуле:-

мкс = F /N

Где

F = статическая сила трения

мкс = коэффициент статического трения

Н = нормальная сила

Примеры статического трения

• Автомобиль, припаркованный на склоне, статическое трение колес о дорогу удерживает автомобиль в его положении.
• Очки на носу — еще один распространенный пример статического трения.
• Носить часы, повесить рубашку на вешалку, кольцо в руке, ремни, удерживающие штаны, — вот некоторые распространенные жизненные примеры статического трения.
• Капля воды на оконном стекле.
• Черепица, которая прилипает к крыше из-за сильных сил цемента, здесь причина трения химическая.

Статическая сила трения

Законы статического трения

1. При статическом трении максимальная сила не зависит от площади контакта.
2. Нормальная сила сравнима с максимальной силой трения покоя, это означает, что если нормальная сила увеличивается, то увеличивается и максимальная внешняя сила, которой объект может обладать, не двигаясь.

Примеры задач

Вопрос 1: На коробку массой 10 кг, все еще стоящую на полу, действует сила 400 Н. Чему равно трение покоя, если коэффициент трения равен 0,3?

Решение:

Дано,

Сила F = 400 N,

Коэффициент трения, μ _S = 0,3

Статическое трение определяется F _S = μ _S F _N

= 0,3 × 4003

F ₄

= 0,3 × 4003

F ₄₄₉

= 0,3 × 4003

F _{4999000 = 0,3 × 4008}

F ₄

= 0,3 × 40085 _{. s} = 120 Н.

Вопрос 2: Сформулируйте законы статического трения.

Ответ:

1. При статическом трении максимальная сила не зависит от площади контакта.
2. Нормальная сила сравнима с максимальной силой трения покоя, это означает, что если нормальная сила увеличивается, то увеличивается и максимальная внешняя сила, которой объект может обладать, не двигаясь.

Вопрос 3: На ящик, стоящий на полу, действует сила 90 Н с коэффициентом трения покоя 0,4. Найдите силу трения.

Решение:

, дано

Применяемая сила или нормальная сила n = 90 N

Коэффициент трения = 0,4

Статическое трение может быть рассчитано как: F = μ _S × N.

F = 0,4 ×  90

= 36 Н

Вопрос 4: Коробка массой 40 кг, стоящая на полу, испытывает горизонтальную силу 60 Н, а ее коэффициент статического трения равен 0,2. Найдите силу трения. Сдвинется ли ящик со своего места.

Решение:

, дано,

Приложил сила = 60 N

Коэффициент трения = 0,2

Нормальная сила F _N = Mg = 40 × 10 = 400 N.

СТАТИЧЕСКАЯ ФРИКЦИЯ. рассчитывается как: F = μ _с × Н.

F = 0,2 ×  400 

= 80 Н

Мы можем видеть, что сила трения покоя, т.е. 80 Н, больше приложенной силы 60 Н, что означает, что коробка останется в его положение.

Вопрос 5: К стоящему на полу ящику приложена сила 50 Н с коэффициентом трения покоя 0,2. Найдите силу трения.

Решение:

, дано

Применяемая сила или нормальная сила n = 50 N

Коэффициент трения = 0,2

Статическое трение может быть рассчитано как: F = μ _S × N.

F = 0,2 ×  50

= 10 Н

Вопрос 6: На ящик массой 20 кг, стоящий на полу, действует горизонтально сила 30 Н с коэффициентом трения покоя 0,3. Найдите силу трения. Определить, будет коробка двигаться или нет?

Решение:

Дано,

Применить силу = 150 N

Коэффициент трения = 0,3

Нормальная сила F _N = Mg = 30 × 10 = 300 N.

СТАТИЧЕСКИЙ FRICTIE рассчитывается как: F = μ _с × Н.

F = 0,3 ×  300

= 90 Н

Мы видим, что статическая сила трения, т.е. 90 Н, больше, чем приложенная сила 30 Н, что означает, что коробка не будет двигаться от своего положения.

Вопрос 7: Ящик массой 20 кг стоит на гладкой поверхности. Статическое трение между этими двумя поверхностями равно 30 Н. Найдите коэффициент статического трения?

Решение:

Дано,

Масса ящика, m = 20 кг

Трение между ними, F = 30 Н

Коэффициент трения покоя μ

4 с ?

Мы знаем, что

Нормальная сила, Н = мг

Итак, N = 20 × 9,81 = 196,2 N (G = 9,81)

Для коэффициента статического трения,

μ _S = F/N

μ _S = 30/196,2

μ _S = 0,153

μ _S = 0,153 9000 3

000 и Armiasis и Armiasis и James и Armiasis и Armiasis и Armiasis и Armiasis и James и Armiasis и James и Armizise и Armiasise и Armiasis и Armiasis и Armiasis.

— Вопрос, связанный с максимальным статическим трением и минимальным $\mu_s$

Задавать вопрос

спросил 3 года, 3 месяца назад

Изменено 3 года, 3 месяца назад

Просмотрено 652 раза

$\begingroup$

Я думаю, что у меня есть правильные формулы для ответа на следующий вопрос, но есть что-то концептуальное, что сбивает меня с толку (см. конец вопроса).

Тело массой $m$ лежит на склоне с углом $\alpha$ (см. рисунок).

A. Какова должна быть величина трения между телом и наклонной плоскостью, если известно, что тело не движется поперек наклонной плоскости, когда наклонная плоскость движется с ускорением $a_0$ вправо?

B.

Создайте выражение для минимального размера $\mu_s$, чтобы это произошло.

Если $a_0$ «маленькое»:

$$ma_x=ma_0\cos\alpha-mg\sin\alpha+F_s=0$$

$$ma_y=N-mg\cos\alpha-ma_0\ sin\alpha=0$$

$$F_s=mg\sin\alpha-ma_0\cos\alpha$$

$$N = mg\cos\alpha + ma_0\sin\alpha$$

$$\mu_s = \frac {mg\sin\alpha-ma_0\cos\alpha}{mg\cos\alpha + ma_0\ sin\alpha}=\frac {g\sin\alpha-a_0\cos\alpha}{g\cos\alpha + a_0\sin\alpha}$$

Если $a_0$ «большой»:

$$ ma_x=ma_0\cos\alpha-mg\sin\alpha -F_s=0$$

$$ma_y=N-mg\cos\alpha-ma_0\sin\alpha=0$$

$$F_s=ma_0\ cos\alpha-mg\sin\alpha$$

$$N = mg\cos\alpha + ma_0\sin\alpha$$

$$\mu_s = \frac {ma_0\cos\alpha-mg\sin\ alpha}{mg\cos\alpha + ma_0\sin\alpha}=\frac {a_0\cos\alpha-g\sin\alpha}{g\cos\alpha + a_0\sin\alpha}$$

Вот вопросы:

1. Я полагаю, что $F_s$ в моем расчете по своей сути относится к максимальному трению статического электричества, но я не уверен в этом.

2. Я понятия не имею, что подразумевается под «минимальным размером» $\mu_s$. Я думал, что это зависит только от материалов, и поэтому всегда имеет одинаковую ценность. Как я должен интерпретировать слово «минимальный» здесь?

• домашние задания и упражнения
• ньютоновская механика
• силы
• трение

$\endgroup$

$\begingroup$

Я считаю, что $F_s$ в моем расчете по своей сути относится к максимальному трению покоя, но я не уверен в этом.

Нет, это не максимальное статическое трение, по крайней мере, пока вы не замените его на $N\mu_s$. Когда у вас просто есть ваши выражения в форме $F_s=\pm mg\sin\alpha\mp ma_0\cos\alpha$, это просто сила трения, необходимая для предотвращения движения объекта вверх или вниз по пандусу. На данный момент вы еще не вводили в свою работу какую-либо модель трения.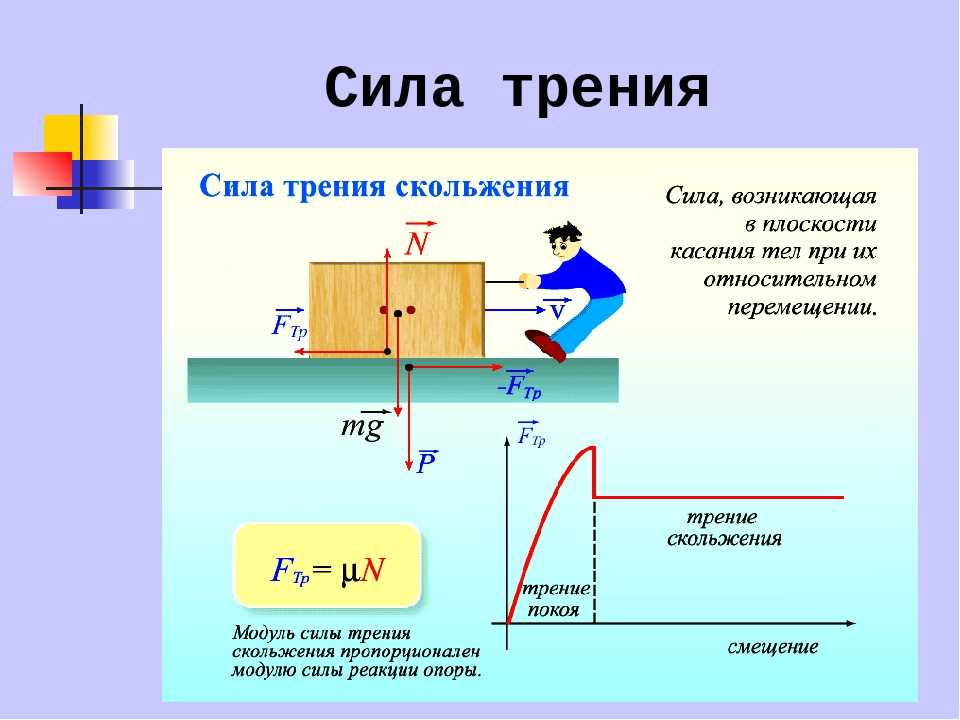

Нам все равно, что $F_s$ может представлять силу, с которой действительно липкий кусок резинки будет воздействовать на блок при заданном ускорении $a_0$. Другими словами, $\mu_s$ может быть бесконечным, и ваши уравнения будут выглядеть точно так же. Следовательно, эти уравнения для $F_s$ не говорят вам, какова максимальная сила трения покоя, по крайней мере сами по себе. Это приводит к вашему следующему вопросу.

Я понятия не имею, что подразумевается под «минимальным размером» $\mu_s$. Я думал, что это зависит только от материалов, и поэтому всегда имеет одинаковую ценность. Как я должен интерпретировать слово «минимальный» здесь?

Как только вы установите $F_s=N\mu_s$, вы предполагаете, что статическое трение максимально. Вы правы в том, что $\mu_s$ зависит только от двух поверхностей. Однако вам не говорят, что такое поверхности. Вопрос пытается заставить вас мыслить в следующих терминах: «Если я хочу ускорить систему с некоторым заданным ускорением $a_0$, то каким, по крайней мере, мне нужно, чтобы $\mu_s$ было?» Конечно, чем меньше $\mu_s$, тем меньший диапазон значений $a_0$ может принять система, прежде чем блок начнет двигаться.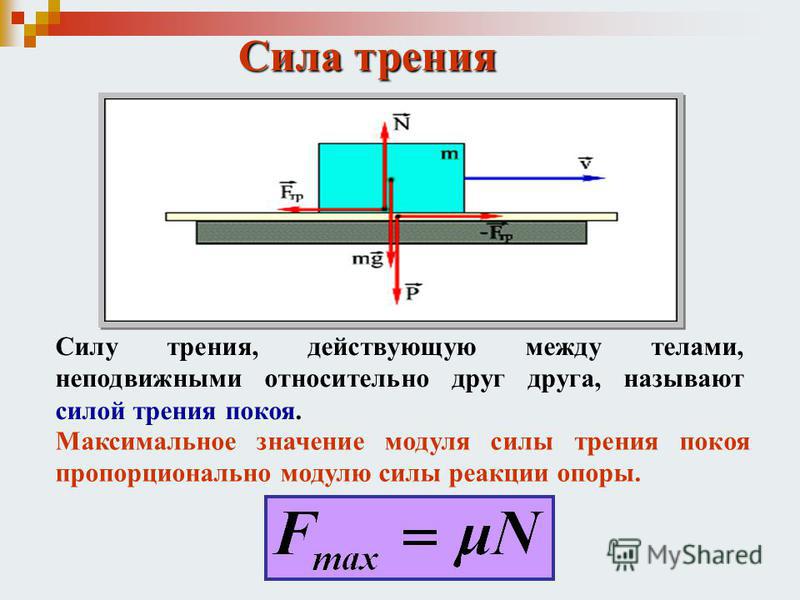

Например, пусть $\mu_s=0$. Тогда у нас нет статического трения, и у нас есть только одно возможное ускорение $a_0=g\tan\alpha$. По мере увеличения $\mu_s$ мы начинаем получать интервал допустимых ускорений, сосредоточенный вокруг этого $a_0=g\tan\alpha$ (каждая половина этого интервала представлена ​​вашими «маленькими» и «большими» случаями).

Таким образом, каждое из значений $\mu_s$, которое у вас есть для каждого случая, является минимальным значением $\mu_s$, которое вам необходимо, чтобы блок не двигался относительно наклона. Если мы опустим $\mu_s$ от этого значения для заданного $a_0$, то сила трения должна быть больше, чем $N\mu_s$, и блок будет двигаться относительно наклона.

Таким образом, подводя итог,

1. В ваших расчетах до реализации $F_s=N\mu_s$ ваши уравнения просто смотрят на то, какая сила $F_s$ требуется, чтобы блок не двигался относительно наклона. Что на самом деле представляет собой эта сила, не имеет значения и еще не вступило в игру. Как только вы предполагаете, что $F_s=N\mu_s$, вы теперь предполагаете, что $F_s$ представляет собой максимальную силу трения для заданного значения $\mu_s$
.
2. Выражения, которые вы получаете для $\mu_s$ в каждом случае, являются минимальным коэффициентом, необходимым для предотвращения проскальзывания при значении $a_0$. Это связано с тем, что если $F_s=N\mu_s$, а затем вы опустили $\mu_s$, сила, необходимая для удержания блока от смещения относительно наклона, должна быть больше, чем $N\mu_s$ сейчас. То, как $a_0$ относится к $g\tan\alpha$, говорит вам, какой случай применить, или вы можете просто обобщить все случаи, используя знаки абсолютного значения с тем, что вы уже разработали: $$\mu_s = \frac {\left|g\sin\alpha-a_0\cos\alpha\right|}{g\cos\alpha + a_0 \sin \alpha}$$

$\endgroup$

13

$\begingroup$

Идея максимального статического трения заключается в том, что трение никогда не превышает силу, которой оно противодействует.