| Взаимодействие зарядов. закон кулона

·  Атом меди содержит 29 электронов и та­кое же количество протонов. Электроны ато­мов меди расположены вокруг ядра на четырех оболочках. На первой находятся два электрона, на второй — восемь, на третьей — восемнадцать, на четвертой, наиболее удален­ной от ядра, — один электрон. Число электронов, расположенных на наиболее удаленной от ядра оболочке, совпадает с номером группы данного элемента в периодической системе Д. И. Менделе­ева, а общий отрицательный заряд электронов атома равен поло­жительному заряду протонов, содержащихся в ядре. Равные по величине положительные и отрицательные заряды по отношению к внешней среде электрически уравновешиваются — взаимно ней­трализуются. В результате этого атомы вещества в обычном состоя­нии электрически нейтральны.

· 

· 

· 

·  [1] Электронная оболочка – область, внутри которой движутся электроны.

·  §2. ВЗАИМОДЕЙСТВИЕ ЗАРЯДОВ. ЗАКОН КУЛОНА

·  Электрические заряды взаимодействуют между собой, т.

е. одноименные заряды взаимно отталкиваются, а разноименные при­тягиваются. Силы взаимодействия электрических зарядов определяются законом Кулона и направлены по прямой линии, соединяю­щей точки, в которых сосредоточены заряды.

·  Согласно закону Кулона, сила взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению количеств электричества в этих зарядах, обратно пропорциональна квадрату расстояния между ними и зависит от среды, в которой находятся заряды:

· 

·  где F — сила взаимодействия зарядов, н (ньютон[2]),

·  q1,  q2, — количество  электричества  каждого  заряда,

к (кулон[3]),

·  r — расстояние между зарядами, м,

·  a— абсолютная  диэлектрическая проницаемость  среды  (ма­териала) ; эта величина характеризует электрические свой­ства той среды, в которой находятся взаимодействующие заряды.

·   В Международной системе единиц (СИ)  a  измеряется в   (ф/м).  Абсолютная диэлектрическая проницаемость среды 

·   

·   где 0 — электрическая  постоянная,  равная  абсолютной  диэлек­трической проницаемости вакуума  (пустоты). Она равна 8,86•10-12 ф/м.

·   Величина , показывающая, во сколько раз в данной среде элек­трические  заряды  взаимодействуют  между собой слабее, чем в вакууме (табл. 1),  называется 

диэлектрической  проницаемостью.

·  Величина   есть отношение абсолютной диэлектрической прони­цаемости  данного  материала  к  диэлектрической  проницаемости вакуума:

·   

·  Для  вакуума  =1.  Диэлектрическая  проницаемость  воздуха практически равна единице.

·  На основании закона Кулона можно сделать вывод, что боль­шие электрические заряды взаимодействуют сильнее, чем малые. С увеличением расстояния между зарядами сила их взаимодей­ствия значительно слабее. Так, с увеличением расстояния между зарядами в 6 раз уменьшается сила их взаимодействия в 36 раз. При сокращении расстояния между зарядами в 9 раз увеличивает­ся сила их взаимодействия в 81 раз.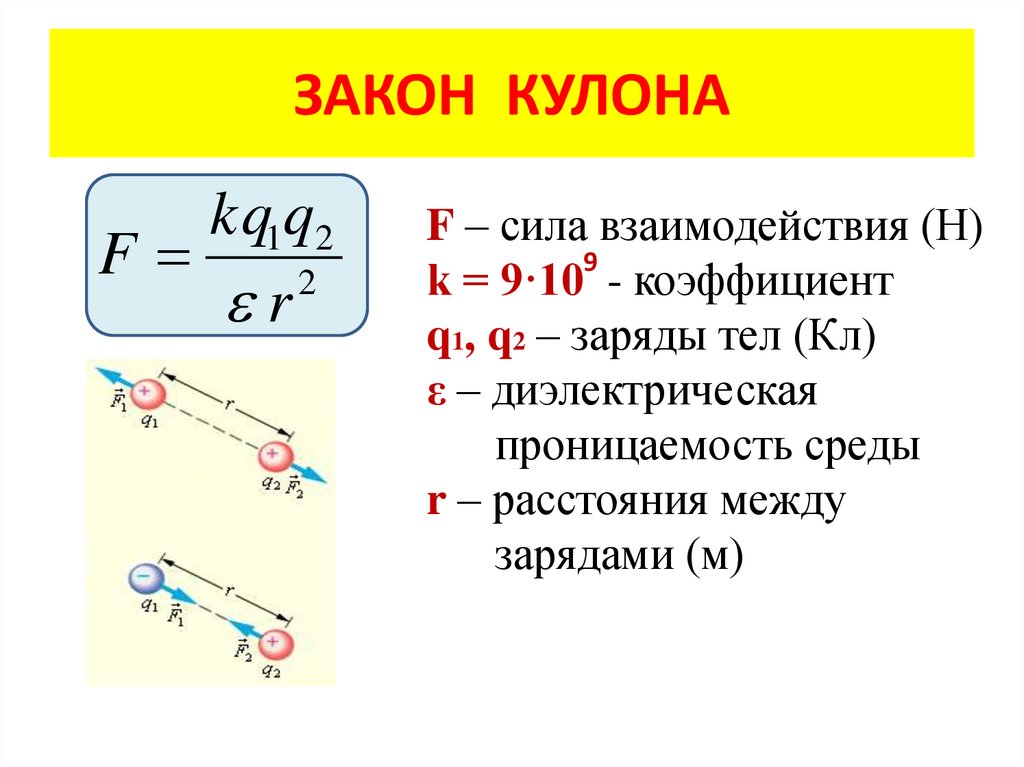

Взаимодействие зарядов также зависит от материала, находящегося между зарядами.

·  Пример. Между электрическими зарядами Q1=2 • 10-6  к и  Q2=4, • 10-6  к, расположенными на расстоянии 0,5 м, помещена слюда (=6). Вычислить силу взаимодействия указанных зарядов.

·  Решение.  Подставляя  в  формулу   значения  известных величин, получим:

· 

·  Если в вакууме электрические заряды взаимодействуют с силой Fв, то, поместив между этими зарядами, например, фарфор, их взаимодействие можно ослабить в 6,5 раз, т. е. в  раз. Это значит, что сила взаимодействия между зарядами может быть определена как отношение

· 

· 

·  Пример. Одноименные электрические заряды взаимодействуют в вакууме с силой Fв =0,25 н. С какой силой будут отталкиваться два заряда, если про­странство между ними заполнено бакелитом? Диэлектрическая проницаемость этого материала равна 5.

·  Решение. Сила взаимодействия электрических зарядов

· 

·  Так как один ньютон 102 г силы, то 0,05 н составляет 5,1 г.

· 

· 

·  [2] Один ньютон содержит  102 г силы

·  [3] Один кулон содержит  6,3• 1018 зарядов  электрона

·  § 3. ЭЛЕКТРИЗАЦИЯ ТЕЛ

· 

·  Известно, что электроны находятся на разном расстоянии от ядра атома. В связи с этим, согласно закону Кулона, взаимодей­ствие положительно заряженных протонов ядра с электронами, расположенными в слое, ближайшем к ядру, значительно сильнее взаимодействия протонов с электронами, находящимися в наиболее удаленном слое.

·  Если от атомов того или иного вещества «оторвать» один или несколько таких слабо связанных (свободных) с ядром электро­нов, то нарушится электрическое равновесие в атомах и вещество будет заряжено положительным электричеством.

·  Наоборот, если у атомов вещества количество электронов боль­ше количества протонов, то тело приобретает отрицательный заряд. Атом с отрицательным зарядом называют отрицательным  ионом.

·  Изменить количество электронов в атомах различных твердых материалов (наэлектризовать тела) можно, например, воздей­ствием световой энергии, нагреванием, использованием химиче­ских процессов, деформацией кристаллов.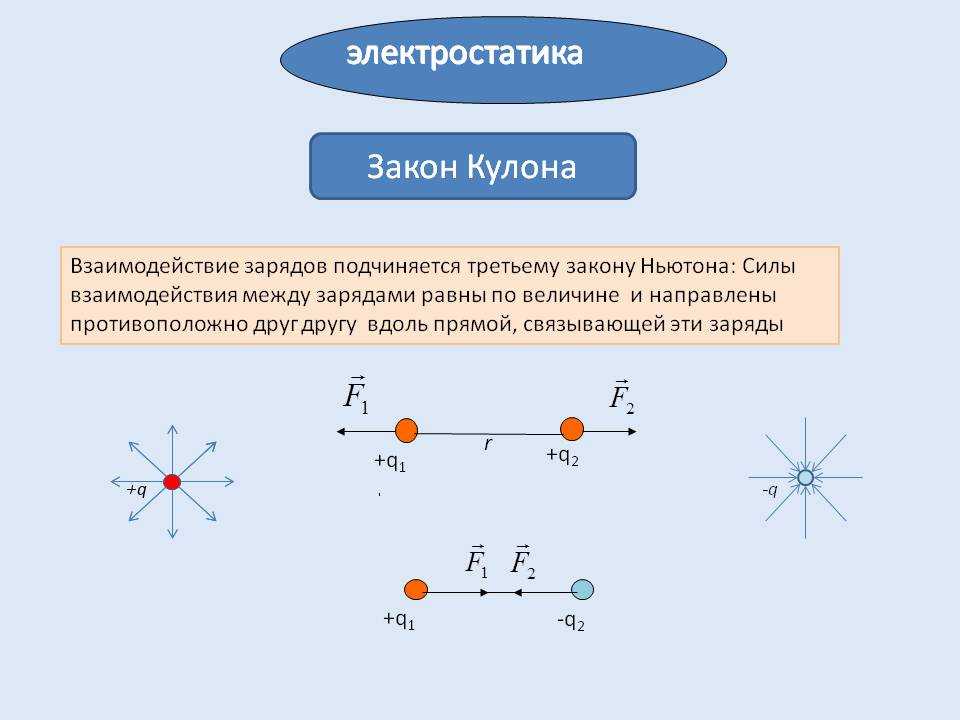

·  Электризация световой энергией. Профессор А. Г. Столетов в 1888 г. установил, что под действием света из таких материалов, как цинк, алюминий, цезий, натрий, свинец, калий и т. п., вылетают электроны и эти материалы заряжаются положительным электри­чеством. В этом можно убедиться на опыте.

·  На стержне электроскопа укрепим полированный диск из цин­ка. При отсутствии электрического заряда на цинке лепестки элек­троскопа будут опущены.

·  Если на диск направить световой поток (рис. 2, а), лепестки электроскопа оттолкнутся и разойдутся на некоторый угол. Это показывает, что диск электроскопа и листочки, прикрепленные к его стержню, зарядились одноименными электрическими заряда­ми. По углу отклонения листочков можно судить о величине заряда.

· 

·  Рис.2 Приборы, определяющие электризацию тел:

·  а — под действием светового потока, б – при нагревании нити.

·  в – под действием химической реакции, г – под давлением кристалла

·    Явление, при котором под воздействием света из материалов вырываются электроны, называется фотоэффектом.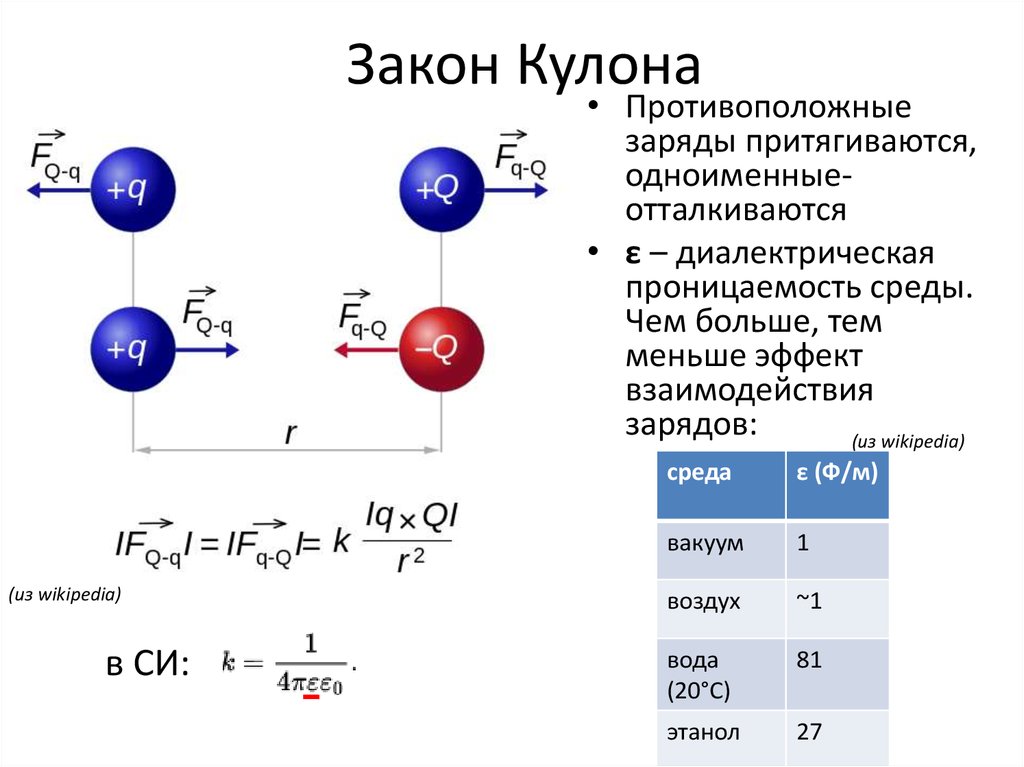 На использо­вании его основано действие фотоэлементов  (см. гл. XIV).

·   Электризация нагреванием. При сильном нагревании металлов электроны приобретают такую энергию, что вылетают за пределы нагретого металла. В результате этого металл «теряет» электроны и заряжается положительно.

·  Если к металлической пластинке

1, помещенной в вакууме (рис. 2, б), присоединить электроскоп и нагреть нить 2, то лепестки электроскопа, отталкиваясь друг от друга, разойдутся на некото­рый угол. Это объясняется тем, что из накаленной нити вылетают электроны. Через пластинку 1 они попадают на электроскоп и заряжают его.

3.1.2 Взаимодействие зарядов. Точечные заряды. Закон Кулона

Видеоурок 1: Закон Кулона — Физика в опытах и экспериментах

Видеоурок 2: Задача на закон Кулона

Лекция: Взаимодействие зарядов.

Точечные заряды. Закон Кулона

В школьном курсе физики рассматриваются неподвижные точечные заряды. В основе их изучения лежит закон Кулона. Если Вы хорошо изучили динамику, то увидите, что данный закон очень похож на Закон гравитационного взаимодействия.

Под точечными зарядами понимают заряды, которые имеют размеры, намного меньшие, чем расстояние между ними.

 

Данная модель введена по примеру материальной точки, позволяющая однозначно говорить о расстояниях между рассматриваемыми зарядами.

Закон Кулона

Сила, с которой взаимодействуют заряды, напрямую зависит от произведения модулей зарядов и обратно пропорциональна квадрату расстояния между ними. 

Данный закон справедлив только для статических зарядов, которые можно принять за точечные.

В данной формуле присутствует коэффициент пропорциональности k:

Данный закон описывает взаимодействие одноименных и разноименных зарядов. В случае, если заряды одноименно заряжены, то по данной формуле можно определить силу, с которой они отталкиваются. Если заряды разноименно заряжены, то таким образом можно определить силу их притяжения.

Закон Кулона в диэлектрической среде

Предыдущая формула описывала силу взаимодействия зарядов в вакууме. Если же заряженные тела находятся в некоторой среде, то имеются некоторые изменения. В знаменатель дроби добавляется диэлектрическая проницаемость среды, которая уменьшает взаимодействие в некоторое количество раз.

Диэлектрическая проницаемость среды — безразмерная величина. Определить её можно с помощью специальных таблиц.

2.2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)

1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д. И.Менделеева и особенностями строения их атомов

2.1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя

1.4.6 Смута. Социальные движения в России в начале XVII в. Борьба с Речью Посполитой и со Швецией

1.2.1 Возникновение государственности у восточных славян. Князья и дружина. Вечевые порядки. Принятие христианства

• Вконтакте
• Сайт

Учебник по физике: Новый взгляд на взаимодействие зарядов

Ранее в Уроке 1 обсуждалось взаимодействие между заряженными объектами с одинаковым и противоположным зарядом. В то время были установлены два фундаментальных взаимодействия зарядов: противоположно заряженные объекты притягиваются и одинаково заряженные объекты отталкиваются. Эти взаимные взаимодействия привели к возникновению электрической силы между двумя заряженными объектами. Эта сила обычно наблюдается в лабораторных занятиях по физике и на демонстрациях в классе. В Уроке 3 мы рассмотрим эти взаимодействия зарядов более подробно и начнем их количественную оценку. Мы введем закон электрической силы Кулона, который является математическим выражением этих взаимодействий зарядов. В конечном счете, мы объединим закон электрической силы Кулона с законами движения Ньютона, чтобы попытаться объяснить разнообразие взаимодействий зарядов, которые мы наблюдали во всем устройстве.

 

Взаимодействие зарядов — это силы

Возможно, вы видели, как два воздушных шара отталкиваются друг от друга дюжину или более раз, и никогда даже не думали о взаимодействии воздушных шаров как о силе. Или, возможно, вы использовали пластиковую трубку для гольфа или другой предмет, чтобы поднимать маленькие кусочки бумаги с лабораторного стола, и никогда не задумывались о законах движения Ньютона. Возможно, даже сейчас вы думаете: «Почему я должен? Это была единица Законов Ньютона, а это единица Статического Электричества». Истинный. Однако физический мир, который мы изучаем, не распадается на отдельные темы, как это делаем мы, учителя и ученики. Физика удивительным образом сочетается друг с другом. Информация, о которой вы забыли из блока законов Ньютона, имеет озорной способ подкрасться к вам в других блоках. Эта забывчивость (или небрежность, или простое невежество) будет преследовать вас, когда вы будете изучать новую физику. Чем больше физики вы изучаете (как в по-настоящему узнать ), тем больше вы начинаете осознавать, что кусочки физической головоломки складываются вместе, чтобы сформировать единую картину мира зрения, звука, осязания и ощущений. Здесь мы исследуем, как законы движения Ньютона согласуются с взаимодействием заряженных объектов.

Предположим, что вы держите заряженную пластиковую трубку для гольфа над горсткой обрывков бумаги, лежащих на столе. Присутствие заряженной трубки, вероятно, поляризует несколько кусочков бумаги, а затем начинает притягивать их вверх. Притяжение между заряженной трубкой и поляризованным (но нейтральным) куском бумаги представляет собой электрическую силу — F _{избрать} . Как и все силы, изучаемые на уроке физики, электрическая сила представляет собой толчок или притяжение, воздействующее на объект в результате взаимодействия с другим объектом. Взаимодействие является результатом электрических зарядов, поэтому его называют электрической силой.

В отличие от многих сил, которые мы изучаем, электрическая сила является бесконтактной силой — она ​​существует несмотря на то, что взаимодействующие объекты не находятся в физическом контакте друг с другом. Два объекта могут действовать на расстоянии разделения и оказывать влияние друг на друга. В этом случае пластиковая трубка для гольфа тянется вверх к бумажному биту, а бумажный бит тянет вниз к трубке для гольфа. В этом случае сила значительно мала. Если бы вы держали в руках трубку для гольфа, вы вряд ли почувствовали бы тягу вниз, оказываемую на нее кусочком бумаги. С другой стороны, сила часто достаточно велика, чтобы уравновесить или даже подавить нисходящее притяжение гравитации (F _grav ) на кусок бумаги и заставить его подняться или даже ускориться над столом. Конечно, фактический результат действия силы на кусок бумаги связан с законами Ньютона и анализом свободного тела. Если бы в какой-то момент электрическая сила превзошла по величине силу гравитации, бумажный кусочек устремился бы вверх. И если в какой-то момент электрическая сила сравняется по величине с силой гравитации, бумажка будет подвешена (или левитирована ) в воздухе. Можно сказать, что бит бумаги находится в равновесие .

Теперь рассмотрим случай с резиновыми шариками, подвешенными на световых нитях к потолку. Если каждый воздушный шар натереть одинаковым образом (шерстью животного), каждый из них станет отрицательно заряженным и будет оказывать друг на друга отталкивающее действие. Это взаимодействие зарядов приводит к тому, что на каждый воздушный шар действует сила, направленная от воздушного шара, с которым он взаимодействует. Еще раз, мы можем идентифицировать этот отталкивающий эффект как электрическую силу. Эта электрическая сила объединяет две другие силы, действующие на воздушный шар, — силу натяжения и силу тяжести.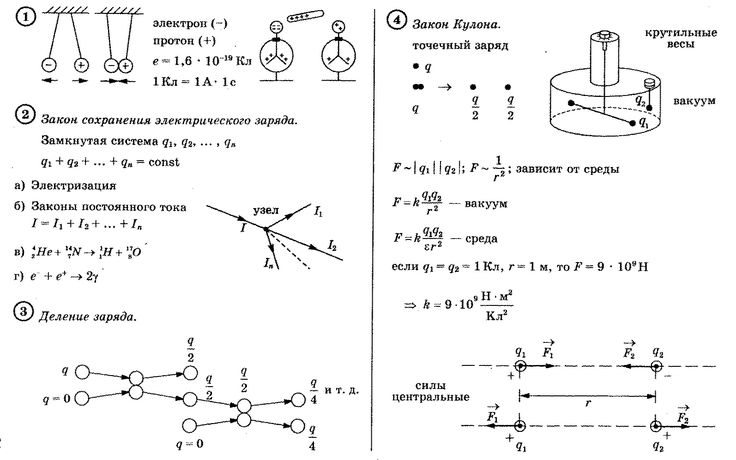 Поскольку воздушные шары покоятся, три силы должны уравновешивать друг друга так, чтобы результирующая сила была равна нулю. Более глубокий анализ компенсации этой силы требует обсуждения векторов и отложен до конца урока 3.

 

Оба этих примера иллюстрируют, как взаимодействие между двумя зарядами приводит к взаимной силе, действующей на заряженные объекты. Электрическое взаимодействие — это сила, которую, как и любую силу, можно проанализировать с помощью диаграммы свободного тела и законов Ньютона. Но какие факторы влияют на величину этой силы? Существует ли уравнение, которое можно использовать для ее количественной оценки так же, как это было сделано для силы тяжести (F _grav = m•g) и силы трения (F _трение = mu•F _норма )? Ответ: Да! Закон Кулона является ключом к пониманию ответа на эти вопросы. Это тема следующего раздела Урока 3.

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного Закона Кулона и/или нашего интерактивного взаимодействия «Поместите заряд в цель». Оба интерактива можно найти в разделе Physics Interactives на нашем веб-сайте. Эти интерактивы предоставляют средства интерактивного изучения действия на расстоянии в увлекательной среде.

Посетите:  Закон Кулона  | Поместите заряд в цель

Следующий раздел:

Перейти к следующему уроку:

Кулоновское взаимодействие — мягкая материя

Автор Yuhang Jin, AP225, осень 2011 г.

Содержание

• 1 Введение
• 2 Основные свойства и формулы кулоновского взаимодействия
• 3 Приложения кулоновского взаимодействия
• 4 Каталожные номера
• 5 Ключевое слово в ссылках:

Введение

Кулоновское взаимодействие представляет собой электростатическое взаимодействие между электрическими зарядами и подчиняется закону Кулона, который является основой классической электродинамики. В общем случае кулоновское взаимодействие может проявляться на различных масштабах от микроскопических частиц до макроскопических тел. Микроскопическая теория кулоновского взаимодействия была развита в рамках квантовой теории поля.

93\mathbf r_2.

Кулоновские силы консервативны, поэтому кулоновское взаимодействие можно описать с помощью кулоновского потенциала. Потенциал, создаваемый точечным зарядом $q\_1$, равен

$U=\backslash frac\{1\}\{4\backslash pi\backslash varepsilon\_0\}\backslash frac\{q\_1\}\{r\}$,

где $r$ — расстояние от заряда $q\_1$. Сила, испытываемая другим точечным зарядом $q\_2$ из-за $q\_1$, определяется выражением

$\backslash mathbf\; F\_\{21\}=-q\_2\backslash nabla\; U$.

Потенциал взаимодействия между двумя точечными зарядами определяется как

$U\_\{12\}=\backslash frac\{1\}\{4\backslash pi\backslash varepsilon\_0\}\backslash frac\{q\_1q\_2\}\{|\backslash mathbf\; r\_1-\backslash mathbf\; r\_2|\}$.

Аналогично потенциал кулоновского взаимодействия двух тел с непрерывным распределением заряда равен

$U\_\{12\}=\backslash int\backslash int\backslash frac\{1\}\{4\backslash pi\backslash varepsilon\_0\}\backslash frac\{\backslash rho(\backslash mathbf\; r\_1)\backslash rho(\backslash mathbf\; r\_2)\}\{|\backslash mathbf\; r\_1-\; \backslash mathbf\; r\_2|\}d^3\backslash mathbf\; r\_1d^3\backslash mathbf\; r\_2$,

Применение кулоновского взаимодействия

Почти все аспекты электротехники более или менее основаны на теории кулоновского взаимодействия.