Главные оси и главные моменты инерции
Оси, относительно
которых центробежный момент инерции
равен нулю, называют главными
осями (иногда
их называют главными
осями инерции). Через
любую точку, взятую в плоскости сечения,
можно провести в общем случае пару
главных осей (в некоторых частных случаях
их может быть бесчисленное множество).
Для того чтобы убедиться в справедливости
этого утверждения, рассмотрим, как
изменяется центробежный момент инерции
при повороте осей на 90′ (рис. б.7). Для
произвольной площадки dA, взятой в первом
квадранте системы осей хОу, обе координаты,
а следовательно, и их произведение
положительны. В новой системе координат
х,Оу„ повернутой относительно
первоначальной на 90′, произведение
координат рассматриваемой площадки
отрицательно. Абсолютное
значение этого
произведения не изменяется, т. е. ху= —
х1у,. Очевидно, то
же самое имеет место и для любой другой
элементарной площадки. Значит, и знак
суммы dAxy, представляющий собой центробежный
момент инерции сечения, при повороте
осей на 90′ меняется на противоположный,
т.
В процессе поворота осей центробежный момент инерции изменяется непрерывно, следовательно, при некотором положении осей он становится равным нулю. Эти оси и являются главными.
Хотя мы и установили, что главные оси можно провести через любую точку сечения, но практический интерес представляют только те из них, которые проходят через центр тяжести сечения — главные центральные оси. В дальнейшем, как правило, для краткости будем называть их просто главными осями, опуская слово «центральные».
В общем случае сечения произвольной формы для определения положения главных осей необходимо провести специальное исследование. Здесь ограничимся рассмотрением частных случаев сечений, имеющих по меньшей мере одну ось симметрии (рис. 6.8).
П
роведем
через. центр тяжести сечения ось Ох,
перпендикулярную оси симметрии Оу, и
определим центробежный момент инерции
J. Воспользуемся известным из курса
математики свойством определенного
интеграла (интеграл суммы равен сумме
интегралов) и представим J s виде двух
слагаемых:
Воспользуемся известным из курса
математики свойством определенного
интеграла (интеграл суммы равен сумме
интегралов) и представим J s виде двух
слагаемых:
так как, для любой элементарной площадки, расположенной справа от оси симметрии, есть соответствующая слева, для которой произведение координат отличается лишь знаком.
Таким образом, центробежный момент инерции относительно осей Ох и Оу оказался равным нулю, т. е. это главные оси. Итак, для нахождения главных осей симметричного сечения достаточно найти положение его центра тяжести. Одной из главных центральных осей является ось симметрии, вторая ось ей перпендикулярна. Конечно, приведенное доказательство остается в силе, если ось, перпендикулярная оси симметрии, проходит и не через центр тяжести сечения, т. е. ось симметрии и любая, ей перпендикулярная, образуют систему главных осей.

Осевые моменты инерции относительно главных центральных осей называют главными центральными (или сокращенно главными) моментами инерции. Относительно одной из главных осей момент инерции максимален, относительно другой — минимален. Например, для сечения, изображенного на рис. 6.8, максимальным является момент инерции J
(относительно оси Ox). Конечно, говоря об экстремальности главных моментов инерции, имеют в виду лишь их сравнение с другими моментами инерции, вычисленными относительно осей, проходящих через ту
 6.9), имеют бесчисленное множество
главных центральных осей. Для этих
сечений любая центральная ось является
главной.
6.9), имеют бесчисленное множество
главных центральных осей. Для этих
сечений любая центральная ось является
главной.Оси инерции. Главные оси и главные моменты инерции Какие моменты инерции сечения называются главными центральными
Оси, относительно
которых центробежный момент инерции
равен нулю, называют главными
осями (иногда
их называют главными
осями инерции). Через
любую точку, взятую в плоскости сечения,
можно провести в общем случае пару
главных осей (в некоторых частных случаях
их может быть бесчисленное множество).
Для того чтобы убедиться в справедливости
этого утверждения, рассмотрим, как
изменяется центробежный момент инерции
при повороте осей на 90″ (рис. б.7). Для
произвольной площадки dA, взятой в первом
квадранте системы осей хОу, обе координаты,
а следовательно, и их произведение
положительны.
В процессе поворота осей центробежный момент инерции изменяется непрерывно, следовательно, при некотором положении осей он становится равным нулю. Эти оси и являются главными.
Хотя мы и установили, что главные оси можно провести через любую точку сечения, но практический интерес представляют только те из них, которые проходят через центр тяжести сечения — главные центральные оси. Вдальнейшем, как правило, для краткости будем называть их просто главными осями, опуская слово «центральные».
В
общем случае сечения произвольной формы
для определения положения главных осей
необходимо провести специальное
исследование.
П роведем через. центр тяжести сечения ось Ох, перпендикулярную оси симметрии Оу, и определим центробежный момент инерции J. Воспользуемся известным из курса математики свойством определенного интеграла (интеграл суммы равен сумме интегралов) и представим J s виде двух слагаемых:
так как, для любой элементарной площадки, расположенной справа от оси симметрии, есть соответствующая слева, для которой произведение координат отличается лишь знаком.
Таким образом, центробежный момент инерции относительно осей Ох и Оу оказался равным нулю, т. е. это
 е. ось
симметрии и любая, ей перпендикулярная,
образуют систему главных осей.
е. ось
симметрии и любая, ей перпендикулярная,
образуют систему главных осей. Нецентральные главные оси, как уже указывалось, интереса не представляют.
Осевые моменты инерции относительно главных центральных осей называют
(относительно
оси Ox). Конечно, говоря об экстремальности
главных моментов инерции, имеют в виду
лишь их сравнение с другими моментами
инерции, вычисленными относительно
осей, проходящих через ту же
точку сечения. Таким
образом, то обстоятельство, что один из
главных моментов инерции максимален,
а другой — минимален, можно рассматривать
как объяснение того, что они (н
соответствующие оси) называются главными.
Равенство же нулю центробежного момента
инерции относительно главных осей —
удобный признак для нх нахождения.
Не приводя доказательства, укажем, что, в случае если два главных центральных момента инерции сечения равны между собой, у этого сечения любая центральная ось главная и все главные центральные моменты инерции одинаковы.
Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
ПРЕДИСЛОВИЕ
Лекция № 1 «Геометрические характеристики
Предисловие …………………………………………………………………….4
плоских сечений» ……………………………………………………………….5
2. Лекция № 2 «Главные оси и главные моменты инерции» ..………………………………………….……………………………13
3. Лекция №3 «Кручение. Расчёты на прочность и жёсткость при кручении» ………………………………………………………………………16
4. Лекция №4 «Срез и смятие. Расчёты на прочность» …….………………………………………………………………. .32
.32
5. Вопросы для проверки пройденного материала… ……………………..36
6. Список литературы …………………………………………………………37
В части 2 конспекта лекций содержаться основные теоретические положения и расчётные формулы по следующим темам: Геометрические характеристики плоских сечений, Кручение, Срез и смятие.
Целью конспекта лекций является оказание помощи студентам при изучении предмета, при решении и защите расчетно-графических работ по сопротивлению материалов.
Лекция №1 «Геометрические характеристики плоских сечений»
К геометрическим характеристикам плоских сечений относятся:
· площадь сечения F ,
· статические моменты площади S x , S y ,
· осевые моменты инерции J x , J y ,
· центробежный момент инерции J xy ,
· полярный момент инерции J ρ ,
· момент сопротивления кручению W ρ ,
· момент сопротивления изгибу W x
1.1. Статические моменты площади S x , S y
Статический момент площади сечения относительно данной оси равен сумме произведений элементарных площадок на расстояние до соответствующей оси.
Единицы измерения S x и S y : [см 3 ], [мм 3 ]. Знак «+» или «-» зависит от расположения осей.
Свойство: Статические моменты площади сечения равны нулю (S x =0 и S y =0), если точка пересечения координатных осей совпадает с центром тяжести сечения. Ось, относительно которой статический момент равен, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения.
Где F — суммарная площадь сечения.
Пример 1:
Определить положение центра тяжести плоского сечения, состоящего из двух прямоугольников с вырезом.
Отрицательная площадь вычитается.
1.2. Осевые моменты инерции J x ; J y
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
Знак всегда «+».
Не бывает равным 0.
Свойство: Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.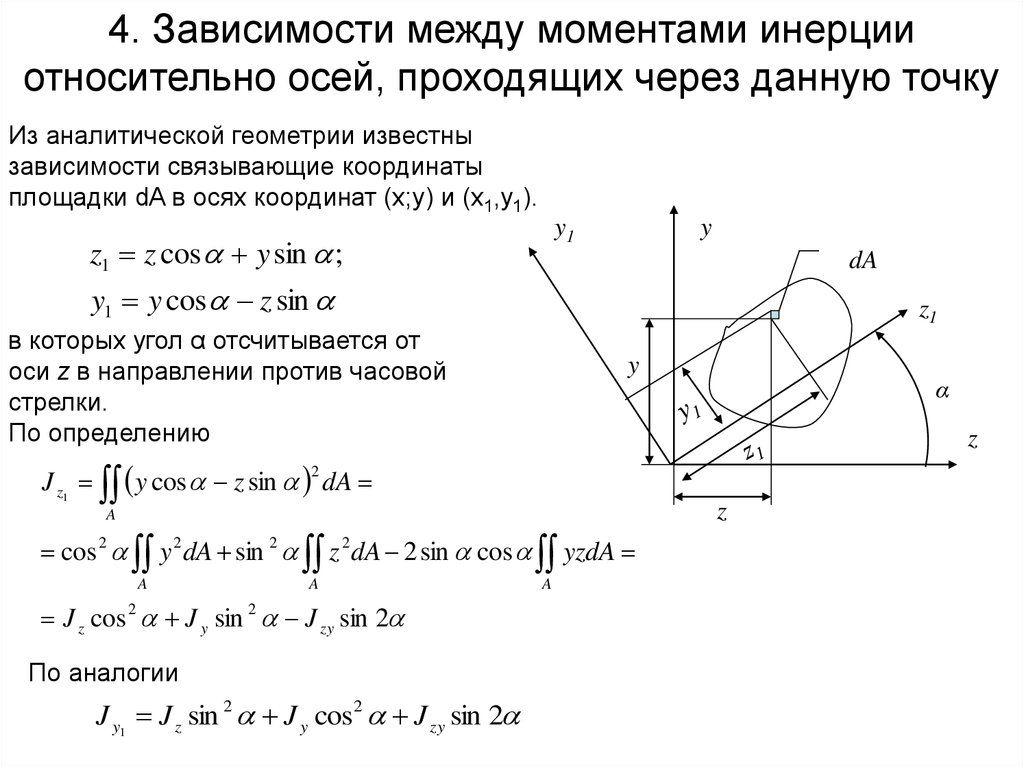
Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения J ρ
Взаимосвязь полярного и осевого моментов инерции:
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство:
при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.
1.4. Центробежный момент инерции сечения J xy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
Единица измерения [см 4 ], [мм 4 ].
Знак «+» или «-».
Если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
Таким образом для симметричных фигур центробежный момент инерции равен 0.
Координатные оси u и v , проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называются главными центральными осями инерции сечения.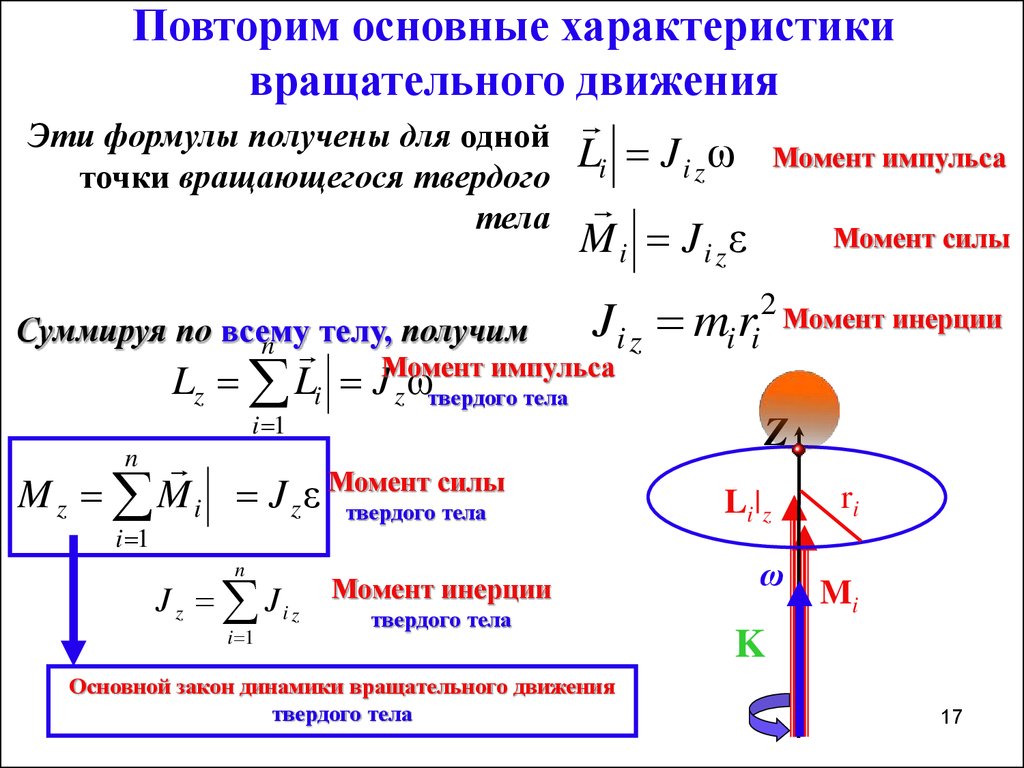 Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.
Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.
У сечений, не обладающих симметрией относительно осей x или y , например у уголка, не будет равен нулю. Для этих сечений определяют положение осей u и v с помощью вычисления угла поворота осей x и y
Центробежный момент относительно осей u и v —
Формула для определения осевых моментов инерции относительно главных центральных осей u и v :
где — осевые моменты инерции относительно центральных осей,
Центробежный момент инерции относительно центральных осей.
Теорема Штейнера:
Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
Доказательство теоремы Штейнера.
Согласно рис. 5 расстояние у до элементарной площадки dF
Подставляя значение у в формулу, получим:
Слагаемое , так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).
Для прямоугольника высотой h и шириной b :
Осевой момент инерции:
Момент сопротивления изгибу:
момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
Для круга:
Полярный момент инерции:
Осевой момент инерции:
Момент сопротивления кручению:
Момент сопротивления изгибу:
Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx .
Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b (ширина) и dy (высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF =bdy . Вычислим значение осевого момента инерции J x
Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF =bdy . Вычислим значение осевого момента инерции J x
По аналогии запишем
Осевой момент инерции сечения относительно центральной
Центробежный момент инерции
Так как оси Сx и Сy являются осями симметрии.
Пример 3. Определить полярный момент инерции круглого сечения.
Решение. Разобьём круг на бесконечно тонкие кольца толщиной радиусом , площадь такого кольца . Подставляя значение в выражение для полярного момента инерции интегрируя, получим
Учитывая равенство осевых моментов круглого сечения и
Получаем
Осевые моменты инерции для кольца равны
с – отношение диаметра выреза к наружному диаметру вала.
Рассмотрим, как изменяются моменты инерции при повороте координатных осей. Положим, даны моменты инерции некоторого сечения относительно осей 0х , 0у (не обязательно центральных)-, — осевые моменты инерции сечения. Требуется определить, — осевые моменты относительно осей u , v , повёрнутых относительно первой системы на угол (рис. 8)
Требуется определить, — осевые моменты относительно осей u , v , повёрнутых относительно первой системы на угол (рис. 8)
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
Исключим u и v в выражениях моментов инерции:
Рассмотрим два первых уравнения. Складывая их почленно, получим
Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. Заметим при этом, что
Где — расстояние от начала координат до элементарной площадки (см. рис.5). Таким образомпо углу и приравнивая производную к нулю, находим
При этом значении угла один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции .
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называются главными центральными осями (u; v). Осевые моменты инерции относительно главных осей называются главными моментами инерции — и
Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называются главными центральными осями (u; v). Осевые моменты инерции относительно главных осей называются главными моментами инерции — и
И их значение определяется по следующей формуле:
Знак плюс соответствует максимальному моменту инерции, знак минус — минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения. Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом инерции сечения относительно некоторой оси, например 0x, называется величина , определяемая из равенства
F – площадь поперечного сечения,
Осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0х до той точки, в которой следует сосредоточить (условно) площадь сечения F, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :
Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :
Радиусы инерции, соответствующие главным осям, называются главными радиусами инерции и определяются по формулам
Если какое-либо тело привести во вращение относительно произвольной оси и затем предоставить самому себе, то положение оси вращения в пространстве, вообще говоря, изменится: ось будет либо поворачиваться, либо перемещаться относительно инерциальной системы отсчета. Для того, чтобы произвольно взятую ось удерживать в неизменном положении, к ней необходимо приложить определенные силы.
Ось вращения тела, положение которой в пространстве сохраняется без приложения извне каких-либо сил, называется свободной осью тела.
Можно показать, что существуют по крайне мере три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Такие оси называются главными осями инерции тела.
Моменты инерции тела относительно главных осей называются главными моментами инерции .
Для тел, обладающих осевой симметрией (например, у однородного цилиндра), одна из главных осей совпадает с осью симметрии, а две любые оси, перпендикулярные к оси симметрии и друг другу и проходящие через центр масс тела, также являются главными (рис. 7.15). Моменты инерции относительно двух последних осей равны друг другу, а момент инерции относительно оси симметрии отличен от них
Такое тело называется симметричным волчком.
Рис. 7.15. Главные оси однородного цилиндра
У тела с центральной симметрией (например, у однородного шара) любые три взаимно перпендикулярные оси, проходящие через центр симметрии, являются главными. Для них
Такие тела называются шаровыми волчками . Любая ось шарового волчка, проходящая через центр симметрии, является главной (а, значит, и свободной).
В общем случае главные моменты инерции тела различны, то есть
Такое тело называется асимметричным волчком . Примером асимметричного волчка может служить однородный прямоугольный параллелепипед (рис. 7.16).
7.16).
Рис. 7.16. Главные оси однородного параллелепипеда
При «почти» свободном вращении на тело могут действовать малые возмущения. Если при таких возмущениях ось вращения мало изменяет свое положение, то вращение называется устойчивым . В противном случае говорят о неустойчивом вращении.
Пусть для асимметричного волчка для определенности имеет место следующее соотношение между главными моментами инерции:
Можно показать, что вращение вокруг осей 1 и 3 (то есть осей с максимальными и минимальными моментами инерции) будет устойчивым, а вокруг оси 2 (с промежуточным по величине моментом инерции) — неустойчивым.
Видео 7.4. Устойчивость полета в воздухе прямоугольного параллелепипеда
Пусть тело вращается вокруг одной из главных осей, например, вокруг оси z. Тогда вектор угловой скорости имеет вид
Посмотрим, как изменяются моменты инерции при повороте осей координат. Положим, даны моменты инерции некоторого сечения относительно осей х, у (не обязательно центральных). Требуется определить J u , J v , J uv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол (рис. 3).
Требуется определить J u , J v , J uv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол (рис. 3).
Проектируем замкнутый четырехугольник ОАВСО на оси и и v. Так как проекция ломаной линии равна проекции замыкающей, находим:
u = y sin +x cos , v = y cos — x sin
В выражениях (3), подставив вместо x 1 и y 1 соответственно u и v, исключаем u и v
Рассмотрим два первых уравнения. Складывая их почленно, получим, что сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. При этом
где — расстояние от начала координат до элементарной площадки (рис. 3). Таким образом,
J x + J y = J p
где J p — полярный момент инерции
величина которого, естественно, не зависит от поворота осей ху.
С изменением угла поворота осей каждая из величин J u и J v меняется, а сумма их остается неизменной. Следовательно, существует такое , при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.
Дифференцируя выражение J u (5) по и приравнивая производную нулю, находим
При этом значении угла один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции J uv при указанном угле обращается в нуль, что легко устанавливается из третьей формулы (5).
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными, то тогда они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Для определения этого первые две формулы (5) перепишем в виде
Для определения этого первые две формулы (5) перепишем в виде
Верхний знак соответствует максимальному моменту инерции, а нижний — минимальному. После того как сечение вычерчено в масштабе и на чертеже показано положение главных осей, нетрудно установить, которой из двух осей соответствует максимальный и которой — минимальный момент инерции.
Если сечение имеет ось симметрии, то эта ось всегда будет главной. Центробежный момент инерции части сечения, расположенной по одну сторону от оси, будет равен моменту части, расположенной по другую сторону, но противоположен ему по знаку. Следовательно, J ху = 0 и оси х и у являются главными.
Главные оси инерции и главные моменты инерции.
При изменении угла величины Ix1, Iy1 и Ix1y1 изменяются. Найдем значение угла, при котором Ix1 и Iy1имеют экстремальные значения; для этого возьмем от Ix1 или Iy1 первую производную по и преравняем ее нулю:илиоткуда(1.28)
Эта
формула определяет положение двух осей,
относительно одной из которых осевой
момент инерции максимален, а относительно
другой — минемален.
Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.
Значения главных моментов инерции найдем из формул (1.23) и (1.24), подставив в них из формулы (1.28), при этом используем известные формулы тригонометрии для функций двойных углов.
После преобразований получим следующую формулу для определения главных моментов инерции: (1.29)
Исследуя вторую производную можно установить, что для данного случая (Ix главной оси, повернутой на угол по отношению к оси х, а минимальный момент инерции — относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфигурации сечений видно, какая из главных осей соответствует максимуму момента инерции.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
Во
многих случаях удается сразу определить
положение главных центральных осей.
Если фигура имеет ось симметрии, то она
является одной из главных центральных
осей, вторая проходит через центр тяжести
сечения перпендикулярно первой. Сказанное
следует из того обстоятельства, что
относительно оси симметрии и любой оси,
ей перпендикулярной, центробежный
момент инерции равен нулю.
Сказанное
следует из того обстоятельства, что
относительно оси симметрии и любой оси,
ей перпендикулярной, центробежный
момент инерции равен нулю.
В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний шестиугольник).
9.Основные геометрические характеристики сечений
Здесь: C — центр тяжести плоских сечений;
A — площадь сечения;
I x , I y — осевые моменты инерции сечения относительно главных осей;
I xI , I yI — осевые моменты инерции относительно вспомогательных осей;
I p — полярный момент инерции сечения;
W x , W y — осевые моменты сопротивления;
W p — полярный момент сопротивления
Прямоугольное сечение
Сечение равнобедренный треугольник
10.
 Основные виды сил, действующие на тело. Момент силы относительно центра. Свойства момента сил.
Основные виды сил, действующие на тело. Момент силы относительно центра. Свойства момента сил.При рассмотрении механических задач большинство сил, действующих на тела, можно отнести к трем основным разновидностям:
Сила всемирного тяготения;
Сила трения;
Сила упругости.
Все окружающие нас тела притягиваются к Земле, это обусловлено действием сил всемирного тяготения. Если мы будем пренебрегать сопротивлением воздуха, то мы уже знаем, что все тела падают на Землю с одинаковым ускорением – ускорением свободного падения.
Как
и всякий предмет, тело, подвешенное
на пружине, стремится упасть
вниз из-за притяжения Земли,
но, когда пружина растянется
до некоторой длины, тело
останавливается, то есть
приходит в состояние
механического равновесия.
Мы уже знаем, что механическое
равновесие наступает,
когда сумма сил, действующих
на тело, равна нулю.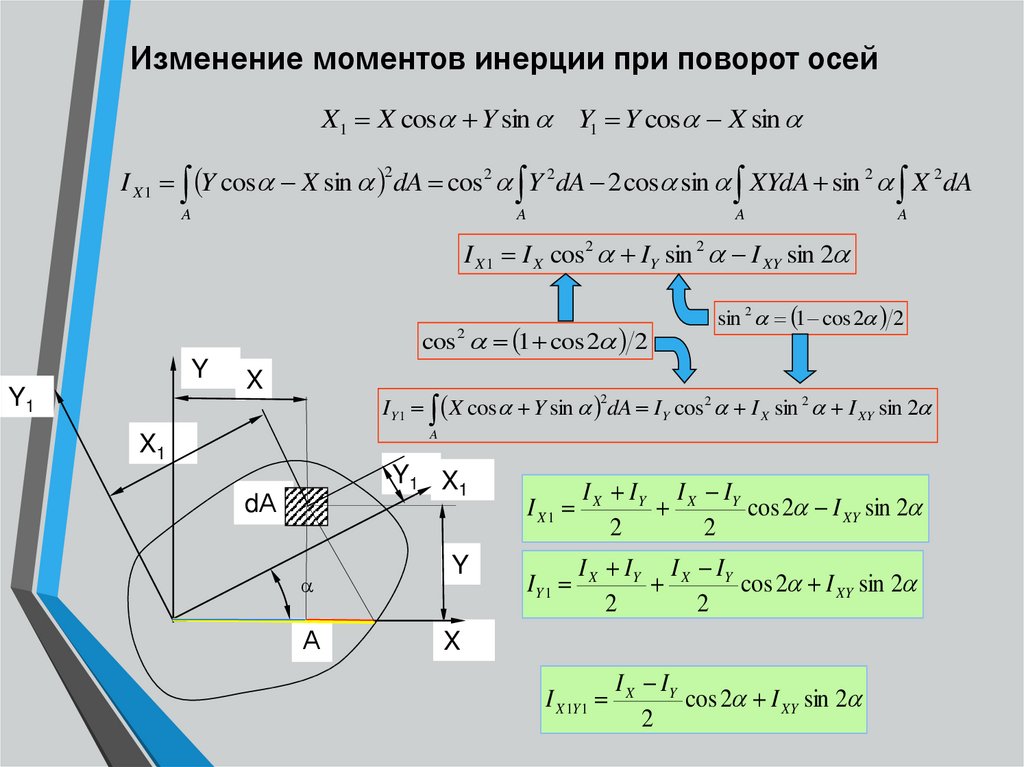 Это означает,
что сила тяжести, действующая
на груз, должна уравновеситься
с некоторой силой, действующей
со стороны пружины. Эта сила,
направленная против силы
тяжести и действующая со
стороны пружины, называется
силой упругости.
Это означает,
что сила тяжести, действующая
на груз, должна уравновеситься
с некоторой силой, действующей
со стороны пружины. Эта сила,
направленная против силы
тяжести и действующая со
стороны пружины, называется
силой упругости.
Пройдя некоторое расстояние, тело останавливается, скорость тела уменьшается от начального значения до нуля, то есть ускорение тела – величина отрицательная. Следовательно, на тело со стороны поверхности действует сила, которая стремится остановить это тело, то есть действует против его скорости. Эта сила называется силой трения.
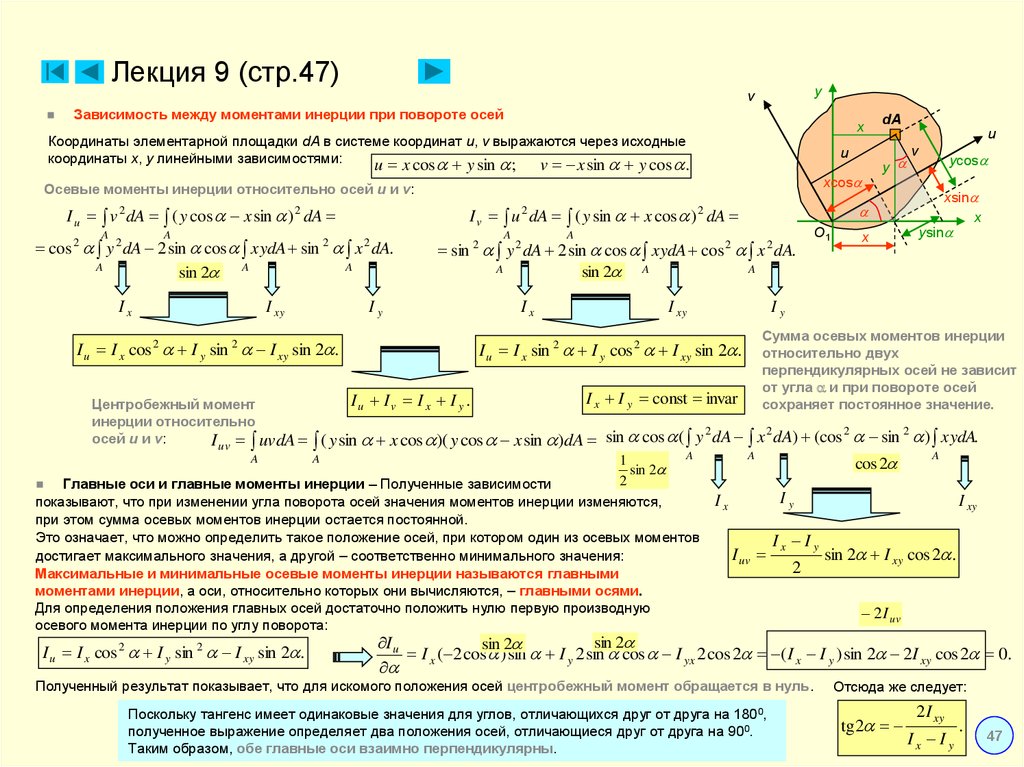
Момент силы относительно центра (точки).
Моментом силы F относительно центра (точки) О называется вектор m o (F) равный векторному произведению радиуса вектора r , проведенного из центра О в точку А приложения силы, на вектор силы F :
где
плечо h перпендикуляр,
опущенный из центра О на
линию действия силы F.
Момент m o (F) характеризует вращательный эффект силы F относительно центра (точки) О .
Свойства момента силы:
1. Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;
2. Если линия действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю .
Основные оси
Главные моменты инерции Как показано в [6] в Inertia Тензор, угловой момент твердого тела относительно начала локальной система отсчета выражается как
Если случайно все недиагональные члены тензора инерции показанные в [1], становятся равными нулю, [1] можно упростить до
Это может произойти при выравнивании осей локальной ссылки
каркас таким образом, чтобы масса корпуса равномерно распределялась вокруг осей, таким образом,
все члены произведения инерции исчезают. Топ Главные оси Как показано в [1], нет гарантии что вектор углового момента имеет то же направление, что и вектор угловой скорости вектор. Это вызывает проблему: если направление углового момента продолжает меняться, развивает крутящий момент, который в конечном итоге заставляет ось вращения двигаться. это главное Причина, вызывающая износ и вибрацию в машинах с вращающимися частями. Но в некоторых особых случаях может выполняться следующее условие, так что векторы углового момента и скорости показывают одно и то же направление:
, где I = эквивалентный скалярный момент инерции
тело вокруг оси вращения. Любая ось вращения тела, которая достаточна [3], называется главной осью .
[3] в основном говорит, что инерция тензор можно заменить одним скалярным моментом инерции, когда ось вращения главная ось. Топ Диагонализация тензора инерции Из [3]:
Или [4] можно упростить до
, где 1 = единичная матрица. I , показанное в [5], называется собственным значением, а w — собственным вектором. [5] — собственное значение уравнение. Чтобы [5] имело нетривиальное решение, определитель коэффициентов должен исчезнуть:
[6] ведет к светскому уравнение , которое в основном является кубическим, дает три корня (собственные значения): я 1 , I 2 и I 3 .
Когда собственные значения известны, можно вычислить главные оси. Пусть
где n = единичный вектор главной оси, таким образом,
Из [4] и [8]:
Для каждого собственного значения можно вычислить соответствующее n x , n y и n z из [9] & [10]. Следует обратить внимание на направление собственный вектор в этом процессе. При анализе движения можно получить главные моменты инерции
от инерционных свойств сегментов тела. Топ
2.18: Определение главных осей
Теперь нам нужно заняться определением главных осей. Пример \(\PageIndex{1}\)Рассмотрим четыре массы, положение и координаты которых следующие:
Относительно первой частицы координаты
Отсюда легко находится, что координаты центра масс относительно первой частицы равны ( −0,7, 3,9, 3,3), а моменты инерции относительно осей, проходящих через первую частицу, равны
Из теорем о параллельных осях можно найти моменты инерции относительно осей, проходящих через центр масс:
Таким образом, тензор инерции равен \[ \left(\begin{array}{c}63. Из того, что было написано ранее, мы понимаем, что если \( \boldsymbol{\omega} \), вектор мгновенной угловой скорости направлен вдоль какой-либо из главных осей, то \( \bf l { \boldsymbol{\omega} } \) будет в том же направлении, что и \( \boldsymbol{\omega} \). Другими словами, если \( (l,m,n)\) — направляющие косинусы главной оси, то \[ \left(\begin{array}{c}A & -H & G \\ -H & B & -F \\ -G & -F & C \end{array}\right)\left( \begin{array}{c}l\\ m \\n\end{массив}\right) = \lambda \left(\begin{array}{c}l\\ m \\n\end{массив}\ справа), \номер \] , где \( \лямбда\) — скалярная величина. Другими словами, вектор с компонентами \( l, m, n \) (направляющие косинусы главной оси) является собственным вектором тензора инерции, а \( \lambda \) — соответствующим главным моментом инерции. Будет три собственных вектора (под прямым углом друг к другу) и три соответствующих собственных значения, которые мы сначала назовем \(\lambda_1, \lambda_2, \lambda_3, \), хотя, как только мы узнаем, какой из них наибольший, а какой самый маленький, мы будем называть \(A_0 ,B_0 ,C_0 \), согласно нашему соглашению \(A_0 ≤ B_0 ≤ C_0 \). где
Три решения для \(\lambda\), которые мы будем называть \(A_0, B_0, C_0 \) в порядке увеличения размера:
и это главные моменты инерции. Из теории уравнений заметим, что сумма корней в точности равна \(a_2\), а также заметим, что она равна \(A+B+C\), что согласуется с тем, что мы писали в разделе 2.16 (уравнение 2.16.2). Сумма диагональных элементов матрицы известна как трассировка матрицы. Математически мы говорим, что «след симметричной матрицы инвариантен относительно ортогонального преобразования». Два других соотношения из теории уравнений можно использовать для проверки правильности арифметических действий. Произведение решений равно \(a_0 \), что также равно определителю тензора инерции, а сумма произведений, взятых по два, равна \(−a_1 \). Теперь мы нашли величины главных моментов инерции; нам еще предстоит найти направляющие косинусы трех главных осей. Начнем с оси наименьшего момента инерции, для которой момент инерции равен \( A_0 = 23,498 256 \). Пусть направляющие косинусы этой оси равны \((l_1 ,m_1 ,n_1 ) \). Поскольку это собственный вектор с собственным значением 23,498 256, мы должны иметь \[ \left(\begin{array}{c} 63,0 & 3,7 & -0,1 \\ 3,7 & 50,2 & -6,3 \\ -0,1 & -6,3 & 25,0 \end{массив}\right)\left(\begin{array}{c}l_1\\ m_1 \\n_1\end{массив}\right) = 23,498256 \left(\begin{массив}{c}l_1\\ m_1 \\n_1\end{массив}\right) \nonumber \] Это три линейных уравнения относительно \( l_1 m_1, n_1, \) без постоянного члена. Из-за отсутствия постоянного члена теория уравнений говорит нам, что третье уравнение, если оно согласуется с двумя другими, должно быть линейной комбинацией первых двух. По сути, у нас есть только два независимых уравнения, и нам понадобится третье, независимое уравнение, если мы хотим найти три направленных косинуса. \[ 39,501744l’ + 3,7m’ — 0,1 = 0 \номер \] \[ 3,7l’ + 26,701744m’ — 6,3 = 0. \номер \] Решения:
Правильность арифметики можно и нужно проверить, проверив, что эти решения также удовлетворяют третьему уравнению. Дополнительное уравнение, которое нам нужно, обеспечивается теоремой Пифагора, которая дает соотношение между тремя направляющими косинусами 92_1 = 1. \)) Неважно, какой знак вы выберете — ведь главная ось идет в обе стороны. Аналогичные расчеты для \( B_0 \) дают
и для \(C_0\)
Для первых двух осей не имеет значения, выберете ли вы верхний или нижний знак. Мы только что видели, что если мы знаем моменты и произведения инерции \(A, B, C, F, G, H \) относительно некоторых осей (т.е. если мы знаем элементы тензора инерции), мы можно найти главные моменты инерции \( A_0, B_0, C_0 \) путем диагонализации тензора инерции или нахождения его собственных значений. Если, с другой стороны, мы знаем главные моменты инерции системы частиц (или твердого тела, представляющего собой совокупность частиц), то как мы можем найти момент инерции I относительно оси, косинусы направления которой относительно главных осей равны \( (l, m, n) \) ? Сначала немного геометрии. Пусть O\(xyz\) — система координат, и пусть P\((x, y, z) \) — точка, вектор положения которой равен \[ { \bf r} = x { \bf i} + y { \bf j } + z { \bf k}. \номер\] Пусть L — прямая, проходящая через начало координат, и пусть направляющие косинусы этой линии равны . |


 Ненулевые диагональные члены тензора инерции
показанные в [2], называются основные моменты
инерция объекта.
Ненулевые диагональные члены тензора инерции
показанные в [2], называются основные моменты
инерция объекта.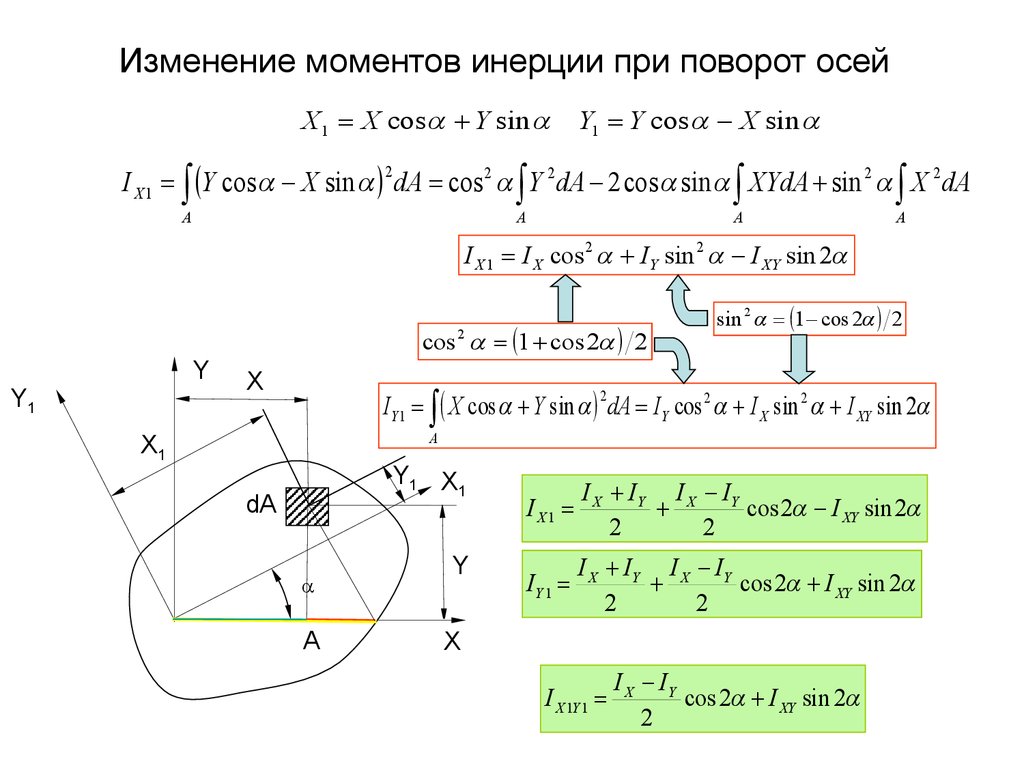 Есть группа
главных осей (теоретически 3) в трехмерном теле. Например, есть
три перпендикулярные главные оси для системы, показанной на рис. 1.
Есть группа
главных осей (теоретически 3) в трехмерном теле. Например, есть
три перпендикулярные главные оси для системы, показанной на рис. 1. Каждому корню соответствует момент
инерция относительно главной оси. На самом деле три корня являются главными моментами
инерция твердого тела, введенная в [2]:
Каждому корню соответствует момент
инерция относительно главной оси. На самом деле три корня являются главными моментами
инерция твердого тела, введенная в [2]: я 1 , я 2 & I 3 каждого сегмента общеизвестны. Данные доступны
в виде отношений радиусов инерции (отношение радиуса инерции к
длина сегмента), уравнения регрессии и коэффициенты масштабирования. Можно также вычислить
главные моменты инерции сегментов тела путем моделирования с использованием некоторых геометрических
формы. См. Индивидуальную оценку BSP для
подробности.
я 1 , я 2 & I 3 каждого сегмента общеизвестны. Данные доступны
в виде отношений радиусов инерции (отношение радиуса инерции к
длина сегмента), уравнения регрессии и коэффициенты масштабирования. Можно также вычислить
главные моменты инерции сегментов тела путем моделирования с использованием некоторых геометрических
формы. См. Индивидуальную оценку BSP для
подробности. В отличие от двумерного случая, у нас нет красивого, простого явного выражения, подобного уравнению 2.12.12, для вычисления ориентации главных осей. Определение лучше всего проводить на числовом примере.
В отличие от двумерного случая, у нас нет красивого, простого явного выражения, подобного уравнению 2.12.12, для вычисления ориентации главных осей. Определение лучше всего проводить на числовом примере. 0 & 3.7 & -0.1 \\ 3.7 & 50.2 & -6.3 \\ -0.1 & -6.3 & 25.0 \end{array}\right) \nonumber \]
0 & 3.7 & -0.1 \\ 3.7 & 50.2 & -6.3 \\ -0.1 & -6.3 & 25.0 \end{array}\right) \nonumber \] 93 =0, \номер\]
93 =0, \номер\]
 Если мы допустим \(l’=l/n\) и \(m’=m/n\), то первые два уравнения примут вид
Если мы допустим \(l’=l/n\) и \(m’=m/n\), то первые два уравнения примут вид Однако для третьих осей, чтобы убедиться, что главные оси образуют правосторонний набор, выберите такой знак, чтобы определитель матрицы направляющих косинусов был равен +1.
Однако для третьих осей, чтобы убедиться, что главные оси образуют правосторонний набор, выберите такой знак, чтобы определитель матрицы направляющих косинусов был равен +1.