Сила Ампера и сила Лоренца – формулы и определение правила правой руки кратко (9 класс)
4.6
Средняя оценка: 4.6
Всего получено оценок: 334.
Обновлено 15 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 334.
Обновлено 15 Января, 2021
Из курса физики 9 класса известно, что электрический ток — это движение заряженных частиц. Опыты показывают, что при движении заряженные частицы взаимодействуют с магнитным полем. Рассмотрим особенности этого взаимодействия.
Сила Ампера и сила Лоренца
Если рассмотреть устройство любого электрического двигателя, то в нём всегда можно найти два элемента:
- статор, создающий магнитное поле;
- ротор, двигающийся под действием статора и состоящий из рамок, проводящих электрический ток.
Магнитное поле, создаваемое статором, порождает силу, которая действует на рамку с электрическим током и поворачивает ее. Сила, которая при этом возникает, называется силой Ампера — именем физика, открывшего ее.
Сила, которая при этом возникает, называется силой Ампера — именем физика, открывшего ее.
Если ток в рамке исчезнет, то и сила Ампера также уменьшится до нуля. А поскольку ток — это движение заряженных частиц, то можно предположить, что сила Ампера возникает при действии магнитного поля на заряженные частицы, и проводник здесь не обязателен.
Опыт полностью подтверждает это предположение. Если в вакууме создать поток заряженных частиц (как правило, электронов) и направить их через магнитное поле, то траектории движения перестанут быть прямыми. А при определенных соотношениях скоростей и силы магнитного поля траектории могут даже стать окружностями или спиралями.
Рис. 2. Движение зарядов в магнитном поле.Сила Ампера, действующая на проводник с током, возникает потому, что магнитное поле действует на заряды, движущиеся в проводнике. Этот механизм возникновения силы Ампера был открыт физиком Х. Лоренцем, и поэтому сила, действующая на движущийся заряд в магнитном поле, была названа его именем.
Можно спросить: определяет ли сила Лоренца закон Ампера? Ответ утвердителен: да, определяет.
Формулы силы Ампера и силы Лоренца
Поскольку сила Ампера — это результат действия силы Лоренца, то и формулы, описывающие эти силы, близки, единицы измерения одинаковы. Сила Ампера и сила Лоренца пропорциональны величине перпендикулярной составляющей индукции $B_\perp=Bsin\alpha$, следовательно, эта часть в обеих формулах будет общей. Кроме того, обе этих силы пропорциональны величине заряда и его скорости движения. То есть формула силы Лоренца примет вид:
$$F_L = qBv sin \alpha$$
Формула силы Ампера будет аналогичной, место заряда займет величина тока $I$ (поскольку ток равен отношению заряда, проходящего по проводнику, ко времени прохождения), место скорости займет длина проводника $Δl$ (поскольку скорость равна отношению длины, которую прошел заряд, ко времени этого прохождения). В результате формула силы Ампера примет вид:
$$F_A = I B Δl sin \alpha$$
Направление силы Ампера и силы Лоренца
В отличие от многих других сил, направление силы Лоренца (а значит, и силы Ампера) не совпадает с направлением движения носителя и не совпадает с направлением на источник магнитного поля.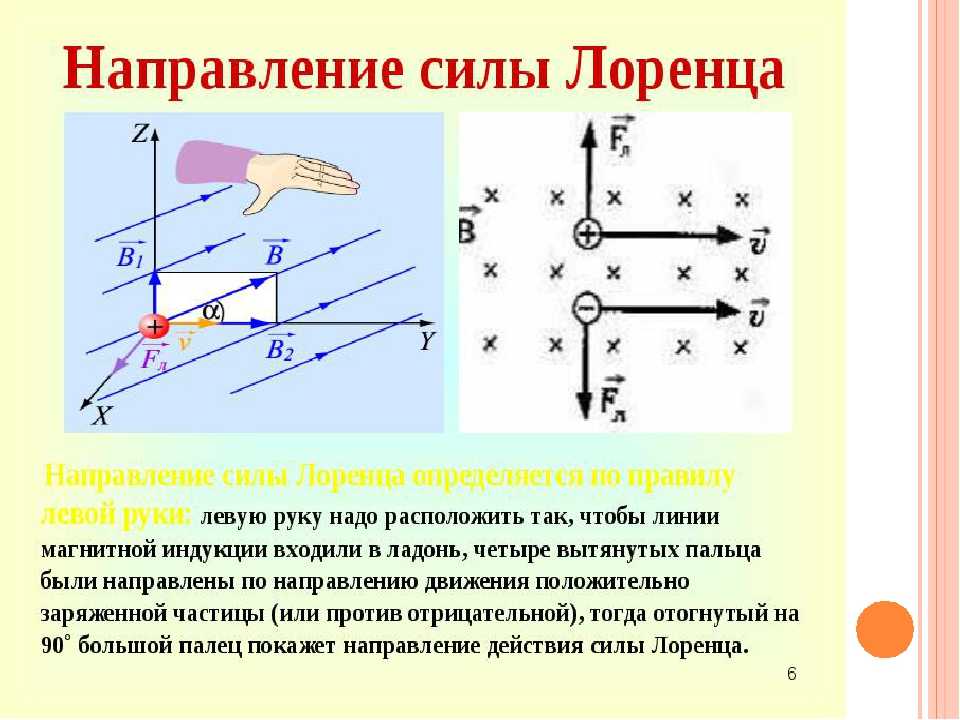
Если расположить левую руку так, чтобы четыре вытянутых пальца указывали на направление движения положительных зарядов (направление тока), а магнитные линии входили в ладонь, «прокалывая» ее, то отставленный большой палец укажет направление действия силы Лоренца (или Ампера).
Например, если линии магнитного поля направлены сверху вниз, то руку надо располагать ладонью вверх. Теперь, если проводник с током направлен вперед и мы расположим четыре вытянутых пальца вперед, то отставленный большой палец укажет направление справа налево. Это и будет направление силы Ампера, действующей на данный проводник, или силы Лоренца, если двигаются заряды.
Что мы узнали?
На заряд, движущийся в магнитном поле, действует сила Лоренца. Поскольку электрический ток — это упорядоченное движение зарядов, то на проводник с током в магнитном поле действует сила Ампера, которая представляет собой сумму сил Лоренца, действующих на движущиеся в проводнике заряды.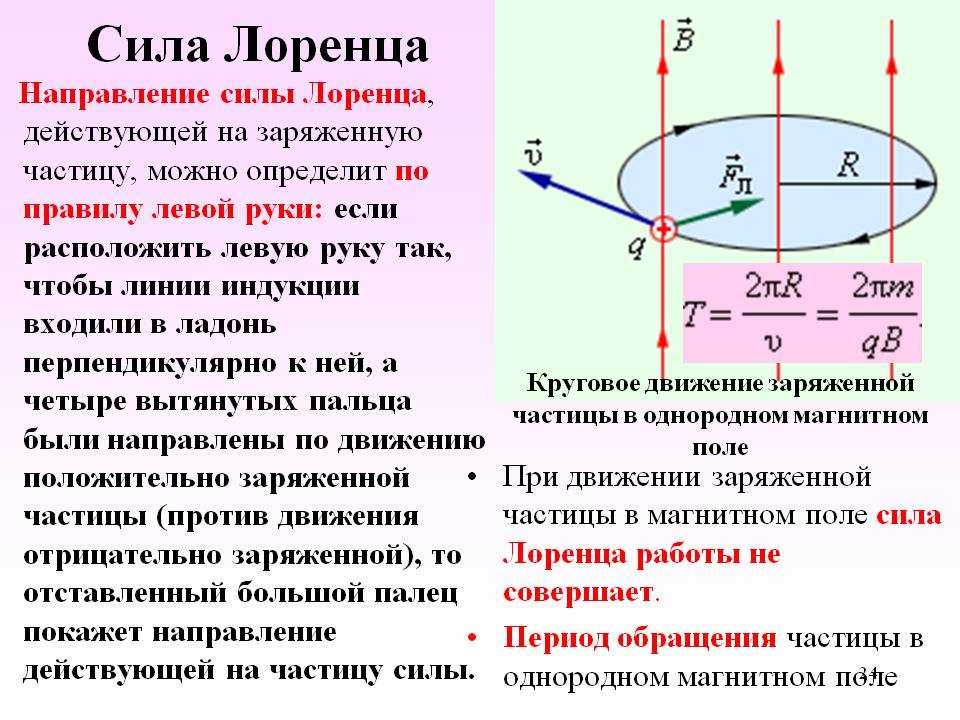
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 334.
А какая ваша оценка?
Помогите решить / разобраться (Ф)
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| ShMaxG |
| |||
11/04/08 |
| |||
| ||||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| T-bin |
| ||
07/12/08 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
электромагнетизм — Альтернативный способ вывода уравнения силы Абрахама Лоренца?
Вы правы в том, что энергия, вложенная в излучение в единицу времени (согласно формуле Лармора), не равна потере кинетической энергии за это время. Однако стандартный аргумент не предполагает этого строгого баланса, а скорее использует баланс энергии на протяжении всего периода колебаний.
Однако стандартный аргумент не предполагает этого строгого баланса, а скорее использует баланс энергии на протяжении всего периода колебаний.
Ваша идея использовать ЭМ импульс для нахождения силы на заряженной сфере должна работать, однако с этим есть трудности.
Очень похожая идея была проанализирована после того, как Лоренц и Абрахам открыли электрон для сферы, а позже Дирак для точечной частицы.
Лоренц и Абрахам работали независимо друг от друга, но они оба предположили заряженную сферу и использовали стандартную электромагнитную теорию для расчета силы, действующей на заряженную сферу из-за того, что одна часть действует на другую часть. Лоренц обнаружил, что получить точное выражение для собственной силы трудно, но с помощью приближений можно получить приближенное выражение для силы в виде ряда, включающего производные положения: во-первых, имеется инерционный член, пропорциональный ускорению $\mathbf a $, который зависит от распределения заряда в сфере, а затем есть член затухания, пропорциональный $\dot{\mathbf a}$, который не зависит от распределения, а только от общего заряда.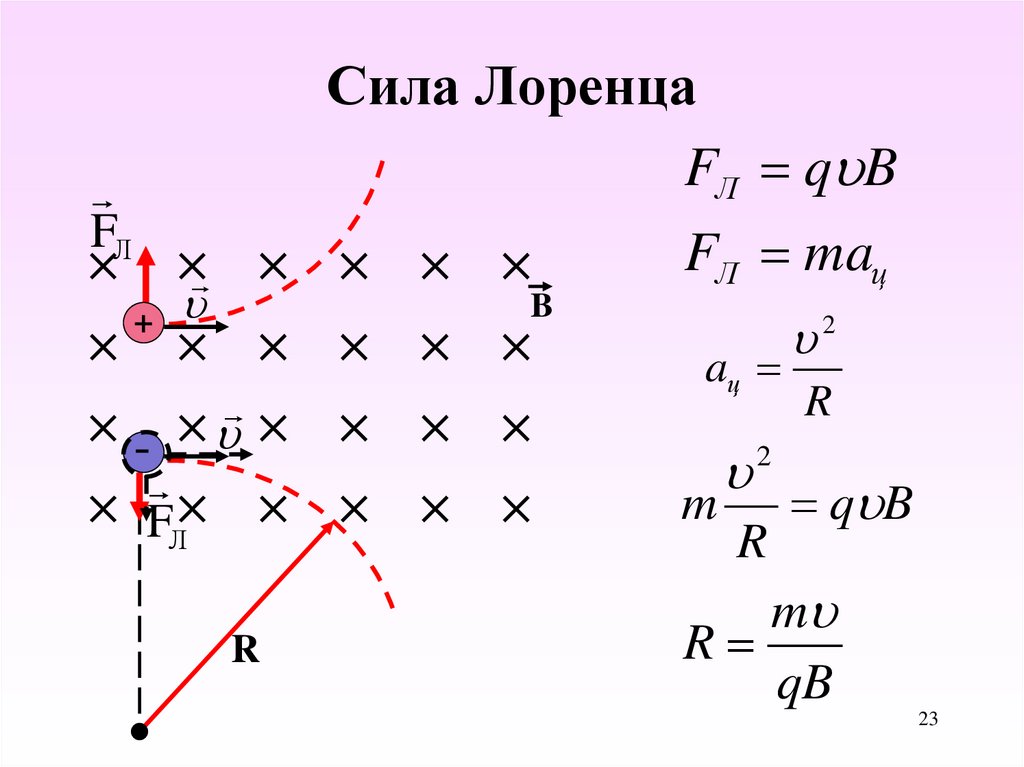 Последний член представляет собой силу Лоренца-Абрахама на заряженной сфере. Есть и другие термины, но они обычно игнорируются.
Последний член представляет собой силу Лоренца-Абрахама на заряженной сфере. Есть и другие термины, но они обычно игнорируются.
Позже Дирак попытался найти влияние излучаемого ЭМ поля на движение точечной заряженной частицы без структуры предложенным Вами способом и пришел к тому же выражению для силы Лоренца-Абрахама (но вдобавок нашел его релятивистское обобщение) [1 ].
Однако анализ Дирака для точечной частицы основан на очень важном и, на мой взгляд, неверном допущении, которое он прямо заявляет в сноске:
Обычный вывод тензора напряжений действителен только для непрерывных распределений заряда, и мы используем его здесь для точечных зарядов. Это предполагает принятие в качестве фундаментального предположения точки зрения, что энергия и импульс локализованы в поле в соответствии с идеями Максвелла и Пойнтинга.
Это предположение плохо, потому что оно вводит в теорию бесконечную ЭМ энергию и неопределенный рабочий термин. Это привело к тому, что многие сбитые с толку люди написали множество статей и книг практически без прогресса.
Это привело к тому, что многие сбитые с толку люди написали множество статей и книг практически без прогресса.
По иронии судьбы сам Дирак ранее в своей статье цитирует статью Френкеля 1925 года, в которой предлагается альтернативный безбесконечный тензор напряжений для электромагнитного поля точечных частиц и приводит к последовательной теории. В варианте Френкеля теории точечных частиц нет самосилы, реакции излучения и связанных с ними загадок, касающихся точечных частиц. С этой точки зрения радиационная реакция, наблюдаемая в макроскопической теории как сопротивление излучения антенны, является всего лишь результатом многих многочастичных взаимодействий.
[1] Дирак П. Классическая теория излучающих электронов (1938), Proc. Рой. Соц А, 167(929), 148-169. https://doi.org/10.1098/rspa.1938.0124
[2] Frenkel J., Zur Elektrodynamik punktfoermiger Elektronen (1925), Zeits. ф. физ., 32, с. 518-534. http://dx.doi.org/10.1007/BF01331692
Итак, если вы хотите пойти дальше и проанализировать импульс электромагнитного поля, чтобы найти силу, действующую на заряженную частицу, вам нужно 1) постулировать некоторый тензор напряжения и 2) работать обратные следствия к уравнению движения, подобно тому, что сделал Дирак. Однако для точечной частицы и стандартного тензора Максвелла-Пойнтинга это приводит к противоречиям из-за бесконечности, поэтому нужно где-то внести изменения, чтобы сделать это стоящим: либо работать с расширенными распределениями зарядов, либо изменить тензор энергии-импульса на что-то, что делает не приводит к бесконечности.
Однако для точечной частицы и стандартного тензора Максвелла-Пойнтинга это приводит к противоречиям из-за бесконечности, поэтому нужно где-то внести изменения, чтобы сделать это стоящим: либо работать с расширенными распределениями зарядов, либо изменить тензор энергии-импульса на что-то, что делает не приводит к бесконечности.
electromagnetism — Получение уравнения силы Лоренца для гравитоэлектромагнетизма
В конце концов я разобрался с этим и просто хотел опубликовать ответ для всех, кому это может быть интересно.
Мы хотим показать, что линеаризованная гравитация предсказывает, что движение масс производит гравитационные эффекты, подобные эффектам электромагнетизма. А именно, в линейном порядке по скорости пробного тела уравнение геодезической дает аналог уравнения силы Лоренца:
$$\mathbf{a} = — \mathbf{E} — 4\mathbf{v} \times \mathbf{B}.$$ 9{аб}$.
«Линеаризованная» гравитация
Для наших расчетов мы будем хранить только члены линейного порядка в $\gamma_{ab}$ , предполагая, что члены более высокого порядка будут достаточно малы.
Ковариантная производная $\nabla_a$
В наших приближениях первого порядка мы можем написать $\partial_a$ вместо $\nabla_a$, если применить к $\gamma_{ab}$ или выражению $\gamma_{ab }$ . Это связано с тем, что члены символа Кристоффеля не будут первого порядка в $\gamma_{ab}$. 9{\,\,a}\gamma$$
$$\Rightarrow \overline{\gamma} = \gamma — \frac{1}{2} (4) \gamma = -\gamma.$$
Заглушка обратно в (3) дает
$$\gamma_{ab} = \overline{\gamma}_{ab} — \frac{1}{2} \eta_{ab} \overline{\gamma}. \;\;\;\;\;\;(4)$$
Уравнение Эйнштейна в аналоге калибровки Лоренца
Поскольку линеаризованная гравитация имеет калибровочную свободу (подробности см. на стр. 75 Вальда), мы можем сделать калибровочное преобразование, чтобы упростить уравнение Эйнштейна до 9{\mu} = (1,0,0,0)$, поэтому в «матричной» форме наш тензор энергии-импульса можно представить как
$$T_{\mu \nu} = \begin{bmatrix} \ро & p_x & p_y & p_z \\ p_x & 0 & 0 & 0 \\ p_y & 0 & 0 & 0 \\ p_z & 0 & 0 & 0 \end{bmatrix},$$
, где $\mathbf{p} = (p_x, p_y, p_z)$ — импульс.



 11.2009, 14:55
11.2009, 14:55  11.2009, 15:31
11.2009, 15:31  11.2009, 17:29
11.2009, 17:29  11.2009, 17:42
11.2009, 17:42 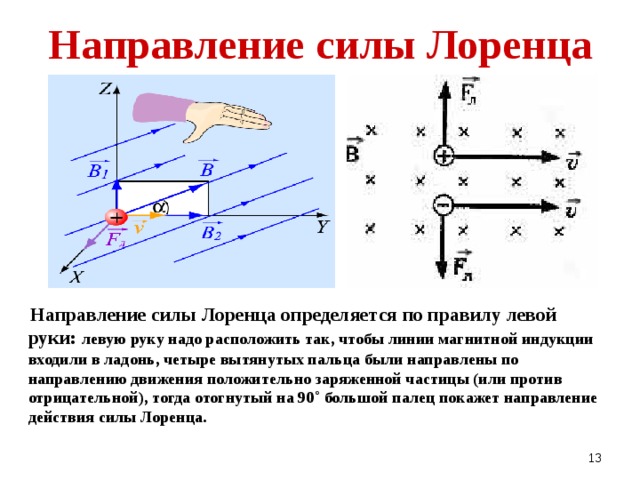 12.2009, 17:04
12.2009, 17:04 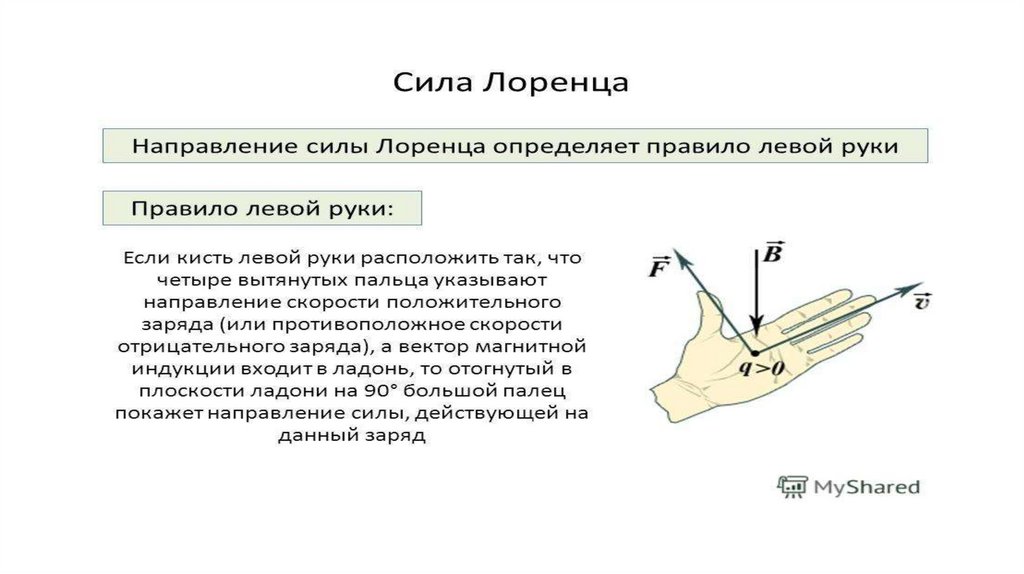 12.2009, 23:33
12.2009, 23:33