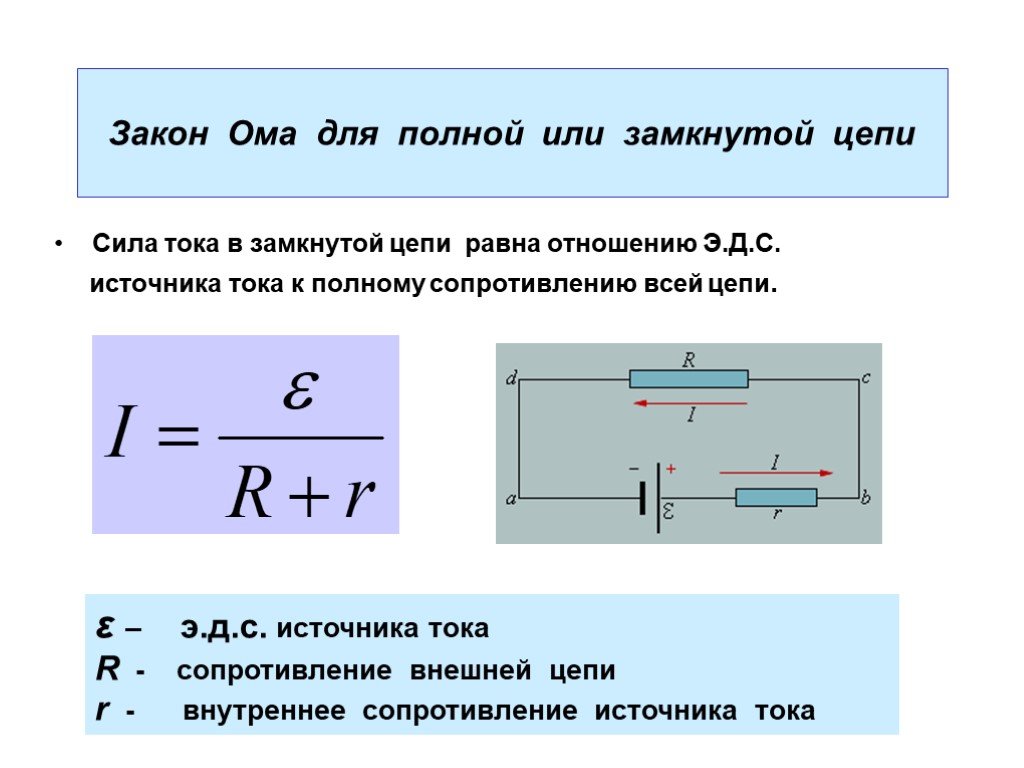
Закон Ома для неоднородного участка: формулы

Содержание

Как звучит закон Ома для участка цепи

Ток в проводнике возникает в электрическом поле, которое, в свою очередь, появляется при наличии разности потенциалов или напряжения. Движение тока направлено в сторону меньшего потенциала. Условно считается, что в этом направлении двигаются положительные заряды, а в обратную сторону происходит движение свободных электронов.

На участке металлического проводника данный процесс будет выглядеть следующим образом. На каждом конце присутствует потенциал – ϕ1 и ϕ2, при этом ϕ1 > ϕ2. Следовательно, напряжение в этом месте равно U = ϕ1 – ϕ2. Немецкий ученый Ом практически установил зависимость, при которой с увеличением напряжения, возрастает и сила тока, протекающего через неполный участок.

Для каждого из проводников, отличающихся материалами, был построен свой график, отражающий зависимость силы тока от напряжения. В дальнейшем, эти графики стали известны, как вольт-амперные характеристики. В результате, было установлено наличие линейной связи между обеими величинами – силой тока и напряжением. То есть, они находятся в прямой пропорциональной зависимости.

Но, как показывают графики, все проводники обладают разными коэффициентами пропорциональности. Следовательно, у них разная степень проводимости, получившая название электрического сопротивления (R). Поэтому, чем ниже будет сопротивление проводника, тем выше сила тока, проходящего через него. При том, что напряжение для всех проводников будет одинаковым.

После всех опытов ученый смог окончательно сформулировать свой закон для участка цепи:

Сила тока в однородном проводнике на отдельном участке, находится в прямой пропорции с напряжением на этом же участке и в обратной пропорциональной зависимости с сопротивлением данного проводника.

Классическая формулировка

Как устроить освещение участка

Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:

I (сила тока) = U (напряжение) /R (электрическое сопротивление).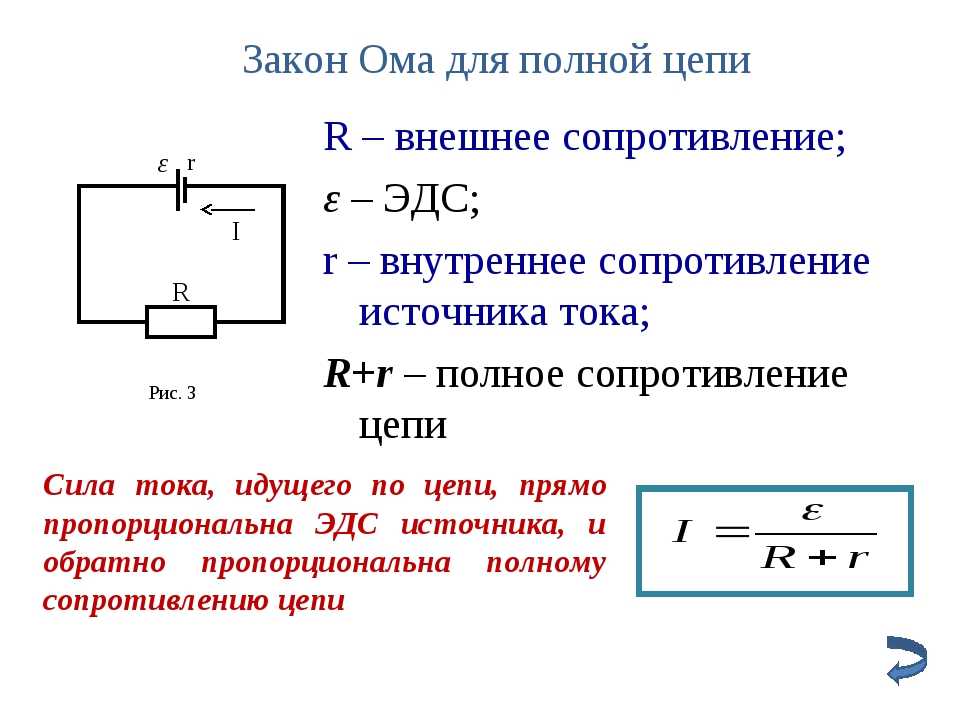

Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:

U = ϕ1 – ϕ2.

Элементарные вычисления показывают взаимные зависимости перечисленных параметров:

• I1 = 24/6 = 4А;
• I2 = 60/6 = 10А.

Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:

I2 > I1.

Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:

• I1 = 24/4 = 6А;
• I2 = 24/12 = 2А.

Основные формулы

Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.

Ток, напряжение и сопротивление

Картинка выше наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.

В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.

При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.

Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.

Электрический ток возникает при наличии электрического поля и свободных носителей заряда. Соединив проводником разноименно заряженные тела, можно получить электрический ток, протекающий в течение короткого промежутка времени. Стационарное электрическое поле — это поле постоянных во времени электрических токов при условии неподвижности проводников с электрическими токами. Участки цепи, где на заряды действует только стационарное поле, называются однородными.

Сторонние силы

Для того, чтобы в проводнике электрический ток был длительное время, необходимо создать определенные условия. Для этого на отдельных участках цепи, кроме сил стационарного поля, действуют, так называемые, сторонние силы. Участки цепи, на которых имеется действие дополнительных, сторонних, сил называются неоднородными. В этом случае перемещение зарядов возникает под действием сил не электростатической природы, действующих в устройствах, называемых источниками постоянного тока.

Силы, приводящие в движение электрические заряды внутри источника постоянного тока против направления действия сил электростатического поля, называются сторонними силами. Сторонние силы в гальваническом элементе или аккумуляторе возникают в результате электрохимических реакций, происходящих между частицами металлического электрода и молекулами электролита. В генераторах постоянного тока сторонней силой является сила, возникающая от действия магнитного поля на движущийся электрический заряд. Работа источника тока похожа на функцию насоса, который заставляет двигаться жидкость (качает) по трубам замкнутого гидравлического контура. Под воздействием сторонних сил заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи длительное время поддерживается постоянный электрический ток.

Рис. 1. Источники постоянного тока, аккумуляторы, гальванические элементы, генераторы.

В организме человека имеется множество химических веществ, которые вступая друг с другом в различные реакции, способствуют возникновению электрической энергии. Например, в сердце есть клетки, которые в процессе поддержания сердечного ритма поглощают натрий и выделяют калий, что приводит к образованию электрических зарядов. При достижении определенной величины заряда, возникает импульс электрического поля, заставляющий сокращаться сердечную мышцу. Эти импульсы регистрируют с помощью кардиографа в больницах и поликлиниках при снятии электрокардиограммы (ЭКГ), дающей информацию о работе сердца..

Неоднородный участок цепи постоянного тока

Определение основных параметров и процессов:

• перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
• при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
• эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):

q = q0*n*V.

Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.

Пример неоднородного участка цепи

Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).

Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.

Ниже приведены формулы, характеризующие рассмотренный пример:

• A12/q = ϕ1 – ϕ2;
• Ast/q = E12;
• U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
• I = (ϕ1 – ϕ2 + E12)/ R.

Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.

К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.

Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:

ϕ1= 20V; ϕ2=10V.

Подставив значения в формулу, можно получить нужный результат:

(20-10+40)/5 = +10А.

Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».

Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:

• кулоновские – Fкул;
• сторонние – Fc;
• сопротивления кристаллической решетки – Fсп.

Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.

Принятые единицы измерения

Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:

• напряжение – в вольтах;
• ток в амперах
• сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.

Переменный ток

Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:

Где «Z» представляет  собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.

Сила тока

Сила тока возникает при наличии частиц со свободными зарядами. Они перемещаются через поперечное сечение проводника из одной точки в другую. Источник питания создает электрическое поле, под действием которого электроны начинают двигаться упорядоченно.

Таким образом, сила тока является количеством электричества, проходящего через определенное сечение за единицу времени. Увеличить этот показатель можно путем увеличения мощности источника тока или изъятия из цепи резистивных элементов.

Международная единица СИ для тока – ампер. Это довольно большая величина, поскольку для человека смертельно опасными считаются всего 0,1 А. В электротехнике малые величины могут выражаться в микро- и миллиамперах.

Определение силы тока можно окончательно сформировать в виде формулы I = q/t, в которой q является зарядом, проходящим через сечение, t – отрезок времени, затраченный на перемещение этого заряда.

Кроме того, сила тока может записываться с помощью основной формулы, когда известны значения напряжения и сопротивления. В числом виде она будет гласить следующее:

• I = U/R

Закон Ома для замкнутой цепи

Подключение светодиода через резистор и его расчет

В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:

I = E/(Rн+Rи).

Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.

Формулировка для полной цепи

Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.

Схема с подключенным с источником

Учитывая «r» ЭДС, формула предстанет в следующем виде:

Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.

Напряжение будет  меньше ЭДС, определить его можно по формуле:

Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.

Использование на практике

Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.

Практически данная схема выглядит так:

U = I x R, I = U/R, R = U/I.

Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.

Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.

Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.

Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.

Формулы для закона Ома

Представленные на рисунке формулы, начали формироваться из основных формул для полной цепи и отдельного участка. С их помощью можно выполнять все основные расчеты, при составлении проектов и в других ситуациях. Формулы полностью пригодны для работы с цепями как постоянного, так и переменного тока.

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.
Применяем закон к любому участку цепи

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

• R=0,2 МОм;
• U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

• R=20 кОм;
• I=10 мА.

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Что мы узнали?

Итак, мы узнали, что участки электрической цепи, на которых кроме стационарного электрического поля имеется действие дополнительных, сторонних сил, называются неоднородными. Сторонние силы возникают в результате работы источников тока: аккумуляторов, гальванических элементов и электрических генераторов тока. Получены уравнения закона Ома для неоднородного участка цепи и для полной цепи.

Вывод

Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.

Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.

Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.

Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.

Видеоурок

Источники

• https://amperof.ru/teoriya/zakon-oma-dlya-neodnorodnogo-uchastka.html
• https://obrazovaka.ru/fizika/zakon-oma-dlya-neodnorodnogo-uchastka-cepi.html
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html

Закон Ома для неоднородного участка цепи

Неоднородный участок цепи постоянного тока

Определение основных параметров и процессов:

• перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
• при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
• эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):

q = q0*n*V.

Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.

Пример неоднородного участка цепи

Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).

Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.

Ниже приведены формулы, характеризующие рассмотренный пример:

• A12/q = ϕ1 – ϕ2;
• Ast/q = E12;
• U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
• I = (ϕ1 – ϕ2 + E12)/ R.

Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.

К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.

Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:

ϕ1= 20V; ϕ2=10V.

Подставив значения в формулу, можно получить нужный результат:

(20-10+40)/5 = +10А.

Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».

Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:

• кулоновские – Fкул;
• сторонние – Fc;
• сопротивления кристаллической решетки – Fсп.

Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.

Действие электродвижущих сил

Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.

Дополнительная информация. Скалярная величина – это когда она может быть выражена только определённым значением. В отличие от векторной величины, которая определяется не только значением, но и направлением.

Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:

• Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
• Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
• Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
• Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
• Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.

В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).

Генераторы тока

ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.

Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.

Советуем изучить Инверторный стабилизатор напряжения

Закон Ома для замкнутой цепи

Закон Ома для участка цепи

В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:

I = E/(Rн+Rи).

Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Классическая формулировка

Закон Ома в дифференциальной форме

Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:

I (сила тока) = U (напряжение) /R (электрическое сопротивление).

Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:

U = ϕ1 – ϕ2.

Элементарные вычисления показывают взаимные зависимости перечисленных параметров:

• I1 = 24/6 = 4А;
• I2 = 60/6 = 10А.

Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:

I2 > I1.

Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:

• I1 = 24/4 = 6А;
• I2 = 24/12 = 2А.

Основные формулы

Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.

Ток, напряжение и сопротивление

Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.

В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.

При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.

Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

В общем, это наиболее распространенные варианты использования этих соединений.

Объяснение закона Ома в классической теории

Формула закона, известная всем со школьных лет, выглядит так:

Из нее легко выводятся формулы для определения \(U\) :

и для определения \(R\) :

Единицами измерения силы тока являются амперы, напряжения — вольты, сопротивление измеряется в омах.

Данный закон верен для линейного участка цепи, на котором зафиксировано стабильное сопротивление.

Дифференциальные уравнения — Неоднородные дифференциальные уравнения

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / DE второго порядка / Неоднородные дифференциальные уравнения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.8: Неоднородные дифференциальные уравнения

Пришло время подумать о том, как решать неоднородные дифференциальные уравнения. Линейное неоднородное дифференциальное уравнение второго порядка имеет вид

. \[\begin{equation}y» + p\left( t \right)y’ + q\left( t \right)y = g\left( t \right)\label{eq:eq1}\end{ уравнение}\]

где \(g(t)\) — ненулевая функция. Обратите внимание, что мы не использовали здесь постоянные коэффициенты, потому что все, что мы собираемся сделать в этом разделе, не требует этого. Кроме того, мы используем коэффициент 1 для второй производной просто для того, чтобы часть работы было немного легче записать.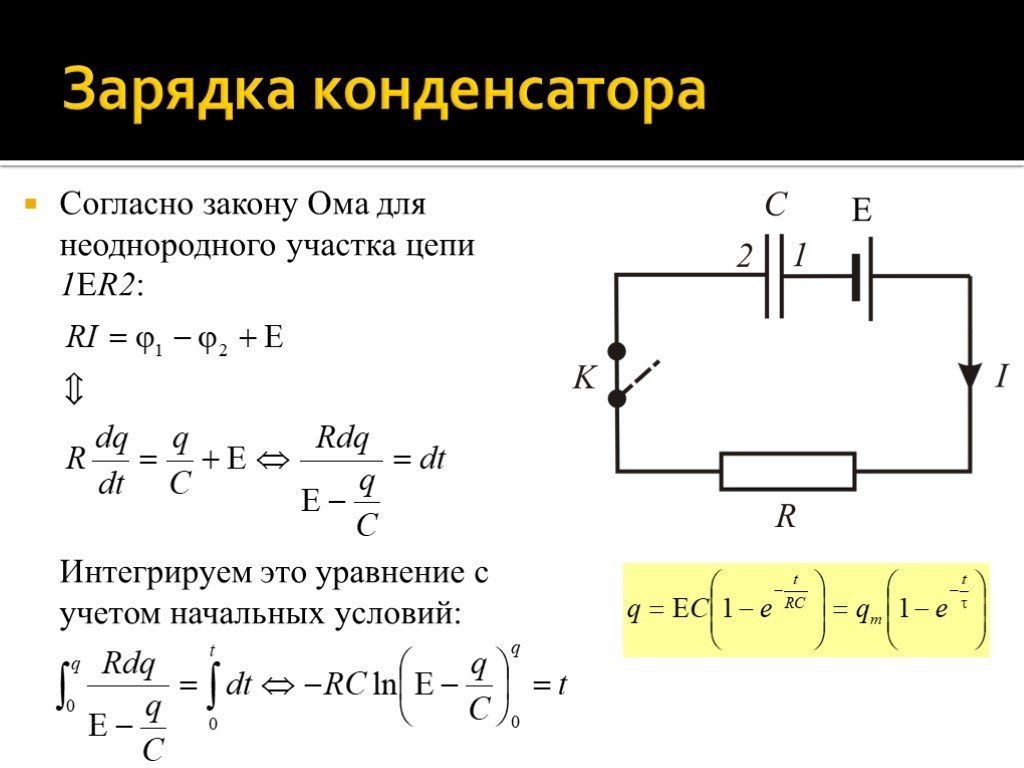

Не обязательно быть 1.

Прежде чем говорить о том, как решить одну из них, нам нужно разобраться с некоторыми основами, что и является целью этого раздела.

Сначала позвоним по номеру

\[\begin{equation}y» + p\left( t \right)y’ + q\left( t \right)y = 0\label{eq:eq2}\end{equation}\]

ассоциированное однородное дифференциальное уравнение с \(\eqref{eq:eq1}\).

Теперь давайте рассмотрим следующую теорему.

Теорема

Предположим, что \(Y_{1}(t)\) и \(Y_{2}(t)\) являются двумя решениями \(\eqref{eq:eq1}\) и что \(y_ {1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений ассоциированного однородного дифференциального уравнения \(\eqref{eq:eq2}\), тогда

\[{Y_1}\влево( t \вправо) — {Y_2}\влево( t \вправо)\]

является решением \(\eqref{eq:eq2}\) и может быть записано как

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

Обратите внимание на используемые здесь обозначения.

Заглавными буквами обозначались решения \(\eqref{eq:eq1}\), а строчными буквами обозначались решения \(\eqref{eq:eq2}\). Это довольно распространенное соглашение при работе с неоднородными дифференциальными уравнениями. 9\prime + q\left( t \right){Y_2} & = g\left( t \right)\end{align*}\]

Итак, мы смогли доказать, что разность двух решений является решением \(\eqref{eq:eq2}\).

Доказательство того, что

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

еще проще. Поскольку \(y_{1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений \(\eqref{eq:eq2}\), мы знаем, что они образуют общее решение поэтому любое решение \(\eqref{eq:eq2}\) можно записать в виде

\[y\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\]

Итак, \(Y_{1}(t) — Y_{2}(t)\) является решением \(\eqref{eq:eq2}\), как мы показали выше, поэтому его можно записывается как

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

Итак, что нам дает эта теорема? Мы можем использовать эту теорему, чтобы записать форму общего решения \(\eqref{eq:eq1}\).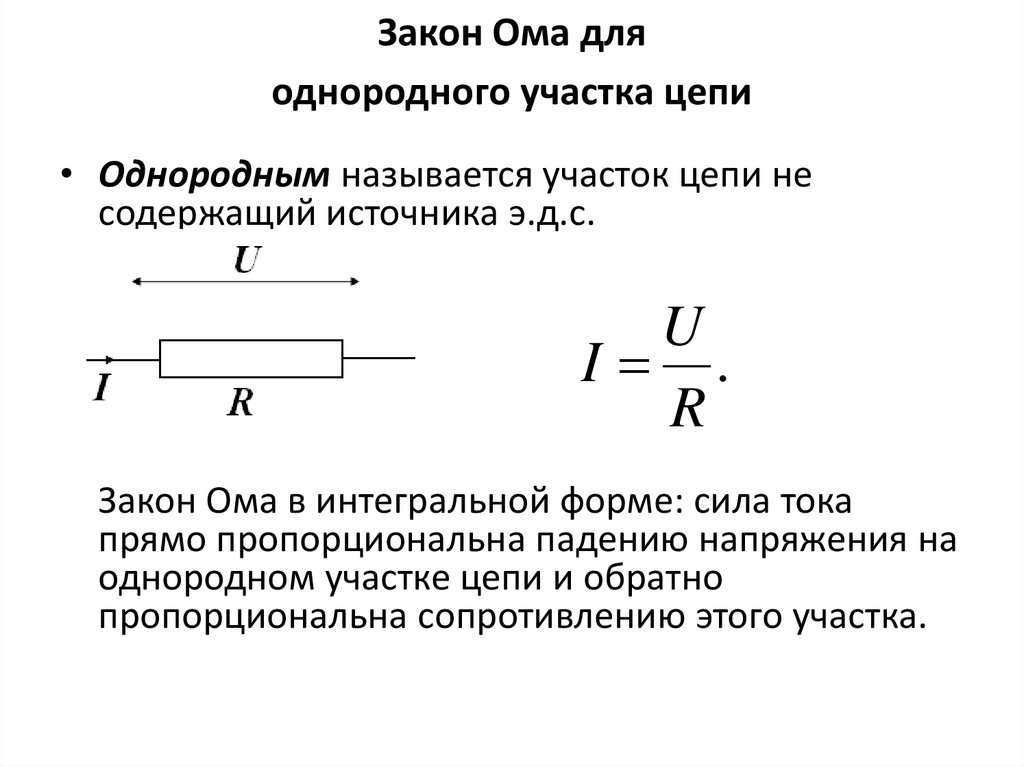

Предположим, что \(y(t)\) является общим решением \(\eqref{eq:eq1}\) и что \(Y_{P}(t)\) является любым решением \(\eqref{eq :eq1}\), которые мы можем получить. Тогда, используя вторую часть нашей теоремы, мы знаем, что

\[y\left( t \right) — {Y_P}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\ ]

где \(y_{1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений для \(\eqref{eq:eq2}\). Решение для \(y(t)\) дает

\[y\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right) + {Y_P}\left( t \right)\ ]

Мы позвоним

\[{y_c}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\]

дополнительное решение и \(Y_{P}(t)\) частное решение. Тогда общее решение дифференциального уравнения можно записать в виде.

\[y\left( t \right) = {y_c}\left( t \right) + {Y_P}\left( t \right)\]

Итак, чтобы решить неоднородное дифференциальное уравнение, нам нужно решить однородное дифференциальное уравнение \(\eqref{eq:eq2}\), что для дифференциальных уравнений с постоянными коэффициентами довольно легко сделать, и нам понадобится решение \(\eqref{eq:eq1}\).

Кажется, это круговой аргумент. Чтобы записать решение \(\eqref{eq:eq1}\) нам нужно решение. Однако это не проблема, как кажется. Есть способы найти решение \(\eqref{eq:eq1}\). Они просто не будут, в общем, общим решением. Фактически, следующие два раздела посвящены именно этому, нахождению частного решения неоднородного дифференциального уравнения.

Существует два распространенных метода поиска конкретных решений: неопределенные коэффициенты и вариация параметров. У обоих есть свои преимущества и недостатки, как вы увидите в следующих нескольких разделах.

Неоднородные цепи и системы Маркова

Перейти к основному содержанию

Книга

Василиу, П.-К.Г. (2022). Неоднородные цепи и системы Маркова: теория и приложения (1-е изд.). Чепмен и Холл/CRC. https://doi.org/10.1201/b23204

АННОТАЦИЯ

Неоднородные цепи Маркова и системы: теория и приложения выполняет две основные цели. Она посвящена изучению неоднородных марковских цепей в первой части и развитию теории и приложений неоднородных марковских систем (популяций) во второй. Книга самодостаточна и требует умеренного знания основ теории вероятностей и линейной алгебры, общих для большинства программ бакалавриата по математике, статистике и прикладной теории вероятностей. Есть некоторые продвинутые части, которые требуют теории меры и другой продвинутой математики, но читатели предупреждены об этом, чтобы они могли сосредоточиться на основных результатах.

Характеристики

• Широкий и доступный обзор неоднородных цепей и систем Маркова
• Заполняет значительный пробел в текущей литературе
• Хороший баланс теории и приложений, с углубленными математическими деталями, отделенными от основных результатов
• Множество иллюстративных примеров потенциальных приложений из различных областей
• Подходит для использования в качестве учебника для аспирантов прикладной теории вероятностей или для самостоятельного изучения
• Включенные потенциальные приложения могут вести к другим количественным областям

Книга в первую очередь предназначена для аспирантов, исследователей и практиков в области прикладных вероятностей и статистики, а презентация была спланирована и структурирована таким образом, чтобы обеспечить гибкость в выборе тем, чтобы текст можно было адаптировать для удовлетворения потребностей различные схемы курса.