Физика, 9 кл. (Буховерцев Б.Б.)

Физика, 9 кл. (Буховерцев Б.Б.)

Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. 9 класс. Учебник. — 6-е изд. — М.: Просвещение, 1982. — 272 с. В учебнике на современном уровне изложены фундаментальные вопросы школьной программы, представлены основные технические применения законов физики, рассмотрены методы решения задач. Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз. Оглавление ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. КОЛИЧЕСТВО ТЕПЛОТЫ 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА? Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. 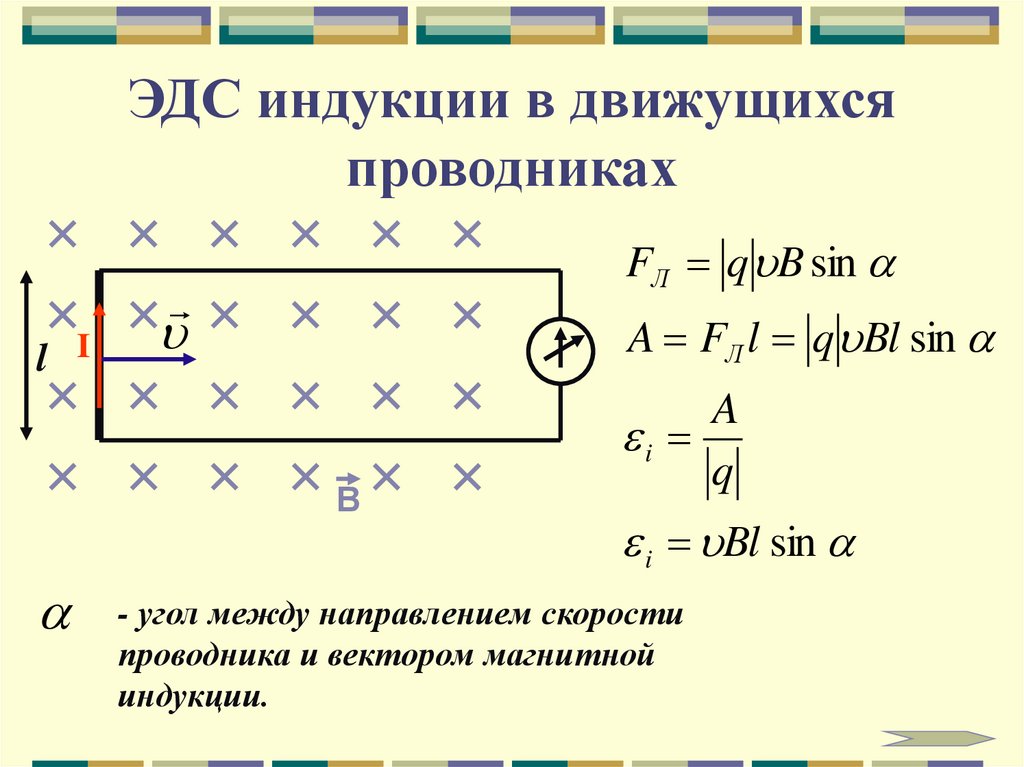СИЛА ЛОРЕНЦА 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ

ЭДС при движении проводника в поле

Основные ссылки

CSS adjustments for Marinelli theme

Объединение учителей Санкт-Петербурга

Форма поиска

Поиск

Вы здесь

Главная » ЭДС при движении проводника в поле

ЭДС при движении проводника в магнитном поле.
Причина возникновения ЭДС — сила Лоренца. При движении перемычки К на электроны действует сила Лоренца, совершающая работу. Электроны перемещаются отС к А. Перемычка – источник ЭДС. Следовательно
Эта формула используется в любом проводнике, движущемся в магнитном поле, если ↑↑.
Если между векторами и  есть угол, то используется формула
Так как
Другой способ вывода формулы эдс в движущемся проводнике. Т.к. – электроны начинают под действием силы Лоренца перемещаться к одному из концов проводника, то возникает электрическое поле. Оно будет возрастать до тех пор, пока электрическая сила не уравновесит силу Лоренца. . Учитывая, что ,  получим: .
Явление существенно при движении проводников значительной длины или с большой скоростью, например, при полете самолета (в магнитном поле Земли).
Знак  можно определить по правилу правой руки Правило правой руки для индукционного тока. Если правую руку расположить так, чтобы линии магнитной индукции (В) входили в ла­донь, а отогнутый большой палец по­казывал направление движения провод­ника, то четыре вытянутых пальца ука­жут направление индукционного тока в проводнике.	Правило правой руки для индукционного тока
Вихревое электрическое поле Электроны в проводниках вторичной обмотки приводятся в движение элект­рическим полем (ЭП), которое порож­дается переменным магнитным полем (МП).
Фундаментальное свойство поля.  Изменяясь во времени, магнитное поле порождает электрическое  (Дж.  Максвелл — английский физик). ЭП, порождаемое переменным МП, не связано с зарядом; силовые линии нигде не начинаются и не кончаются, т. е. линии замкнутые. Такое поле — вихревое электрическое.
Токи Фуко Индукционный ток в массивных проводниках называют то­ками Фуко. Используют: плавка металлов в вакууме. Вредное действие: бесполезная потеря энергии в сердечниках трансформаторов и в генераторах.

Теги: 

конспект

ЭДС движения | Физика

Цели обучения

К концу этого раздела вы сможете:

• Вычислять ЭДС, силу, магнитное поле и работу, обусловленную движением объекта в магнитном поле.

Как мы видели, любое изменение магнитного потока индуцирует противодействующую этому изменению ЭДС — процесс, известный как индукция. Движение является одной из основных причин индукции. Например, магнит, перемещаемый по направлению к катушке, создает ЭДС, а катушка, перемещаемая по направлению к магниту, создает аналогичную ЭДС. В этом разделе мы сконцентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что условно называется ЭДС движения . Одна ситуация, когда возникает ЭДС движения, известна как эффект Холла и уже была исследована. На заряды, движущиеся в магнитном поле, действует магнитная сила F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает ЭДС f = Bℓv . Мы видели, что эффект Холла имеет приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и обнаружим, что ЭДС движения можно использовать в качестве источника энергии. Рассмотрим ситуацию, показанную на рис. 1. Стержень движется со скоростью v вдоль пары проводящих рельсов, отстоящих друг от друга на расстоянии ℓ в однородном магнитном поле B . Рельсы неподвижны относительно B и соединены с неподвижным резистором R . Резистор может быть любым, от лампочки до вольтметра. Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором. B перпендикулярен этой области, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается. При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.

 

Рис. 1. (а) ЭДС движения = B ℓ v индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. RHR-2 дает показанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на ту же полярность стержня. (Обратите внимание, что буквенный символ E, используемый в эквивалентной схеме в нижней части части (b), представляет ЭДС.)

Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака:

[латекс]\текст{ЭДС} = \text{N}\frac{\Delta\Phi}{\ Дельта т}\\[/латекс].

Здесь и далее под «ЭДС» подразумевается величина ЭДС. В этом уравнении N = 1 и поток Φ = BA  cos θ . У нас есть θ = 0º и cos  θ  = 1, так как B перпендикулярно A . Теперь Δ Φ = Δ( BA ) = B Δ A , так как B является однородным. Обратите внимание, что площадь, заметаемая стержнем, составляет Δ A = ℓ Δ x . Ввод этих величин в выражение для ЭДС дает

[латекс]\text{ЭДС}=\frac{B\Delta A}{\Delta t}=B\frac{\ell\Delta x}{\Delta t}\ \[/латекс].

Наконец, обратите внимание, что Δ x / Δ t = v , скорость стержня. Ввод этого в последнее выражение показывает, что

ЭДС = Bℓv  ( B ,ℓ и v перпендикулярно)

— ЭДС движения. Это то же самое выражение, которое было дано ранее для эффекта Холла.

Установление связей: объединение сил

Между электрической и магнитной силами существует много связей. Тот факт, что движущееся электрическое поле создает магнитное поле и, наоборот, движущееся магнитное поле создает электрическое поле, является частью того, почему электрические и магнитные силы теперь считаются разными проявлениями одной и той же силы. Это классическое объединение электрических и магнитных сил в то, что называется электромагнитной силой, является источником вдохновения для современных усилий по объединению других основных сил.

Чтобы найти направление индуцируемого поля, направление тока и полярность индуктируемой ЭДС, мы применяем закон Ленца, как описано в Законе индукции Фарадея: Закон Ленца. (См. рис. 1(b).) Поток увеличивается, так как увеличивается закрытая площадь. Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. Таким образом, RHR-2 требует, чтобы I было направлено против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано на рисунке.

ЭДС движения также возникает, если магнитное поле движется, а стержень (или другой объект) неподвижен относительно Земли (или какого-либо наблюдателя). Мы видели пример этого в ситуации, когда движущийся магнит индуцирует ЭДС в неподвижной катушке. Важно относительное движение. В этих наблюдениях проявляется связь между магнитными и электрическими полями. Движущееся магнитное поле создает электрическое поле за счет ЭДС индукции. Мы уже видели, что движущееся электрическое поле создает магнитное поле — движущийся заряд подразумевает движущееся электрическое поле, а движущийся заряд создает магнитное поле.

ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, при обычных движениях. Например, простой расчет ЭДС движения стержня длиной 1 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает ЭДС = Бℓv = (5,0 × 10 ⁻⁵ Тл)(1,0 м)(3,0 м /с) = 150 мкВ. Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля «Шаттл» были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и стационарные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.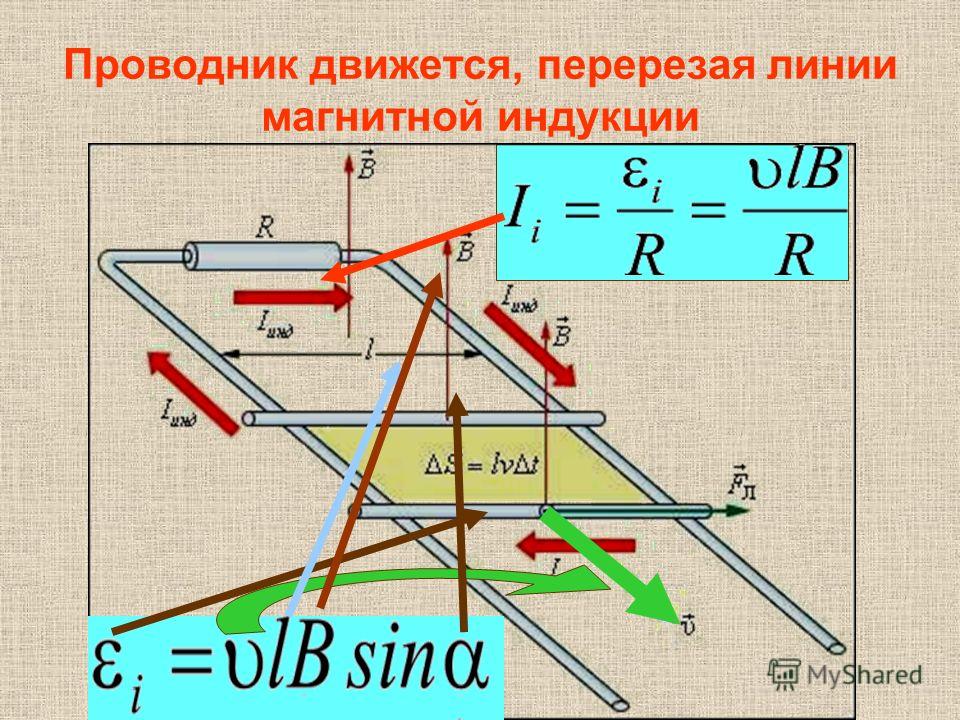 ) на ток в кабеле за счет магнитной силы F = IℓB sin θ  выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовать ее в электрическую энергию. Оба испытания оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Следующий пример указывает на принципиальную осуществимость.

Пример 1. Расчет большой ЭДС движения объекта на орбите

Рис. 2. ЭДС движения как преобразование электроэнергии для космического челнока является мотивацией для эксперимента с привязанным спутником. Было предсказано, что ЭДС 5 кВ будет индуцироваться в тросе длиной 20 км при движении с орбитальной скоростью в магнитном поле Земли. Цепь завершается обратным путем через стационарную ионосферу.

Рассчитайте ЭДС движения вдоль проводника длиной 20,0 км, движущегося с орбитальной скоростью 7,80 км/с перпендикулярно магнитному полю Земли 5,00 × 10 ⁻⁵ Тл.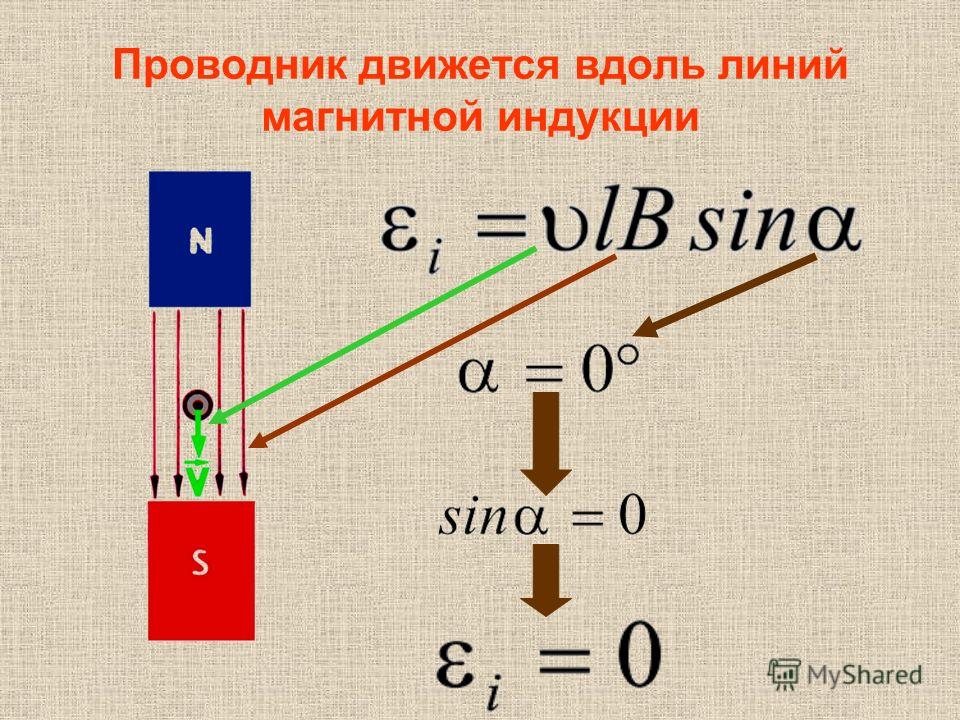 {3}\text{ V}\end{массив}\\[/latex].

Обсуждение

Полученное значение превышает измеренное напряжение 5 кВ для эксперимента с челноком, поскольку фактическое орбитальное движение троса не перпендикулярно полю Земли. Значение 7,80 кВ — это максимальная ЭДС, полученная при θ = 90º и sin θ = 1.

• ЭДС, индуцированная движением относительно магнитного поля B , называется ЭДС движения

  ЭДС = Bℓv  ( B ,ℓ и против перпендикулярно)

  , где ℓ — длина объекта, движущегося со скоростью v  относительно поля.

Концептуальные вопросы

1. Почему часть цепи должна двигаться относительно других частей, чтобы иметь полезную ЭДС движения? Рассмотрим, например, что рельсы на рисунке 1 неподвижны относительно магнитного поля, а стержень движется.
2. Мощную индукционную пушку можно сделать, поместив металлический цилиндр внутрь катушки соленоида. Цилиндр принудительно выталкивается при быстром включении соленоидного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает. Почему цилиндр может стать активным/горячим при выстреле из пушки?
3. Индукционная плита нагревает кастрюлю с катушкой переменного тока, расположенной под кастрюлей (и без горячей поверхности). Может ли поверхность печи быть проводником? Почему не работает катушка с постоянным током?
4. Объясните, как можно оттаять замерзшую водопроводную трубу, обернув вокруг нее катушку с переменным током. Имеет ли значение, является ли труба проводником? Объяснять.

Задачи и упражнения

1. Используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что магнитная сила, действующая на ток в движущемся стержне на рисунке 1, направлена ​​в направлении, противоположном его скорости.

2. Если в спутниковом тросе, показанном на рисунке 2, течет ток, используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что на трос действует магнитная сила в направлении, противоположном его скорости.

3. (a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м/с. Какая ЭДС индуцируется между законцовками крыльев, если вертикальная составляющая поля Земли равна 3,00 × 10 ⁻⁵   Тл? б) Может ли ЭДС такой величины иметь какие-либо последствия? Объяснять.

4. (a) Отвертка из цветного металла используется в магнитном поле 2,00 Тл. Какая максимальная ЭДС может быть наведена на его длине 12,0 см при движении со скоростью 6,00 м/с? (б) Вероятно ли, что эта ЭДС будет иметь какие-либо последствия или даже будет замечена?

5. С какой скоростью должен двигаться скользящий стержень на рисунке 1, чтобы создать ЭДС 1,00 В в поле 1,50 Тл, если длина стержня составляет 30,0 см?

6. Стержень длиной 12,0 см на рисунке 1 движется со скоростью 4,00 м/с. Какова напряженность магнитного поля, если индуцируется ЭДС 95,0 В?

7. Докажите, что когда B , ℓ и v не взаимно перпендикулярны, ЭДС движения определяется выражением ЭДС = Bℓv  sin θ .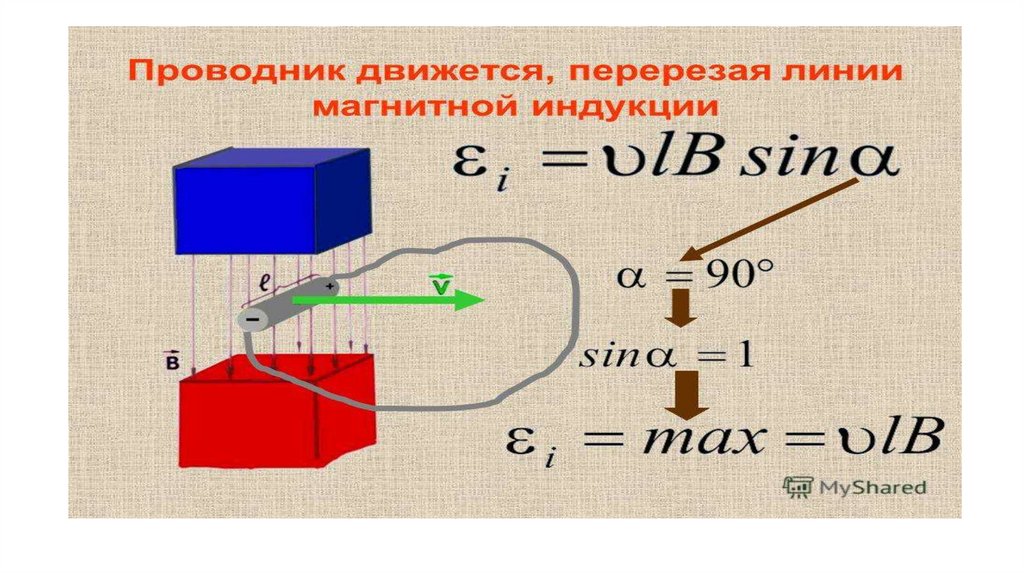 Если v перпендикулярно B , тогда θ — это угол между ℓ и B . Если ℓ перпендикулярно B , то θ является углом между v и B .

8. Во время полета космического корабля «Шаттл» в августе 1992 года можно было выпустить только 250 м троса, рассмотренного в примере 1 (выше). ЭДС движения 40,0 В создавалась в поле Земли 5,00 × 10 ⁻⁵ Тл при движении со скоростью 7,80 × 10 ³ м/с. Каков угол между скоростью шаттла и полем Земли, если предположить, что проводник перпендикулярен полю?

9. Комплексные концепции Выведите выражение для тока в системе, подобной показанной на рис. 1, при следующих условиях. Сопротивление между рельсами Р , рельсы и подвижный стержень одинаковы по сечению А и имеют одинаковое удельное сопротивление ρ . Расстояние между рельсами равно l, и стержень движется с постоянной скоростью v перпендикулярно однородному полю B . В нулевой момент времени подвижный стержень находится рядом с сопротивлением Р .

10. Интегрированные концепции  Привязной спутник на рис. 2 имеет массу 525 кг и находится на конце троса длиной 20,0 км и диаметром 2,50 мм с прочностью на растяжение стали. а) На сколько растянется трос, если к спутнику приложить силу 100 Н? (Предположим, что спутник и шаттл находятся на одной высоте над Землей.) (b) Какова эффективная силовая постоянная троса? в) Сколько энергии запасается в нем при растяжении силой 100 Н?

11. Интегрированные концепции  Привязанный спутник, обсуждаемый в этом модуле, вырабатывает 5,00 кВ и течет ток 10,0 А. а) Какую силу магнитного сопротивления это создает, если система движется со скоростью 7,80 км/с? б) Сколько кинетической энергии отводится от системы за 1,00 ч, если пренебречь изменением высоты или скорости за это время? в) Как изменится скорость, если масса системы равна 100 000 кг? (d) Обсудите долгосрочные последствия (скажем, недельный полет) на орбите космического корабля «Шаттл», отметив, какое влияние оказывает снижение скорости, и оценив величину этого эффекта.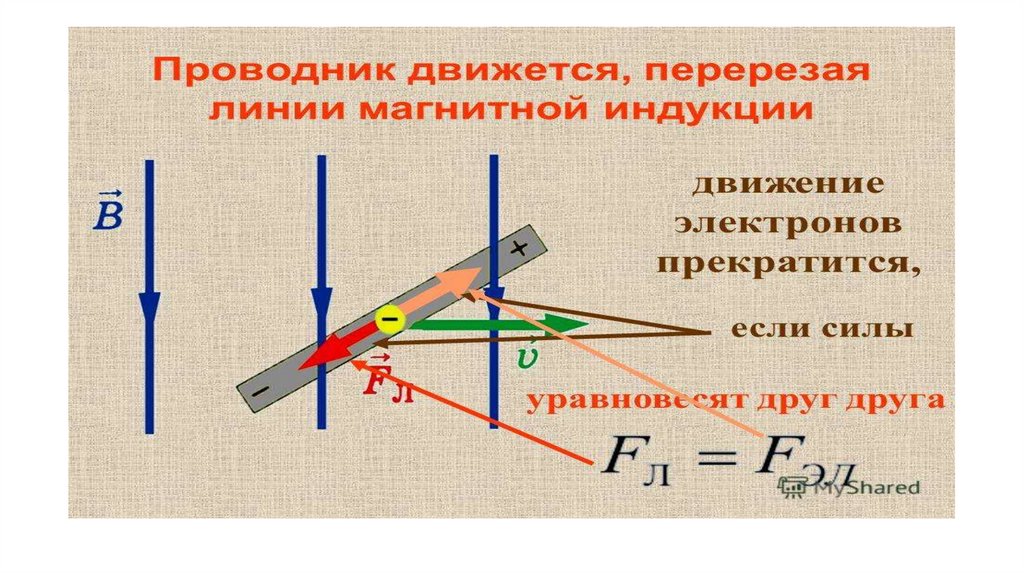

Избранные решения задач и упражнений

1. (а) 0,630 В (б) Нет, это очень маленькая ЭДС.

5. 2,22 м/с

11.(а) 10,0 Н (б) 2,81 × 10 ⁸ Дж (в) 0,36 м/с (г) Для недельного полета (168 часов) изменение по скорости будет 60 м/с, или примерно 1%. В общем, уменьшение скорости приведет к тому, что орбита начнет двигаться по спирали внутрь, потому что скорости больше не будет достаточно для поддержания круговой орбиты. Долгосрочные последствия заключаются в том, что шаттлу потребуется немного больше топлива для поддержания желаемой скорости, иначе орбита будет немного спиральной внутрь.

ЭДС, индуцированная в движущемся проводнике

Такие устройства, как генераторы или батареи, работают таким образом, что электрический заряд передается внутри устройства, и в этом процессе энергия преобразуется из одной формы в другую. Клеммы этих устройств образуют противоположные полярности. Одна клемма становится отрицательно заряженной, тогда как другая становится положительно заряженной.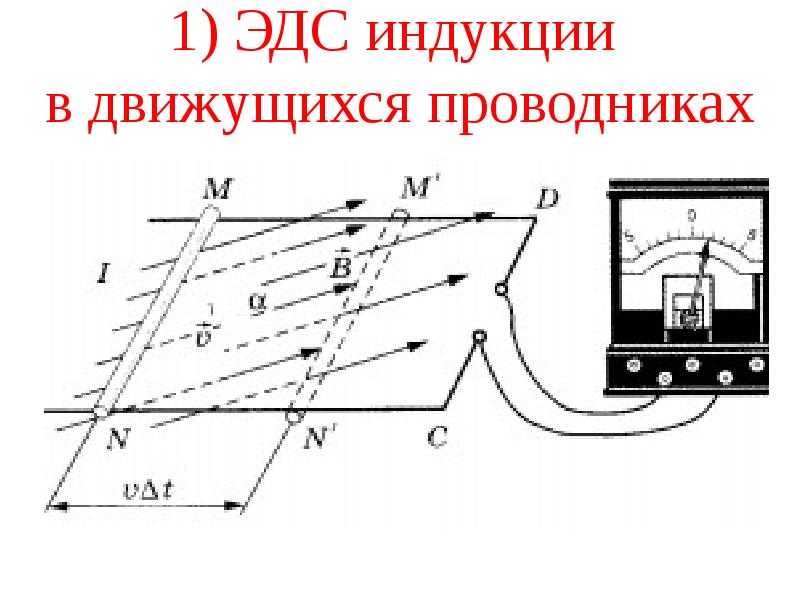 Энергия, получаемая в этих устройствах, или работа, совершаемая над единицей электрического заряда, называется электродвижущей силой или ЭДС. Измеряется в вольтах. Процесс, при котором ЭДС индуцируется в цепи с помощью переменных магнитных или электрических полей, называется электромагнитной индукцией.

Закон электромагнитной индукции Фарадея

Майкл Фарадей ввел два закона, известные как закон электромагнитной индукции Фарадея.

Первый закон Фарадея

Если изменить величину или направление магнитного поля, в проводе возникнет ЭДС, и эта индуцированная ЭДС или индуцированное напряжение приведет к индуцированному току. Этого можно добиться различными способами:

• Путем перемещения магнита вперед и назад
• Путем изменения величины магнитного поля
• Путем изменения ориентации катушки
• Путем перемещения катушки в магнитное поле и из него

Второй закон Фарадея

Скорость изменения магнитного потока, связанная с катушки равна величине ЭДС индукции в катушке. Индуцированный поток равен произведению количества витков в катушке на поток, связанный с катушкой.

E=NdΦ/dt … 1

Закон Ленца

Закон Ленца гласит, что направление ЭДС индукции таково, что она противодействует изменению, вызвавшему ее. Возьмем в качестве примера стержневой магнит. Если мы будем перемещать стержневой магнит в катушке и из нее, будет индуцироваться ЭДС. Перемещение северного полюса магнита из катушки также вызвало бы ЭДС, и ее направление было бы противоположным изменению. В этом случае удаление от северного полюса индуцирует ЭДС. Следовательно, изменение попытается противодействовать этому, то есть полярность на одном конце катушки станет южной, чтобы притянуть северный полюс.

Теперь, используя закон Ленца в уравнении 1

E= -NdΦ/dt… 2

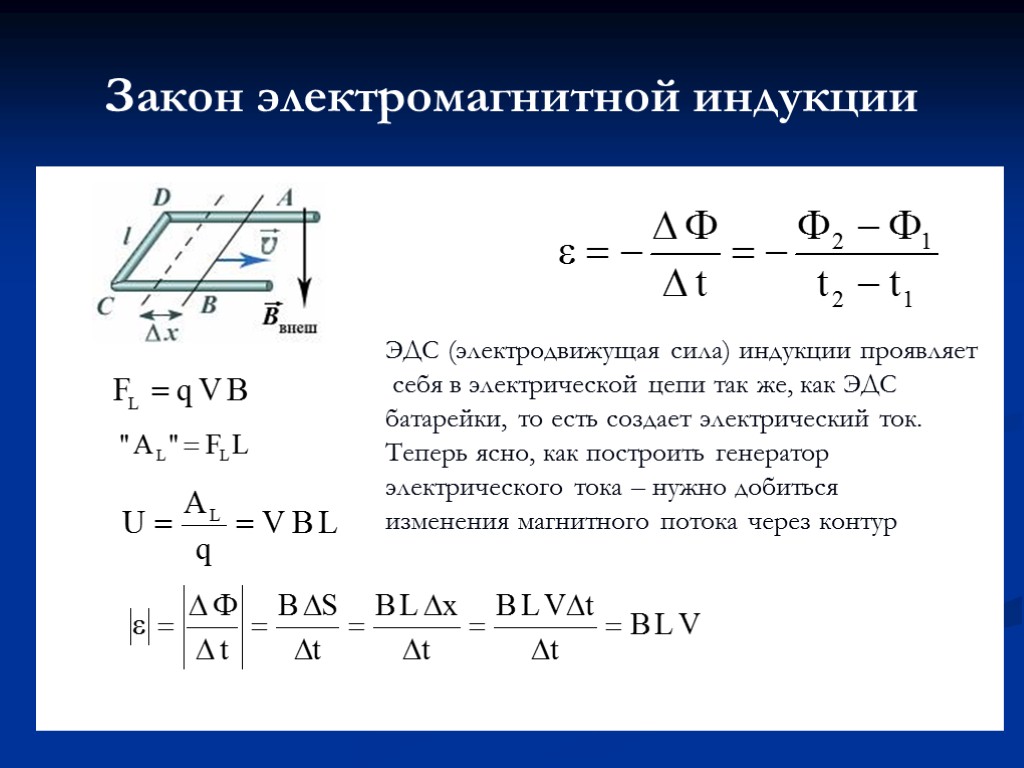
ЭДС, индуцируемая в движущемся проводнике

Всякий раз, когда проводник перемещается в однородном магнитном поле, в проводнике возникает ЭДС.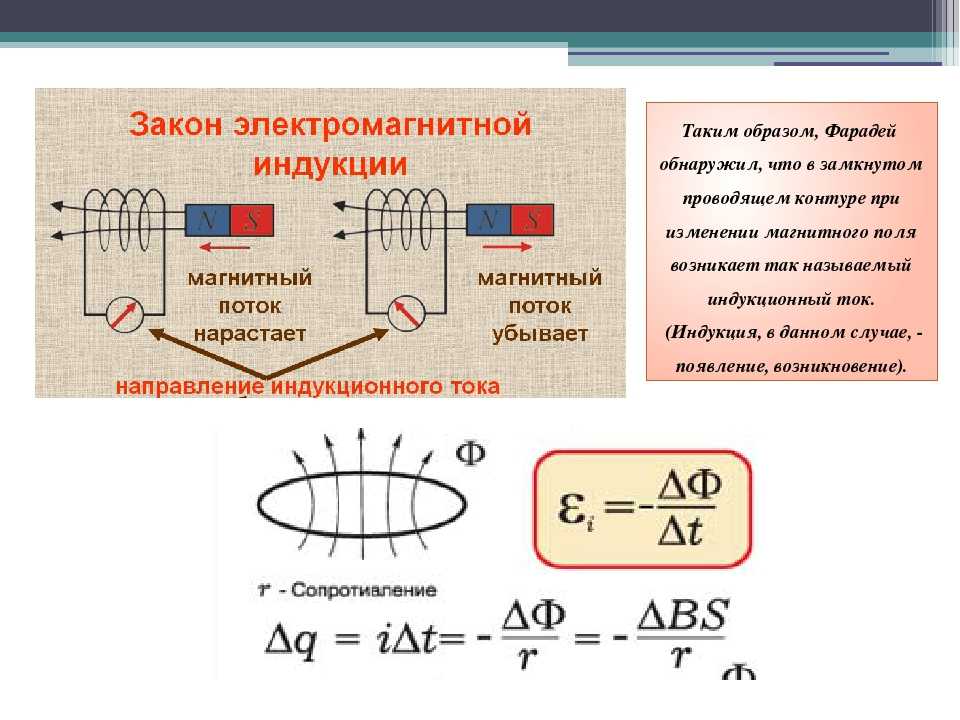 ЭДС индуцируется поперек проводника из-за изменения площади проводника, который покидает и входит в магнитное поле. Таким образом изменяется магнитный поток, что приводит к индукции ЭДС. ЭДС индукции также известна как ЭДС движения. Теперь давайте получим выражение для величины ЭДС индукции.

По закону Фарадея

E=ΔΦ/Δt

Рассмотрим металлический стержень длины l, движущийся со скоростью v. Он пройдет расстояние x,

за время t.

Скорость = расстояние/время

Или, v=Δx/Δt

Поскольку площадь контура (ЭДС индуцирования) постоянно меняется, величина, на которую она изменится, будет:

ΔA=lΔx

Магнитное поток равен произведению магнитного поля на изменение площади.

Следовательно, 3 становится

E=B∆A/∆t

=Blv∆t/∆t

=Blv

Следовательно, ЭДС, индуцируемая в проводнике, будет e=Blv.

Направление ЭДС индукции, согласно закону Ленца, противоположно вызывающему ее изменению.

Задачи

• Рассчитайте ЭДС провода, движущегося со скоростью 5 м/с через однородное магнитное поле силой 0,5 Тл.