Способы определения ЭДС индукции в движущихся проводниках

 

Нахождение ЭДС индукции через силу Лоренца

Магнитный поток через контур может изменяться по следующим причинам:

В обоих этих случаях будет выполняться закон электромагнитной индукции. При этом происхождение электродвижущей силы в этих случаях различное. Рассмотрим подробнее второй из этих случаев

В данном случае проводник движется в магнитном поле. Вместе с проводником совершают движение и все заряды, которые находятся внутри проводника. На каждый из таких зарядов со стороны магнитного поля будет действовать сила Лоренца. Она и будет способствовать перемещению зарядов внутри проводника.

• ЭДС индукции в данном случае будет иметь магнитное происхождение.

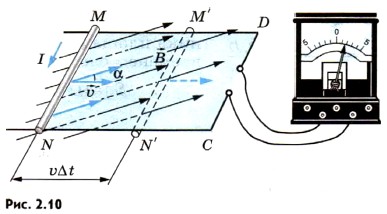
Рассмотрим следующий опыт: магнитный контур, у которого одна сторона подвижная, помещают в однородное магнитное поле. Подвижная сторона длиной l начинает скользить вдоль сторон MD и NC с постоянной скоростью V. При этом она постоянно остаётся параллельной стороне СD. Вектор магнитной индукции поля будет перпендикулярен проводнику и составлять угол а с направлением его скорости. На следующем рисунке представлена лабораторная установка для этого опыта:

Сила Лоренца, действующая на движущуюся частицу, вычисляется по следующей формуле:

Fл = |q|*V*B*sin(a).

Сила Лоренца будет направлена вдоль отрезка MN. Рассчитаем работу силы Лоренца:

A = Fл*l = |q|*V*B*l*sin(a).

ЭДС индукции — это отношение работы, совершаемой силой при перемещении единичного положительного заряда, к величине этого заряда. Следовательно, имеем:

Ei = A/|q| = V*B*l*sin(a).

Эта формула будет справедлива для любого проводника, движущегося в с постоянной скоростью в магнитном поле. ЭДС индукции будет только в этом проводнике, так как остальные проводники контура остаются неподвижными. Очевидно, что ЭДС индукции во всем контуре будет равняться ЭДС индукции в подвижном проводнике.

ЭДС из закона электромагнитной индукции 

Магнитный поток через тот же контур, что и в примере выше, будет равняться: 

Ф = B*S*cos(90-a) = B*S*sin(a).

Здесь угол (90-а) = угол между вектором магнитной индукции и нормалью к поверхности контура. За некоторое время ∆t площадь контура будет изменяться на ∆S = -l*V*∆t. Знак «минус» показывает, что площадь уменьшается. При этом за это время магнитный поток изменится:

∆Ф = -B*l*V*sin(a).

Тогда ЭДС индукции равна:

Ei = -∆Ф/∆t = B*l*V*sin(a).

Если весь контур будет двигаться внутри однородного магнитного поля с постоянной скоростью, то ЭДС индукции будет равняться нулю, так как будет отсутствовать изменение магнитного потока.

• ЭДС индукции будет возникать и при повороте рамки внутри магнитного поля.

Нужна помощь в учебе?

Предыдущая тема: Закон электромагнитной индукции:магнитный поток и электродвижущая сила
Следующая тема:&nbsp&nbsp&nbspЭлектродинамический микрофон: самоиндукция

Все неприличные комментарии будут удаляться.

ЭДС индукции в движущихся проводниках

ЭДС индукции в движущихся проводниках

Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.

На электрические заряды, перемещающиеся вместе с проводником в магнитном поле, действует сила Лоренца:

Fл = /q/vB sin a

Её направление можно определить по правилу левой руки.

Под действием силы Лоренца внутри проводника происходит распределение положительных и отрицательных зарядов вдоль всей длины проводника l.
Сила Лоренца является в данном случае сторонней силой, и в проводнике возникает ЭДС индукции, а на концах проводника АВ возникает разность потенциалов.

Причина возникновения ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца на свободные заряды.

Готовимся к проверочной работе!

1. При каком направлении движения контура в магнитном поле в контуре будет возникать индукционный ток?

2. Укажите направление индукционного тока в контуре при введении его в однородное магнитное поле.

3. Как изменится магнитный поток в рамке, если рамку повернуть на 90 градусов из положения 1 в положение 2 ?

4. Будет ли возникать индукционный ток в проводниках, если они движутся так, как показано на рисунке?

5. Определить направление индукционного тока в проводнике АБ, движущемся в однородном магнитном поле.

6. Указать правильное направление индукционного тока в контурах.

Следующая страница «Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе»
Назад в раздел «10-11 класс»

Электромагнитное поле — Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера — Действие магнитного поля на движущийся заряд.Магнитные свойства вещества — Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца — ЭДС электромагнитной индукции. Вихревое электрическое поле — ЭДС индукции в движущихся проводниках
— Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе

Т. ЭДС индукции в движ. проводниках — PhysBook

ЭДС индукции в движущихся проводниках

Выясним механизм возникновения ЭДС индукции в проводнике, движущемся в постоянном магнитном поле.

Пусть металлический проводник движется со скоростью \(~\vec v\), перпендикулярной вектору магнитной индукции \(~\vec B\) (рис. 1). Вместе с проводником, естественно, движутся свободные электроны. Следовательно, на электроны будет действовать сила Лоренца. Под действием этой силы свободные электроны перемещаются к одному из торцов проводника (на рис. 1, а к левому торцу), в результате происходит разделение зарядов: положительные заряды накапливаются на одном конце проводника, отрицательные — на другом. Эти заряды создадут внутри проводника электростатическое поле. Перераспределение зарядов будет происходить до тех пор, пока электрическая сила \(~\vec {F_e} = q \vec {E}\) не скомпенсирует силу Лоренца.

Рис. 1

Пусть средняя скорость упорядоченного движения электронов, обусловленная действием силы Лоренца, в системе отсчета, связанная с проводником, равна \(~\vec u \). Тогда скорость \(~\vec {v_0}\) движения электронов в инерциальной системе отсчета, в которой существует магнитное поле, будет равна \(~\vec{v_0} = \vec u + \vec v\), причем вектор \(~\vec {v_0}\) составляет угол α со скоростью \(~\vec v\) движения проводника. Сила Лоренца будет перпендикулярна \(~\vec {v_0}\) (рис. 1, б), и ее модуль \(~F_L = qBv_0\). Разложим вектор \(~\vec {F_L}\) на две составляющие: направленные вдоль проводника \(~\vec F_{L \parallel}\) и перпендикулярно проводнику \(~\vec F_{L \perp}\).

Продольная составляющая \(~\vec F_{L \parallel}\) и выполнит работу по разделению зарядов.

Из рис. 1, б видим, что \(~F_{L \parallel} = F_L \cos \varphi = qBv_0 \cos \varphi\), а \(~v_0 \cos \varphi = v\). Следовательно, \(~F_{L \parallel} = qBv\). Перемещение электронов прекратится, когда \(~F_{L \parallel} = F_e \), т.е. \(~ qBv = qE \). Напряженность электростатического поля связана с разностью потенциалов \(~ E = \dfrac Ul\). Из этих уравнений найдем \(~U = Bνl\). Таким образом, между концами проводника возникла разность потенциалов. Следовательно, сторонней силой, вызывающей разделение зарядов, является продольная составляющая силы Лоренца

. Работа, которую совершает эта сила при перемещении электрического заряда (электрона) вдоль проводника, \(~ A_1 = F_{L \parallel} l = qBvl \). ЭДС индукции в этом случае \(~ \varepsilon _i =\dfrac Aq = Bνl.\)

Если такой проводник замкнуть, то в цепи пойдет индукционный ток, направление которого можно определить по правилу правой руки (оно является частным случаем правила Ленца):

если правую руку расположить вдоль проводника так, чтобы перпендикулярная составляющая магнитной индукции \(~\vec {B_{\perp}}\) входила в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике.

Если \(~\vec v\) не перпендикулярно \(~\vec B\), то

\(~\varepsilon_i = Bvl \sin \alpha, \)

где α — угол между \(~\vec v\) и \(~\vec B\).

Пусть проводник перемещается в магнитном поле в направлении действия внешней силы \(~\vec F\). За время t, в течение которого электрон, движущийся со скоростью \(~\vec u\) вдоль проводника, пройдет расстояние \(~ l = ut\), проводник переместится на \(~\Delta r.\) \(~\Delta r = vt = v \dfrac lu\). Работа, которую совершит за это время перпендикулярная составляющая силы Лоренца,

\(~A_2 = F_{L \perp}\Delta r \cos 180 =-F_{L \perp}\Delta r = -F_L \sin \varphi \Delta r = -qBv_0 \sin \varphi \Delta r. \)

Из рисунка 1, б \(~\sin \varphi_0 = \dfrac u{v_0}\). Тогда \(~A_2 =-qBv_0 \dfrac u{v_0} v\dfrac lu = -qBvl.\)

Так как \(~A_2<0\), то происходит торможение движения проводника в магнитном поле. Для того чтобы проводник двигался равномерно, к нему необходимо приложить внешнюю силу, по модулю равную перпендикулярной составляющей силы Лоренца. Полная работа силы Лоренца \(~A = A_1-A_2=qBvl — qBvl = 0 .\) В данном случае имеет место превращение механической энергии источника внешней силы \(~\vec F\) в энергию индукционного тока. Это превращение происходит в соответствии с законом сохранения и превращения энергии.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 348-350.

План – конспект урока «ЭДС индукции в движущихся проводниках» (11 класс)

План – конспект урока

«ЭДС индукции в движущихся проводниках»

Выполнила студентка 5 курса

группы ФМ-112

очной формы обучения

физико-математического образования

Кежутина Ольга Владиславовна

Дата проведения: 21.09.16

Владимир 2016

Тема урока: ЭДС индукции в движущихся проводниках.

Класс: «11б»

Тип урока: урок усвоения новых знаний.

Методы изучения: объяснительно-иллюстративный с элементами эвристической беседы

Вид урока: урок-беседа.

Цель: выяснить условия возникновения ЭДВ в движущихся проводниках.

Задачи:

Образовательные: Дать понятие об энергетической характеристике индукционного электрического тока, возникающего в движущихся проводниках.

Воспитательные: Формирование умения культуры общения (внимательно слушать друг друга, анализировать услышанное), умения работать коллективно и в парах.

Развивающие: Развитие физического мышления учащихся, расширение понятийного аппарата учащихся, формирование умений анализировать информацию, делать выводы из наблюдений и опытов.

Оборудование: Гальванометр, магнит, проводник.

Ход урока:

Организационный этап.

12.00 – 12.01

-Здравствуйте, ребята, садитесь.

Представляется.

Ученики настраиваются на урок.

Актуализация знаний.

12.02–12.06

Фронтальный опрос:

1. В чем заключается явление электромагнитной индукции?

2. Сформулируйте закон электромагнитной индукции.

3. Что называется магнитным потоком?

4. Формула нахождения магнитного потока.

Ученики отвечают на вопросы:

1.явление электромагнитной индукции заключается в том, что ток возникает, когда изменяется магнитный поток, пронизывающий контур.

2. ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

.

3.Магнитным потоком Ф (потоком вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции В на площадь S и косинус угла а между векторами В и n.

4.

Мотивационный этап.

12.07 -12.09

На сегодняшнем уроке мы продолжаем исследовать причины возникновения индукционного тока в замкнутом проводящем контуре. На прошлых уроках мы с вами установили тот факт, что индукционный ток в контуре возникает либо если контур покоится в переменном магнитном поле, либо если он движется в постоянном магнитном поле. Первое условие возникновения индукционного тока мы с вами уже рассмотрели, и теперь двигаемся дальше. (Делаем схему)

Запись темы на доске: «ЭДС индукции в движущихся проводниках».

Наблюдают, отвечают на вопросы, вступают в дискуссию, делают выводы.

Изучение нового материала.

12.10– 12.25

 Итак, В первом случае, когда проводник покоится в переменном магнитном поле, мы уже научились определять направление индукционного тока. По какому правилу мы сможем определить направление индукционного тока в этом случае? Правильно. Необходимо теперь научится определять направление индукционного тока в случае если проводник движется в постоянном магнитном поле.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она-то и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

На многих электростанциях земного шара именно сила Лоренца вызывает перемещение электронов в движущихся проводниках.

Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (рис. 2.10). Пусть сторона контура MN длиной Iскользит с постоянной скоростью 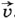 вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции  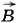однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Из закона электромагнитной индукции мы знаем что: .

Рассмотрим чему в этом случае будет равно изменение магнитного потока.

Обратите внимание на то что угол α это угол между векторами скорости и магнитной индукции, однако в определении магнитного потока берется угол между вектором нормали к плоскости проводника и вектором магнитной индукции, поэтому в нашем случае мы берем угол .

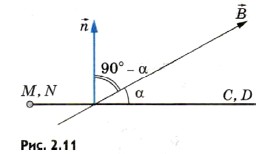
Отсюда получаем:

Теперь обратим внимание на те величины, которые не меняются (константы), их можно вынести за знак . Это и с учетом формул приведения.

Получаем:

Рассмотрим (из рисунка).

Окончательно получим:

– ЭДС индукции в движущихся проводниках, где

скорость движения проводника,

магнитная индукция,

l— длина активной части проводника,

угол между векторами и .

Итак, мы выяснили, как вычислить ЭДС индукции в движущихся проводниках, теперь давайте выясним, как определить направление индукционного тока в движущихся проводниках.

Причиной появления этой ЭДС является сила Лоренца, действующая на свободные заряды в движущемся проводнике. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

С учетом этого можно сформулировать следующее для определения направления индукционного тока в движущемся проводнике (правило левой руки):

нужно расположить левую руку так, чтобы вектор магнитной индукции B⃗  входил в ладонь, четыре пальца совпадали с направлением скорости υ⃗ проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока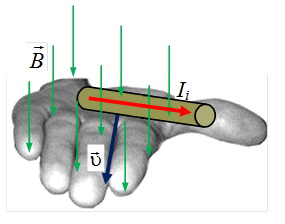

Примеры: Самолет, поезда.

Отвечают на вопросы, вступают в дискуссию, делают выводы, делают записи в тетрадях.

По правилу Ленца.

Вспомним чему равен магнитный поток.

Закрепление изученного материала

12.26 -12.40

Предлагает решить задачу:

№912.

На рисунке 100 представлены различные случаи электромагнитной индукции. Решить задачу для каждого случая.

№928. Найти ЭДС индукции в проводнике с длиной активной части 0,25 м, перемещающемся в однородном магнитном поле индукцией 8 мТл со скоростью 5 м/с под углом 30° к вектору магнитной индукции.

№930.

Решают задачи у доски и на местах.

Подведение итогов. Домашнее задание.

12.41-12.43

Выставление и обоснование отметок. Запись домашнего задания.

Д/З: §12 -13, №929

Записывают домашнее задание

Рефлексия

12.44 -12.45

Организуется беседа с целью осмысления участниками урока своих собственных действий в ходе урока.

Вопросы:

1. Что нового вы для себя узнали на уроке?

2. Понятен ли был материал урока?

3. Понравился ли вам урок?

Принимают участие в беседе

«ЭДС индукции в движущихся проводниках.» (11 класс)

Тема урока: ЭДС индукции в движущихся проводниках.

Тип урока: Комбинированный урок.

Цель урока: Дать понятие об энергетической характеристике индукционного электрического тока, возникающего в движущихся проводниках.

Демонстрации: Правила буравчика, правила левой руки, правила Ленца.

Используются технологии ИКТ для сопровождения изучения нового материала

Ход урока:

I. Организационный момент.

На сегодняшнем уроке мы продолжаем исследовать причины возникновения индукционного тока в замкнутом проводящем контуре. На прошлой неделе мы с вами установили тот факт, что индукционный ток в контуре возникает либо если контур покоится в переменном магнитном поле, либо если он движется в постоянном магнитном поле. Первое условие возникновения индукционного тока мы с вами уже рассмотрели, и теперь двигаемся дальше.

Тема сегодняшнего нашего урока » ЭДС индукции в движущихся проводниках».

Цель урока: познакомиться с понятием энергетической характеристики индукционного электрического тока, возникающего в движущихся проводниках.

II. Актуализация знаний.

К настоящему моменту мы с вами познакомились с рядом правил, которые используются для определения направления вектора магнитной индукции, индукционного тока, силы Ампера и Лоренца.

1. Правило буравчика.

2. Правило левой руки.

— Для движущегося участка проводника (формулировка и математическая запись закона Ампера)

— Для движущейся частицы (количественное определение силы Лоренца)

3. Правило Ленца (алгоритм применения правила к решению задач)

Все эти правила так или иначе связаны с явлением электромагнитной индукции.

— Когда и кем оно было открыто и в чем оно заключается?

(29 августа 1831 г., Майклом Фарадеем. Явление эл/м индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется)

— Сформулируйте закон электромагнитной индукции.

(ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром )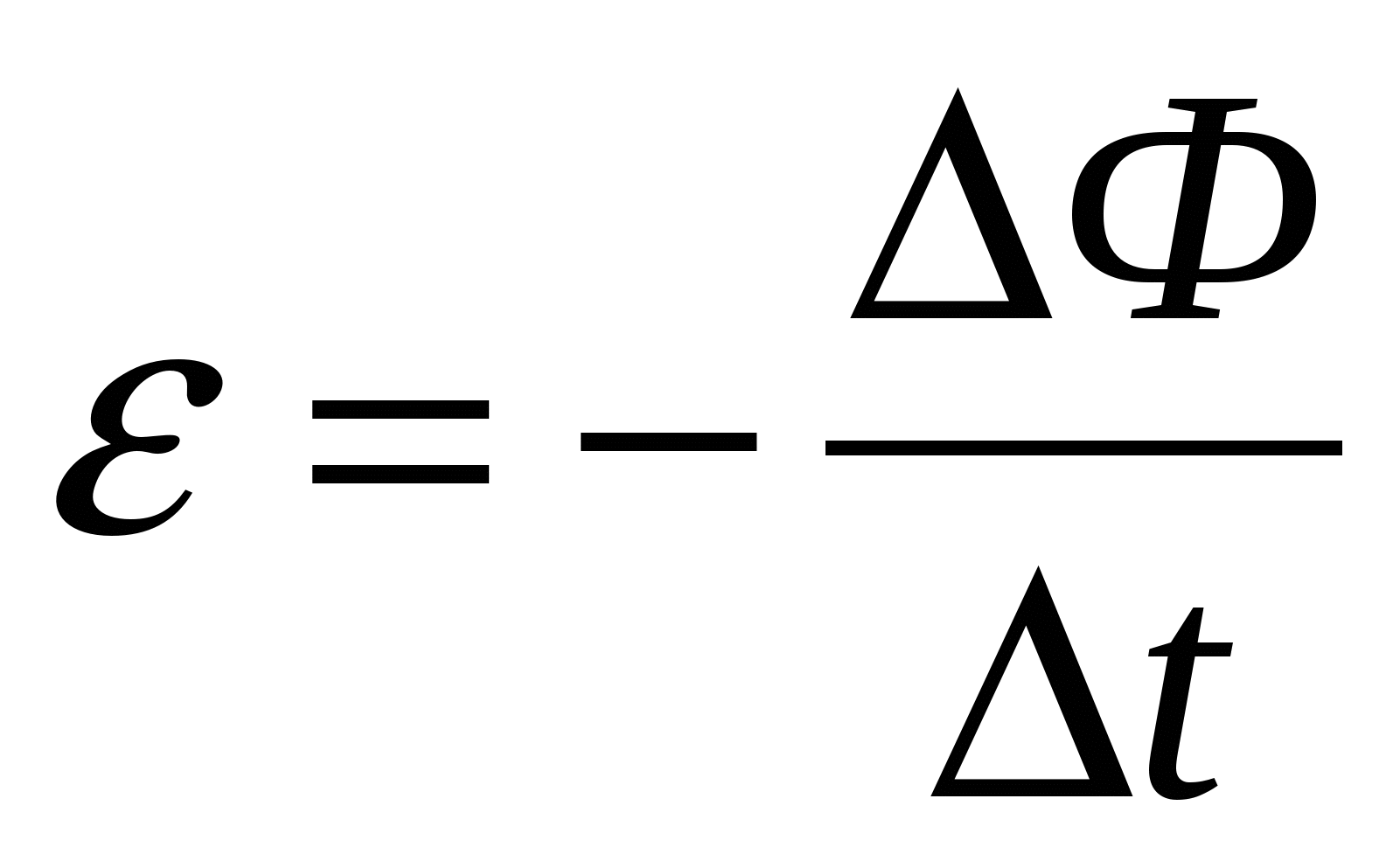

— Что является причиной возникновения индукционного тока в проводнике, покоящемся в переменном магнитном поле?

(Индукционный ток в неподвижном замкнутом контуре, находящемся в переменном магнитном поле, вызывается электрическим полем, порождаемым переменным магнитным полем, которое называется вихревым)

— Чему равна работа этого электрического поля?

(работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике)

III. Изучение нового материала.

1. Если проводник движется в постоянном магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на них со стороны магнитного поля действует сила Лоренца. Она-то и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле.

Пусть сторона контура MN длиной l скользит с постоянной скоростью υ вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции 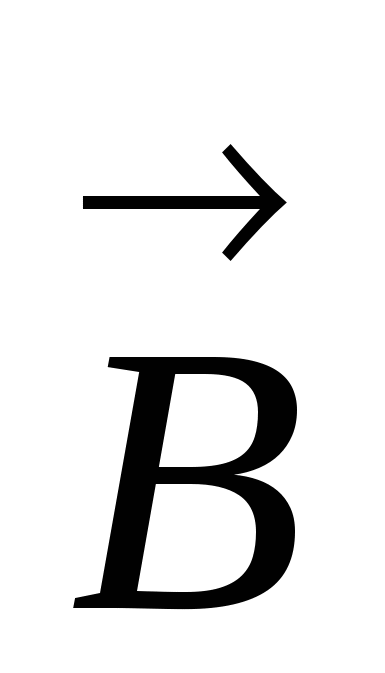однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю .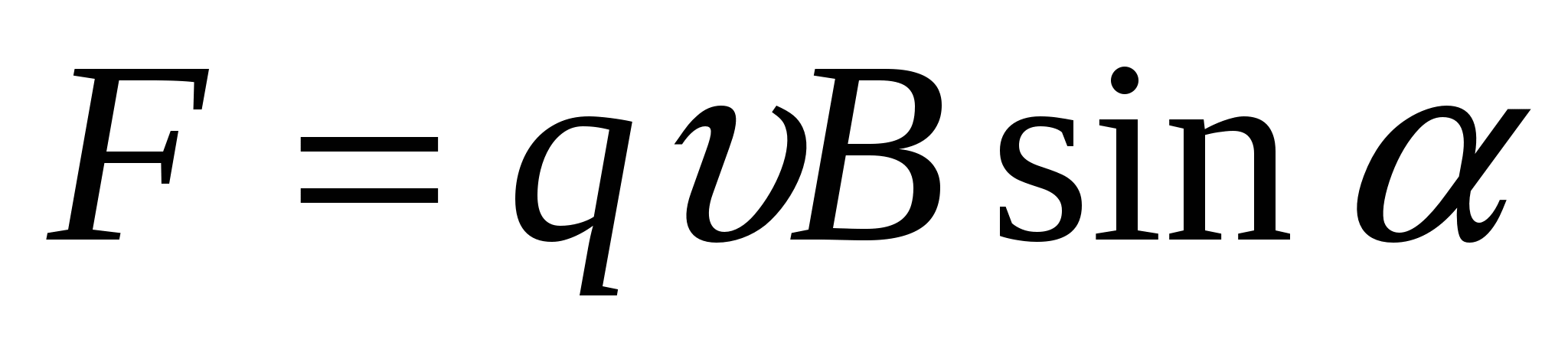

Направлена она вдоль проводника MN.

Работа данной силы на пути l положительна и равна .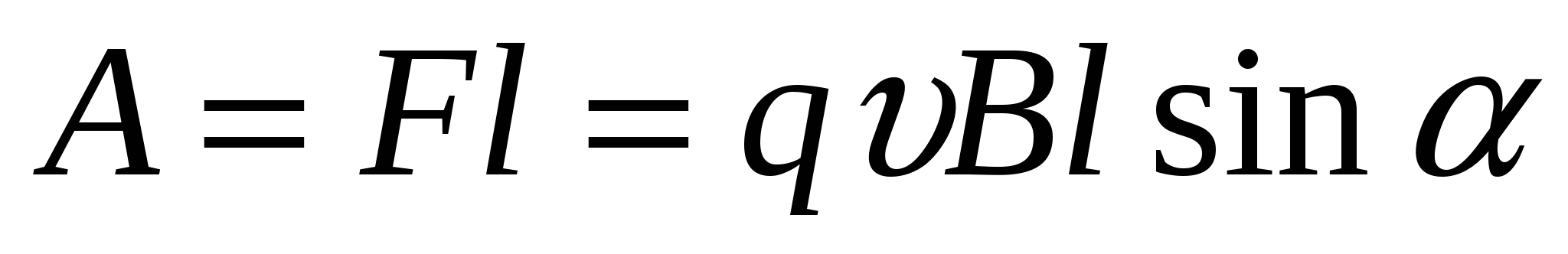

ЭДС индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду. .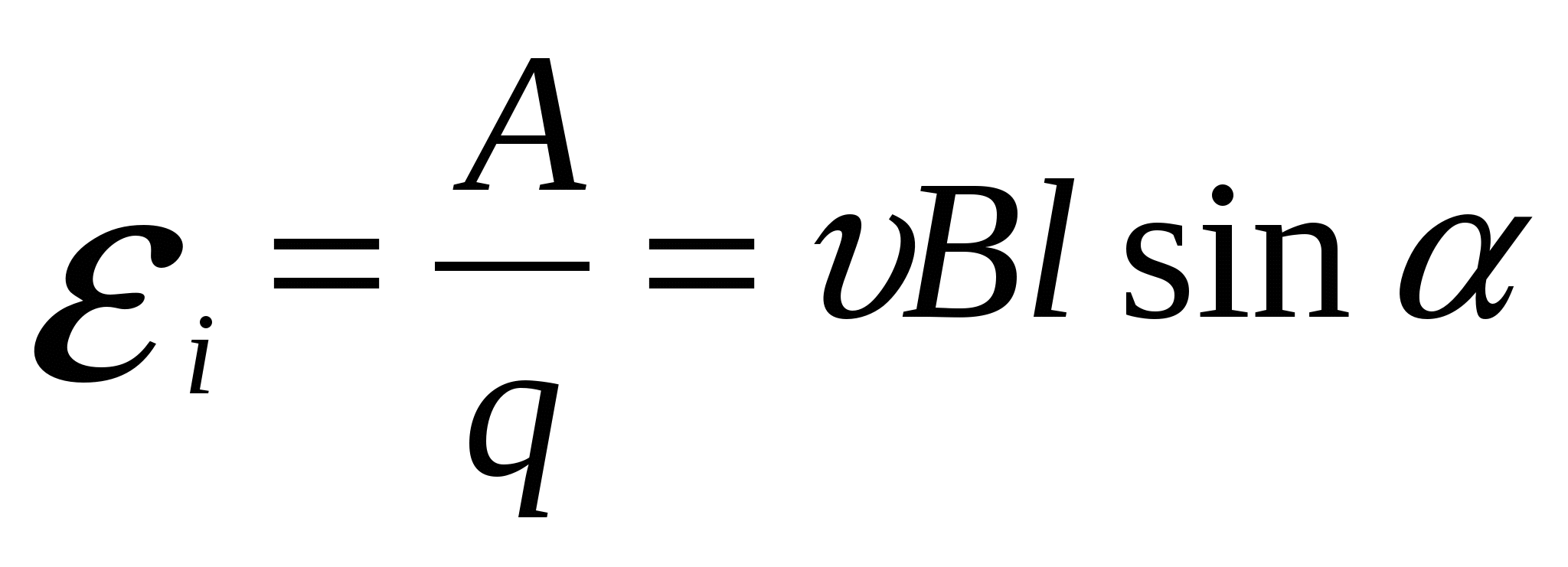

2. С другой стороны, ЭДС индукции можно вычислить с помощью закона эл/м индукции.

Магнитный поток через контур MNCD равен ,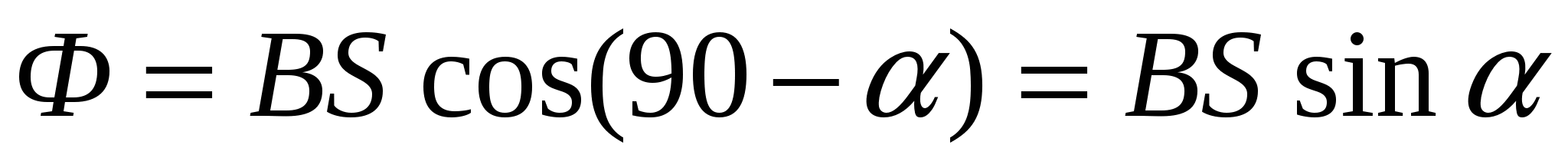

где угол 90°- есть угол между вектором 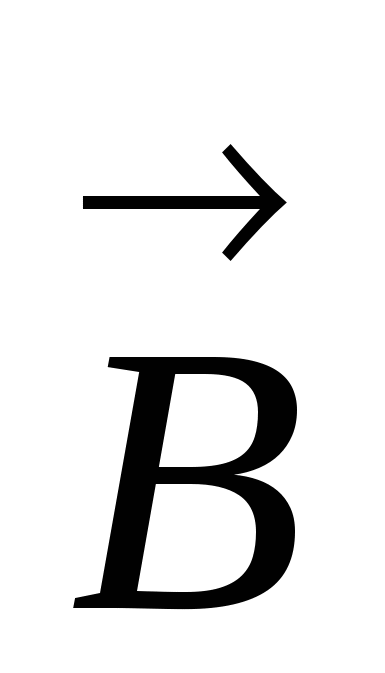и нормалью 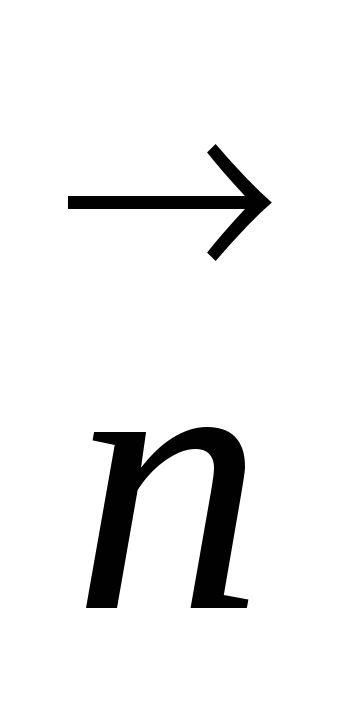к плоскости контура,

а S — площадь контура MNCD.

При перемещении проводника площадь S изменяется со временем следующим образом

За время площадь контура меняется на 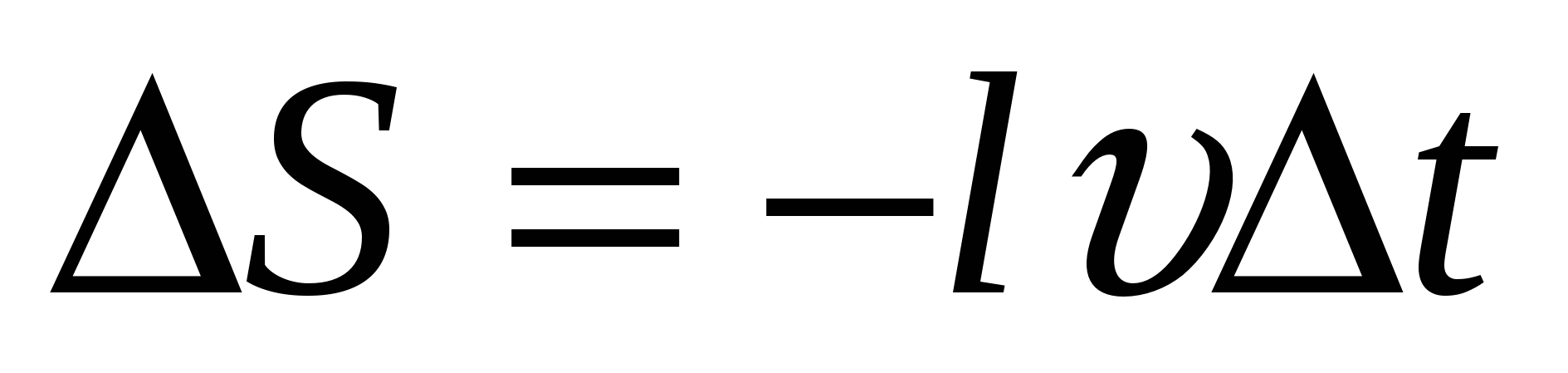. Знак минус указывает на то, что она уменьшается.

Изменение магнитного потока за это время равно .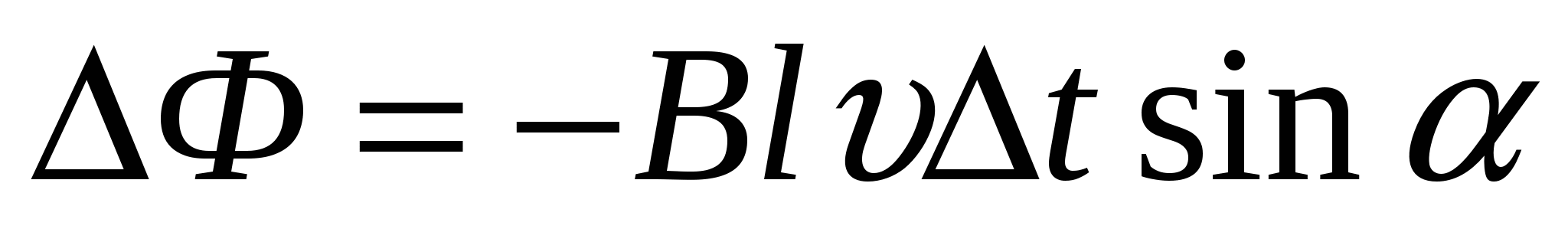

Следовательно, .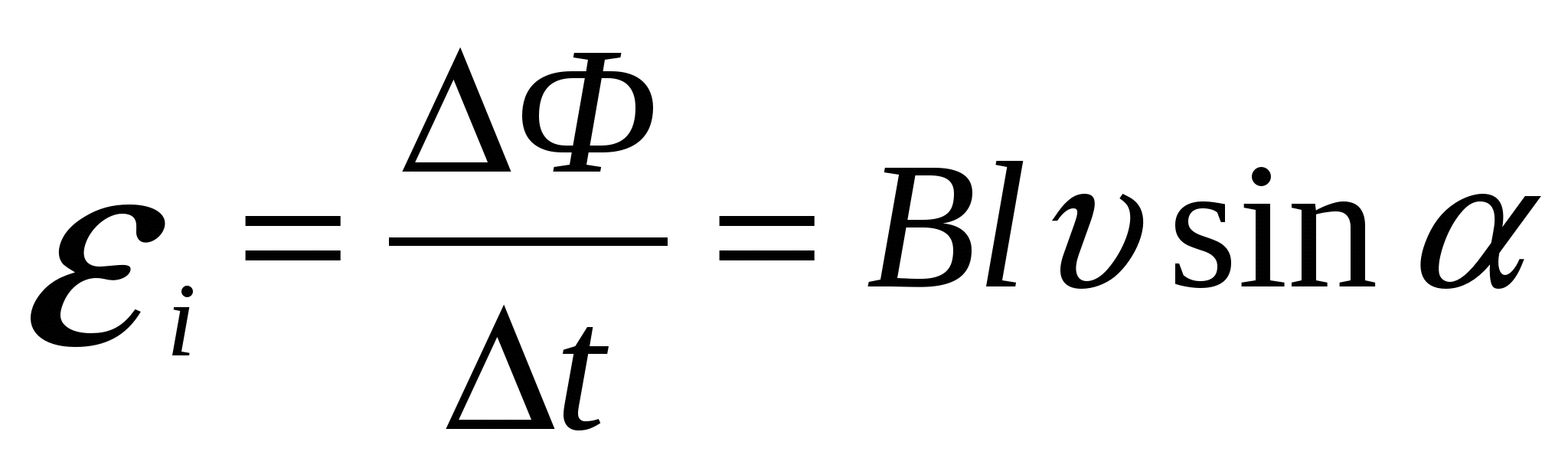

IV. Закрепление изученного.

Решение задач.

1. Найти ЭДС индукции в проводнике с длиной активной части 25 см, перемещающемся в однородном магнитном поле индукцией 8мТл со скоростью 5 м/с под углом 30° к вектору магнитной индукции. (0,005 В)

2. С какой скоростью надо перемещать проводник, длина активной части которого 1 м, под углом 60° к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции 1В? Индукция магнитного поля равна 0,2 Тл. (5,8 м/с)

V. Итог урока.

Итак, на сегодняшнем уроке мы с вами выяснили, что ЭДС индукции в проводниках, движущихся в постоянном магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца.

Для количественного определения ЭДС нам необходимо знать индукцию постоянного магнитного поля, длину активной части проводника, скорость движения проводника в магнитном поле и угол между вектором магнитной индукции и вектором скорости движения.

VI. Домашнее задание.

§ 13, упр.2(9), №902(1,3)

38. Вывод эдс индукции из закона сохранения энергии. Механизм возникновения эдс индукции. Вихревые токи (Токи Фуко)

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции 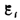 определяются только скоростью изменения магнитного потока, т. е.

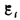
Теперь необходимо выяснить знак 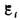. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.

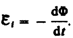(123.2)

Знак минус показывает, что увеличение потока 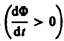вызывает э. д. с.  т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока 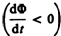вызывает  т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

Механизм возникновения э.д.с. индукции можно пояснить на простом примере. Пусть изменение магнитного потока, пронизывающего контур, проис-ходит за счет изменения площади контура вследствие движения одного из проводников, составляющих контур. Пусть, например, контур образован п-образным проводником 1 и скользящей перемычкой 2 (рис. 3.12), и пусть линии индукции магнитного поля В перпендикулярны плоскости контура и направлены от нас (показаны крестиками).

П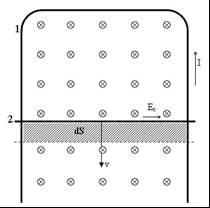ри скольжении перемычки вниз площадь контура S будет возрастать, что приведет к возрастанию магнитного потока, равного ВS. При этом, со-гласно закону Фарадея должна возникнуть э.д.с. индукции. Непосредственной физической причиной возникновения индукционного тока в контуре в данном случае является сила Лоренца. Действительно, при движении перемычки вниз со скоростью v, с той же скоростью будут перемещаться находящиеся в ней электроны. Сила Лоренца, действующая на каждый электрон, будет равна evB (где е — заряд электрона) и направлена влево. Формально эту силу можно рассматривать как проявление поля сторонних сил, имеющего напряженность Е_с. Из формулы (2.22) вытекает, что   Е_с = vB. Электродвижущая сила индукции Е_i, создаваемая полем Е_сво всей движущейся перемычке длиной l будет согласно (2.24) равна

Е_i = òЕ_сldl = Е_сl = vBl (3.25)

Скорость v движения перемычки представим как производную dx/dt. Тогда

Е_i = В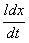= В(3.26)

В (3.26) учтено, что произведение ldx представляет со-бой приращение dS площади контура.  В свою очередь произведение BdS равно приращению dФ магнитного потока. В итоге мы получаем, что э.д.с. индукции равна производной dФ/dt от магнитного потока

Е_i = dФ/dt,(3.27)

то есть мы пришли к закону Фарадея. В проведенных рассуждениях мы для простоты оперировали модулями векторов Е_с,  v  и  В, поэтому ве-личину э.д.с. индукции в формуле (3.27)  определили также лишь по модулю.

Рассмотренное объяснение механизма возникновения э.д.с. индукции относится к случаю, когда изменение магнитного потока происходит за счет подвижных проводников. Но магнитный поток может меняться также и путем изменения величины В при неизменной геометрии контура. Тогда сила Лоренца не возникает, а ин-дукционный ток возбуждается в этом случае вихревым электрическим полем, порождае-мым меняющимся во времени магнитным полем. Этот более общий случай возникновения э.д.с. индукции будет рассмотрен в следующем разделе (тема 4).

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.

Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и др.

Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.

Опыты Фарадея. Закон Фарадея. Правило Ленца. ЭДС индукции в неподвижных проводниках.

1. Опыты Фарадея

а) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится.

б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра. Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток.

Возникновение индукционного тока означает, что в контуре действует электродвижущая сила _i – ЭДС индукции.

 

ЭДС индукции, возникающая в проводящем контуре, равна скорости изменения магнитного потока через площадь, ограниченную этим контуром – закон Фарадея.

Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Знак минус в законе Фарадея является математическим выражением правила Ленца.

Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из N витков (например, соленоид), то если витки соединены последовательно, _i будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности:

— потокосцепление или полный магнитный поток.

Если Ф₁ =Ф₂=…=Ф_n, то

Т.к. Ф_B=BScosα,то для того чтобы изменить магнитный поток Ф можно изменить:

1) магнитное поле 2) площадь S3) угол α.

 

Индуктивность соленоида.

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) , которая выражается в системе СИ в тесла [Тл], внутри катушки является фактически постоянной и (приближённо) равна

где − магнитная постоянная, − число витков, − ток, записанный в амперах [А] и − длина катушки в метрах [м]. Пренебрегая краевыми эффектами на концах соленоида, получим^[16], что потокосцепление через катушку равно плотности потока [Тл], умноженному на площадь поперечного сечения [м²] и число витков :

Отсюда следует формула для индуктивности соленоида (без сердечника):

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель — относительную магнитную проницаемость^[17] сердечника:

В случае, когда , можно (следует) под S понимать площадь сечения сердечника [м²] и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.