Site Loader
Posted on 08.06.2020

Сложение векторов

Откладывание вектора от данной точки

Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Определение 1

Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).

$\overrightarrow{a}$ отложенный от точки $A$

Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

Теорема 1

От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

  1. Вектор $\overrightarrow{a}$ — нулевой.

    В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.

  2. Вектор $\overrightarrow{a}$ — ненулевой.

Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)

Иллюстрация теоремы 1

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Сложение векторов. Правило треугольника

Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.

Определение 2

Суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ называется вектор $\overrightarrow{c}=\overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $\overrightarrow{AB}=\overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $\overrightarrow{BC}=\overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис. 3).

Сумма векторов

Рисунок 3. Сумма векторов

Замечание 1

Иначе, определение 2, еще называют

правилом треугольника для сложения двух векторов.

Из этого правила следует несколько свойств сложения двух векторов:

  1. Для любого вектора $\overrightarrow{a}$ выполняется равенство

    \[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\]

  2. Для любых произвольных точек $A,\ B\ и\ C$ выполняется равенство

    \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]

Замечание 2

Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.

Правило параллелограмма

Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.

Теорема 2

Для любых треух векторов $\overrightarrow{a},\ \overrightarrow{b}\ и\ \overrightarrow{c}$ справедливы следующие два закона:

  1. Переместительный закон:
\[\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\]
  1. Сочетательный закон:
\[\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)\]

Доказательство.

Переместительный закон:

  1. Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ не коллинеарны.

    Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $\overrightarrow{a}+\overrightarrow{b}\ и\ \overrightarrow{b}+\overrightarrow{a}$. Получим следующий рисунок (рис 4).

    Иллюстрация переместительного закона

    Рисунок 4. Иллюстрация переместительного закона

    Очевидно, что $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, а $\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$

    Следовательно, $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$.

  2. Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ коллинеарны.

    Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $\left|\overrightarrow{a}+\overrightarrow{b}\right|и\ |\overrightarrow{b}+\overrightarrow{a}|$.

Сочетательный закон:

Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $\overrightarrow{AB}=\overrightarrow{a}$, от полученной точки $B$ — вектор $\overrightarrow{BC}=\overrightarrow{b}$ и от точки $C$ — вектор $\overrightarrow{CD}=\overrightarrow{c}$ (Рис. 5).

Иллюстрация сочетательного закона

Рисунок 5. Иллюстрация сочетательного закона

Из свойства правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:

Следовательно, $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$.

Теорема доказана.

Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $\overrightarrow{AB}=\overrightarrow{a}$ и $\overrightarrow{AD}=\overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$.

Пример задачи на сложение векторов

Пример 1

Дан четырехугольник $ABCD$. Доказать, что $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD}$

Иллюстрация сочетательного закона

Рисунок 6.

Доказательство.

Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:

\[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\]

ч. т. д.

Сложение векторов

Суммой x+y векторов x и y называется вектор, проведенный из начала x к концу у, если вектор у параллельно перемещен так, что конец x и начало y совмещены.

Сложение векторов

Рис. 1

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим сумму z=x+y векторов Сложение векторов

и Сложение векторов.

Для построения суммы векторов z=x+y, нужно переместить параллельно вектор y так, чтобы начало вектора y совпало с концом вектора x. Тогда конец полученного вектора y’ будет конечной точкой суммы векторов z=x+y.

Таким образом, для получения суммы векторов x и y достаточно сложить соответствующие координаты векторов x и y:
Сложение векторовСложение векторов

На рисунке Рис. 1 в двухмерном пространстве представлен процесс сложения векторов x=(9,1) и y=(2,4).

Вычислим z=x+y=(9+2, 1+4)=(11,5). Сравним полученный результат с геометрической интерпретацией. Действительно, после параллельного перемещения вектора y на позицию y’ и сложения x и y’, получим вектор z=(11,5).

Вариант 2. Начальные точки векторов произвольные.

Рассмотрим процесс сложения двух векторов x и y. Пусть вектор x имеет начальную точку Сложение векторов и конечную точкуСложение векторов

, а вектор y — начальную точку Сложение векторов и конечную точку Сложение векторов. Для того, чтобы параллельно переместить вектор y, нужно каждый элемент i точек C и D увеличить на соответствущую величину γi:

Сложение векторов(1)

а для того, чтобы точка C переместилась в точку B, должны выполняться условия

Сложение векторов(2)

Следовательно

Сложение векторов(3)

Подставляя (3) в (1), получим:

Из выражений (4) видно, что точка C’ совпала с точкой B, и, следовательно, вектор Сложение векторовпереместился в нужную позицию BD’. Таким образом, начальная точка вектора x+y будет точка A, а конечная точка — будет точка D’, которая вычисляется из выражения в (4).

Сложение векторов

Рис. 2

На рисунке Рис.2, для получения суммы векторов x и y, вектор y перемещается параллельно так, чтобы его начало совмещалось с концом вектора x (вектор y’ ). Вектор z=x+y получится соединив начало x и конец вектора y’.

Рассмотрим процесс сложения векторов, начальные точки которых не совпадают с началом координат. На Рис.2 представлен процесс сложения векторов x=AB и y=CD, где A(1,1), B(10,-3), C(1,2), D(2,7). Из выражений (4) вычисляем координаты точки D’:

Сумма векторов z=x+y будет иметь начальную точку A(1,1) и конечную точку D'(11,2).

Операция сложения векторов обладает следующими свойствами:

1. x+y=y+x (коммутативность).

2.(x+y)+w=x+(y+w) (ассоциативность).

3. x+0=x (наличие нулевого вектора).

4. x+(-x)=0 (наличие противоположного вектора).

Пример сложения двух векторов

Пример 1. Вычислить сумму векторов AB и CD, где A(2,2), B(7,6), C(5,6), D(10,7).

Вычислим новое расположение точек C и D, используя выражения (4). Тогда

C'(7,6), D'(10+7-5, 7+6-6)=D(12,7).

Сумма векторов AB и CD будет вектор AD’, где A(2,2), D‘(12,7).

Пример 2. Вычислить сумму векторов AB и у, где A(4,3), B(5,8), y=(7,3).

Так как вектор y представлен в виде координат, то это означает, что начальная точка вектора y является C(0,0) а конечная точка — D(7,3).

Вычисляя новое расположение вектора y, получим новые точки

C'(5,8), D'(7+5-0, 3+8-0)=D'(12,11).

Наконец, сумма векторов AB и y будет вектор AD’, где A(4,3), D’(12,11).

Сложение и вычитание векторов. Геометрия, 9 класс: уроки, тесты, задания.

1. Сложение векторов

Сложность: среднее

1
2. Сложение векторов по правилу многоугольника

Сложность: среднее

1
3. Сложение и вычитание векторов

Сложность: среднее

1
4. Сложение векторов по закону многоугольника

Сложность: среднее

2
5. Сложение векторов в четырёхугольнике

Сложность: среднее

1
6. Разность векторов в ромбе

Сложность: среднее

1
7. Выражение вектора в четырёхугольнике

Сложность: среднее

1
8. Сложение перпендикулярных векторов

Сложность: сложное

3

12-г. Сложение и вычитание векторов

      § 12-г. Сложение и вычитание векторов

На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.

Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).

Укрупнённый чертёж перемещения груза до середины моста (повтор чертежа предыдущего параграфа).

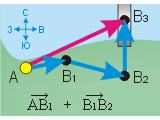
Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое, сумму векторов AВ1 и В1В2.

Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).

Иллюстрация сложения двух векторов по правилу параллелограмма.

Итак, мы нашли вектор суммы или сумму векторов: _?_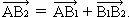

Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив правило паралеллограмма.

Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.

Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.

Другими словами, сейчас мы ищем вектор разности: _?_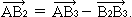

На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.

Иллюстрация вычитания двух векторов по правилу треугольника.

Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.

Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом». Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде (см. § 12-л, а также § 13-з, § 13-и).

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!