Эффект Холла
a
b
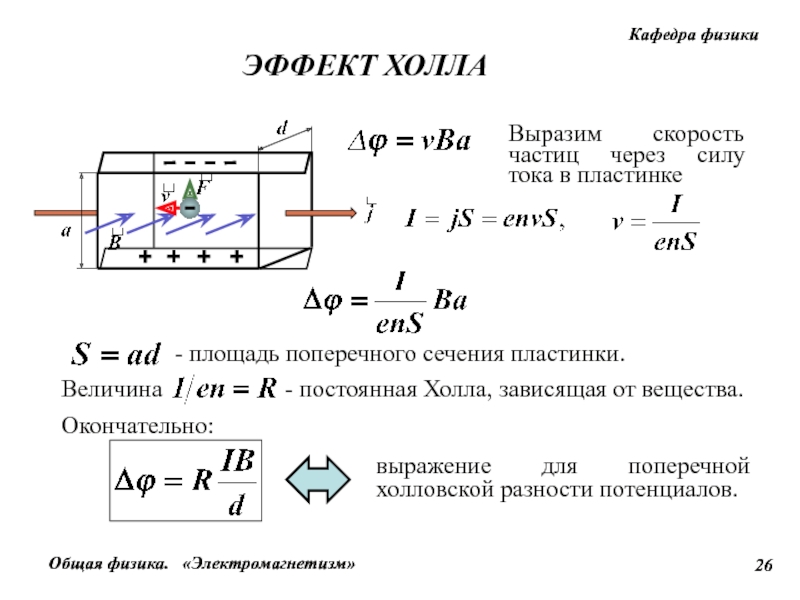
Рисунок
1.6. — Схема эксперимента
Холла: a – геометрия
опыта; b – поле Холла
в стационарном режиме (при
установившейся дрейфовой
скорости v). Индукция
магнитного поля направлена
перпендикулярно плоскости
чертежа, к наблюдателю.
Схема эксперимента Холла изображена на рис. 1.6. Имея дело с немагнитными и слабомагнитными материалами можно считать магнитным полем величину H, поскольку разница между H и B в этом случае чрезвычайно мала. К проводнику, расположенному вдоль оси , приложено электрическое поле , вызывающее электрический ток . Помимо того, имеется магнитное поле , параллельное оси . В результате появляется сила Лоренца:
 31)
31)
отклоняющая
электроны в отрицательном
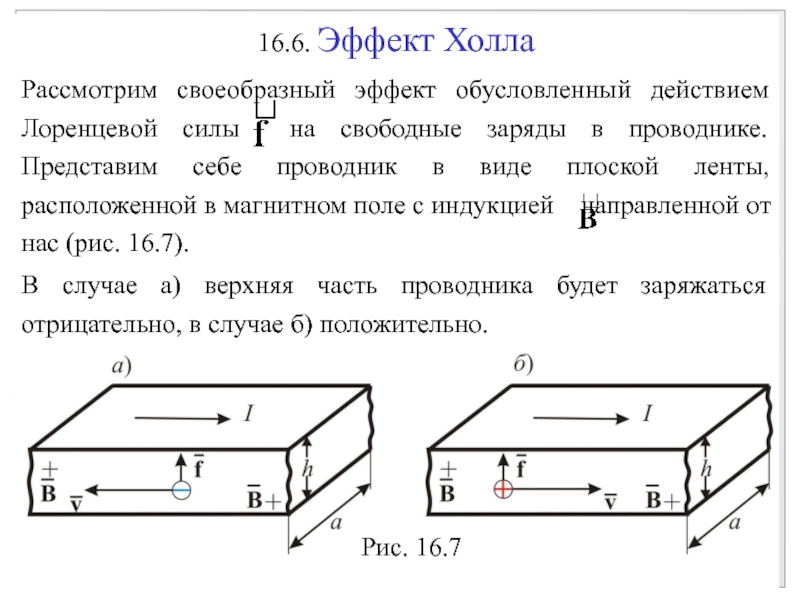
Две величины представляют здесь интерес. Одна из них — это отношение поля вдоль проводника Ех к плотности тока jx:
 32)
32)
Холл обнаружил, что эта величина (магнетосопротивление) не зависит от поля. Другой характеристикой является величина поперечного поля Е
Следует обратить внимание на то, что, поскольку поле Холла направлено против оси у (рис. 1.6), коэффициент RH должен быть отрицательным. С другой стороны, если бы заряд носителей был положительным, знак их
 В результате поле Холла имело
бы направление, противоположное тому,
которое оно имеет при отрицательно заряженных
носителях. Этот вывод очень важен, поскольку
он означает, что измерения поля Холла
позволяют определить знак носителей
заряда. Экспериментальные данные, впервые
полученные Холлом, находились в согласии
со знаком заряда электрона, определенным
позднее Томсоном. Одна из замечательных
особенностей эффекта Холла заключается,
однако, в том, что в некоторых металлах
коэффициент Холла положителен, и поэтому
носители в них должны, видимо, иметь заряд,
противоположный заряду электрона.
В результате поле Холла имело
бы направление, противоположное тому,
которое оно имеет при отрицательно заряженных
носителях. Этот вывод очень важен, поскольку
он означает, что измерения поля Холла
позволяют определить знак носителей
заряда. Экспериментальные данные, впервые
полученные Холлом, находились в согласии
со знаком заряда электрона, определенным
позднее Томсоном. Одна из замечательных
особенностей эффекта Холла заключается,
однако, в том, что в некоторых металлах
коэффициент Холла положителен, и поэтому
носители в них должны, видимо, иметь заряд,
противоположный заряду электрона.Чтобы рассчитать коэффициент Холла, определим в начале плотности тока jx и jy в случае, когда имеется электрическое поле с произвольными компонентами Ех и Еу, а также магнитное поле Н, направленное вдоль оси z. На каждый электрон, движущийся с дрейфовой скоростью действуют электрическое и магнитное поля, следовательно действует (не зависящая от пространственных координат) сила:
 34)
34)
поэтому уравнение движения электронов для импульса в расчете на один электрон будет выглядеть так:
где второй член в правой части введён, чтобы учесть электрическое сопротивление; — импульс электрона; — время между последовательными соударениями (время свободного пробега).

Для геометрии опыта, представленном на (рис. 1.6), представим в записи по компонентам:
где используются обозначения для циклотронной частоты обращения электронов по спиральным орбитам в магнитном поле:
В стационарном
состоянии ток и дрейфовая
скорость не зависит от времени и
поэтому (2.37) имеет вид:
 39)
39)
Запишем закон Ома по компонентам:
где — статическая удельная электропроводность.
Умножив обе части равенств (2.39) на и учитывая (2.40) получим:
Учтём геометрию опыта (рис. 1.6): , и нет тока в направлении Y, , в результате (2.41) примет вид:
 42)
42)
Поле , существующее благодаря действию силы Лоренца, и получило название поля Холла:
где введена постоянная Холла:
Коэффициент Холла не зависит ни от каких параметров металла, кроме плотности носителей. Выше мы уже вычисляли n, предполагая, что валентные электроны атома в металле превращаются в электроны проводимости. Измерение коэффициента Холла дает прямой способ проверки справедливости такого предположения .
При выводе
уравнения для ЭДС Холла сделан
ряд допущений, связанных с тем, что
полная скорость электронов принимается
раной дрейфовой скорости, т.
При попытках
определить плотность электронов n, используя результаты измерений
коэффициентов Холла, возникает трудность,
связанная с тем, что в действительности
в противоречие с формулой (2.44) эти коэффициенты
обычно зависят от магнитного поля. Кроме
того, они зависят от температуры и от
того, насколько тщательно приготовлен
образец. Это кажется довольно странным,
поскольку время релаксации, которое может
сильно зависеть от температуры и состояния
образца, в (2.44) не фигурирует. Тем не менее,
при самых низких температурах для очень
чистых, тщательно приготовленных образцов
в чрезвычайно сильных полях измеряемые
значения постоянной Холла, по-видимому,
действительно стремятся к некоторому
пределу .
Отрицательное значение соответствует электронам. Вообще, знак константы Холла зависит от типа носителей зарядов и, например, в дырочном полупроводнике . Важным следствием формулы (2.44) является возможность экспериментального определения концентрации заряженных частиц с помощью эффекта Холла и в металлах, и в полупроводниках.
Коэффициенты
Холла для некоторых металлов
приведены в таблице №2.
| Металл | Металл | ||||
| Эксперимент | Расчёт | Эксперимент | Расчёт | ||
| Li | -1.70 | -1.33 | Cu | -0.54 | -0.74 |
| Na | -2.34 | -2.3 | Ag | -0. 90 90 | -1.07 |
| K | -4.45 | -4.45 | Au | -0.72 | -1.06 |
| Rb | -5.04 | -5.4 | |||
Таблица №2. Экспериментальные и вычисленные значения константы Холла.
Расчёт по формуле (2.44) в предположении, что число электронов равно числу атомов .
Применение
константы Холла для расчёта
электрофизических свойств твёрдых
тел показало ошибочность теории
Друде для некоторых металлов.
Теоретический результат Друде подтверждает
экспериментальное наблюдение Холл, не
обнаружившего зависимости сопротивления
от поля. Действительно, при (как это имеет место в стационарном
состоянии, когда поле Холла уже установилось)
первое из уравнений (2.41) сводится к уравнению , то есть проводимость имеет такую
же величину, как и в нулевом магнитном
поле. Однако, как показали более точные
эксперименты на многих металлах, в действительности
сопротивление обнаруживает зависимость
от магнитного поля, в ряде случаев очень
сильную. Объяснение того, почему теория
Друде оказывается применимой для одних
металлов, а для других возникают такие
разительные расхождения, должна дать
квантовая теория твердого тела (Ашкрофт).
Объяснение того, почему теория
Друде оказывается применимой для одних
металлов, а для других возникают такие
разительные расхождения, должна дать
квантовая теория твердого тела (Ашкрофт).
Фактически
формула (2.44) справедлива для произвольной
сферы в — пространстве, заполненной носителями.
Теория эффекта Холла и других гальваномагнитных
явлений основывается очевидно, на существенном
использовании теоремы Блоха и на описании
электронных состояний в пространстве
обратной решётки. В неупорядоченной системе,
когда компоненты вектора уже не есть хорошие квантовые числа,
выводы, полученные с помощью кинетического
уравнения, сразу же попадают под сомнение.
Фактически, однако, пока ещё нет точной
теории, с помощью которой можно заменить
можно заменить простую формулу (2.44). Последняя
формула дает вполне удовлетворительное
согласие с опытными данными для жидких
металлов, несмотря на то что длина свободного
пробега электрона оказывается там порядка
межатомного расстояния. Неясно, однако,
можно ли наблюдать эффект Холла в предельном
случае прыжковой проводимости по локализованным
состояниям .
Неясно, однако,
можно ли наблюдать эффект Холла в предельном
случае прыжковой проводимости по локализованным
состояниям .
Для характеристики
напряженности магнитного поля удобно
использовать безразмерную величину , играющую в теории важную роль. Когда
величина мала, из уравнений (2.41) следует, что
ток j почти параллелен Е, как это
было бы в отсутствие магнитного поля.
В общем случае ток j направлен к Е под углом (называемым углом Холла). Из уравнений
(2.41) следует, что . Величина , называемая циклотронной частотой,
представляет собой просто круговую частоту
вращения свободного электрона в магнитном
поле H. Произведение мало, если электроны между столкновениями
могут проделать лишь малую часть оборота,
и велико, если они могут совершить много
оборотов. Иначе говоря, когда , магнитное поле лишь слегка деформирует
орбиты электронов, а когда величина сравнима с единицей и больше, то влияние
магнитного поля на орбиты электронов
становится преобладающим. Для численной
оценки циклотронной частоты удобна формула:
Для численной
оценки циклотронной частоты удобна формула:
Исследование эффекта Холла в полупроводниках. Построение графиков и определение концентрации зарядов
Физика \ Физика
Страницы работы
16 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
Министерство информационных технологий и связи
ГОУ ВПО СибГУТИ
Кафедра физики
Лабораторная работа №6.10 на тему:
«Исследование эффекта холла в полупроводниках»
Проверил:
Черевко А.Г.
Выполнил:
студент группы П-62
Илларионов В.В.
Новосибирск 2007
Содержание:
1. Цель
работы…………………………………………………………………………стр 3
Цель
работы…………………………………………………………………………стр 3
2. Краткая теория…………………………………………………………………… стр 4
3. Описание установки………………………………………………………… стр 8
4. Выполнение работы………………………………………………………… стр 9
5. Результаты измерений…………………………………………………… стр 12
6. Контрольные вопросы…………………………………………………… стр 15
7. Выводы………………………………………………………………………………… стр 16
Цель работы
· Изучить теорию эффекта Холла
· Исследовать зависимость ЭДС Холла (Ux) от величины индукции внешнего магнитного поля (B) и силы тока(I), протекающего через образец.
· Определить концентрацию основных носителей заряда (n) и их подвижность(µ).
Краткая теория
Эффектом
Холла называют явление возникновения э.д.с. в помещённом в магнитное поле
полупроводнике, по которому протекает электрический ток. Пусть полупроводник
имеет форму параллелепипеда длиной L и сечением, a *Ь и по нему протекает ток L перпендикулярно сечению. Полупроводник находится в однородном магнитном поле с индукцией В, направление
которой перпендикулярно направлению тока и указано на рисунке 10.1
Полупроводник находится в однородном магнитном поле с индукцией В, направление
которой перпендикулярно направлению тока и указано на рисунке 10.1
Рисунок 10.1- Механизм возникновения холловской э.д.с.
Опыт показывает, что между точками А и С .расположенными
на нижней и верхней гранях образца, возникает разность потенциалов, названная
э.д.с. Холла, которая возрастает с увеличением тока I и вектора магнитной
индукции В: Ux ~ I В. Объясняется возникновение Uxсмещением движущихся
зарядов к верхней или нижней грани образца под действием силы Лоренца. Если основными
носителями заряда являются дырки, то силой Лоренца (см. рисунок 10.1) они
отклоняются к нижней грани образца, и там накопится положительный заряд, а на
верхней останется не скомпенсированный отрицательный заряд. Если основными
носителями заряда являются электроны, то они будут также отклоняться и
накапливаться на нижней грани, создавая на ней отрицательный заряд. (Вспомните
правило левой руки, по которому в данном случае определяем направление силы
Лоренца).
Величина силы Лоренца определяется соотношением:
где q — заряд носителя, vd— его дрейфовая скорость. Смещение носителей заряда в поперечном (по отношению vd и В) направлении прекратится тогда, когда сила Лоренца уравновесится силой F электрического поля, создаваемого сместившимися зарядами. Если B┴vd, то:
Дрейфовая скорость может быть выражена из формулы для плотности дрейфового тока:
Если плотность тока Jодинакова во всех точках сечения а * b, то:
После подстановки уравнений (4) и (3) в формулу (2) получим:
Считая возникшее поле однородным, найдем холловское напряжение на контактах АС, используя связь напряженности Ехи разности потенциалов Ux :
Предложенный вывод выражения для Uxнагляден, но недостаточно
строг. Не был учтён статистический характер распределения носителей заряда по
скоростям. Это значит, что уравнение (2) не может выполняться одновременно для
всех электронов (или дырок), имеющих различные по величине и направлению
скорости. Поэтому стационарное состояние наступает не тогда, когда сила Лоренца
уравновешивает силу электрического поля Холла для каждого электрона, а тогда,
когда ток, созданный холловским электрическим полем Ux, компенсирует ток,
созданный действием силы Лоренца. Однако результат строгой теории эффекта Холла
для униполярных полупроводников на основе Geи Siпрактически не отличается
от полученного нами. В нашей лабораторной работе используется датчик, Холла
изготовленный из кремния.
Это значит, что уравнение (2) не может выполняться одновременно для
всех электронов (или дырок), имеющих различные по величине и направлению
скорости. Поэтому стационарное состояние наступает не тогда, когда сила Лоренца
уравновешивает силу электрического поля Холла для каждого электрона, а тогда,
когда ток, созданный холловским электрическим полем Ux, компенсирует ток,
созданный действием силы Лоренца. Однако результат строгой теории эффекта Холла
для униполярных полупроводников на основе Geи Siпрактически не отличается
от полученного нами. В нашей лабораторной работе используется датчик, Холла
изготовленный из кремния.
Итак, измеренное значение напряжения Холла Ux изнание условий эксперимента (размеры образца, величина тока L, вектор магнитной индукции В) дают возможность определить знак и концентрацию носителей заряда в полупроводнике. А параллельное измерение удельной электропроводности <т:
того же образца позволяет вычислить и подвижность носителей заряда µ:
Подвижность электрона µn и подвижность дырки µp численно равна
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Изучение определения, шаги для получения, использование
1
Сохранить
Скачать публикацию в формате PDF Эффект Холла описывает накопление заряда на одной стороне проводника, по которому течет ток и который находится в магнитном поле. Он назван в честь своего первооткрывателя Э. Х. Холла в 1879 году, когда небольшой ток возник в проводнике, несущем электрический ток в магнитном поле. Полярность, возникшая в эффекте Холла, также доказала, что электроны текут, проводя ток. Вывод эффекта Холла можно выполнить с использованием таких параметров, как ток, электрическое поле, разность потенциалов и напряжение Холла.
В этой статье мы рассмотрим эффект Холла, вывод эффекта Холла и его применение.
Эффект Холла
Когда ток течет по проводнику в присутствии магнитного поля, носители заряда, которыми являются электроны, испытывают поперечную силу, которая отталкивает их к одной стороне проводника. Это вызывает избыточный положительный заряд на другой стороне проводника.
За счет этого накопления носителей заряда на одной стороне проводника возникает разность потенциалов между сторонами проводника. Существование этого поперечного напряжения, которое можно измерить, известно как эффект Холла.
Вывод эффекта Холла
Если в проводнике течет ток I, то его можно определить как \(I = nev_dA\), где n — число электронов в единице объема, e — заряд электронов, \( v_d\) — небольшая единица объема, а A — площадь поперечного сечения проводника.
Уравнения \(v_d\) и I можно объединить, чтобы получить следующее уравнение:
\(I = ne(\frac {E}{B})A\), где B — плотность магнитного потока в Тесла и E электрическое поле.
Электрическое поле E связано с разностью потенциалов В соотношением :
\(E = \frac{V}{l}\) где В — разность потенциалов на проводнике и l длина проводника, на котором измеряется напряжение.
Объединяя уравнения для E и I , получаем дирижера.
Эффект Холла также может быть получен другим способом.
Если магнитное поле B приложено в положительном направлении Z к проводнику, по которому течет ток в положительном направлении Y, то сила Лоренца, действующая на электроны, определяется выражением:
\(F_l = -Bev_d\), где e — величина заряд и \(v_d[/latex} — скорость дрейфа.
Сила Лоренца действует в отрицательном направлении Y, и, таким образом, из-за эффекта Холла на одной стороне накапливается заряд, который вызывает накопление положительного заряда на другой стороне. тоже
Из-за этого генерируется электрическое поле, которое определяется формулой:
Поскольку сила Лоренца и электрическая сила уравновешены в нейтральной ситуации, таким образом,
\(F_e = F_l\)
Таким образом, мы получаем \(E_h = Bv_d \)
Если b — ширина проводника, то \(E_h = \frac{V_h}{b}\) или \(V_h = E_h b\), что можно выразить как \(V_h = Bv_d b\) … …. .1
.1
Теперь, если J — плотность тока, ее можно выразить как \(J = -n_e ev_d\).
Подставив приведенное выше уравнение в уравнение 1, мы получим,
\(V_h = – Bb \frac{J}{n_e e}\)
Но \(V_h = E_h b\) получаем,
\(E_h = \frac{BJ}{n_e e}\) что является формулой для электрического поля, создаваемого из-за эффекта Холла.
Коэффициент Холла
Коэффициент Холла выражается как \(R_H \), который определяется выражением \(R_H = \frac{1}{ne}\), где n — количество электронов.
Формула коэффициента Холла для полупроводников становится отрицательной, когда число электронов больше числа дырок.
Эффект Холла для полупроводников 9{2}}{e(p\mu _{H}+n\mu _{e})}\).
Где,
- n — концентрация электронов
- p — концентрация дырок
- \(\mu_e\) — подвижность электрона
- \(\mu_H\) — подвижность дырки
- e — элементарная заряд
Применение эффекта Холла
Эффект Холла применяется в следующих областях:
- Используется в датчиках на эффекте Холла
- При измерении магнитного поля
- Применение в определении положения
Надеюсь, что эта статья о лазерных диодах помогла правильно объяснить концепцию. Вы также можете ознакомиться с другими разделами по физике. Чтобы узнать больше о таких интригующих концепциях и их практическом применении, посетите веб-сайт Testbook или приложение Testbook. Загрузите приложение Testbook прямо сейчас!
Вы также можете ознакомиться с другими разделами по физике. Чтобы узнать больше о таких интригующих концепциях и их практическом применении, посетите веб-сайт Testbook или приложение Testbook. Загрузите приложение Testbook прямо сейчас!
Часто задаваемые вопросы о выводе эффекта Холла
В.1 Какова формула эффекта Холла?
Ans.1 Формула для напряжения Холла задается как \(V = \frac{IBL}{neA}\), а для электрического поля из-за эффекта Холла \(E_h = \frac{ BJ}{n_e e}\).
Q.2 Что такое выражение, полученное с помощью эффекта Холла, для напряжения Холла?
Ответ 2 Выражение, полученное на основе эффекта Холла, для напряжения Холла: [Latex]V = \frac{IBL}{neA}[Latex]
Q.3 В чем заключается польза эффекта Холла?
Ответ 3 Эффект Холла используется во множестве вещей, особенно в датчиках на эффекте Холла, в магнитометрах и т. д.
д.
В.4 Каков принцип работы датчика Холла?
Ans.4 Датчик Холла работает по принципу разности потенциалов, возникающей по ширине проводника благодаря эффекту Холла.
Q.5 Что такое поле Холла?
Ans.5 Электрическое поле, возникающее по ширине проводника, в котором протекает электрический ток под действием внешнего магнитного поля, благодаря эффекту Холла известно как поле Холла.
Q.6 Каковы компоненты вывода эффекта Холла?
Ans.6 Компоненты вывода эффекта Холла:
VH — напряжение Холла
EH — поле Холла
v — скорость дрейфа
b — ширина металлической пластины
B — магнитное поле
Bev — сила, действующая на электрон
| Выпрямители: определение, типы и применение |
| Расширенная форма: запись расширенной формы чисел и десятичных чисел с решенными примерами |
| Основы алгебры: изучите основные формулы, операции и правила, используя примеры значения с использованием примеров! |
Вывод на эффекте Холла – метод, применение и часто задаваемые вопросы
Прежде чем перейти к выводу на эффекте Холла, учащиеся должны отметить, что эффект Холла возникает из-за разности потенциалов. Он возникает поперек электрического проводника и поперек этого электрического тока. По сути, это относится к произведению магнитной индукции и плотности тока, когда магнитное поле работает перпендикулярно потоку тока, связанному с тонкой пленкой.
Он возникает поперек электрического проводника и поперек этого электрического тока. По сути, это относится к произведению магнитной индукции и плотности тока, когда магнитное поле работает перпендикулярно потоку тока, связанному с тонкой пленкой.
Что такое эффект Холла?
Эффект Холла, также называемый эффектом Холла-Эру, представляет собой влияние поперечной составляющей электрического тока на магнитное поле в поперечном стержне Холла. Когда ток течет в плоскости, перпендикулярной направлению магнитного поля, сила Лоренца действует на магнитные заряды (магнитный поток), окруженные поперечным током.
Сила Лоренца — это сила, испытываемая магнитным зарядом под действием внешнего силового поля, которым в данном случае является поперечный электрический ток. Поскольку электрический ток имеет определенную полярность, сила Лоренца толкает замкнутый магнитный заряд в направлении, параллельном электрическому току.
Это движение магнитного заряда создает магнитное поле, перпендикулярное току, и по закону Фарадея результирующая сила Лоренца создает тангенциальное магнитное поле. Таким образом, эффект Холла также называют поперечным эффектом Холла-Эру.
Таким образом, эффект Холла также называют поперечным эффектом Холла-Эру.
Напряжение Холла, возникающее в магнитном поле, называется эффектом Холла. В физике напряжение Холла — это напряжение, возникающее при протекании тока перпендикулярно магнитному полю. Он пропорционален плотности тока и, следовательно, обратно пропорционален толщине образца (эффект Холла не работает с планарными устройствами).
История
Эффект Холла был независимо открыт в 1890 году Орестом Чволсоном и Эдвином Пауэллом в США и в России Владимиром И. Вернадским. Эдвин Пауэлл и Орест Чволсон сообщили о своих открытиях эффекта Холла в журнале Nature в октябре 1890 г., где они описали этот эффект как «закон Холла». статья, опубликованная в 1892 году. Статья не была хорошо принята Физическим обществом в Нью-Йорке из-за неортодоксальной терминологии, которую использовал Чвольсон. После дальнейшего исследования, проведенного Э. М. Перселлом и Джозефом Генри, вторая статья Чвольсона была принята Физическим обществом, и в ней использовалась терминология «эффект Холла».
Теория
Эффект Холла может быть определен двумя переменными:
Магнитное поле
В эффекте Холла электрический ток проходит через проводник с током. Магнитное поле, окружающее проводник, обратно пропорционально радиусу проводника. Ток через проводник можно представить как два потока (ток, текущий в противоположных направлениях) в квадратуре; произведение потоков дает полный поток через проводник.
Если проводник тонкий и общий поток очень мал, магнитное поле вокруг проводника примерно однородно. Это дает приблизительную формулу для магнитного поля, которое при умножении на постоянную дает напряжение Холла, измеренное на проводнике
Напряжение
Когда электрический ток проходит через проводник, он создает электростатическое поле вокруг проводника из-за электрические заряды тока. Заряды тока создают разность потенциалов на проводнике. Если проводник состоит из одного или нескольких проводников с токами в одном направлении, это обычный случай, когда напряжение Холла возникает на проводнике и измеряется как выход.
Электромагнитный эффект
Эффект Холла — это электромагнитное явление, которое можно применять ко многим электромагнитным устройствам. Это связано с тем, что проводник с током, пластина Холла и магнитное поле имеют электрический заряд и создают электрическое поле в окружающем их пространстве. Например, магнит создает магнитное поле, и когда ток электронов проходит через магнитное поле, электроны меняют направление и создают электрическое поле в окружающем пространстве.
Электронный эффект
Когда электроны проходят через проводник, движение электронов создает напряжение между электронами и проводником. Это потому, что все они отрицательны, и если бы они были заряжены так же, как батарея, они отталкивались бы друг от друга и образовывали положительное пространство между ними и проводником.
Напряжение, создаваемое этим, пропорционально току в проводнике. Этот ток можно получить, измерив напряжение Холла и применив формулу.
Каковы применения эффекта Холла?
Понимание этой концепции на начальном уровне включает в себя объяснение сферы практического применения вывода эффекта Холла. К ним относятся следующие:
Эффект Холла помогает измерять магнитное поле вокруг электрического заряда и, таким образом, квалифицируется как магнитометр.
Формула эффекта Холла позволяет определить, служит ли материал полупроводником или изолятором.
Определение эффекта Холла находит широкое применение в интегральных схемах (ИС) в виде датчиков Холла.
Приборы Холла используются для измерения тока и потенциала в цепи. Это полезно во многих приложениях, таких как проектирование и тестирование интегральных схем. Общие реализации включают устройства Холла верхнего и нижнего плеча.
Это небольшие твердотельные полупроводниковые устройства, используемые для измерения магнитных полей, например, создаваемых магнитным полем Земли, и используемые в ряде других приложений, таких как датчики для транспортных средств, аэрокосмических и электронных устройств. Датчики Холла также являются популярной альтернативой герконам для использования в небольших бытовых приборах, таких как микроволновые печи, микроволновые тостеры для хлеба и беспроводные пылесосы.
Датчики Холла также являются популярной альтернативой герконам для использования в небольших бытовых приборах, таких как микроволновые печи, микроволновые тостеры для хлеба и беспроводные пылесосы.
В металлическом проводнике электроны могут свободно перемещаться из одной точки в другую. Благодаря этой свободе движения проводник может поляризоваться магнитным полем. Движение электронов вызывает изменение сопротивления проводника, которое можно измерить холловским вольтметром. Это изменение сопротивления зависит от направления и силы электрического поля. При этом удельное сопротивление проводника и величина сопротивления изменяется в зависимости от направления и силы магнитного поля.
Способность эффекта Холла измерять электрическое поле позволяет применять его для измерения удельного сопротивления и поверхностной проводимости неметаллических материалов. Металлические материалы не имеют магнитного поля, создающего электродвижущую силу, но по металлическим проводам может течь ток.
Величина напряжения пропорциональна напряженности электрического поля, что позволяет разрабатывать холловские вольтметры с высоким разрешением.
Кратко пролив свет на его приложения, давайте перейдем к тому, как вы можете вывести эффект Холла с нуля.
Как получить эффект Холла?
(Изображение будет загружено в ближайшее время)
Физика эффекта Холла включает в себя металлическое тело, которое содержит одну форму носителей заряда, таких как электроны. Кроме того, металл гарантирует отсутствие движения зарядов по оси Y.
Таким образом, необходимо рассмотреть следующие компоненты компонентов выражения эффекта Холла, чтобы лучше понять происхождение –
Abbreviations | Components |
| Hall Voltage |
| Hall field |
| Скорость дрейфа |
| Ширина металлического корпуса |
| Magnetic field |
| Force acting on an electron |
However, the ‘I’ component within the Hall effect calculation stands для –невА.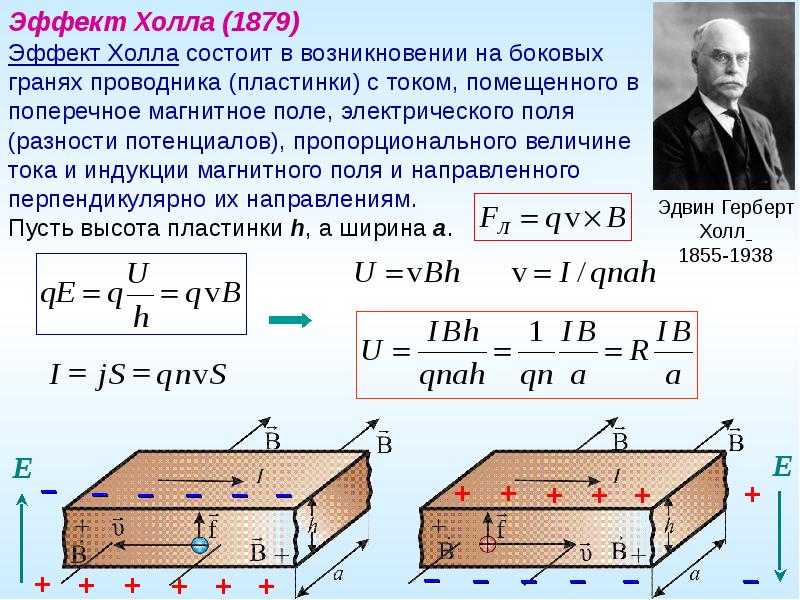 В этом случае «I» означает электрический ток, «n» означает количество электронов в единице объема, а «A» — площадь поперечного сечения проводника.
В этом случае «I» означает электрический ток, «n» означает количество электронов в единице объема, а «A» — площадь поперечного сечения проводника.
Таким образом, вывод эффекта Холла относится к следующему –
\[eE_{H}Bev\frac{evH}{d}=BevV_{H}=Bvd\]
Однако этот вывод предполагает, что сила направлена вниз из-за магнитного поля (равного восходящему электрическому сила), в случае равновесия.
Другой способ найти точное значение VH — использовать следующее уравнение:
\[V_{H}=\frac{-Bi}{net} \frac{EH}{JB}=-\frac{1} {ne}\]
Это конкретное уравнение использует вывод коэффициента эффекта Холла, который равен –
\[\frac{EH}{JB}\]
Кроме того, коэффициент Холла (RH) подразумевает отношение между произведением плотности тока и магнитного поля и наведенным электрическим полем.
Однако при расчете RH учитываются следующие факторы:
E = электрическое поле.



 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305