Что такое высота над уровнем моря?

Высота над уровнем моря… Этот термин, пожалуй, известен каждому школьнику. Мы достаточно часто встречаем его в газетах, на сайтах, в научно-популярных журналах, а также при просмотре документальных фильмов.

Теперь же попробуем дать ему более точное определение.

Раздел 1. Высота над уровнем моря. Общая информация

Под этим термином следует понимать абсолютную высоту или же абсолютную отметку, т. е. такую координату в трехмерном пространстве, которая показывает, на какой высоте по отношению к уровню моря находится тот или иной объект.

Двумя другими показателями географического месторасположения предмета являются долгота и широта.

Вот, к примеру, Москва. Высота над уровнем моря этого города весьма различна: максимальная составляет 255 м (недалеко от ст. м. «Теплый стан»), а минимальная — 114,2 м — находится вблизи Бесединских мостов, именно там, где река Москва покидает город.

Вообще же, если оперировать чисто физическими измерениями, то высота над уровнем моря является ничем иным как расстоянием по вертикали от, собственно, самого отдельно взятого предмета до среднего уровня морской поверхности, которая не должна быть нарушена ни приливами, ни волнениями.

Данная величина бывает как положительной, так и отрицательной. Ну, тут все относительно просто: то, что находится выше моря, приобретает знак «плюс», а ниже, соответственно, «минус».

Кстати, нельзя не отметить тот факт, что при увеличении ее значения наблюдается снижение атмосферного давления.

Если говорить о нашей стране, то самой высокой точкой суши в РФ по праву считается 5642-метровый Эльбрус, а вот самой низкой можно назвать Каспийское море с абсолютной высотой около 28 м.

Раздел 2. Высота над уровнем моря. Самое высокое место на планете

Ну, конечно же, это Эверест — хорошо известная гора, расположенная в центральной части горной системы Гималаи, как раз на границе двух южноазиатских государств, Непала и Тибета.

На сегодняшний день его высота составляет 8848 метров. Слова «на сегодняшний день» не случайны. По мнению ученых, земная поверхность все еще продолжает формироваться, поэтому и этот пик, хотя это и незаметно, растет с каждым годом.

Если углубиться в историю, то практически сразу же можно обнаружить информацию о том, что первыми отважными покорителями Джомолунгмы были Эдмунд Хиллари (Новая Зеландия) и Тензинг Норгей (Непал). Свое на самом деле героическое восхождение они совершили 28 мая 1953 года. С тех пор Эверест стал своеобразной Меккой для сотен и тысяч скалолазов, альпинистов и других смелых искателей приключений.

Раздел 3. Высота над уровнем моря. Самое низкое место на планете

В этом случае все немного сложнее. Дело в том, что таких точек на Земле сразу две: одна из них — побережье Мертвого моря — расположена на суше, а вторая носит название Марианской впадины и находится глубоко под толщей воды Тихого океана.

Остановимся на каждой из них более подробно.

Итак, Мертвое море, как известно, можно обнаружить на границе трех стран: Израиля, Палестины и Иордании. Оно является не только самым соленым водоемом на планете, но самым низким участком суши.

Сейчас уровень воды в нем составляет 427 метров, но и это еще не предел, т. к. ежегодно он, по мнению специалистов, падает в среднем на 1 метр.

Высота над уровнем моря… Москва, как было упомянуто выше, располагается в пределах от 114 до 255 м. Для нас это, в принципе, норма. Если учесть, что столицу РФ вряд ли можно назвать очень холмистой, то эту разницу почувствовать почти невозможно.

А теперь давайте возьмем в руки глобус или физическую карту земной поверхности: где-то глубоко-глубоко в Тихом океане, недалеко от островов Гуам, можно рассмотреть пометку с надписью «Марианский желоб». Так вот, он уходит под воду на глубину чуть больше 11 км.

Высота над уровнем моря — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Высота над уровнем моря, абсолютная высота, абсолютная отметка или альтиту́да (лат. altitudo — высота (точки земной поверхности над уровнем океана)) — одна координата в трёхмерном геопространстве (две другие — широта и долгота), показывающая, на каком уровне относительно принятого за ноль уровня моря находится тот или иной объект.

Высота над уровнем моря может быть приблизительно определена как расстояние по вертикали от объекта до среднего уровня поверхности моря, не нарушенного волнением и приливами, или (если объект располагается на суше) до поверхности геоида. Высота точки, лежащей выше уровня моря, считается положительной, ниже — отрицательной.

Определение высоты объектов над уровнем моря в России

В России и в странах СНГ^[1] высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, зафиксированного отметкой на Кронштадтском футштоке.

Примеры

• Самая высокая точка суши в мире — гора Джомолунгма в Гималаях: высота 8848 м над уровнем моря^[2][3].
• Самый низкий участок суши в мире — побережье Мёртвого моря: на 417,5 м ниже уровня моря.
• Самая высокая точка суши в России — гора Эльбрус: высота 5642 м над уровнем моря.
• Самый низкий участок суши в России — побережье Каспийского моря: абсолютная высота около −28 м.

См. также

Напишите отзыв о статье «Высота над уровнем моря»

Примечания

Ссылки

Отрывок, характеризующий Высота над уровнем моря

– Не…е…т, – проговорил сквозь зубы Долохов, – нет, не кончено, – и сделав еще несколько падающих, ковыляющих шагов до самой сабли, упал на снег подле нее. Левая рука его была в крови, он обтер ее о сюртук и оперся ею. Лицо его было бледно, нахмуренно и дрожало.

– Пожалу… – начал Долохов, но не мог сразу выговорить… – пожалуйте, договорил он с усилием. Пьер, едва удерживая рыдания, побежал к Долохову, и хотел уже перейти пространство, отделяющее барьеры, как Долохов крикнул: – к барьеру! – и Пьер, поняв в чем дело, остановился у своей сабли. Только 10 шагов разделяло их. Долохов опустился головой к снегу, жадно укусил снег, опять поднял голову, поправился, подобрал ноги и сел, отыскивая прочный центр тяжести. Он глотал холодный снег и сосал его; губы его дрожали, но всё улыбаясь; глаза блестели усилием и злобой последних собранных сил. Он поднял пистолет и стал целиться.
– Боком, закройтесь пистолетом, – проговорил Несвицкий.
– 3ак’ойтесь! – не выдержав, крикнул даже Денисов своему противнику.
Пьер с кроткой улыбкой сожаления и раскаяния, беспомощно расставив ноги и руки, прямо своей широкой грудью стоял перед Долоховым и грустно смотрел на него. Денисов, Ростов и Несвицкий зажмурились. В одно и то же время они услыхали выстрел и злой крик Долохова.
– Мимо! – крикнул Долохов и бессильно лег на снег лицом книзу. Пьер схватился за голову и, повернувшись назад, пошел в лес, шагая целиком по снегу и вслух приговаривая непонятные слова:
– Глупо… глупо! Смерть… ложь… – твердил он морщась. Несвицкий остановил его и повез домой.
Ростов с Денисовым повезли раненого Долохова.
Долохов, молча, с закрытыми глазами, лежал в санях и ни слова не отвечал на вопросы, которые ему делали; но, въехав в Москву, он вдруг очнулся и, с трудом приподняв голову, взял за руку сидевшего подле себя Ростова. Ростова поразило совершенно изменившееся и неожиданно восторженно нежное выражение лица Долохова.
– Ну, что? как ты чувствуешь себя? – спросил Ростов.

Уровень моря — Википедия

Материал из Википедии — свободной энциклопедии

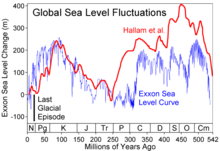График, демонстрирующий колебания уровня Мирового океана за последние 550 млн лет

У́ровень мо́ря — положение свободной поверхности Мирового океана, измеряемое по отвесной линии относительно некоторого условного начала отсчёта. Это положение определяется законом тяготения, моментом вращения Земли, температурой, приливами и другими факторами. Различают «мгновенный», приливной, среднесуточный, среднемесячный, среднегодовой и среднемноголетний уровни моря.

Под воздействием ветрового волнения, приливов, нагревания и охлаждения поверхности моря, колебаний атмосферного давления, осадков и испарения, речного и ледникового стока уровень моря непрерывно изменяется. Среднемноголетний уровень моря не зависит от этих колебаний поверхности моря. Положение среднемноголетнего уровня моря определяется распределением силы тяжести и пространственной неравномерностью гидрометеорологических характеристик (плотность воды, атмосферное давление и др.).

Постоянный в каждой точке среднемноголетний уровень моря принимается за исходный уровень, от которого отсчитываются высоты на суше. Для отсчёта глубин морей с малыми приливами этот уровень принимается за нуль глубин — отметку уровня воды, от которой отсчитываются глубины в соответствии с требованиями судоходства. В России и большинстве других стран бывшего СССР, а также в Польше, абсолютные высоты точек земной поверхности отсчитывают от среднемноголетнего уровня Балтийского моря, определённого от нуля футштока в Кронштадте^[1]. Глубины и высоты в западноевропейских странах исчисляются по Амстердамскому футштоку (замер уровня Средиземного моря делается по Марсельскому футштоку)

[2]. Для США и Канады точка отсчёта находится у канадского города Римуски, а для КНР — у города Циндао^[3]. Для измерения и регистрации колебаний уровня моря используют мареограф.

Поскольку существует множество факторов, влияющих на глобальные изменения погоды, (например, Глобальное потепление), то предсказания и оценки изменений уровня океана в ближайшем будущем не отличаются особой точностью.

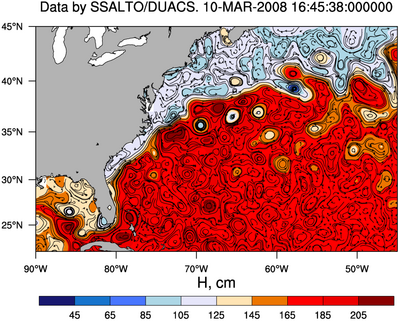Абсолютная высота морской поверхности (в сантиметрах) в районе течения Гольфстрим на 10 марта 2008 года, полученная по данным спутника Jason 1. Стрелочками показаны геострофические течения, ассоциированные с изменениями высоты морской поверхности.

Высота морской поверхности (ВМП) — это высота (или топография или рельеф) поверхности океана. В течение суток она, очевидно, наиболее подвержена влиянию приливных сил Луны и Солнца, действующих на Землю. На больших временных масштабах на ВМП влияет циркуляция океана. Обычно циркуляция океана вызывает отклонения топографии от среднего уровня максимум на ± 1 м^[4]. Самые медленные изменения ВМП происходят за счёт изменений в гравитационном поле Земли (геоид) в результате перераспределения континентов, образования подводных гор и тому подобного.

Поскольку гравитационное поле Земли относительно стабильно в масштабах десятилетий и столетий, циркуляция океана играет более значительную роль в наблюдаемой изменчивости ВМП. Сезонные изменения в распределении тепла и ветрового воздействия влияют на циркуляцию океана, а та, в свою очередь, на ВМП. Вариации ВМП могут быть измерены при помощи спутниковой альтиметрии (например, спутники TOPEX/Poseidon, Jason 1) и используются для определения, например, повышения уровня моря, расчёта содержания тепла и геострофических течений, обнаружения и изучения вихрей в океане.

Высота над уровнем моря Википедия

Системы высот в Европе.

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте). В исходном пункте высота принимается равной нулю.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

• высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
• высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (т. е. вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

История понятия

К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов ^[1], следуя французскому академику Л. Пюиссану ^[2][3] отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г.

[4] Лаплас ^[5] дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд

[6], Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта ^[7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля ^[8]. Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. ^[9]

Основные системы высот над уровнем моря

1. Динамическая высота (перевод разности потенциалов на линейную меру делением на постоянную величину, близкую к средней силе тяжести, например, среднее значение нормальной силы тяжести на широте 45°). Динамические высоты удобно применять вблизи одной и той же уровенной поверхности замкнутого водоёма или гидротехнического сооружения, в этом случае измеренные превышения не будут отличаться от соответствующей разности динамических высот. Применение динамических высот для решения геодезических задач неудобно, поскольку потребуется вводить поправку за переход к динамическим даже в линии нивелирования низкой точности.
2. Ортометрическая высота (отрезок силовой линии реального поля силы тяжести от геоида Брунса до точки земной поверхности; разность потенциалов переводится в линейную меру делением на среднее интегральное значение реальной силы тяжести вдоль этого отрезка). Приращения ортометрической высоты по вертикали в точности равны приращению длины.
3. Нормальная высота (отрезок силовой линии нормального поля силы тяжести от поверхности уровенного эллипсоида вверх до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка). Отметки нормальных высот, хотя и в общем случае непостоянны для одной и той же уровенной поверхности, лучше характеризуют уровенные поверхности с разными потенциалами, чем ортометрические. Приращения нормальной высоты по вертикали не равны приращению длины и соответствуют затуханию аномального гравитационного поля с высотой.
4. Нормально-ортометрическая высота (отрезок силовой линии нормального поля силы тяжести от земной поверхности вниз до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка).

Исходный пункт счёта высот

В России и в Казахстане высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, зафиксированного отметкой на Кронштадтском футштоке.

Балтийская система высот

В России в качестве государственной системы высот используется Балтийская система нормальных высот 1977 года, определенная по результатам уравнивания измерений на пунктах государственной нивелирной сети I и II классов главной высотной основы, выполненного ГУГК СССР в 1977 году. Отсчёт нормальных высот в Балтийской системе нормальных высот 1977 года ведется от нуля Кронштадтского футштока. За нуль Кронштадтского футштока принята горизонтальная черта на медной пластине Тонберга, укрепленной в устое Синего моста через Обводной канал в г. Кронштадте. Отметка горизонтальной черты пластины Тонберга равна 0,000 м. Строго говоря, исходным пунктом служит вековой репер вблизи футштока, связанный с началом счёта высот.

Примеры

Высоты горных вершин над уровнем моря определены наклонным визирным лучом из тригонометрическим нивелированием с точностью около 1 м, тогда как геодезическая высота вершины над отсчётным эллипсоидом может быть определена с точностью до 1 см с помощью геодезических ГНСС-приёмников.

См. также

Комментарии

Примечания

1. ↑ Болотов А. П. Геодезия или руководство к исследованию общего вида Земли, построению карт и производству тригонометрической и топографической съемок и нивелировок. Часть II: проекции карт, нивелирование, топография.. — СПб.: К. Вингебер, 1837. — 445 с.
2. ↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 1. — Paris: Courcier, 1807. — С. 230.
3. ↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 2. — Paris: Courcier, 1819. — С. 350.
4. ↑ Puissant L. Traité de topographie, d’arpentage et de nivellement. — Paris: Courcier, 1807. — 332 с.
5. ↑ Laplace Pierre-Simon. Traité de Mécanique céleste, t. 4. — 1. — Paris: L’Imprimerie Royale, 1805.
6. ↑ Wand Th. Die Principien der mathematischen Physik und Potentialtheorie. — Leipzig: B. G. Teubner, 1871. — 184 с.
7. ↑ F. R. Helmert. Zur Theorie des geometrischen Nivellirens (Deutsch) // Astronomische Nachrichten : журнал. — 1873. — Т. 81, № 19. — С. 298-300. — ISSN 1521-3994.
8. ↑ Молоденский М. С. Основные вопросы геодезической гравиметрии. — Труды ЦНИИГАиК, вып. 42. — Москва: Геодезиздат, 1945. — 108 с.
9. ↑ Еремеев В. Ф., Юркина М. И. Теория высот в гравитационном поле Земли. — Труды ЦНИИГАиК, вып. 191. — Москва: Недра, 1972. — 144 с.
10. ↑ Mount Everest — Peakbagger.com
11. ↑ BBC Russian — В мире — Китай согласился «приподнять» Эверест на 4 метра

Источники

Ссылки

• Гравиметрия и геодезия (Бровар Б.В., Юркина М.И., Тулин В.А., Спиридонов А.И., Демьянов Г.В., Галаганов О.Н., Родкин М.В., Таранов В.А., Кафтан В.И., Жаров В.Е., Авсюк Ю.Н., Светлосанова З.П., Толчельникова С.А., Пик М.В., Молоденский С.М., Денисов В.И., Мельников В.Н., Измайлов В.П., Карагиоз О.В., Колосницын Н.И., Нейман Ю.М., Бывшев В.А., Гусев Н.А., Баграмянц В.О., Копаев А.В., Сорока А.И., Непоклонов В.Б., Кузнецов Ю.Г., Майоров А.Н., Щеглов С.Н., Медведев П.П., Лебедев С.А., Зуева А.Н., Плешаков Д.И., Дубовской В.Б., Конопихин А.А., Соловьев Ю.Ю., Чуйкова Н.А., Пасынок С.Л., Максимова Т.Г., Казарян С.А., Васин М.Г., Попков Д.И., Леонтьев В.И., Сбитнев А.В., Жильников В.Г., Латышев Д.Д., Четверикова А.А.) М.: Научный мир, 2010, 562 с. ISBN: 978-5-91522-189-4

Литература

Абсолютная высота поверхности земли как узнать. Что такое высота над уровнем моря

Все мы изучали в школе географию и с термином «высота над уровнем моря» знакомы не понаслышке. Это определение можно встретить в научно-популярных телевизионных передачах, на страницах журналов, газетах и других средствах информации. Давайте рассмотрим современные способы ее определения.

Уровень моря, относительно которого измеряется расстояние до объекта, представляет собой водную поверхность в состоянии покоя, находящуюся перпендикулярно по отношению к равнодействующим силам, приложенным к массе воды. Водный уровень изменяется очень часто и виной этому фазы Луны, сила Солнца и ветра, испарение. Поэтому для вычисления среднего значения, вести необходимые расчеты нужно годами.

Высотой над уровнем моря является точка (координата) в трехмерной площади, которая указывает, на какой высоте находится определенный объект по отношению к уровню моря, принятого за ноль. Также она может быть ориентировочно определена как вертикаль от предмета до средней высоты над уровнем моря, не беря во внимание приливы и отливы. Высота точки, расположенной выше уровня, считается положительной, ниже — отрицательной. Две другие координаты географического месторасположения объекта — долгота и широта.

Если взять Россию за пример, то ее самой высокой точкой является Эльбрус — 5642 метра, а самой низкой — Каспийское море, высшая точка которого составляет примерно 28 м.

Как узнать высоту над уровнем моря

По старинке высоту над уровнем моря можно посмотреть в специальных топографических картах, в которых отображены все высоты. Но есть более современные методы.

1. Узнать какая высота над уровнем моря можно с помощью спутникового навигатора, работающего от определенной программы, например, Гугл или Гугл Земля (Google Earth). Для начала нужно загрузить одно из приложений на свой смартфон или компьютер и с помощью подсказок определить расстояние от уровня моря до нужного вам объекта. Работать с программами очень просто: наводите курсор на нужное место на карте, и информация выдается автоматически.
2. Измерение уровня конкретной местности доступно на GPS-устройствах. Приборы определяют высоты на основании информации, полученной со спутников. Наибольшую точность показателей имеют GPS-приемники со встроенным барометром-альтиметром.
3. В поисковой строке браузера Яндекс вбиваете «высота над уровнем моря» и нужный вам город, страну, гору и т. д. Особенно эта информация будет полезна путешественникам, которые собираются покорять горные вершины. Так вы сможете заранее узнать, какие высоты придется преодолевать и подготовиться к восхождению.
4. Как определить высоту знает приложение под названием Altitude, устанавливаемое на смартфоны. Она определяет точку над уровнем моря в реальном времени, а также скорость передвижения и другие данные. Результаты могут быть не совсем точными с расхождением в полтора-два деления.

Также измерения высоты местности над уровнем моря можно проводить с помощью альтиметра — инструмента, который используется для измерения высот подъема или точки над уровнем моря. Пользоваться альтиметром очень просто:

• запустите устройство и определите величину АД, соответствующую текущим погодным условиям;
• откалибруйте прибор и удержите кнопку «Set». После этого устройство само переключится на нужный режим и укажет давление высоты в текущем времени;
• снизьте показатели до нормальных, используя кнопку «Set». Сохранив полученные параметры в главном меню, на экране высветится высота над уровнем моря искомого объекта.

Альтиметр – прибор для измерения высоты над уровнем моря

Как узнать высоту над уровнем моря, используя тот или иной метод — дело сугубо индивидуальное, но альтиметр выдаст более точные показания, по сравнению с мобильными приложениями и GPS.

Самый высокий и низкий участок суши над уровнем моря

Если говорить о самых высоких и низких точках в мировом масштабе, то к первой относится гора Эверест, настоящее название Джомолунгма. Расположена она в Гималайской горной системе на высоте 8848 м над уровнем моря. Вторая вершина горы возвышается на высоте 8760 метро.

Эверест — явный победитель среди всех гор планеты по уровню возвышенности. Еще в 19 веке работник геодезической службы Радханат Сикдар из Индии измерил ее высоту. Но с тех пор данные изменялись, и гора оказалась еще выше, чем было заявлено изначально.

Самой низкой точкой над уровнем моря считается не одна, а сразу две. Первая находится на суше. Это побережье Мёртвого моря на границе Израиля и Иордании. Расположена точка на отметке 417 метрах ниже уровня моря, но как заявляют специалисты, ежегодно этт показатель увеличивается на 1 метр.

Вторая точка носит название Марианской впадины и находится глубоко под водами Тихого океана. Это бездонный кратер, который в своей самой низкой точке имеет глубину более 11 тысяч метров ниже уровня моря.

Зависимость давления от высоты над уровнем моря

На различной высоте показатели атмосферного давления также будут разными. Многие люди регулярно сталкиваются с проблемой тесной взаимосвязи плохого самочувствия и колебаний атмосферных показателей. По этой причине невозможно совершать походы в горы и летать на самолетах, особенно на дальние расстояния.

Как заявляют исследователи, зависимость давления от высоты над уровнем моря определяется такими показателями: повышение на 10 метров вызывает снижение давления на одну отметку, т.е. на каждые 100 м в среднем идет снижение на 7,5 мм. рт. ст. Пока высота не достигнет 500 м

Высота над уровнем моря Википедия

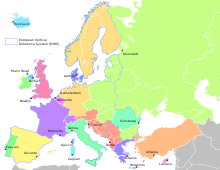Системы высот в Европе.

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте). В исходном пункте высота принимается равной нулю.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

• высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
• высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (т. е. вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

История понятия[ | ]

К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов ^[1], следуя французскому академику Л. Пюиссану ^[2][3] отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. ^[4] Лаплас ^[5] дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд ^[6], Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта ^[7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля ^[8]. Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. ^[9]

Основные системы высот над уровнем моря[ | ]

1. Динамическая высота (перевод разности потенциалов на линейную меру делением на постоянную величину, близкую к средней силе тяжести, например, среднее значение нормальной силы тяжести на широте 45°). Динамические высоты удобно применять вблизи одной и той же уровенной поверхности з

Высота над уровнем моря Википедия

Системы высот в Европе.

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте). В исходном пункте высота принимается равной нулю.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

• высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
• высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (т. е. вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов ^[1], следуя французскому академику Л. Пюиссану ^[2][3] отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. ^[4] Лаплас ^[5] дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд ^[6], Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта ^[7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля ^[8]. Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. ^[9]