Выполняется ли закон ома для полупроводников
По значению удельного электрического сопротивления полупроводники занимают промежуточное положение между хорошими проводниками и диэлектриками. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и др.), огромное количество сплавов и химических соединений. Почти все неорганические вещества окружающего нас мира – полупроводники. Самым распространенным в природе полупроводником является кремний, составляющий около 30 % земной коры.
Качественное отличие полупроводников от металлов проявляется прежде всего в зависимости удельного сопротивления от температуры. С понижением температуры сопротивление металлов падает (см. рис. 1.12.4). У полупроводников, напротив, с понижением температуры сопротивление возрастает и вблизи абсолютного нуля они практически становятся изоляторами (рис. 1.13.1).
| Рисунок 1.13.1. |
Такой ход зависимости ρ () показывает, что у полупроводников концентрация носителей свободного заряда не остается постоянной, а увеличивается с ростом температуры. Механизм электрического тока в полупроводниках нельзя объяснить в рамках модели газа свободных электронов. Рассмотрим качественно этот механизм на примере германия (Ge). В кристалле кремния (Si) механизм аналогичен.
Атомы германия на внешней оболочке имеют четыре слабо связанных электрона. Их называют валентными электронами . В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной , т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум атомам (рис. 1.13.2). Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах; поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках на много порядков меньше, чем у металлов. Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.
| Рисунок 1.13.2. |
При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок . Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой, восстанавливается электронная связь между атомами германия. Этот процесс называется рекомбинацией . Электронно-дырочные пары могут рождаться также при освещении полупроводника за счет энергии электромагнитного излучения. В отсутствие электрического поля электроны проводимости и дырки участвуют в хаотическом тепловом движении.
Если полупроводник поместить в электрическое поле, то в упорядоченное движение вовлекаются не только свободные электроны, но и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток в полупроводнике складывается из электронного и дырочного токов:
Концентрация электронов проводимости в полупроводнике равна концентрации дырок: . Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.
При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков. Такое сильное влияние примесей может быть объяснено на основе изложенных выше представлений о строении полупроводников.
Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.
Проводимость полупроводников при наличии примесей называется примесной проводимостью . Различают два типа примесной проводимости – электронную и дырочную .
Электронная проводимость возникает, когда в кристалл германия с четырехвалентными атомами введены пятивалентные атомы (например, атомы мышьяка, As).
| Рисунок 1.13.3. |
На рис. 1.13.3 показан пятивалентный атом мышьяка, оказавшийся в узле кристаллической решетки германия. Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказался излишним; он легко отрывается от атома мышьяка и становится свободным. Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки. Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью . В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника – в тысячи и даже миллионы раз. Удельное сопротивление проводника с большим содержанием примесей может приближаться к удельному сопротивлению металлического проводника.
В кристалле германия с примесью мышьяка есть электроны и дырки, ответственные за собственную проводимость кристалла. Но основным типом носителей свободного заряда являются электроны, оторвавшиеся от атомов мышьяка. В таком кристалле . Такая проводимость называется электронной , а полупроводник, обладающий электронной проводимостью, называется полупроводником -типа .
| Рисунок 1.13.4. |
Дырочная проводимость возникает, когда в кристалл германия введены трехвалентные атомы (например, атомы индия, In). На рис. 1.13.4 показан атом индия, который с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия. Примесь атомов, способных захватывать электроны, называется акцепторной примесью . В результате введения акцепторной примеси в кристалле разрывается множество ковалентных связей и образуются вакантные места (дырки). На эти места могут перескакивать электроны из соседних ковалентных связей, что приводит к хаотическому блужданию дырок по кристаллу.
Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов, которые возникли из-за механизма собственной электропроводности полупроводника: . Проводимость такого типа называется дырочной проводимостью . Примесный полупроводник с дырочной проводимостью называется полупроводником -типа . Основными носителями свободного заряда в полупроводниках -типа являются дырки.
Следует подчеркнуть, что дырочная проводимость в действительности обусловлена эстафетным перемещением по вакансиям от одного атома германия к другому электронов, которые осуществляют ковалентную связь.
Для полупроводников — и -типов закон Ома выполняется в определенных интервалах сил тока и напряжений при условии постоянства концентраций свободных носителей.
Цель работы: изучение движения зарядов внутри проводника и проверка закона Ома для проводников.
Электропроводность проводника определяется наличием в нем свободных носителей заряда (электроны в металле, положительные и отрицательные ионы в электролитах). Предположим, что носители тока слабо взаимодействуют друг с другом, а взаимодействие их с другими частицами сводится к соударениям. Кроме того, будем считать, что движение этих частиц подчиняется законам классической механики, что справедливо для полупроводников или электролитов, но не справедливо для металлов.
В отсутствие электрического поля частицы в проводнике (которые приближенно можно считать свободными) совершают хаотическое движение, сталкиваясь при этом с ионами на узлах кристаллической решетки, с атомами примесей и т.д. Все направления движения свободных частиц равноправны, и какого-нибудь потока частиц, то есть тока, не возникает. Поэтому усредненные по всему коллективу частиц проекции скорости равны нулю. Если проводник находится в электрическом поле, то на частицы действуют направленные силы. Если следить за какой-нибудь частицей, то можно обнаружить, что на тепловое хаотическое движение частицы накладывается направленное движение ее под действием силы со стороны электрического поля (так называемый дрейф).
Рассмотрим движение одной частицы. Пусть заряженная частица с зарядом е и массой m движется в однородном электрическом поле. Сила, действующая на частицу со стороны поля, равна , где – напряженность поля, которую можно считать постоянной. Тогда уравнение ее движения имеет вид:
Пусть вектор напряженности направлен по оси Ох, тогда ускорение частицы тоже направлено по этой оси и равно . Если начальная скорость частицы равна нулю, то в момент времени t она равна , а средняя скорость вдвое меньше, за некоторый промежуток времени τ она равна
Примем такую модель. Будем считать, что движущиеся заряженные частицы сталкиваются с другими частицами через одинаковое время τ, которое можно отождествить со средним временем между соударениями. Будем считать, что в среднем в результате соударения частицы останавливаются, а после этого они снова начинают движение в электрическом поле с нулевой начальной скоростью. По этой причине можно считать, что частицы движутся в электрическом поле со средней скоростью, даваемой формулой (1).
Сила тока – это заряд, переносимый движущимися частицами за единицу времени, а плотность тока равна силе тока через сечение проводника с площадью, равной единице. Найдем связь между плотностью тока и скоростью направленного движения частиц. Пусть частицы движутся влево со скоростью v (рис. 1). За время t они проходят путь, равный l = vt. Таким образом, за это время сечение S проводника пересекут только те частицы, которые отстоят от него на расстояние, меньшее или равное l, т.е. те частицы, которые находятся внутри цилиндра высотой l = vt и объема V = S(vt). Если концентрация частиц равна n, то их число в этом объеме равно N = nV = nS(vt). Пусть заряд одной частицы равен q. Тогда за время t через сечение проводника протекает суммарный заряд N частиц, равный Q = qN = qnSvt. Следовательно, сила тока через проводник равна , а плотность тока – .
В рассматриваемом нами случае вектор плотности тока направлен в направлении приложенного поля, т.е. вдоль оси Ох. Величина j пропорциональна средней скорости направленного движения, а именно j = еnavn. Подставляя сюда avn из формулы (1), получим:
Это выражение называют законом Ома в дифференциальной форме. Величина
называется коэффициентом электропроводности или просто электропроводностью данного проводника, а коэффициент пропорциональности между средней скоростью направленного движения зарядов avn и напряженностью приложенного электрического поля Е называют подвижностью носителей тока. Из формулы (2) видно, что подвижность выражается следующим образом:
Электропроводность и подвижность связаны друг с другом соотношением: s = enl.
Смысл закона Ома заключается в том, что средняя скорость направленного движения носителей тока пропорциональна напряженности электрического поля, т.е. пропорциональна действующей на частицы силе. Закон Ома выполняется для металлов, полупроводников, электролитов, т.е. для тех веществ, в которых носители тока испытывают большое число соударений. При этом данный закон выполняется при не слишком сильных полях, когда роль соударений велика. Закон Ома не выполняется при токах в вакууме, так как в этом случае носители тока практически не испытывают столкновений. Закон Ома очень ограниченно выполняется в плазме, так как в плазме обычно непостоянно число носителей тока. Отметим, что выражение для коэффициента электропроводности (3) соответствует опыту гораздо хуже, чем сам закон Ома. Это выражение более или менее применимо для полупроводников или электролитов, но совершенно не пригодно для металлов, в то время как сам закон Ома для металлов выполняется достаточно хорошо.
Обычно в физике и особенно в электротехнике применяется закон Ома в другом виде – в так называемой интегральной форме. Получим вид этого закона.
Рассмотрим участок однородного проводника, имеющего для простоты цилиндрическую форму (рис. 2). Пусть площадь поперечного сечения проводника S, а длина l. К концам проводника приложена разность потенциалов U = j1– j2, то есть внутри проводника действует электрическое поле . Поэтому в проводнике возникает электрический ток, плотность тока, согласно закону Ома, j = sЕ. Если ток распределен равномерно по сечению проводника, то сила тока I = jS = sES.
В случае однородного поля напряженность поля Е связана с потенциалом соотношением: . Поэтому сила тока в проводнике , откуда .
Величина (удельное сопротивление ) называется сопротивлением данного участка проводника. Тогда закон Ома в интегральной форме имеет вид:
Главное меню
| Интегральный закон Ома |
| Обзорные статьи |
Закон Ома — физический закон, описывающий связь между силой тока, напряжением и сопротивлением проводника в одной электрической цепи. Закон назван в честь Георга Ома — его первооткрывателя. Он гласит, что величина сила тока участка цепи прямо пропорциональна величине напряжения между концами цепи, если свойства проводника при прохождении по нему тока не изменяются. Также следует учитывать, что закон Ома – это фундаментальный закон, который может применяться к любой физической системе, включающей в себя действующие поля или потоки частиц, преодолевающие сопротивление. То есть, он может быть применен для расчёта гидравлических, электрических, световых, пневматических, тепловых, магнитных потоков и т. д., подобно правилам Кирхгофа, но такая реализация этого закона применяется крайне редко, только в рамках узко специализированных расчётов. Для ряда случаев математическая форма закона Ома может несколько различаться. По-другому математическое выражение закона Ома для участка цепи называется интегральным законом Ома. То есть предполагается, что электрическая цепь состоит из проводников, индивидуальное сопротивление которых усредняется относительно объема проводника. Первоначально закон Ома был установлен путем экспериментального изучения и анализа зависимости между напряжением (разностью потенциалов) U на концах проводника и силой тока I в самом проводнике. Как выяснилось, в широком диапазоне величин I и U соблюдается их пропорциональная зависимость: где U — падение напряжения на концах цепи, I — сила тока, R – сопротивление. Величина R называется электрическим сопротивлением проводника. Этой формулой выражается закон Ома в интегральной форме. Величины, которые входят в данное выражение, в случае с постоянным током являются действительными. Но закон Ома справедлив и для переменного тока. Если величина тока изменяется во времени, но по форме сигнал не является синусоидальным, то его можно представить суммой синусоидальных Фурье-компонент. В случае с линейными цепями компоненты фурье-разложения тока можно считать действующими независимо. Следует отметить тот факт, что данный закон есть лишь простейшее приближение для описания зависимости величины тока от разности потенциалов, а для некоторых систем он справедлив лишь в очень узком диапазоне значений. При описании более сложных (нелинейных) структур, в которых зависимостью сопротивления от силы тока пренебрегать нельзя, принято анализировать вольт-амперную характеристику. На физическом уровне суть закона Ома заключается в пропорциональности средней скорости направленного движения заряженных частиц напряженности электрического поля, т.е. скорость прямо пропорциональна силе, действующей на частицы. Если электрическое поле отсутствует, частицы в проводнике (которые можно считать свободными приближенно) совершают хаотическое движение, при этом сталкиваясь с ионами, расположенными на узлах кристаллической решетки, а также с атомами примесей и т.д. Любые направления движений свободных частиц являются равноправными, и не возникает никакого потока частиц, другими словами, ток отсутствует. Поэтому усредненные по всей совокупности частиц проекции скорости, соответственно, равны нулю. При внедрении проводника в электрическое поле на частицы начинают действовать направленные силы. Если проследить за одной из частиц, то можно обнаружить, что на ее тепловое хаотическое движение накладывается ее направленное движение под воздействием силы электрического поля (дрейф). Закон Ома справедлив для электролитов, полупроводников, металлов, т.е. для веществ, носители тока в которых испытывают большое число соударений. Но при этом закон выполняется даже при не очень сильных полях, когда соударения имеют большую роль. Закон Ома не работает при токах в вакууме, поскольку в этом случае частицы практически не имеют столкновений. В плазме закон Ома выполняется очень ограниченно, поскольку в таких условиях число носителей тока обычно непостоянно. |
3.2. Экспериментальный закон Ома для дрейфового тока
Рассмотрим
цилиндрический проводник (рис. 9) между
контактами 1,2 которого существует
постоянная разность потенциалов  .
При наличии внешнего электрического
поля свободные электроны и дырки
проводника приобретают направленное
движение (дрейф), создаваядрейфовый
поток носителей заряда. Таким образом,
электрический ток есть явление
электронного переноса через поперечное
сечение проводника при наличии градиента
потенциала внешнего электрического
поля.
.
При наличии внешнего электрического
поля свободные электроны и дырки
проводника приобретают направленное
движение (дрейф), создаваядрейфовый
поток носителей заряда. Таким образом,
электрический ток есть явление
электронного переноса через поперечное
сечение проводника при наличии градиента
потенциала внешнего электрического
поля.

Рис. 9.
Поток электрического
заряда  через элемент поверхностиdS
за время dt
определяется законом, аналогичным
закону Фика
через элемент поверхностиdS
за время dt
определяется законом, аналогичным
закону Фика
 . (13)
. (13)
Легко видеть, что выражение (13) представляет собой электродинамический закон Ома:
 , (14)
, (14)
где  – кинетический коэффициент переноса,
называемыйудельной
электропроводностью проводника.
– кинетический коэффициент переноса,
называемыйудельной
электропроводностью проводника.
Выведем формулу
для  из молекулярно-кинетических представлений.
из молекулярно-кинетических представлений.
3.3. Соотношение Эйнштейна для коэффициентов диффузии и электропроводности. Вывод формулы для электропроводимости

Рис. 10. Диффузия и дрейф заряда в полупроводнике.
Поместим
полупроводниковый образец между
обкладками плоского конденсатора. В
начальный момент времени после зарядки
конденсатора в полупроводнике возникнет
дрейфовый поток электронов и дырок под
действием внешнего электрического
поля. В результате этого на концах
проводника с координатами  возникнут области индуцированного
пространственного заряда определенной
толщины, которые создадут свое внутреннее
поле в объеме полупроводника. Накопление
индуцированного заряда происходит до
тех пор, пока внутреннее индуцированное
поле не скомпенсирует внешнее электрическое
поле конденсатора, благодаря чему
суммарное электрическое поле внутри
полупроводника будет равно нулю.
Рассмотренное явление получило названиеэффекта поля.
возникнут области индуцированного
пространственного заряда определенной
толщины, которые создадут свое внутреннее
поле в объеме полупроводника. Накопление
индуцированного заряда происходит до
тех пор, пока внутреннее индуцированное
поле не скомпенсирует внешнее электрическое
поле конденсатора, благодаря чему
суммарное электрическое поле внутри
полупроводника будет равно нулю.
Рассмотренное явление получило названиеэффекта поля.
В состоянии равновесия в полупроводнике устанавливается некоторый градиент концентрации электронов вдоль оси x. Распределение концентрации электронов вдоль оси x соответствует распределению Больцмана:
 . (15)
. (15)
При наличии градиента концентрации возникает диффузионный ток, определяемый законом Фика
 . (16)
. (16)
Дрейфовый ток определяется законом Ома
 . (17)
. (17)
Состояние равновесия характеризуется равенством диффузионного и дрейфового токов
 . (18)
. (18)
С другой стороны из распределения Больцмана (15) имеем
 . (19)
. (19)
Подставляя (19) в (18), получаем
 –соотношение
Эйнштейна. (20)
–соотношение
Эйнштейна. (20)
Согласно (12) коэффициент диффузии
 (21)
(21)
где использованы
формулы  (22)
(22)
 –время релаксации.
–время релаксации.
Подставляя (21) в (20), получаем формулу для электропроводимости
 (23)
(23)
Такой же результат следует из квантовой теории, однако в (23) масса электрона заменяется его эффективной массой m*.
§4. Концентрация носителей заряда в невырожденном полупроводнике n-типа
На рис. 11 представлена схема энергетических уровней в объеме полупроводника. Следует подчеркнуть, что наличие запрещенных зон энергии непосредственно не влияет на распределение электронов. Это значит, что при заданном положении уровня Ферми заполнение электронами тех или иных состояний в зоне проводимости совершенно не зависит от наличия под зоной проводимости запрещенного участка.

Рис.11.
В нормальном состоянии валентная зона целиком заполнена, а зона проводимости – пуста. Электроны в зону проводимости и дырки в валентную зону доставляются примесью – соответственно донорной и акцепторной. Кроме того, при достаточно высоких температурах электроны могут возбуждаться непосредственно из валентной зоны в зону проводимости, давая начало собственной проводимости. Заметим, что механизмы возбуждения могут быть самыми различными: тепловое возбуждение, фотовозбуждение и др.
В настоящем
параграфе мы рассмотрим лишь полупроводник
n-типа
(примесь донорного типа). Допустим, что
все донорные уровни характеризуются
одной и той же энергией –  .
Обозначим концентрацию примесных
центров черезNd.
.
Обозначим концентрацию примесных
центров черезNd.
Никакие расчеты
статистического характера невозможны
до тех пор, пока неизвестно, сколько
состояний соответствует данной энергии.
Плотность квантовых состояний
соответствует данной энергии. Плотность
квантовых состояний  – это количество состояний на единичный
интервал энергии. Функция
– это количество состояний на единичный
интервал энергии. Функция для полупроводника представлена в
правой части рис.11. Она состоит из трех
частей:
для полупроводника представлена в
правой части рис.11. Она состоит из трех
частей:
1). У краев зоны
проводимости и валентной зоны  меняется как
меняется как и дается формулой
и дается формулой
 (24)
(24)
2). В запрещенной
зоне  отлична от нуля только при энергии,
соответствующей примесному уровню.
отлична от нуля только при энергии,
соответствующей примесному уровню.
3). При  плотность состояний
плотность состояний ведет себя как
ведет себя как -функция
-функция
 (25)
(25)
Концентрация электронов в зоне проводимости вычисляется интегрированием (метод Гиббса)
 (26)
(26)
Опуская весьма громоздкую процедуру определения уровня Ферми и вычисления интеграла, запишем окончательное выражение для концентрации свободных электронов
 (27)
(27)
Экспонента в (27)
появилась потому, что при рассмотрении
полупроводника n-типа
мы исходим из функции распределения
Ферми, но в конце-концов аппроксимировали
ее (с большой точностью) функцией
Больцмана (см. формулу (10)). Действительно,
несмотря на то, что к электронам
полупроводника в принципе необходимо
применять статистику Ферми, большая
часть электронов, участвующих в
электропроводности, находится на
уровнях, отстоящих от уровня Ферми на
значительном (по сравнению с kT)
расстоянии и потому подчиняется
распределению Максвелла-Больцмана. Это
соответствует относительно слабой
ионизации примесей при достаточно
низких температурах, когда уровень
Ферми лежит в запрещенной зоне примерно
посредине между уровнями  и
и (см. рис. 11).
(см. рис. 11).
При этих условиях
из формулы (27) следует, что концентрация
свободных электронов растет лишь как
корень квадратный из концентрации
примесных центров. При достаточно
высоких температурах все электроны,
естественно, переходят с донорных
уровней в зону проводимости. Число
свободных электронов при этом равно  .
Соответствующий интервал температур
носит название области насыщения.
.
Соответствующий интервал температур
носит название области насыщения.
Из формулы (27)
следует, что с ростом температуры
величина  уменьшается, при этом экспонента
отрицательного аргумента увеличивается,
т.е. концентрация электронов проводимости
растет по закону, близкому к
экспоненциальному.
уменьшается, при этом экспонента
отрицательного аргумента увеличивается,
т.е. концентрация электронов проводимости
растет по закону, близкому к
экспоненциальному.
1.2.Электрический ток в полупроводниках. Полупроводниковые приборы.
К полупроводникам относятся материалы проводимость, которых больше, чем у диэлектриков, поменьше, чем у проводников. К полупроводникам относят кремний (Si), фосфор(P), германий (Ge), индий (In), мышьяк (As).
Полупроводники имеют ряд особенностей:
Электрический ток в полупроводниках обусловлен как движением свободных электронов, так и движением связанных электронов, так называемых дырок. Поэтому различают электронную и дырочную проводимости. Место, покинутое электронами условно положительно заряжено – дырка. Полупроводники, имеющие преимущественно электронную проводимость, называются полупроводниками (-)n-типа. Полупроводники, имеющие преимущественно дырочную проводимость , называются полупроводниками (+)р-типа.
Проводимость полупроводников очень сильно зависит от температуры, эта зависимость в десятки раз больше, чем у металлов. С увеличением температуры проводимость полупроводников увеличивается, а сопротивление уменьшается, т.к. увеличивается количество пар носителей зарядов ē и дыр.
Проводимость полупроводников сильно зависит от примесей и называется примесной проводимостью. Проводимость чистых полупроводников совсем невелика, чтобы увеличить проводимость к чистому полупроводнику добавляют примесь.
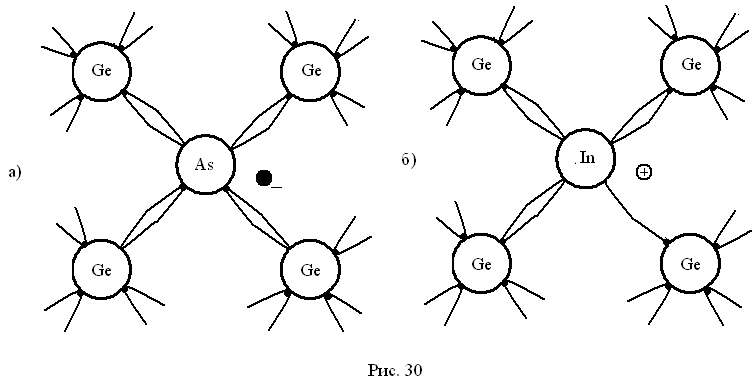
рис.44
Примесь может увеличить во много раз либо число свободных электронов, либо дырок. В первом случае (рис.44(а)) примесь выполняет роль донора (отдает электроны) – проводимость n – типа, а во втором (рис.44(б)) – роль акцептора (отбирает электроны) – проводимость р – типа.
Полупроводниковый диод p-n переход.
Полупроводниковый прибор, имеющий одностороннюю проводимость, основанный на работе p-n перехода. Ток через диод может проходить только в одном направлении.
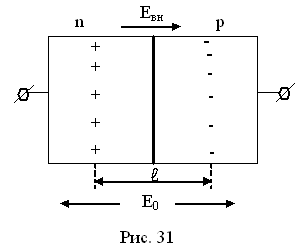
На границе раздела двух полупроводников с разной проводимостью, вследствие разной концентрации электронов и дырок, возникает диффузия, в результате которой образуется разность потенциалов (в области n– типа возникает (+) заряд, а в области р – типа (-) заряд). Имеет место напряженность поля Евн
Если приложить к р – n– переходу внешнее поле Е0, то в зависимости от его направления, будет следующее:
1. Е0совпадает по направлению с Евн; Е = Е0+ Евн, размеры ℓ увеличатся и тока не будет
2. Если Е0 противоположно Евн, то Е = Евн – Е0; Евн = Е0; Е = 0 через переход будет протекать электрический ток.
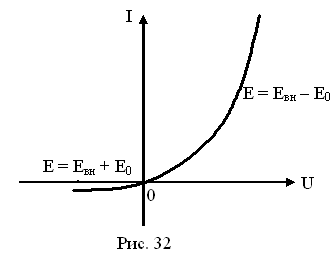
Вольт-амперная характеристика полупроводникового диода.
Полупроводниковый триод
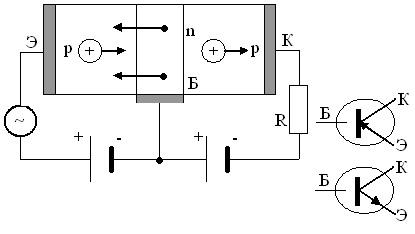
Полупроводниковый триод состоит из двух полупроводников одного типа проводимости разделенных тонким слоем полупроводника другого типа проводимости (p-n-p) или (n-p-n).
Ток в этой системе регулируется засчет напряжения между базой и эмиттером, изменение тока в цепи эмиттера будет вызывать изменение тока в цепи коллектора, причем изменение напряжения будет значительным (усиление напряжения). П/nтриоды (транзисторы) так же как и электронные лампы – триоды применяются для усиления и генерирования электрических колебаний. Транзисторы имеют ряд преимуществ перед электронными лампами — не требуют питания для накала катода, виброустойчивы, малогабаритны и др., однако их характеристики зависят от температуры.
Выполняется ли закон Ома для электрического тока в газах? Решите пожалуйста по физике
C чего вдруг НЕ ВЫПОЛНЯЕТСЯ???? при определенных условиях до тока насыщения и пробоя КОНЕЧНО ВЫПОЛНЯЕТСЯ ВАХ — ЛИНЕЙНАЯ при I< Iнас ЗНАЧИТ НАПРЯЖЕНИЕ U прямо пропорционально току I- ЭТО И ЕСТЬ ЗАКОН ОМА вроде в школе это объясняют.. — в ПРЕДЫДУЩЕМ ОТВЕТЕ — ВАМ ВЕРНО НАПИСАЛИ!! ! читаем ВОЛЬТ- АМПЕРНАЯ ХАРАКТЕРИСТИКА для ГАЗОВ
Нет, не выполняется.
Не выполняется. Даже вопрос так нельзя ставить: Георг Ом выводил в 1830 г. свою знаменитую формулу I=U/R только для металлов, о газах даже не помышлял.
Если условия опыта стабильны, то сила тока всегда равна отношению напряжения к сопротивлению. Другое дело, что при изменении Давления, температуры и т. д. меняеться сопротивление газов, а значит сила тока меняется, но закон Ома всё равно выполняется уже длоя новых условий. Вот, если строить воль-амперную характеристику, то она будет нелинейной.

