Выполняется ли закон ома для полупроводников

По значению удельного электрического сопротивления полупроводники занимают промежуточное положение между хорошими проводниками и диэлектриками. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и др.), огромное количество сплавов и химических соединений. Почти все неорганические вещества окружающего нас мира – полупроводники. Самым распространенным в природе полупроводником является кремний, составляющий около 30 % земной коры.

Качественное отличие полупроводников от металлов проявляется прежде всего в зависимости удельного сопротивления от температуры. С понижением температуры сопротивление металлов падает (см. рис. 1.12.4). У полупроводников, напротив, с понижением температуры сопротивление возрастает и вблизи абсолютного нуля они практически становятся изоляторами (рис. 1.13.1).

Рисунок 1. 13.1.

Такой ход зависимости ρ () показывает, что у полупроводников концентрация носителей свободного заряда не остается постоянной, а увеличивается с ростом температуры. Механизм электрического тока в полупроводниках нельзя объяснить в рамках модели газа свободных электронов. Рассмотрим качественно этот механизм на примере германия (Ge). В кристалле кремния (Si) механизм аналогичен.

Атомы германия на внешней оболочке имеют четыре слабо связанных электрона. Их называют валентными электронами . В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной , т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум атомам (рис. 1.13.2). Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах; поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках на много порядков меньше, чем у металлов.

Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.

Рисунок 1.13.2.

При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок . Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой, восстанавливается электронная связь между атомами германия. Этот процесс называется рекомбинацией .

(adsbygoogle = window.adsbygoogle || []).push({}); Электронно-дырочные пары могут рождаться также при освещении полупроводника за счет энергии электромагнитного излучения. В отсутствие электрического поля электроны проводимости и дырки участвуют в хаотическом тепловом движении.

Если полупроводник поместить в электрическое поле, то в упорядоченное движение вовлекаются не только свободные электроны, но и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток в полупроводнике складывается из электронного и дырочного токов:

Концентрация электронов проводимости в полупроводнике равна концентрации дырок: . Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.

При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков. Такое сильное влияние примесей может быть объяснено на основе изложенных выше представлений о строении полупроводников.

Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.

Проводимость полупроводников при наличии примесей называется примесной проводимостью . Различают два типа примесной проводимости – электронную и дырочную .

Электронная проводимость возникает, когда в кристалл германия с четырехвалентными атомами введены пятивалентные атомы (например, атомы мышьяка, As).

Рисунок 1.13.3.

На рис. 1.13.3 показан пятивалентный атом мышьяка, оказавшийся в узле кристаллической решетки германия. Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказался излишним; он легко отрывается от атома мышьяка и становится свободным.

Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки. Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью . В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника – в тысячи и даже миллионы раз. Удельное сопротивление проводника с большим содержанием примесей может приближаться к удельному сопротивлению металлического проводника.

Читайте также:  Выход из строя компрессора холодильника

В кристалле германия с примесью мышьяка есть электроны и дырки, ответственные за собственную проводимость кристалла. Но основным типом носителей свободного заряда являются электроны, оторвавшиеся от атомов мышьяка. В таком кристалле . Такая проводимость называется электронной , а полупроводник, обладающий электронной проводимостью, называется полупроводником -типа .

Рисунок 1.13.4.

Дырочная проводимость возникает, когда в кристалл германия введены трехвалентные атомы (например, атомы индия, In). На рис. 1.13.4 показан атом индия, который с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия. Примесь атомов, способных захватывать электроны, называется акцепторной примесью . В результате введения акцепторной примеси в кристалле разрывается множество ковалентных связей и образуются вакантные места (дырки). На эти места могут перескакивать электроны из соседних ковалентных связей, что приводит к хаотическому блужданию дырок по кристаллу.

Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов, которые возникли из-за механизма собственной электропроводности полупроводника: . Проводимость такого типа называется дырочной проводимостью . Примесный полупроводник с дырочной проводимостью называется полупроводником -типа . Основными носителями свободного заряда в полупроводниках -типа являются дырки.

Следует подчеркнуть, что дырочная проводимость в действительности обусловлена эстафетным перемещением по вакансиям от одного атома германия к другому электронов, которые осуществляют ковалентную связь.

Для полупроводников — и -типов закон Ома выполняется в определенных интервалах сил тока и напряжений при условии постоянства концентраций свободных носителей.

Цель работы: изучение движения зарядов внутри проводника и проверка закона Ома для проводников.

Электропроводность проводника определяется наличием в нем свободных носителей заряда (электроны в металле, положительные и отрицательные ионы в электролитах). Предположим, что носители тока слабо взаимодействуют друг с другом, а взаимодействие их с другими частицами сводится к соударениям. Кроме того, будем считать, что движение этих частиц подчиняется законам классической механики, что справедливо для полупроводников или электролитов, но не справедливо для металлов.

В отсутствие электрического поля частицы в проводнике (которые приближенно можно считать свободными) совершают хаотическое движение, сталкиваясь при этом с ионами на узлах кристаллической решетки, с атомами примесей и т.д. Все направления движения свободных частиц равноправны, и какого-нибудь потока частиц, то есть тока, не возникает. Поэтому усредненные по всему коллективу частиц проекции скорости равны нулю. Если проводник находится в электрическом поле, то на частицы действуют направленные силы. Если следить за какой-нибудь частицей, то можно обнаружить, что на тепловое хаотическое движение частицы накладывается направленное движение ее под действием силы со стороны электрического поля (так называемый дрейф).

Рассмотрим движение одной частицы. Пусть заряженная частица с зарядом е и массой m движется в однородном электрическом поле. Сила, действующая на частицу со стороны поля, равна , где – напряженность поля, которую можно считать постоянной. Тогда уравнение ее движения имеет вид:

Читайте также:  Vives maori goroka grafito

Пусть вектор напряженности направлен по оси Ох, тогда ускорение частицы тоже направлено по этой оси и равно . Если начальная скорость частицы равна нулю, то в момент времени t она равна , а средняя скорость вдвое меньше, за некоторый промежуток времени τ она равна

Примем такую модель. Будем считать, что движущиеся заряженные частицы сталкиваются с другими частицами через одинаковое время τ, которое можно отождествить со средним временем между соударениями. Будем считать, что в среднем в результате соударения частицы останавливаются, а после этого они снова начинают движение в электрическом поле с нулевой начальной скоростью. По этой причине можно считать, что частицы движутся в электрическом поле со средней скоростью, даваемой формулой (1).

Сила тока – это заряд, переносимый движущимися частицами за единицу времени, а плотность тока равна силе тока через сечение проводника с площадью, равной единице. Найдем связь между плотностью тока и скоростью направленного движения частиц. Пусть частицы движутся влево со скоростью v (рис. 1). За время t они проходят путь, равный l = vt. Таким образом, за это время сечение S проводника пересекут только те частицы, которые отстоят от него на расстояние, меньшее или равное l, т.е. те частицы, которые находятся внутри цилиндра высотой l = vt и объема V = S(vt). Если концентрация частиц равна n, то их число в этом объеме равно N = nV = nS(vt). Пусть заряд одной частицы равен q. Тогда за время t через сечение проводника протекает суммарный заряд N частиц, равный Q = qN = qnSvt. Следовательно, сила тока через проводник равна , а плотность тока – .

В рассматриваемом нами случае вектор плотности тока направлен в направлении приложенного поля, т.е. вдоль оси Ох. Величина j пропорциональна средней скорости направленного движения, а именно j = еnavn. Подставляя сюда avn из формулы (1), получим:

Это выражение называют законом Ома в дифференциальной форме. Величина

называется коэффициентом электропроводности или просто электропроводностью данного проводника, а коэффициент пропорциональности между средней скоростью направленного движения зарядов avn и напряженностью приложенного электрического поля Е называют подвижностью носителей тока. Из формулы (2) видно, что подвижность выражается следующим образом:

Электропроводность и подвижность связаны друг с другом соотношением: s = enl.

Смысл закона Ома заключается в том, что средняя скорость направленного движения носителей тока пропорциональна напряженности электрического поля, т. е. пропорциональна действующей на частицы силе. Закон Ома выполняется для металлов, полупроводников, электролитов, т.е. для тех веществ, в которых носители тока испытывают большое число соударений. При этом данный закон выполняется при не слишком сильных полях, когда роль соударений велика. Закон Ома не выполняется при токах в вакууме, так как в этом случае носители тока практически не испытывают столкновений. Закон Ома очень ограниченно выполняется в плазме, так как в плазме обычно непостоянно число носителей тока. Отметим, что выражение для коэффициента электропроводности (3) соответствует опыту гораздо хуже, чем сам закон Ома. Это выражение более или менее применимо для полупроводников или электролитов, но совершенно не пригодно для металлов, в то время как сам закон Ома для металлов выполняется достаточно хорошо.

Обычно в физике и особенно в электротехнике применяется закон Ома в другом виде – в так называемой интегральной форме. Получим вид этого закона.

Рассмотрим участок однородного проводника, имеющего для простоты цилиндрическую форму (рис. 2). Пусть площадь поперечного сечения проводника S, а длина l. К концам проводника приложена разность потенциалов U = j₁– j₂, то есть внутри проводника действует электрическое поле . Поэтому в проводнике возникает электрический ток, плотность тока, согласно закону Ома, j = sЕ. Если ток распределен равномерно по сечению проводника, то сила тока I = jS = sES.

В случае однородного поля напряженность поля Е связана с потенциалом соотношением: . Поэтому сила тока в проводнике , откуда .

Читайте также:  Датчик сухого хода danfoss

Величина (удельное сопротивление ) называется сопротивлением данного участка проводника. Тогда закон Ома в интегральной форме имеет вид:

Главное меню

Интегральный закон Ома

Обзорные статьи

Закон Ома — физический закон, описывающий связь между силой тока, напряжением и сопротивлением проводника в одной электрической цепи. Закон назван в честь Георга Ома — его первооткрывателя. Он гласит, что величина сила тока участка цепи прямо пропорциональна величине напряжения между концами цепи, если свойства проводника при прохождении по нему тока не изменяются. Также следует учитывать, что закон Ома – это фундаментальный закон, который может применяться к любой физической системе, включающей в себя действующие поля или потоки частиц, преодолевающие сопротивление. То есть, он может быть применен для расчёта гидравлических, электрических, световых, пневматических, тепловых, магнитных потоков и т. д., подобно правилам Кирхгофа, но такая реализация этого закона применяется крайне редко, только в рамках узко специализированных расчётов. Для ряда случаев математическая форма закона Ома может несколько различаться. По-другому математическое выражение закона Ома для участка цепи называется интегральным законом Ома. То есть предполагается, что электрическая цепь состоит из проводников, индивидуальное сопротивление которых усредняется относительно объема проводника. Первоначально закон Ома был установлен путем экспериментального изучения и анализа зависимости между напряжением (разностью потенциалов) U на концах проводника и силой тока I в самом проводнике. Как выяснилось, в широком диапазоне величин I и U соблюдается их пропорциональная зависимость: где U — падение напряжения на концах цепи, I — сила тока, R – сопротивление. Величина R называется электрическим сопротивлением проводника. Этой формулой выражается закон Ома в интегральной форме. Величины, которые входят в данное выражение, в случае с постоянным током являются действительными. Но закон Ома справедлив и для переменного тока. Если величина тока изменяется во времени, но по форме сигнал не является синусоидальным, то его можно представить суммой синусоидальных Фурье-компонент. В случае с линейными цепями компоненты фурье-разложения тока можно считать действующими независимо. Следует отметить тот факт, что данный закон есть лишь простейшее приближение для описания зависимости величины тока от разности потенциалов, а для некоторых систем он справедлив лишь в очень узком диапазоне значений. При описании более сложных (нелинейных) структур, в которых зависимостью сопротивления от силы тока пренебрегать нельзя, принято анализировать вольт-амперную характеристику. На физическом уровне суть закона Ома заключается в пропорциональности средней скорости направленного движения заряженных частиц напряженности электрического поля, т.е. скорость прямо пропорциональна силе, действующей на частицы. Если электрическое поле отсутствует, частицы в проводнике (которые можно считать свободными приближенно) совершают хаотическое движение, при этом сталкиваясь с ионами, расположенными на узлах кристаллической решетки, а также с атомами примесей и т.д. Любые направления движений свободных частиц являются равноправными, и не возникает никакого потока частиц, другими словами, ток отсутствует. Поэтому усредненные по всей совокупности частиц проекции скорости, соответственно, равны нулю. При внедрении проводника в электрическое поле на частицы начинают действовать направленные силы. Если проследить за одной из частиц, то можно обнаружить, что на ее тепловое хаотическое движение накладывается ее направленное движение под воздействием силы электрического поля (дрейф). Закон Ома справедлив для электролитов, полупроводников, металлов, т.е. для веществ, носители тока в которых испытывают большое число соударений. Но при этом закон выполняется даже при не очень сильных полях, когда соударения имеют большую роль. Закон Ома не работает при токах в вакууме, поскольку в этом случае частицы практически не имеют столкновений. В плазме закон Ома выполняется очень ограниченно, поскольку в таких условиях число носителей тока обычно непостоянно.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2. 1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4. 1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5. 5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Соблюдает ли полупроводник закон Ома?

спросил 3 года 10 месяцев назад

Изменено 7 месяцев назад

Просмотрено 2к раз

\$\начало группы\$

Закон Ома справедлив для металлов, но справедлив ли он для полупроводников? Там работает?

Я не говорю здесь о PN-переходе.

Если у меня есть блок кремния и я пропускаю через него напряжение, увижу ли я протекание тока в соответствии с законом Ома?

• полупроводники
• закон Ома

\$\конечная группа\$

11

\$\начало группы\$

Да. Все материалы в нормальных условиях и при фиксированной температуре следуют* закону Ома, хотя он становится менее полезным в хороших изоляторах, где пробой происходит до того, как может протекать какой-либо значительный ток.

Неомические эффекты возникают на границах между различными материалами, такими как p-n переходы, переходы Шоттки, термопары, гальванические элементы и т.д. Их также можно наблюдать при явлениях разряда, когда протекание тока вызывает ионизацию и химические изменения в проводящем материале.

*Здесь «следовать» означает «вести себя так, как близко». В зависимости от того, насколько точно вы измеряете вещи, может иметь значение, что это не совсем точно.

Редактировать: стоит отметить, что наличие (изменяющихся) магнитных полей может все усложнить. Например, считается, что трансформаторы и катушки индуктивности не подчиняются закону Ома в динамических условиях.

Для получения дополнительной информации о том, что становится неясным, см. этот вопрос.

\$\конечная группа\$

7

\$\начало группы\$

Закон Ома является приблизительным. В нем говорится, что напряжение и ток линейно связаны с константой, называемой сопротивлением (постоянному току). Это может быть верно в широком диапазоне приложенного напряжения или только в небольшом диапазоне. В некоторых случаях это понятие используется для описания небольших изменений вокруг конкретной точки (динамический импеданс — R = dV/di вокруг конкретной точки смещения).

Металлические проводники следуют ему очень хорошо, потому что движение электронов, вызванное разумными токами, мало по сравнению с их ранее существовавшими тепловыми случайными движениями. Если ток настолько велик, что происходит нагрев, то «закон Ома» не соблюдается в точности.

Полупроводники имеют больше ограничений. Может быть ограниченное количество доступных носителей, поэтому их скорость значительна по сравнению с тепловым движением — и тогда закон Ома не соблюдается. Кроме того, более высокие напряжения влияют на граничные условия на поверхности полупроводника, что также влияет на сопротивление постоянному току (большое сопротивление сигнала).

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Правда ли, что не все компоненты подчиняются закону Ома?

спросил 1 год, 4 месяца назад

Изменено 3 месяца назад

Просмотрено 1к раз

\$\начало группы\$

После объяснения закона Ома человеку, который ничего не смыслил в электронике, меня поправил другой парень, указав, что не все компоненты подчиняются закону Ома. Я ответил как обычно: «Я знаю, поэтому я сказал в простой резистивной цепи».

Однако, поскольку я также очень мало разбираюсь в электронике, мне стало любопытно, правда ли это. Существует ли какая-либо компонента, для которой нарушается соотношение I = V/R?

Я всегда считал, что это просто означает, что это отношение было постоянным, а не то, что я мог ожидать, что R будет постоянным и/или независимым от двух других значений или времени. Интересно, когда люди говорят, что диод (например) не подчиняется закону Ома, они на самом деле просто имеют в виду, что вы не можете использовать его для установки I, независимо изменяя V или R?

Диод ведет себя иначе, чем переменный резистор, который пытается поддерживать постоянное падение напряжения на нем и обеспечивает максимальное сопротивление при обратном напряжении на клеммах?

После прочтения принятого ответа здесь Действительно ли диод следует закону Ома? Я заключаю, что ответ на последний вопрос «нет», то есть диод действительно «подчиняется» закону Ома. Могу ли я также заключить, что это верно для всех компонентов, если мы используем исходную формулировку Ома, а не более поздние упрощения?

Имеет ли вообще смысл говорить, что закон Ома может быть «нарушен»?

• закон Ома

\$\конечная группа\$

12

\$\начало группы\$

Статья в Википедии объясняет это довольно хорошо:

Если сопротивление непостоянно, предыдущее уравнение нельзя назвать законом Ома, но его все же можно использовать для определения статического/постоянного сопротивления. [4] Закон Ома — это эмпирическое соотношение, которое точно описывает проводимость подавляющего большинства электропроводящих материалов при силе тока многих порядков. Однако некоторые материалы не подчиняются закону Ома; они называются неомическими.

Диоды не имеют линейной зависимости между током и напряжением, поэтому их нельзя смоделировать так же просто, как резистор с использованием закона Ома, В = IR . Однако мы можем упростить и смоделировать их в диапазоне токов как комбинацию резистора и источника напряжения.

Рис. 1. Этот зеленый светодиод имеет «сопротивление» 15 Ом со смещением напряжения 2,0 В. Источник изображения: сопротивление светодиода.

Рисунок 2. Если бы это была наша область интереса, мы могли бы использовать значение сопротивления 37,5 Ом и смещение напряжения 1,5 В.

Диод ведет себя иначе, чем переменный резистор, который пытается поддерживать постоянное падение напряжения на нем и обеспечивает максимальное сопротивление, когда напряжение на клеммах меняется на противоположное?

Посмотрите, поможет ли моя статья Что такое светодиод с аналогией с обратным клапаном.

Есть ли вообще смысл говорить, что закон Ома можно «нарушить»?

Не думаю. Имеет смысл сказать, что это относится к резисторам, а не к другим вещам.

\$\конечная группа\$

5

\$\начало группы\$

Ом Первоначальная работа заключалась в попытке понять взаимосвязь между длиной телеграфного кабеля и величиной напряжения, необходимой для получения определенного тока. Когда он делал эту работу, концепция резистора как компонента, который вы можете преднамеренно ввести в схему специально для того, чтобы выбросить ценные биты ЭДС, была неслыханной.

Его главным вкладом было открытие — или, по крайней мере, проделанная работа, на которую указывала большая толстая стрелка — того факта, что падение напряжения в металлической цепи пропорционально току. Дело было не в том, что напряжение было пропорционально квадрату тока, или квадратному корню из тока, или току, возведенному в степень, отличную от единицы.

Как неоднократно упоминалось, закон Ома не является основным законом физики — это кульминация огромного количества эмпирического опыта, преднамеренного и непреднамеренного, который привел нас к пониманию того, что для большинства проводящих материалов , мы можем сделать кусок указанного материала и присвоить ему такое сопротивление, что \$E = I\R\$.

Он занял прочное место в анализе цепей, потому что если предположить, что ему подчиняются все резистивные элементы, то (наряду с некоторыми другими упрощающими предположениями для других компонентов, которые обычно достаточно верны для этой цели) он сводит системный анализ к решению систем линейных дифференциальных уравнений — и, хотя решение линейных дифференциальных уравнений слегка сбивает с толку, нет вообще никакого общего решения для решения нелинейное дифференциальных уравнения.

Итак, все ли компоненты подчиняются закону Ома? Нет. Соответствует ли закону Ома каждый резистор ? Нет, если вы принимаете во внимание нагрев, нет (если присутствуют высокие напряжения), если вы принимаете во внимание коронный разряд или другие пути утечки, а не если вы принимаете во внимание старение и т. д.

Но есть достаточно компонентов, которые следуют это то, что это полезно. Кроме того, поскольку вы можете взять большую часть остатка и превратить описание схемы в линейное дифференциальное уравнение, которое можно проанализировать на бумаге, полезно. Именно эта невероятная полезность поддерживала его жизнь все эти годы и придавала ему ту форму, которую мы все знаем и любим.

\$\конечная группа\$

\$\начало группы\$

Все сопротивления подчиняются закону. Просто идеальные чистые сопротивления найти где-либо еще, кроме как в учебниках, будет сложно. Тем не менее, это полезная концепция.

Даже резисторы в реальном мире не являются чистыми сопротивлениями, поскольку они имеют паразитную индуктивность и паразитную емкость над ними, поэтому резистор 100 Ом при постоянном токе не будет выглядеть как резистор 100 Ом при измерении на частоте 10 ГГц. Резистор на 100 Ом может быть аппроксимирован как идеальный резистор на 100 Ом при использовании в некотором разумном диапазоне частот, токов и напряжений.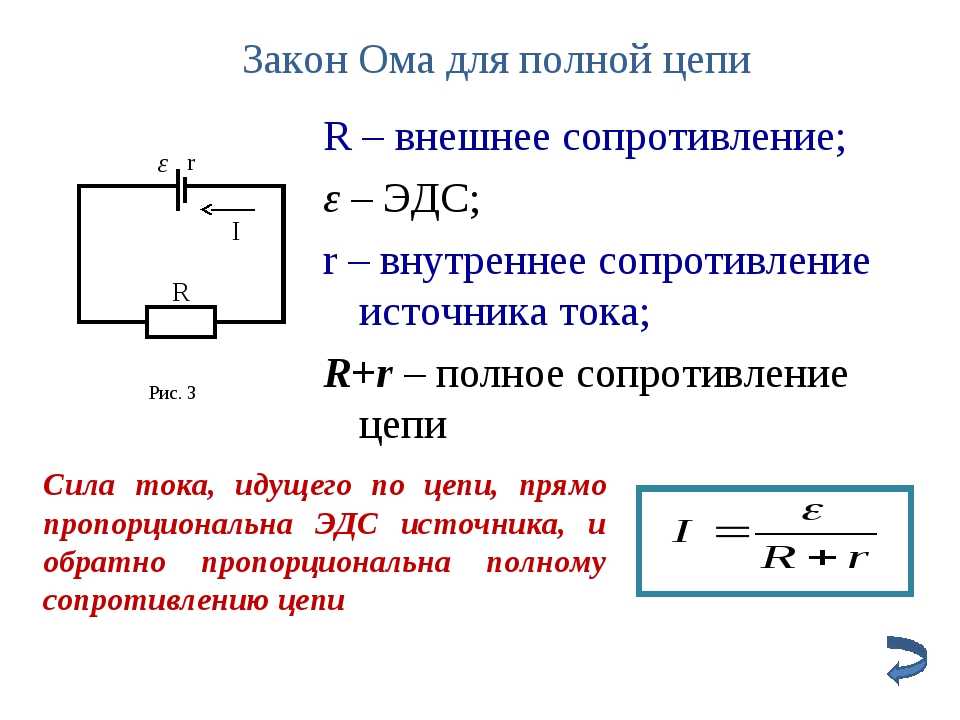 Если вы приложите 200 вольт к резистору, он, скорее всего, будет измерять сопротивление, отличное от 100 вольт, из-за любых нелинейностей, которые он может иметь.

Диоды и другие полупроводники не являются сопротивлениями, поэтому закон к ним не применяется, но идеальный резистор как часть моделирования полупроводникового диода может быть достаточно хорошим приближением, в зависимости от того, насколько точно вы хотите смоделировать диод.

\$\конечная группа\$

\$\начало группы\$

Я попытаюсь ответить на свой вопрос в виде резюме.

Кажется, все сводится к тому, подразумевает ли закон Ома, что R постоянно или нет. Я всегда доводил до , а не подразумевают, что это простое математическое соотношение, которое утверждает, что I = V/R, независимо от того, является ли R постоянным или нет. Таким образом, это можно рассматривать как формулу определения R в форме R = V / I.

Я сослался на другой ответ электроники SE, в котором утверждалось следующее: действительно ли диод следует закону Ома? Он утверждает, что вывод о том, что R должен быть постоянным, исходит из более позднего упрощения Максвелла. Это казалось очень убедительным, потому что на самом деле восходило к первоисточнику, сотням страниц, написанных самим Омом по этому вопросу.

Однако другой ответчик здесь сослался на https://en.wikipedia.org/wiki/Ohm%27s_law, заявив, что, когда R непостоянно, его нельзя назвать законом Ома, даже если его можно использовать в качестве формулы определения для R В Википедии есть анонимные авторы, но в статье содержится ссылка на университетский учебник, который, безусловно, имеет большой вес: https://books.google.no/books?vid=ISBN9780321501219&redir_esc=y

С этой точки зрения закон Ома является скорее эмпирическим законом, который можно использовать, если вы знаете константу R, чтобы определить V из I или наоборот. Но это справедливо только для компонентов с постоянным R.

Думаю, не так уж важно, что изначально имел в виду Ом. Из ответов здесь становится ясно, что если я скажу «закон Ома», подавляющее большинство инженеров-электронщиков и любителей сочтут это подразумевающим, что R является постоянным. Главная цель – быть правильно понятым.

\$\конечная группа\$

1

\$\начало группы\$

Есть ли какой-либо компонент, для которого нарушается соотношение I = V/R?

И из комментария (чтобы быть уверенным, что я правильно истолковал вопрос): —

Как указано в вопросе, я хотел знать, может ли это быть сказал для всех компонентов, а не только для диодов.

Здесь вы говорите о любых (или всех) компонентах , т.е. вы не говорите о идеальных компонентах , потому что вы сказали любой компонент . Все практичные, настоящие компоненты могут быть изготовлены из композитов идеальные компоненты и, действительно, связь между V и I не определяется постоянной величиной, называемой R. Даже некоторые идеальные компоненты (например, конденсатор или катушка индуктивности) не имеют линейной зависимости между напряжением и током. В конденсаторе например: —

Картинка отсюда. В этом «идеальном» примере связь между током и напряжением не является простой «Х»: —

$$I = C\cdot\dfrac{dv}{dt}$$

Другими словами, ток пропорционален скорость изменения напряжения на клеммах компонента. Аналогичная история с индуктором.

Если вы сосредоточитесь на токе и напряжении при идеальном сопротивлении, тогда закон Ома верен, но в более широкой картине это не так ясно, потому что у всех реальных компонентов есть паразиты, которые мутят чистую воду закона Ома.

\$\конечная группа\$

\$\начало группы\$

Вы поняли, что R не обязательно является постоянным для многих компонентов.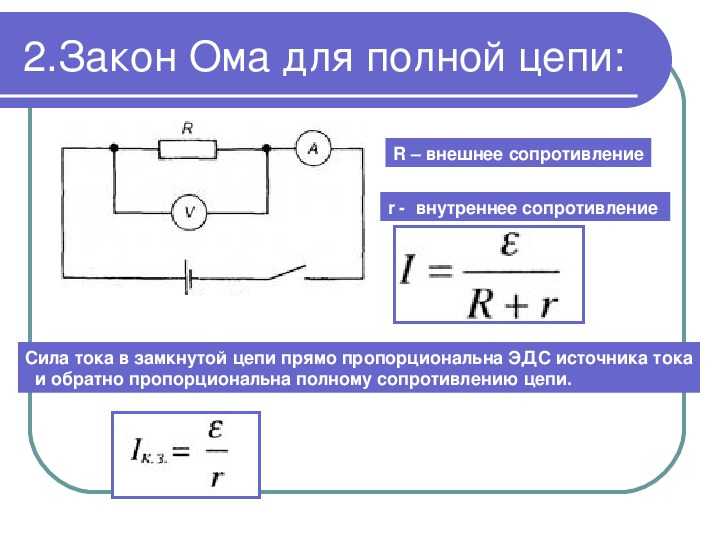 Это не только полупроводники. Даже лампа накаливания с вольфрамовой нитью имеет сопротивление, которое зависит от того, насколько горяча нить накала.

Значит, закон Ома применим ко всем компонентам? Если вы допускаете, что R является функцией V или I, то вы можете утверждать, что любая двухполюсная компонента подчиняется закону Ома. Вы измеряете V и I, вычисляете R, используя R = V/I , а затем обнаруживаете, что I = V/R . Но это становится бессмысленным круговым аргументом.

\$\конечная группа\$

\$\начало группы\$

Закон Ома представляет собой эмпирическое утверждение о связи между напряжением и током в проводнике. Его также можно получить, используя упрощенные атомарные модели проводников. В любом случае он описывает простое линейная зависимость между напряжением и током через проводящие материалы: металлические проводники или неметаллические проводники, такие как почва, бетон, электролиты, плазма, биологические ткани и т. д.

Основная проблема заключается в том, что это линейная зависимость между напряжением устройства и текущий, и который идентифицируется линией , которая проходит через начало координат на плоскости IV.

С этой точки зрения любое электрическое устройство, кривая i-v которого не является линией или которое не проходит через начало координат, называется

.0116 нелинейное устройство , а закон Ома недействителен для нелинейных устройств.

При этом все полупроводниковые электронные устройства, такие как диоды, транзисторы, фотоэлементы и т. д., или многие электрические устройства, такие как люминесцентные лампы, будут глобально нарушать закон Ома.

Обратите внимание, однако, что инженеры-электрики могут говорить о линеаризации нелинейного устройства (или цепи с нелинейными устройствами) через рабочую точку и использовать анализ слабых сигналов для вывода его поведения вокруг этой конкретной рабочей точки.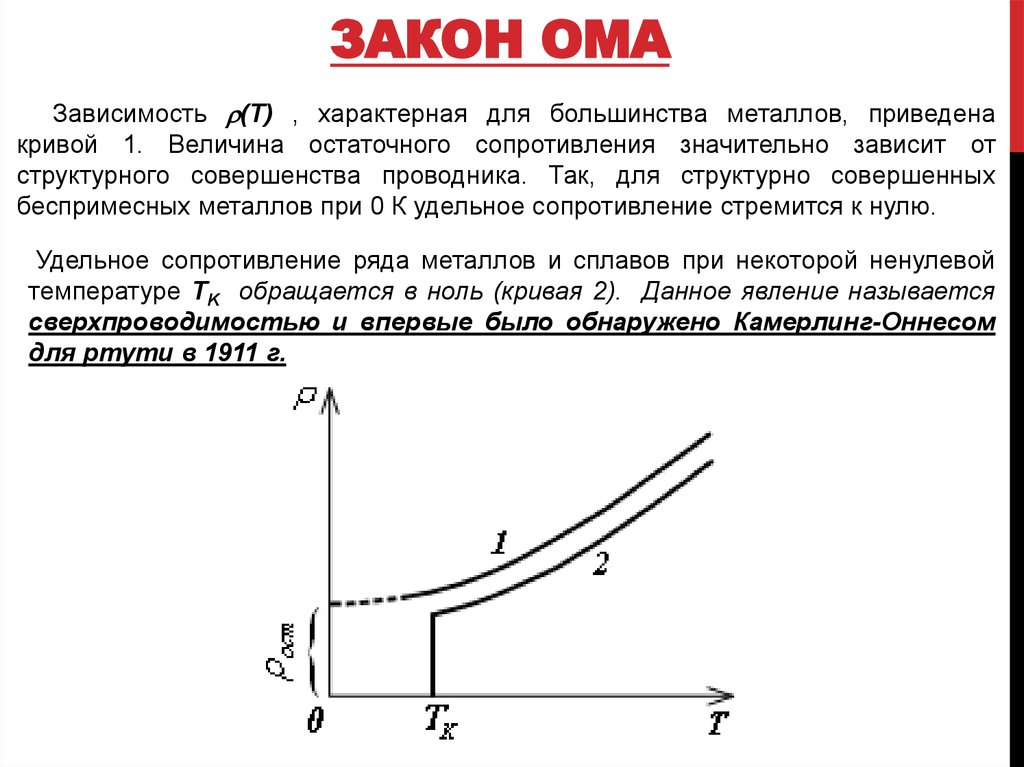 В таком случае устройство или вся схема будет заменена его линейная модель с линейными резисторами, поведение которых будет подчиняться закону Ома в этом ограниченном диапазоне анализа. Но это не делает такие устройства омическими. В конечном итоге они являются нелинейными устройствами и нарушают закон Ома.

\$\конечная группа\$

\$\начало группы\$

Закон Ома описывает линейную зависимость между током, напряжением и сопротивлением.

Если вы построите график зависимости тока от напряжения, подаваемого на резистор, вы получите прямую линию — это линейная функция.

Если построить график зависимости тока от напряжения, приложенного к диоду, то график не будет прямой линией.

В этом смысле диод не подчиняется закону Ома.

С другой стороны, для любой точки на графике диода вы можете записать закон Ома в виде \$R=\frac{E}{I}\$, чтобы рассчитать эквивалентное сопротивление для этой точки.

Вы не можете применить закон Ома к любой цепи и ожидать, что линейная зависимость будет верна — если вы измерите ток, потребляемый цепью при напряжении 5 В, вы не сможете использовать закон Ома, чтобы предсказать, какой ток она будет потреблять при 10В. Нет, то есть, если цепь не является чисто резистивной.

Кроме того, есть туннельные диоды.

Уравнение \$E=IR\$ полностью искажено для туннельных диодов. На графике зависимости тока от напряжения есть места, где вы получаете одно и то же сопротивление более одного раза.

Закон Ома не выполняется для всех компонентов при любых условиях. Даже для простых резисторов это лишь приближение к реальному поведению. Для нелинейных устройств (диоды, транзисторы и т. д.) он не описывает их поведение в целом, хотя его можно использовать для расчета эквивалентного сопротивления при заданном токе и напряжении в конкретной цепи.

\$\конечная группа\$

1

\$\начало группы\$

Действительно, закон Ома применяется к очень немногим нагрузкам: резистивным нагрузкам.