1.7. Моменты силы относительно точки и оси
Сила может не только перемещать тело поступательно, но и оказывать на него вращательное действие, которое зависит не только от величины силы, но и от расстояния до центра поворота.
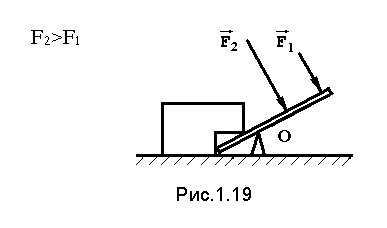
Например, для того, чтобы повернуть тело с помощью рычага (рис.1.19), наименьшую по модулю силу нужно приложить к концу рычага, чем ближе к центру, тем величина силы должна быть больше, если же сила будет проходить через точку О, то повернуть тело будет невозможно, какой большой бы она не была.
|
Для характеристики вращательного действия силы вводится понятие момента силы относительно точки.
Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние между точкой и линией действия силы (плечо):
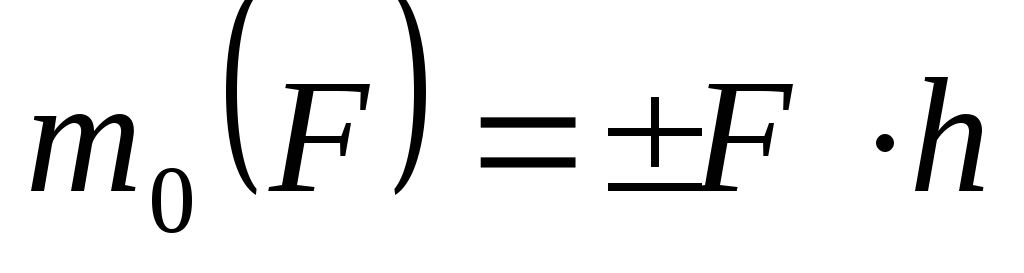 (1.5)
(1.5)
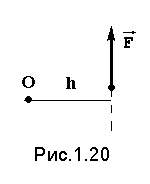
Знак момента определяется следующим образом: если сила стремится повернуть тело вокруг данной точки против часовой стрелки, то он считается положительным (рис.1.20), в противном случае — отрицательным.
Момент силы относительно точки равен нулю только в том случае, если линия действия силы проходит через данную точку. Единицы измерения момента [HM] и в соответствующих кратных единицах.
Момент
силы относительно оси характеризует
вращательное действие силы относительно
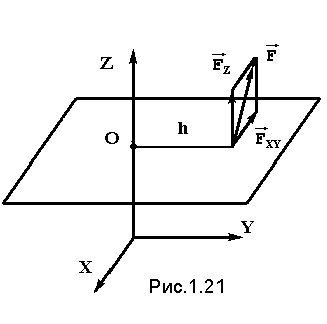
оси. Если силу 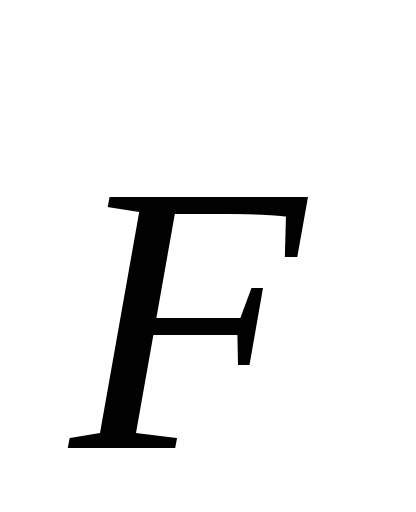 разложить на составляющие
разложить на составляющие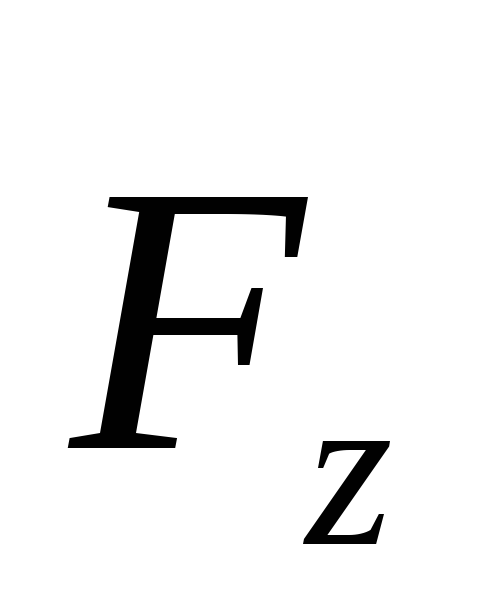 и
и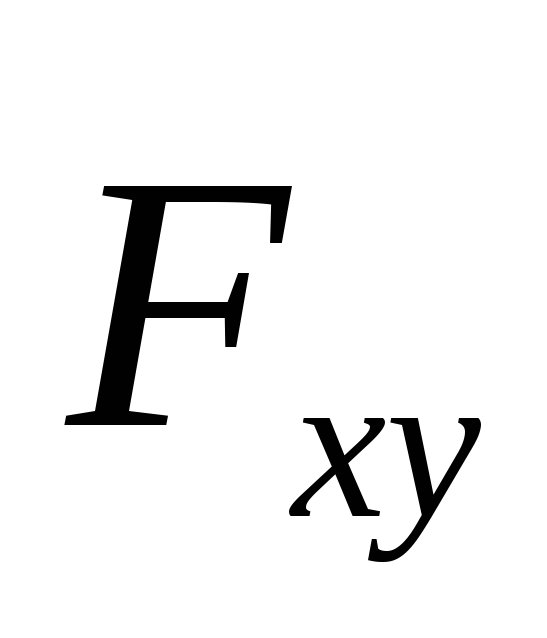 ,
одна из которых параллельна, а другая
перпендикулярна оси Z (рис.1.21), то увидим,
что сила
,
одна из которых параллельна, а другая
перпендикулярна оси Z (рис.1.21), то увидим,
что сила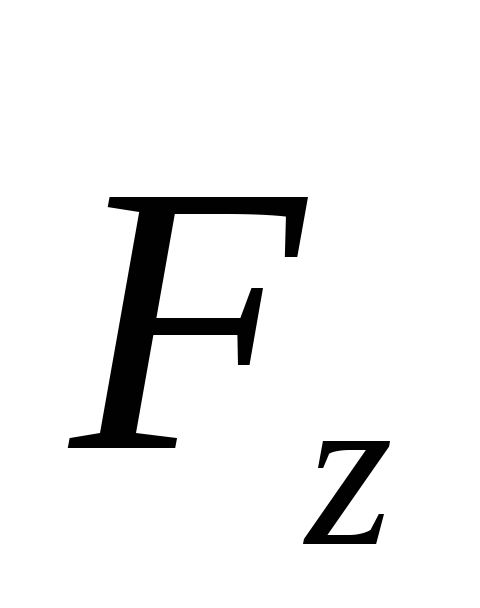
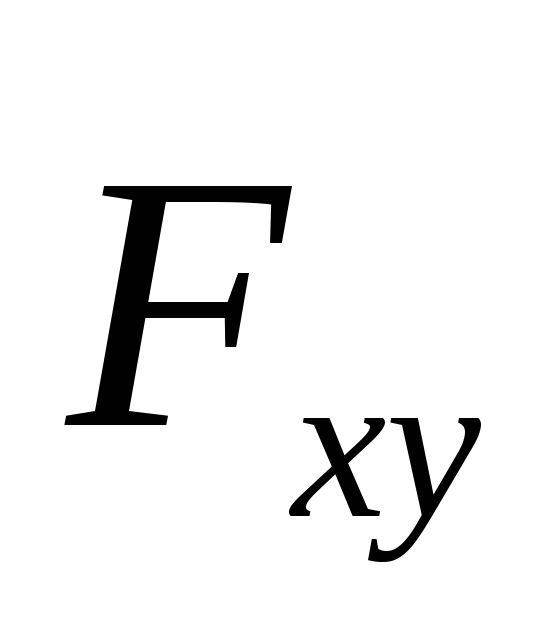 определится ее моментом относительно
точки О.
определится ее моментом относительно
точки О.
|
Следовательно, для определения момента силы относительно оси нужно силу спроектировать на плоскость, перпендикулярную оси и найти момент проекции относительно точки пересечения оси с этой плоскостью:
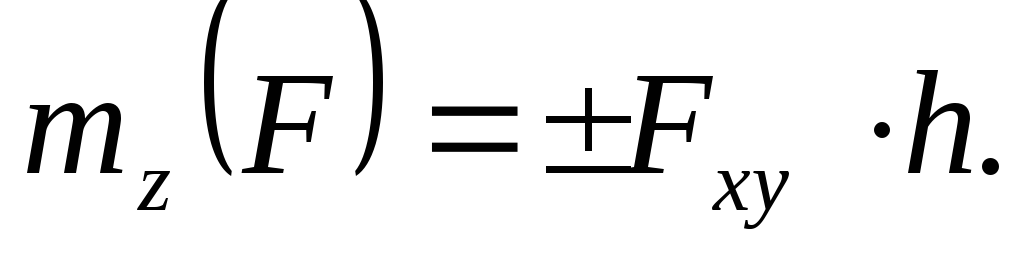 (1.6)
(1.6)
Знак момента определяется следующим образом: момент считается положительным, если, глядя с положительного конца оси поворот тела будет виден против часовой стрелки. Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ее.
При определении момента силы относительно точки часто бывает затруднительно определить плечо силы. В этом случае можно воспользоваться теоремой Вариньона: момент равнодействующей плоской системы сил относительно точки равен алгебраической сумме моментов составляющих сил относительно той же точки.
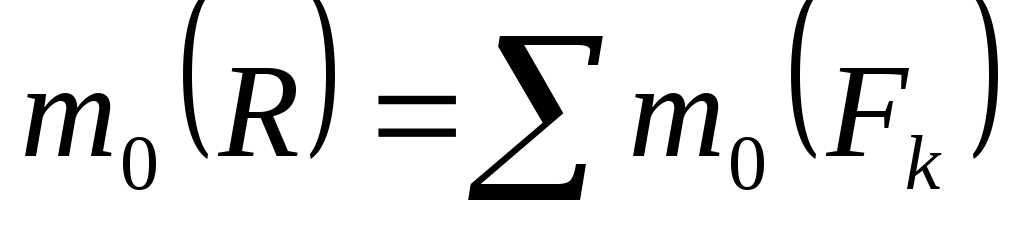 (1.7)
(1.7)
Аналогичная теорема применима и для определения момента силы относительно оси.
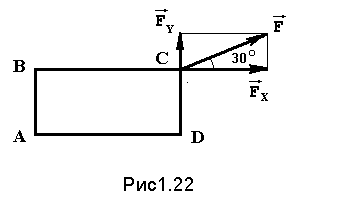
Пример: найти момент силы F = 10 H относительно точки А, если АВ=0,2 м, ВС=0,5 м (рис.1.22). Разложим силу F на две составляющих Fx=Fcos(30), Fy=Fsin(30). Тогда |
|
Тогда
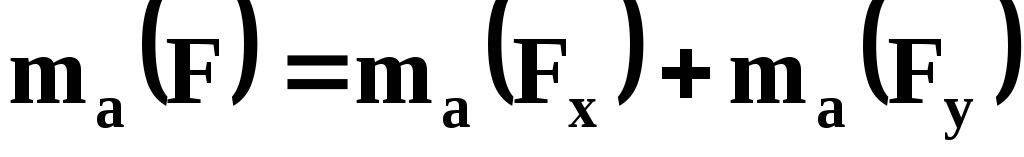
или 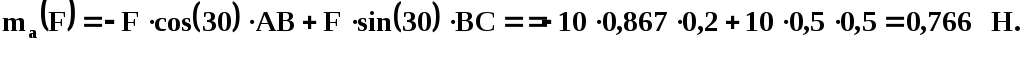
1.8. Пара сил и ее свойства
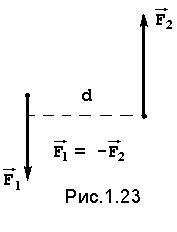
Парой сил называется система, состоящая из двух сил, равных по модулю, противоположных по направлению и не лежащих на одной прямой (рис.1.23). |
|
Плоскость, в которой лежат силы пары называется плоскостью действия пары, а кратчайшее расстояние между силами пары называется плечом пары. Сумма сил пары равна нулю, поэтому пара сил не имеет равнодействующей, однако она оказывает на тело вращательное действие, характеризуемое ее моментом.
Моментом пары называется алгебраическая величина, модуль которой равен произведению одной из сил на плечо пары:
m = F1d = F2 d (1.8)
Момент пары считается положительным, если пара стремится повернуть тело против часовой стрелки и отрицательный, если пара стремится повернуть тело по часовой стрелке.
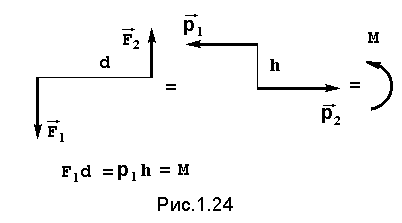
Эффект действия пары на твердое тело не зависит от ее положения в плоскости, поэтому ее можно переносить в плоскости действия в любое положение. Кроме того, не изменяя действия пары на тело, ее можно заменить другой парой с равным моментом. Поэтому часто пары изображают в виде круговой стрелки и называют пару сосредоточенным моментом (рис.1.24).
|
Поскольку действие пары определяется ее моментом, то если на
тело
действует несколько пар, лежащих в
одной плоскости, то их можно заменить
одной парой с моментом, равным сумме
моментов слагаемых пар: М=M
Mk=0 (1.9)
Отметим еще одно важное свойство пары сил: сумма моментов сил пары относительно любой точки равна моменту пары. Возьмем пару сил F1 и F2 и произвольную точку А (рис.1.25). |
|
Тогда
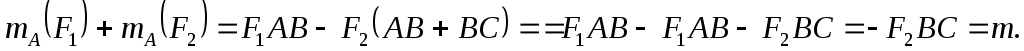
Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)
10
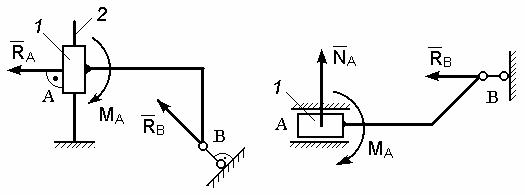
и) Другие виды связей
|
|
Ползун 1 на стержне 2 | Ползун 1 в направляющих |
Рис. XII
На рис. XII приведена расчетная схема для рамы AB.
11
Задача С.1. Проекция силы на ось и момент силы относительно оси
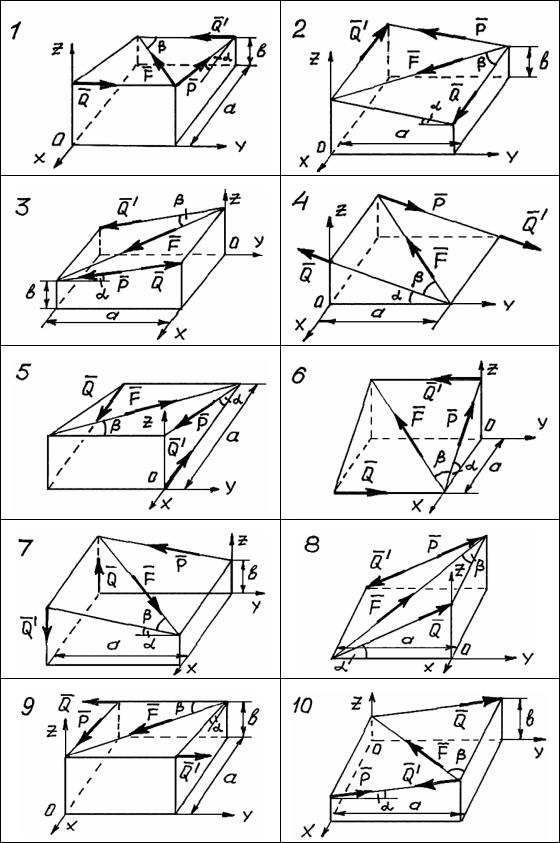
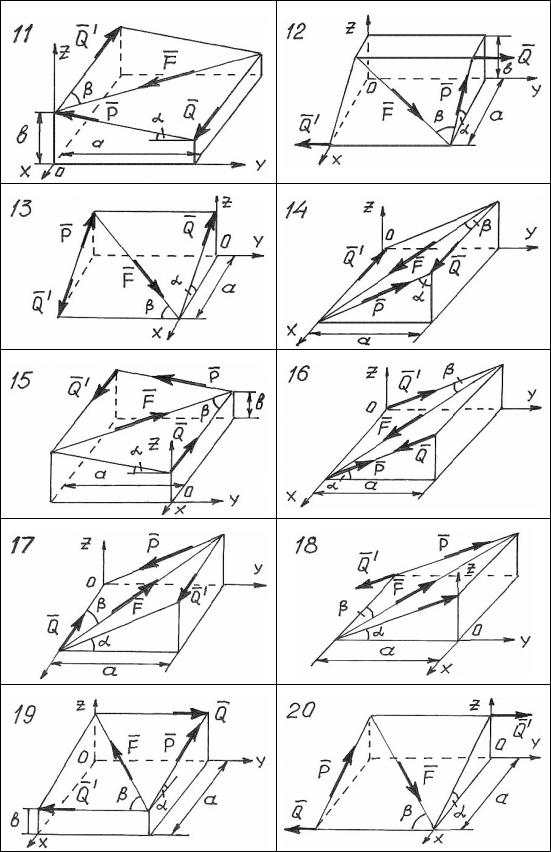
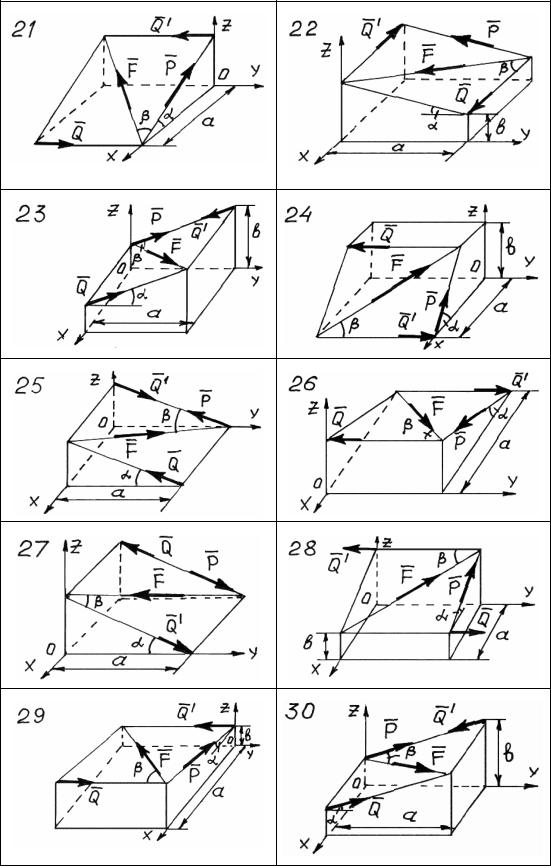
На схемах рис. 2 – 4 показаны системы сил {Q,Q’,P,F} в прямо-
угольной системе координат. Геометрические размеры a, b и углы α, β – известны.
Во всех вариантах схем требуется найти проекции всех сил на оси координат и моменты этих сил относительно осей координат Oxyz двумя способами – аналитическим и графо-аналитическим.
1. Момент силы
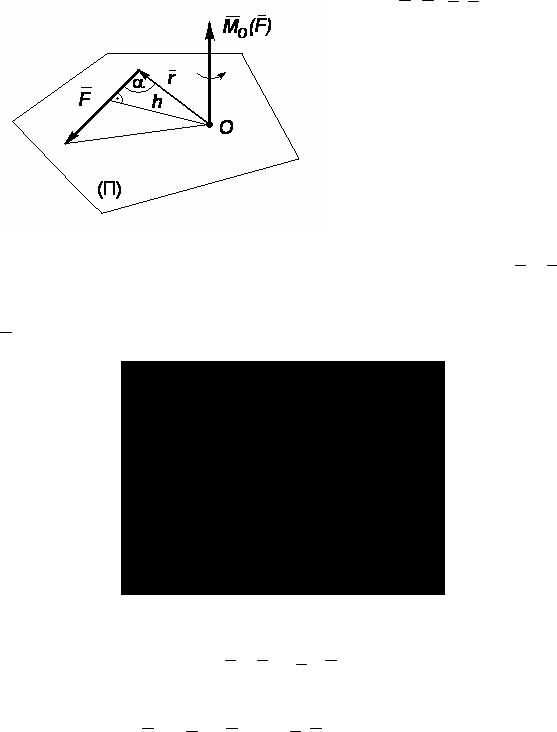
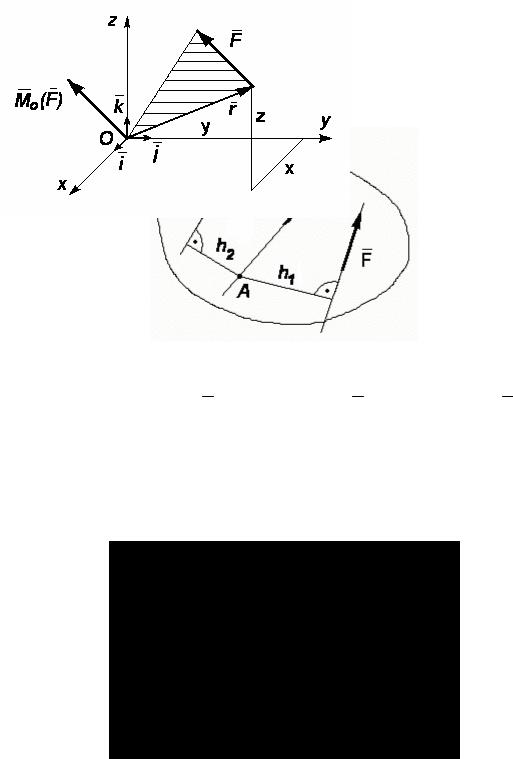
Момент силы относительно точки O (рис. 1) – это вектор Mo (F), который всегда будет перпендикулярен плоскости (П), где лежит сила F .
Рис. 1
Вектор – момент
Mo (F) = r ×F,
а по модулю
Mo (F) =| r | | F | sin(r, F) = Frsinα= Fh.
15
Момент силы относительно точки, это алгебраическая величина, взятая со знаком « + » или « – » и равна произведению силы F на “плечо” h.
h – перпендикуляр, опущенный из точки O на линию действия силыF .
Если сила F стремится вращать плоскость (П) против хода часовой стрелки, то принимается знак « + », в обратном направлении – знак « – ».
Рис. 5
Для схемы рис. 5: MA(F)= +F h2 ; MA(P)= -P h3 ; MA(Q)= 0.
Если линия действия силы пересекает заданную точку, то момент этой силы относительно данной точки всегда будет равен нулю.
Теперь рассмотрим аналитический способ вычисления момента силы относительно координатных осей.
16
На рис. 6 показан вектор-момент Mo (F) силы F относительно точки O начала координатных осей.
В проекциях на оси координат xOyz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M | O (F) = Mx i + My j + Mzk . | (1) | |||||||||||||||||||||||
С другой стороны, |
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| i |
|
| j |
|
|
| k |
|
|
| |
|
|
|
|
| = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| M | O (F) | ×F | = | x | y |
| z | , |
| |||||||||||||||
| r |
|
| ||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| Fx | Fy |
| Fz |
|
| |||||||
где i, j,k – орты осей координат,
x, y, z – проекции радиус-вектора r на оси координат, Fx, Fy, Fz – проекции силы F на те же оси координат.
Раскрывая определитель, можно записать
|
|
|
|
|
|
|
|
|
|
|
|
M | O (F) = i(yFz — zFy )+ j(zFx — xFz )+ k(xFy — yFx ). | (2) | |||||||||
Сравнивая (1) и (2), окончательно запишем аналитический способ вычисления момента силы относительно осей координат.
Mx = yFz — zFy , My = zFx — xFz , Mz = xFy — yFx .
Запишем определение для вычисления момента силы F относительно оси графо-аналитическим способом.
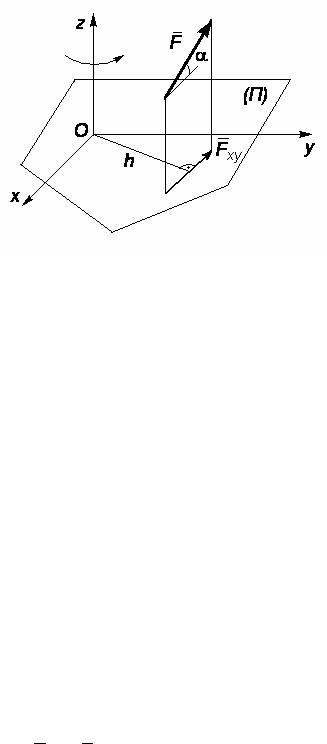
Чтобы вычислить момент силы F относительно оси, нужно (рис.7) провести плоскость (П) перпендикулярную этой оси и на эту плоскость спроецировать вектор силы Fxy = Fcosα; а затем взять
момент этой проекции Fxy относительно точки O пересечения оси z
с плоскостью (П).
Тогда Mz(F) = Fxy h = Fhcosα.
17
|
|
|
|
|
|
|
|
|
|
|
|
| Рис. 7 | ||
Частные случаи: | |||||||
а) |
|
|
|
|
| ||
Mz(F) | = 0; F ≠ 0; cosα ≠ 0; h = 0 — линия действия силы F | ||||||
пересекает ось Oz. | |||||||
б) |
|
|
|
| |||
Mz(F)= 0; F ≠ 0; h ≠ 0; cosα = 0 — линия действия силы F | |||||||
параллельна данной оси.
В этих двух случаях момент силы относительно оси всегда будет равен нулю.
Если смотреть на ось сверху и видеть, что проекция Fxy стремит-
ся вращать плоскость (П) против хода часовой стрелки, то момент силы будет иметь знак « + », а в другом направлении – знак « – ».
2. Момент пары сил
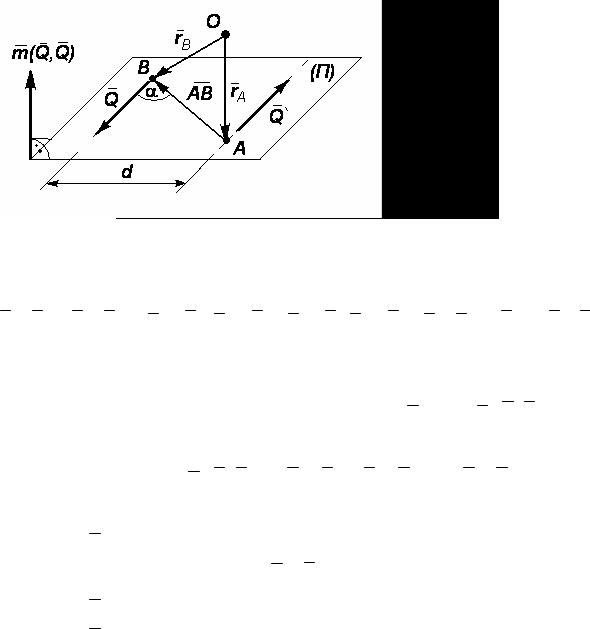
Парой сил называется система двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 8).
По определению Q ‘= -Q . Расстояние d между силами называется плечом пары. Плоскость (П), в которой лежит пара сил, называется плоскостью действия пары сил. Пару сил нельзя привести к равнодействующей силе, поэтому она сама является простейшей системой.
Действие пары сил удобно задавать с помощью вектора момента
18
Рис. 8 пары сил. Вычислим сумму моментов сил, составляющих пару, относительно произвольной точки O.
Mo (Q)+ Mo (Q’ )= rB ×Q + rA ×Q’ = rB ×Q — rA ×Q = (rB — rA )×Q = AB ×Q.
Из полученного результата видно, что сумма моментов не зависит от положения моментной точки, а определяется только параметрами пары сил. Эта сумма обозначается m или m(Q,Q’ )и называется вектором момента пары сил.
Таким образом, m(Q,Q’ )= Mo (Q)+ Mo (Q’ )= AB ×Q.
Напомним, что A и B произвольные точки на линии действия сил. Вектор m полностью характеризует действие пары сил.
По модулю он равен m =| AB ×Q |= Q AB sinα = Q d .
Вектор m перпендикулярен плоскости действия пары сил (П). Вектор m по правилу векторного произведения всегда направлен туда, откуда поворот, который стремится вызвать пара сил, будет
виден против хода часовой стрелки (правило правого винта). Моменты пары сил относительно координатных осей можно вы-
числять аналитическим и графо-аналитическим способами. Момент пары сил по существу является моментом одной из сил
относительно произвольной точки на линии действия другой силы. Поэтому для аналитического расчета моментов можно использовать полученные ранее формулы. Применительно для пары сил, они имеют следующий вид

19
mx = ( AB )y Qz — ( AB )zQy ; my = ( AB )zQx — ( AB )x Qz ; mz = ( AB )x Qy — ( AB )y Qx .
Здесь ( AB )x , ( AB )y , ( AB )z — проекции вектора AB соединяю-
щего любые две точки на линии действия сил.
Qx , Qy , Qz — проекции силы Q , к которой направлен векторAB .
При графо-аналитическом расчете необходимо:
-на схеме показать вектор m , направив его в любом месте перпендикулярно плоскости действия пары в ту сторону, откуда вращение пары будет видно против хода часовой стрелки;
-вычислить модуль момента пары m = Q d ;
-спроецировать вектор m на оси координат и в полученные выражения подставить модуль момента пары сил.
Пример решения задачи
Для системы сил на рис. 9 требуется найти проекции всех сил на оси координат и моменты этих сил относительно осей координат Oxyz двумя способами – аналитическим и графо-аналитическим.
Моменты силы P
Аналитический способ
Запишем формулы для аналитического расчета моментов силы P
Mx (P)= yPz — zPy ;
My (P) = zPx — xPz ; Mz(P) = xPy — yPx .
Выберем на линии действия силы P произвольную точку, например точку K, и запишем ее координаты. x = DA; y = 0; z = DE.
1. Понятие алгебраического момента силы.
2. Момент силы относительно точки.
3. Теорема Вариньона для системы сходящихся сил.
Момент силы относительно оси.
1. То, что понятия силы явно недостаточно для решения многих задач механики, знали еще в Древней Греции. Новый элемент — произведение силы на ее расстояние до точки опоры, приводящий тело во вращение, был введен Архимедом при изложении им теории равновесия рычага. В современной трактовке, введенный Архимедом новый силовой фактор, называется алгебраическим моментом. К необходимости введения этого понятия мы приходим при попытке ответить, например, на следующий вопрос: при каком соотношении длин L1 , L2 и весов P1 , P2 невесомый стержень (рис. 1.21) будет находиться в равновесии в горизонтальном положении?
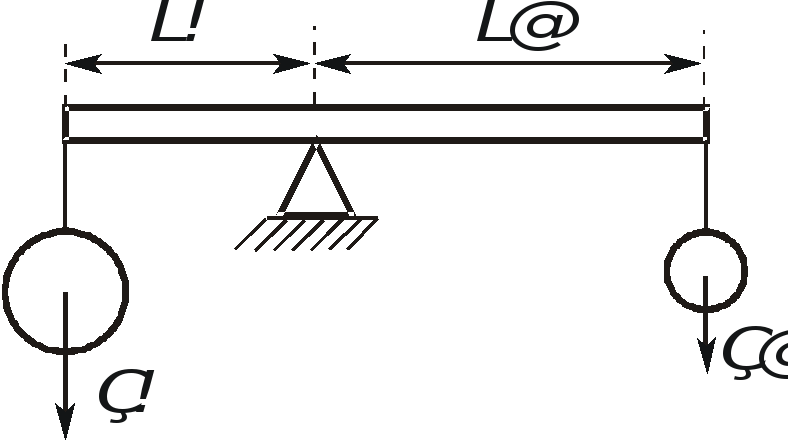
Рис. 1.21. К определению алгебраического момента
Ответ на этот вопрос следующий: стержень будет в равновесии, если:
P1 L1 = P2 L2
или
P1 L1 — P2 L2 = 0.
Другими словами, при равновесии рычага должны быть равны произведения сил, расположенных справа и слева от точки опоры О, на кратчайшие расстояния от точки О до линий действия этих сил.
Если отвлечься от рассмотренной выше задаче о равновесии рычага, то алгебраический момент силы относительно произвольного центра О можно определить как взятое со знаком плюс или минус произведение модуля силы на плечо. При этом плечом называют кратчайшее расстояние от центра О до линии действия силы (рис. 1.22)

Рис. 1.22. К определению алгебраического момента
Правило знаков: если сила стремится повернуть тело, к которому она приложена, против часовой стрелки, то момент считается положительным, если по часовой — отрицательным. Понятия алгебраического момента вполне достаточно для описания действия на тело плоских систем сил. Для описания действия пространственной системы сил вводится понятие вектора-момента относительно точки и понятие осевого момента.
2. Момент силы относительно точки
Моментом силы 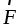 относительно точкиО называется вектор
относительно точкиО называется вектор 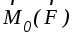 ,
равный
векторному произведению
,
равный
векторному произведению 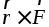 ,
где
,
где 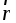 — радиус-вектор, определяющий положение
точки приложения силы
— радиус-вектор, определяющий положение
точки приложения силы 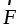 относительно точкиO.
относительно точкиO.
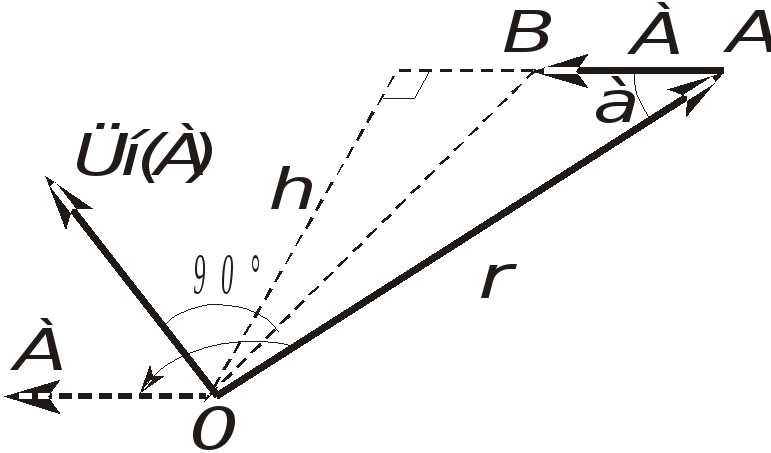
Рис. 1.23. К определению момента силы относительно точки
По определению
векторного произведения вектор 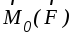 приложен в точкеO и направлен перпендикулярно плоскости,
содержащей перемножаемые векторы (
плоскость треугольника OАВ)
в ту сторону, откуда поворот от вектора
приложен в точкеO и направлен перпендикулярно плоскости,
содержащей перемножаемые векторы (
плоскость треугольника OАВ)
в ту сторону, откуда поворот от вектора 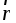 к вектору
к вектору 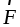 виден происходящим против хода часовой
стрелки (рис.1.23). Модуль вектора-момента
равен:
виден происходящим против хода часовой
стрелки (рис.1.23). Модуль вектора-момента
равен:
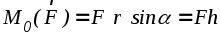 ,
,
где h — плечо силы 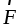 относительно точкиO.
относительно точкиO.
Введенный таким образом момент, полностью определяет вращательный эффект приложенной к телу силы: его линия действия определяет плоскость вращения, его направление — направление вращения, его модуль — интенсивность вращательного воздействия силы на тело.
Теорема Вариньона для системы сходящихся сил
Момент равнодействующей, относительно некоторой точки О, равен сумме моментов составляющих сил относительно той же точки.
Данная теорема справедлива для любой системы сил, имеющей равнодействующую. Приведем здесь ее доказательство для системы сходящихся сил.
Пусть 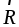 является равнодействующей системы
сходящихся сил
является равнодействующей системы
сходящихся сил 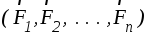 ,
т.е.
,
т.е.
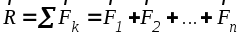 .
.
Тогда по определению момента
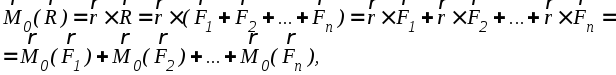
что и требовалось доказать.
Момент силы относительно оси
Моментом силы относительно оси называется проекция на эту ось вектора момента данной силы относительно любой точки, лежащей на этой оси.
Пусть необходимо
вычислить момент силы 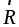 относительно осиZ.
Выберем на этой оси (рис. 1.24) произвольную
точку O и проведем через нее оси X и Y.
По определению момент силы
относительно осиZ.
Выберем на этой оси (рис. 1.24) произвольную
точку O и проведем через нее оси X и Y.
По определению момент силы 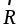 относительно точкиO равен
векторному произведению
относительно точкиO равен
векторному произведению 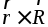 :
:
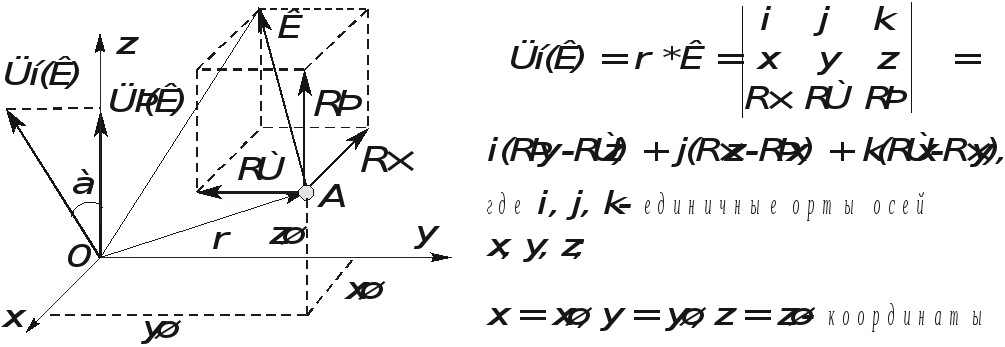
Рис. 1.24. Определение осевых моментов
Из векторной
алгебры известно, что выражения, стоящие
в скобках при единичных ортах 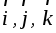 представляют собой проекции векторного
произведения на оси x, y, z соответственно:
представляют собой проекции векторного
произведения на оси x, y, z соответственно:
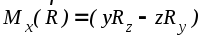 ,
,
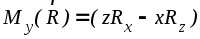 ,
(1.3)
,
(1.3)
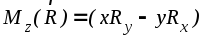 .
.
Анализируя последнее из выражений (1.3) можно заметить, что оно не содержит координаты z. Это значит, что значение осевого момента Mz не зависит от выбора точки О на оси z. Отсутствие в данном выражении Rz говорит о том, что осевой момент создают лишь перпендикулярные данной оси составляющие силы. Это означает, что если сила параллельна какой-либо оси, то ее момент относительно этой оси равен нулю. Кроме того, отсюда же (и из теоремы Вариньона) следует простое правило вычисления осевых моментов:
Момент силы ™ относительно какой-либо оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси, взятому относительно точки пересечения оси с плоскостью.
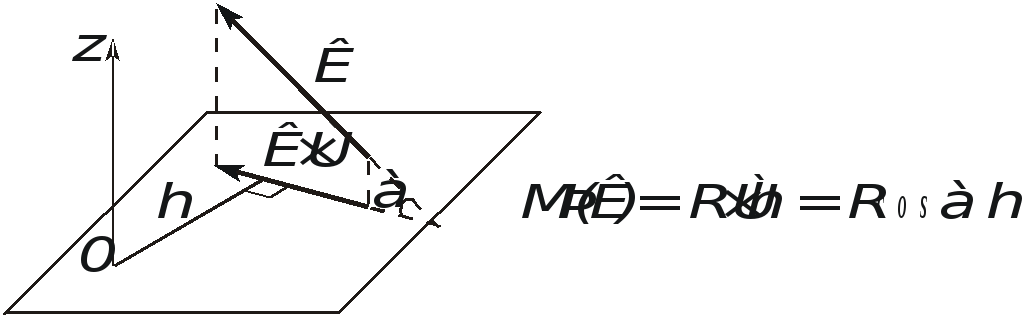
Рис. 1.25. Вычисление осевого момента
Момент будет иметь
знак плюс, когда с положительного конца
оси поворот, который стремится совершить
сила 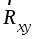 ,
виден происходящим против хода часовой
стрелки. Из рис. 1.25 видно, что если
линия действия силы
,
виден происходящим против хода часовой
стрелки. Из рис. 1.25 видно, что если
линия действия силы 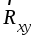 , а,
следовательно и силы , пересекает ось Z, то ее осевой момент
будет равен нулю ( т.к. в этом случае h
= 0 ).
, а,
следовательно и силы , пересекает ось Z, то ее осевой момент
будет равен нулю ( т.к. в этом случае h
= 0 ).
Лекция 5
Вопросы
Сложение параллельных сил.
Пара сил и ее момент.
Теорема о параллельном переносе силы.
1. Рассмотрим вопрос о сложении двух параллельных и направленных в одну сторону сил (рис. 1.26)
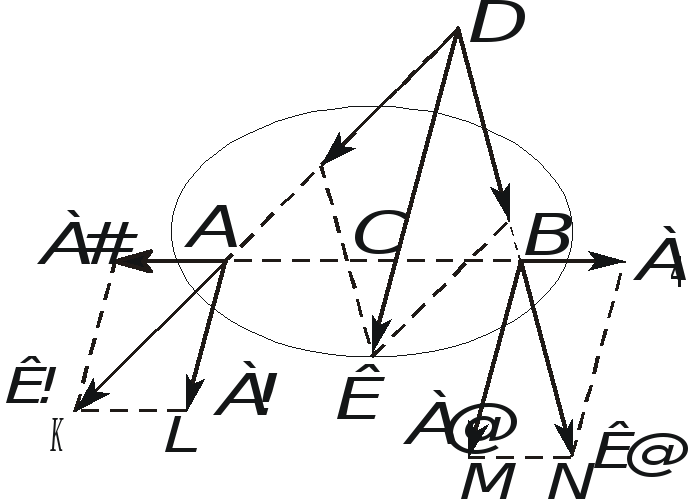
Рис. 1.26. Сложение двух параллельных сил, направленных в одну сторону
Пусть на твердое
тело в точках А и В действуют параллельные силы 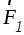 и
и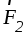 (рис. 1.26). Приложим в этих точках
уравновешенную систему двух равных по
величине сил
(рис. 1.26). Приложим в этих точках
уравновешенную систему двух равных по
величине сил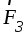 и
и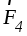 и направленных вдольАВ в противоположные
стороны. Заменим системы сил
и направленных вдольАВ в противоположные
стороны. Заменим системы сил 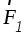 ,
,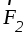 и
и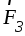 ,
,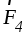 их равнодействующими
их равнодействующими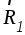 и
и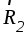 .
Затем перенесем
.
Затем перенесем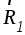 и
и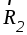 вдоль их линий действий в точкуD и заменим их одной силой К,
являющейся равнодействующей сил А!
и А@:
вдоль их линий действий в точкуD и заменим их одной силой К,
являющейся равнодействующей сил А!
и А@:
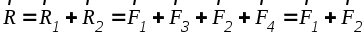 .
.
Найдем линию
действия силы 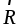 .
Из подобия треугольниковACD и BMN следует
.
Из подобия треугольниковACD и BMN следует
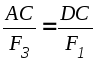 ,
, 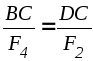 .
.
Учитывая, что F3 = F4 , получаем 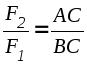
или 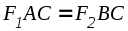 .
(1.5)
.
(1.5)
Таким образом, система двух параллельных и одинаково направленных сил имеет равнодействующую, равную сумме этих сил и направленную в ту же сторону.
Согласно (1.5), линия
действия равнодействующей делит отрезок АВ на части, обратно пропорциональные
величинам сил 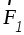 и
и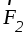 .
.
Аналогичным образом рассматривается случай сложения двух параллельных не равных по величине и противоположно направленных сил. Ниже приводятся без доказательства лишь результаты такого сложения.
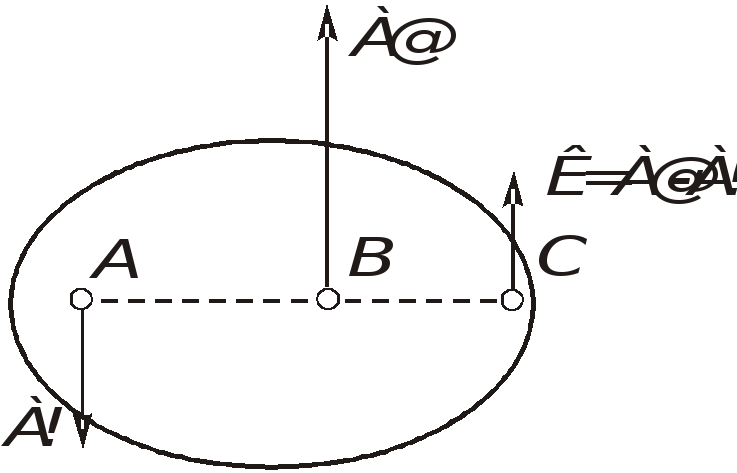
Рис. 1.27. Сложение двух параллельных и противоположно направленных сил
Изображенная на
рис 1.27 система сил имеет равнодействующую 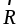 ,
которая равна разности сил
,
которая равна разности сил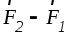 и направлена в сторону большей по
величине силы. Ее линия действия делит
отрезокАВ на части обратно пропорциональные силам F1 и F2 внешним образом (точка С лежит за большей по величине силой F2 ):
и направлена в сторону большей по
величине силы. Ее линия действия делит
отрезокАВ на части обратно пропорциональные силам F1 и F2 внешним образом (точка С лежит за большей по величине силой F2 ): 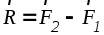 ,
,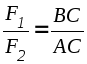 .
(1.6)
.
(1.6)
Еще раз обращаем
внимание на то, что в рассматриваемом
случае 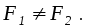
2. Пара сил и ее момент
Займемся не рассмотренным в предыдущем пункте случаем, когда складываются две равные, параллельные, не лежащие на одной прямой и противоположно направленные.
Если использовать
формулу (1.6) для вычисления равнодействующей
такой системы сил, то мы получим  ,
что казалось бы, должно означать
уравновешенность данной системы сил.
Вместе с тем, очевидно, что под действием
такой системы сил тело начнет вращаться.
Остается признать, что такая система
является исключением среди систем двух
параллельных сил и не имеет равнодействующей.
Именно поэтому ее рассматривают как
самостоятельный силовой фактор и
называют парой
сил.
,
что казалось бы, должно означать
уравновешенность данной системы сил.
Вместе с тем, очевидно, что под действием
такой системы сил тело начнет вращаться.
Остается признать, что такая система
является исключением среди систем двух
параллельных сил и не имеет равнодействующей.
Именно поэтому ее рассматривают как
самостоятельный силовой фактор и
называют парой
сил.
Так как вращательный эффект сил характеризуется их моментом, вычислим момент пары сил относительно произвольного центра О, как сумму моментов отдельных сил пары (рис. 1.28)
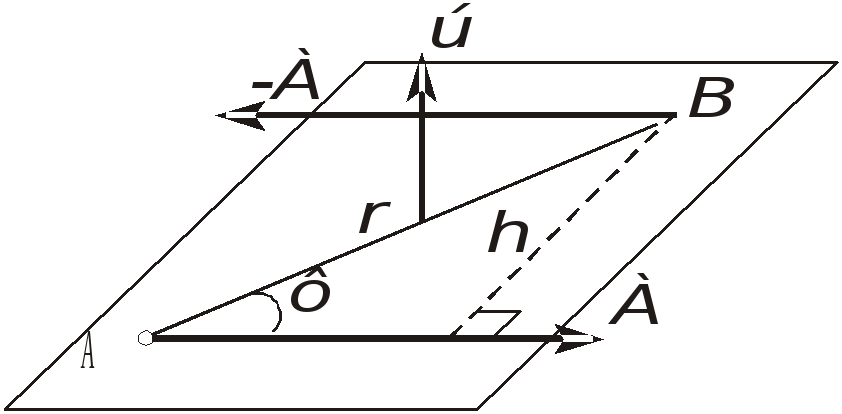
Рис. 1.28. К определению момента пары сил
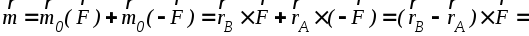
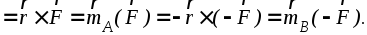 (1.7)
(1.7)
Данный результат означает, что момент пары сил не зависит от выбора точки О и равен моменту одной из сил пары относительно точки приложения другой силы, т.е.
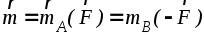 .
(1.8)
.
(1.8)
Модуль момента
пары сил равен m = F r sin = F h, где h — расстояние между линиями действия сил
пары, называемое плечом
пары. Вектор 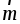 направлен перпендикулярно плоскости
действия пары в ту сторону, откуда
вращение видно против хода часовой
стрелки.
направлен перпендикулярно плоскости
действия пары в ту сторону, откуда
вращение видно против хода часовой
стрелки.
Из принятого определения момента пары, как суммы моментов отдельных сил пары относительно произвольного центра (1.7) и независимости момента пары сил от выбора центра О (1.8), следует:
a) две пары сил, имеющие одинаковые моменты, эквивалентны (т.е. оказывают на тело одинаковое механическое действие). Это означает, что две пары сил, независимо от их расположения в данной ( или в параллельной) плоскости, независимо от того, чему равны в отдельности модули их сил и плечи, будут эквивалентны, если будут равны их моменты;
б) момент пары является свободным вектором (т.е. его можно считать приложенным в любой точке тела).
Примеры эквивалентных по действию на тело пар сил (рис. 1.29):
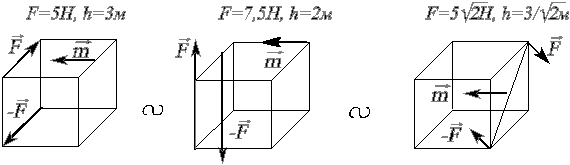
Рис. 1.29. Примеры эквивалентных по действию пар сил
в) если на тело
действуют несколько пар сил, то сумма
моментов всех сил, образующих эти пары,
относительно любого центра будет равна
геометрической сумме моментов отдельных
пар сил и, следовательно, вся совокупность
этих пар будет эквивалентна одной паре
с моментом 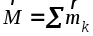 ,
(1.9)
,
(1.9)
где 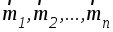 — моменты отдельных пар сил.
— моменты отдельных пар сил.
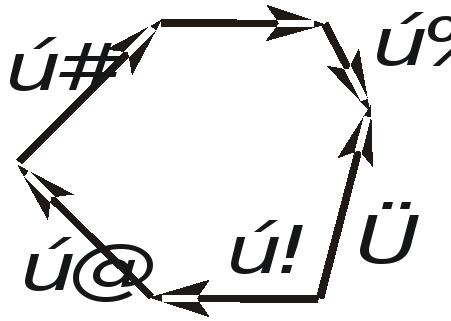
Рис. 1.22. Векторный многоугольник моментов пар сил
3. Теорема о параллельном переносе силы
Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, параллельно перенести в любую другую точку тела, добавив при этом пару сил с моментом, равным моменту переносимой силы относительно ее новой точки приложения. Докажем эту теорему.
Пусть в точке А приложена сила, которую мы хотим перенести
в точку В.
Приложим в точке В уравновешенную систему двух сил, равных
по величине переносимой силе, как
показано на рисунке. Заменив образовавшуюся
при этом пару сил 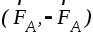 (которую называют присоединенной) ее
моментом и перенеся данный момент, как
свободный вектор, в точку В,
получаем формулируемое в теореме
утверждение.
(которую называют присоединенной) ее
моментом и перенеся данный момент, как
свободный вектор, в точку В,
получаем формулируемое в теореме
утверждение.

Рис. 1.24. Эквивалентные преобразование при параллельном переносе силы
Пример 1.
На барабан 1 радиуса r намотаны в противоположных направлениях
две нити, к концам которых прикладывают
силы 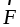 и
и 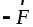 .
На барабан 2 того же радиуса намотана
одна нить, к которой прикладывают силу
.
На барабан 2 того же радиуса намотана
одна нить, к которой прикладывают силу 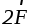 (рис.
1.29). Рассмотрим, чем будут отличаться
действия этих сил.
(рис.
1.29). Рассмотрим, чем будут отличаться
действия этих сил.
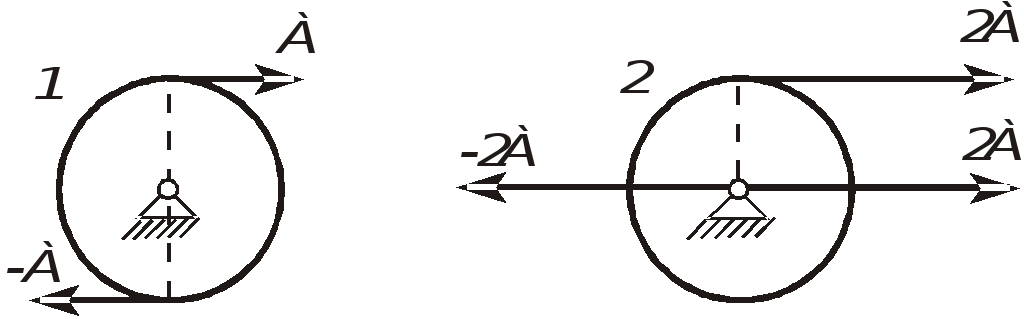
Рис. 1.29. Примеры действия пар сил
На барабан 1
действует только пара сил 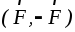 с моментом, численно равным2rF,
вращающим барабан. Силу, действующую
на барабан 2, можно заменить силой
с моментом, численно равным2rF,
вращающим барабан. Силу, действующую
на барабан 2, можно заменить силой 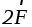 ,
приложенной к оси барабана, и парой сил
,
приложенной к оси барабана, и парой сил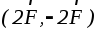 с моментом2rF . Итак, оба
барабана будут вращаться одинаково. Но
при этом ось второго барабана будет
испытывать давление, равное 2F,
а ось первого барабана никакого давления
не испытывает.
с моментом2rF . Итак, оба
барабана будут вращаться одинаково. Но
при этом ось второго барабана будет
испытывать давление, равное 2F,
а ось первого барабана никакого давления
не испытывает.
Лекция 6
Вопросы
2.8. Момент силы относительно точки. Теорема Вариньона о моменте равнодействующей
1. Момент силы относительно точки. Понятие момента силы возникло в связи с определением вращательного действия силы, приложенной к телу, имеющему неподвижную точку или неподвижную ось.
П редставим
себе твердое тело, имеющее в точкеО сферическую опору (рисунок 39, а, б).
Рассмотрим силу
редставим
себе твердое тело, имеющее в точкеО сферическую опору (рисунок 39, а, б).
Рассмотрим силу  ,
приложенную в точкеА этого тела. Очевидно, что сила
,
приложенную в точкеА этого тела. Очевидно, что сила  будет поворачивать тело вокруг неподвижной
точкиО.
Длина перпендикуляра d,
опущенного из точки О на линию действия силы
будет поворачивать тело вокруг неподвижной
точкиО.
Длина перпендикуляра d,
опущенного из точки О на линию действия силы  ,
называется плечом этой силы относительно
точкиО.
Так как точку приложения силы можно
произвольно перемещать вдоль линии
действия, то, очевидно, вращательный
эффект силы
,
называется плечом этой силы относительно
точкиО.
Так как точку приложения силы можно
произвольно перемещать вдоль линии
действия, то, очевидно, вращательный
эффект силы  будет зависеть: 1) от модуляF силы
будет зависеть: 1) от модуляF силы  и длины плечаd;
2) от положения плоскости поворота ОАВ,
проходящей через точку О и силу
и длины плечаd;
2) от положения плоскости поворота ОАВ,
проходящей через точку О и силу  ;
3) от направления поворота в этой
плоскости.
;
3) от направления поворота в этой
плоскости.
Ограничимся здесь пока рассмотрением плоской системы сил, т. е. когда линии действия сил системы расположены в одной плоскости. В этом случае плоскость поворота для всех сил системы является обшей и в дополнительном задании не нуждается, а направление поворота в этой плоскости можно охарактеризовать соответствующим знаком, считая поворот вокруг точки О против хода часовой стрелки положительным, а в направлении противоположном – отрицательным.
Тогда для
количественного измерения вращательного
эффекта силы  можно ввести следующее понятие о моменте
этой силы относительно некоторой точкиО на плоскости: моментом
силы относительно некоторой точки О на
плоскости называется скалярная величина,
равная взятому с соответствующим знаком
произведению модуля силы на ее плечо
относительно этой точки.
При этом будем считать, что момент силы
можно ввести следующее понятие о моменте
этой силы относительно некоторой точкиО на плоскости: моментом
силы относительно некоторой точки О на
плоскости называется скалярная величина,
равная взятому с соответствующим знаком
произведению модуля силы на ее плечо
относительно этой точки.
При этом будем считать, что момент силы  относительно точкиО имеет знак «плюс», если эта сила стремится
повернуть тело вокруг точки О против хода часовой стрелки (рисунок
39, а),
и знак «минус»,— если по ходу часовой
стрелки (рисунок 39, б).
относительно точкиО имеет знак «плюс», если эта сила стремится
повернуть тело вокруг точки О против хода часовой стрелки (рисунок
39, а),
и знак «минус»,— если по ходу часовой
стрелки (рисунок 39, б).
Момент силы  относительно точкиО будем обозначать символом
относительно точкиО будем обозначать символом 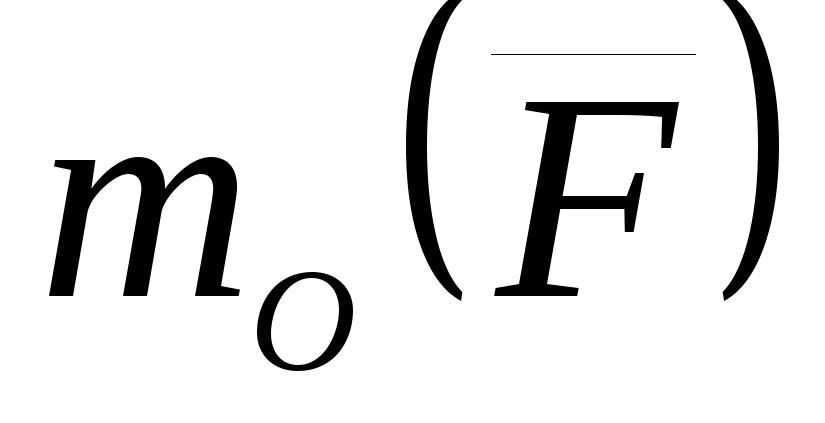 .
Следовательно,
.
Следовательно,
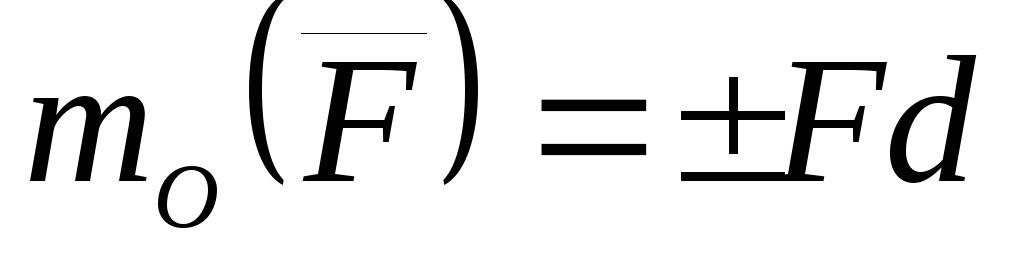 .
(1)
.
(1)
Заметим, что момент силы относительно точки О можно принимать за скалярную (алгебраическую) величину лишь в тех случаях, когда имеем дело с плоской системой сил. В случае же пространственной систем сил, т. е. когда линия действия всех сил системы расположены в различных непараллельных плоскостях, правило знаков момента силы относительно точки теряет свои силы.
Таким образом, мы установили, что момент силы относительно точки О сил плоской системы отличаются друг от друга численным значением и знаком. При этом численное значение момента сил относительно точки О равно произведению модуля силы на длину ее плеча относительно этой точки.
Отметим в заключение,
что геометрически численное значение
момента силы  относительно точкиО выражается удвоенной площадью треугольника OAB (рисунок 40), вершиной которого является
данная точка О,
а основанием – данная сила
относительно точкиО выражается удвоенной площадью треугольника OAB (рисунок 40), вершиной которого является
данная точка О,
а основанием – данная сила  :
:
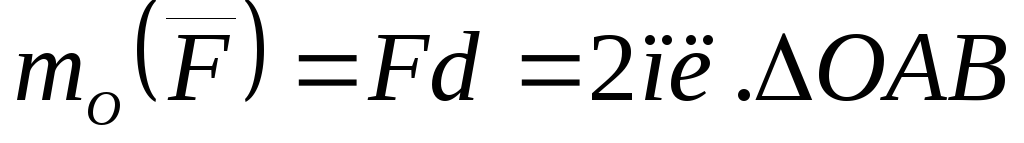 .
(2)
.
(2)
Единица момента
силы определяется по формуле (1), или 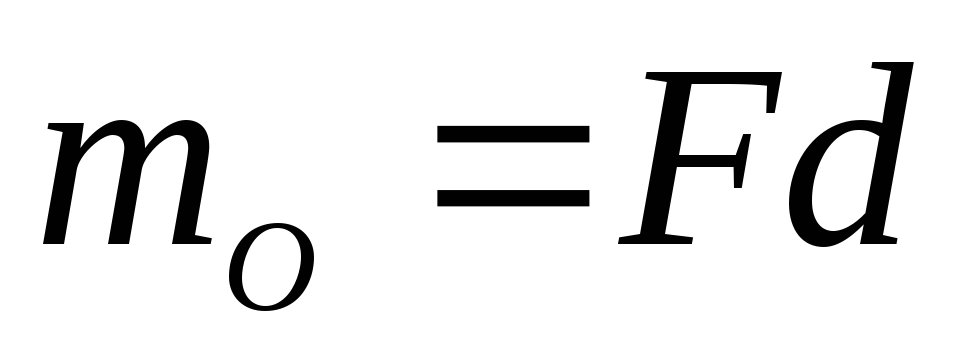 .
.
Положив в этой формуле F = 1 кг, d = 1 м, получим:
1 единица момента
сил 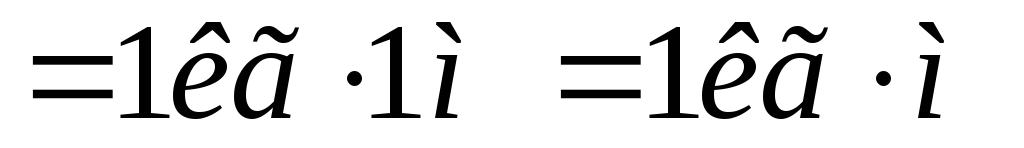
Размерность единицы момента силы в системе МКГСС
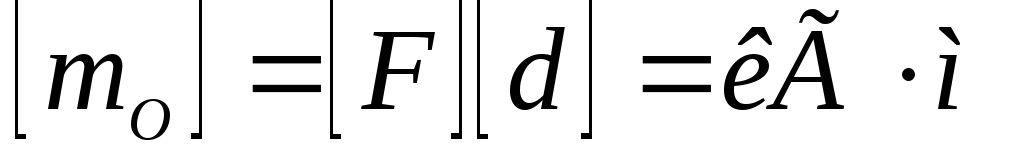 .
.
Если же модуль силы выражен в ньютонах (F = 1 H), а длина плеча в метрах (d = 1 м), то, очевидно, размерность единицы момента в системе СИ выражается в виде
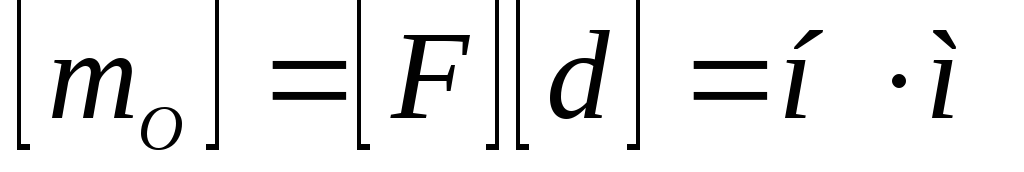 .
.

Отметим теперь следующие свойства момента силы относительно точки:
1. Момент силы относительно точки не изменится при переносе точки приложения силы вдоль ее линии действия, так как при этом не изменяется ни модуль силы, ни длина ее плеча.
2. Момент силы относительно точки равен нулю только тогда, когда модуль силы равен нулю или когда линия действия силы проходит через точку, так как в этом последнем случае длина плеча равна нулю
2. Теорема Вариньона о моменте равнодействующей. Докажем теперь следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно некоторой точки, лежащей в плоскости сил, равен алгебраической сумме моментов слагаемых сил относительно той же точки.
Рассмотрим
плоскую систему сходящихся сил 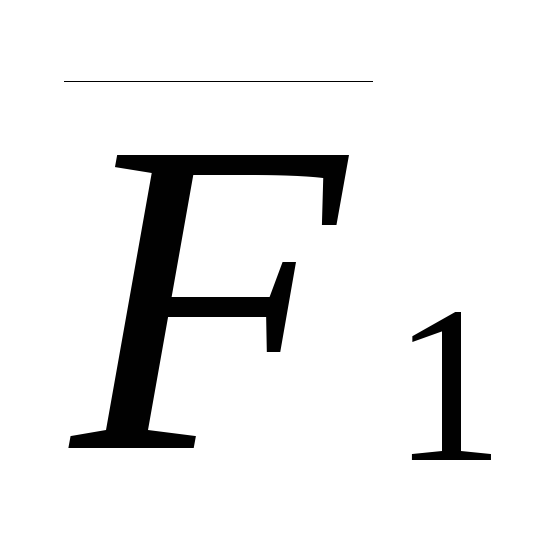 ,
, ,
…,
,
…, 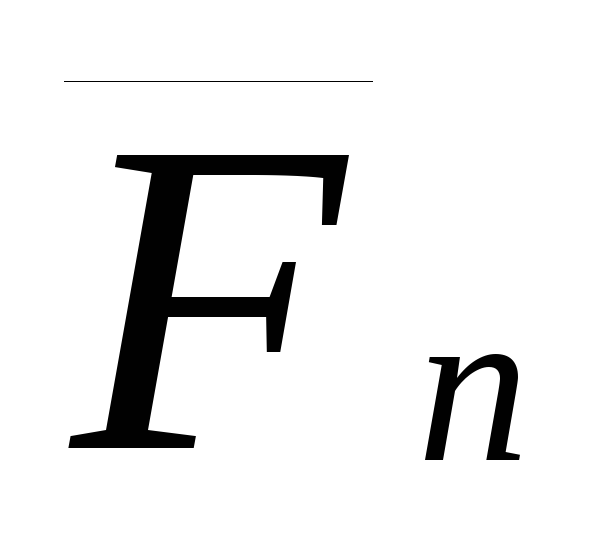 ,
приложенных в точке А твердого
тела (рисунок 41). Их равнодействующая
,
приложенных в точке А твердого
тела (рисунок 41). Их равнодействующая 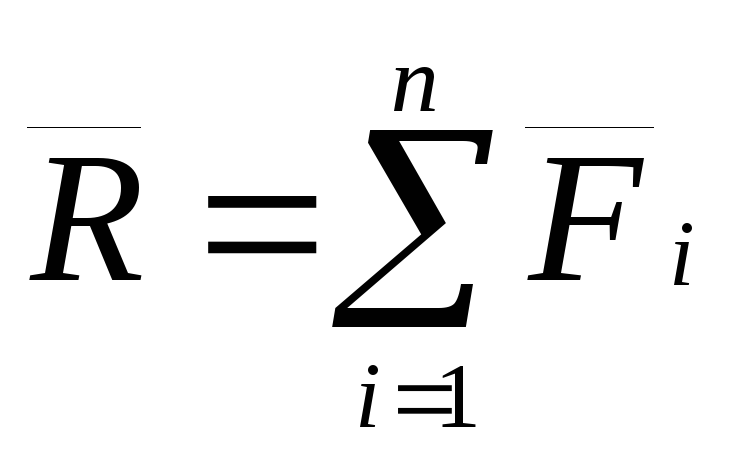 будет приложена в той же точке. По теореме
о проекции равнодействующей на ось
получим
будет приложена в той же точке. По теореме
о проекции равнодействующей на ось
получим 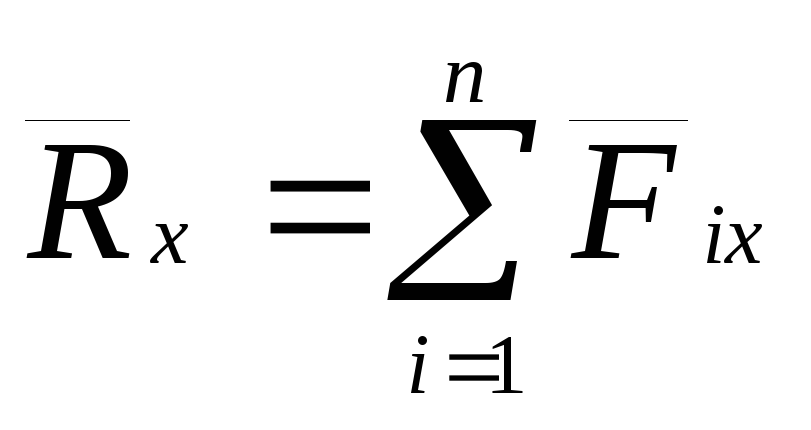 .Умножая
обе части этого равенства на ОА,
получим
.Умножая
обе части этого равенства на ОА,
получим
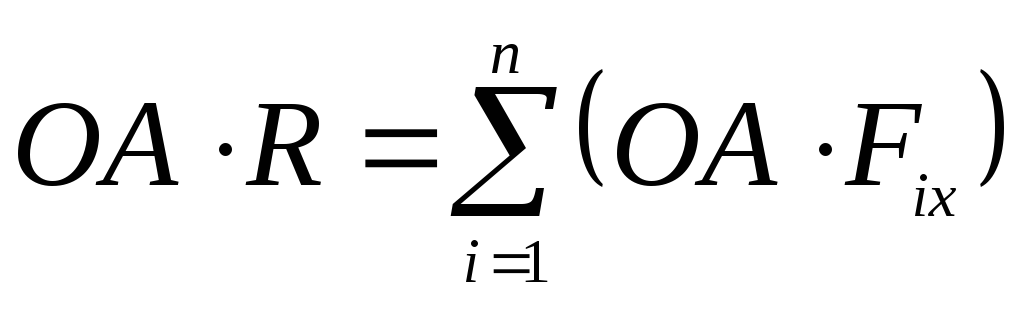 .
(3)
.
(3)
Преобразуем
эту формулу, для чего найдем момент
относительно точки О любой из сил системы, например силы 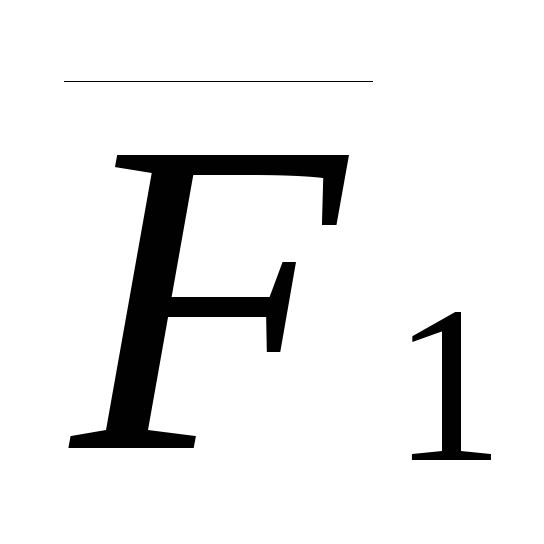 .
Очевидно,
.
Очевидно,
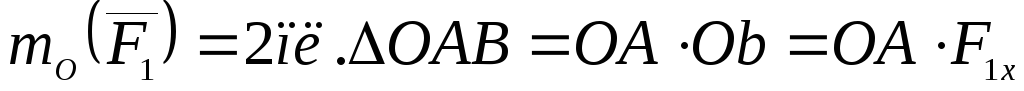 ,
(4)
,
(4)
где 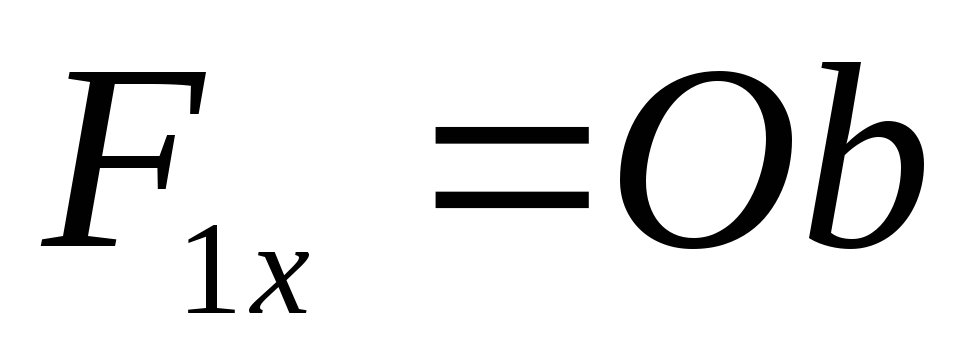 — проекция силы
— проекция силы 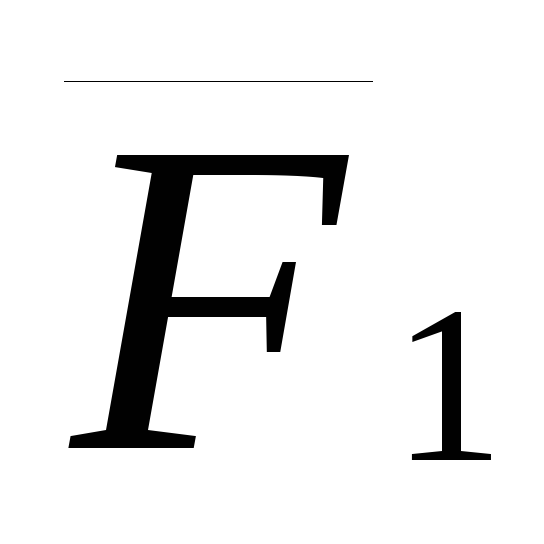 на ось Ох,
перпендикулярную к ОА.
на ось Ох,
перпендикулярную к ОА.
Согласно формуле (4) можно преобразовать формулу (3) к виду
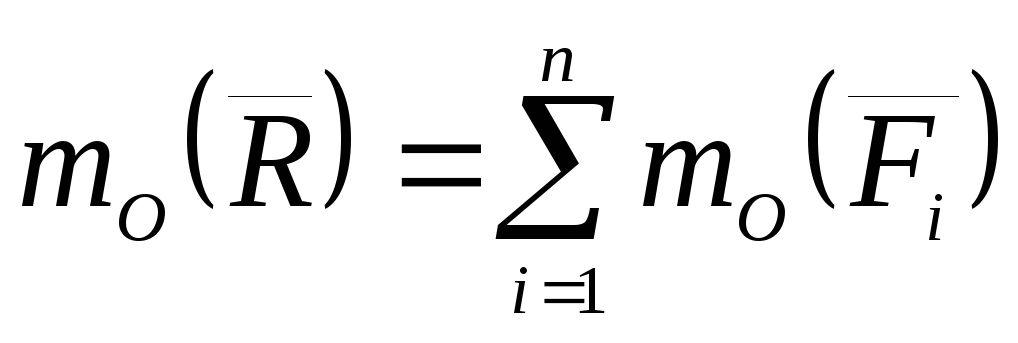 .
(5)
.
(5)
Эта формула и дает математическое выражение теоремы Вариньона о моменте равнодействующей.
Моментом пары сил называется сумма моментов сил, образующих пару, вычисленная относительно произвольно выбранной точки.
Аксиомы статики. Момент силы относительно центра оси.
Аксиомы устанавливают простейшие правила действия над силами и системами сил.
Аксиома 1. Две силы, приложенные в одной точке тела, эквивалентны одной силе, приложенной в той же точке и равной геометрической сумме этих сил (Рис. 1.3).
  | ||||
| Рис. 1.3 1.4 | Рис. 1.4 |
Аксиома 2. Не изменяя действия системы сил на тело, к ней можно добавить или от неё отнять уравновешенную систему сил.
Аксиома 3. Система двух сил, приложенных к абсолютно твёрдому телу, эквивалентна нулю тогда и только тогда, когда эти силы равны по модулю и действуют по одной прямой в противоположные стороны (Рис. 1.4).
Аксиомы позволяют рассматривать систему сил, приложенную к абсолютно твёрдому телу, как систему скользящих векторов.
  |
| Рис.1.5 Рис.1.6 |
Моментом силы относительно точки называется вектор, равный векторному произведению радиуса-вектора, проведённого из данного центра в точку приложения силы, и этой силы: 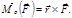 Моментом силы относительно оси называется проекция на ось вектора момента силы, вычисленного относительно любой точки этой оси.
Моментом силы относительно оси называется проекция на ось вектора момента силы, вычисленного относительно любой точки этой оси.
Главный вектор и главный момент системы сил.
Главным вектором системы сил называется геометрическая сумма всех сил системы: 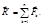
Главным моментом системы сил относительно некоторого центра O называется геометрическая сумма моментов всех сил системы относительно точки O:
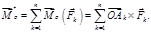
Вектор главного момента изображают приложенным в той точке 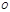 , относительно которой он вычисляется.
, относительно которой он вычисляется.
Главный вектор и главный момент системы сил представляют собой чисто геометрические величины и не могут рассматриваться как некоторая сила или момент некоторой силы.
Пара сил и ее момент.
Парой сил называется система двух сил, равных по модулю и действующих по параллельным прямым в противоположные стороны.
Плоскость, в которой расположены силы пары, называется плоскостью действия пары сил. Кратчайшее расстояние между линиями действия сил пары называется плечом пары сил.
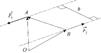 | 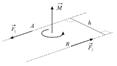 | |
| Рис. 1.7 | Рис. 1.8 |
Вычислим сумму моментов сил, образующих пару, относительно произвольно выбранной точки 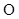 (Рис. 1.7):
(Рис. 1.7):
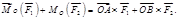
Учитывая, что 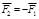 и
и 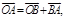 получаем:
получаем:
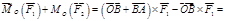
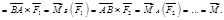
Как видно, сумма моментов сил, образующих пару сил, не зависит от точки, относительно которой эта сумма вычисляется, и может быть принята за характеристику пары сил.
Моментом пары сил называется сумма моментов сил, образующих пару, вычисленная относительно произвольно выбранной точки.
Момент пары сил можно вычислить как момент одной из сил пары относительно точки приложения другой силы той же пары, поскольку эта вторая сила не создаёт момент относительно своей точки приложения:
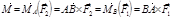
Момент пары сил – вектор свободный; он располагается перпендикулярно плоскости действия пары сил, причём направлен в ту сторону, откуда возможный поворот тела под действием пары виден против хода часовой стрелки (Рис. 1.8). Модуль момента пары равен произведению модуля одной из сил пары на её плечо: 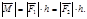
Содержание метода Пуансо о приведении системы сил к одному центру.
Теорема.(метод Пуансо).Произвольная система сил эквивалентна системе, состоящей из одной силы, равной геометрической сумме всех сил системы, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен сумме моментов всех сил системы относительно этой точки.
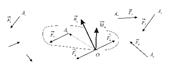 |
| Рис. 2.1 |
Две важнейшие характеристики системы сил:
1) главным вектором системы сил называется геометрическая сумма всех сил системы: 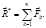
2) главным моментом системы сил относительно некоторого центра O называется геометрическая сумма моментов всех сил системы относительно точки O: 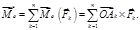
Теорема о приведении системы сил к одному центру можно сформулировать в виде:
произвольная система сил эквивалентна системе, состоящей из одной силы, равной главному вектору системы сил, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен главному моменту системы сил относительно этой точки. 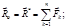
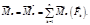
5.Необходимые и достаточные условия равновесия системы сил.
Система сил эквивалентна нулю (уравновешена) тогда и только тогда, когда её главный вектор и главный момент относительно произвольной точки равны нулю.
Таким образом, Для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх взаимно перпендикулярных осей координат равнялась нулю и сумма моментов всех сил системы относительно каждой из этих осей равнялась нулю.
Момент относительно точки — Лекции и примеры решения задач технической механики
Моментом силы относительно точки O называется результат векторного произведения радиуса-вектора, проведенного из точки O в точку приложения силы, на вектор силы:
MO(F) = r × F. (1.4)
Вектор MO(F) (рисунок 1.15) перпендикулярен плоскости, в которой лежат радиус-вектор r и вектор силы F, и направлен так, что если смотреть навстречу ему, видно силу, стремящуюся повернуть плоскость, в которой она лежит, против хода часовой стрелки.
Наш короткий видеоурок про момент силы с примерами:
Момент силы относительно точки (видео)
Численно момент силы равен
MO = r ∙ F sinα;
r ∙ sinα = h;
MO= F ∙ h. (1.5)
На рисунке 1.15 видно, что если силу перенести вдоль линии действия в другую точку, то величина и знак момента не изменятся:
MO= r ∙ F sinα = r1∙ F1 sinα1 = F ∙ h = F1∙ h. (1.6)
Рисунок 1.15
Можно также сказать, что численно момент силы относительно точки равен удвоенной площади треугольника (OAB), основанием которого является сила, а высотой – плечо h (рисунок 1.16):
S∆OAB = 1/2 F ∙ h;
MO(F) = F ∙ h = 2S∆OAB (1.7)
Рисунок 1.16
>> Теорема Вариньона
Момент сил относительно точки и оси — Мегаобучалка
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы (рисунок 4).
Рисунок 4 – Момент силы F относительно точки О
При закреплении тела в точке О сила F стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а называется плечом силы относительно центра момента.
Момент силы F относительно О определяется произведением силы на плечо.
МО(F) = F·a.
Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке, а отрицательным — против часовой стрелки. Когда линия действия силы проходит через данную точку, момент силы относительно этой точки равен нулю, так как в рассматриваемом случае плечо а = 0 (рисунок 5).
Рисунок 5 – Определение знака момента силы относительно точки
Между моментом пары и моментом силы есть одно существенное различие. Численное значение и направление момента пары сил не зависят от положения этой пары в плоскости. Значение и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Уравнения равновесия плоской системы сил
Условия равновесия сил на плоскости: для равновесия системы сил, произвольно расположенных в плоскости, необходимо и достаточно, чтобы главный вектор и главный момент этих сил относительно любого центра каждый в отдельности равнялся нулю.
FГЛ = 0; МГЛ = Σ МО (Fi) = 0.
Получим основную форму уравнения равновесия:
Теоретически уравнений моментов можно записать бесконечное множество, но практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия:
1. Первая форма уравнений равновесия
2. Вторая форма уравнений равновесия
3. Третья форма уравнений равновесия
Для системы параллельных сил (рисунок 43), можно составить только два уравнения равновесия:
Пример.
Дано: F = 24 кH; q = 6 кН/м; М = 12 кН·м α = 60°; а = 1,8 м; b = 5,2 м; с = 3,0 м. Определить реакции VA, HA и VВ (рисунок 6).
Рисунок 6 – Заданная двухопорная балка
Решение:
Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и HА (горизонтальная). Подвижная опора — реакцию VB (вертикальная). Выбираем систему координат ХУ с началом в левой опоре, определяем равнодействующую распределенной нагрузки:
Q = q·a2 = 6·5,2 = 31,2 кН.
Чертим расчетную схему балки (рисунок 7).
Рисунок 7 – Расчётная схема балки
Для полученной произвольной плоской системы сил составляем уравнения равновесия:
∑Fix = 0; HA – F·cos60° = 0;
∑Fiу = 0; VA – F·cos30° – Q + VB = 0;
∑МА(Fi) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – М – VB·(1,8 + 5,2 + 3) = 0.
Решаем систему уравнений.
HA = F·cos60° = 24·0,5 = 12 кН;
VA = F·cos30° + Q – VB = 24·0,866 + 31,2 – 27,08 = 24,9 кН.
Для проверки правильности решения составим сумму моментов относительно точки приложения наклонной силы F:
∑МА(Fi) = VA·(1,8 + 5,2) – Q·2,6 – М – VB·3 = 24,9·7 – 31,2·2,6 – 12 – 27,08·3 = – 0,06.
Ответ: опорные реакции балки равны VA = 24,9 кН; VВ = 27,08 кН; НА = 12 кН.
Контрольные вопросы:
1. Что определяет эффект действия пары сил?
2. Зависит ли эффект действия пары сил от её положения в плоскости?
3.Зависят ли значения и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
4. Когда момент силы относительно точки равен нулю?
5. Сколь независимых уравнений равновесия можно составить для плоской системы параллельных сил?