| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | ||
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
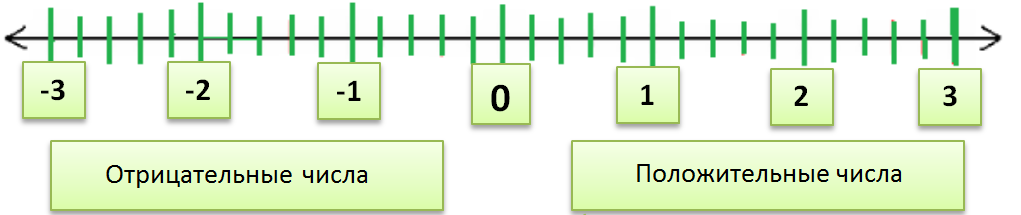
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
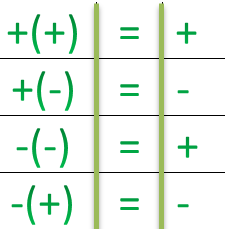
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Дальнозоркость — это плюс или минус?
Чтобы ответить на вопрос: дальнозоркость — это плюс или минус, очки с какими диоптриями подбирать, стоит разобраться в природе патологии и особенностях функционирования зрительной системы.
Эту рефракционную аномалию в офтальмологической практике принято называть гиперметропией, при таком отклонении фокус изображения при рассмотрении того или иного предмета передается не на сетчатку, как у человека со здоровым зрением, а за нее. Как правило, глазное яблоко при дальнозоркости короче, чем при зрении в пределах нормы. Патология может возникнуть у детей при рождении или быть приобретенной.
Особенности строения человеческого глаза
Зрительная система работает благодаря сложнейшим механизмам, которые функционируют в человеческом организме. Глаза преобразуют световые лучи в изображения, за каждый процесс комплексного преобразования отвечает определенный элемент зрительной системы. Так, свет, отраженный от предметов, транслируется на роговичную оболочку, именно она фокусирует лучи, а затем преломляет их. Сквозь камеру с бесцветной жидкостью световые лучи проникают к радужке, здесь в центральной части располагается зрачок, через его отверстие проходят лишь центральные лучи, а остальная их часть отфильтровывается пигментными клетками радужной оболочки.
Центральный поток лучей света в дальнейшем попадает на хрусталик (естественную двояковыпуклую линзу), он более точно фокусирует этот поток. Через стекловидное тело лучи переходят на сетчатку, она является неким экраном, проецирующим картинки с перевернутом виде.
Близорукость/дальнозоркость: особенности аномалий
Рефракционные аномалии зрения могут возникать у любого человека вне зависимости от возраста, нередко они бывают врожденными. Как правило, такие заболевания спровоцированы изменениями в процессе преломления, когда очертания объектов становятся размытыми или вовсе не различаются глазом. «Минус» и «плюс» —это обозначения степени преломления световых лучей в офтальмологии.
Зрение при близорукости (миопии) становится размытым, когда человек пытается рассмотреть объекты, находящиеся вдали от него, но зато ближние предметы ему видны хорошо. К примеру, пациент с миопией может отлично воспринимать текст, работать с мелкими предметами, шить или писать, но не сможет прочитать вывеску на другой стороне улицы.При дальнозоркости все происходит ровно наоборот. Зрение человека с такой аномалией позволяет ему отлично видеть лишь отдаленные картинки, а то, что находится вблизи, ему кажется размытым.
Как правило, дальнозоркость (близорукость чаще наблюдается у детей в связи большим нагрузками на глаза) проявляется у взрослых пациентов, если она не является врожденной, что связано с генетической предрасположенностью к такой рефракционной аномалии.
Дальнозоркость — плюс или минус?
Патологию преломляющей функции зрения или рефракционное нарушение чаще всего корректируют с помощью очков «плюс» диоптрий со специальными линзами. Очки на плюс при дальнозоркости преломляют световые лучи таким образом, что они фокусируются непосредственно на сетчатке, а не за ней. Показатели рефракции, а также кривизна (изгиб) глазного яблока у каждого человека индивидуальны, поэтому очки плюс подбираются пациенту только специалистом после комплексного компьютерного обследования. Важно понимать, что самостоятельный выбор линз может привести к ухудшению зрения и дискомфортным ощущениям во время ношения.
Какие очки носят при пресбиопии?
Если аномалия не является врожденной, она редко проявляется у детей, чаще она развивается у взрослых и может быть связана с чрезмерным напряжением зрительных органов. Помимо этого, у людей после 40 лет неизбежно наступает возрастная пресбиопия — это дальнозоркость, которая связана с естественными изменениями в зрительной системе. У человека возникает ослабление аккомодационной способности за счет изменения эластичности хрусталика и структуры ресничных мышц.
Контактные линзы при дальнозоркости — плюс или минус?
Средства контактной коррекция зрения — это отличная альтернатива плюсовым очкам. Оптические изделия не сковывают движения, совершенно незаметны на глазах и обеспечивают максимально широкий угол обзора. Офтальмологи рекомендуют заменить неудобные оправы контактными линзами людям, которые ведут активный образ жизни. Помимо этого, контактная оптика отлично подходит для детей, поскольку она не вызывает дискомфорта и позволяет беспрепятственно играть и веселиться.
Плюс линз для дальнозоркости и в том, что они могут выполнять эстетическую роль: Вы можете выбрать оттеночные средства контактной коррекции зрения для того, чтобы усилить природный цвет глаз или совсем изменить его. Ответ на вопрос, контактные линзы при дальнозоркости имеют плюс или минус, такой же: как и очки, линзы имеют показатели со знаком «плюс».
Степени заболевания
Итак, мы нашли ответ на вопрос, дальнозоркость — это плюс или минус. Очки плюсовые стоит подбирать исходя из степени патологии. Офтальмологи выделяют три степени дальнозоркости:
- слабая — до +3 дптр, сопровождается головными болями и быстрой утомляемостью глаз;
- средняя — от +3 до +6 дптр, стабильное зрение вдаль, размытость очертаний близко расположенных предметов;
- высокая — от +6 дптр, размытые контуры не только близко находящихся объектов, но и удаленных. Утрачивается способность зрения фокусироваться.
Диагностика дальнозоркости
Если человек обнаружил проблемы со зрением, необходимо незамедлительно обратиться к офтальмологу. Он проведет несколько тестов для выявления наличия дальнозоркости с использованием специализированных таблиц: Головина, Сивцева или Орловой. После этого он приступит к исследованию глазного дна при помощи специального зеркала, либо ультразвукового прибора. Также потребуется компьютерная диагностика, которая позволит подобрать специалисту необходимые средства коррекции зрения, выписать рецепт и дать важные рекомендации.
Математический калькулятор. Подробный онлайн калькулятор всех математических операции.
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
С ← ( ) ±
7 8 9 ÷ %
4 5 6 х √
1 2 3 — x2
0 . = + 1/x
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1/x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Пример:
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Пример:
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Пример:
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Пример:
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Пример:
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Пример:
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Пример:
{ 1/3 = 0,33 }
{ ½ = 0,5 }
Вычисление процентов от числа
Пример:
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Почему минус на минус дает плюс?
«Враг моего врага — мой друг».

Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов

