Three.js

.isVector3

Свойство используется для проверки, является ли данный класс и производные от него классы трехмерными векторами (Vector3). Значением по умолчанию является

true

.
Не изменяйте это свойство, так как оно используется для оптимизации внутри three.js.

.x

.y

.z

.add( v )

Метод добавляет к данному вектору вектор

v

.

.addScalar( s )

Метод добавляет скалярное значение

s

к значениям данного вектора

x

,

y

и

z

.

.addScaledVector( v, s )

Добавляет к данному вектору множество из вектора (

v

) и скаляра (

s

).

.addVectors( a, b )

Устанавливает данный вектор как сумму векторов

a + b

.

.angleTo( v )

Метод возвращает угол в радианах между данным вектором и вектором, указанном в параметре

v

.

.applyAxisAngle( axis, angle )

axis — нормализованный вектор Vector3.

angle — угол в радианах.

Метод применяет к данному вектору поворот, определяемый осями (параметр

axis

) и углом (параметр

angle

).

.applyEuler( euler )

Метод конвертирует угол Эйлера, заданный в параметре

euler

, в кватернион и применяет его к данному вектору.

.applyMatrix3( m )

Метод умножает данный вектор на матрицу, указанную в параметре

m

.

.applyMatrix4( m )

Перемножает данный вектор (с подразумеваемой 

1

в четвертом измерении) с матрицей

m

и делит согласно перспективы.

.applyQuaternion( quaternion )

Метод перемножает данный вектор с кватернионом, переданным в аргументе

quaternion

.

.ceil( )

Компоненты вектора

x

,

y

и

z

округляются вверх до ближайшего целочисленного значения.

.clamp( min, max )

min — минимальные значения x, y и z в желаемом диапазоне.

max — максимальные значения x, y и z в желаемом диапазоне.

Если значение

x

,

y

или

z

данного вектора больше значения

x

,

y

или

z

вектора, указанного в параметре

max

, оно заменяется этим соответствующим значением.
Если значение

x

,

y

или

z

данного вектора меньше значения

x

,

y

или

z

вектора, указанного в параметре

min

, оно заменяется этим соответствующим значением.

.clampLength( min, max )

min — минимальное значение длины, на котором она будет зафиксирована (зажата).

max — максимальное значение длины, на котором она будет зафиксирована (зажата).

Если длина данного вектора больше значения, указанного в параметре

max

, она заменяется на значение

max

.
Если длина данного вектора меньше значения, указанного в параметре

min

, она заменяется на значение

min

.

.clampScalar( min, max )

min — минимальное значение компонентов, на котором они будут зафиксированы (зажаты).

max — максимальное значение компонентов, на котором они будут зафиксированы (зажаты).

Если значение

x

,

y

или

z

данного вектора больше значения, указанного в параметре

max

, оно заменяется на значение

max

.
Если значение

x

,

y

или

z

данного вектора меньше значения, указанного в параметре

min

, оно заменяется на значение

min

.

.clone( )

Возвращает новый Vector3 с такими же значениями

x

,

y

и

z

, что и у данного вектора.

.copy( v )

Копирует значения свойств

x

,

y

и

z

из вектора, переданного в параметре

v

, в данный трехмерный вектор.

.cross( v )

Метод устанавливает данный вектор как векторное произведение (в англоязычном варианте это cross product) самого себя и вектора, указанного в параметре

v

.

.crossVectors( a, b )

Устанавливает данный вектор как векторное произведение (в англоязычном варианте это cross product) векторов, указанных в параметрах

a

и

b

.

.distanceTo( v )

Метод вычисляет расстояние от данного вектора до вектора, указанного в параметре

v

.

.distanceToManhattan( v )

Метод вычисляет манхэттенское расстояние (Manhattan length) от данного вектора до вектора, указанного в параметре

v

.

.distanceToSquared( v )

Вычисляет квадрат расстояния от данного вектора до вектора, указанного в параметре

v

. При простом сравнении одного расстояния с другим взамен следует сравнивать именно квадраты расстояний, так как это вычисление несколько более эффективно.

Примечание переводчика: Вычисление расстояния методом distanceTo это вычисление квадратного корня из результата, полученного методом distanceToSquared.

.divide( v )

Метод делит данный вектор на вектор, указанный в параметре 

v

.

.divideScalar( s )

Делит данный вектор на скалярное значение 

s

. Если значение скаляра равно нулю (

s = 0

), вектор устанавливается как 

(0, 0, 0)

.

.dot( v )

Метод вычисляет скалярное произведение (dot product) данного вектора и вектора, переданного в параметре

v

.

.equals( v )

Метод проверяет точное равенство данного вектора и вектора, переданного в параметре

v

.

.floor( )

Этим методом компоненты вектора округляются вниз, до ближайшего целочисленного значения.

.fromArray ( array, offset )

array — исходный массив в виде [x, y, z, w].

offset — смещение массива (дополнительный, необязательный параметр). Значение по умолчанию равно 0.

Метод устанавливает для данного вектора значение

x

равное

array[ offset + 0 ]

, значение

y

равное

array[ offset + 1 ]

и значение

z

равное

array[ offset + 2 ]

.

.fromBufferAttribute( attribute, index )

attribute — исходный атрибут.

index — индекс в атрибуте.

Устанавливает значения

x

,

y

и

z

данного вектора из атрибута, указанного в параметре

attribute

.

.getComponent( index )

index — целочисленное значение, может быть 0, 1 или 2.

Если индекс равен 

0

, возвращается значение 

x

.
Если индекс равен 

1

, возвращается значение 

y

.
Если индекс равен 

2

, возвращается значение 

z

.

.length( )

Вычисляет евклидову длину(Euclidean length), т. е. расстояние по прямой линии, от точки начала координат

(0, 0, 0)

до точки с заданными координатами

(x, y, z)

.

.lengthManhattan( )

Метод вычисляет манхэттенское расстояние (Manhattan length) данного вектора.

.lengthSq( )

Метод вычисляет квадрат евклидовой длины(Euclidean length), т.е. квадрат расстояния по прямой линии, от точки начала координат

(0, 0, 0)

до точки с заданными координатами

(x, y, z)

. При сравнении длин векторов, взамен сравнения длин, следует сравнивать квадраты длины, так как для расчета это несколько более эффективно.

Примечание переводчика: Вычисление длины вектора методом length это вычисление квадратного корня из результата, полученного методом lengthSq.

.lerp( v, alpha )

v — трехмерный вектор (Vector3), до которого будет проводится операция интерполирования.

alpha — коэффициент интерполяции в закрытом интервале [0, 1].

Метод выполняет операцию линейного интерполирования между данным вектором и вектором, переданным в параметре 

v

, с коэффициентом интерполяции 

alpha

, причем 

alpha

можно рассматривать как расстояние вдоль линии соединения этих двух векторов — при

alpha = 0

, он будет равен данному вектору, а при

alpha = 1

— вектору 

v

.

.lerpVectors( v1, v2, alpha )

v1 — начальный трехмерный вектор (Vector3).

v2 — трехмерный вектор (Vector3), до которого будет проводится операция интерполирования.

alpha — коэффициент интерполяции в закрытом интервале [0, 1].

Метод устанавливает данный вектор как линейно интерполированный вектор между векторами 

v1

и 

v2

, и где

alpha

— это расстояние вдоль линии соединения этих двух векторов — при

alpha = 0

, он будет равен вектору 

v1

, при

alpha = 1

— вектору 

v2

.

.max( v )

Если значение

x

,

y

или

z

данного вектора меньше значения

x

,

y

или

z

вектора, переданного в параметре

v

, то это значение заменяется соответствующим значением вектора

v

.

.min( v )

Если значение

x

,

y

или

z

данного вектора больше значения

x

,

y

или 

z

вектора, переданного в параметре 

v

, то это значение заменяется соответствующим значением вектора 

v

.

.multiply( v )

Метод умножает данный вектор на вектор, указанный в параметре 

v

.

.multiplyScalar( s )

Метод умножает данный вектор на скаляр, переданный в параметре 

s

.

.multiplyVectors( a, b )

Устанавливает данный вектор равным произведению

a × b

.

.negate( )

Метод инвертирует данный вектор, т.е. устанавливает

x = -x

,

y = -y

и

z = -z

.

.normalize( )

Метод преобразовывает данный вектор в единичный вектор (unit vector) — то есть, направление его остается тем же самым, а длина вектора (

length

) устанавливается равной 

1

.

.project( camera )

camera — камера, используемая в проекции.

Метод проецирует вектор на камеру.

.projectOnPlane( planeNormal )

planeNormal — вектор, представляющий нормаль к плоскости.

Метод проецирует данный вектор на плоскость путем вычитания из данного вектора проекции данного вектора на нормаль к этой плоскости.

.projectOnVector( Vector3 )

Метод проецирует данный вектор на другой вектор (параметр

Vector3

).

.reflect( normal )

normal — нормаль (перпендикуляр) к плоскости отражения.

Метод отражает вектор от плоскости, перпендикулярной (ортогональной) к нормали (параметр

normal

). Предполагается что нормаль имеет единичную длину.

.round( )

Метод округляет компоненты вектора до ближайшего целочисленного значения.

.roundToZero( )

Метод округляет компоненты вектора к нулю (если значение отрицательно — происходит округление вверх, если положительное — вниз) до целочисленного значения.

.set( x, y, z )

Устанавливает компоненты

x

,

y

и

z

данного вектора.

.setComponent( index, value )

index — целочисленное значение, может быть 0, 1 или 2.

value — число с плавающей запятой.

Если индекс равен 

0

, устанавливается значение 

x

.
Если индекс равен 

1

, устанавливается значение 

y

.
Если индекс равен 

2

, устанавливается значение 

z

.

.setFromCylindrical( c )

Метод устанавливает данный вектор из координат в цилиндрической системе, переданных в 

c

.

.setFromMatrixColumn( matrix, index )

Устанавливает компоненты

x

,

y

и

z

данного вектора равными колонке матрицы (аргумент

matrix

), определяемой по индексу (

index

).

.setFromMatrixPosition( m )

Метод устанавливает данный вектор равным элементам положения матрицы преобразования, переданной в аргументе 

m

.

.setFromMatrixScale( m )

Метод устанавливает данный вектор равным элементам масштабирования матрицы преобразования, переданной в аргументе 

m

.

.setFromSpherical( s )

Метод устанавливает данный вектор из координат в сферической системе, переданных в 

s

.

.setLength( l )

Метод устанавливает данный вектор как вектор с тем же самым направлением, но длиной (

length

) равной значению, переданному в 

l

.

.setScalar( scalar )

Устанавливает значения компонентов

x

,

y

и

z

данного вектора равными скалярному значению, указанному в параметре

scalar

.

.setX( x )

Метод заменяет значение

x

данного вектора на значение, переданное в параметре 

x

.

.setY( y )

Метод заменяет значение

y

данного вектора на значение, переданное в параметре

y

.

.setZ( z )

Метод заменяет значение

z

данного вектора на значение, переданное в параметре

z

.

.sub ( v )

Метод вычитает из данного вектора вектор, указанный в параметре 

v

.

.subScalar( s )

Метод вычитает из компонентов

x

,

y

и

z

данного вектора скалярное значение, указанное в параметре 

s

.

.subVectors( a, b )

Метод устанавливает данный вектор как разность векторов

a — b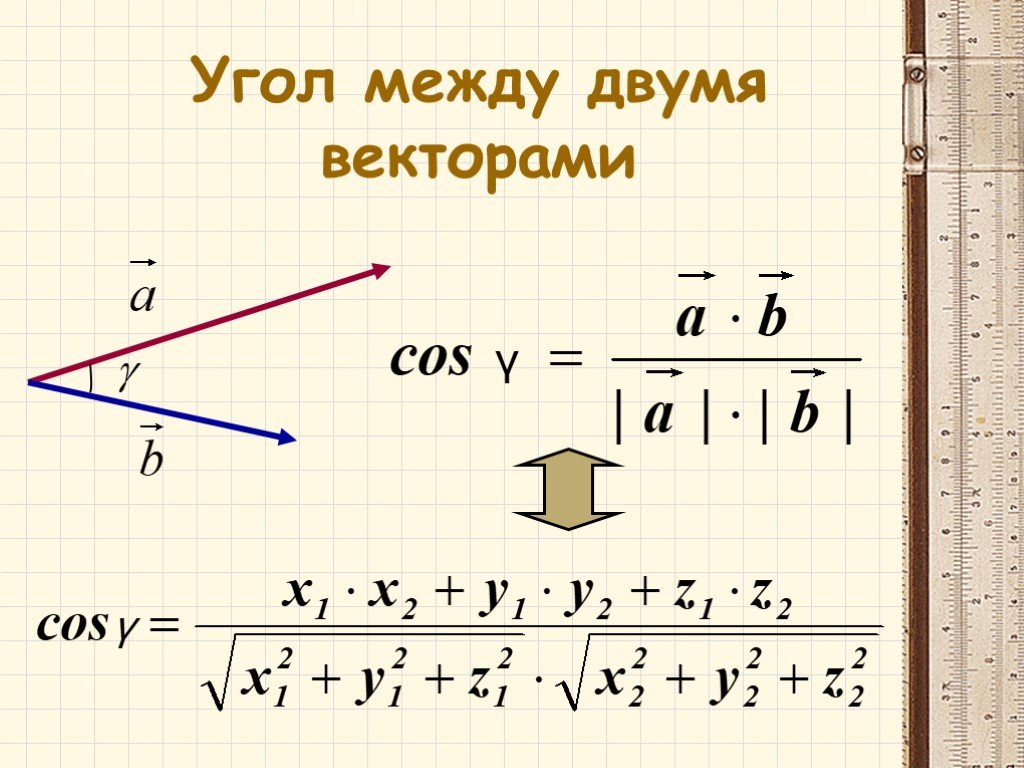

.

.toArray( array, offset )

array — дополнительный, необязательный массив для хранения вектора. Если он не предоставлен, создается новый массив.

offset — дополнительное, необязательное смещение в массиве.

Возвращает массив в виде

[x, y, z]

, или копирует

x

,

y

и

z

в предоставленный (

array

) массив.

.transformDirection( m )

Метод изменяет данный вектор на матрицу (набор

3 × 3

вверху слева в матрице, переданной в параметре

m

) и затем нормализует результат.

.unproject( camera )

camera — камера, используемая в проекции.

Отменяет проецирование вектора на проекционную матрицу камеры.

Алгоритм вектора ориентации устройства | Microsoft Learn

Twitter LinkedIn Facebook Адрес электронной почты

• Статья
• 09/27/2022
• Чтение занимает 2 мин

В этой статье описывается алгоритм, используемый пакетом Windows Hardware Lab Kit (Windows HLK) для определения различий между полученным и ожидаемым вектором для точности данных 9 осей в расширенных тестах датчика ориентации. Тесты проверяют правильность интеграции датчиков и правильность интеграции всех датчиков, необходимых для слияния датчиков.

Примечание

В некоторых случаях вы можете использовать средство диагностики датчиков для проверки трехмерного инклинометра и агрегированного датчика ориентации устройства, который находится в тестируемом режиме.

Алгоритм вектора кватерниона

Алгоритм использует дугу 4-точечный продукт двух векторов, разделенный на произведение величины двух векторов и разделенный на 2. Этот алгоритм показан на рисунке 1 Формула векторного алгоритма кватерниона:

Матричные значения поворота преобразуются в значения кватерниона для проверки точности. Вычисляемый вектор кватерниона должен отклоняться не более +/- 5 градусов от ожидаемого вектора кватерниона (допуска по сравнению с угловой формой между векторами кватерниона) (точность **+/- 10 градусов, разрешенная в направлении оси заголовка). Тест Windows HLK позволяет использовать дельту Øt до 15 градусов.

Вычисление угла дельта между полученными и ожидаемыми векторами Кватерниона

В этом разделе описывается вычисление, вычисляющее угол дельты между полученными и ожидаемыми векторами кватерниона в расширенных тестах ориентации в Windows HLK.

Следующие два значения данных представляют интерес к отчету об агрегированном датчике ориентации устройства:

• Вектор кватерниона

• Матрица поворота

Тест состоит из следующих двух проверок:

1. Проверка полученного вектора Quaternion в отчете о данных датчика. Вектор Quaternion имеет форму (xi + yj + zk + w).

   1. Ожидается, что значение w всегда будет положительным.

   2. Ожидается, что вектор кватерниона будет нормализован и ненулевым. Например, величина вектора должна быть близка к 1,0. Для округления ошибок в расчете величины предоставляется один процент (1%) литерал.

   3. Разностный угол вычисляется с помощью delta = 2 * Acos( Exp. Rec ) / ( | Exp | * | Rec | ) ), где:

      \* указывает скалярное умножение.

      . indicates dot product

      Exp — ожидаемый вектор Quternion

      Rec — полученный вектор Кватерниона

      | Q | указывает величину вектора квтерниона.

      дельта — угол в градусах

   4. Если дельта больше 360 градусов, дельта вычисляется повторно как delta = delta — 360.

   5. На этом этапе разностное значение должно быть меньше или равно допустимому значению погрешности; например, 10 градусов.

2. Проверка полученной матрицы поворота. Ожидается, что матрица поворота будет матрицей 3×3.

   1. Каждый столбец и вектор строки матрицы поворота должен быть нормализован и ненулевым. Для округления ошибок в расчете величины предоставляется один процент (1).

   2. Полученная матрица поворота преобразуется в вектор кватерниона.

   3. Все шаги от <a> до <e> проверки (1) используются повторно.

Тестирование функциональных возможностей датчика с помощью средства диагностики датчиков

Интеграция датчиков движения и ориентации

2 }\\ d = \sqrt{ 11 } \end{align}

Следовательно, расстояние между точками $P$ и $Q$ равно $\sqrt{11}$.

Предположим, что у нас есть вектор $\vec{u}$. Если этот вектор умножить на скаляр $k$, то норма вектора $k\vec{u}$ будет в k раз больше, чем $k$. Однако есть проблема. Мы определяем норму как величину или длину вектора, поэтому норма должна быть положительной. Отсюда получаем следующее соотношение:

(4)

\begin{align} \| к \vec{u} \| = \ середина к \ середина \ | \vec{и} \| \end{выравнивание}

Заметим, что $\mid k \mid$ представляет абсолютное значение k , то есть:

(5)

\begin{align} \mid k \mid = \left\{\begin{matrix} k & \mathrm{if \: k >0}\\ -k & \mathrm{if \: k < 0} \ конец{матрица}\справа. \end{align}

Таким образом, если $k$ отрицательное, то мы берем положительное значение $k$, иначе $k$ остается прежним. Например, $\mid -3 \mid = 3$. Обратите внимание, что иногда для обозначения абсолютного значения будет использоваться обозначение $\mathrm{abs} (k)$.

Из этого мы можем вывести соотношение между скалярным множителем вектора и его нормой, то есть:

(6)

\begin{align} \| к \vec{u} \| = \ середина к \ середина \ | \vec{и} \| \end{align}

Пример 4

Учитывая, что $\| \vec{и} \| = 4$, найти $\| -3\vec{u} \|$.

Из приведенной формулы заметим, что $\| -3 \vec{u} \| = \середина -3 \середина \| \vec{и} \| = (3)(4) = 12$.

Как рассчитать единичный вектор?

Физические величины делятся на два типа: «векторные» и «скалярные». Термин «вектор» относится к физической величине, которая имеет как величину, так и направление. Это физические величины, которые подчиняются треугольному закону сложения векторов. Некоторыми примерами векторных величин являются электрическое поле, смещение, импульс, скорость, сила и ускорение. Все эти величины имеют как величину, так и направление. С другой стороны, «скалярные» величины имеют только величину. Некоторыми примерами скалярных величин являются расстояние, длина, объем, температура и площадь.

Типы векторов

• Равные векторы: Векторы, имеющие одинаковую величину и одинаковое направление, называются равными векторами.
• Коллинеарные векторы: Векторы, направленные либо в одном, либо в противоположном направлении друг другу, называются коллинеарными векторами.
• Параллельные векторы: Параллельные векторы также известны как подобные векторы . Коллинеарные векторы с одинаковыми направлениями называются параллельными векторами. Угол между этими векторами равен нулю.
• Антипараллельные векторы: Антипараллельные векторы также известны как непохожие векторы. Коллинеарные векторы с противоположными направлениями называются антипараллельными векторами. Угол между этими векторами 180°.
• Копланарные векторы: Все векторы, лежащие в одной плоскости, называются копланарными векторами.
• Нулевые векторы: Вектор с одинаковыми начальной и конечной точками называется нулевым вектором. Его также называют .Нулевой вектор . Величина такого вектора равна 0, а его направление неопределенно.

Вычисление единичного вектора

Единичный вектор представляет собой вектор величины 1 и с направлением вдоль заданного вектора. Он представляет направление данного вектора. Единичный вектор вектора находится путем деления вектора на его модуль. Модуль вектора — это величина вектора.

Он представлен символом ‘  ‘(шляпа или кепка) над переменной как  и определяется как,

Где |А| — модуль вектора A, а для вектора |A| определяется как,

Таким образом, для вектора единичный вектор определяется как,

.

Найдите .

Решение:

Модуль вектора,

= = √9

= 3

Вектор единиц,

=

=

=

=

=

=

Проблема 2: Является ли вектор, заданный , также единичным вектором?

Решение:

Модуль вектора, 

=  = √3

Величина этого вектора не равна 1. Следовательно, это не единичный вектор.

Задача 3. Найдите единичный вектор в направлении .

Решение:

Модуль вектора, 

=  = √3

Единичный вектор, 

= 

=

Задача 4. Если — единичный вектор, найдите значение z.

Solution:

Magnitude of a unit vector is 1, which means:

which means, 

Squaring both sides,

Question 5: Find единичный вектор .