Перевод чисел из шестнадцатеричной системы в двоичную и восьмеричную
Алгоритм перевода чисел из шестнадцатеричной системы счисления двоичную крайне прост. Необходимо только заменить каждую цифру шестнадцатеричного числа ее эквивалентом в двоичной системе счисления (в случае положительных чисел). Как и в предыдущих параграфах, удобно и полезно воспользоваться таблицей соответствия, приведенной в Приложении. Отметим только, что каждое шестнадцатеричное число следует заменять двоичным, дополняя его до 4 разрядов (в сторону старших разрядов).
Пусть требуется перевести шестнадцатеричное число F116 в двоичное число. Воспользовавшись Таблицей соответствия из Приложения, получим:
F116=111100012,
поскольку F16 = 11112, 116 = 00012. Этот пример иллюстрирует тот факт, что
следует дополнять младшие разряды до
4 разряда в двоичном числе. Естественно,
дополнять старший разряд двоичного
числа до 4 старших битов нулями не имеет
смысла, другими словами пишут
Этот пример иллюстрирует тот факт, что
следует дополнять младшие разряды до
4 разряда в двоичном числе. Естественно,
дополнять старший разряд двоичного
числа до 4 старших битов нулями не имеет
смысла, другими словами пишут
1F16=111112, а не000111112
Обычно при переводе чисел из шестнадцатеричной в восьмеричную систему счисления вначале шестнадцатеричное число переводят в двоичное, затем разбивают его на триады, начиная с младшего бита, а потом заменяют триады соответствующими им эквивалентами в восьмеричной системе. Для рассмотренных примеров имеем:
1F16=111112=011 111
F116=111100012=011 110 0012=3618
Непосредственное
преобразование чисел из шестнадцатеричной
системы счисления в восьмеричную требует
выполнения арифметических действий в
этой системе счисления. Об этом речь
пойдет позже, в IV главе нашего курса.
Отмечу только, что программная реализация
вышеприведенного алгоритма проще и
надежнее, поскольку при выполнениях
операций деления неизбежно возникают
дробные числа и переполнения разрядной
сетки, необходимость округления, и, как
следствие, потеря точности, не говоря
уже о скорости выполнения компьютером
такого типа алгоритмов.
Об этом речь
пойдет позже, в IV главе нашего курса.
Отмечу только, что программная реализация
вышеприведенного алгоритма проще и
надежнее, поскольку при выполнениях
операций деления неизбежно возникают
дробные числа и переполнения разрядной
сетки, необходимость округления, и, как
следствие, потеря точности, не говоря
уже о скорости выполнения компьютером
такого типа алгоритмов.
Задание
Перевести аргумент 1 и аргумент 2 из лабораторной № 2 в другие системы счисления:
десятичную
восьмеричную
шестнадцатеричную
Выполнить суммирование в десятичной системе счисления.
Перевести результаты суммирования из лабораторной № 1 в десятичную систему счисления. Сравнить результаты с п. 2.
Выполнить умножение в десятичной системе счисления.
Перевести результаты умножения из лабораторной № 1 в десятичную систему счисления.
 Сравнить результаты с п. 2.
Сравнить результаты с п. 2.Перевести результаты умножения из десятичной системы счисления в другие системы:
восьмеричную
шестнадцатеричную
Перевести числа из п. 6 из восьмеричной и шестнадцатеричной системы в двоичную. Сравнить результаты.
для нечетного варианта: 1700 + № своего варианта. Для вариантов x8 иx9 взять числа:
вариант 8 — 1726
вариант 9 — 1727
вариант 18 — 1736
вариант 19 — 1737
для четного варианта: 2000 + № своего варианта. Для вариантов x8 иx9 взять числа:
вариант 8 — 2026
вариант 9 — 2027
вариант 18 — 2036
вариант 19 — 2037
Литература
1. 2. И.Я. Депман «История арифметики» // М.: изд. «Просвящение», –1965. – 415 с. 3. Е.А. Башков «Аппаратное и программное обеспечение зарубежных ЭВМ» // Учеб. пособие. – К.: Выща школа. – 1990. – 207 с. 4. С.Д. Погорелый, Т.Ф. Слободянюк «Программное обеспечение микропроцессорных систем: Справочник» // 2-е изд., перераб. и доп. – К.: Тэхника. – 1989. – 301 с. 5. Р. Токхайм «Микропроцессоры: Курс и упражнения» // пер. с англ., под ред. В.Н. Грасевича. М.: Энергоатомиздат. – 1988. – 336 с. 6. В. Юров «Assembler» // СПб: Издательство «Питер». – 2000. – 624 с. 7. У. Девис «Операционные системы. Функциональный подход» // Пер. с англ., М.: изд. «Мир». – 1980. – 436 с. 8. Д.В. Иртегов
«Введение в операционные системы»
// СПб.: БХВ-Петербург, – 2002. 9. С.В. Зубков «Assembler для DOS, Windows и Unix» // М.: ДМК Пресс. – 2000. – 608 с. 10. Э. Таненбаум «Архитектура компьютера» // пер. с анг., под ред. А.В. Гордеева. СПб.: Питер. – 2002. – 704 с. 11. З.Л. Рабинович, В.А. Раманаускас «Типовые операции в вычислительных машинах» // К.: Техніка, -1980. -264 с. 12. Б. Бериан «Программирование на языке ассемблера системы IBM/370. Упрощенный подход» // М.: «Мир», -1980. -640 с. |
Число 31, 0x00001F, тридцать один
Энциклопедия чисел
Свойства натурального числа 31, 0x00001F, 0x1F:
Системы счисления Основные свойства Степени, корни
Тригонометрия Хэши, криптография Языки программирования
Дата и время Цвет по числу Интернет
Другие свойства
Рейтинг 6.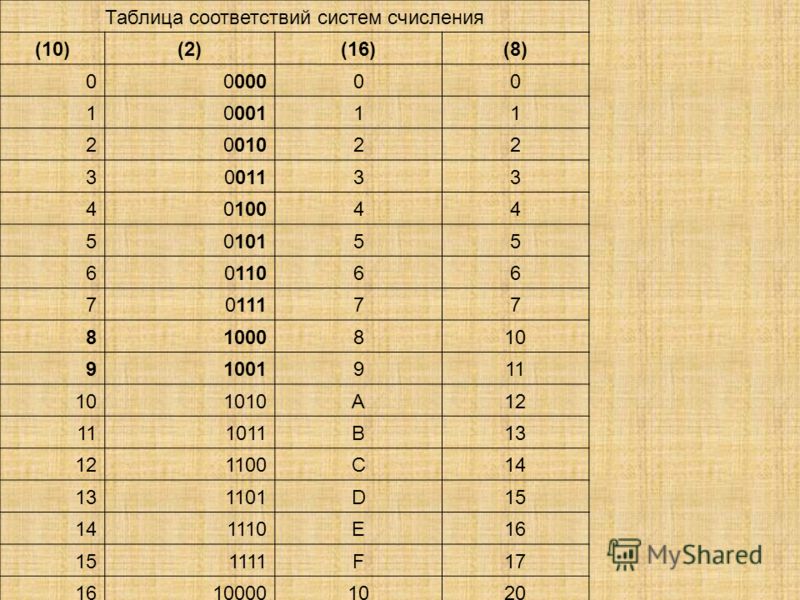 4 из 10,
оценок: 7.
4 из 10,
оценок: 7.
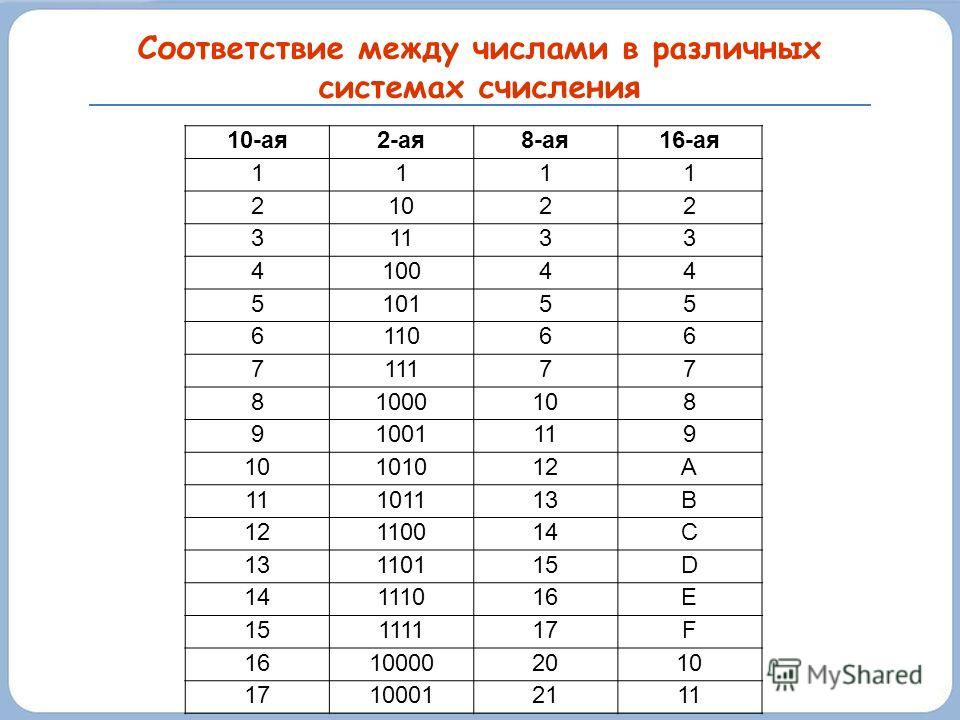
Системы счисления, перевод в систему счисления
Десятичное число 31
- 31 в шестнадцатеричной системе счисления
- 1F
- 31 в двоичной системе счисления
- 11111
- 31 в восьмеричной системе счисления
- 37
Шестнадцатеричное число 1F
- 1F в десятичной системе
- 31
- 1F в двоичной системе
- 11111
- 1F в восьмеричной системе
- 37
Двоичное число 11111
- 11111 в десятичной системе
- 31
- 11111 в шестнадцатеричной системе
- 1F
- 11111 в восьмеричной системе
- 37
Восьмеричное число 37
- 37 в десятичной системе
- 31
- 37 в шестнадцатеричной системе
- 1F
- 37 в двоичной системе
- 11111
Основные арифметические и алгебраические свойства
- Число 31 на русском языке, number in Russian, число 31 прописью:
- тридцать один
- Четность
- Нечетное число 31
- Разложение на множители, делители числа 31
- 31, 1
- Простое или составное число
- Простое число 31
- Числа делящиеся на целое число 31
- 62, 93, 124, 155, 186, 217, 248, 279
- Число 31 умноженное на число два
- 62
- 31 деленное на число 2
- 15.
 5
5
- Список 8-ми простых чисел перед числом
- 29, 23, 19, 17, 13, 11, 7, 5
- Сумма десятичных цифр
- 4
- Количество цифр
- 2
- Десятичный логарифм 31
- 1.4913616938343
- Натуральный логарифм 31
- 3.4339872044851
- Это число Фибоначчи?
- Нет
- Число на 1 больше числа 31,
следующее число - число 32
- Число на 1 больше числа 31,
- Число на 1 меньше числа 31,
предыдущее число - 30
- Число на 1 меньше числа 31,
Степени числа, корни
- 31 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 961
- 31 во второй степени (в квадрате)
- В третьей степени (в кубе, 31 в степени 3, x³) равно
- 29791
- Корень квадратный из 31
- 5.56776436283
- Корень кубический из числа 31 =
- 3.1413806523914
Тригонометрические функции, тригонометрия
- Синус, sin 31 градуса, sin 31°
- 0.
 5150380749
5150380749
- Косинус, cos 31 градуса, cos 31°
- 0.8571673007
- Тангенс, tg 31 градуса, tg 31°
- 0.600860619
- Синус, sin 31 радиан
- -0.40403764532307
- Косинус, cos 31 радиан
- 0.91474235780453
- Тангенс, tg 31 радиан равно
- -0.4416955680207
- 31 градус, 31° =
- 0.54105206811824 радиан
- 31 радиан =
- 1776.1691649056 градуса, 1776.1691649056°
Контрольные суммы, хэши, криптография
- MD-5 хэш(31)
- c16a5320fa475530d9583c34fd356ef5
- CRC-32, CRC32(31)
- 3832313845
- SHA-256 hash, SHA256(31)
- eb1e33e8a81b697b75855af6bfcdbcbf7cbbde9f94962ceaec1ed8af21f5a50f
- SHA1, SHA-1(31)
- 632667547e7cd3e0466547863e1207a8c0c0c549
- ГОСТ Р 34.
 11, GOST R 34.11-94, GOST(31)
11, GOST R 34.11-94, GOST(31) - b34c3cca0f60e634c0f9b476764511f09c1fe7ecd05b705ffba23312df2cf268
- ГОСТ Р 34.
- Base64
- MzE=
Языки программирования
- C++, CPP, C значение 31
- 0x00001F, 0x1F
- Delphi, Pascal значение числа 31
- $00001F
Дата и время
- 31-й день простого и високосного года
- 31 января
- Конвертация UNIX timestamp 31 в дату и время
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
- Конвертация в IPv4 адрес Интернет
- 0.0.0.31
- 31 в Википедии:
- 31
Другие свойства числа
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/31
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x1F
- Номер телефона
- 31
- Телефонный код страны
- +31 Нидерланды
Цвет по числу 31, цветовая гамма
- html RGB цвет 31, 16-ричное значение
- #00001F — (0, 0, 31)
- HTML CSS код цвета #00001F
- .color-mn { color: #00001F; }
.color-bg { background-color: #00001F; }
Цвет для данного числа 31
Здесь вы можете изменить составляющую цвета для данного числа 31 или цвета 00001F:
как преобразовать шестнадцатеричный 1f в десятичный
Как написать 1f в десятичном (основание 10)?
1f равно 31 в десятичной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа.
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | 11009 |
| 13 | D | 9000 15||
| 1101 | |||
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |||
| 17 | 11 | 21 | 10001 | |||
| 18 | 12 | 0008 2210010 | ||||
| 19 | 13 | 23 | 10011 | |||
| 20 | 14 | 24 | 10100 | |||
| 21 | 15 | 25 | 10101 | |||
| 22 | 16 | 26 | 10110 | |||
| 23 | 17 | 27 | 10111 | |||
| 24 | 18 | |||||
| 18 | 30 | 0008 11000 | ||||
| 25 | 19 | 31 | 11001 | |||
| 26 | 1A | 32 | 11010 | |||
| 27 | 1B | 33 | 11011 | |||
| 28 | 1C | 34 | 11100 | |||
| 29 | 1D | 35 | 11101 | |||
| 30 | 1E | 36 | 1111111111109 | 1E | 36 | 11111111109 |
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |||||||
| 33 | 21 | 41 | 100001 | |||||||
| 34 | 22 | 42 | 100010 | |||||||
| 23 | 43 | |||||||||
| 0008 100011 | ||||||||||
| 36 | 24 | 44 | 100100 | |||||||
| 37 | 25 | 45 | 100101 | |||||||
| 38 | 26 | 46 | 100110 | |||||||
| 39 | 27 | 47 | 100111 | |||||||
| 40 | 28 | 50 | 101000 | |||||||
| 41 | 29 | 51 | 101001 | 29 | 51 | 101001 | 29 | 51 | 101001 | 0009|
| 42 | 2A | 52 | 101010 | |||||||
| 43 | 2B | 53 | 101011 | |||||||
| 44 | 2C | 54 | 101100 | |||||||
| 45 | 2D | 55 | 101101 | |||||||
| 46 | 2E | 56 | 101110 | |||||||
| 47 | 2F | 57 | 101111 | 2F | 57 | 101111999 | 0060
|
9000
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | |
| 241 | F1 | 361 | 11110001 | |
| 242 | F2 | 362 | 11110010 | |
| 243 | F3 | 363 | 11110011 | |
| 244 | F4 | 364 | 11110100 | 0009 |
| 245 | F5 | 365 | 11110101 | |
| 246 | F6 | 366 | 11110110 | |
| 247 | F7 | 367 | 11110111 | |
| 248 | F8 | 370 | 11111000 | |
| 249 | F9 | 371 | 11111001 | |
| 250 | FA | 372 | 0008 11111010 | |
| 251 | FB | 373 | 11111011 | |
| 252 | FC | 374 | 11111100 | |
| 253 | FD | 375 | 11111101 | |
| 254 | FE | 376 | 11111110 | |
| 255 | FF | 377 | 1111111111119 |
Номерная конвертер базы
021 Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 180 hexadecimal to octal
- 1961 decimal to octal
- 1111110000 binary to octal
- decimal to binary
- 15200 octal to binary
- hexadecimal to octal
- 162 decimal to hexadecimal
- hexadecimal to octal
- 6000 шестнадцатеричный код в восьмеричный
1F Hex to Decimal: (1F)16 = (?)10
- Home
- Цифровые числа
- Hex Calculator
- (1F)16 в десятичной системе
- Каждая цифра данного шестнадцатеричного числа 1F должна быть заменена эквивалентным десятичным числом перед умножением на 16 значений степени, но это преобразование не является фактическим десятичным эквивалентом (1F)16.
- Десятичный эквивалент самого правого числа F в шестнадцатеричном формате 1F следует умножить на 16 0
- Десятичный эквивалент самой левой цифры 1 в шестнадцатеричном формате 1F следует умножить на 16 (количество цифр в шестнадцатеричном формате — 1) .

(1F) 16 в десятичном виде равно:
1F 16 = 31 10
0x1F = 31 10
Следовательно,
шестнадцатеричное число (1F)16 равно десятичному числу (31)10.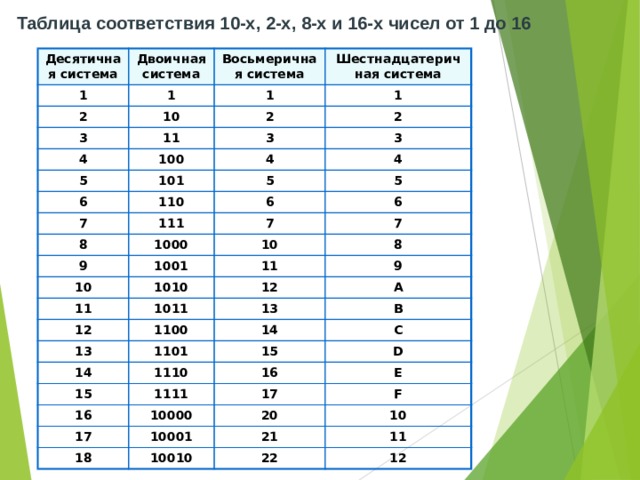
, где,
1F 16 -данное число шестигранников,
16 в 1F 16 представляет базовый-16 или гексадецимный номер,
31 10 7-й децимляльный номер,
31 10 , децимляльный номер,
31 10 , децимляльный номер,
31 10 . 10 в 31 10 представляет десятичную систему счисления с основанием 10.
Важные примечания: (1F)16 в десятичной системе счисления
Ниже приведены некоторые важные примечания, которые следует помнить при преобразовании шестнадцатеричного числа (1F)16 в десятичный эквивалент (с основанием 10).
Для шестнадцатеричных значений, отличных от 1F, используйте следующий инструмент:
В приведенном ниже пошаговом решении показано, как преобразовать шестнадцатеричное число (1F)16 в десятичное. Чтобы найти десятичный эквивалент (1F)16, замените каждую цифру данного шестнадцатеричного числа эквивалентным десятичным числом, чтобы (1F)16 стало 1 15. Найдите произведение 16 0 и 15, 16 1 и 1. Сумма всех отдельных произведений представляет собой десятичный эквивалент шестнадцатеричного числа 1F.
Решено Пример:Преобразуйте шестнадцатеричное число (1f)16 в десятичный эквивалент.
step 1 Observe the input parameters, values and what to be found:
Input values:
Hexadecimal Number = (1F) 16
What to be found:
What is the десятичный эквивалент шестнадцатеричного (1f)16?
(1F)16 = (?)10
Шаг 2 Замените каждую цифру данного шестнадцатеричного числа (1F)16 эквивалентным десятичным числом, используя приведенную ниже таблицу шестнадцатеричных и десятичных систем счисления.


 Сравнить результаты с п. 2.
Сравнить результаты с п. 2. О. Нейгебавуэр
«Точные науки в древности» // М.:
пер. с англ., изд. «Наука», – 1968. –
224 с.
О. Нейгебавуэр
«Точные науки в древности» // М.:
пер. с англ., изд. «Наука», – 1968. –
224 с. – 624 с.
– 624 с. 5
5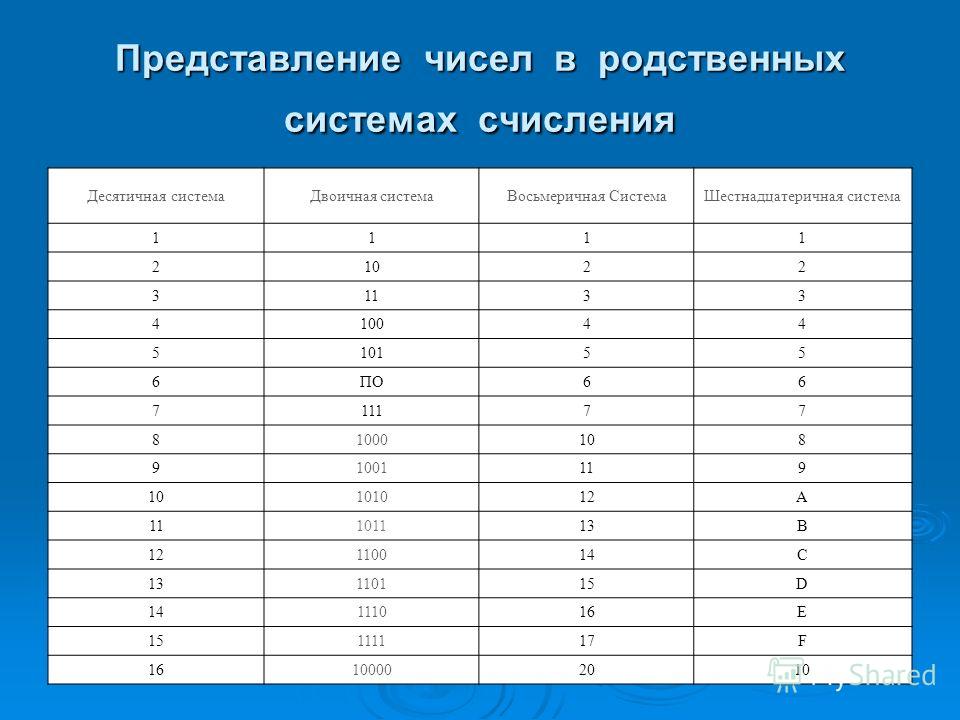 5150380749
5150380749 11, GOST R 34.11-94, GOST(31)
11, GOST R 34.11-94, GOST(31) 0070
0070 н.э.
н.э. 0009
0009