Формула
Наиболее легко эта задача решается для тел простых форм, вращающихся вокруг оси, проходящей через центр инерции тела С. В этом случае, для вычисления Ic можно модифицировать формулу (6.2.1),
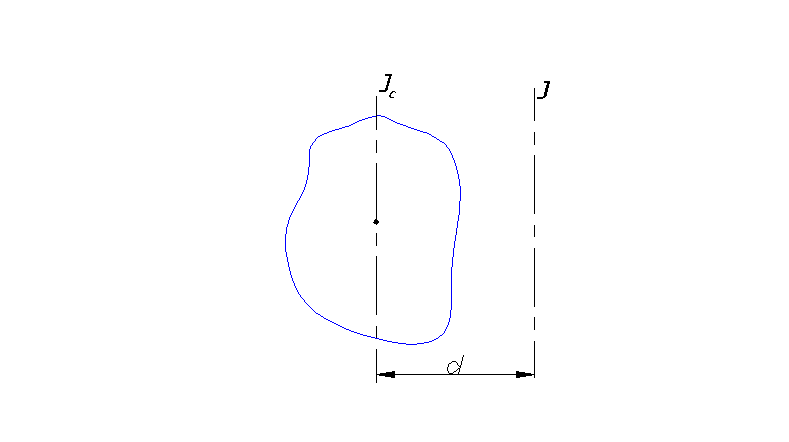
Ic = kmR2. Моменты инерции шара, диска и стержня приведены на рис. 6.6. При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции (рис. 6.7), следует пользоваться теоремой о
Например: стержень массой m длиной l вращается вокруг оси, проходящей через конец стержня (рис. 6.8). , .
|
Вычисление момента инерции некоторых тел
J = 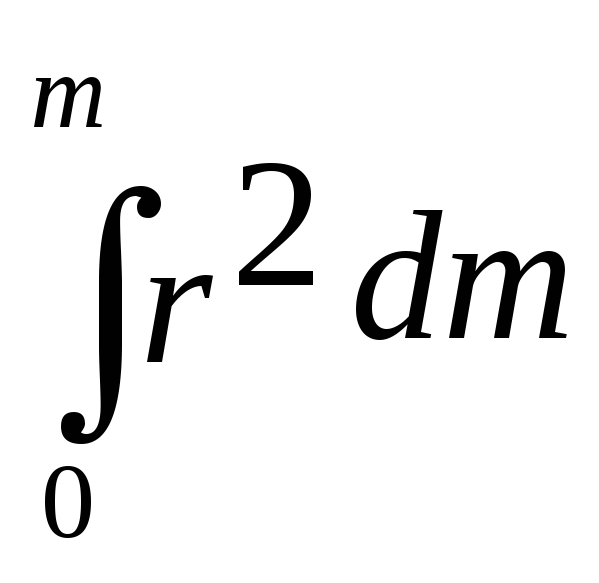 ;
;
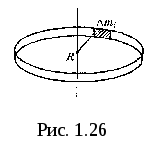
1. Момент инерции однородного обруча относительно оси, перпендикулярной к плоскости обруча и проходящей через его центр.
Будем считать
толщину обруча постоянной, разобьем
обруч на малые элементы mi;.
Момент инерции относительно оси
выразится выражениями 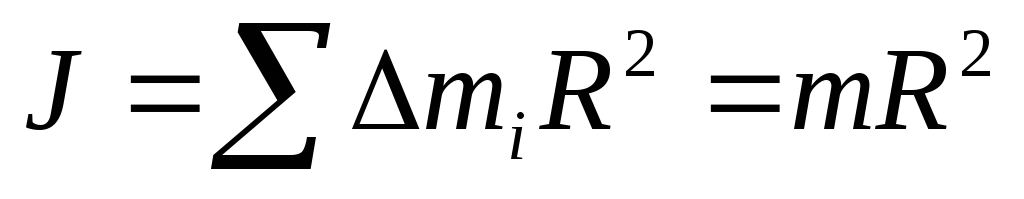
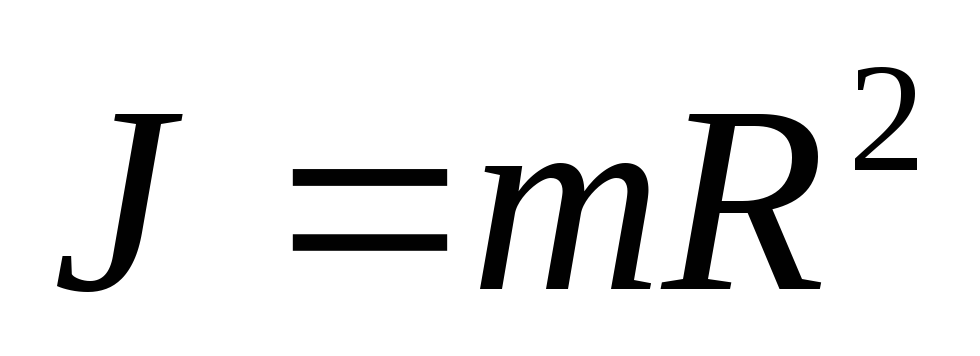 ;
;
2. Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через центр масс и через один из концов стержня.
Разобьем стержень
на малые элементы. Момент инерции
относительно оси одной половины
стержня равен 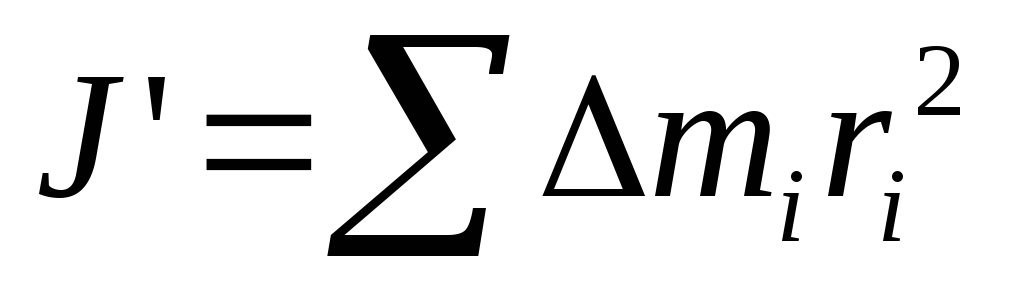 ,
а всего стержня
,
а всего стержня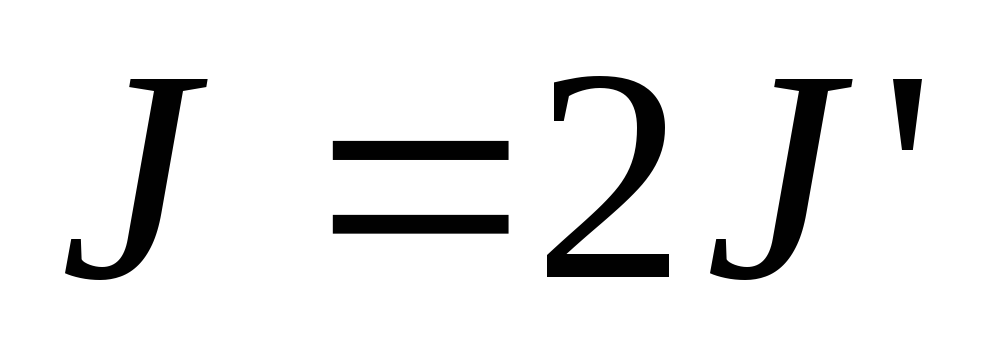 ,
,
Если S — сечение стержня, — плотность материала, то m = Sr;
JC=2Sri2r=2Sri2r в пределе операция суммирования переходит
в интегрирование  ;
;
Так как m = Sl — масса стержня, то момент инерции стержня относительно центра
JC =
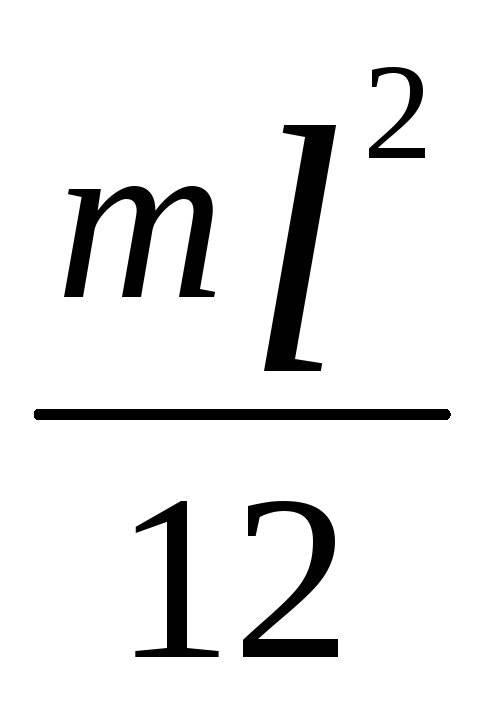 ;
;Момент инерции шара
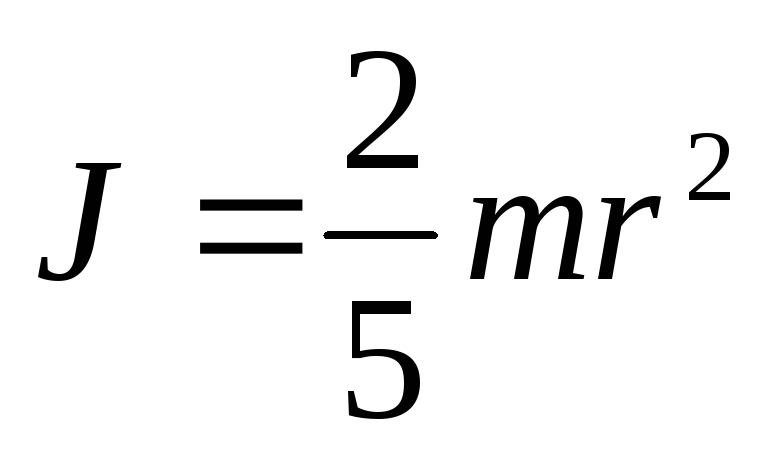
Момент инерции сплошного цилиндра или диска
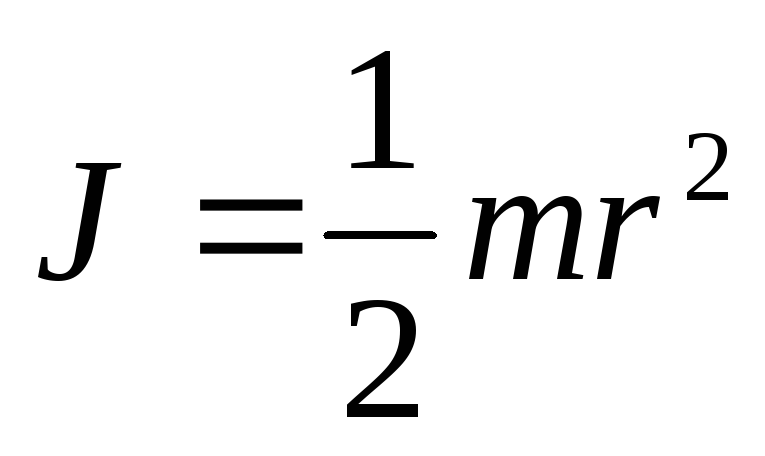
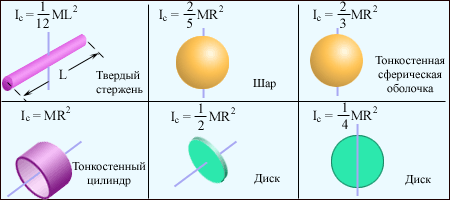
Момент инерции тела зависит от формы тела, относительно какой оси вращается тело и от распределения массы по объему тела.
Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен моменту инерции

Кинетическая энергия вращающегося твердого тела.
Работа внешних сил при вращении твердого тела.
Рассмотрим теперь
вращение тела с энергетической точки
зрения. Допустим, что в некоторой точке
тела приложена сила (в плоскости,
перпендикулярной оси вращения),
направление которой совпадает с
вектором линейной скорости этой точки.
Поэтому речь идет о силе 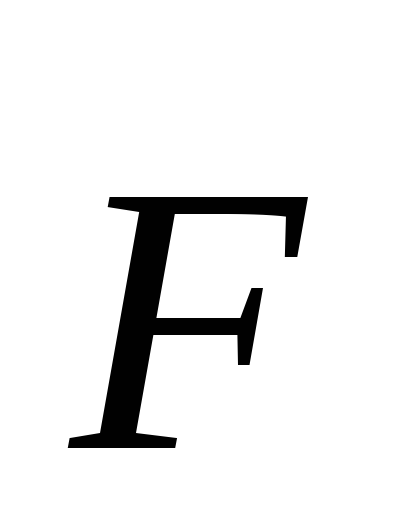
 .
.Элементарная работа этой силы равна
dA = Fds,
где ds — элемент дуги окружности, связанный,
как известно, с ее радиусом  и углом поворота следующим образом:
и углом поворота следующим образом:
dS = rd;
Тогда
dA =
dA = Md .
Если М = const, то при повороте тела на конечный угол , формула для работы имеет вид
A = M;
Найдем теперь кинетическую энергию вращающегося тела. Очевидно, эта энергия должна быть равна сумме кинетических энергий отдельных материальных точек, т.е.
WК =  ,
,
i = ri и, принимая во внимание, что момент инерции тела относительно оси вращения
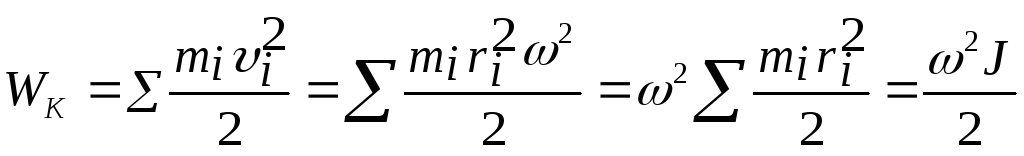
WK = 
Сравнивая
полученное выражение с выражением для
кинетической энергии тела, движущегося
поступательно WK = 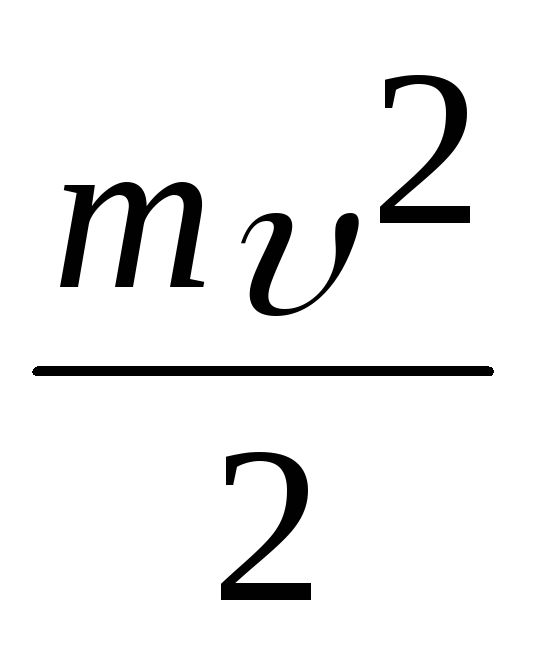 , приходим к выводу, что момент
инерции вращательного движения — мера
инертности тела.
, приходим к выводу, что момент
инерции вращательного движения — мера
инертности тела.
Работа А, совершенная моментом внешних сил на протяжении угла поворота
A =  ;
;
где 2 и 1— угловые скорости тела в моменты, когда его угловые координаты равны соответственно 2 и 1.
В случае, например, скатывающегося цилиндра с наклонной плоскости без скольжения энергия движения складывается из энергии поступательного движения и энергии вращения
 +
+ 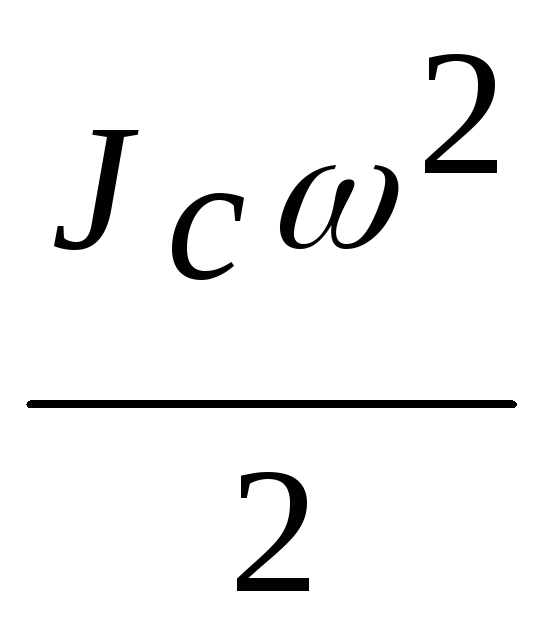
где т — масса катящегося тела; C — скорость центра масс тела;
Jc — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.
Элементы механики жидкостей и газов.
Давление в жидкости и газе.
Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т.е. объем газа определяется объемом того сосуда, который газ занимает.
Как и газ, жидкость принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.
Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика — раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми или твердыми телами — использует единый подход к изучению жидкостей и газов.
В механике жидкости и газы рассматриваются как сплошные, непрерывно распределенные тела в занятой ими части пространства.
Плотность жидкости мало зависит от давления и во многих задачах можно пользоваться понятием несжимаемой жидкости — жидкости, плотность которой всюду одинакова и не изменяется со временем.
Жидкости имеют следующие наиболее характерные свойства.
Типичные жидкости (вода, бензин, спирт и т.п.) не имеют трения покоя, частицы их очень подвижны. В других жидкостях имеется вязкость (внутреннее трение) — это мед, масло, вар и т.п. Однако при продолжительном действии силы частицы вязкой жидкости тоже становятся подвижными. Это свойство выражается так: жидкости не имеют упругости формы, для них модуль сдвига равен нулю.
Практически все жидкости несжимаемы. Это значит, что для них коэффициенты сжатия имеют очень малые значения. Следовательно,
приближенно можно считать все жидкости невязкими и несжимаемыми: такие жидкости называются идеальными.
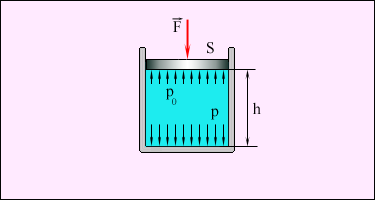

[P]=Па=н/м2
Действие силы тяжести приводит к возникновению разности давлений между горизонтальными слоями жидкости находящимися на различной глубине. Разность сил давления в слоях АВ и СД (рис. 1.27) равна весу вертикального столба жидкости с основанием S и высотой h1. При поперечном сечении S столба жидкости, его высоте h и плотности сила давления на слой находящийся на глубине h находится по формуле:
F =ghS, а давление на нижнее основание
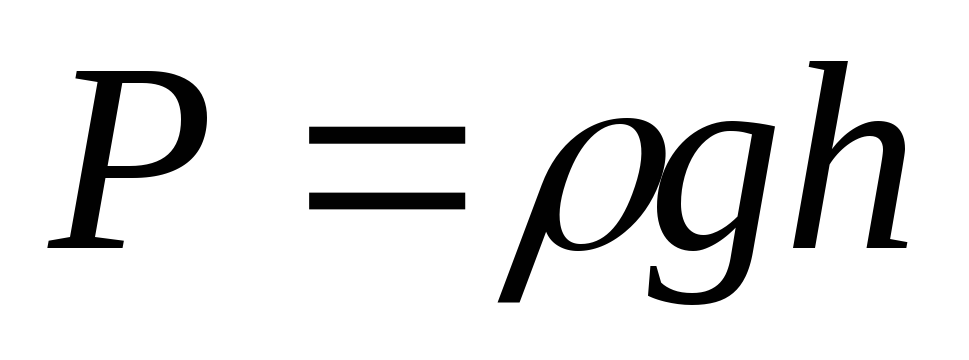 давление столба жидкости
давление столба жидкости
 (1.2)
(1.2)
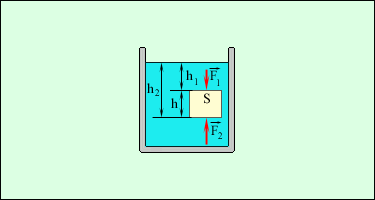
Если давление на поверхности P0, то в любом горизонтальном слое давление постоянно и будет зависеть от глубины слоя АВ:
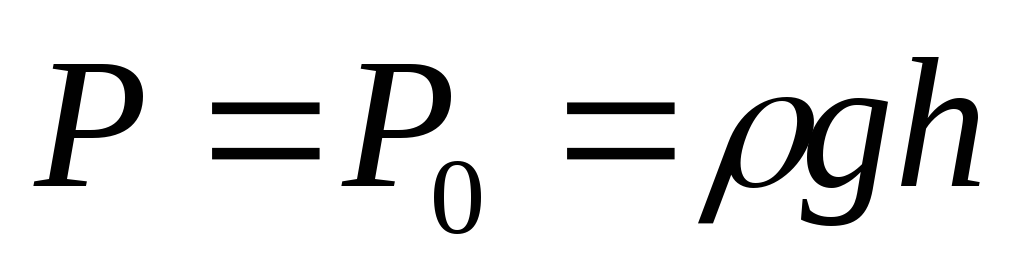 (1.2)
(1.2)
Согласно формуле (1.82) сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу жидкости (газа) вытесненной телом.
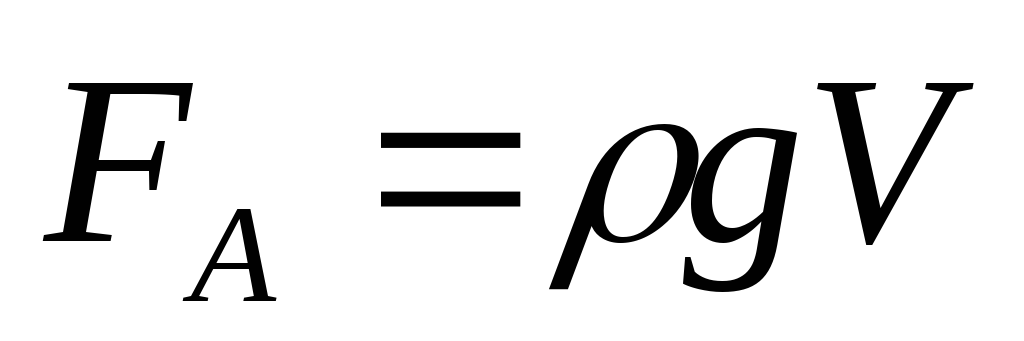 (1.2)
(1.2)
где  — плотность жидкости,V
— объем
погруженного в жидкость тела.
— плотность жидкости,V
— объем
погруженного в жидкость тела.
Примеры расчета момента инерции.
1. Стержень
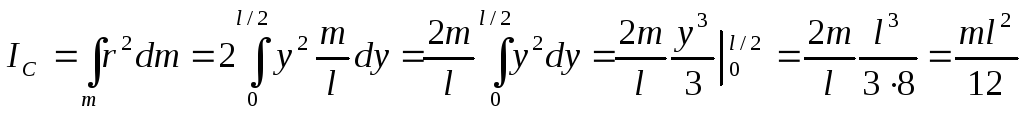
2. Кольцо (тонкостенный цилиндр).
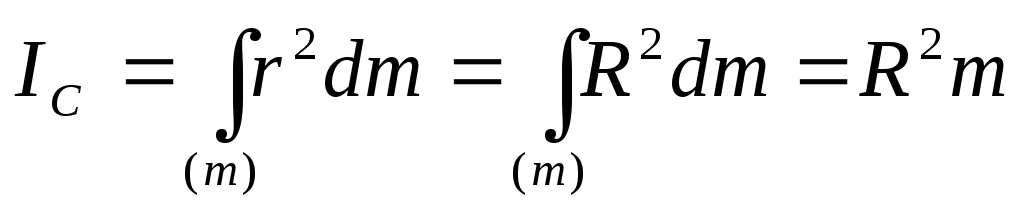
3. Диск (сплошной цилиндр).

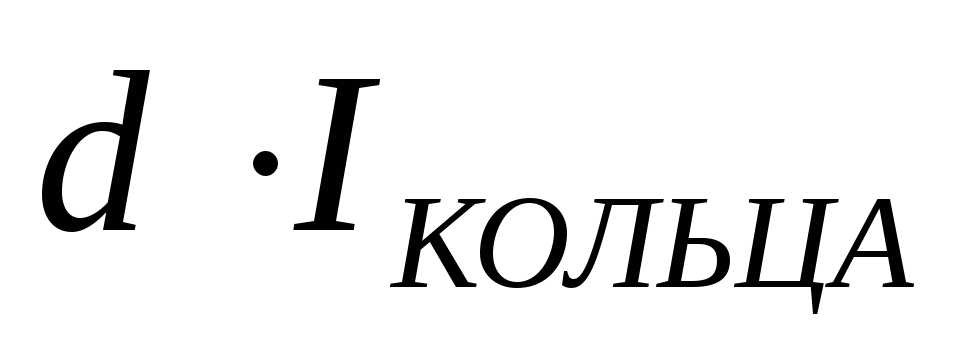 =
=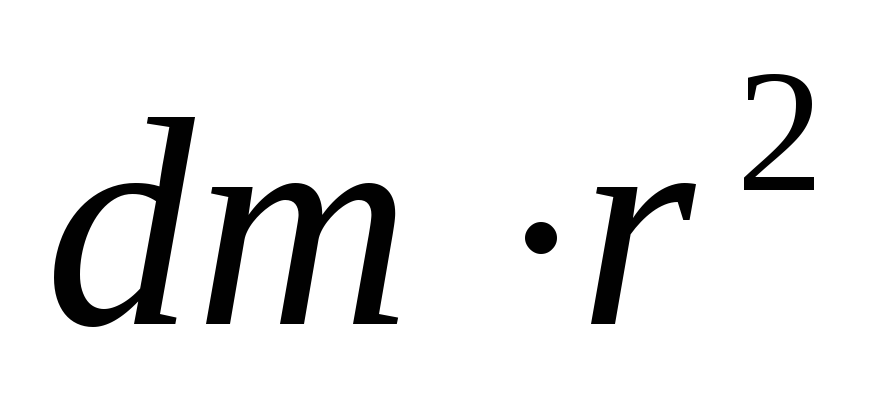
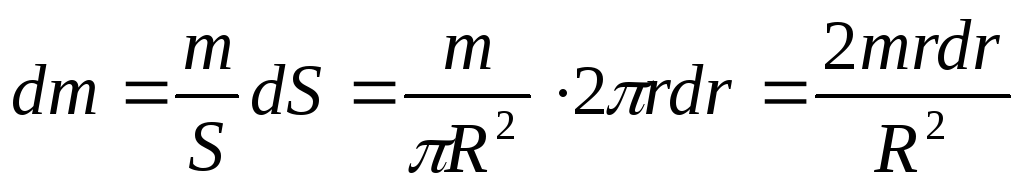

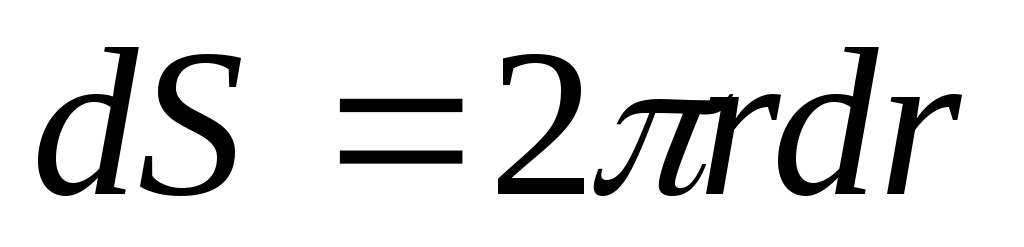
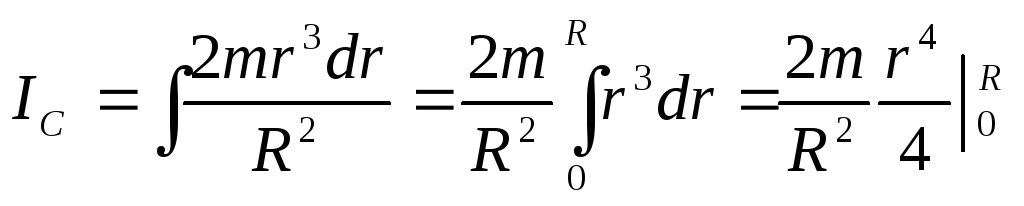
4. Толстостенный цилиндр.
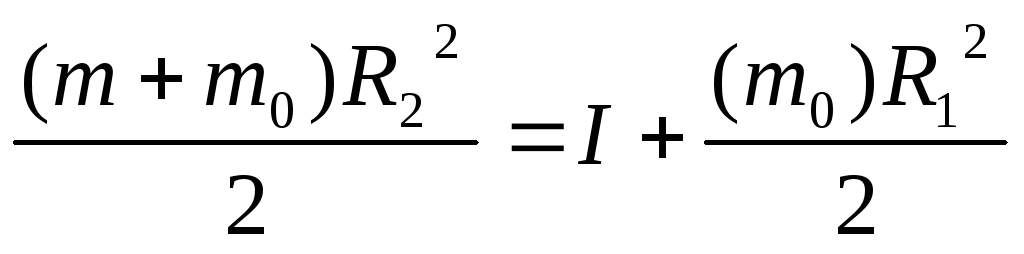
5. Сферическая оболочка. (В декартовый координатах).

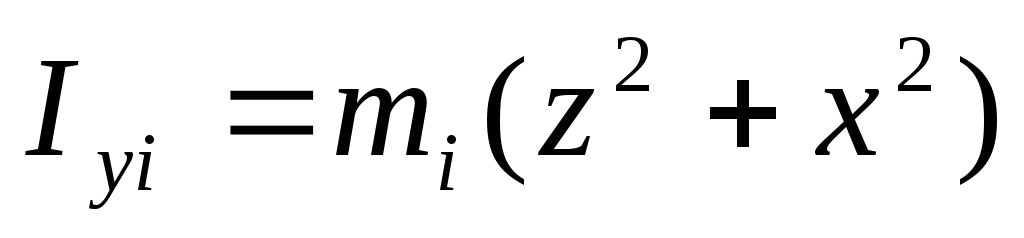

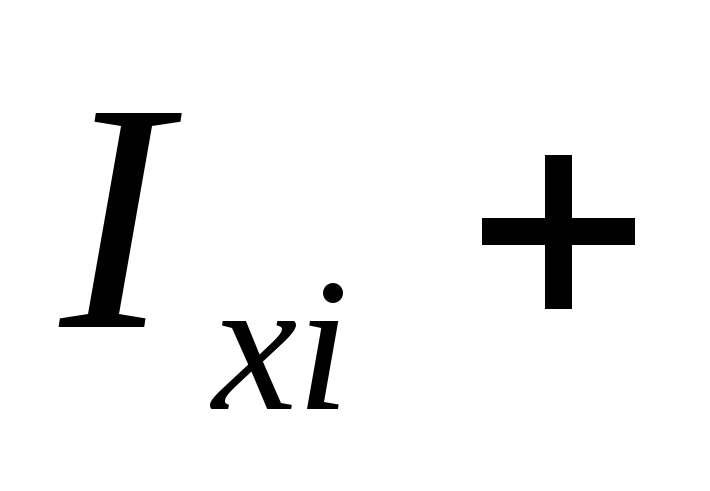
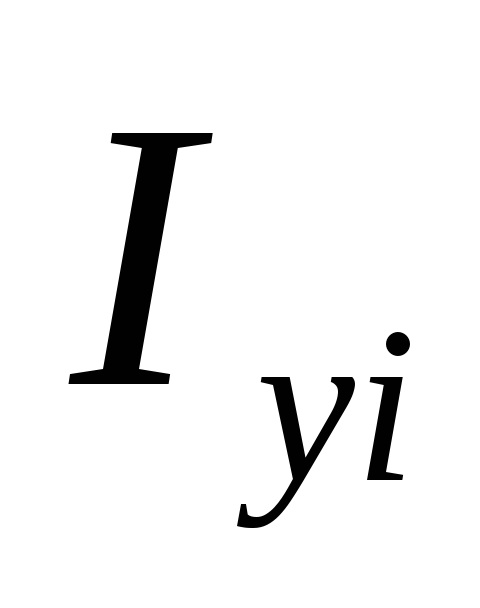 +
+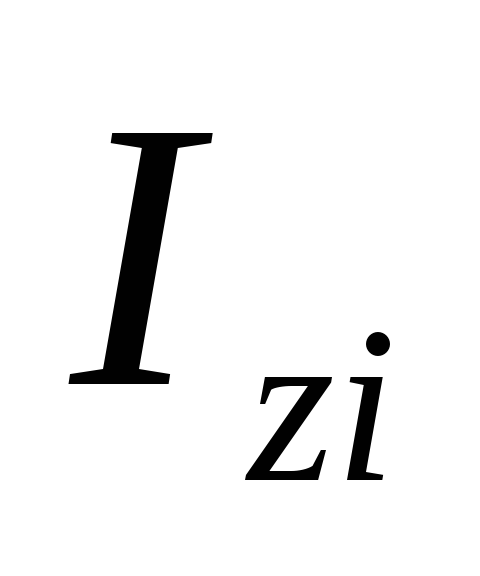 =
=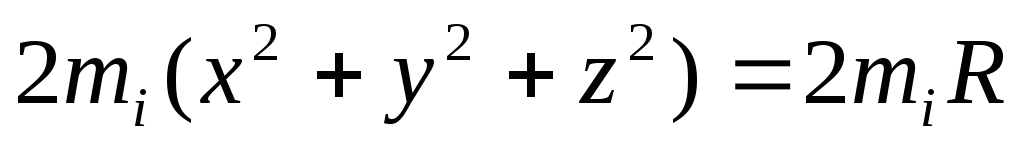
 +
+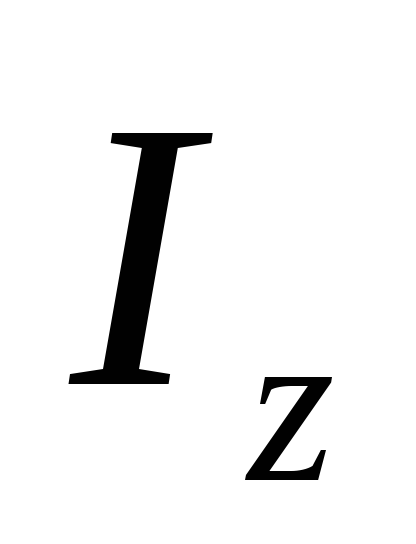 =
=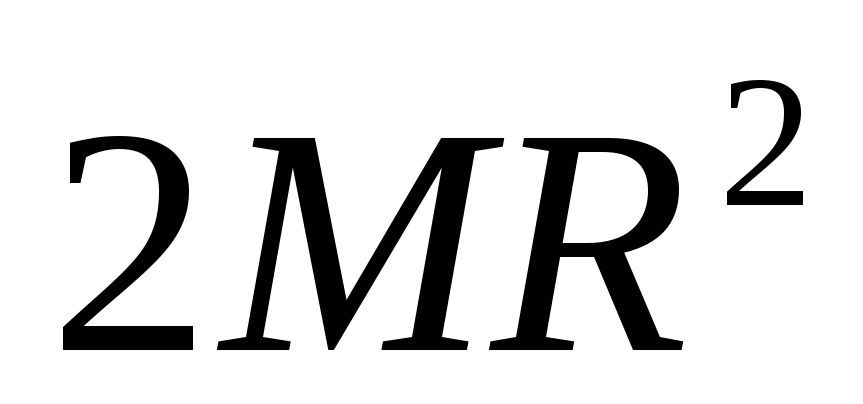

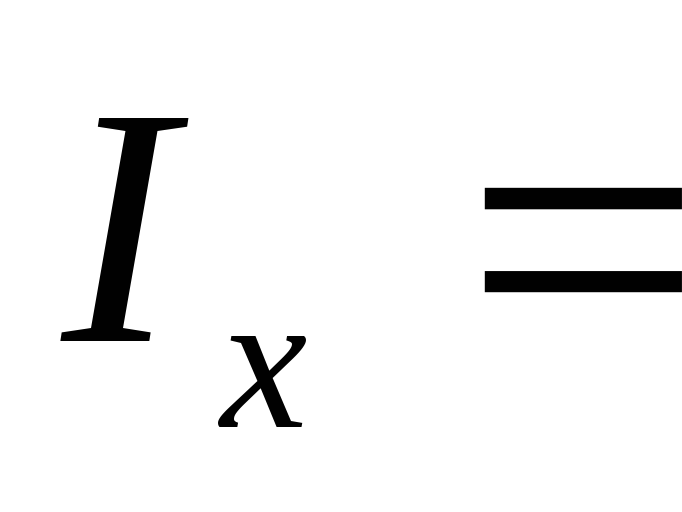
 =
=
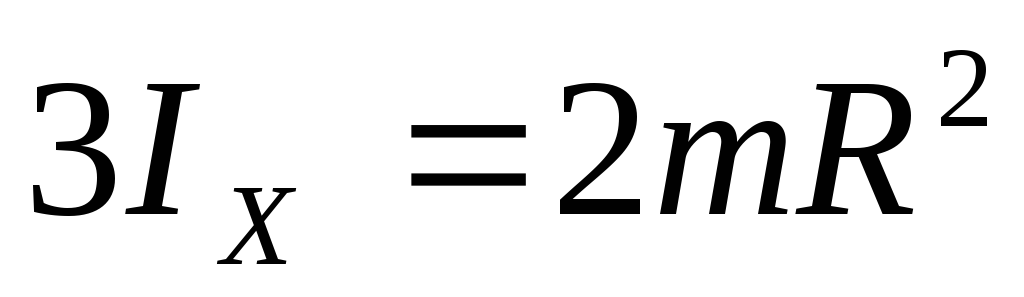
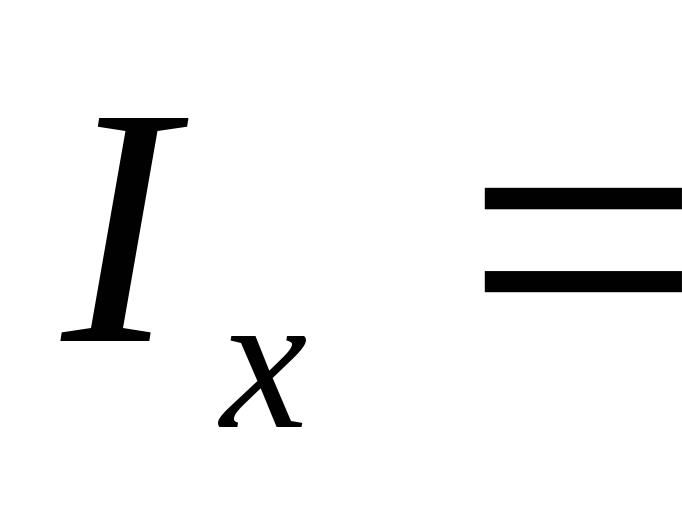
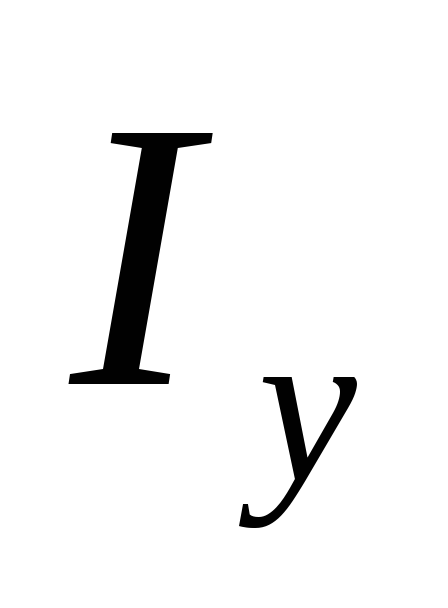 =
= =
=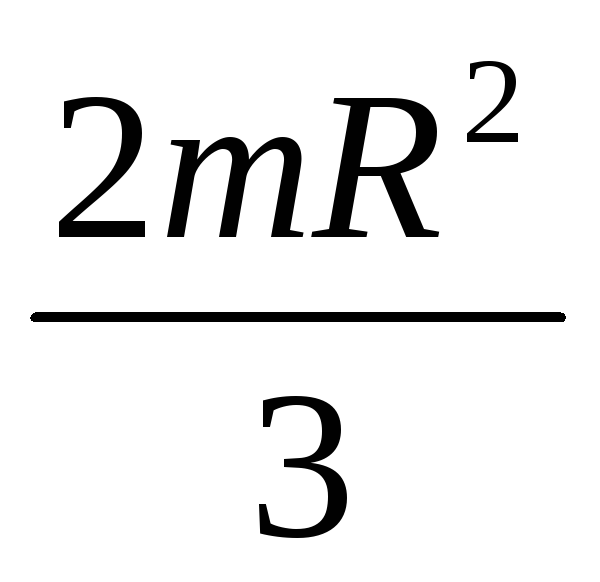
6. Шар.

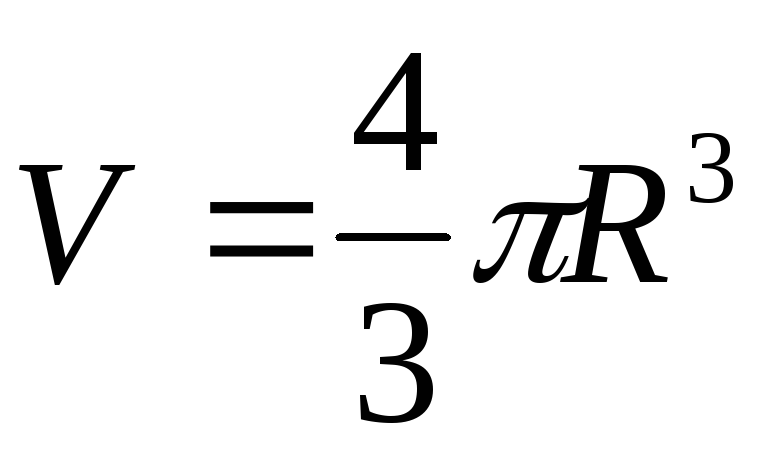
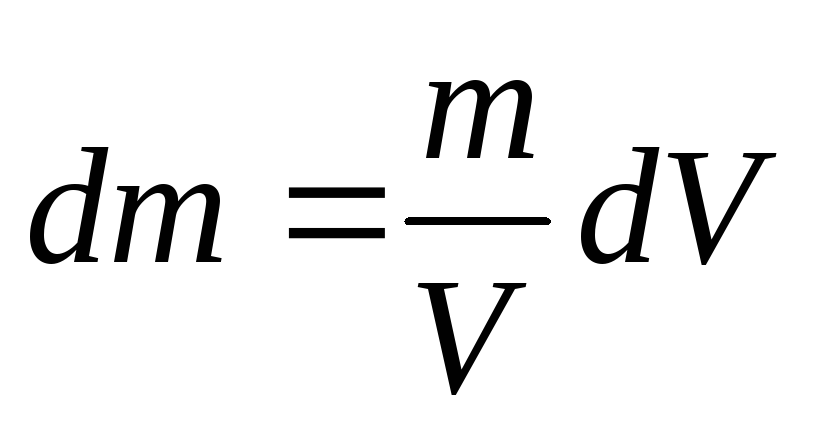
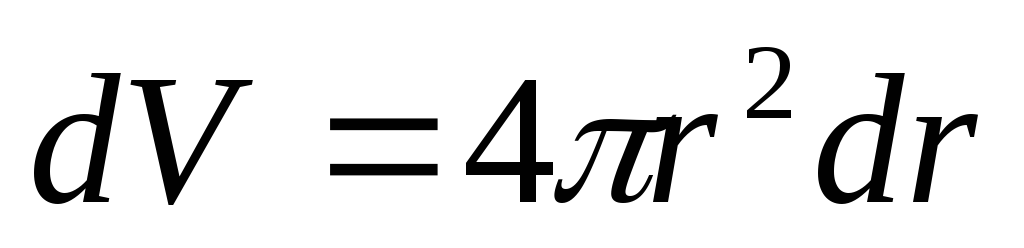
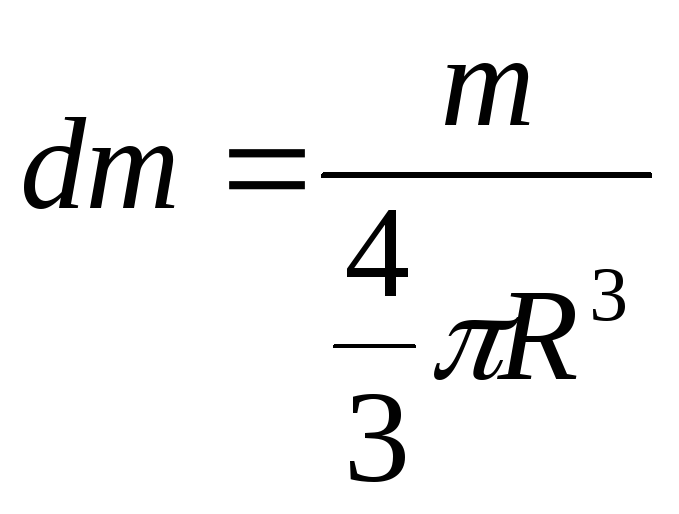
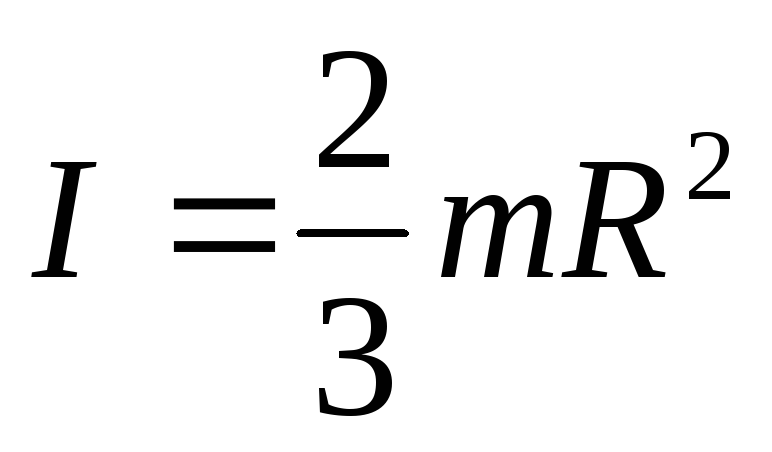
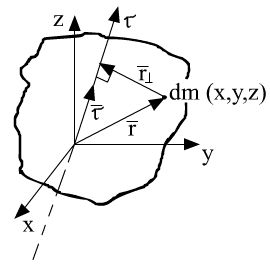
БИЛЕТ 14. Тензор инерции.
 -?
-?
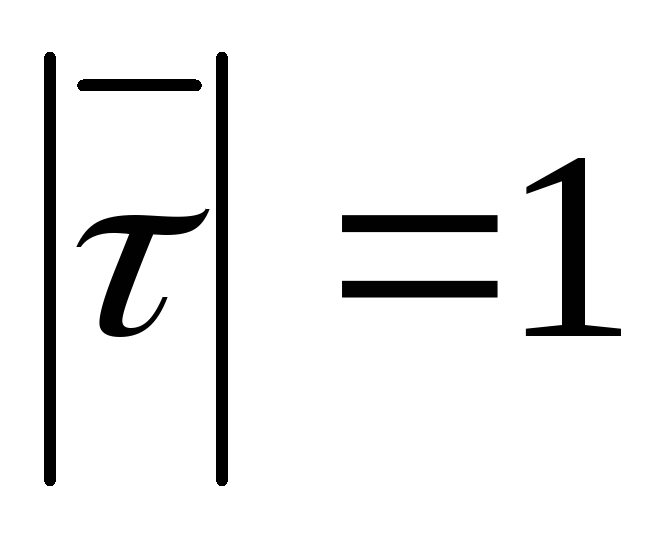

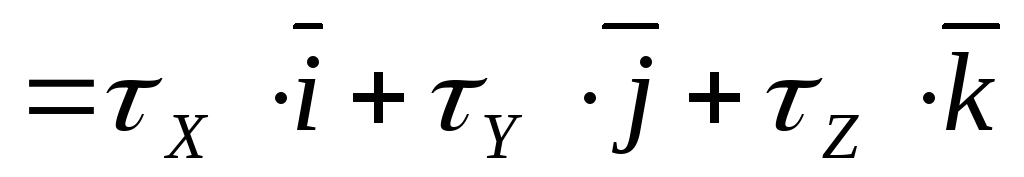

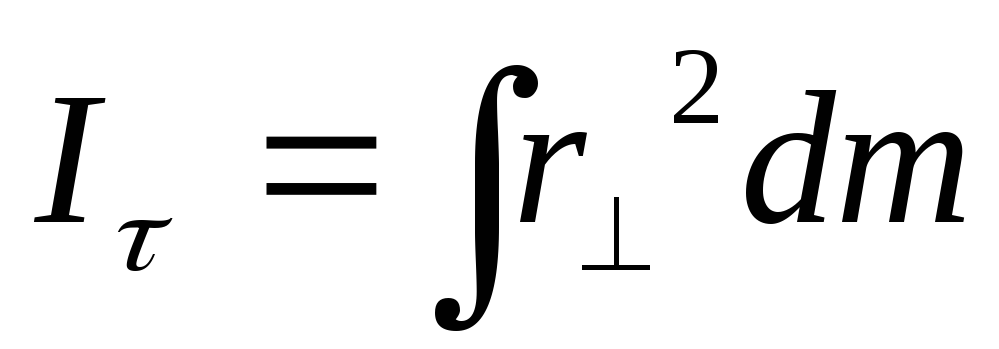

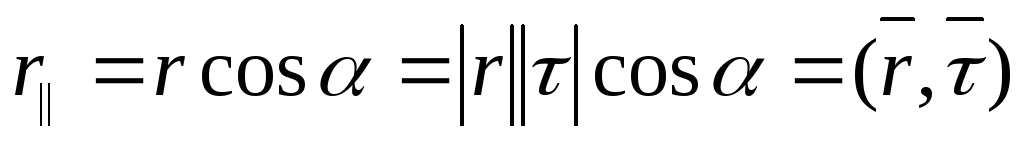


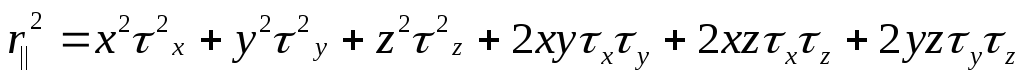



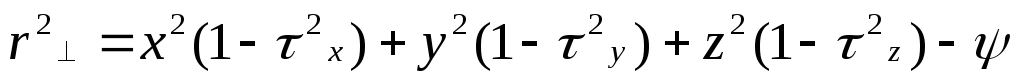
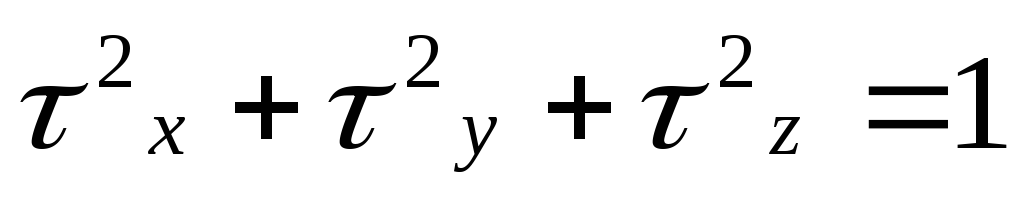
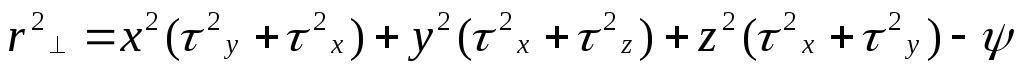
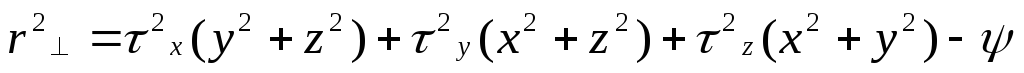
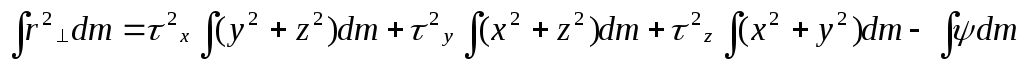
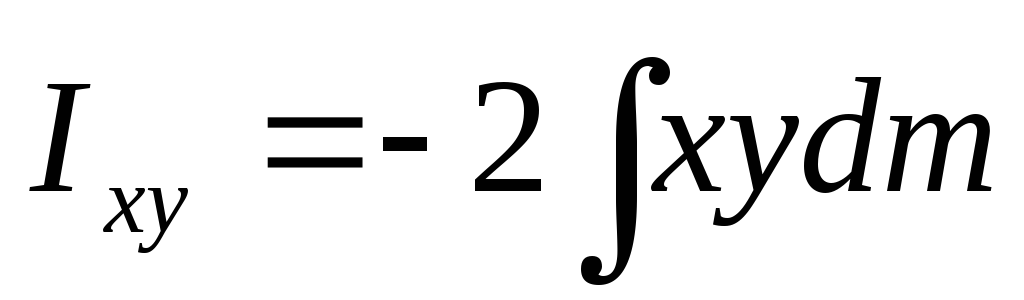

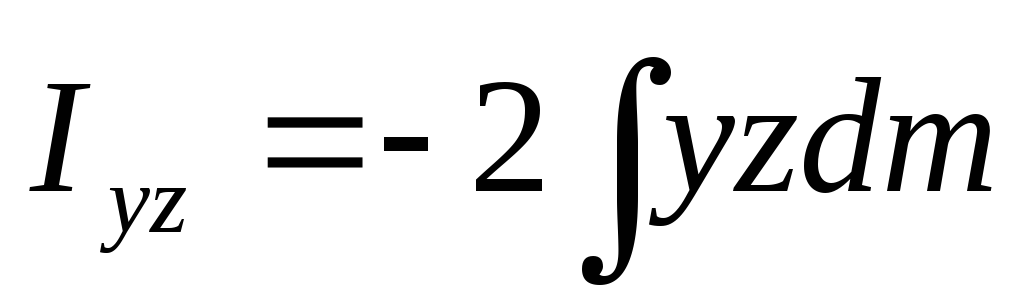
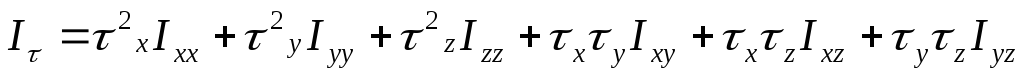
Тензор
инерции— 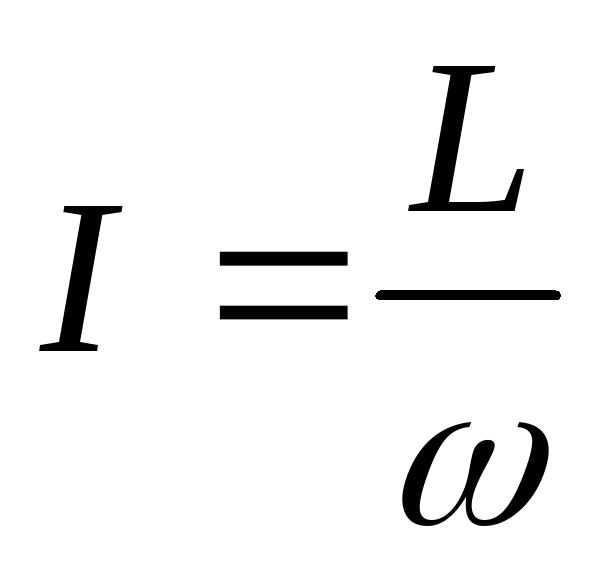 .
Это некоторая матрица:
.
Это некоторая матрица:
 ,
где
,
где 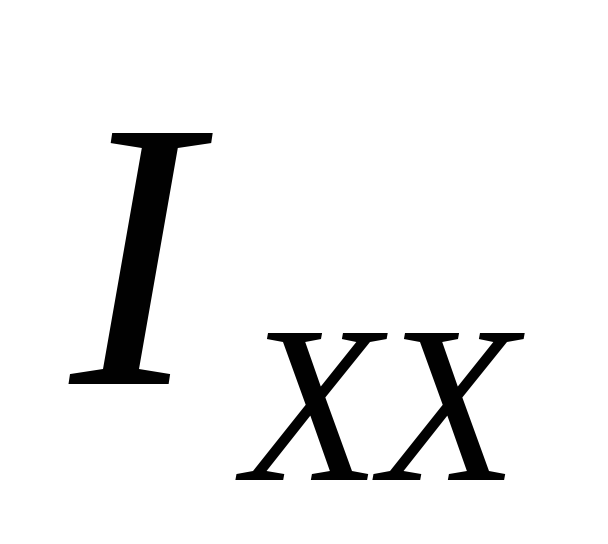 ,
,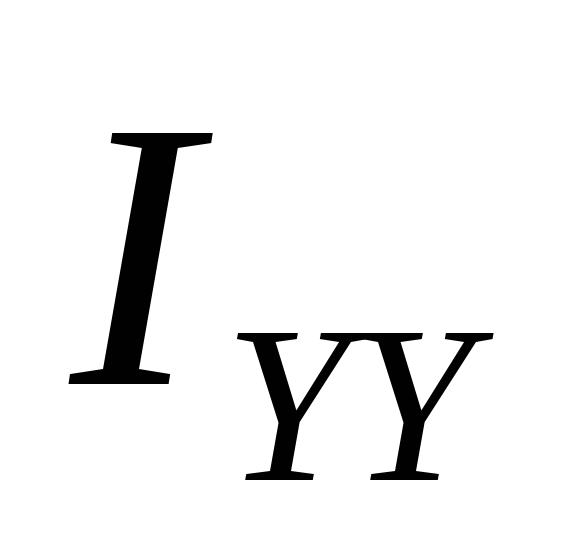 ,
,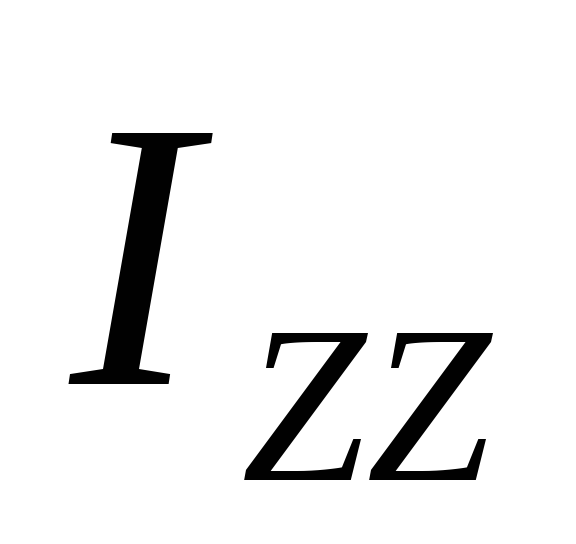 -осевые
моменты инерции, а все остальные числа-
центробежные моменты инерции.
-осевые
моменты инерции, а все остальные числа-
центробежные моменты инерции.
БИЛЕТ 15. Уравнение моментов относительно неподвижной точки и центра масс. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса.
Уравнение моментов
— относительно неподвижной точки (оси).
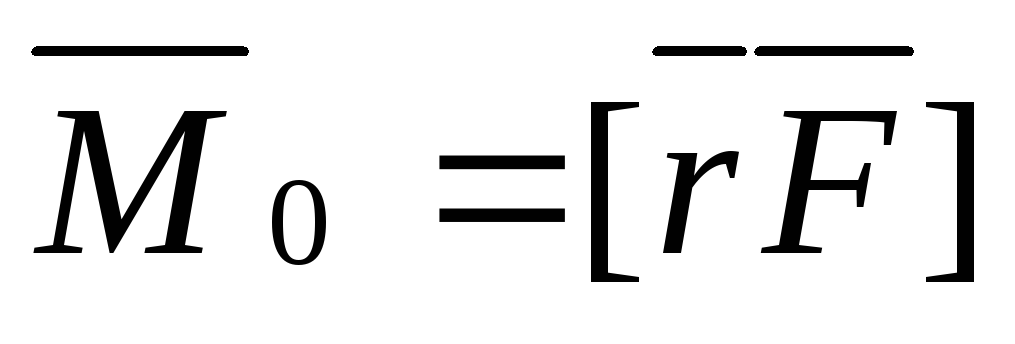
Материальная точка.
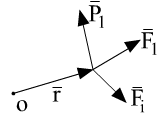
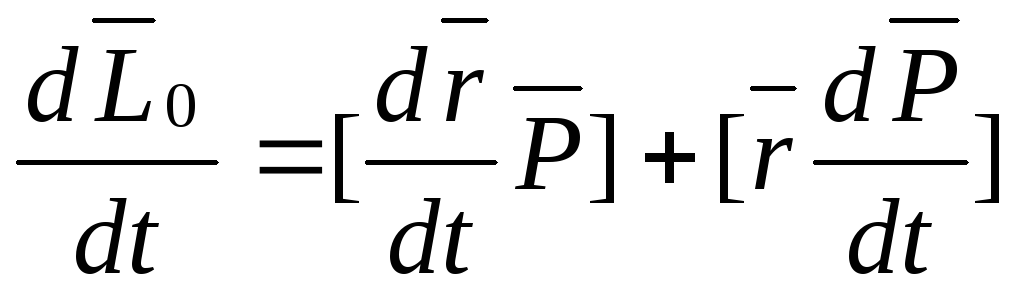

0
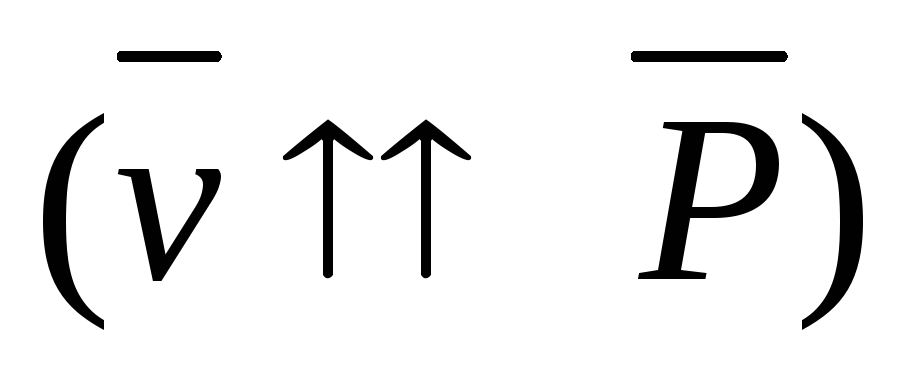
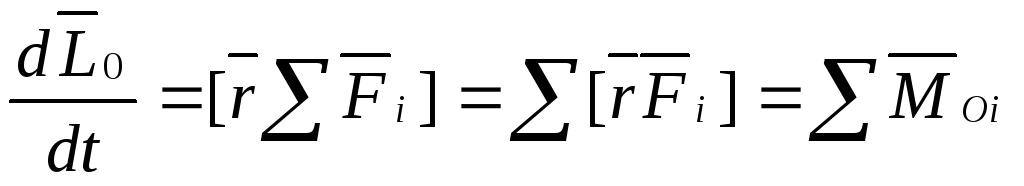
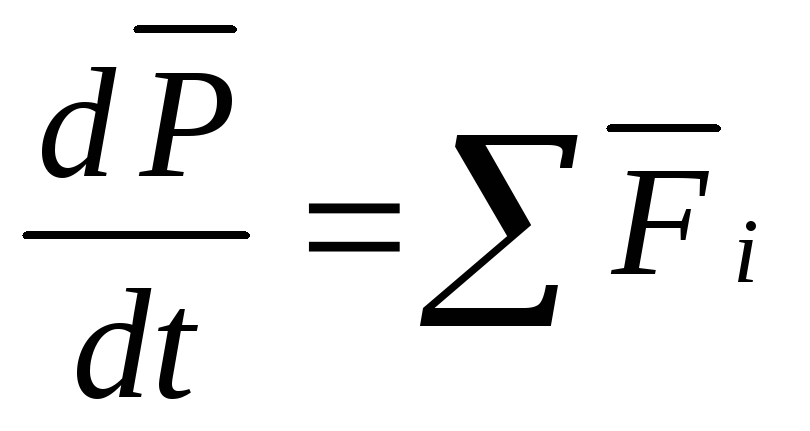
 -Закон
Изменения Момента Импульса для
Материальной Точки.
-Закон
Изменения Момента Импульса для
Материальной Точки.
Система материальных точек.
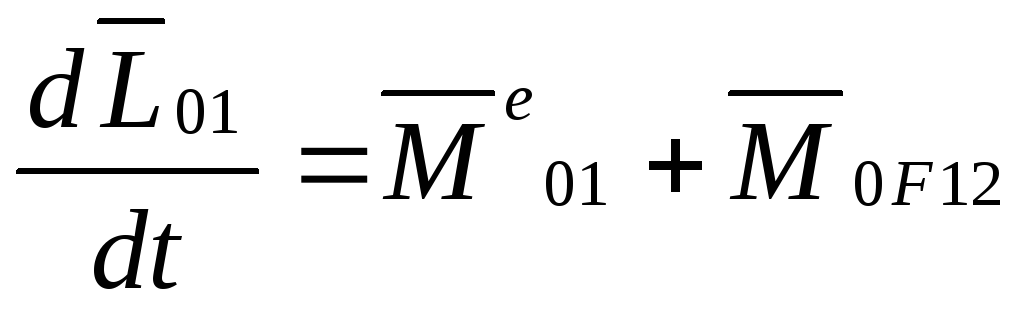
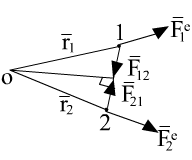
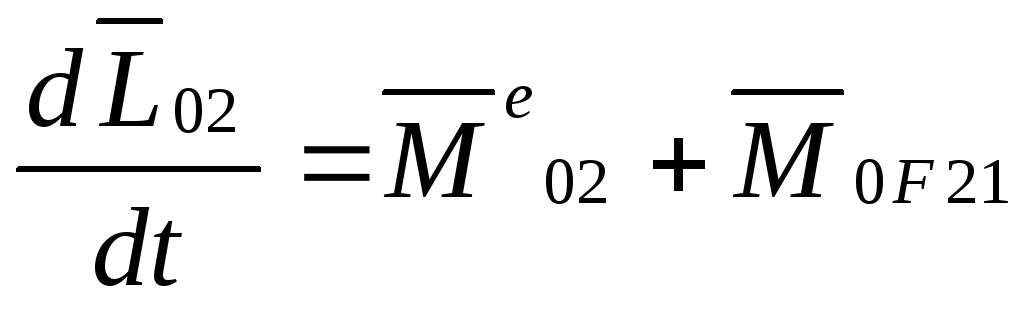


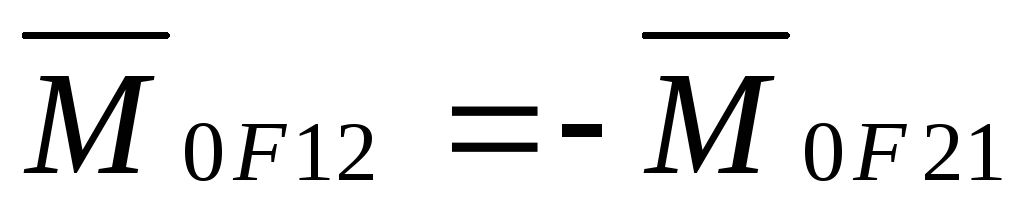

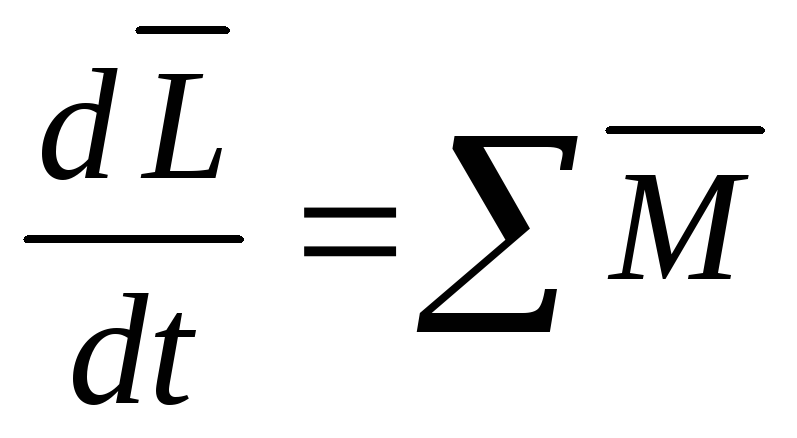
Абсолютно твердое тело.
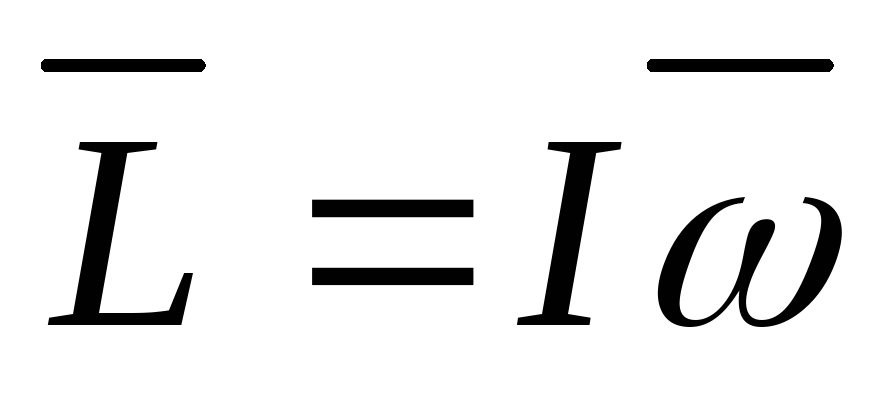

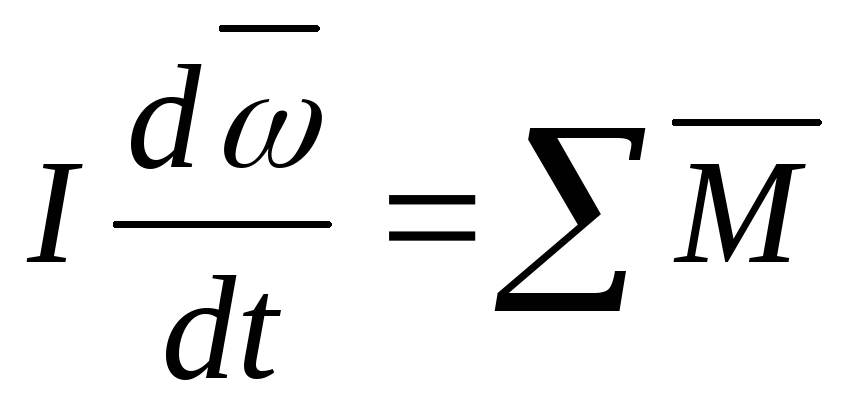
 —основное
уравнение динамики вращательного
движения.
—основное
уравнение динамики вращательного
движения.
— относительно центра масс.
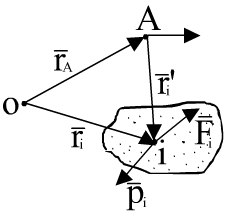
— система материальных точек.
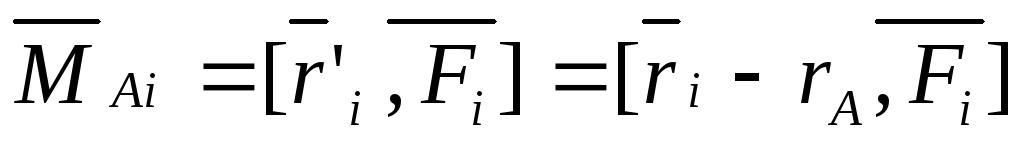
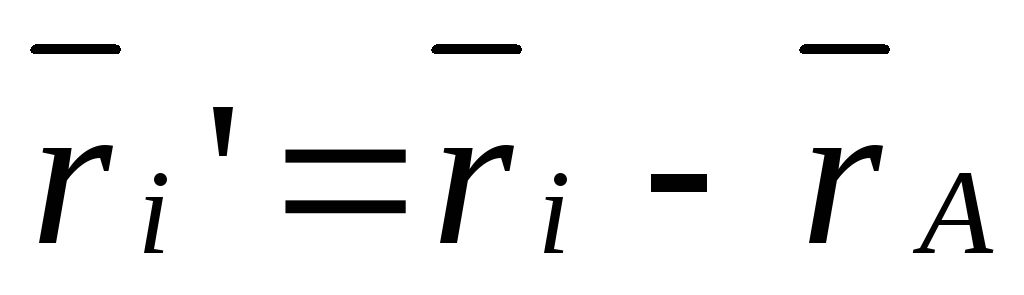
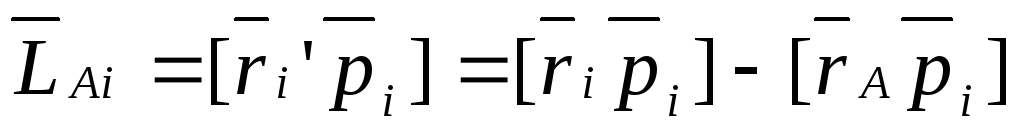
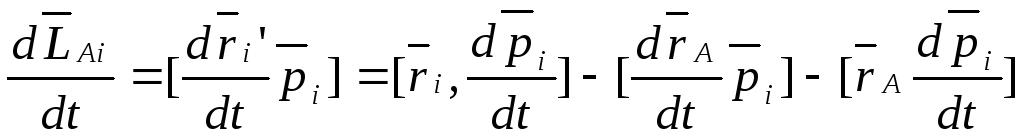

0
( )
)
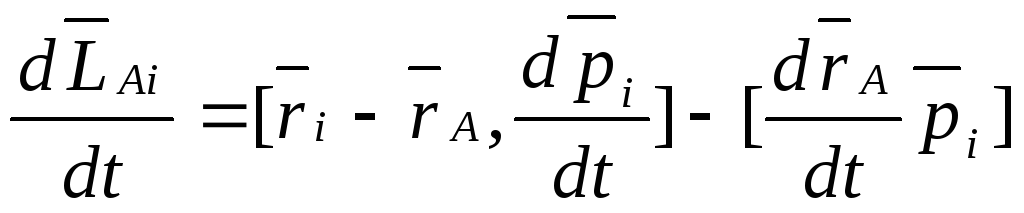
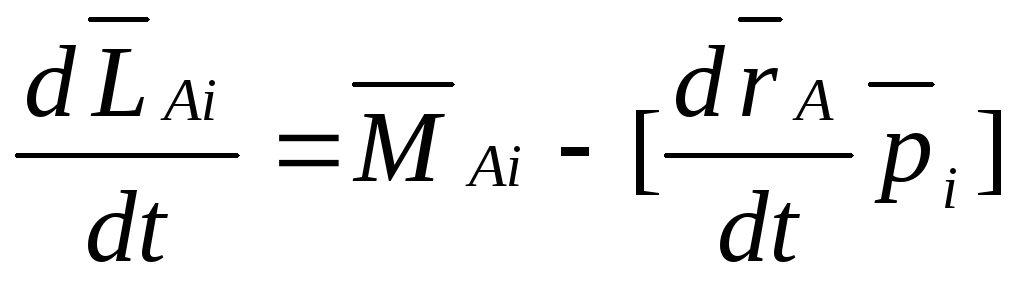
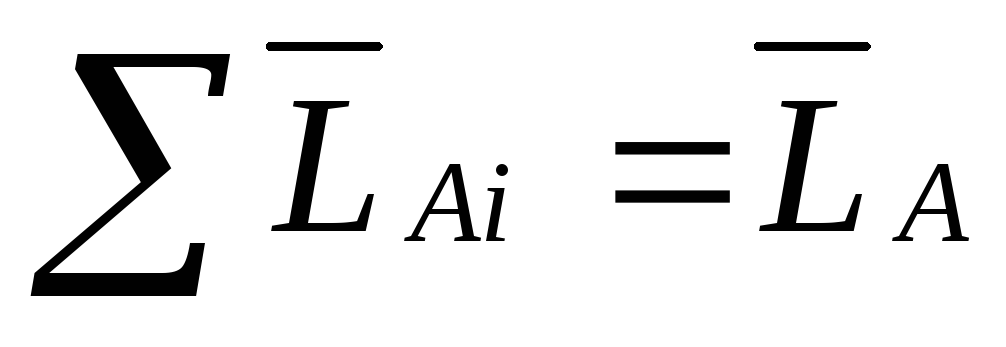
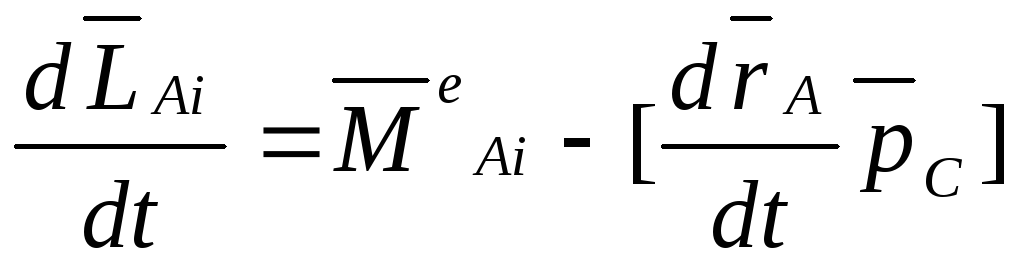
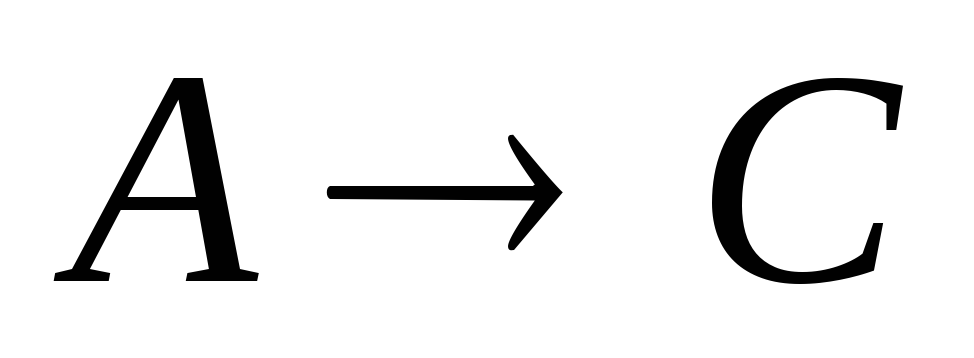
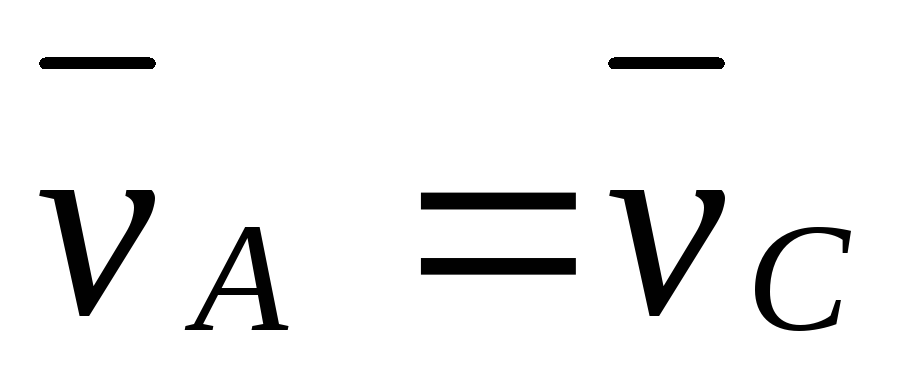


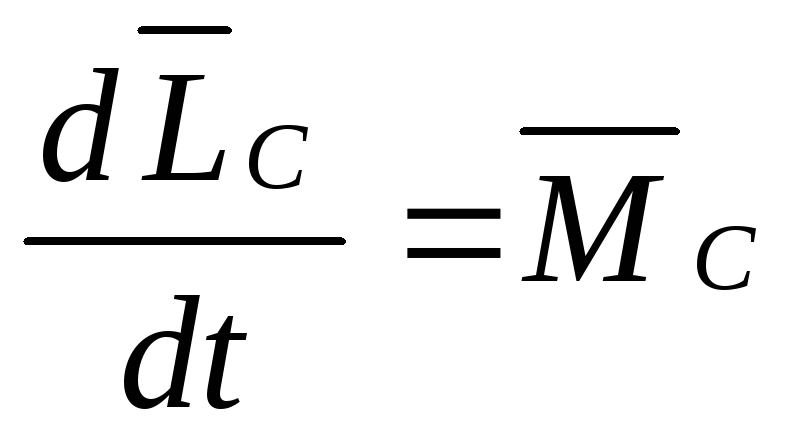

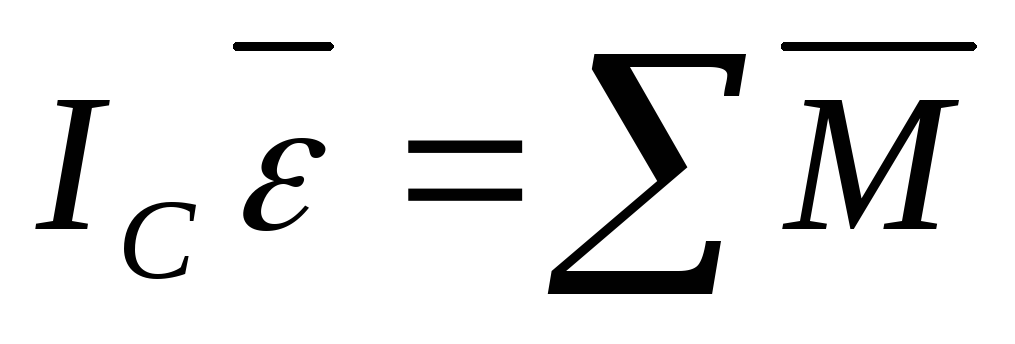 -относительно
оси, проходящей через центр масс системы.
-относительно
оси, проходящей через центр масс системы.
Закон сохранения момента импульса.
Для
замкнутой системы момент внешних сил 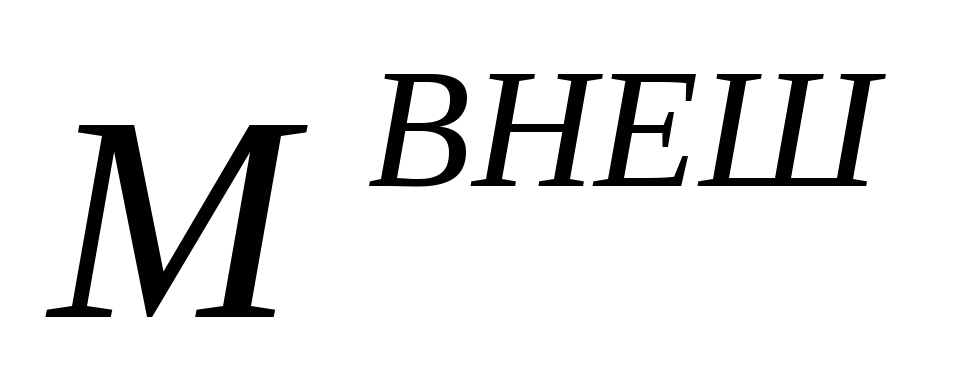 всегда
равен нулю, так как на нее внешние силы
не действуют. Поэтому ЗСМИ формулируется
следующим образом:
всегда
равен нулю, так как на нее внешние силы
не действуют. Поэтому ЗСМИ формулируется
следующим образом:
«Момент импульса замкнутой системы не изменяется с течением времени».
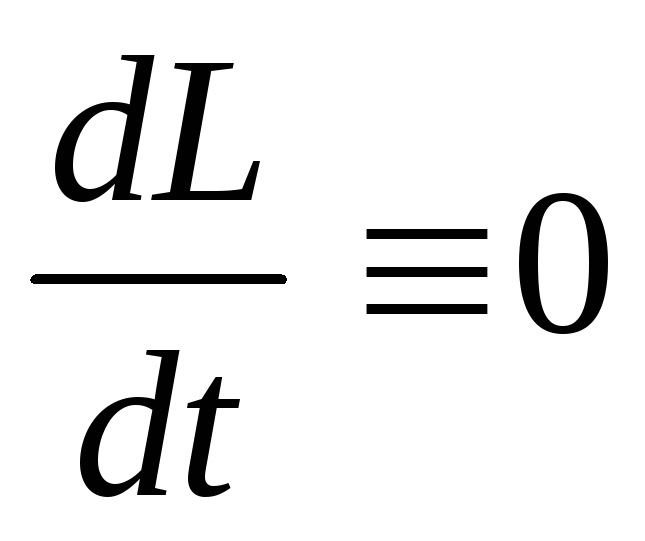 и
и 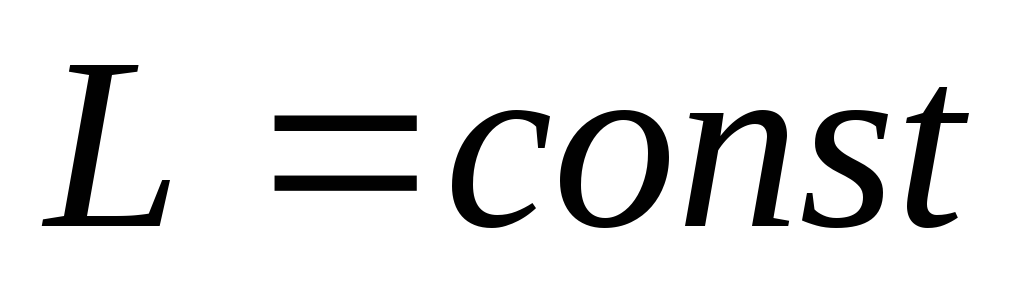
Кроме
того закон выполняется для случая
относительно любой неподвижной оси и
центра масс:  и
и .
.
БИЛЕТ 16. Работа при вращательном движении. Кинетическая энергия вращающегося тела.
Работа при вращательном движении.
Е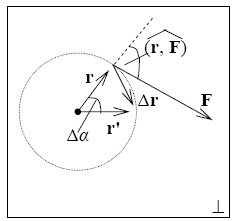 сли
сли ,
то
,
то
,
где  —
смещение точки приложения силы.
—
смещение точки приложения силы.





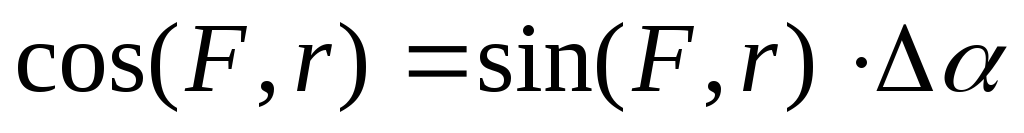





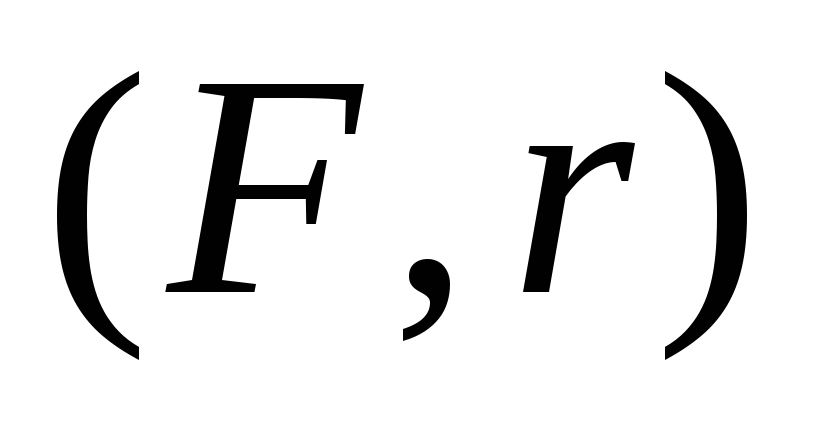 =
= =
=


{



Кинетическая энергия вращающегося тела.

Представим энергию всего тела, как сумму энергий материальных точек.
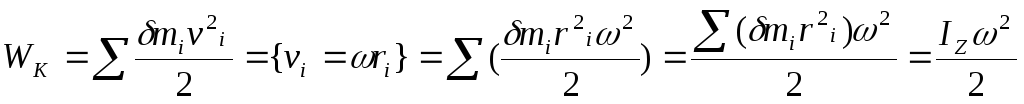
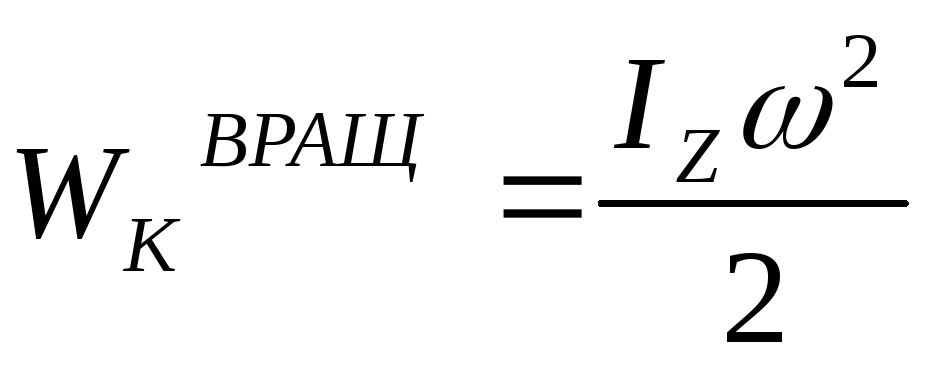
БИЛЕТ 17. Принцип относительности Галилея. Специальная теория относительности. Постулаты Эйнштейна.
Принцип относительности Галилея— Электронная База Знаний (с.51-53).
Постулаты Эйнштейна:
Все законы физики одинаковы во всех инерциальных системах отсчета.
Скорость света- величина постоянная и не зависит от скорости источника или приемника.
БИЛЕТ 18. Преобразования Лоренца.
Электронная База Знаний (с.54-56).
БИЛЕТ 19. Следствия из преобразования Лоренца (относительность одновременности, замедление хода движущихся часов, сокращение длины).
Электронная База Знаний (с.57-60).
БИЛЕТ 20. Преобразование скоростей (СТО).
Электронная База Знаний (с.59-60). (V. Закон сложения скоростей)
БИЛЕТ 21. Релятивистский импульс. Релятивистское выражение для энергии.
Электронная База Знаний (с.61, 62-63 III. кинетическая энергия).
БИЛЕТ 22. Интервал (СТО).
Справочник Детлафа (с. 94-95).
БИЛЕТ 23. Инварианты преобразования Лоренца.
???????????????????????????????????????????
БИЛЕТ 24. Основное уравнение молекулярно-кинетической теории.
Электронная База Знаний (С.69-71)
БИЛЕТ 25. Число степеней свободы. Закон равномерного распределения энергии по степеням свободы.
Электронная База Знаний (С.72-74)
БИЛЕТ 26. Внутренняя энергия термодинамической системы. Работа. Количество теплоты. Теплоемкость.
Электронная База Знаний (74-75, 80-83)
БИЛЕТ 27. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам. Уравнение Майера.
Электронная База Знаний (76-79)
Справочник Детлафа (с. 121).
БИЛЕТ 28. Адиабатный процесс. Уравнение адиабаты.
Электронная База Знаний (77-78)
Справочник Детлафа (с. 122-124).
БИЛЕТ 29. Политропный процесс. Уравнение политропы. Теплоемкость в политропном процессе.
Электронная База Знаний (78-79)
Справочник Детлафа (с. 124-125).
БИЛЕТ 30. Распределение Максвелла (распределение молекул по скоростям). Средняя, наиболее вероятная и средняя квадратичная скорости молекул идеального газа.
Справочник Детлафа (с. 128-132).
БИЛЕТ 31. Идеальный газ во внешнем потенциальном поле. Барометрическая формула. Распределение Больцмана.
Справочник Детлафа (с. 133-135).
БИЛЕТ 32. Эффективное сечение. Длина свободного пробега.
Эффективное сечение.
Справочник Детлафа (с. 136).
БИЛЕТ 33. Второе начало термодинамики.
Справочник Детлафа (с. 149, 158-161).
БИЛЕТ 34. Тепловые машины и их КПД. Тепловой насос. Холодильная установка.
Электронная База Знаний (84-85)
БИЛЕТ 35. Цикл Карно. КПД цикла Карно. Теорема Карно. Изменение энтропии в цикле Карно.
Электронная База Знаний (86-88)
Справочник Детлафа (с. 150-153).
БИЛЕТ 36. Неравенство Клаузиуса. Энтропия. Изменение энтропии в изолированных системах.
Электронная База Знаний (88-89)
Справочник Детлафа (с. 153-154).
БИЛЕТ 37. Энтропия и вероятность. Статистическое толкование второго начала термодинамики.
Электронная База Знаний (90-93)
Справочник Детлафа (с. 162-164).
2. Момент инерции и его вычисление
Согласно
определению, момент
инерции тела относительно оси равен
сумме произведений масс частиц на
квадраты их расстояний до оси вращения или 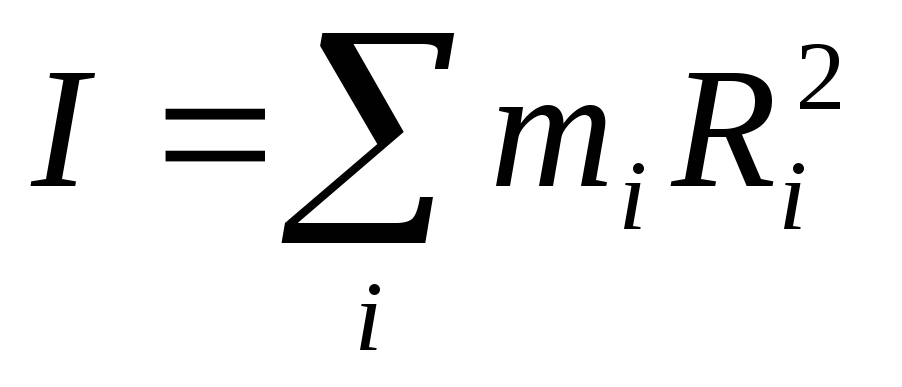
Однако, эта формула непригодна для вычисления момента инерции; так как масса твердого тела распределена непрерывно, то сумму следует заменить на интеграл. Поэтому для вычисления момента инерции тело разбивают на бесконечно малые объемы dV с массой dm=dV. Тогда
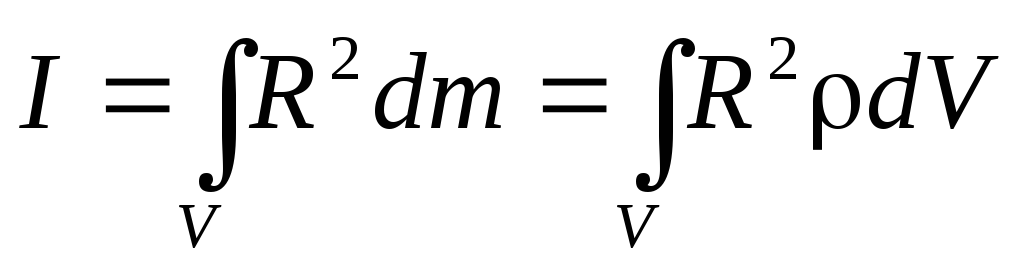
где R — расстояние элемента dV от оси вращения.
Если момент инерции IC относительно оси, проходящей через центр масс, известен, то можно легко вычислить момент инерции относительно любой параллельной оси О, проходящей на расстоянии d от центра масс или
IO=IC+md2,
Это соотношение называется теоремой Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси параллельной ей и проходящей через центр масс и произведения массы тела на квадрат расстояния между осями.
3. Кинетическая энергия вращения
Кинетическая энергия вращающегося вокруг закрепленной оси твердого тела
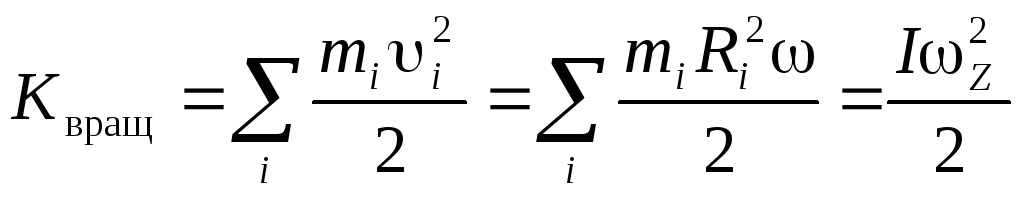
Дифференцируя формулу по времени, получим закон изменения кинетической энергии вращающегося вокруг закрепленной оси твердого тела:
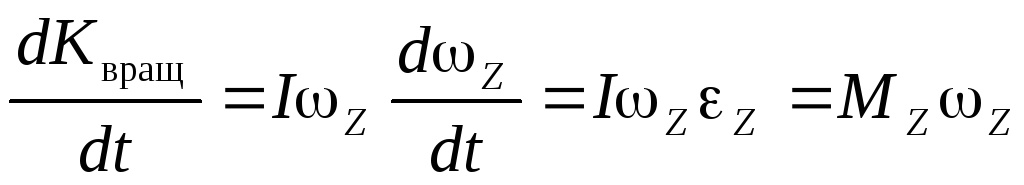 –
–
скорость изменения кинетической энергии вращательного движения равна мощности момента силы.
Отсюда
dKвращ=MZZdt=MZd
K
K2-K1=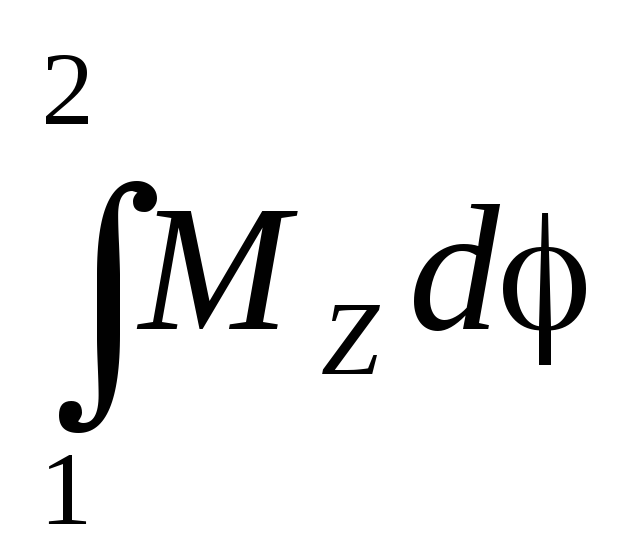
т.е. изменение кинетической энергии вращения равно работе момента сил.
4. Плоское движение
Движение твердого тела, при котором центр масс перемещается в фиксированной плоскости, а ось его вращения, проходящая через центр масс, остается перпендикулярной к этой плоскости, называется плоским движением. Это движение можно свести к совокупности поступательного движения и вращения вокруг неподвижной (закрепленной) оси, так как в Ц-системе ось вращения, действительно, остается неподвижной. Поэтому плоское движение описывается упрощенной системой двух уравнений движения:
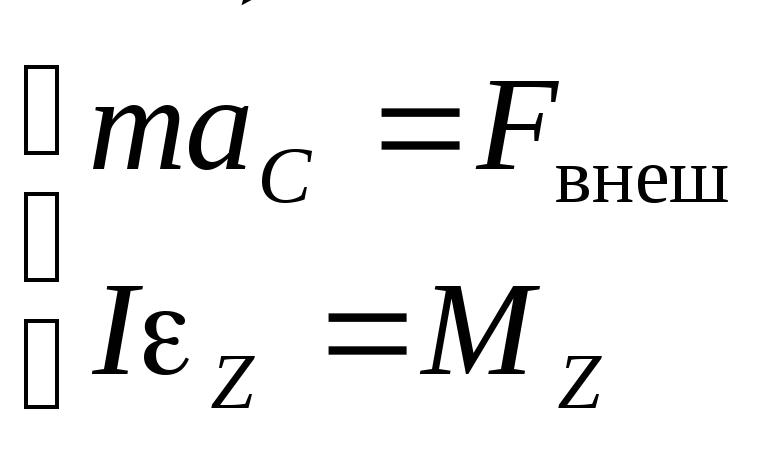 (8.10)
(8.10)
Кинетическая энергия тела, совершающего плоское движение, будет:
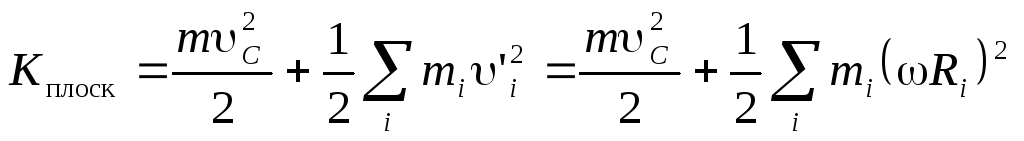
и окончательно
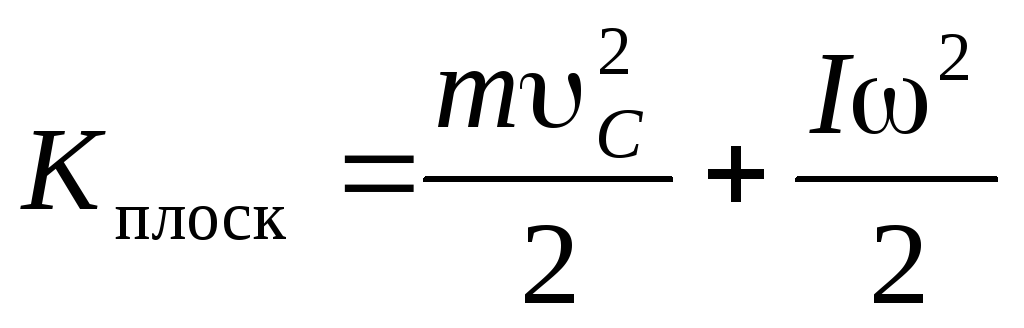 ,
,
так как в данном случае i‘ — скорость вращения i-ой точки вокруг неподвижной оси.
Колебания
1. Гармонический осциллятор
Колебаниями вообще называются движения, повторяющиеся во времени.
Если эти повторения следуют через равные промежутки времени, т.е. x(t+T)=x(t), то колебания называются периодическими. Система, совершающая
колебания, называется осциллятором. Колебания, которые совершает система, предоставленная самой себе, называются собственными, а частота колебаний в этом случае — собственной частотой.
Гармоническими колебаниями называются колебания, происходящие по закону sin или cos. Например,
x(t)=A cos( t+0),
где x(t) — смещение частицы от положения равновесия, A — максимальное
смещение
или амплитуда,
t+0 — фаза колебаний, 0 —
начальная фаза (при t=0), 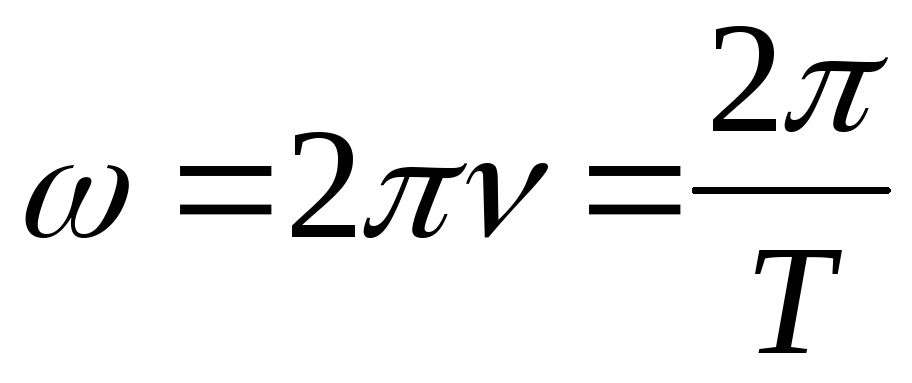 —циклическая
частота,
—циклическая
частота,  — просто частота колебаний.
— просто частота колебаний.
Система, совершающая гармонические колебания, называется гармоническим осциллятором. Существенно, что амплитуда и частота гармонических колебаний постоянны и не зависят друг от друга.
Условия возникновения гармонических колебаний:на частицу (или систему частиц) должна действовать сила или момент сил, пропорциональные смещению частицы из положения равновесия и
стремящиеся вернуть ее в положение равновесия. Такая сила (или момент сил)
называется квазиупругой;
она имеет вид 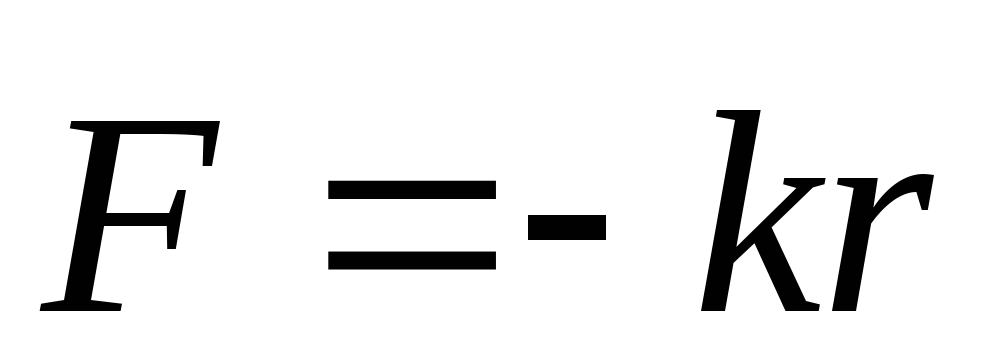 ,
где k называется квазижесткостью.
,
где k называется квазижесткостью.
В частности это может быть и просто упругая сила, приводящая в колебания пружинный маятник, колеблющийся вдоль оси x. Уравнение движения такого маятника имеет вид:
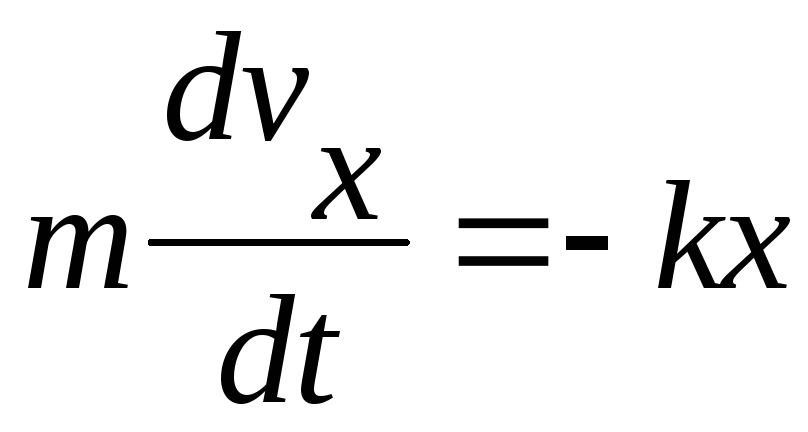 или
или  ,
,
где
введено обозначение 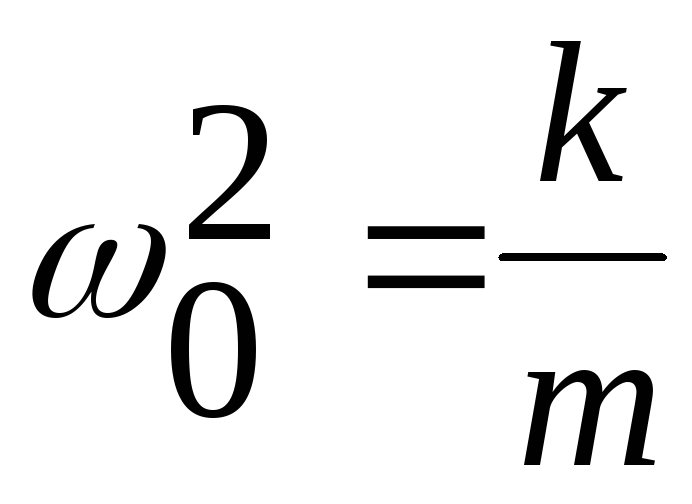 .
.
Непосредственной подстановкой нетрудно убедиться, что решением уравнения
является функция
x=A cos( 0t+0),
где A и 0 — постоянные величины, для определения которых следует задать два начальных условия: положение x(0)=x0 частицы и ее скорость vх(0)=v0 в начальный (нулевой) момент времени.
Это уравнение представляет собою динамическое уравнение любых
гармонических колебаний с собственной частотой 0. Для грузика на
пружинке период колебаний пружинного маятника
 .
.
4.3. Моменты инерции простых фигур
Как уже отмечалось выше, к числу простых плоских фигур относятся три фигуры: прямоугольник, треугольник и круг. Простыми эти фигуры считаются потому, что положение центра тяжести этих фигур заранее известно. Все остальные фигуры могут быть составлены из этих простых фигур и считаются сложными. Вычислим осевые моменты инерции простых фигур относительно их центральных осей.
1. Прямоугольник.Рассмотрим сечение
прямоугольного профиля размерами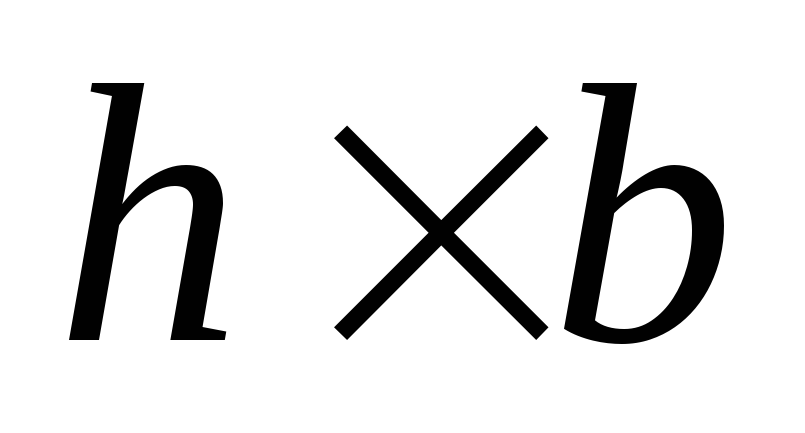 (Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии
(Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии от
центральной оси
от
центральной оси .
.
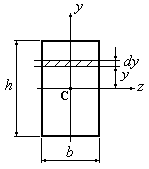
Рис.4.6
Вычислим момент инерции прямоугольного сечения относительно оси :
 .
(4.10)
.
(4.10)
Момент
инерции прямоугольного сечения
относительно оси  найдем аналогично. Здесь вывод не
приводится.
найдем аналогично. Здесь вывод не
приводится.
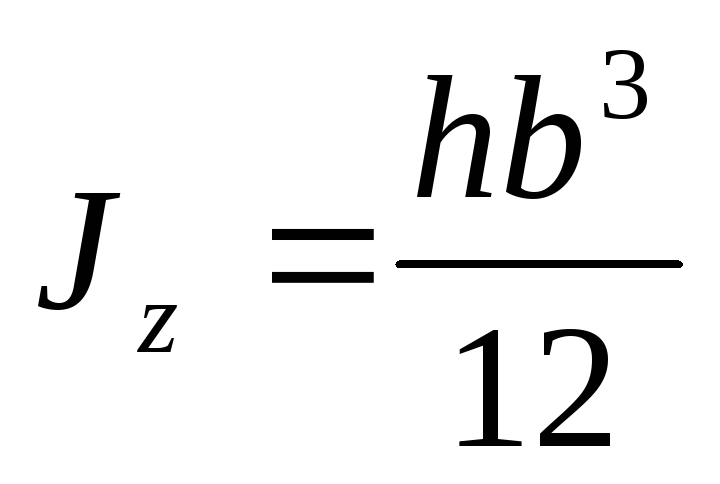 .
(4.11)
.
(4.11)
Центробежный
момент инерции относительно осей  и
и равен нулю, так как оси
равен нулю, так как оси и
и являются осями симметрии, а, следовательно,
главными осями.
являются осями симметрии, а, следовательно,
главными осями.
2. Равнобедренный треугольник.Рассмотрим сечение треугольного профиля
размерами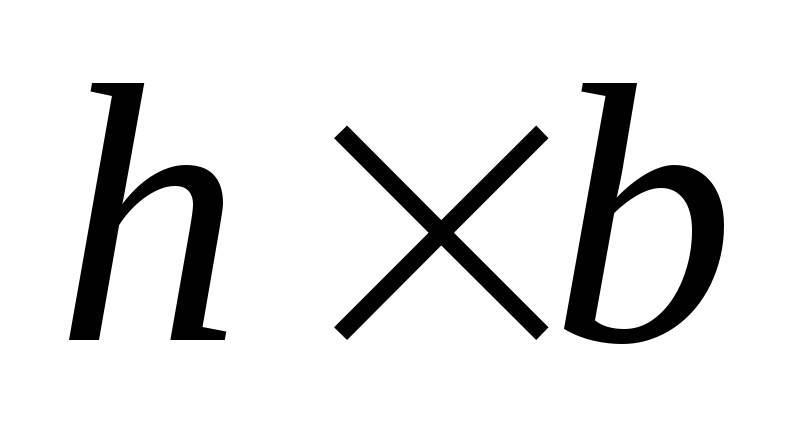 (Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии
(Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии от центральной оси
от центральной оси .
Центр тяжести треугольника находится
на расстояни
.
Центр тяжести треугольника находится
на расстояни от основания. Треугольник принимается
равнобедренным, так что ось
от основания. Треугольник принимается
равнобедренным, так что ось сечения является осью симметрии.
сечения является осью симметрии.
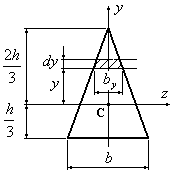
Рис.4.7
Вычислим
момент инерции сечения относительно
оси  :
:
 .
(4.12)
.
(4.12)
Величину  определим из подобия треугольников:
определим из подобия треугольников:
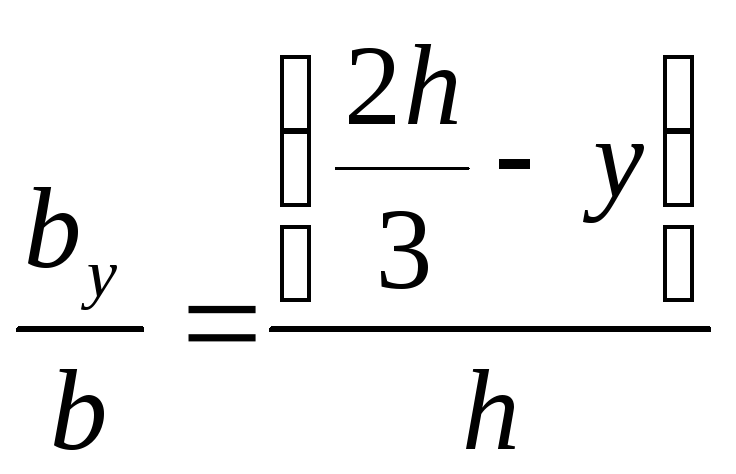 ;
откуда
;
откуда  .
.
Подставляя
выражения для  в (4.12) и интегрируя, получим:
в (4.12) и интегрируя, получим:
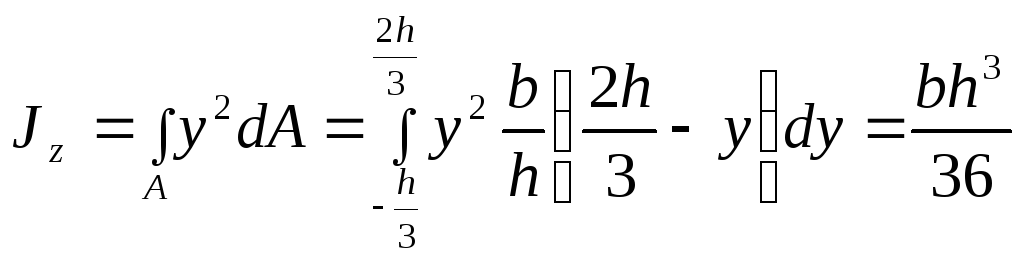 .
(4.13)
.
(4.13)
Момент
инерции для равнобедренного треугольника
относительно оси  находится аналогичным образом и равен:
находится аналогичным образом и равен:
 (4.14)
(4.14)
Центробежный
момент инерции относительно осей  и
и равен нулю, так как ось
равен нулю, так как ось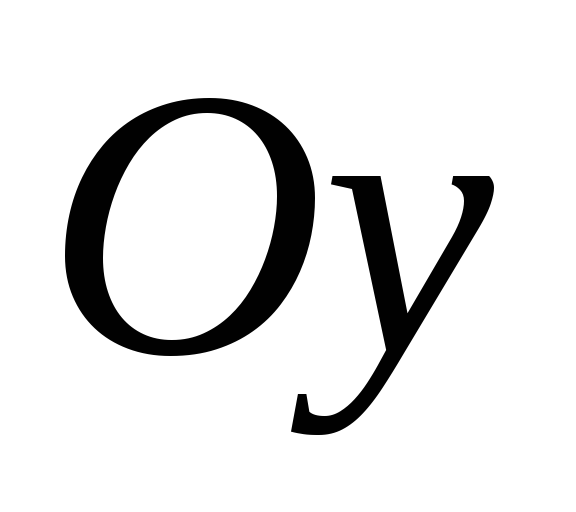 является осью симметрии сечения.
является осью симметрии сечения.
3. Круг. Рассмотрим сечение круглого
профиля диаметром (Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянии
(Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянии от центра тяжести круга
от центра тяжести круга .
.

Рис.4.8
Вычислим полярный момент инерции круга, воспользовавшись выражением (4.5):
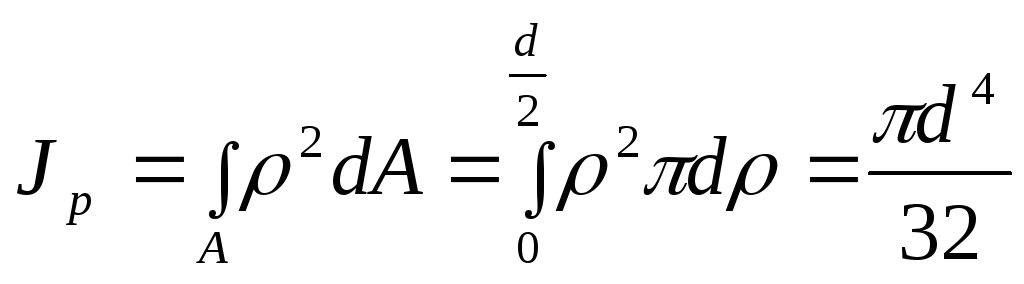 .
(4.15)
.
(4.15)
Используя условие инвариантности для
суммы осевых моментов инерции относительно
двух взаимно перпендикулярных осей
(4.6) и учитывая, что для круга в силу
симметрии 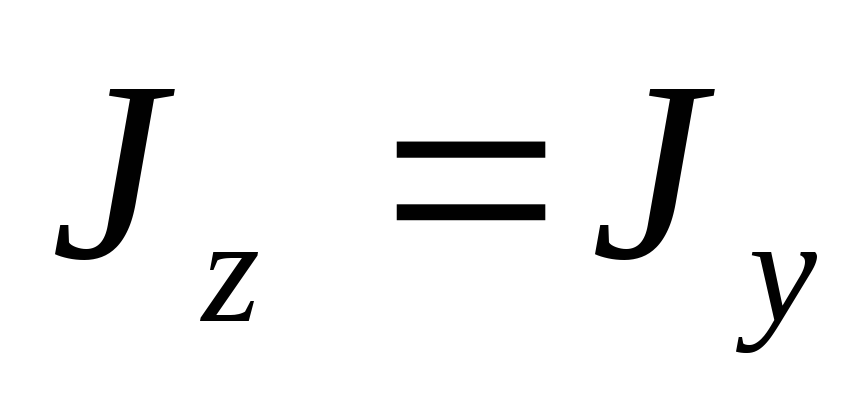 ,
определяем величину осевых моментов
инерции:
,
определяем величину осевых моментов
инерции:
 .
(4.16)
.
(4.16)
Откуда:
 .
(4.17)
.
(4.17)
Центробежный
момент инерции относительно осей 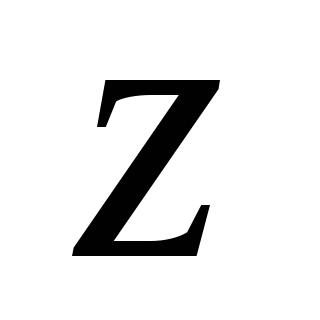 иравен нулю, так как оси
иравен нулю, так как оси и
и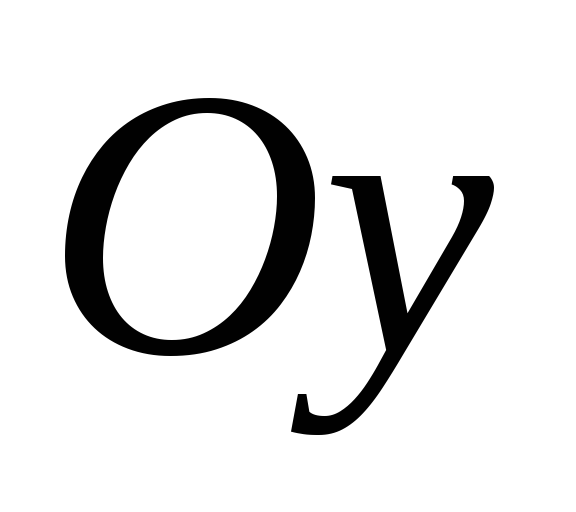 являются осями симметрии сечения.
являются осями симметрии сечения.
4.4. Зависимости между моментами инерции относительно параллельных осей
При вычислении моментов инерции для сложных фигур следует запомнить одно правило: значения для моментов инерции можно складывать, если они вычислены относительно одной и той же оси. Для сложных фигур чаще всего центры тяжести отдельных простых фигур и всей фигуры не совпадают. Не совпадают, соответственно, и центральные оси для отдельных простых фигур и всей фигуры. В связи с этим существуют приемы приведения моментов инерции к одной оси, например, центральной оси всей фигуры. Это может быть связано с параллельным переносом осей инерции и дополнительными вычислениями.
Рассмотрим определение моментов инерции относительно параллельных осей инерции, изображенных на рис.4.9.

Рис.4.9
Пусть
осевые и центробежный моменты инерции
изображенной на рис.4.9. фигуры относительно
произвольно выбранных осей  ис началом координат в точке
ис началом координат в точке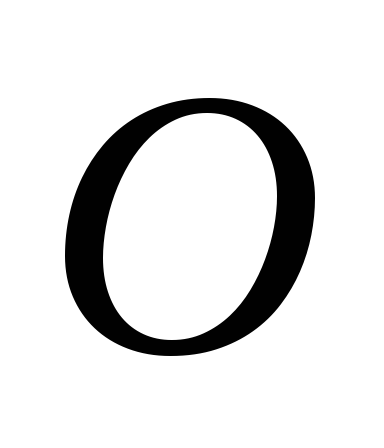 известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осей
известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осей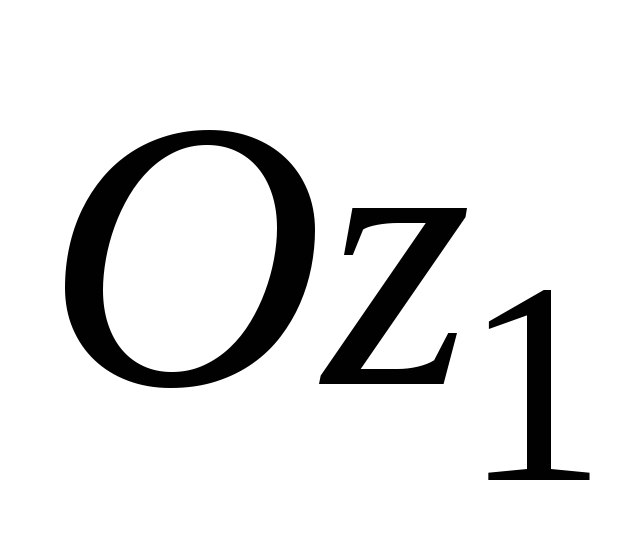 и
и с началом координат в точке
с началом координат в точке .
Оси
.
Оси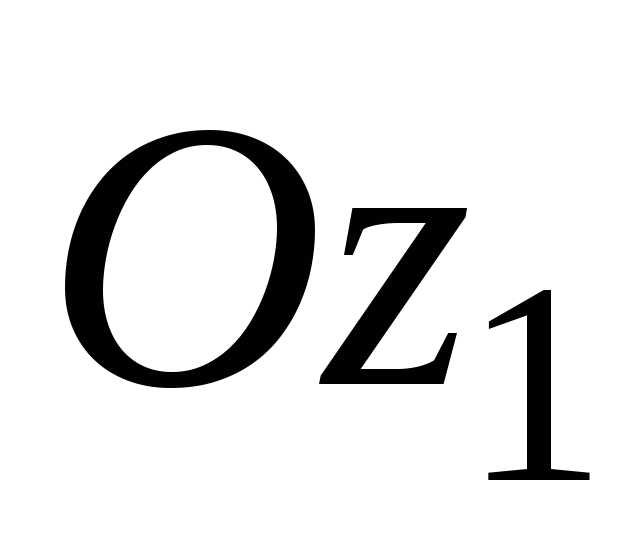 и
и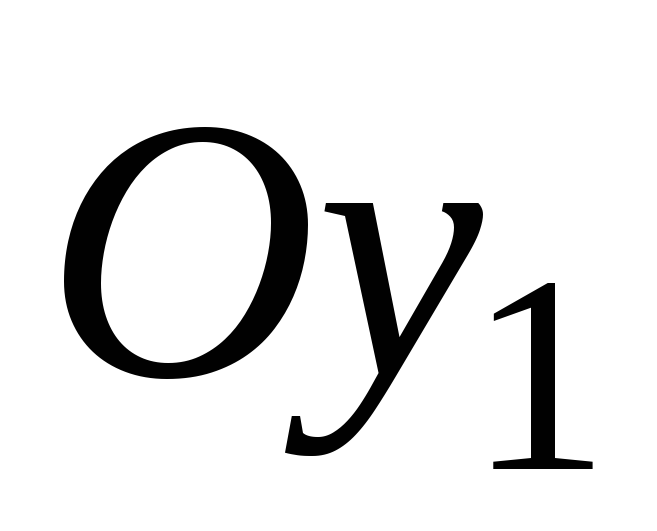 проведены на расстояниях
проведены на расстояниях и
и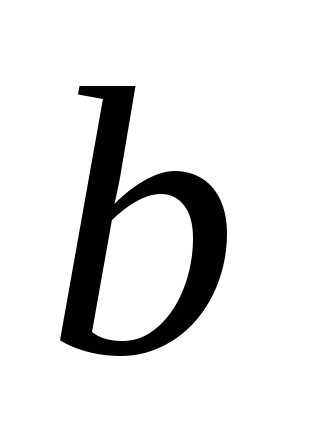 соответственно от осей
соответственно от осей и
и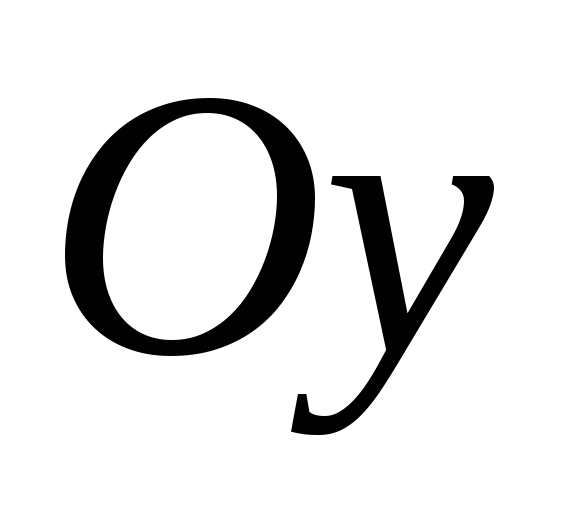 .
.
Воспользуемся
выражениями для осевых моментов инерции
(4.4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат  и
и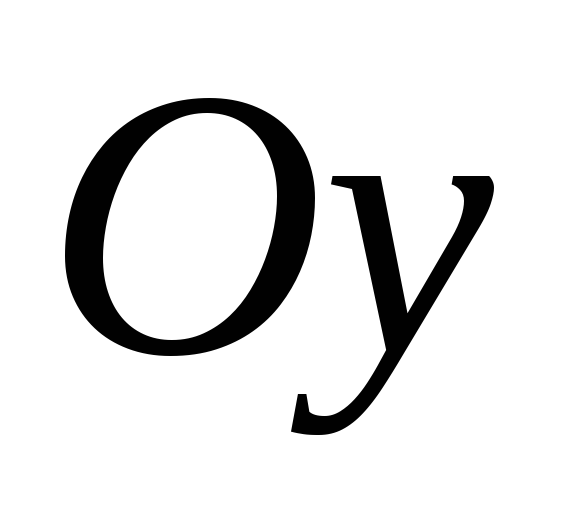 элемента с бесконечно малой площадью
координаты
элемента с бесконечно малой площадью
координаты и
и в новой системе координат. Получим:
в новой системе координат. Получим:
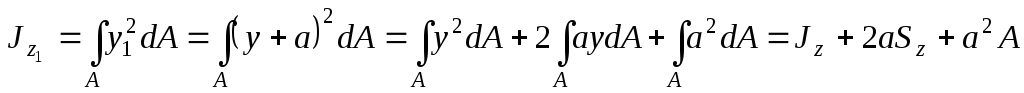 .
(4.18)
.
(4.18)
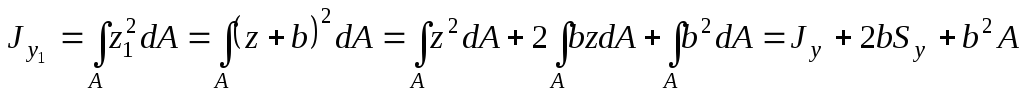 .
(4.19)
.
(4.19)
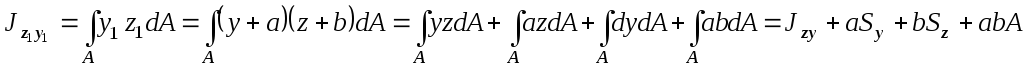 .
.
(4.20)
Анализируя полученные выражения, приходим к выводу, что при вычислении моментов инерции относительно параллельных осей к моментам инерции, вычисленных относительно исходных осей инерции, следует призводить добавки в виде дополнительных членов, которые могут оказаться намного больше значений для моментов инерции относительно исходных осей. Поэтому пренебрегать этими дополнительными членами ни в коем случае нельзя.
Рассмотренный случай представляет собой самый общий случай параллельного переноса осей, когда в качестве исходных были взяты произвольные оси инерции. В большинстве расчетов встречаются частные случаи определения моментов инерции.
Первый частный случай. Исходные оси являются центральными осями инерции фигуры. Тогда, используя основное свойство для статического момента площади, можно исключить из уравнений (4.18)(4.20) члены уравнений, в которые входит статический момент площади фигуры. В результате получим:
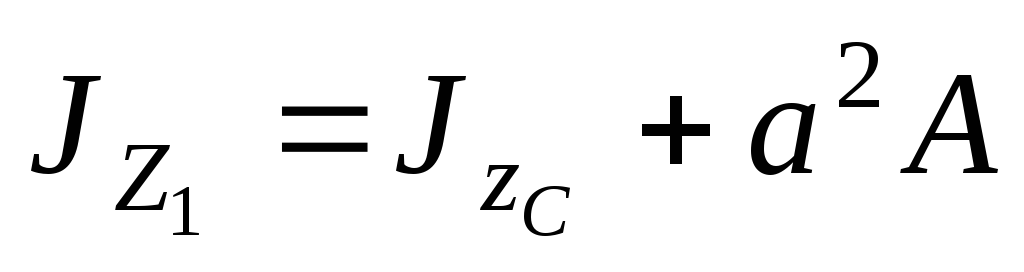 .
(4.21)
.
(4.21)
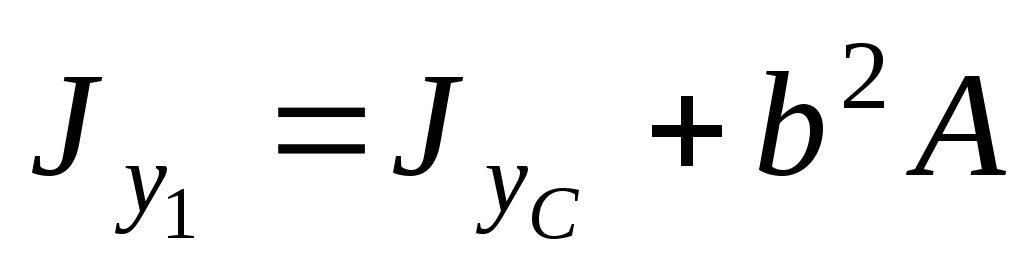 .
(4.22)
.
(4.22)
 .
(4.23)
.
(4.23)
Здесь оси 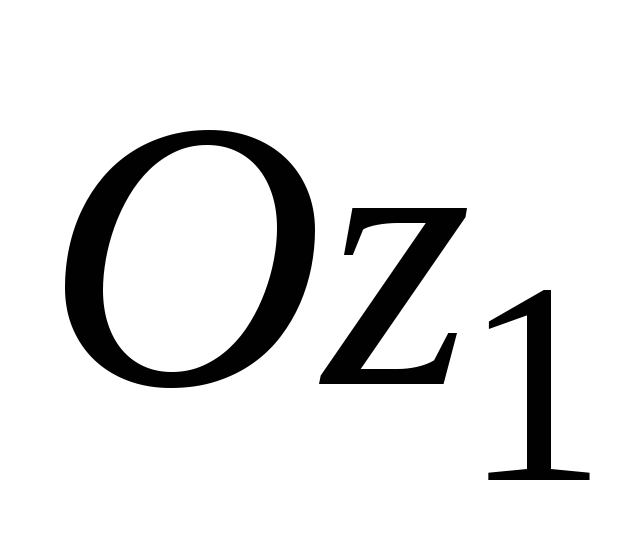 и
и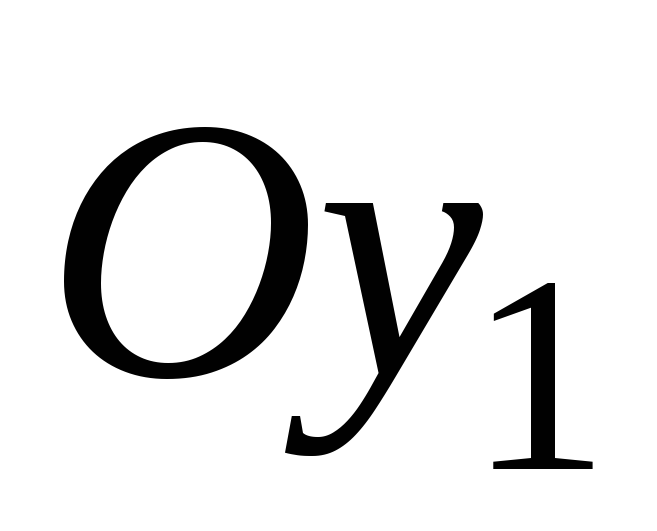 центральные оси
инерции.
центральные оси
инерции.
Второй частный случай. Исходные оси являются главными осями инерции. Тогда, учитывая, что относительно главных осей инерции центробежный момент инерции равен нулю, получим:
 .
(4.24)
.
(4.24)
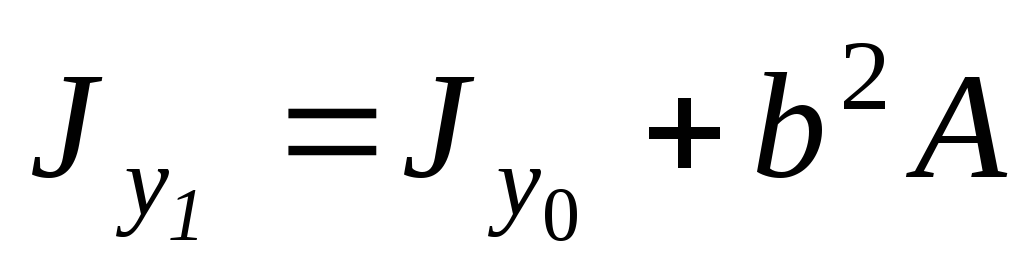 .
(4.25)
.
(4.25)
 .
(4.26)
.
(4.26)
Здесь оси  и
и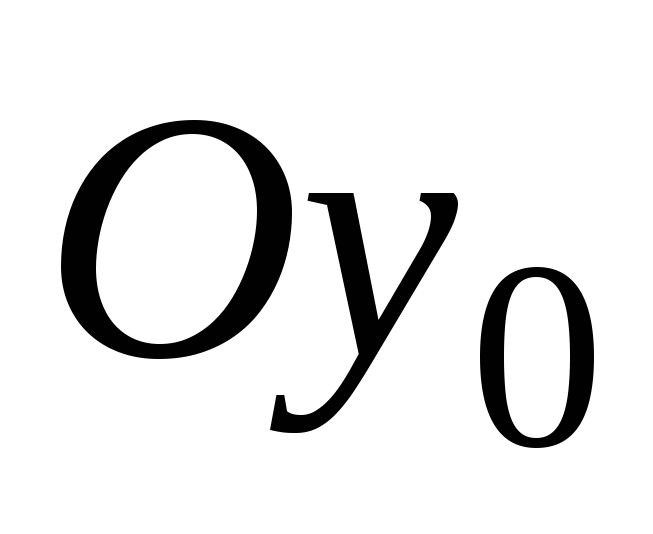 главные оси инерции.
главные оси инерции.
Воспользуемся полученными выражениями и рассмотрим несколько примеров вычисления моментов инерции для плоских фигур.
Пример 4.2.Определить осевые моменты
инерции фигуры, приведенной на рис.
4.10, относительно центральных осей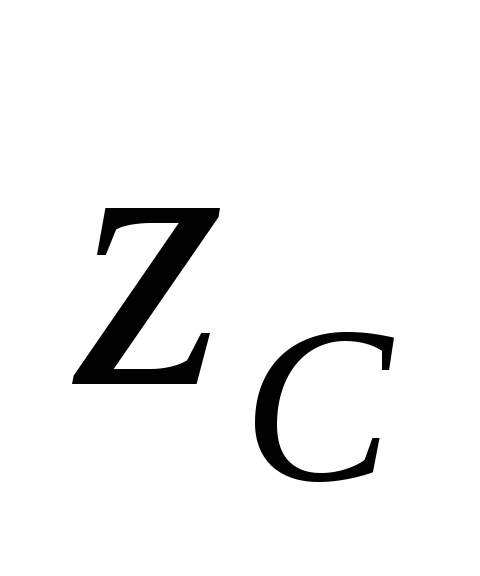 и
и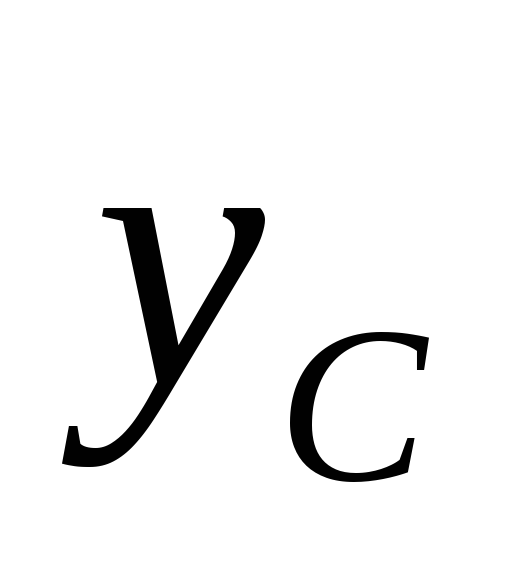 .
.
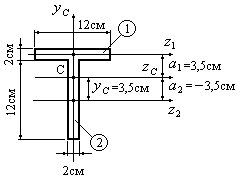
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной
на рис.4.10 фигуры было определено положение
центра тяжести С. Координата центра
тяжести откладывалась от оси 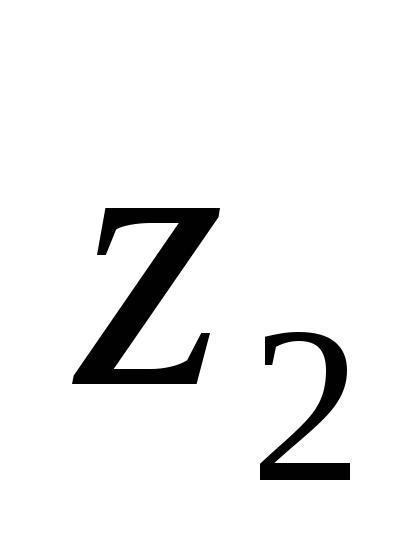 и составила
и составила .
Вычислим расстояния
.
Вычислим расстояния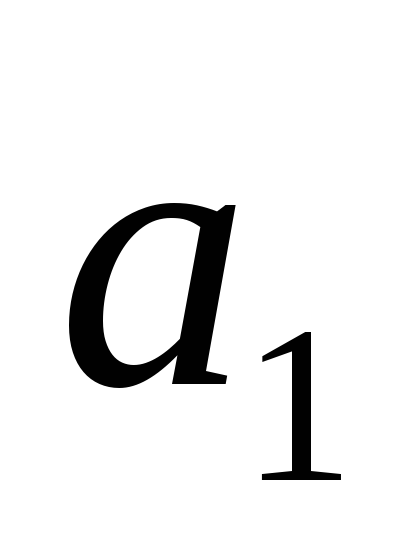 и
и между осями
между осями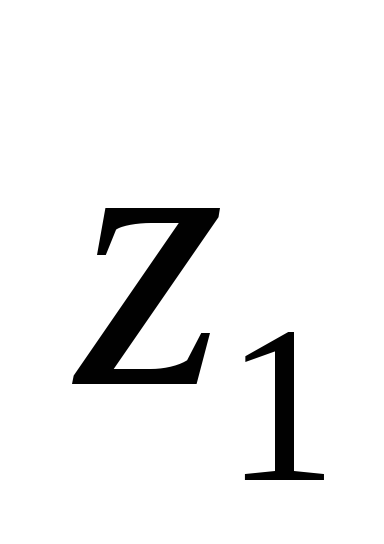 и
и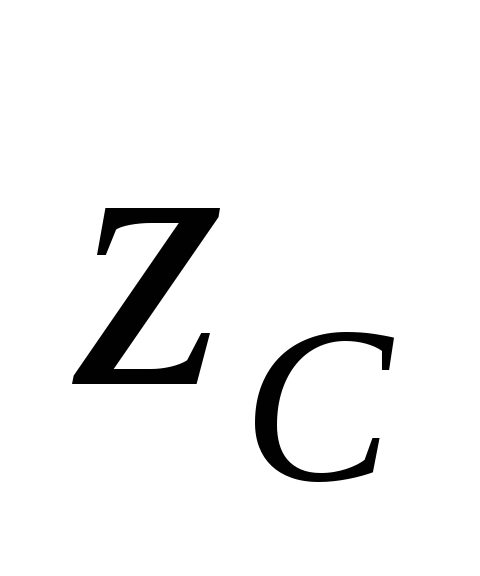 и осями
и осями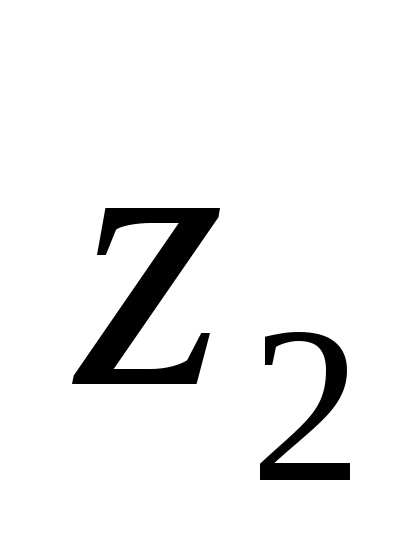 и
и .
Эти расстояния составили соответственно
.
Эти расстояния составили соответственно и
и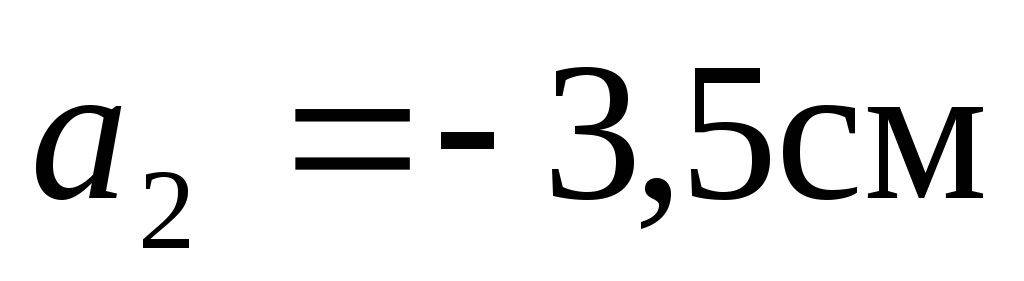 .
Так как исходные оси
.
Так как исходные оси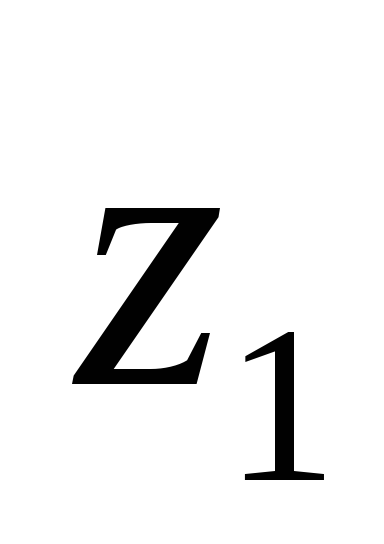 и
и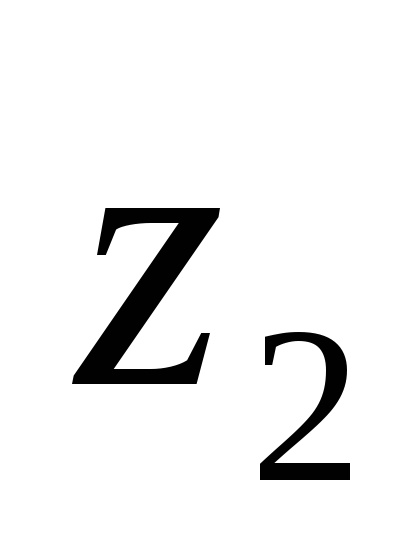 являются центральными осями для простых
фигур в виде прямоугольников, для
определения момента инерции фигуры
относительно оси
являются центральными осями для простых
фигур в виде прямоугольников, для
определения момента инерции фигуры
относительно оси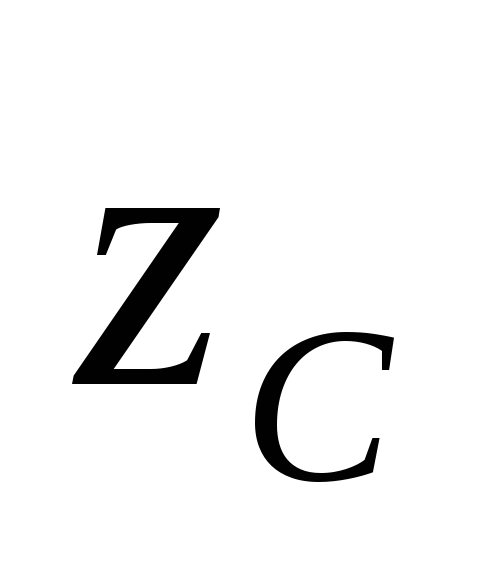 воспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).
воспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).
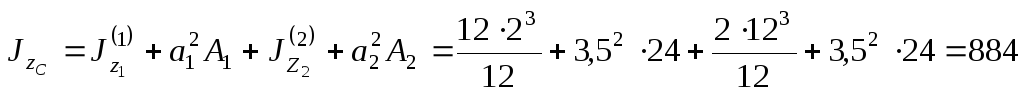 см4.
см4.
Момент инерции относительно оси 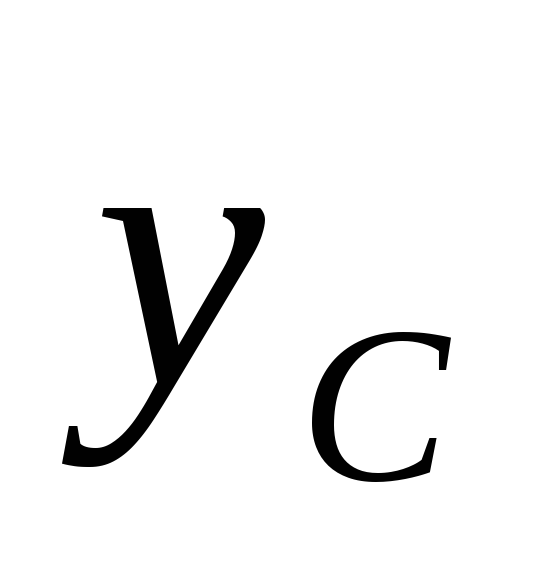 получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как ось
получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как ось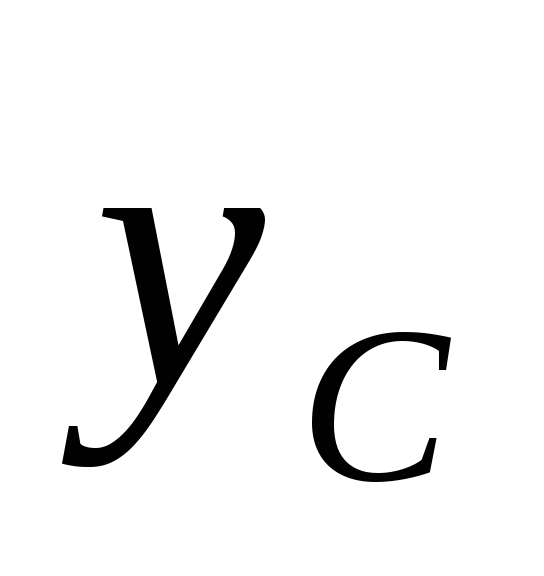 является общей центральной осью для
простых фигур и для всей фигуры.
является общей центральной осью для
простых фигур и для всей фигуры.
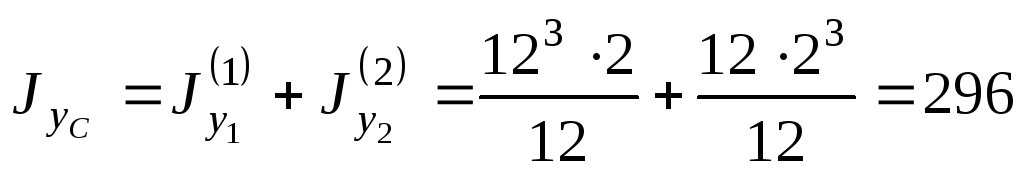 см4.
см4.
Центробежный момент инерции относительно
осей 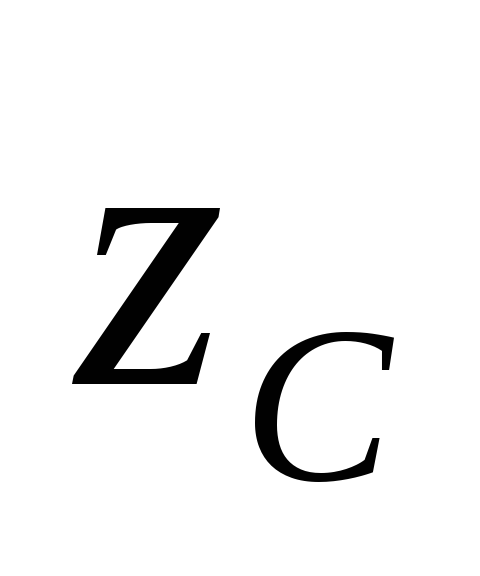 и
и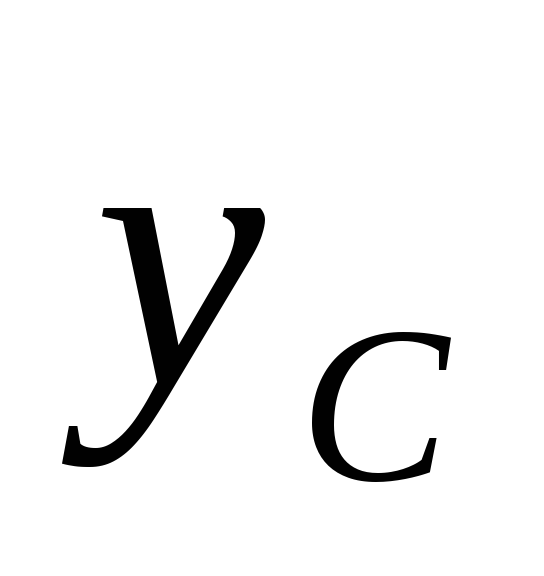 равен нулю, так как ось инерции
равен нулю, так как ось инерции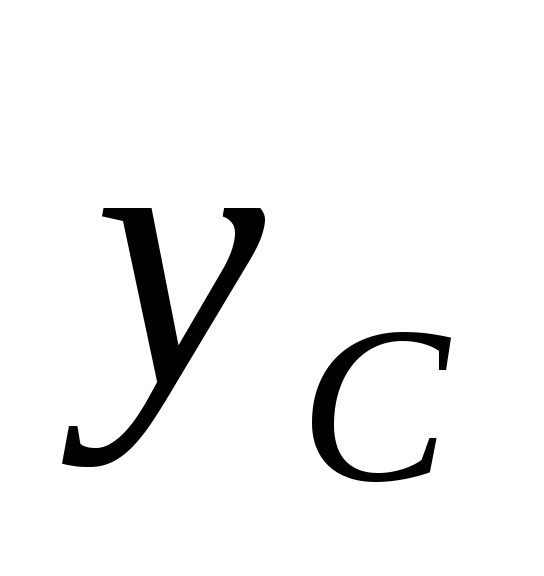 является главной осью (осью симметрии
фигуры).
является главной осью (осью симметрии
фигуры).
Пример
4.3. Чему равен
размер b (в см) фигуры,
изображенной на рис. 4.11, если момент
инерции фигуры относительно оси 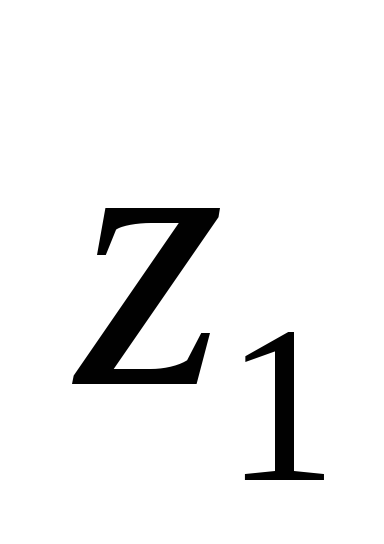 равен 1000 см4?
равен 1000 см4?
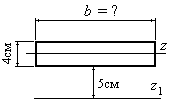
Рис.4.11
Решение:
Выразим момент инерции относительно
оси 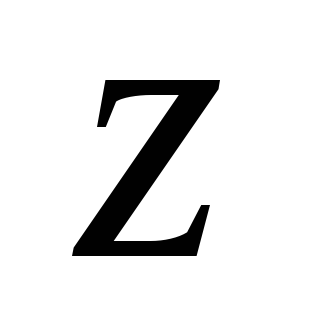 через неизвестный размер сечения
через неизвестный размер сечения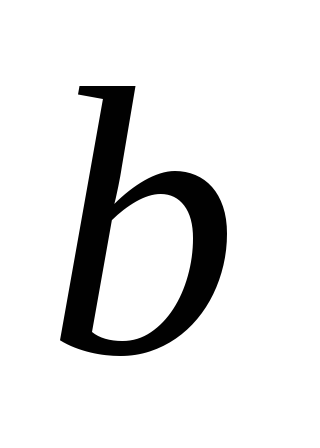 ,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осями
,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осями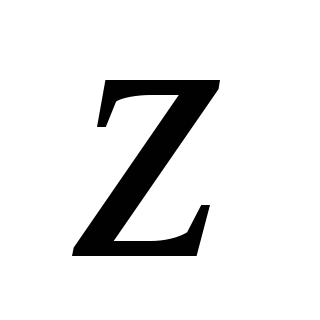 и
и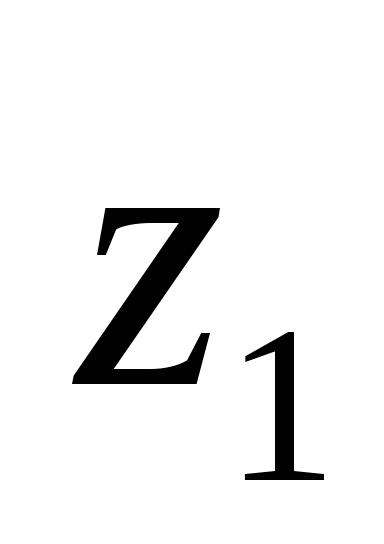 равно 7см:
равно 7см:
 см4.
(а)
см4.
(а)
Решая выражение (а) относительно размера
сечения  ,
получим:
,
получим:
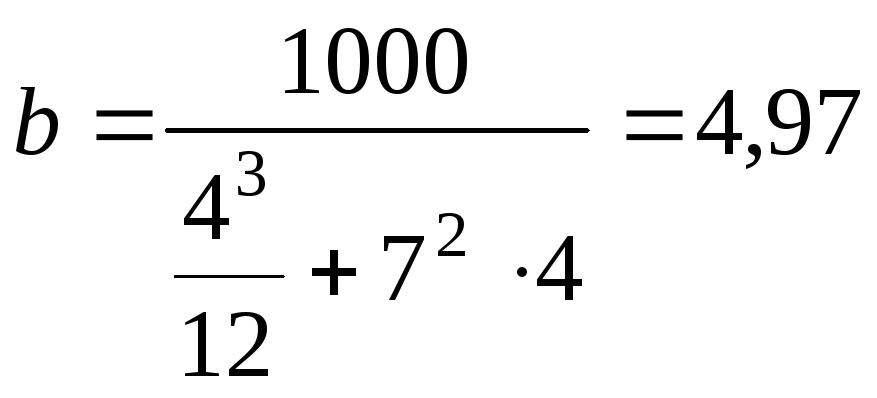 см.
см.
Пример.4.4. Какая из фигур, изображенных на рис.4.12
, имеет больший момент инерции относительно
оси 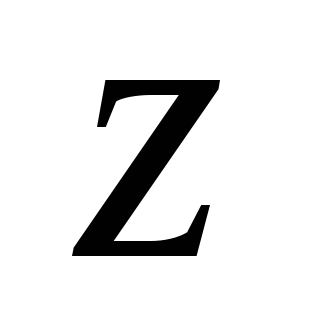 ,
если обе фигуры имеют одинаковую площадь
,
если обе фигуры имеют одинаковую площадь см2?
см2?

Рис.4.12
Решение:
1. Выразим площади фигур через их размеры и определим:
а) диаметр сечения для круглого сечения:
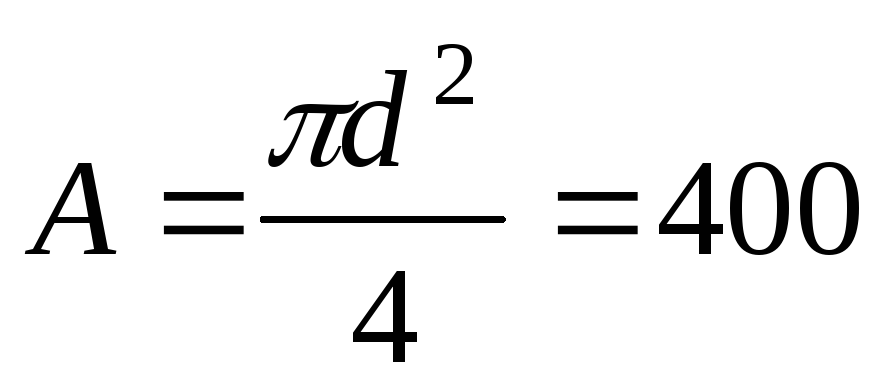 см2; Откуда
см2; Откуда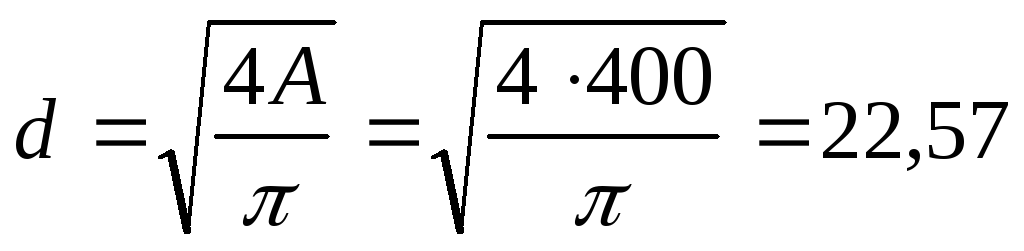 см.
см.
б) размер стороны квадрата:
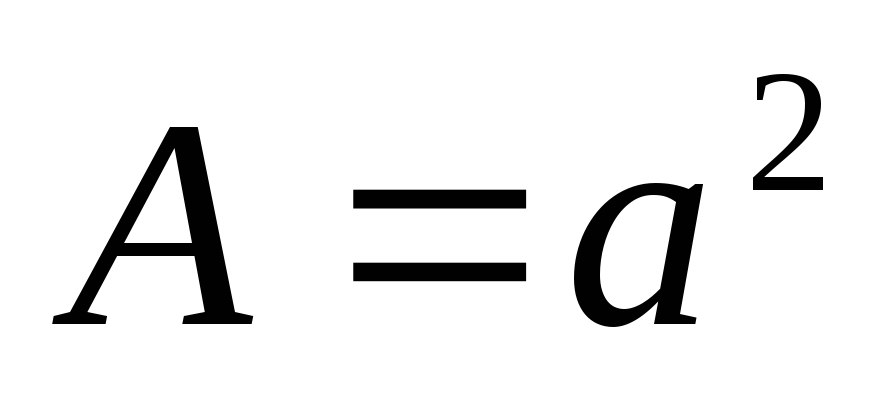 ;
Откуда
;
Откуда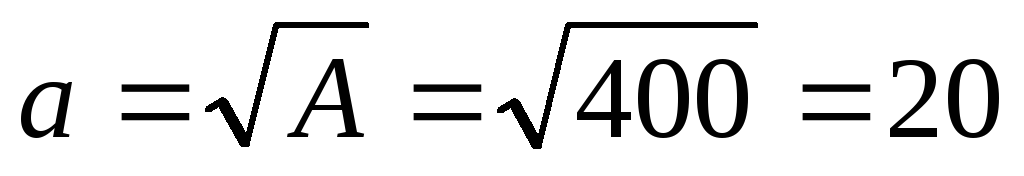 см.
см.
2. Вычисляем момент инерции для круглого сечения:
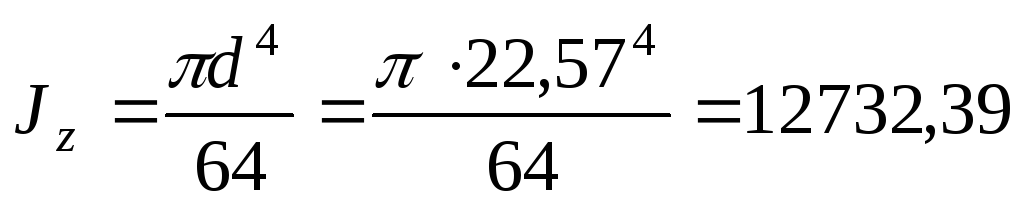 см4.
см4.
3. Вычисляем момент инерции для сечения квадратной формы:
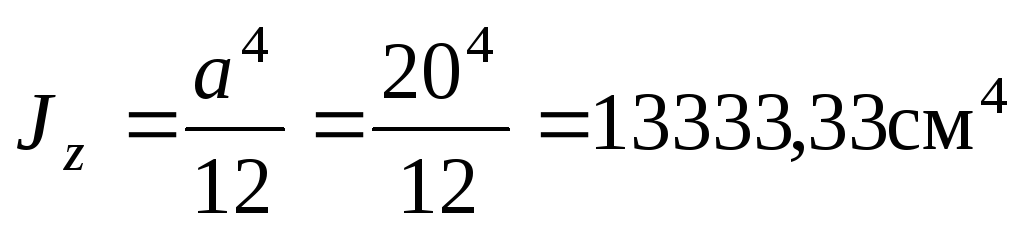 см4.
см4.
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 4.5.Определить полярный момент
инерции (в см4) сечения прямоугольной
формы относительно его центра тяжести,
если ширина сечения 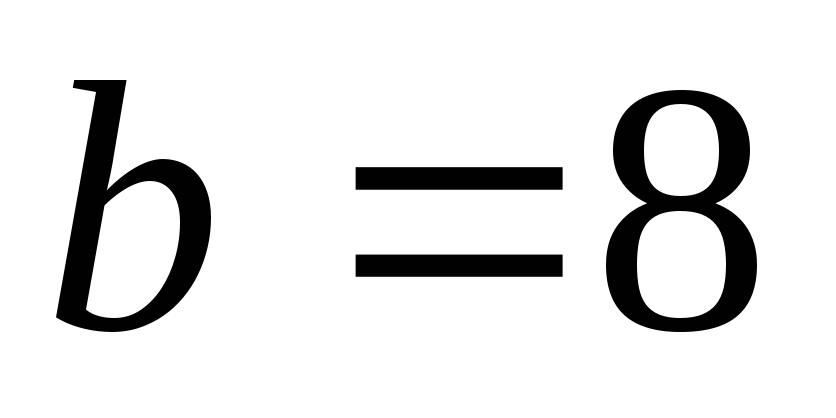 см,
высота сечениясм.
см,
высота сечениясм.
Решение:
1. Найдем моменты инерции сечения
относительно горизонтальной 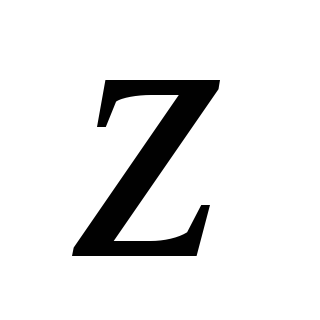 и вертикальной
и вертикальной центральных осей инерции:
центральных осей инерции:
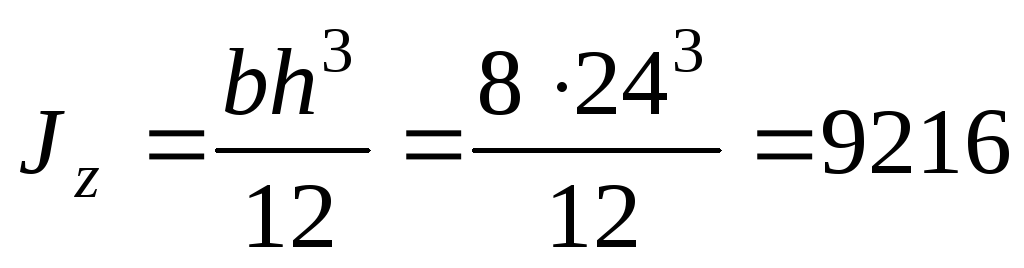 см4;
см4;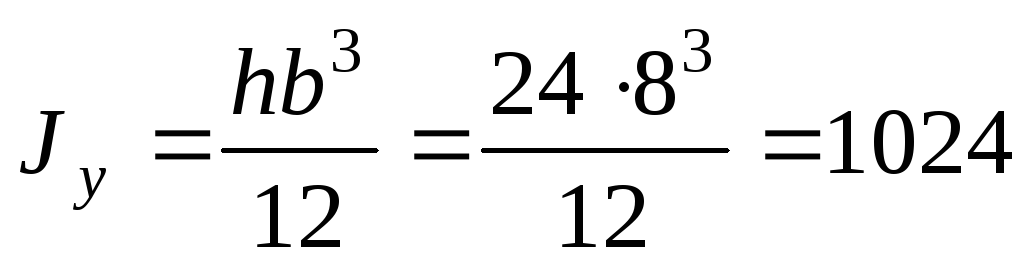 см4.
см4.
2. Определяем полярный момент инерции сечения как сумму осевых моментов инерции:
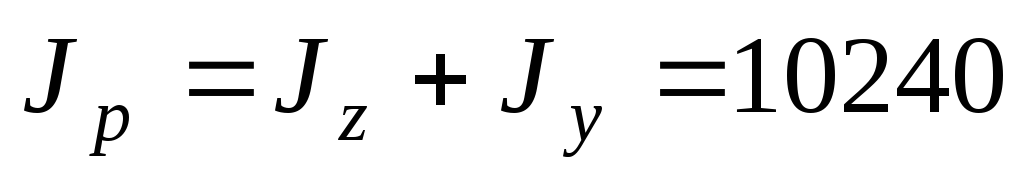 см4.
см4.
Пример
4.6. Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси 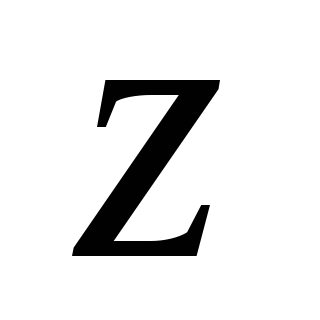 ,
если момент инерции фигуры относительно
оси
,
если момент инерции фигуры относительно
оси равен 2400 см4.
равен 2400 см4.
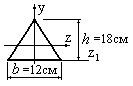
Рис.4.13
Решение:
Момент инерции сечения треугольной
формы относительно главной оси инерции 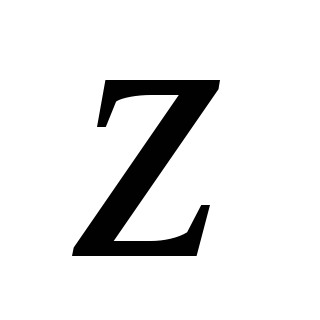 будет меньше по сравнению с моментом
инерции относительно оси
будет меньше по сравнению с моментом
инерции относительно оси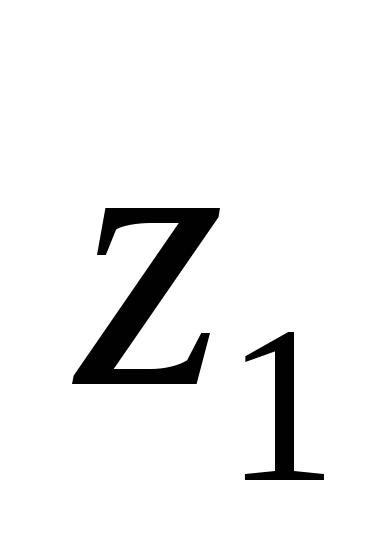 на величину
на величину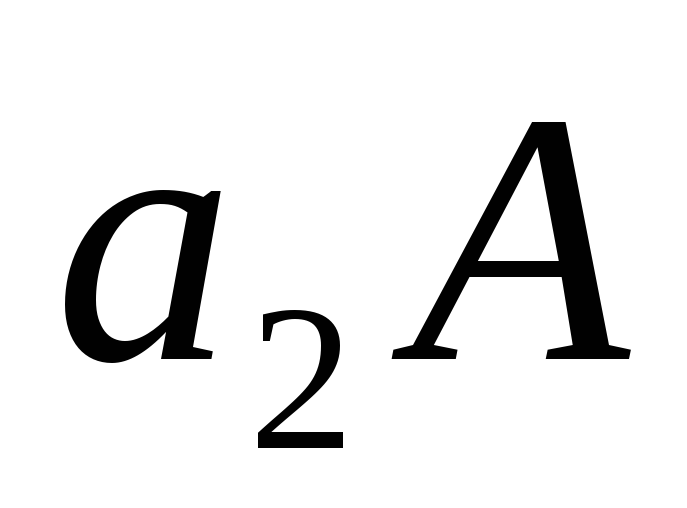 .
Поэтому при
.
Поэтому при см
момент инерции сечения относительно
оси
см
момент инерции сечения относительно
оси найдем следующим образом:
найдем следующим образом:
 см4.
см4.

