Закон всемирного тяготения – формула, определение, кто открыл

4.1

Средняя оценка: 4.1

Всего получено оценок: 433.

4.1

Средняя оценка: 4.1

Всего получено оценок: 433.

Закон всемирного тяготения был открыт еще в XVII веке и дал колоссальное развитие для физики того времени. Так кто открыл этот закон, и почему он так важен для науки?

Определение закона всемирного тяготения

Датский астроном Тихо Браге, долгие годы наблюдавший за движением планет, накопил огромное количество интересных данных, но не сумел их обработать. Зато это смог сделать его ученик Иоганн Кеплер. Используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, Кеплер установил законы движения планет вокруг Солнца. Однако и он не смог объяснить динамику этого движения, то есть почему планеты движутся именно по таким законам.

И вот тогда настало время Исаака Ньютона, уже открывшего три основных закона динамики. Ньютон предположил, что ряд явлений, казалось бы не имеющих между собой ничего общего, вызваны одной причиной – силами тяготения.

2}$ не зависит от массы тела. И это представляется возможным только в том случае, если сила, с которой Земля притягивает тело, изменяется пропорционально массе тела.

По третьему закону Ньютона силы, с которыми взаимодействуют тела, равны по модулю. Если сила, действующая на одно тело, пропорциональна массе этого тела, то равная ей сила, действующая на второе тело, очевидно, пропорциональна массе второго тела.

Но силы, действующие на оба тела, равны, следовательно они пропорциональны массе как первого, так и второго тела.

Исаак Ньютон открыл этот закон в возрасте 23 лет, но на протяжении девяти лет не опубликовал его, так как имевшиеся тогда неверные данные о расстоянии между Землей и Луной не подтверждали его идею. Лишь в 1667 году, после уточнения этого расстояния, закон всемирного тяготения был наконец отдан в печать.

Вот формулировка и определение закона всемирного тяготения: все тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Эту силу называют силой тяготения.

Рис. 2. Формула закона всемирного тяготения.

Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет большую массу (планета, звезда).

Рис. 3. Планеты солнечной системы.

Из этого закона следует еще один существенный признак массы: масса отражает свойство тела притягиваться к другим телам и определяет силу этого притяжения.

Применение закона всемирного тяготения

Как и любые другие законы, закон всемирного тяготения имеет определенные границы применимости. Он справедлив для:

• материальных точек;
• тел, имеющих форму шара;
• шара большого радиуса, взаимодействующего с телами, размеры которых много меньше размеров шара.

Закон неприменим, например, для взаимодействия бесконечного стержня и шара. В этом случае сила тяготения обратно пропорциональна только расстоянию, а не квадрату расстояния. А, скажем, сила притяжения между телом и бесконечной плоскостью вообще не зависит от расстояния.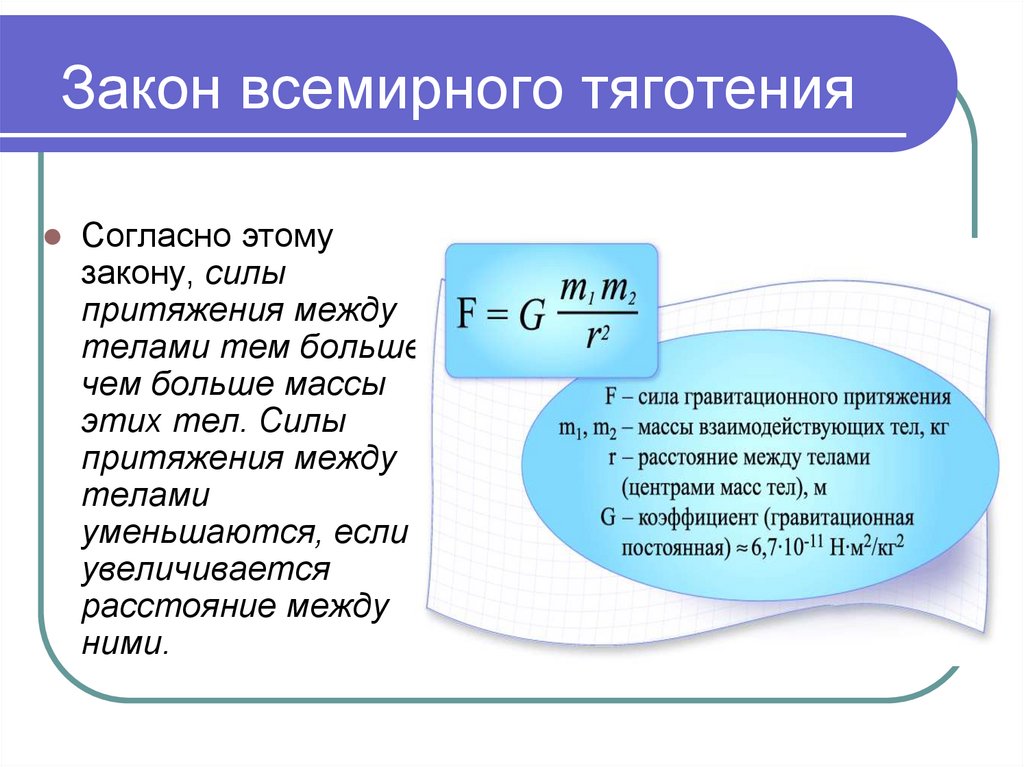

Что мы узнали?

В 9 классе очень важной является тема всемирного тяготения. В этой статье кратко рассказывается про открытие и применение этого закона, а также об ученых, которые внесли свой вклад для развития этого закона.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.1

Средняя оценка: 4.1

Всего получено оценок: 433.

---

А какая ваша оценка?

Всемирное тяготение

Всемирное тяготение

§6. Всемирное тяготение

Закон всемирного тяготения гласит: две материальные точки притягивают друг друга с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними. При этом силы определяют относительно центра масс системы этих точек. Они равны по величине и направлены по одной прямой навстречу друг другу (см. рис.61, на котором m₁ и m₂ — массы точек, относительные величины и направления сил указаны стрелками).

Рис.61.

При увеличении расстояния в два раза силы уменьшаются в четыре раза.

Математическая запись закона имеет вид:

где G — гравитационная постоянная, r — радиус-вектор с началом в первой точке и концом во второй, F₁ и F₂ векторы сил.

В случае материальных точек, о которых говорилось в формулировке закона, размеры тел пренебрежимо малы в сравнении с расстоянием между ними. Как доказал Ньютон, шары, расстояние между центрами которых больше суммы их радиусов, притягиваются точно так же, как и материальные точки тех же масс, помещённые в центры шаров. При этом предполагается, что либо шары однородны, либо плотность вещества внутри них зависит только от расстояния от центра.

Это замечательное свойство шаров позволяет, например, довольно точно вычислить силу, с которой шарообразная Земля притягивает человека массы на её поверхности. Ввиду того, что размеры человека пренебрежимо малы в сравнении с радиусом планеты, его можно рассматривать как материальную точку. С другой стороны, огромная Земля, притягивая человека, ведёт себя, как материальная точка той же массы и помещённая в центр Земли. Поэтому искомая сила равна

где m_Е и R_Е масса и средний радиус Земли, а

g — ускорение свободного падения, равное 9,8 м/с² (вращение Земли вокруг оси здесь не учитывалось). Учёт некоторой сплюснутости Земли у полюсов и центробежной силы инерции, вызванных вращением Земли, приводит к приближённой формуле:

где f — географическая широта пункта. Отсюда следует, что на полюсах вес человека (не гравитационная сила, действующая на него) увеличивается по сравнению с экватором в 1,0053 раза (на 0,53 %).

Приливообразующим ускорением называют разность ускорений к Луне (Солнцу) данной точки Земли и её центра. Например, в случае Луны справедлива формула:

где g’ — приливообразующее ускорение, m и r — масса Луны и расстояние до неё от центра Земли, причём величина g’ определяется здесь для точек А и В, показанных на рис.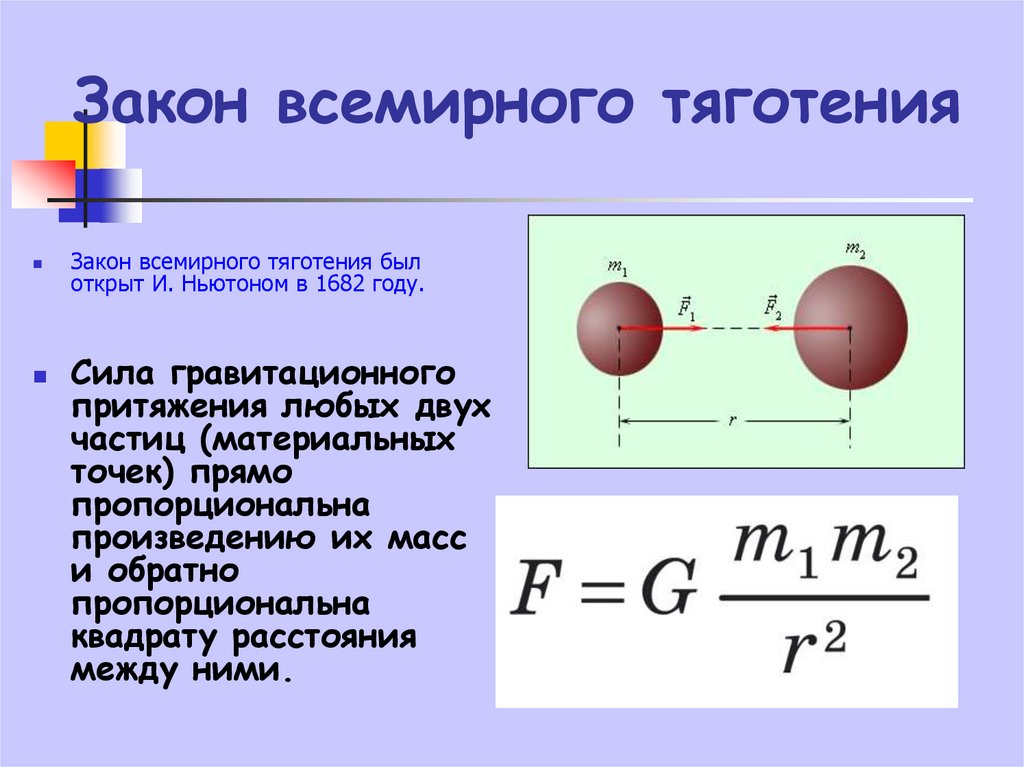

48. Ввиду того, что точка В отстоит от Луны дальше, чем центр Земли, и лунная гравитация там слабее, чем в точке О, приливообразующее ускорение здесь направлено прочь от Луны. Величина его почти такая же, как и в точке А.

Ньютон и гравитация: универсальный закон всемирного тяготения

Закон Ньютона

Качественно закон всемирного тяготения Ньютона утверждает, что:

Каждая массивная частица притягивает любую другую массивную частицу с сила прямо пропорциональна произведению их масс на обратно пропорциональна квадрату расстояния между ними

В векторной записи, если это позиция вектор массы м ₁ и является вектором положения масса м ₂ , то сила на м ₁ за счет м ₂ определяется по формуле:

Разность двух векторов в числителе дает направление силы. Появление куба вместо квадрата в знаменатель для того, чтобы отменить этот определяющий направление фактор | — | в числителе.

Рисунок %: Направление силы – это разность векторов положения.

Эта сила обладает некоторыми замечательными свойствами. Во-первых, отметим, что это действует на расстояние , означает, что независимо от любого промежуточного вопроса, каждый частица во Вселенной оказывает гравитационное воздействие на любую другую частицу. Более того, гравитация подчиняется принципу суперпозиции. Это означает, что для нахождения гравитационной силы на любую частицу надо только найти векторную сумму всех сил от всех частиц в системе. Например, сила Земли на Луне находится векторной суммой всех сил между всеми частиц Луны и Земли. Это звучит как огромная задача, но на самом деле упрощает расчет.

Гравитация как центральная сила

Универсальный закон всемирного тяготения Ньютона создает центральную силу. Сила находится в радиальном направлении и зависит только от расстояния между объектами. Если одна из масс находится в начале координат, тогда () = F ( r ). Который то есть сила является функцией расстояния между частицами и полностью в направлении . Очевидно, сила также зависит от G и массы, но они просто постоянны — единственная координата, по которой сила зависит от радиальной.

Легко показать, что когда частица находится в центре силы, угловая импульс сохраняется, а движение происходит в самолете. Сначала рассмотрим угловой момент:

= (×) = × + × = ×( м ) + × = 0

Последнее равенство следует из того, что векторное произведение с самим собой равно нулю, а так как полностью в направлении векторного произведения этих двух векторов также равно нулю. С угловой момент не меняется со временем, он сохраняется. Это по существу более общее выражение второго закона Кеплера, которое мы видели (здесь), также утверждало сохранение угловых импульс.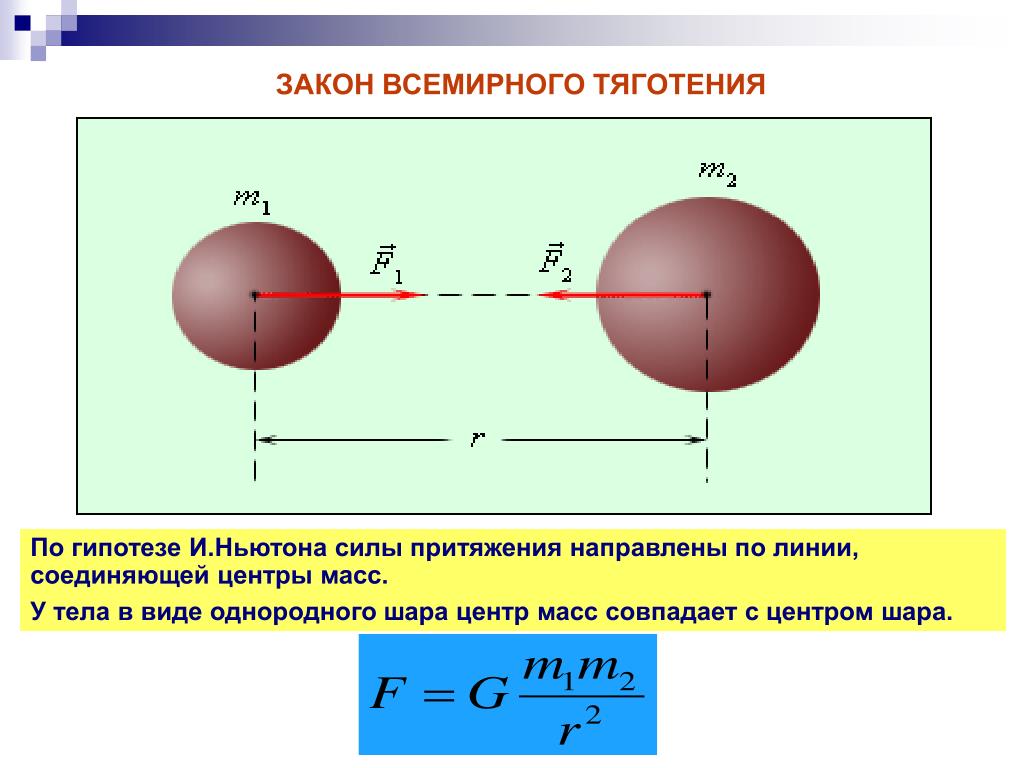

В некоторый момент времени t ₀ у нас есть вектор положения и вектор скорости движения, которые определяют плоскость P с нормальный задается = ×. В предыдущем доказательстве мы показали, что × не меняется во времени. Это означает, что = × также не меняется во времени. Следовательно, × = для всех t . Поскольку должен быть ортогонален , он всегда должен лежать в самолете P .

Универсальный закон всемирного тяготения

Ключевые понятия

• Сила гравитации
• Закон всемирного тяготения
• Значение всемирного закона тяготения

Напомним: 

• Все тела на Земле, вращаясь вокруг Земли и падая на Землю, находятся под действием гравитационной силы, создаваемой земным притяжением.
• Гравитационная сила является силой притяжения.
• Второй закон Ньютона: ускорение, создаваемое определенной силой, обратно пропорционально массе тела.
• Третий закон движения Ньютона: Каждое действие имеет равное и противоположное противодействие.

Введение:  

Обычно мы видим, как предметы падают на Землю. Такие движения вызваны гравитационным притяжением Земли к этим объектам. Однако 3-й закон движения Ньютона гласит: «Каждое действие имеет равное и противоположное противодействие». Это означает, что гравитационное притяжение, которое Земля оказывает на падающие тела, также должно иметь силу противодействия. Говорят, что эта сила реакции равна по величине и противоположна по направлению гравитационному притяжению Земли. Сила реакции есть не что иное, как другая гравитационная сила, которую падающее тело оказывает на землю. Удивительно, но эта сила реакции точно равна по величине гравитационному притяжению, которое Земля оказывает на падающее тело и действует в противоположном ему направлении. Сказав это, может возникнуть естественный вопрос, то есть, почему Земля не движется к телу, несмотря на то, что объект подвергается равному гравитационному притяжению.

Объяснение:  

Ответ на поставленный выше вопрос лежит во втором законе движения Ньютона. В нем говорится, что ускорение, создаваемое определенной силой, обратно пропорционально массе тела.

Математически,                           a α 1/м  

Если манго падает на Землю, на него действует сила, равная по величине и противоположная по направлению силе притяжения Земли, как показано на рис. 2.1 ниже. Манго движется к Земле. Однако кажется, что Земля не движется к манго, хотя и находится под действием силы того же размера. Это связано с пренебрежимо малой массой манго по сравнению с массой Земли. А согласно второму закону Ньютона ускорение, приобретаемое телом при приложении определенной силы, обратно пропорционально его массе.

Mathematically,                            m _mango <<<  m _earth  

     a _mango >>>  a _earth  

The mango, being пренебрежимо малой массы, получает значительное ускорение, чтобы двигаться к Земле. Однако сила того же размера создает чрезвычайно малое ускорение для движения Земли. Таким образом, Земля также перемещает к манго из-за гравитационного притяжения манго на Земле. Однако ускорение Земли по направлению к манго пренебрежимо мало и, следовательно, не очевидно .

По той же причине кажется, что Земля не приближается ни к одному падающему объекту, включая Луну.

Итак, если существует сила, с которой манго действует на Землю, должна существовать какая-то сила притяжения между любыми двумя объектами. На самом деле это правда. Подобная сила притяжения существует между любыми двумя объектами в этой вселенной. Это было предложено сэр Исаак Ньютон в год 1687 как универсальный закон всемирного тяготения.

Универсальный закон всемирного тяготения  

Этот закон позволяет измерить количество гравитационной силы притяжения между любыми двумя объектами в этой вселенной, используя факторы, от которых зависит эта сила.

В нем говорится: « Каждый объект во вселенной притягивает любой другой объект с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. ” 

Эта сила представляет собой бесконтактную и притягивающую гравитационную силу. Гравитационная сила измеряется в подразделении Si ‘ Newton ‘ Сокращена как N . ₂ , разделенные расстоянием r . Сила F между двумя объектами определяется выражением

F α m ₁

×

m ₂  

F α 1/r ²  

On combining the above equations, we get , 

F α m ₁

××

m ₂ / r ²  

F = G (m ₁ m ₂ /r ² )  

where G (Universal gravitational constant) = 6.