Как найти работу в физике все формулы. Механическая работа

Прежде чем раскрывать тему «В чём измеряется работа», необходимо сделать небольшое отступление. Всё в этом мире подчиняется законам физики. Каждый процесс или явление можно объяснить на основе тех или иных законов физики. Для каждой измеряемой величины существует единица, в которой её принято измерять. Единицы измерения являются неизменными и имеют единое значение во всём мире.

Причиной этого является следующее. В тысяча девятьсот шестидесятом году на одиннадцатой генеральной конференции по мерам и весам была принята система измерений, которая признана во всём мире. Эта система получила наименование Le Système International d’Unités, SI (СИ система интернационал). Эта система стала базовой для определений принятых во всём мире единиц измерения и их соотношения.

Физические термины и терминология

В физике единица измерения работы силы называется Дж (Джоуль), в честь английского учёного физика Джеймса Джоуля, сделавшего большой вклад в развитие раздела термодинамики в физике. Один Джоуль равен работе, совершаемой силой в один Н (Ньютон), при перемещении её приложения на один М (метр) в направлении действия силы. Один Н (Ньютон) равен силе, массой в один кг (килограмм), при ускорении в один м/с2 (метр в секунду) в направлении силы.

К сведению. В физике всё взаимосвязано, выполнение любой работы связано с выполнением дополнительных действий. В качестве примера можно взять бытовой вентилятор. При включении вентилятора в сеть лопасти вентилятора начинают вращаться. Вращающиеся лопасти воздействуют на поток воздуха, придавая ему направленное движение. Это является результатом работы. Но для выполнения работы необходимо воздействие других сторонних сил, без которых выполнение действия невозможно. К ним относятся сила электрического тока, мощность, напряжение и многие другие взаимосвязанные значения.

Электрический ток, по своей сути, – это упорядоченное движение электронов в проводнике в единицу времени. В основе электрического тока лежит положительно или отрицательно заряжённые частицы.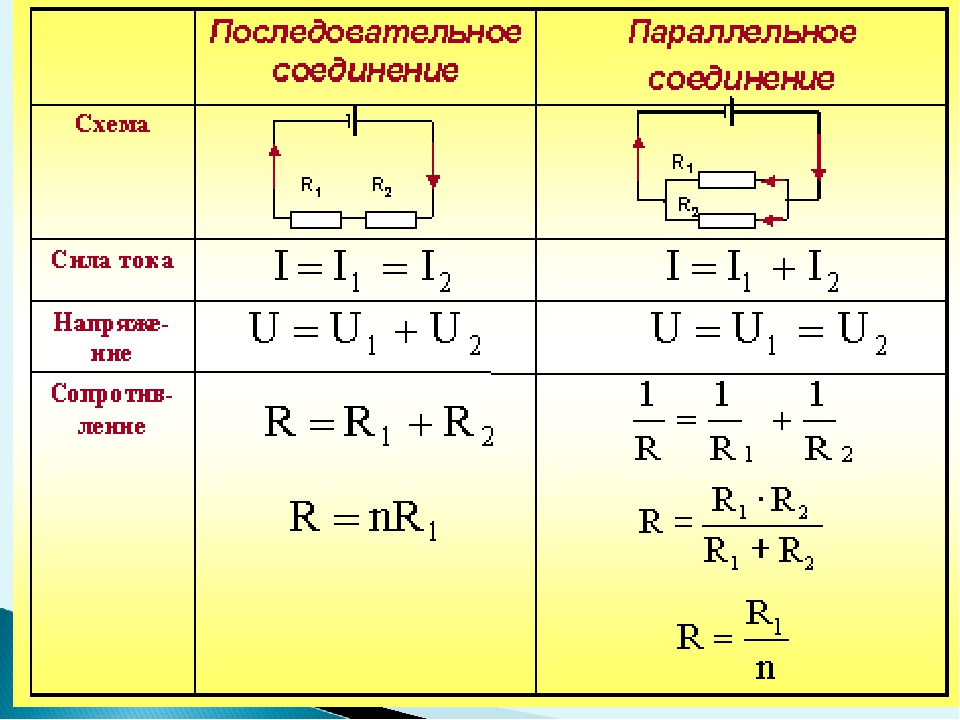 Они носят название электрических зарядов. Обозначается буквами C, q, Кл (Кулон), названо в честь французского учёного и изобретателя Шарля Кулона. В системе СИ является единицей измерения количества заряженных электронов. 1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.

Сила электрического тока обозначается буквой А (ампер). Ампер – это единица в физике, характеризующая измерение работы силы, которая затрачивается для перемещения зарядов по проводнику. По своей сути, электрический ток – это упорядоченное движение электронов в проводнике под воздействием электромагнитного поля. Под проводником подразумевается материал или расплав солей (электролит), имеющий небольшую сопротивляемость прохождению электронов. На силу электрического тока влияют две физические величины: напряжение и сопротивление. Они будут рассмотрены ниже.

Сила тока всегда прямо пропорциональна по напряжению и обратно пропорциональна по сопротивлению.

Как было сказано выше, электрический ток – это упорядоченное движение электронов в проводнике. Но есть один нюанс: для их движения нужно определённое воздействие. Это воздействие создаётся путём создания разности потенциалов. Электрический заряд может быть положительным или отрицательным. Положительные заряды всегда стремятся к отрицательным зарядам. Это необходимо для равновесия системы. Разница между количеством положительно и отрицательно заряжённых частиц называется электрическим напряжением.

Мощность – это количество энергии, затрачиваемое на выполнение работы в один Дж (Джоуль) за промежуток времени в одну секунду. Единицей измерения в физике обозначается как Вт (Ватт), в системе СИ W (Watt). Так как рассматривается мощность электрическая, то здесь она является значением затраченной электрической энергии на выполнение определённого действия в промежуток времени.

Лошадь тянет телегу с некоторой силой, обозначим её F тяги. Дедушка, сидящий на телеге, давит на неё с некоторой силой. Обозначим её F давл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что

F тяги совершает работу над телегой, а F давл не совершает работу над телегой.

Итак, работа силы над телом или механическая работа – физическая величина, модуль которой равен произведению силы на путь, пройденный телом вдоль направления действия этой сил ы:

В честь английского учёного Д.Джоуля единица механической работы получила название 1 джоуль (согласно формуле, 1 Дж = 1 Н·м).

Если на рассматриваемое тело действует некоторая сила, значит, на него действует некоторое тело. Поэтому работа силы над телом и работа тела над телом – полные синонимы. Однако, работа первого тела над вторым и работа второго тела над первым – частичные синонимы, поскольку модули этих работ всегда равны, а их знаки всегда противоположны.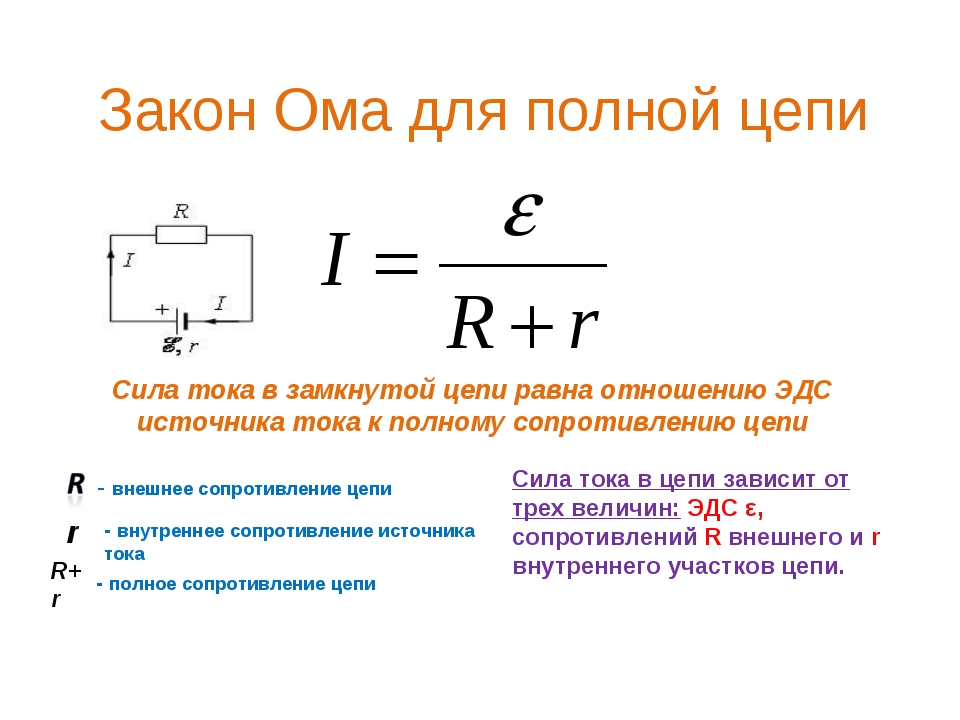

Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.

Числовые значения силы и пути – всегда неотрицательные величины. В отличие от них механическая работа может иметь как положительный, так и отрицательный знаки. Если направление силы совпадает с направлением движения тела, то работу силы считают положительной. Если направление силы противоположно направлению движения тела, работу силы считают отрицательной (берём «–» из «±» формулы). Если направление движения тела перпендикулярно направлению действия силы, то

такая сила работу не совершает, то есть A = 0.

Рассмотрите три иллюстрации по трём аспектам механической работы.

Совершение силой работы может выглядеть по-разному с точек зрения различных наблюдателей. Рассмотрим пример: девочка едет в лифте вверх. Совершает ли она механическую работу? Девочка может совершать работу только над теми телами, на которые действует силой. Такое тело лишь одно – кабина лифта, так как девочка давит на её пол своим весом. Теперь надо выяснить, проходит ли кабина некоторый путь. Рассмотрим два варианта: с неподвижным и движущимся наблюдателем.

Пусть сначала мальчик-наблюдатель сидит на земле. По отношению к нему кабина лифта движется вверх и проходит некоторый путь. Вес девочки направлен в противоположную сторону – вниз, следовательно, девочка совершает над кабиной отрицательную механическую работу: A дев A дев = 0.

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

где A – работа, F – сила, s – пройденный путь.

ПОТЕНЦИА́Л (потенциальная функция), понятие, характеризующее широкий класс физических силовыхполей (электрических, гравитационных и т.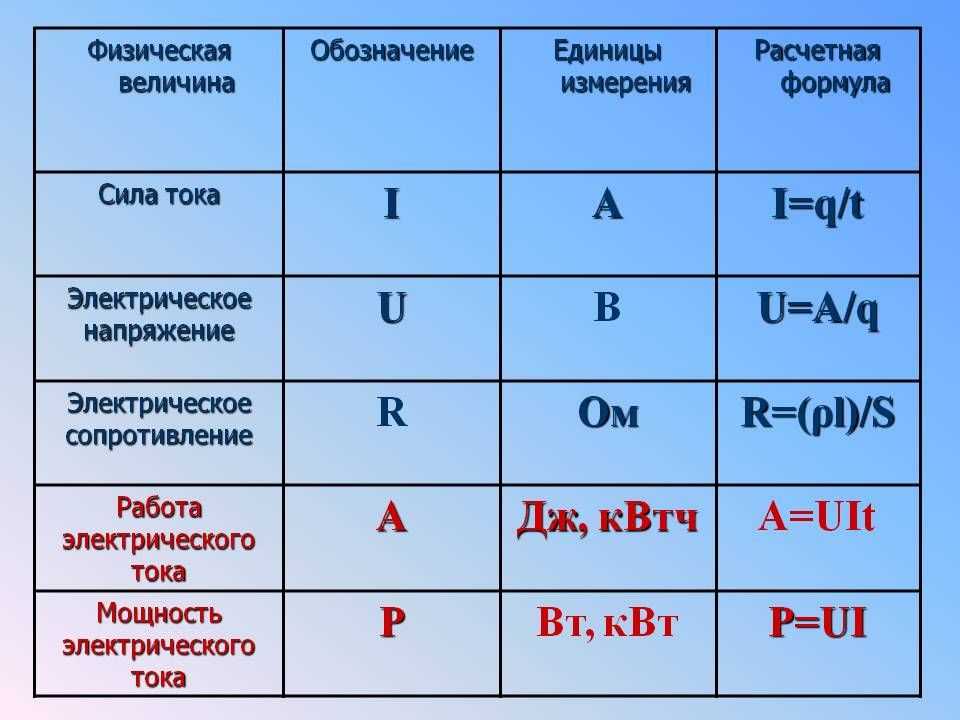 п.) и вообще поля физических величин, представляемыхвекторами (поле скоростей жидкости и т. п.). В общем случае потенциал векторного поля a(x ,y ,z ) — такаяскалярная функция u (x ,y ,z ), что a=grad

35. Проводники в электрическом поле. Электроемкость.

Проводники в электрическом поле. Проводники — это вещества, характеризующиеся наличием в них боль­шого количества свободных носителей зарядов, способ­ных перемещаться под действием электрического поля. К проводникам относятся металлы, электролиты, уголь. В металлах носителями свободных зарядов являются электроны внешних оболочек атомов, которые при взаи­модействии атомов полностью утрачивают связи со «своими» атомами и становятся собственностью всего проводника в целом. Свободные электроны участвуют в тепловом движении подобно молекулам газа и могут перемещаться по металлу в любом направлении. Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками

36. Емкость плоского конденсатора.

Емкость плоского конденсатора.

Т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.

37. Магнитное взаимодействие токов в вакууме. Закон Ампера.

Закон Ампера. В 1820 году Ампер (французский ученый (1775-1836)) установил экспериментально закон, по которому можно рассчитать силу, действующую на элемент проводника длины с током .

где – вектор магнитной индукции,– вектор элемента длины проводника, проведенного в направлении тока.

Модуль силы , где– угол между направлением тока в проводнике и направлением индукции магнитного поля.Для прямолинейного проводника длиной с токомв однородном поле

Направление действующей силы может быть определено с помощью правила левой руки :

Если ладонь левой руки расположить так, чтобы нормальная (к току) составляющая магнитного поля входила в ладонь, а четыре вытянутых пальца направлены вдоль тока, то большой палец укажет направление, в котором действует сила Ампера.

38.Напряженность магнитного поля. Закон Био-Савара-Лапласа Напряжённость магни́тного по́ля (стандартное обозначение Н ) — векторная физическая величина , равная разности вектора магнитной индукции B и вектора намагниченности J .

В Международной системе единиц (СИ) : где-магнитная постоянная .

Закон БСЛ. Закон, определяющий магнитное поле отдельного элемента тока

39. Приложения закона Био-Савара-Лапласа. Для поля прямого тока

Для кругового витка.

И для соленоида

40. Индукция магнитного поля Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля (векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства). МИ. (В) это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле: B=F / (I*l) (Словестно: Модуль вектора МИ. (B) равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l . Магнитная индукция зависит только от магнитного поля. В связи с этим индукцию можно считать количественной характеристикой магнитного поля. Она определяет, с какой силой(Сила Лоренца) магнитное поле действует назаряд, движущийся со скоростью. Измеряется МИ в теслах (1 Тл). 2/R играет роль центростремительной силы. Период обращения равен T=2пиR/V=2пиm/qB и он не зависит от скорости частицы (Это справедливо только при V

Сила Л. определяется соотношением: Fл = q·V·B·sina (q — величина движущегося заряда; V — модуль его скорости; B — модуль вектора индукции магнитного поля; aльфа — угол между вектором V и вектором В) Сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно. Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.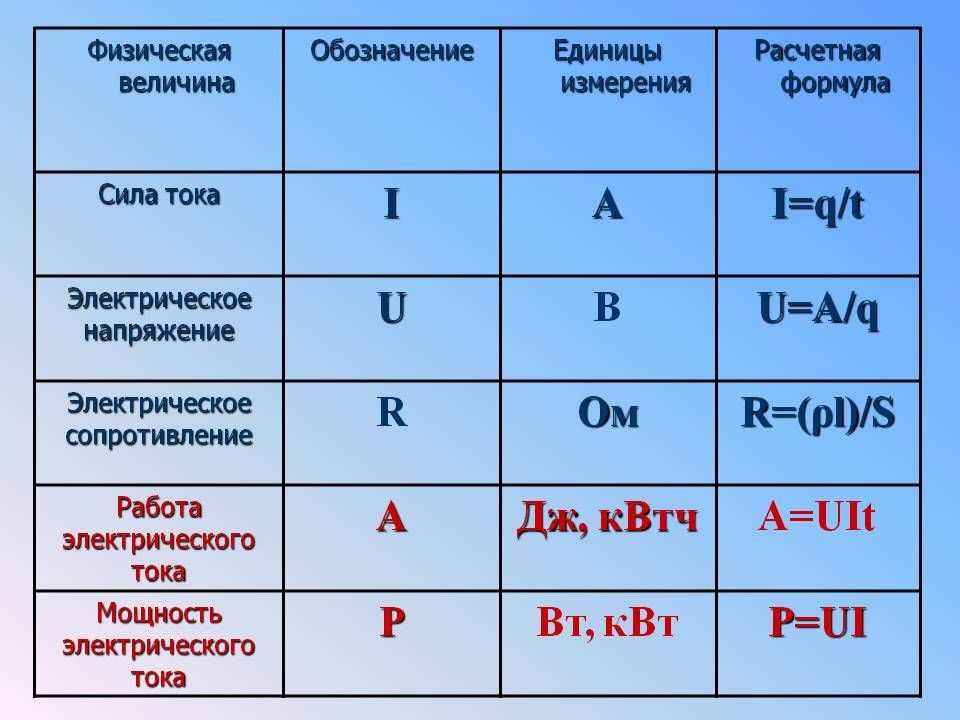

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Определение 1

Работа А, совершаемая постоянной силой F → , — это физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α , располагаемого между векторами силы F → и перемещением s → .

Данное определение рассматривается на рисунке 1 . 18 . 1 .

Формула работы записывается как,

A = F s cos α .

Работа – это скалярная величина. Это дает возможность быть положительной при (0 ° ≤ α

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1 . 18 . 1 . Работа силы F → : A = F s cos α = F s s

При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:

A = ∑ ∆ A i = ∑ F s i ∆ s i .

Данная сумма работы вычисляется из предела (Δ s i → 0) , после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s (x) рисунка 1 . 18 . 2 .

Рисунок 1 . 18 . 2 . Графическое определение работы Δ A i = F s i Δ s i .

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 1 . 18 . 3 .

Рисунок 1 . 18 . 3 . Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.

F → у п р = — F →

Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 1 . 18 . 4 . Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.

Определение 2

Если на тело действует несколько сил, то формула общей работы будет выглядеть, как сумма всех работ, совершаемых над ним. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Рисунок 1 . 18 . 5 . Модель механической работы.

Определение мощности

Определение 3

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

Определение 4

Система С И использует в качестве единицы мощности ватт (В т) , равняющийся мощности силы, которая совершает работу в 1 Д ж за время 1 с.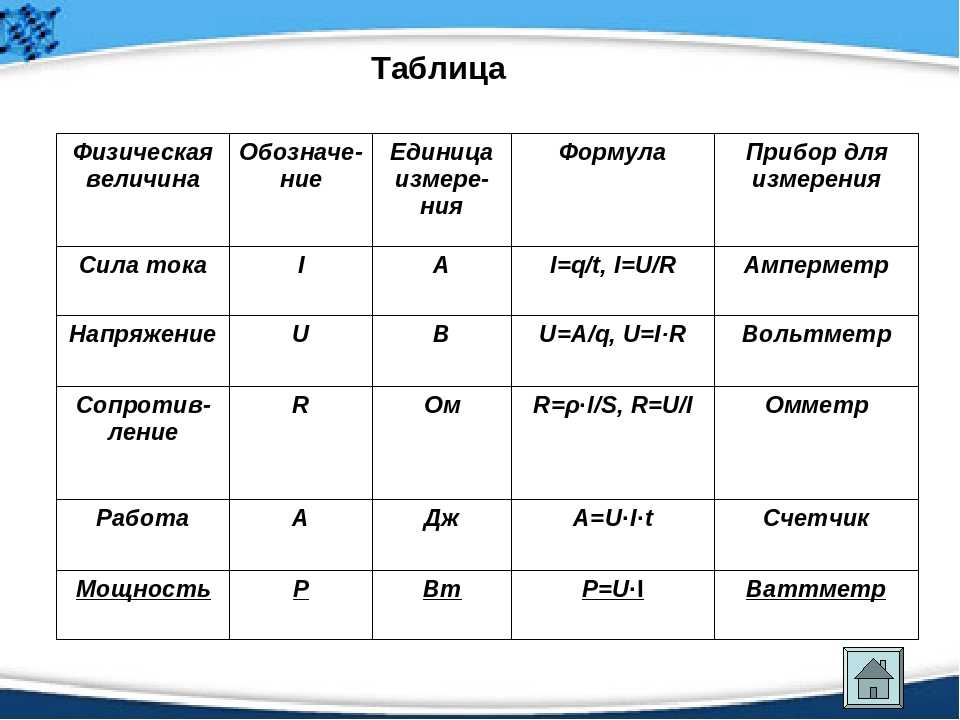

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

2 . Постоянный электрический ток Основные формулы и законы

Сила тока

(если ).

Плотность тока

, ,

где – площадь поперечного сечения проводника, – средняя скорость упорядоченного движения зарядов в проводнике, – концентрация зарядов, – элементарный заряд.

Зависимость сопротивления от параметров проводника

,

где – длина проводника, – площадь поперечного сечения проводника, – удельное сопротивление, – удельная проводимость.

Зависимость удельного сопротивления от температуры для металлических проводников

,

где – температурный коэффициент сопротивления, – удельное сопротивление при , – температура проводника.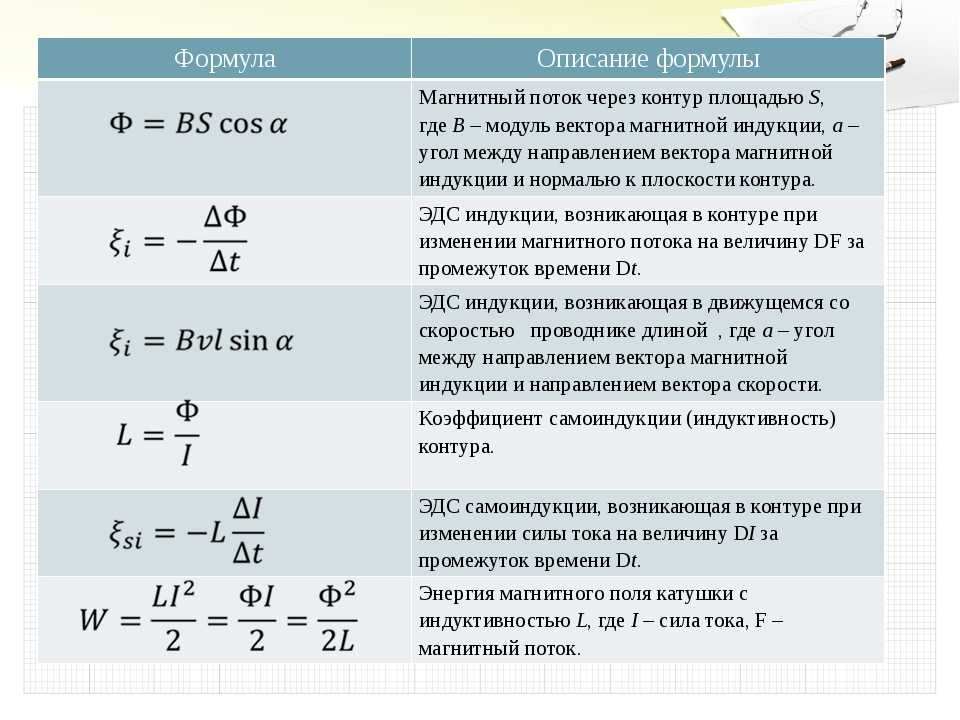

Сопротивление системы проводников: при последовательном (а) и параллельном (б) соединениях

а) , б) ,

где – сопротивление -го проводника, – число проводников.

Сопротивления, необходимые для расширения пределов измерения приборами силы тока ( ) и напряжения ( ) в раз

, .

Законы Ома:

для однородного участка цепи

,

для неоднородного участка цепи

 ,

для замкнутой цепи

,

где – напряжение на однородном участке цепи, – разность потенциалов на концах участка цепи, – ЭДС источника, – внутреннее сопротивление источника тока, в дифференциальной форме

,

где – плотность тока, – удельная проводимость, –напряжённость поля.

Сила тока короткого замыкания

.

Работа тока за время

.

.

Мощность тока, выделяемая в нагрузке (полезная),

.

Полная мощность, выделяемая в цепи,

.

Мощность, теряемая в источнике,

.

Коэффициент полезного действия источника тока

.

Правила Кирхгофа

1) – для узлов;

2) – для контуров,

где – алгебраическая сумма сил токов, сходящихся в узле, – алгебраическая сумма ЭДС в контуре.

2.1. В сеть включены четыре последовательно соединённых резистора одинакового сопротивления. Как изменится сопротивление цепи, если эти резисторы соединить параллельно? [уменьшится в 16 раз].

2.2. В сеть с напряжением 120 В включены две лампы сопротивлением 200 Ом каждая. Какой ток пойдёт через каждую лампу при параллельном и последовательном их соединениях? [0,6 А; 0,3 А].

2.3. Общее сопротивление двух последовательно соединённых проводников 5 Ом, а параллельно соединённых 1,2 Ом. Определите сопротивление каждого проводника. [3 Ом и 2 Ом].

2.4. Сопротивление одного из последовательно включённых проводников в n раз больше сопротивления другого. Во сколько раз изменится сила тока в цепи (напряжение постоянно), если проводники включить параллельно? [увеличится в (n+1)²/n раз].

2.5. На концах медного провода длиной 5 м поддерживается напряжение 1 В. Определите плотность тока в проводе (удельное сопротивление меди 1,7^.10^-8 Ом ^. м). [1,18^.10⁷А/м²].

2. 6. Во сколько раз изменится сопротивление проводника (без изоляции), если его свернуть пополам и скрутить? [уменьшится в 4 раза].

2.7. Гальванический элемент даёт на внешнее сопротивление 0,5 Ом силу тока 0,2 А. Если внешнее сопротивление заменить на 0,8 Ом, то ток в цепи 0,15 А. Определите силу тока короткого замыкания. [0,45A] .

2.8. Резистор сопротивлением 5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение 10 В. Если заменить резистор другим с сопротивлением 12 Ом, то вольтметр покажет напряжение 12 В. Определите ЭДС и внутреннее сопротивление источника тока. Током через вольтметр пренебречь. [14 В; 2 Ом].

2.9. Найдите внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт. [0,2 Ом; 12 В].

2.10. Определите силу тока в цепи, состоящей из двух элементов с ЭДС, равными 1,6 В и 1,2 В и внутренними сопротивлениями 0,6 Ом и 0,4 Ом соответственно, соединённых одноимёнными полюсами. [0,4 A] .

2.11. Электрическую лампу сопротивлением 240 Ом, рассчитанную на напряжение 120 В, надо питать от сети напряжением 220 В. Какой длины нихромовый проводник с площадью поперечного сечения 0,55 мм² надо включить последовательно с лампой? (удельное сопротивление нихрома 1,1^.10^-6 Ом^.м). [100 м].

2.12. Цепь состоит из трёх последовательно соединённых проводников, подключенных к источнику напряжения 24 В. Сопротивление первого проводника 4 Ом, второго 6 Ом, а напряжение на концах третьего проводника 4 В. Найдите силу тока в цепи, сопротивление третьего проводника и напряжения на концах первого и второго проводников. [2 А; 2 Ом; 8 В; 12 В].

2.13. К источнику тока с ЭДС 12 В присоединена нагрузка. Напряжение на клеммах источника 8 В. Определите КПД источника тока. [68%] .

2.14. Внешняя цепь источника тока потребляет мощность 0,75 Вт.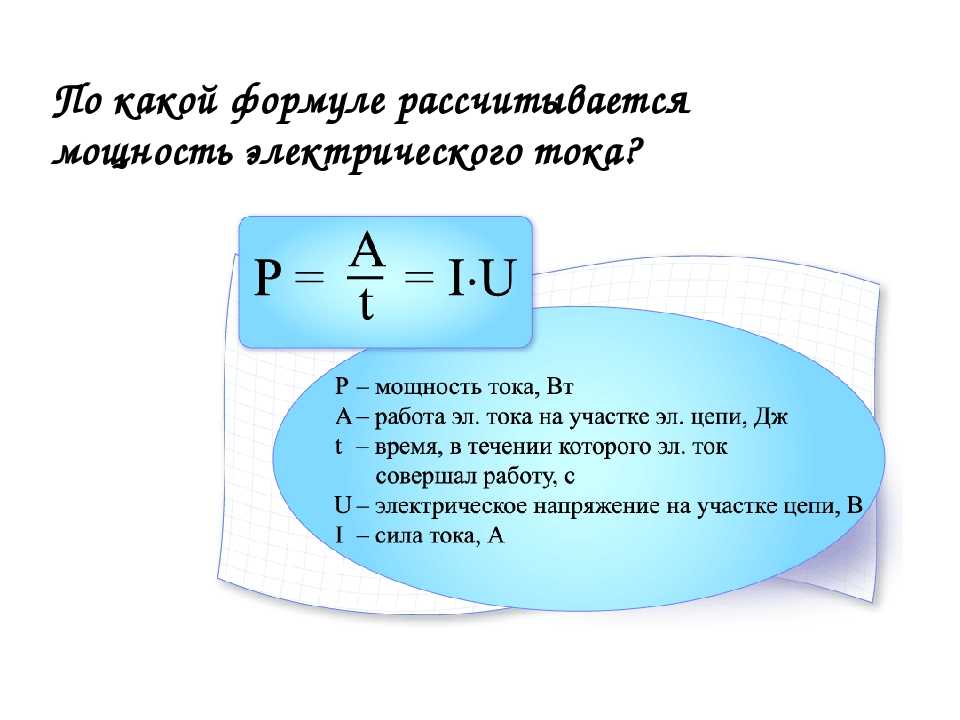 Определите силу тока в цепи, если ЭДС источника 2 В и внутреннее сопротивление 1 Ом. [0,5 А и 1,5 А] .

2.15. Источник тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён к нагрузке сопротивлением 9 Ом. Найдите: 1) силу тока в цепи, 2) мощность, выделяемую во внешней части цепи, 3) мощность, теряемую в источнике тока, 4) полную мощность источника тока, 5) КПД источника тока. [1)1,2 A; 2)12,96 Вт; 3)1,44 Вт; 4)14,4 Вт; 5)90%].

2.16. Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через 10 мин, если другая, то через 20 мин. Через сколько минут закипит вода, если обе секции включить последовательно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми. [30 мин].

2.17. Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через 10 мин, если другая, то через 20 мин. Через сколько минут закипит вода, если обе секции включить параллельно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми. [6,67 мин] .

2.18. Амперметр сопротивлением 0,18 Ом предназначен для измерения силы тока до 10 А. Какое сопротивление надо взять и как его включить, чтобы этим амперметром можно было измерять силу тока до 100 А? [0,02 Ом, параллельно].

2.19. Вольтметр сопротивлением 2000 Ом предназначен для измерения напряжения до 30 В. Какое сопротивление надо взять и как его включить, чтобы этим вольтметром можно было измерять напряжение до 75 В? [3000 Ом, последовательно].

2.20. Ток в проводнике сопротивлением 100 Ом равномерно нарастает от 0 до 10 А в течение 30 с. Чему равно количество теплоты, выделившееся за это время в проводнике? [100 кДж].

2.21. Ток в проводнике сопротивлением 12 Ом равномерно убывает от 5 А до 0 в течение 10 с. Какое количество теплоты выделяется в проводнике за это время? [1 кДж].

2.22. По проводнику сопротивлением 3 Ом течёт равномерно возрастающий ток. Количество теплоты, выделившееся в проводнике за 8 с, равно 200 Дж. Определите заряд, протекший за это время по проводнику. В начальный момент времени ток был равен нулю. [20 Кл].

2 .23. Ток в проводнике сопротивлением 15 Ом равномерно возрастает от 0 до некоторого максимума в течение 5 с. За это время в проводнике выделилось количество теплоты 10 кДж. Найдите среднее значение силы тока в проводнике за этот промежуток времени. [10 А] .

2.24. Ток в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение 10 с. За это время в проводнике выделилось количество теплоты 1 кДж. Определите скорость нарастания тока в проводнике, если сопротивление его 3 Ом. [1А/с].

2.25. На рис. 2.1 = = , R₁ = 48 Ом, R₂ = 24 Ом, падение напряжения U₂ на сопротивлении R₂ равно 12 В. Пренебрегая внутренним сопротивлением элементов, определите силу тока во всех участках цепи и сопротивление R₃. [I₁=0,25 A, I₂=0,5 A, I₃=0,75 A, R₃=16 Ом].

R₄

Рис. 2.1. Рис.2.2.

Рис. 2.3

2.26. На рис. 2.2 =2В, R₁= 60 Ом, R₂= 40 Ом, R₃=R₄= 20 Ом, R_G= 100 Ом. Определите силу тока I_Gчерез гальванометр. [1,49 мА].

2.27. Найдите силу тока в отдельных ветвях мостика Уитстона (рис. 2.2) при условии, что сила тока, идущего через гальванометр, равна нулю. ЭДС источника 2В, R₁= 30 Ом, R₂= 45 Ом, R₃= 200 Ом. Внутренним сопротивлением источника пренебречь. [I₁=I₂=26,7 мА, I₃=I₄= 4 мА].

2.28. На рис. 2.3 =10 В, = 20 В, = 40 В, а сопротивления R₁=R₂=R₃= 10 Ом. Определите силу токов через сопротивления (I) и через источники ( ). Внутренним сопротивлением источников пренебречь. [I₁=1A, I₂=3A, I₃=2A, =2A, =0, =3A].

2.29. На рис. 2.4 = 2,1 В, = 1,9 В, R₁=45 Ом, R₂= 10 Ом, R₃= 10 Ом. Найдите силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь. [I₁=0,04 A, I₂=0,01 A, I₃=0].

Рис. 2.4 Рис. 2.5

Рис. 2.6

2.30. На рис. 2.5 сопротивления вольтметров равны R₁=3000 Ом и R₂=2000 Ом; R₃=3000 Ом, R₄=2000 Ом; =200 В. Найдите показания вольтметров в случаях: а) ключ К разомкнут, б) ключ К замкнут. Внутренним сопротивлением источника пренебречь. [а) U₁=120 В, U₂=80 В; б) U₁=U₂=100 В].

2.31. На рис. 2.6 = =1,5 В, внутренние сопротивления источников r₁=r₂=0,5 Ом, R₁=R₂= 2 Ом, R₃= 1 Ом. Сопротивление миллиамперметра 3 Ом. Найдите показание миллиамперметра. [75 мА].

2.32. На рис. 2.7 = = 110 В, R₁=R₂= 200 Ом, сопротивление вольтметра 1000 В. Найдите показание вольтметра. Внутренним сопротивлением источников пренебречь. [100 В].

Рис. 2.7 Рис. 2.8

Рис. 2.9

2.33. На рис. 2.8 = = 2В, внутренние сопротивления источников равны 0,5 Ом, R₁= 0,5 Ом, R₂= 1,5 Ом. Найдите силу тока во всех участках цепи. [2,22 А; 0,44 А; 1,78 А].

2.34. На рис. 2. 9 = = 100 В, R₁= 20 Ом, R₂= 10 Ом, R₃= 40 Ом, R₄= 30 Ом. Найдите показание амперметра. Внутренним сопротивлением источников и амперметра пренебречь. [1 А].

2.35. Какую силу тока показывает амперметр на рис. 2.10, сопротивление которого R_A=500 Ом, если = 1 В, = 2 В, R₃=1500 Ом и падение напряжения на сопротивлении R₂ равно 1 В. Внутренним сопротивлением источников пренебречь.[1 мА].

2.36. На рис. 2.11 =1,5 В, =1,6 В, R₁=1 кОм, R₂=2 кОм. Определите показания вольтметра, если его сопротивление R_V=2 кОм. Сопротивлением источников пренебречь. [0,35 В].

Рис. 2.10 Рис. 2.11

Рис. 2.12

2.37. На рис. 2.12 сопротивления R₁= 5Ом, R₂= 6 Ом, R₃= 3 Ом. Найдите показание амперметра, если вольтметр показывает 2,1 В. Сопротивлением источника и амперметра пренебречь. [0,2 А].

2.38. Определите ЭДС источника в схеме на рис. 2.13, если сила тока, текущего через него, равна 0,9 А, внутреннее сопротивление источника 0,4 Ом. R₁=30 Ом, R₂=24 Ом, R₃ =50 Ом, R₄ =40 Ом, R₅ =60 Ом.

2.39. Найдите показания амперметра в схеме на рис. 2.14, если ЭДС равна 19,8 В, внутреннее сопротивление 0,4 Ом, R₁=30 Ом, R₂=24 Ом, R₃=50 Ом, R₄=40 Ом, R₅=60 Ом.

E₁

E₂

Рис. 2.13 Рис. 2.14

Рис. 2.15

2.40. Найдите величины всех сопротивлений в схеме на рис. 2.15, если через сопротивление R₁ течёт ток 0,4 мкА, через сопротивление R₂ ток 0,7 мкА, через сопротивление R₃ – 1,1 мкА, через сопротивление R₄ ток не течёт. Внутренним сопротивлением элементов пренебречь. =1,5 В; =1,8 В.

Рис. 2.16 Рис. 2.17

Рис. 2.18

2.41. Определите и в схеме на рис. 2.16, если R₁=R₄=2 Ом, R₂=R₃= 4 Ом. Ток, текущий через сопротивление R₃, равен 1А, а через сопротивление R₂ ток не течёт. Внутренние сопротивления элементов r₁=r₂=0,5 Ом.

2.42. Определите силу тока во всех участках цепи в схеме на рис. 2.17, если =11 В, =4 В, =6 В, R₁=5 Ом, R₂=10 Ом, R₃=2 Ом. Внутренние сопротивления источников r₁=r₂=r₃=0,5 Ом.

2.43. В схеме на рис. 2.18 R₁=1 Ом, R₂=2 Ом, R₃=3 Ом, сила тока через источник равна 2А, разность потенциалов между точками 1 и 2 равна 2 В. Найдите сопротивление R₄.

Буклет с формулами 12 класс физики Текущее электричество

Формулы физики

Скорость зарядного тока в любой части провода называется протекающим по нему электрическим током.

Электрический ток (I) = q/t. Его единицей СИ является ампер (А).

Обычное направление электрического тока – это направление движения положительного заряда.

Ток одинаков для всех участков проводника неоднородного сечения. Подобно потоку воды, зарядка течет быстрее, когда проводник мал в противоположном направлении, и замедляется, когда проводник более протяженный в поперечном сечении, так что уровень заряда остается неизменным.

При зарядке q вращается по окружности с частотой f, равной мощности,

я = qf

(Ток в металлическом проводнике течет за счет движения свободных электронов, в то время как электролиты и ионизированные газы теперь текут за счет электронов и направлений. )

Виды электрического тока

По величине и направлению электрический ток бывает двух видов

1. Постоянный ток (DC) Его величина и направление не меняются со временем. Сеть, батарея или динамо-машина постоянного тока являются наиболее постоянными источниками тока.
2. Переменный ток (AC) Электрический ток, величина которого непрерывно изменяется и время от времени меняет свое направление, называется переменным током. Динамо-машина переменного тока является текущим источником обмена.

• Сопротивление R= V/i

Где I = сила тока

я = текущий

• Изменение сопротивления в зависимости от температуры:

R = R0(1 + αΔT)

Где-R _t -сопротивление при температуре t°C,

R ₀ -стойкость при температуре 0°С,

α -температурный коэффициент сопротивления.

Проводимость = обратная величина удельного сопротивления или σ = 1/ρ = 1/RA

• Напряжение на клеммах:

Случай-1 : Когда батарея подает ток

V = E – ir

Где – V-концевой P. D., E – ЭДС ячейки, r-внутреннее сопротивление ячейки,

R- внешнее сопротивление.

Случай-2 : Когда аккумулятор заряжается

V = E + ir

• Законы Кирхгофа:

1. Первый закон Кирхгофа: ∑i = 0 на любом перекрестке
2. Второй закон Кирхгофа: ∑i R = 0 в замкнутом контуре.

• Условие балансировки для моста из пшеничного камня: p/q = r/s, где P, Q, R и S — сопротивления моста 9.0026
• Метровый мост

Где – x – неизвестное сопротивление данного провода, R – сопротивление в коробке сопротивлений, l ₁ – балансировочная длина от левого конца моста до жокея.

ρ=Lπr2X

Где — ρ-удельное сопротивление провода,

Х-сопротивление провода,

А – Площадь поперечного сечения провода,

l-длина провода.

• Измеритель потенциала:

ЭДС ячейки во вторичной цепи

E _с = Iρ

(i) Сравнение ЭДС двух ячеек

E1/E2 = L1/L2

Где – E ₁ – ЭДС первой ячейки, E ₂ – ЭДС второй ячейки, l ₁ и l ₂ – балансировочные длины отдельных ячеек соответственно.

(ii) Для определения внутреннего сопротивления ячейки:

r = R (L1 — L2)/L2

Следуйте решениям NCERT для класса 12 по физике , подготовленным Physics Wallah. Если каким-либо учащимся необходимо пройти онлайн-тест, чтобы проверить свои концепции или понимание, они могут посетить викторину по текущему электричеству.

Загрузите PDF-файл буклета с формулами класса 12​t физика главы Current Electricity по ссылке, указанной ниже

List of Current Electricity Formulas

Электрический ток — это движение зарядов по проводу. Если вам нужна помощь в отношении текущих концепций электричества, взгляните на текущие формулы электричества. Извлеките максимальную пользу из Шпаргалки по текущему электричеству и получите хорошее представление о концепциях. Вы можете увидеть различные формулы, такие как закон Ома, скорость дрейфа, плотность тока, подвижность и т. д. Поднимите свою подготовку на новый уровень, обратившись за помощью к формулам физики и улучшите свои предметные знания.

1. Электрический ток

Скорость протекания заряда
I = \(\frac{d q}{d t}\)
Единица → Ампер

2. Закон Ома

Если физические условия , давление и т. д.) проводника без изменений, то
В ∝ I или V = RI

3. Удельное сопротивление (удельное сопротивление)

Если l → длина проводника.
A → площадь поперечного сечения проводника.
, затем
R = ρ \(\frac{\ell}{A}\)
Удельное сопротивление ρ = \(\frac{RA}{\ell}\) Ом-м
Значение ρ зависит только от природы материала и температуры материала.

4. Скорость дрейфа. }}\right) \overrightarrow{\mathrm{E}}\)
v _d = \(\frac{\mathrm{eE} \tau}{\mathrm{m}}\)
где τ — время релаксации m – масса электрона.
Если n — числовая плотность носителей заряда (электронов), то ток

9{2} \tau}{\mathrm{m}}\right)\) E = σE
Проводимость
σ = \(\frac{J}{E}=\frac{1}{\rho}\) mho/ m

Другая форма закона Ома.

6. Подвижность (μ)

μ = \(\frac{v_{d}}{E}=\frac{e \tau}{m}\) m ² /V-s

7 Температурная зависимость сопротивления

R _t ≈ R _o (1 + αt)
α называется температурным коэффициентом сопротивления
α = \(\frac{\mathrm{R}_{\mathrm{t} }-\mathrm{R}_{0}}{\mathrm{R}_{0} \mathrm{t}}\) на °C

8. Комбинация сопротивлений

Комбинация серий
R = R ₁ + R ₂ + ……… + R _n
Через все сопротивления протекает одинаковый ток.
В параллельной комбинации
\(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\ldots \ldots \ldots+1 / R_ {n}\)
Разность потенциалов на всех сопротивлениях одинакова.
Для двух сопротивлений параллельно.

R = \(\ frac {\ mathrm {R} _ {1} \ mathrm {R} _ {2}} {\ mathrm {R} _ {1} + \ mathrm {R} _ {2}} \ ) ; \(\frac{I_{1}}{I_{2}}=\frac{R_{2}}{R_{1}}\)
I ₁ = \(\frac{\mathrm{R}_{2}}{\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}\) I, I ₂ = \(\frac{\mathrm{R}_{1}}{\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}\ ) I.

9. Законы Кирхгофа

Первый закон (Текущий закон или Закон соединения): В каждом узле Σi = 0
, т.е. i ₁ + i ₂ + i _{3 … i n = 0
Первый закон, основанный на сохранении заряда}

Второй закон (закон напряжения или закон петли):
В каждом замкнутом контуре сумма падений потенциала на различных компонентах в направлении протекания тока равна полной ЭДС, приложенной к контуру.
ΣiR = Σ э.д.с.
Второй закон сохранения энергии

10. Мост Уитстона

В уравновешенном состоянии моста.
(I _g = o)
\(\frac{P}{Q}=\frac{R}{S}\)

Если \(\frac{P}{Q}>\frac{R} {S}\), V _D > V _B
Если \(\frac{P}{Q}<\frac{R}{S}\), V _B > V _D
P.O. Box и Meter Bridge также основаны на этом принципе.

11. Гальванометр с подвижной катушкой

Катушка (участок A), подвешенная в магнитном поле (B), отклоняется, когда через катушку проходит ток.
Отклоняющая пара niAB = восстанавливающая пара Cθ
i = \(\frac{\mathrm{C} \theta}{\mathrm{nAB}}\) = Kθ
Чувствительность = \(\frac{\theta}{i}= \frac{n A B}{C}\)

12. Амперметр

Устройство для измерения тока.

Шунтирующее сопротивление S амперметра для диапазона i ампер равно –
S = \(\frac{\mathrm{i}_{\mathrm{g}} \times \mathrm{G}}{\left(\mathrm {i} — \ mathrm {i} _ {\ mathrm {g}} \ right)} \ приблизительно \ frac {\ mathrm {i} _ {\ mathrm {g}}} {\ mathrm {i}} \) G
где i _g — ток в гальванометре для полного отклонения шкалы. S — это маленькое (низкое) сопротивление, включенное параллельно.
Чистое сопротивление амперметра равно \(\left(\frac{\mathrm{SG}}{\mathrm{S}+\mathrm{G}}\right)\)

13. Вольтметр

Используется для измерения разности потенциалов. Это делается путем последовательного включения надлежащего высокого сопротивления с катушкой гальванометра. Для вольтметра диапазона V вольт значение сопротивления равно
R = \(\left(\frac{\mathrm{V}}{\mathrm{i}_ {\mathrm{g}}}-\mathrm{G}\right)\)
R → последовательное соединение с высоким сопротивлением.
Чистое сопротивление вольтметра равно (R + G)

14. Ячейка

Преобразует химическую энергию в электрическую.
Первичная ячейка:
Химические реакции необратимы. Ячейка Лекланша, ячейка Даниэля и т. д.

Вторичная ячейка:
Химические реакции обратимы. После разрядки аккумулятор можно снова зарядить. Свинцовый аккумулятор, щелочной элемент и т. д.

15. Электродвижущая сила (ЭДС)

Эквивалентна разности потенциалов между клеммами элемента, когда ток из элемента не поступает.

16. Напряжение на клеммах (В)

Это разность потенциалов между выводами ячейки, когда от ячейки отводится ток.
V = E – IR (разрядка), V = E + IR (зарядка)

17. Внутреннее сопротивление (r)

Обусловлено столкновениями при движении ионов в электролите ячейки. Это зависит от природы электролита, температуры, потребляемого тока и дефектов.
r = \(\frac{E-V}{I}\)
= \(\frac{E-V}{V}\)R.

18. Группировка ячеек

Для n одинаковых ячеек
Группировка рядов: I = \(\frac{n E}{R+n r}\)

Параллельная группировка: I = \(\frac{\mathrm{E}}{\mathrm{R} +\mathrm{r} / \mathrm{n}}=\frac{\mathrm{nE}}{\mathrm{nR}+\mathrm{r}}\)

Смешанная группировка: m строк из n ячеек, всего количество ячеек N = mn
I = \(\frac{n E}{R+n r / m}=\frac{m n E}{m R+n r}\)
Для максимального тока nr =mR.

19. Теорема о максимальной передаче мощности

• Для передачи максимальной мощности от источника постоянного тока: 9{2}}{R}\) Вт
  1 кВтч (1 единица) = 1000 × 3600 Дж
  Для двух ламп мощностью P ₁ и P ₂ :
  При параллельном соединении с номинальным напряжением:
  P = P ₁ + P ₂
  При последовательном соединении с номинальным напряжением:
  \(\frac{1}{P}=\frac{1}{P_{1}}+\frac{1}{P_{ 2}}\)
  или P = \(\frac{P_{1} P_{2}}{P_{1}+P_{2}}\)

  Посетите единый ресурс для формул, например, Onlinecalculator.