Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
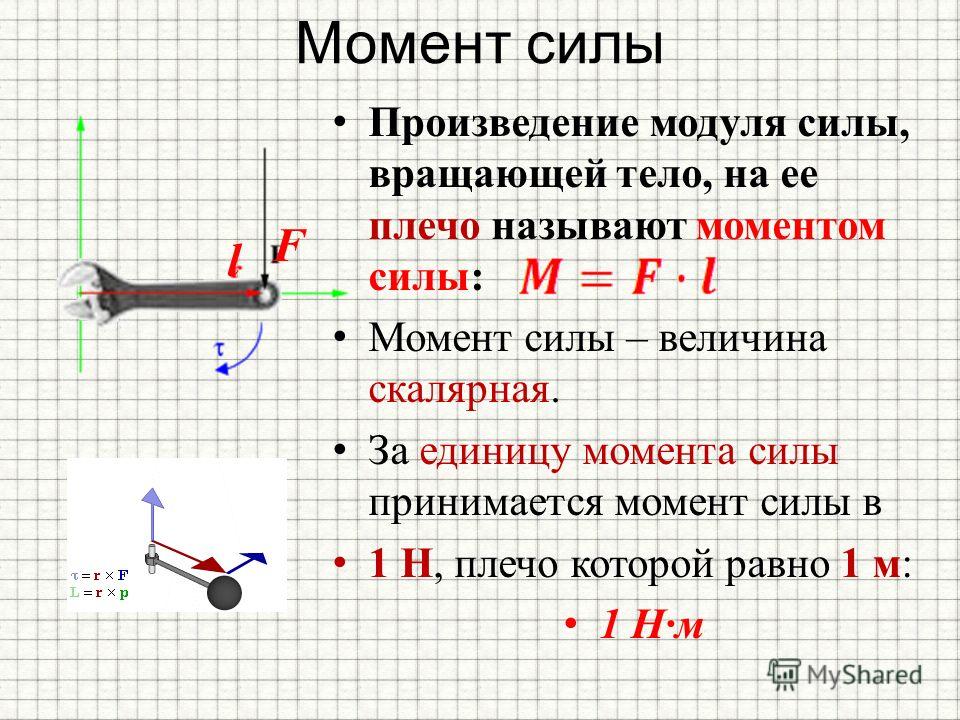
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила».
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.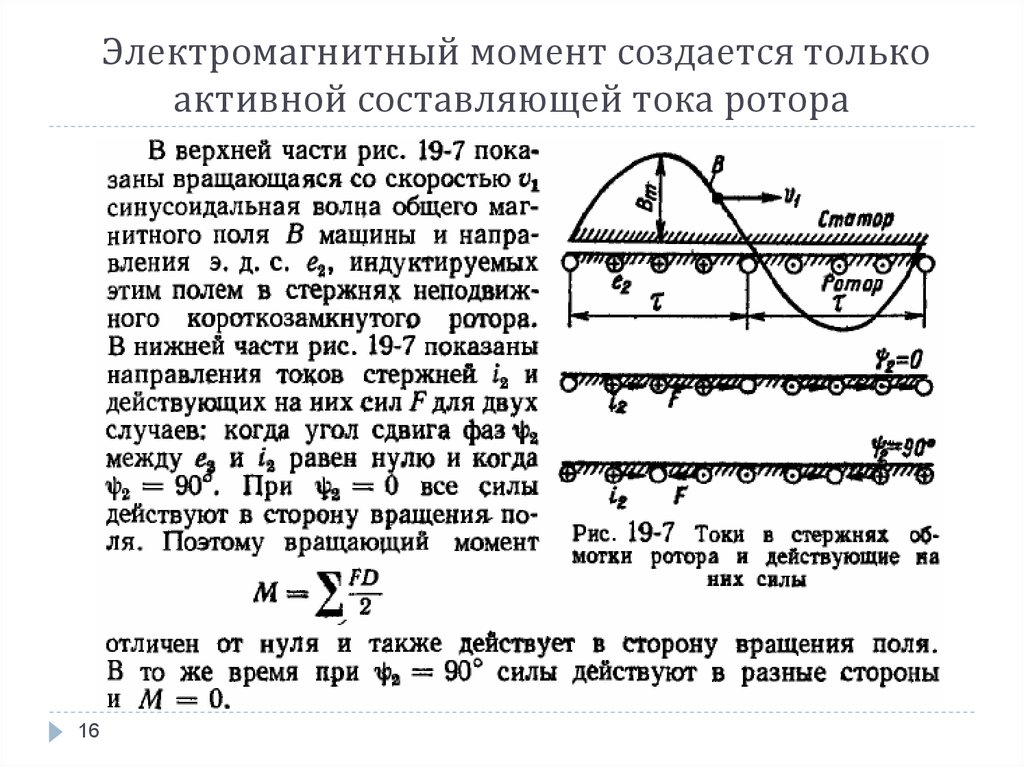
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.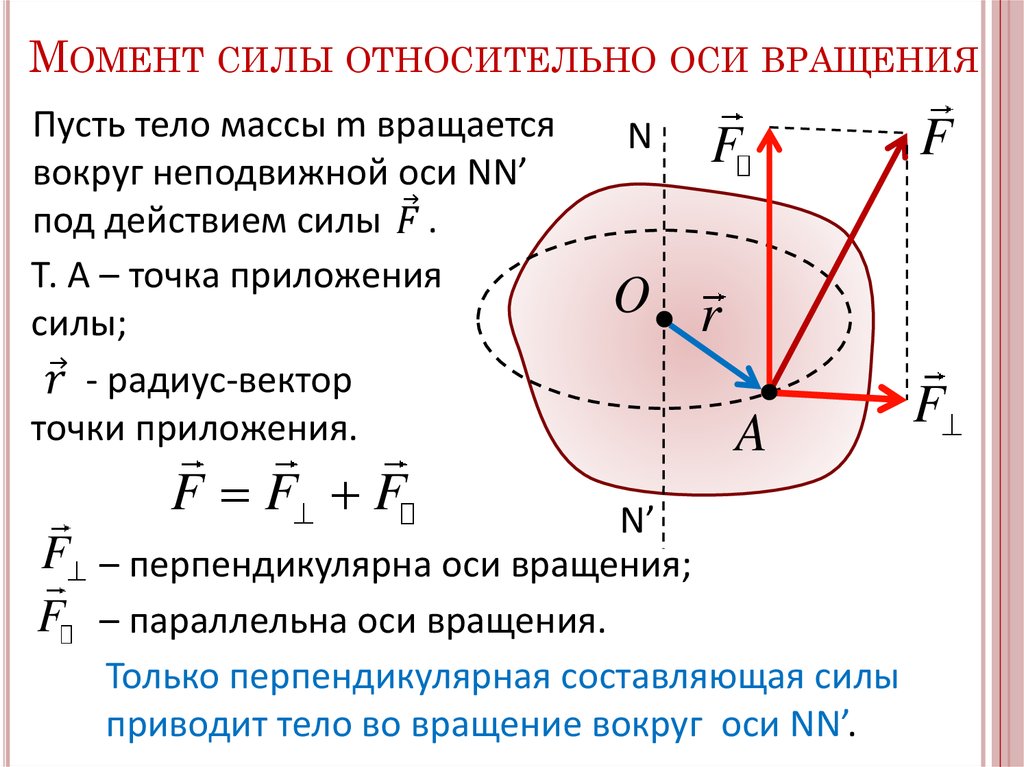
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.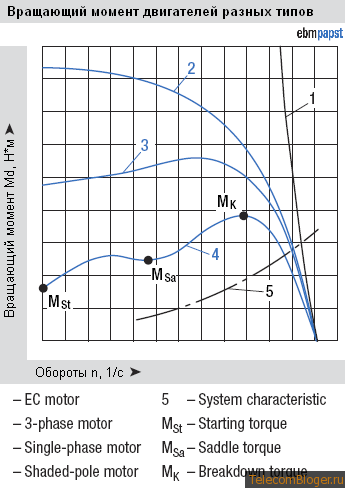
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Вращающий момент | это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Содержание
|
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Что такое крутящий момент в автомобилях
Крутящий момент — это крутящая сила, которая говорит о вращательной силе двигателя и измеряет, какая часть этой крутящей силы доступна, когда двигатель работает.
Крутящий момент присутствует в повседневных делах, таких как нажатие дверной ручки, открытие бутылки содовой, использование гаечного ключа или вращение педалей на велосипеде. Это крутящий момент, который выполняет свою работу!
Давайте разберем это дальше. Представьте, что вы затягиваете болт с помощью гаечного ключа. Вы приложите некоторое усилие к концу ключа, которое будет передано болту на другом конце. Это прикладывает к болту крутящий момент или силу скручивания.
Хотя мощность просто измеряется в лошадиных силах, крутящий момент обычно измеряется в фунтах на фут (фунт-фут).
Вот как это работает: если мы продолжим наш пример с гаечным ключом, и вы представите, что используете специальный гаечный ключ длиной в один фут для затягивания болта. Приложение силы в один фунт к концу этого гаечного ключа длиной в один фут оказывает крутящий момент в один фунт-фут на болт. Увеличить крутящий момент можно, добавив больший вес или используя более длинный ключ.
Приложение силы в один фунт к концу этого гаечного ключа длиной в один фут оказывает крутящий момент в один фунт-фут на болт. Увеличить крутящий момент можно, добавив больший вес или используя более длинный ключ.
Кольцевые гайки, которыми колеса крепятся к вашему автомобилю, обычно необходимо затягивать с крутящим моментом около 100 фунтов на фут — это означает, что оператор должен приложить усилие в 100 фунтов к концу гаечного ключа длиной в фут.
Как работает крутящий момент в автомобилеВсе двигатели, будь то бензиновые или гибридные, генерируют определенное количество лошадиных сил и крутящего момента. Они связаны друг с другом и по-разному выражают мощность двигателя. Крутящий момент используется даже при расчете мощности двигателя. И мощность, и крутящий момент измеряются, чтобы дать покупателям представление о производительности, которую они могут ожидать от своего автомобиля.
Двигатели обычных легковых и грузовых автомобилей обычно развивают крутящий момент от 100 до 400 фунто-футов. Этот крутящий момент создается поршнями внутри двигателя, когда они совершают возвратно-поступательные движения вверх и вниз по коленчатому валу двигателя, заставляя его непрерывно вращаться (или скручиваться). Затем этот крутящий момент передается на колеса автомобиля через трансмиссию и трансмиссию.
Этот крутящий момент создается поршнями внутри двигателя, когда они совершают возвратно-поступательные движения вверх и вниз по коленчатому валу двигателя, заставляя его непрерывно вращаться (или скручиваться). Затем этот крутящий момент передается на колеса автомобиля через трансмиссию и трансмиссию.
Выходной крутящий момент является результатом многих переменных, в том числе размера двигателя и его конструкции.
Проще говоря, чем больше крутящий момент у двигателя, тем лучше он подходит для тяжелых работ, таких как буксировка, буксировка или преодоление крутых подъемов. Вот почему крутящий момент часто имеет первостепенное значение при перемещении чего-то большого и тяжелого, например, грузовика с прицепом.
Крутящий момент и мощность в лошадиных силах — в чем разницаМощность и крутящий момент — это разные способы выражения характеристик двигателя автомобиля.
Что такое лошадиная сила? Лошадиная сила передает общую способность двигателя в любых условиях. И наоборот, выходной крутящий момент передает пиковую мощность, доступную этому двигателю, в определенный момент, когда он выполняет свою самую тяжелую работу.
И наоборот, выходной крутящий момент передает пиковую мощность, доступную этому двигателю, в определенный момент, когда он выполняет свою самую тяжелую работу.
Для иллюстрации давайте представим, что вы покупаете новую стереосистему. Вы могли бы рассмотреть, насколько громко звучит стерео. Максимально возможная громкость прослушивания для непрерывного воспроизведения подобна лошадиным силам двигателя: хороший показатель того, какой мощностью обладает эта стереосистема.
Теперь рассмотрим бас стереосистемы. Бас — это часть прослушивания, которая играет на максимальной громкости (в лошадиных силах), хотя бас, скорее всего, будет оцениваться по его пиковому уровню «напора», созданному на короткий момент.
Таким образом, мощность в лошадиных силах подобна громкости стереосистемы, а крутящий момент подобен басу: оба атрибута стоит знать, и для определенных типов музыки (или транспортных средств) один может быть важнее другого.
Основные различия между лошадиными силами и крутящим моментом Мощность в лошадиных силах определяет общую производительность двигателя. Крутящий момент обеспечивает простое измерение максимального крутящего усилия, которое двигатель может создать при интенсивной работе.
Крутящий момент обеспечивает простое измерение максимального крутящего усилия, которое двигатель может создать при интенсивной работе.
Вот почему у пикапов есть двигатели с высоким крутящим моментом, которые развивают больший крутящий момент, чем небольшой автомобиль.
Например, 5,7-литровый двигатель i-FORCE V8 автомобиля Toyota Tundra имеет мощность 381 л.с. и крутящий момент в 401 фунт-фут. Такой высокий уровень крутящего момента дает водителям широкие возможности для выполнения сложных работ, таких как буксировка, транспортировка и преодоление крутых подъемов.
И наоборот, Toyota Corolla Hatchback оснащен четырехцилиндровым двигателем Dynamic Force мощностью 168 лошадиных сил и крутящим моментом 151 фунт-фут. В этом автомобиле нет необходимости в высоком крутящем моменте, а экономия топлива является приоритетом, поэтому мощность и крутящий момент устанавливаются инженерами так, чтобы сбалансировать приятную производительность с отличной топливной экономичностью.
Наконец, рассмотрим гибридный автомобиль, в котором используется бензиновый двигатель, усиленный электродвигателем.
Электрические двигатели являются суперзвездами крутящего момента, поскольку они мгновенно обеспечивают полный крутящий момент. Вы увидите это в следующий раз, когда будете использовать блендер: как только вы включите его, его электродвигатель немедленно и без ожидания приложит максимальный крутящий момент к вращающимся лезвиям.
Именно такой мгновенный и мощный выходной крутящий момент помогает гибридным автомобилям, таким как Toyota Prius , Corolla Hybrid и RAV4 Hybrid , обеспечивать снижение расхода топлива и повышение производительности.
Найди и создай свою следующую Toyota
Простое объяснение технологии: Крутящий момент в автомобилях
Время считывания 6 минут
Мощность двигателя, максимальная скорость, ускорение от 0 до 60 миль в час (от 0 до 100 км/ч) — вот ключ номера машин, о которых знают даже дети. Тем не менее, когда дело доходит до крутящего момента, даже заядлым фанатикам моторов может быть трудно объяснить это. Его значение при вождении автомобиля гораздо больше, чем многие думают. Итак, что такое крутящий момент? И как это влияет на автомобили? Читайте дальше, чтобы узнать ответы.
Тем не менее, когда дело доходит до крутящего момента, даже заядлым фанатикам моторов может быть трудно объяснить это. Его значение при вождении автомобиля гораздо больше, чем многие думают. Итак, что такое крутящий момент? И как это влияет на автомобили? Читайте дальше, чтобы узнать ответы.
13 апреля 2021 г.
Включите push-уведомления
Инновационная мобильность, захватывающие тенденции будущего и высокие обороты в минуту: подпишитесь сейчас, чтобы получать уведомления о новом контенте.
Подписка успешная .
Подписка не удалась . Если вам нужна помощь, перейдите по ссылке для получения поддержки.
Как это звучит?
Эту статью также можно прослушать в официальном подкасте BMW «Changing Lanes».
Помимо этой и других озвученных статей, «Changing Lanes» каждую неделю предлагает вам свежие новые эпизоды, наполненные эксклюзивной информацией о технологиях, образе жизни, дизайне, автомобилях и многом другом, которую вам принесут ведущие Ники и Джонатан.
Найдите и подпишитесь на Change Lanes на всех основных платформах подкастинга.
applepodcast googlepodcast Spotify Deezer
- Объяснение BMW
- Опыт вождения
- Технологии
Краткие факты
В физике крутящий момент определяется силой, которая действует на тело посредством рычага.
Применительно к двигателям внутреннего сгорания или электродвигателям крутящий момент указывает силу, которой подвергается приводной вал.
Крутящий момент выражается в фунт-футах (lb-ft) или ньютон-метрах (Нм).
- Взаимодействие крутящего момента и частоты вращения двигателя (об/мин) определяет мощность двигателя.
Если вы никогда не путешествовали на электромобиле (➜ Подробнее: Объяснение электромобилей и подключаемых гибридов), время пришло. Это не только хорошо для вашей зеленой совести, но и удовольствие от вождения (➜ Читать далее: Развенчание мифов об электромобилях), безусловно, тоже не осталось без внимания. Одной из причин этого является крутящий момент. Или, точнее: мгновенность, с которой это применяется, когда вы нажимаете на акселератор. Но какую роль в этом играет мощность двигателя, т.е. показатель в кВт или в л.с.?
Одной из причин этого является крутящий момент. Или, точнее: мгновенность, с которой это применяется, когда вы нажимаете на акселератор. Но какую роль в этом играет мощность двигателя, т.е. показатель в кВт или в л.с.?
Чтобы ответить на этот вопрос, вам нужно вернуться на шаг назад, как объясняет эксперт BMW Михаэль Гризе: «Важно то, что вы, как водитель, ожидаете от своего автомобиля. Это высокий уровень мощности двигателя или крутящего момента?» В конце концов, все сводится к тому, действительно ли вам нужна высокая максимальная скорость или быстрая реакция на педаль акселератора.
Начнем с теории. В физике крутящий момент определяется как сила, действующая на точку вращения с помощью плеча рычага. Формула крутящего момента, закон рычага: крутящий момент = сила (Н) х плечо рычага (м). Единицами крутящего момента являются ньютон-метры (Нм) или фунт-футы (фунт-фут). Ньютон (или фунт) обозначает действующую силу, а метры (или футы) обозначают длину плеча рычага. Другое название крутящего момента, которое, возможно, дает более четкое представление о его значении, — вращательная сила. Как следует из этого названия, сила вращения или крутящий момент обеспечивают вращение объекта. Таким образом, он указывает силу, действующую на приводной вал автомобиля при его вращении. Сила (N), с другой стороны, линейно ускоряет объекты. Мощность двигателя есть произведение силы и скорости действия этой силы. Мощность двигателя и крутящий момент являются показателями, которые зависят от частоты вращения двигателя.
Другое название крутящего момента, которое, возможно, дает более четкое представление о его значении, — вращательная сила. Как следует из этого названия, сила вращения или крутящий момент обеспечивают вращение объекта. Таким образом, он указывает силу, действующую на приводной вал автомобиля при его вращении. Сила (N), с другой стороны, линейно ускоряет объекты. Мощность двигателя есть произведение силы и скорости действия этой силы. Мощность двигателя и крутящий момент являются показателями, которые зависят от частоты вращения двигателя.
Высокий крутящий момент обеспечивает эффективное и энергосберегающее вождение. Высокая мощность двигателя позволяет автомобилю быстро разгоняться и достигать высокой максимальной скорости.
Михаэль Гризе
Руководитель проекта по системам электропривода, BMW Group
Итак, это была теория, а теперь перейдем к практике. В конструкции двигателя внутреннего сгорания цель состоит в том, чтобы обеспечить водителю высокий крутящий момент даже при низких оборотах двигателя (вращения). В то же время крутящий момент следует прикладывать в максимально возможном диапазоне частоты вращения двигателя. С точки зрения опыта вождения, высокий крутящий момент означает максимально короткую задержку между нажатием водителем на педаль газа и реакцией двигателя. Высокий крутящий момент воспринимается водителем как отличная тяга при трогании с места или обгоне.
В то же время крутящий момент следует прикладывать в максимально возможном диапазоне частоты вращения двигателя. С точки зрения опыта вождения, высокий крутящий момент означает максимально короткую задержку между нажатием водителем на педаль газа и реакцией двигателя. Высокий крутящий момент воспринимается водителем как отличная тяга при трогании с места или обгоне.
Таким образом, заблаговременное применение мощного крутящего момента означает высокую степень уверенности (при обгоне), большое удовольствие от вождения и эффективную тягу для водителя. Тем не менее, со всеми двигателями внутреннего сгорания всегда есть мгновенная задержка (хотя и небольшая, в зависимости от конструкции) перед тем, как крутящий момент начнет действовать — в отличие от двигателя электромобиля, как мы увидим ниже. Короче говоря, высокий крутящий момент, доступный на раннем этапе, дает только преимущества для водителей.
Крутящий момент и его значение для водителей лучше всего иллюстрируется его отличием от термина «мощность двигателя» или «выходная мощность». Здесь также лучше привести краткий теоретический фон в качестве основы для объяснения эксперта BMW: с мощностью двигателя в игру вступает фактор времени. Проще говоря, это указывает на энергию, преобразованную в данный период времени. Физическая формула такова: мощность = сила х скорость. Он указывается в киловаттах (кВт), ранее в лошадиных силах (л.с.). Один ватт (Вт) соответствует одному ньютон-метру в секунду, а 1 лошадиная сила — это мощность, необходимая для подъема 33 000 фунтов ровно на один фут за одну минуту. Двигатель достигает высокой мощности либо за счет высокого крутящего момента, либо за счет высокой скорости вращения двигателя. Максимальная мощность двигателя, заявленная производителями, а также указанная в техпаспорте автомобиля, обычно доступна при высоких оборотах двигателя.
Здесь также лучше привести краткий теоретический фон в качестве основы для объяснения эксперта BMW: с мощностью двигателя в игру вступает фактор времени. Проще говоря, это указывает на энергию, преобразованную в данный период времени. Физическая формула такова: мощность = сила х скорость. Он указывается в киловаттах (кВт), ранее в лошадиных силах (л.с.). Один ватт (Вт) соответствует одному ньютон-метру в секунду, а 1 лошадиная сила — это мощность, необходимая для подъема 33 000 фунтов ровно на один фут за одну минуту. Двигатель достигает высокой мощности либо за счет высокого крутящего момента, либо за счет высокой скорости вращения двигателя. Максимальная мощность двигателя, заявленная производителями, а также указанная в техпаспорте автомобиля, обычно доступна при высоких оборотах двигателя.
Измерение стандартного ускорения (➜ Подробнее: От 0 до 60: Набрать скорость при разгоне) сюда хорошо вписывается: передачи полностью выдвинуты, двигатель работает в высоких (вращательных) диапазонах скоростей, максимальные номинальные можно призвать силу. Чтобы понять крутящий момент и мощность двигателя, а также повседневное использование автомобиля, важно знать, что двигатель внутреннего сгорания достигает своего максимального крутящего момента при частоте вращения ниже максимальной выходной мощности. Поэтому, когда мы говорим о хорошей мощности в нижнем диапазоне оборотов двигателя, мы имеем в виду высокий крутящий момент даже при низких оборотах двигателя. Это полезно знать для ограничения переключения передач при вождении автомобилей с механической коробкой передач. Или для буксировки прицепов в вашем автомобиле и для движения в гору.
Чтобы понять крутящий момент и мощность двигателя, а также повседневное использование автомобиля, важно знать, что двигатель внутреннего сгорания достигает своего максимального крутящего момента при частоте вращения ниже максимальной выходной мощности. Поэтому, когда мы говорим о хорошей мощности в нижнем диапазоне оборотов двигателя, мы имеем в виду высокий крутящий момент даже при низких оборотах двигателя. Это полезно знать для ограничения переключения передач при вождении автомобилей с механической коробкой передач. Или для буксировки прицепов в вашем автомобиле и для движения в гору.
Пример иллюстрирует разницу между крутящим моментом и мощностью двигателя. Если, как водитель автомобиля с двигателем внутреннего сгорания, вы будете следить за циферблатами на дисплее, вы увидите, что по мере увеличения частоты вращения двигателя (об/мин) вы достигнете точки, в которой крутящий момент равен его максимум. В то же время мощность двигателя увеличивается с увеличением оборотов двигателя. Когда водитель чувствует, что мощность двигателя, производительность двигателя падает по отношению к оборотам двигателя, он переключается на более высокую передачу (конечно, автомат делает это сам). Затем обороты двигателя падают, и игра начинается сначала.
Когда водитель чувствует, что мощность двигателя, производительность двигателя падает по отношению к оборотам двигателя, он переключается на более высокую передачу (конечно, автомат делает это сам). Затем обороты двигателя падают, и игра начинается сначала.
Вопреки распространенному мнению (то есть тому, что думают ваши друзья), в повседневной жизни с автомобилем крутящий момент двигателя играет более важную роль, чем (максимальная) мощность двигателя. Это потому, что для сохранения ресурсов — окружающей среды, кошельков людей и их нервов — инженеры хотят, чтобы водители ехали с хорошей тягой в диапазоне низких оборотов двигателя. Что подводит нас к двигателю электромобиля. В чем большой плюс электромобилей? Они обеспечивают полный крутящий момент с самого начала. Безо всяких задержек. Вот почему ускорение электромобилей (➜ Подробнее: Факты об электромобилях со всего мира) так запоминается как водителям, так и пассажирам. И не только это, но и без рывков и без переключения передач, так как многие электромобили идут с одноступенчатой автоматической коробкой передач.
При низких оборотах двигателя важен крутящий момент, при высоких оборотах — мощность двигателя.
Михаэль Гризе
Руководитель проекта по системам электропривода, BMW Group
Эксперт BMW Гриз объясняет, в чем особенность электромобилей. «Высокий крутящий момент электродвигателя позволяет транспортным средствам с такими двигателями эффективно передвигаться и экономить энергию». Максимально возможная скорость, которая достигается за счет высокой мощности двигателя, — не единственная цель электромобилей. Электромобили обладают отличным сцеплением с дорогой, что обеспечивает комфортное и эффективное вождение, но они также не пренебрегают удовольствием от вождения!
Другими словами, максимальный крутящий момент электродвигателя фактически достигается при низких оборотах. «И она остается близкой к постоянной до тех пор, пока вы не достигнете максимальной мощности двигателя», — поясняет далее инженер Гризе. Оттуда крутящий момент падает, а мощность двигателя остается постоянной.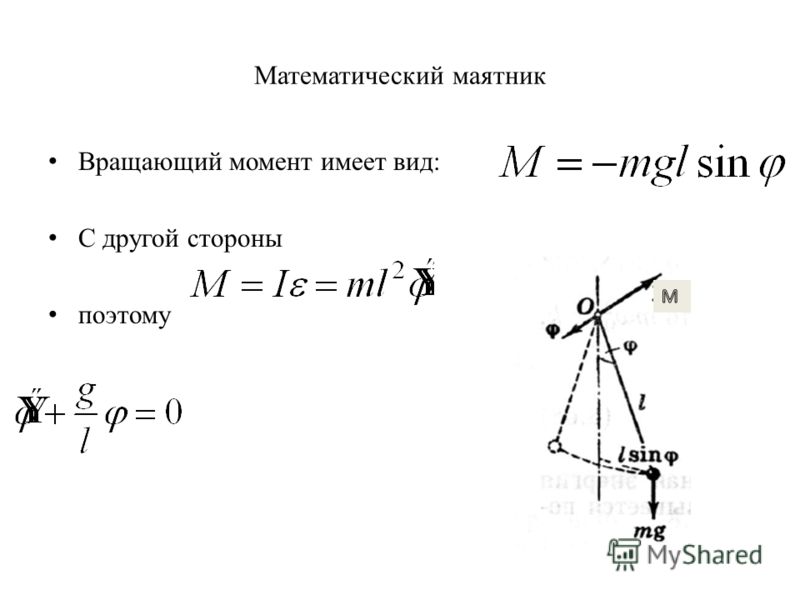 Как только достигается точка максимального крутящего момента, автомобиль больше не разгоняется быстрее. Эксперт BMW Гриз резюмирует следующим образом: «При низких оборотах двигателя важен крутящий момент, при высоких — мощность двигателя».
Как только достигается точка максимального крутящего момента, автомобиль больше не разгоняется быстрее. Эксперт BMW Гриз резюмирует следующим образом: «При низких оборотах двигателя важен крутящий момент, при высоких — мощность двигателя».
Что важнее, высокая мощность двигателя или высокий крутящий момент? Все сводится к тому, что вам как водителю нужно. Если, например, вы предпочитаете высокую максимальную скорость, вы найдете ее в автомобиле с высокой номинальной выходной мощностью. Если, с другой стороны, вы предпочитаете эффективный и комфортный стиль вождения с быстрым стартом на светофоре, вы полагаетесь на фактор крутящего момента — как в случае с электромобилями.
Что такое крутящий момент в автомобиле?
Крутящий момент представляет собой физическую величину, которая указывает тяговое усилие в конструкции двигателя. Физической единицей крутящего момента является ньютон-метр (Нм). Для автомобилей с двигателем внутреннего сгорания цель состоит в том, чтобы как можно раньше достичь высокого крутящего момента при низких оборотах двигателя. В электромобилях крутящий момент доступен сразу, и это преимущество.
В электромобилях крутящий момент доступен сразу, и это преимущество.
Автор: Нильс Арнольд; Иллюстрации: Майкл Блосс; Фото/Видео: BMW
- Automotive Life
- Insight
- Performance
- Technology
10.6 Torque – University Physics Volume 1
10 Fixed Цели обучения
К концу этого раздела вы сможете:
- Описывать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
- Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
- Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент
Важной величиной для описания динамики вращающегося твердого тела является крутящий момент. Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт.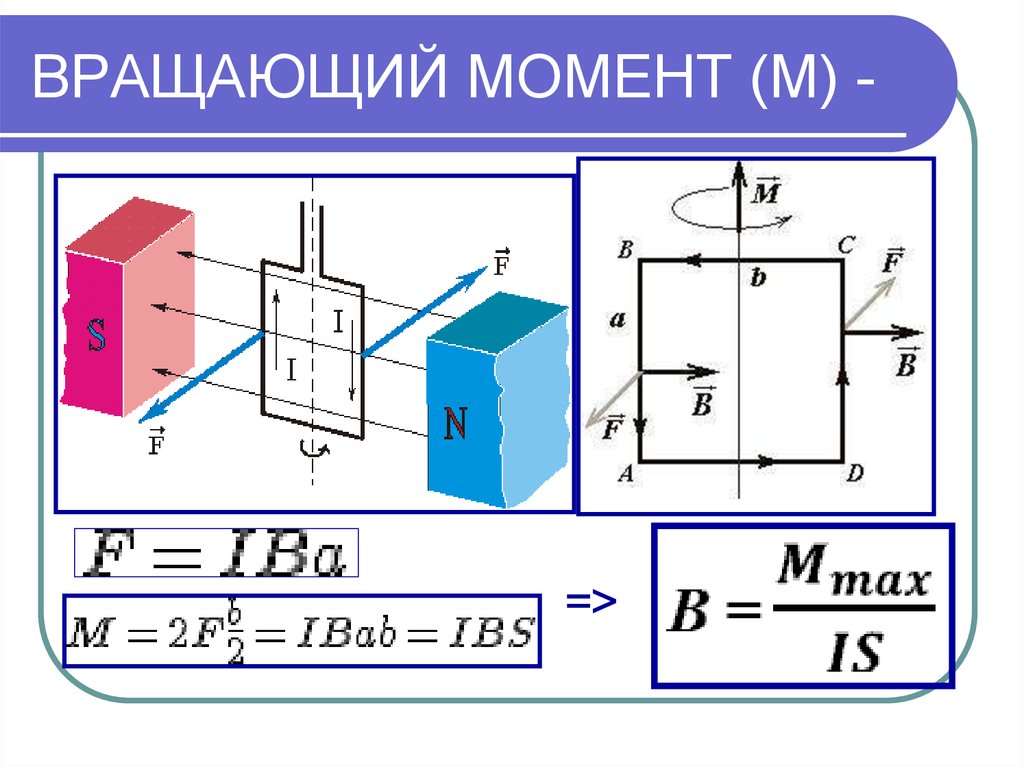 Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Определение крутящего момента
До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .
В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке показано вращение против часовой стрелки.
Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке показано вращение против часовой стрелки. 9\циркуляр[/латекс].
9\циркуляр[/латекс].
Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.
Крутящий момент
Когда сила [латекс]\mathbf{\overset{\to} {F}}[/латекс] приложена к точке P , положение которой равно [латекс]\mathbf{\overset{\ до }{r}}[/latex] по отношению к O (рисунок), крутящий момент [латекс]\mathbf{\overset{\to }{\tau}}[/latex] вокруг O составляет
[ латекс]\mathbf{\overset{\to }{\tau}}=\mathbf{\overset{\to}}{r}}\times \mathbf{\overset{\to}}{F}}.[/latex]
{F}}[/latex] и его направление определяется по правилу правой руки.
Из определения перекрестного произведения крутящий момент [латекс]\mathbf{\overset{\to }{\tau}}[/latex] перпендикулярен плоскости, содержащей [латекс]\mathbf{\overset{\to} {r}}\,\text{and}\,\mathbf{\overset{\to}}{F}}[/latex] и имеет величину
[латекс]|\mathbf{\overset{\to }{\ тау}}|=|\mathbf{\overset{\to}}{r}}\times \mathbf{\overset{\to}}{F}}|=rF\text{sin}\,\theta,[/latex ]
, где [латекс]\тета[/латекс] — угол между векторами [латекс]\mathbf{\overset{\to }{r}}[/латекс] и [латекс]\mathbf{\overset{\to {F}}[/латекс]. Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как [латекс]\текст{Н}\cdot \текст{м}[/латекс]. Величина [latex]{r}_{\perp }=r\text{sin}\,\theta[/latex] представляет собой расстояние по перпендикуляру от O до линии, определяемой вектором [latex]\mathbf{\ перетянут {\to} {F}}[/латекс] и называется плечом рычага . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В пересчете на плечо рычага величина крутящего момента составляет
Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как [латекс]\текст{Н}\cdot \текст{м}[/латекс]. Величина [latex]{r}_{\perp }=r\text{sin}\,\theta[/latex] представляет собой расстояние по перпендикуляру от O до линии, определяемой вектором [latex]\mathbf{\ перетянут {\to} {F}}[/латекс] и называется плечом рычага . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В пересчете на плечо рычага величина крутящего момента составляет
[латекс]|\mathbf{\overset{\to }{\tau}}|={r}_{\perp}F.[/latex]
Перекрестное произведение [латекс]\mathbf{\overset{ \to }{r}}\times \mathbf{\overset{\to }{F}}[/latex] также сообщает нам знак крутящего момента. На рисунке перекрестное произведение [латекс]\mathbf{\overset{\to }{r}}\times \mathbf{\overset{\to }{F}}[/latex] расположено вдоль положительной оси z , что условно является положительным крутящим моментом. Если [латекс]\mathbf{\overset{\to }{r}}\times \mathbf{\overset{\to }{F}}[/latex] расположен вдоль минус 9\circ[/latex], крутящий момент максимальный и диск вращается с максимальным угловым ускорением.
Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно указанной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:
[латекс] {\ mathbf {\ overset {\ to }{\tau}}}_{\text{net}}=\sum _{i}|{\mathbf{\overset{\to}}{\tau}}}_{i}|.[/latex]
Расчет чистого крутящего момента для твердых тел на неподвижной оси
В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу.
Сначала мы представляем стратегию решения проблем.
Стратегия решения проблем: определение чистого крутящего момента
- Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
- Определите угол между плечом рычага [латекс]\mathbf{\overset{\to }{r}}[/латекс] и вектором силы.

- Возьмите векторное произведение [латекс]\mathbf{\overset{\to }{r}}\,\text{and}\,\mathbf{\overset{\to }{F}}[/latex], чтобы определить если крутящий момент положительный или отрицательный относительно точки вращения или оси.
- Оцените величину крутящего момента, используя [латекс]{r}_{\perp}F[/латекс].
- Присвойте величине соответствующий знак, положительный или отрицательный.
- Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.
Пример
Расчет крутящего момента
Четыре силы показаны на рисунке в определенных местах и ориентациях по отношению к данному xy -система координат. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.
Рисунок 10.34 Четыре силы, создающие крутящие моменты.
Стратегия
Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя перекрестное произведение [латекс]\mathbf{\overset{\to}}{r}}[/латекс] и вектора силы [латекс]\mathbf{\overset{\ в {F}}[/latex]. 9\circ=10\,\text{N}\cdot \text{m}[/latex].
Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя перекрестное произведение [латекс]\mathbf{\overset{\to}}{r}}[/латекс] и вектора силы [латекс]\mathbf{\overset{\ в {F}}[/latex]. 9\circ=10\,\text{N}\cdot \text{m}[/latex].
Перекрестное произведение [латекс]\mathbf{\overset{\to }{r}}[/латекс] и [латекс]\mathbf{\overset{\to }{F}}[/латекс] не соответствует страница.
Таким образом, чистый крутящий момент равен [латекс]{\tau}_{\text{net}}=\sum _{i}|{\tau}_{i}|=160-60+120+10=230\ ,\text{N}\cdot \text{m}\text{.}[/latex]
Значение
Обратите внимание, что каждая сила, действующая в направлении против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая в направлении по часовой стрелке направление имеет отрицательный крутящий момент.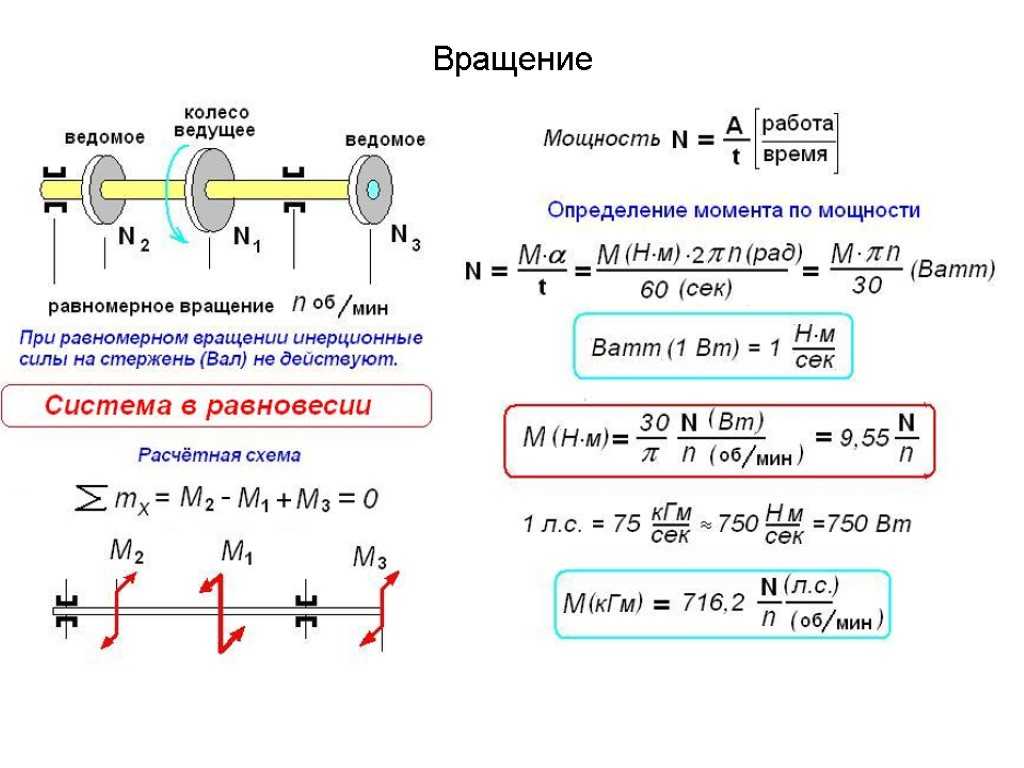 Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.
Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.
Пример
Расчет крутящего момента на твердом телеНа рисунке показано несколько сил, действующих в разных местах и под разными углами на маховик. У нас есть [латекс]|{\mathbf{\overset{\to}}{F}}}_{1}|=20\,\text{N},[/latex] [латекс]|{\mathbf{\overset {\to }{F}}}_{2}|=30\,\text{N}[/латекс], [латекс]|{\mathbf{\overset{\to}}{F}}}_{3 }|=30\,\text{N}[/latex] и [latex]r=0,5\,\text{m}[/latex]. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.
Рисунок 10.35 Три силы, действующие на маховик. 9\circ=-0.5\,\text{m}(30\,\text{N})=-15.0\,\text{N}\cdot \text{m}.[/latex] Когда мы оцениваем крутящий момент из-за [латекса] {\ mathbf {\ overset {\ to } {F}}} _ {3} [/ латекса], мы видим, что угол, который он образует с [латексом] \ mathbf {\ overset {\ to} {r}}[/latex] равно нулю, поэтому [latex]\mathbf{\overset{\to }{r}}\times {\mathbf{\overset{\to}}{F}}}_{3}=0 . [/latex] Следовательно, [latex]{\mathbf{\overset{\to}}{F}}}_{3}[/latex] не создает крутящего момента на маховике.
[/latex] Следовательно, [latex]{\mathbf{\overset{\to}}{F}}}_{3}[/latex] не создает крутящего момента на маховике.
Оцениваем сумму моментов:
[латекс] {\ tau} _ {\ text {net}} = \ sum _ {i} | {\ tau } _ {i} | = 5-15 = -10 \, \ text {N} \ cdot \ text{m}.[/latex]
Значение
Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был закреплен на месте, [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {3} [/ латекс] заставил бы маховик перемещаться, а также [ латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} [/ латекс]. Его движение было бы комбинацией поступательного движения и вращения. 9{7}\text{N}\cdot \text{m}[/latex].
Резюме
- Величина крутящего момента относительно фиксированной оси рассчитывается путем нахождения плеча рычага в точке приложения силы и использования соотношения [латекс]|\mathbf{\overset{\to}{\tau} }|={r}_{\perp}F[/latex], где [latex]{r}_{\perp}[/latex] — расстояние по перпендикуляру от оси до линии, на которой лежит вектор силы.

- Знак крутящего момента находится по правилу правой руки. Если страница представляет собой плоскость, содержащую [латекс]\mathbf{\overset{\to }{r}}[/latex] и [латекс]\mathbf{\overset{\to }{F}}[/латекс], то [латекс]\mathbf{\overset{\to }{r}}\times \mathbf{\overset{\to }{F}}[/latex] находится за пределами страницы для положительных крутящих моментов и на странице для отрицательных крутящих моментов .
- Чистый крутящий момент можно найти путем суммирования отдельных крутящих моментов относительно заданной оси.
Концептуальные вопросы
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
Показать решениеВеличина силы, длина плеча рычага, угол плеча рычага и вектор силы
Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила действует на малый крутящий момент.
При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
Момент инерции колес уменьшен, поэтому для их ускорения требуется меньший крутящий момент.
Может ли одна сила создать нулевой крутящий момент?
Может ли набор сил иметь чистый крутящий момент, равный нулю, и результирующую силу, отличную от нуля?
Показать решениеда
Может ли набор сил иметь результирующую силу, равную нулю, и результирующий крутящий момент, отличный от нуля?
В выражении [латекс]\mathbf{\overset{\to }{r}}\times \mathbf{\overset{\to }{F}}[/latex] может [латекс]|\mathbf{\overset {\to }{r}}|[/latex] всегда меньше, чем плечо рычага? Может ли оно быть равно плечу рычага?
Показать решение[латекс]|\mathbf{\overset{\to }{r}}|[/латекс] может быть равно плечу рычага, но не меньше, чем плечо рычага
Проблемы
Два маховика незначительной массы и разных радиусов соединены вместе и вращаются вокруг общей оси (см.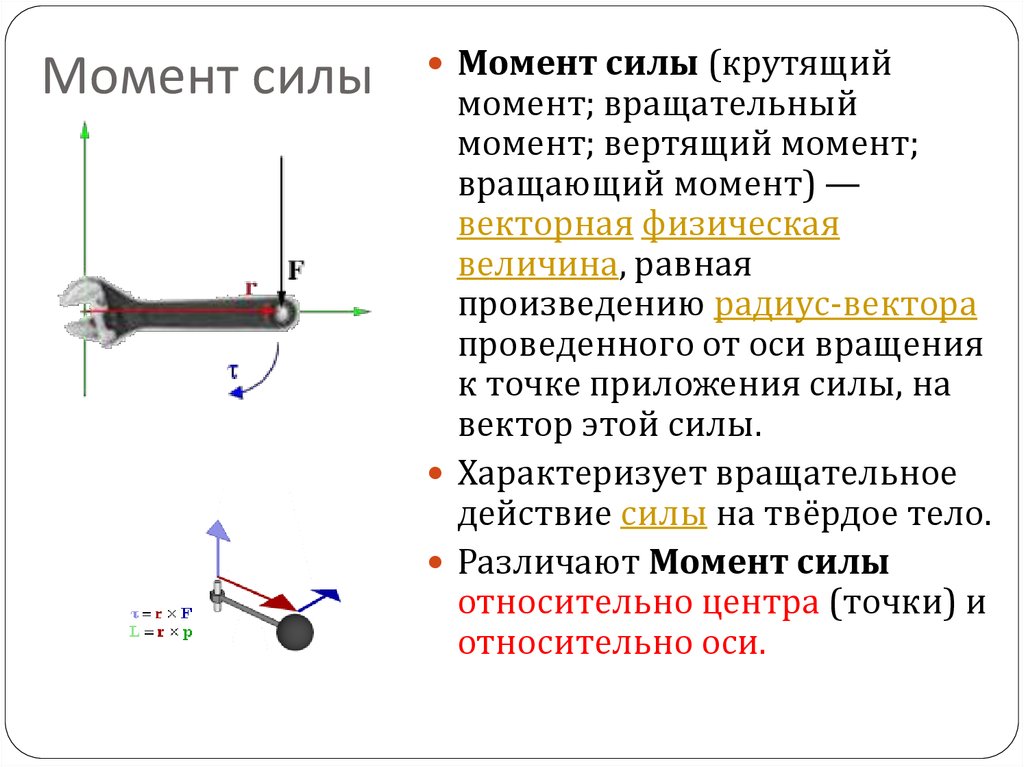 ниже). Меньший маховик радиусом 30 см имеет шнур, на который действует тяговое усилие 50 Н. Какую тяговую силу нужно приложить к шнуру, соединяющему больший маховик радиусом 50 см, чтобы комбинация не вращалась?
ниже). Меньший маховик радиусом 30 см имеет шнур, на который действует тяговое усилие 50 Н. Какую тяговую силу нужно приложить к шнуру, соединяющему больший маховик радиусом 50 см, чтобы комбинация не вращалась?
[латекс]F=30\,\текст{N}[/латекс]
Болты с цилиндрической головкой на автомобиле затягивать с моментом 62,0 Н[латекс]\cdot \text{м}[/латекс]. Если механик использует ключ длиной 20 см, какую перпендикулярную силу он должен приложить к концу ключа, чтобы правильно затянуть болт?
(а) Открывая дверь, вы толкаете ее перпендикулярно с силой 55,0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете к петлям? (b) Имеет ли значение, если вы нажмете на той же высоте, что и петли? Есть только одна пара петель.
Показать раствора. [латекс]0,85\,\текст{м}(55,0\,\текст{N})=46,75\,\текст{N}\cdot \текст{м}[/латекс]; б. Неважно, на какой высоте вы нажимаете.
При затяжке болта ключ нажимают перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. \circ[/латекс] к земле (см. следующий рисунок). Стержень расположен на высоте 6,0 м. Какую силу необходимо приложить перпендикулярно качелям на поднятом конце, чтобы качели едва начали вращаться? 9{3}\text{N}\cdot \text{m}\,[/latex] требуется, чтобы поднять разводной мост (см. следующий рисунок). Какое напряжение необходимо для создания этого крутящего момента? Было бы легче поднять разводной мост, если бы угол [латекс]\тета[/латекс] был больше или меньше?
\circ[/латекс] к земле (см. следующий рисунок). Стержень расположен на высоте 6,0 м. Какую силу необходимо приложить перпендикулярно качелям на поднятом конце, чтобы качели едва начали вращаться? 9{3}\text{N}\cdot \text{m}\,[/latex] требуется, чтобы поднять разводной мост (см. следующий рисунок). Какое напряжение необходимо для создания этого крутящего момента? Было бы легче поднять разводной мост, если бы угол [латекс]\тета[/латекс] был больше или меньше?
Горизонтальная балка длиной 3 м и массой 2,0 кг имеет массу 1,0 кг и ширину 0,2 м на конце балки (см. следующий рисунок). Чему равен крутящий момент системы относительно опоры у стены?
Показать ответ[латекс]\сумма\тау =57.82\,\текст{N}\cdot \текст{м}[/латекс]
Какую силу необходимо приложить к концу стержня вдоль оси x длиной 2,0 м, чтобы создать крутящий момент на стержне относительно начала координат [латекс]8,0\mathbf{\hat{k}}\, \text{N}\cdot \text{m}[/latex]?
Каков крутящий момент относительно источника силы [латекс](5,0\mathbf{\шляпа{i}}-2,0\mathbf{\шляпа{j}}+1,0\mathbf{\шляпа{k}})\ ,\text{N}[/latex], если применяется в точке, положение которой равно: [latex]\mathbf{\overset{\to }{r}}=(-2.


 также
также также
также
