Восьмеричная система счисления
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
Основание S = 8
Базис – степени числа 8: 80, 81, 82, 83, …или1, 8, 64, 512, …
Представим любое восьмеричное число через его цифры и веса разрядов:
35728 = 2×80 + 7×81 + 5×82 + 3×83 = 2×1 + 7×8 + 5×64 + 3×512 = 191410
Этим же способом любое восьмеричное число переводится в десятичную систему счисления.
Обратный перевод – из десятичной в восьмеричную систему счисления – осуществляется последовательным деление десятичного числа на основание восьмеричной системы счисления
1914/8 = 239остаток2
239/8 = 29остаток7
29/8 = 3остаток5
3/8 = 0остаток3, получаем 35728.
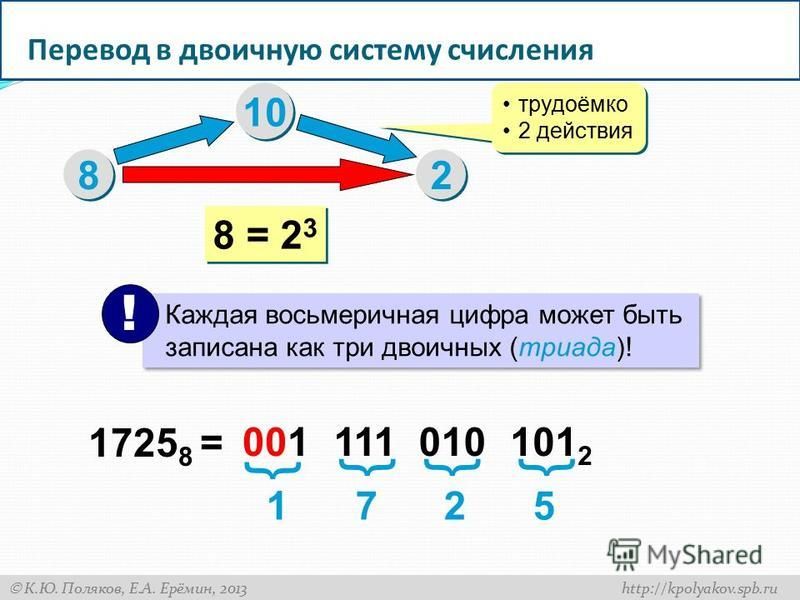
Особый случай перевода – двоично-восьмеричный
Для перевода двоичного числа в восьмеричное необходимо:
1.разбить двоичное число справа налево потрицифры (недостающие слева дополнить нулями):
10011000101
2.каждую тройку цифр представить числом в восьмеричной системе счисления:
010 011 000 1012 = 23058
2 3 0 5
Для перевода восьмеричного числа в двоичное необходимо каждую цифру восьмеричного числа представить ее трехразряднымдвоичным эквивалентом:
23058 = 010 011 000 1012
2 3 0 5
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,

Основание S = 16
Базис – степени числа 16: 160, 161, 162
Представим любое 16-ричное число через его цифры и веса разрядов:
A5D16 = D×160 + 5×161 + A×162 = 13×1 + 5×16 + 10×256 = 265310
Этим же способом любое 16-ричное число переводится в десятичную систему счисления.
Обратный перевод – из десятичной в 16-ричную систему счисления – осуществляется последовательным деление десятичного числа на основание 16-ричной системы счисления
2653/16 = 165остаток13, то естьD
165/16 = 10остаток5
10/16 = 0остаток10, то естьA, получаем A5D16.
Особый случай перевода – двоично-шестнадцатеричный
Для перевода двоичного числа в 16-ричное необходимо:
1.разбить двоичное число справа налево почетырецифры (недостающие слева дополнить нулями):
100110001012 = 0100 1100 01012
2.каждую четверку цифр представить числом в 16-ричной системе счисления:
0100 1100 01012 = 4C516
4 12=C 5
Для перевода 16-ричного числа в двоичное необходимо каждую цифру 16-ричного числа представить ее четырехразряднымдвоичным эквивалентом:
A
A 5 D
Для быстрого перевода чисел из одной системы счисления в другую полезно запомнить следующую таблицу соответствия:
10-я | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
2-я | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
16-я | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Системы счисления — презентация онлайн
Составила учитель информатики школы №841
Марина С. А.
А.
Цели урока:
1) Закрепить понятия «число», «цифра»
2) Раскрыть понятия «система счисления»,
«алфавит» системы счисления
3) Ознакомить учащихся с историей развития
систем счисления и дать их классификацию
4) Закрепить умения:
— представление числа в различных системах счисления
— представление числа в развернутой и свернутой формах
— научиться переводить числа из различных систем
счисления в десятичную
Содержание
1. Основные понятия. Виды систем счисления
2. Непозиционные системы счисления
3. Позиционные системы счисления
4. Десятичная система счисления
5. Двоичная система счисления
6. Восьмеричная система счисления
7. Шестнадцатеричная система счисления
8. Перевод чисел в десятичную сс
9. Задания для самостоятельного выполнения
Основные понятия
Система счисления — это способ записи чисел и
правила действий над этими
числами
Число — это величина, а не символьная запись
Цифра — набор символов, участвующих в
записи числа
Алфавит
— совокупность различных цифр,
используемых для записи числа
Позиционные
Непозиционные
значение цифры
зависит
не зависит
от ее позиции в числе
323
Три
сотни
XIX
Три
единицы
десять
десять
Непозиционные системы счисления
• единичная
• древнеегипетская
• вавилонская
• римская
I,V,X,L,C,D,M
• алфавитная
колода
Позиционные системы счисления
Каждая
позиционная
система
определенный алфавит и основание.
счисления
имеет
Количество цифр – основание (p)
системы счисления
Совокупность всех цифр – алфавит
Позиционные системы могут иметь различный алфавит (2,3,4 знака).
Позиция цифры в числе называется разрядом.
Для записи чисел в позиционной системе с основанием р нужно
иметь алфавит из р цифр. При р > 10 к десяти арабским
цифрам добавляют латинские буквы.
Алфавиты систем счисления
Основание Название
Алфавит
р=2
Двоичная
01
р=3
Троичная
012
р=8
Восьмеричная
01234567
р = 16
Шестнадцатеричная
0123456789ABCDEF
ПРИМЕРЫ: (перепиши, вставляя пропущенные числа)
1. p = 10 (десятичная с/c)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 и т.д.
2. p = 4 (четверичная с/c)
31 32
33 100
1 2 3 10 11 12 13 20 21 22 23 30 __
__ __
__
3. p = 2 (двоичная с/c)
10011010 1011 ____
1100 ___
1101
1 10 11 100 101 110 111 1000 ___
1110
___ 1111
___ 10000 10001
_____ 10010
_____
4. p = 16 (шестнадцатеричная с/c)
p = 16 (шестнадцатеричная с/c)
1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18
1C ___
1D ___
1E ___
1F
19 1A 1B ___
Вопрос для обсуждения
В наше время для записи чисел чаще всего используются
две системы счисления:
— арабская десятичная (цифры 0,1,2,3,4,5,6,7,8,9)
— римская (цифры I,V,X,L,C,M)
1.Где сегодня
используется
римская
система счисления для записи чисел?
Рассмотрим 2 числа: XXX и 333.
2.Чем
отличается
принцип
записи
многозначных чисел в римской и арабской
системах счисления?
Десятичная система счисления
Получив название арабской эта система счисления, в XII веке
распространилась по всей Европе.
Система счисления, применяемая в современной
математике, является позиционной десятичной
системой.
Её основание равно десяти, т.к. запись любых
чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — алфавит.
Рассмотрим десятичное число 555:
Число записано в привычной для нас свернутой
форме:
В зависимости от позиции цифра 5 обозначает единицы,
десятки, сотни.
5 5 5 10
с
о
т
н
и
д
е
с
я
т
к
и
е
д
и
н
и
ц
ы
Из двух написанных
рядом одинаковых цифр
левая в десять раз
больше правой.
В развернутой форме записи числа умножение
цифр производится в явной форме:
Любое число в нулевой
степени равно 1
55510 = 5·102 + 5·101 + 5·100
Для записи десятичных дробей используются
разряды с отрицательными значениями степеней
основания:
Любое число в отрицательной степени =
единица / число в положительной степени:
10 -1 =1/10 1 , 10-2 = 1/102
555,5510 = 5·102 + 5·101 + 5·100 + 5·10-1 + 5·10-2
2 1 0 -1 -2
Степень основания
Первый разряд цифры, стоящей слева от
Основание системы счисления
запятой равен 0
Номер разряда стоящей в нем цифры равен
значению степени основания
Вопрос для обсуждения
1) В какой системе счисления удобнее считать?
2) Почему арабская система называется
десятичной?
Двоичная система счисления
Информация в компьютере представлена в двоичном коде.
Используется двоичная система счисления.
Двоичная
система
счисления
позиционной системой счисления.
является
Алфавит двоичной системы – две цифры (0,1),
основание равно 2.
Из двух написанных рядом одинаковых цифр левая в два раза
больше правой.
Число в свернутой форме записывается так:
101,012
В развернутой форме число записывается в виде
суммы
ряда
степеней
основания
2
с
коэффициентами, в качестве цифр 0 или1.
101,012 = 1·22 + 0·21 + 1·20 + 0·2-1 + 1·2-2 = 5,2510
2 1 0 -1 -2
Степень основания
Первый разряд цифры, стоящей слева от
Основаниезначение
Вычислив
системысуммы,
счисления
получаем число
запятой равен 0
в десятичной
системе
счисления
Номер разряда
стоящей
в нем
цифры равен
значению степени основания
Восьмеричная система счисления
Широко используется в информатике.
Восьмеричная система счисления
позиционной системой счисления.
является
Алфавит восьмеричной системы – цифры
(0,1,2,3,4,5,6,7), основание равно 8.
Из двух написанных рядом одинаковых цифр левая в восемь раз
больше правой.
Число в свернутой форме записывается так:
137,28
В развернутой форме число записывается в виде
суммы
ряда
степеней
основания
8
с
коэффициентами, в качестве цифр от 0 до 7.
137,28 = 1·82 + 3·81 + 7·80 + 2·8-1 = 95,2510
2 1 0 -1
Степень основания
Первый разряд цифры, стоящей слева от
Основаниезначение
Вычислив
системысуммы,
счисления
получаем число
запятой равен 0
в десятичной
системе
счисления
Номер разряда
стоящей
в нем
цифры равен
значению степени основания
Шестнадцатеричная система
счисления
Широко используется в информатике.
Шестнадцатеричная система счисления является
позиционной системой счисления.
Алфавит шестнадцатеричной системы – цифры
(0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), основание равно
16.
(Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15)
Из двух написанных рядом
одинаковых цифр левая в
шестнадцать раз больше правой.
Число в свернутой форме записывается так:
12A,416
В развернутой форме число записывается в виде
суммы ряда степеней основания 16 с
коэффициентами, в качестве цифр от 0 до F,
выражая шестнадцатеричные цифры через их
десятичное значение (A=10, F=15).
12A,416 = 1·162 + 2·161 + 10·160 + 4·16-1 = 298,2510
2 1 0
-1
Степень основания
Первый разряд цифры, стоящей слева от
Вычислив
Основание
значение
системы
суммы,
счисления
получаем число
запятой равен 0
в десятичной
системе
счисления
Номер разряда
стоящей
в нем
цифры равен
значению степени основания
Алгоритм перевода чисел,
записанных в произвольной системе счисления,
в десятичную систему счисления
1. Записать число в развернутой форме в виде сумм ряда
степеней
основания
системы
счисления
с
коэффициентами в качестве цифр данной системы
счисления.
2. Вычислить полученную сумму.
231,24 = 2·42 + 3·41 + 1·40 + 2·4-1 = 45,510
2 1 0
-1
Переведи в десятичную
сс: основания = номер разряда цифры
Степень
2 + 1·31 системы
Основание
1123 = 1·3
+ 2·30 =счисления
1410
1346 = 1·62 + 3·61 + 4·60 = 5810
Задания для самостоятельного
выполнения
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Какое минимальное основание должна иметь
система счисления, если в ней можно записать
числа:
а) 341
б) 123
в) 222
г) 111
Ответ:
а) 341 (р=5)
б) 123 (р=4)
в) 222 (р=3)
г) 111 (р=2)
Какое число ошибочно записано в:
а) троичной СС – 79, 212, 531
б) девятеричной СС – 419, 832, 4А
Ответ:
а) в троичной СС для записи чисел
используются цифры 0 1 2 , значит цифры 79 и
531 записаны неверно
б) в девятиричной СС для записи чисел
используются цифры 0 1 2 3 4 5 6 7 8, значит
цифры 419 и 4А записаны неверно
Какое максимальное число можно записать в
двоичной
системе
счисления
четырьмя
цифрами?
Переведите полученное число в десятичную
систему счисления.
Ответ:
11112 = 1510.
Определите четное число или нечетное:
а) 1012
б) 1102
в) 10012
г) 1002
Сформулируйте критерий четности в двоичной
системе счисления.
Ответ: четное число в двоичной системе
счисления оканчивается на 0, а нечетное – на 1.
а) 1012 = 510
б) 1102 = 610
в) 10012 = 910
г) 1002 = 410
Было 11 яблок. После того как каждое яблоко
разрезали пополам, стало 110 половинок.
Возможно ли это? Обоснуйте ответ.
Ответ: да,
если считать числа в задаче,
представленными
в
двоичной
системе
счисления:
112= 1 21 + 1 20 = 310;
1102 = 1 22 + 1 21 + 0 20 = 4 + 2 = 610
Выпишите алфавит традиционной позиционной
пятеричной системы счисления.
Переведите число 325
счисления.
в десятичную систему
Ответ: алфавит пятеричной системы счисления
– цифры (0,1,2,3,4).
325 = 3 51 + 2 50 = 15 + 2 = 1710
Домашнее задание:
1) § 4.1.1 стр.104
2) выполнить «задания для самостоятельного
выполнения» № 4. 1, 4.4 на стр.108
1, 4.4 на стр.108
Урок окончен
С этим файлом связано 1 файл(ов). Среди них: Финансовая грамотность .docx. Показать все связанные файлы Подборка по базе: Компьютерное 3D моделирование. Презентация.pptx, Тест по информатике за курс 5 класса.docx, Турченко презентация.pdf, Приложение 1. Презентация 3-5 классы.pptx, Кремовый Базовый Презентация Шаблон.pptx, уланов презентация.pptx, КИМ для промежуточной аттестации по математике и информатике 2 к, Важнейшие особенности рельефа России презентация.ppt, ГДМВ Презентация по неплановому ремонту.pptx Системы счисления Усольцева А.М. Цели презентации: 1) Закрепить понятия «число», «цифра» 2) Раскрыть понятия «система счисления», «алфавит» системы счисления 3) Ознакомить учащихся с историей развития систем счисления и дать их классификацию 4) Закрепить умения: Содержание 1. 2. Непозиционные системы счисления 3. Позиционные системы счисления 4. Десятичная система счисления 5. Двоичная система счисления 6. Восьмеричная система счисления 7. Шестнадцатеричная система счисления 8. Перевод чисел в десятичную сс 9. Задания для самостоятельного выполнения Основные понятия Система счисления — это способ записи чисел и правила действий над этими числами Число — это величина, а не символьная запись Цифра — набор символов, участвующих в записи числа Алфавит — совокупность различных цифр, используемых для записи числа Позиционные Непозиционные зависит не зависит значение цифры от ее позиции в числе 323 XIX Виды систем счисления Непозиционные системы счисления единичная колода I,V,X,L,C,D,M Единичная («палочная система») Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе. или Обозначение: = 3 4 5 — единицы — десятки — сотни Обозначение: Иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Древнеегипетская система 2-ой разряд 1-ый разряд = 60 +20+2 = 82 Вавилонская шестидесятеричная система (2 тысячи лет до н.э.) Первая известная нам система счисления, основанная на позиционном принципе. — единицы — десятки — 60 ; 602 ; 603 ; … ; 60n Обозначение: X X X I I = 32 D X L I I = 542 1000 500 100 50 10 5 1 M D C L X V I Римская система В качестве цифр в римской системе используются: Величина числа суммируется из значений цифр. При этом применяется следующее правило: Значение каждой меньшей цифры, поставленной слева от большей, вычитается из значения большей цифры. Если меньшая цифра стоит справа от большей, их значения складываются. Найдите значения чисел: Алфавитные системы Алфавитной нумерацией пользовались южные и восточные славянские народы. Над буквой, обозначавшей цифру, ставился специальные значок «» («титло»). Обозначение: 1 2 3 4 5 6 7 8 9 10 – основание (p) Совокупность всех цифр – алфавит Количество цифр Позиционные системы могут иметь различный алфавит (2,3,4 знака). Позиционные системы счисления Каждая позиционная система счисления имеет определенный алфавит и основание. системы счисления
Алфавиты систем счисления Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из р цифр. Позиция цифры в числе называется разрядом. ПРИМЕРЫ: (перепиши, вставляя пропущенные числа) 31 32 33 100 1001 1100 1101 1110 1111 10001 10010 1C 1D 1E 1F В наше время для записи чисел чаще всего используются две системы счисления: — римская (цифры I,V,X,L,C,M) Вопрос для обсуждения Рассмотрим 2 числа: XXX и 333. 2.Чем отличается принцип записи многозначных чисел в римской и арабской системах счисления? — арабская десятичная (цифры 0,1,2,3,4,5,6,7,8,9) 1. Десятичная система счисления Получив название арабской эта система счисления, в XII веке распространилась по всей Европе. Система счисления, применяемая в современной математике, является позиционной десятичной системой. Её основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр: Рассмотрим десятичное число 555: 5 5 5 10 единицы десятки сотни Число записано в привычной для нас свернутой форме: В зависимости от позиции цифра 5 обозначает единицы, десятки, сотни. Из двух написанных рядом одинаковых цифр левая в десять раз больше правой. В развернутой форме записи числа умножение цифр производится в явной форме: 55510 = 5·102 + 5·101 + 5·100 Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания: 555,5510 = 5·102 + 5·101 + 5·100 + 5·10-1 + 5·10-2 2 1 0 -1 -2 Номер разряда стоящей в нем цифры равен значению степени основания Первый разряд цифры, стоящей слева от запятой равен 0 Основание системы счисления Степень основания Любое число в нулевой степени равно 1 Любое число в отрицательной степени = единица / число в положительной степени: 10 -1 =1/10 1 , 10-2 = 1/102 1) В какой системе счисления удобнее считать? 2) Почему арабская система называется десятичной? Вопрос для обсуждения Двоичная система счисления Информация в компьютере представлена в двоичном коде. Двоичная система счисления является позиционной системой счисления. Алфавит двоичной системы – две цифры (0,1), основание равно 2. Из двух написанных рядом одинаковых цифр левая в два раза больше правой. В развернутой форме число записывается в виде суммы ряда степеней основания 2 с коэффициентами, в качестве цифр 0 или1. Число в свернутой форме записывается так: 101,012 101,012 = 1·22 + 0·21 + 1·20 + 0·2-1 + 1·2-2 Номер разряда стоящей в нем цифры равен значению степени основания 2 1 0 -1 -2 Первый разряд цифры, стоящей слева от запятой равен 0 Основание системы счисления Степень основания Вычислив значение суммы, получаем число в десятичной системе счисления = 5,2510 Восьмеричная система счисления Широко используется в информатике. Восьмеричная система счисления является позиционной системой счисления. Алфавит восьмеричной системы – цифры (0,1,2,3,4,5,6,7), основание равно 8. Из двух написанных рядом одинаковых цифр левая в восемь раз больше правой. В развернутой форме число записывается в виде суммы ряда степеней основания 8 с коэффициентами, в качестве цифр от 0 до 7. Число в свернутой форме записывается так: 137,28 137,28 = 1·82 + 3·81 + 7·80 + 2·8-1 Номер разряда стоящей в нем цифры равен значению степени основания 2 1 0 -1 Первый разряд цифры, стоящей слева от запятой равен 0 Основание системы счисления Степень основания Вычислив значение суммы, получаем число в десятичной системе счисления = 95,2510 Шестнадцатеричная система счисления Широко используется в информатике. Шестнадцатеричная система счисления является позиционной системой счисления. Алфавит шестнадцатеричной системы – цифры (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), основание равно 16. Из двух написанных рядом одинаковых цифр левая в шестнадцать раз больше правой. (Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15) В развернутой форме число записывается в виде суммы ряда степеней основания 16 с коэффициентами, в качестве цифр от 0 до F, выражая шестнадцатеричные цифры через их десятичное значение (A=10, F=15). Число в свернутой форме записывается так: 12A,416 12A,416 = 1·162 + 2·161 + 10·160 + 4·16-1 Номер разряда стоящей в нем цифры равен значению степени основания 2 1 0 -1 Первый разряд цифры, стоящей слева от запятой равен 0 Основание системы счисления Степень основания Вычислив значение суммы, получаем число в десятичной системе счисления = 298,2510 Алгоритм перевода чисел, 1. Записать число в развернутой форме в виде сумм ряда степеней основания системы счисления с коэффициентами в качестве цифр данной системы счисления. 2. Вычислить полученную сумму. 231,24 = 2·42 + 3·41 + 1·40 + 2·4-1 2 1 0 -1 Основание системы счисления Степень основания = номер разряда цифры = 45,510 1123 = 1346 = 1·32 + 1·31 + 2·30 = 1410 1·62 + 3·61 + 4·60 = 5810 Переведи в десятичную сс: Задания для самостоятельного выполнения Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Ответ: а) 341 (р=5) в) 222 (р=3) Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: Ответ: а) в троичной СС для записи чисел используются цифры 0 1 2 , значит цифры 79 и 531 записаны неверно б) в девятиричной СС для записи чисел используются цифры 0 1 2 3 4 5 6 7 8, значит цифры 419 и 4А записаны неверно Какое число ошибочно записано в:
б) девятеричной СС – 419, 832, 4А Ответ: 11112 = 1510.  Какое максимальное число можно записать в двоичной системе счисления четырьмя цифрами? Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1. Определите четное число или нечетное: Ответ: да, если считать числа в задаче, представленными в двоичной системе счисления: Было 11 яблок. После того как каждое яблоко разрезали пополам, стало 110 половинок. Ответ: алфавит пятеричной системы счисления – цифры (0,1,2,3,4). Выпишите алфавит традиционной позиционной пятеричной системы счисления. |
Системы счисления. Перевод чисел в десятичную систему счисления презентация, доклад
Системы счисления. Перевод чисел в десятичную систему счисления.
Основные понятия
Система счисления
— это способ записи чисел и правила действий над этими числами
Число
— это величина, а не символьная запись
Цифра
— набор символов, участвующих в записи числа
Алфавит
— совокупность различных цифр, используемых для записи числа
зависит
не зависит
Непозиционные системы счисления
– основание (p)
Совокупность всех цифр
– алфавит
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит и основание.
системы счисления
Алфавиты систем счисления
Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из р цифр. При р > 10 к десяти арабским цифрам добавляют латинские буквы.
Позиция цифры в числе называется разрядом.
Система счисления, применяемая в современной математике, является позиционной десятичной системой.
Её основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — алфавит.
Развернутая запись числа:
54610 = 5·102 + 4·101 + 6·100
2 1 0
Двоичная система счисления является позиционной системой счисления.
Алфавит двоичной системы – две цифры (0,1), основание равно 2.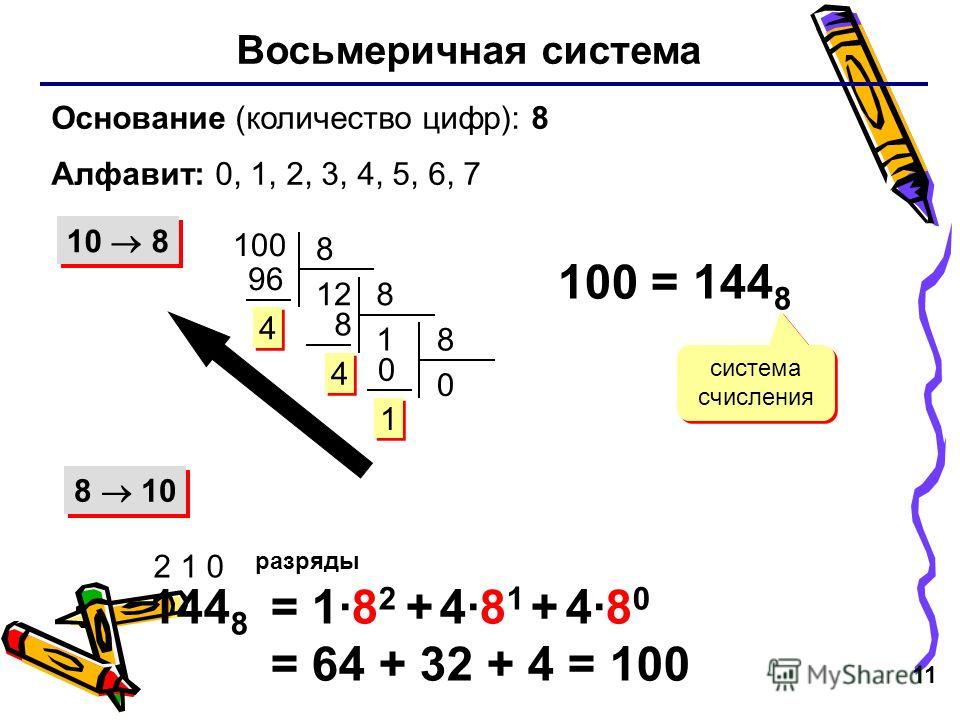
Из двух написанных рядом одинаковых цифр левая в два раза больше правой.
В развернутой форме число записывается в виде суммы ряда степеней основания 2 с коэффициентами, в качестве цифр 0 или1, сумма является десятичной записью двоичного числа.
Число в свернутой форме записывается так:
1012
101012 = 1·24 + 0·23 + 1·22 + 0·21 + 1·20
2 1 0
= 510
1012 = 1·22 + 0·21 + 1·20
1002 = 1·22 + 0·21 + 0·20
4 3 2 1 0
2 1 0
= 2110
= 410
Восьмеричная система счисления
Восьмеричная система счисления является позиционной системой счисления.
Алфавит восьмеричной системы – цифры (0,1,2,3,4,5,6,7), основание равно 8.
Из двух написанных рядом одинаковых цифр левая в восемь раз больше правой.
В развернутой форме число записывается в виде суммы ряда степеней основания 8 с коэффициентами, в качестве цифр от 0 до 7, сумма является десятичной записью восьмеричного числа.
Число в свернутой форме записывается так:
1378
1378 = 1·82 + 3·81 + 7·80
2 1 0
= 9510
378 = 3·81 + 7·80
15618 = 1·83 + 5·82 + 6·81 + 1·80
1 0
3 2 1 0
= 3110
= 88110
Шестнадцатеричная система счисления является позиционной системой счисления.
Алфавит шестнадцатеричной системы – цифры (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), основание равно 16.
Из двух написанных рядом одинаковых цифр левая в шестнадцать раз больше правой.
(Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15)
В развернутой форме число записывается в виде суммы ряда степеней основания 16 с коэффициентами, в качестве цифр от 0 до F, выражая шестнадцатеричные цифры через их десятичное значение (A=10, F=15), сумма является десятичной записью шестнадцатеричного числа.
Число в свернутой форме записывается так:
12A,416
12A16 = 1·162 + 2·161 + 10·160
2 1 0
= 29810
Алгоритм перевода чисел,
записанных в произвольной системе счисления,
в десятичную систему счисления
1. Записать число в развернутой форме в виде сумм ряда степеней основания системы счисления с коэффициентами в качестве цифр данной системы счисления.
2. Вычислить полученную сумму.
2314 = 2·42 + 3·41 + 1·40
2 1 0
= 45,510
1123 =
1346 =
1·32 + 1·31 + 2·30 = 1410
1·62 + 3·61 + 4·60 = 5810
Переведи в десятичную сс:
2 1 0
2 1 0
Задания для тренировки
Ответ: а) 341 (р=5) в) 222 (р=3)
б) 123 (р=4) г) 111 (р=2)
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа:
а) 341
б) 123
в) 222
г) 111
Ответ: а) в троичной СС для записи чисел используются цифры 0 1 2 , значит цифры 79 и 531 записаны неверно
б) в девятиричной СС для записи чисел используются цифры 0 1 2 3 4 5 6 7 8, значит цифры 419 и 4А записаны неверно
Какое число ошибочно записано в:
а) троичной СС – 79, 212, 531
б) девятеричной СС – 419, 832, 4А
Ответ: 11112 = 1510.
Какое максимальное число можно записать в двоичной системе счисления четырьмя цифрами?
Переведите полученное число в десятичную систему счисления.
Ответ: алфавит пятеричной системы счисления – цифры (0,1,2,3,4).
325 = 3⋅51 + 2⋅50 = 15 + 2 = 1710
Выпишите алфавит традиционной позиционной пятеричной системы счисления.
Переведите число 325 в десятичную систему счисления.
Домашнее задание:
Переведите число 368 в десятичную систему счисления.
Переведите число 3916 в десятичную систему счисления.
Переведите число 101102 в десятичную систему счисления.
Переведите число 1001112 в десятичную систему счисления.
Переведите число 1678 в десятичную систему счисления.
Переведите число 1E16 в десятичную систему счисления.
Переведите число 2438 в десятичную систему счисления.
Переведите число 1658 в десятичную систему счисления.
Переведите число 100000012 в десятичную систему счисления.
Переведите число 11016 в десятичную систему счисления.
Переведите число 10001012 в десятичную систему счисления.
Доклад Системы счисления по информатике 5, 8 класс сообщение
- Энциклопедия
- Разное
- Системы счисления
Мы привыкли к цифрам, которые называются арабскими. Называются они так, потому что впервые были обоснованны и напечатаны на арабском языке. Это несложно и не составляет проблем для понимания. В системе счисления эти же самые цифры будут называться десятичными. Почему? Ответ на этот вопрос также не труден. Всё потому, что при счёте мы используем всего 10 цифр от 0 до 9, а затем они начинают повторяться.
Но десятичная система счисления – не единственная. Их существует множество. Рассмотрим самые популярные из них:
Двоичная система счисления
В этой системе счисления используются только две цифры: 0 и 1. Единица представляет собой степень двойки. Чем больше единиц в записи, тем больше число. На двоичной системе вычисления построена работа многих современных вычислительных машин. Например, число 1001 в двоичной системе счисления, это тоже самое что 9 в десятичной. Расчёт ведётся так: справа – налево в двоичном числе проставляются степени, затем единицы «заменяются» на двойки возводятся в степень и складываются между собой. Так, если мы проведём эту процедуру с числом 1001. То мы получим: 2 в 0 степени + 2 в третьей степени или 1 + 8 получим 9.
Чем больше единиц в записи, тем больше число. На двоичной системе вычисления построена работа многих современных вычислительных машин. Например, число 1001 в двоичной системе счисления, это тоже самое что 9 в десятичной. Расчёт ведётся так: справа – налево в двоичном числе проставляются степени, затем единицы «заменяются» на двойки возводятся в степень и складываются между собой. Так, если мы проведём эту процедуру с числом 1001. То мы получим: 2 в 0 степени + 2 в третьей степени или 1 + 8 получим 9.
Пятеричная система счисления
В этой системе счисления существует всего пять цифр. Поэтому основанием данной системы является пятёрка. Чтобы возвести число из десятичной системы в пятеричную, необходимо делить это число на пять записывая остатки. После того, как при делении не останется целой части, деление прекращается, а остатки складываются снизу вверх. Например число 24( 10-чная система счисления) в пятеричной системе будет выглядеть как 44. 24/5 = 4 и 4 в остатке. 4/5 = 0 и 4 в остатке, остатки записываем считая снизу вверх. То есть, если бы при первом делении у нас получилось пять, то число выглядело бы как 45, а не 54.
То есть, если бы при первом делении у нас получилось пять, то число выглядело бы как 45, а не 54.
Восьмеричная система счисления
В ней действуют все те же законы и правила, что и в пятеричной. Единственным отличием является только то, что основанием системы здесь является восьмёрка, тот же принцип, существует и во всех остальных системах счисления, для наглядности, переведём число 45 десятичной системы в восьмеричную: 45/8 = 5 и 5 остаток. 5/8 = 0 и 5 остаток. В итоге получается число 55. В шестнадцатеричной системе это число будет выглядеть как 2D( после 9 все числа заменяются на буквы английского алфавита по порядку A – 10 B -11 C – 12 и так далее).
Вариант №2
Системы счисления (СС) – это последовательность цифр и английских букв, записанная по определенным правилам. СС бывают позиционными и непозиционными. Позиционные системы – это такие системы, в которых определенный символ числа имеет различное значение, находясь на различных позициях. Например, десятичная система является позиционной. Число 25 не равно числу 52, так как определенный символ, например 5, зависит от местоположения. В непозиционных системах счисления символ не зависит от расположения в числе.
Число 25 не равно числу 52, так как определенный символ, например 5, зависит от местоположения. В непозиционных системах счисления символ не зависит от расположения в числе.
Самые распространенные системы: десятичная, восьмеричная, двоичная, шестнадцатеричная. В десятичной системе алфавит состоит из цифр от 0 до 9. Можно производить над числами этой системы такие операции, как сложение, вычитание, деление и умножение.
Алфавит восьмеричной системы имеет 8 символов и состоит из цифр от 0 до 7; алфавит двоичной – из двух цифр: 0 и 1. Самая необычная СС – шестнадцатеричная. В ее алфавит входят арабские цифры от 0 до 9, а так же английские большие буквы от A до F. Операции над числами можно проводить такие же, как с числами десятичной системы счисления.
Самая неклассическая СС – это троичная система. Это позиционная СС с основанием 3. Она бывает двух видов: несимметричная и симметричная троичная система. В несимметричную систему входят цифры: 0,1,2. Симметричная система состоит из цифр -1,0,1. Такая система встречается в физике. Например, ток может течь как в одну сторону, так и в другую. В первом случае можно использовать цифру 1, во втором случае -1, а отсутствия тока можно обозначить цифрой 0.
Такая система встречается в физике. Например, ток может течь как в одну сторону, так и в другую. В первом случае можно использовать цифру 1, во втором случае -1, а отсутствия тока можно обозначить цифрой 0.
Таким образом, системы счисления – это очень важный раздел в информатике. Одно и то же число в разной системе может быть представлено по-разному. В информатике самая распространенная система – двоичная. Компьютер работает с двоичным кодом, поэтому двоичная СС – одна из интересных и сложных тем в информатике.
5, 8 класс по информатике
Системы счисления
Популярные темы сообщений
- Иммунитет
Каждый человек в мире хоть раз болел какой-нибудь болезнью. Кто-то переносит ее легко, кто-то с осложнениями. Но что же нам помогает избавиться от болезни или даже вообще не дает нам заболеть? Руки? Ноги? Глаза? Нос? Конечно же, нет.
- Ян Гус
Каждый год 6 июля во всей Чехии зажигаются костры – так жители этой страны чтят память о своем национальном герое – Яне Гусе.
 Почему же, по прошествии почти 650 лет, чехи помнят об этом человеке и считают его героем?
Почему же, по прошествии почти 650 лет, чехи помнят об этом человеке и считают его героем? - Дания
На Севере Европы есть небольшое Королевство, называется оно Дания. Живет здесь около 6 миллионов человек, именуются датчанами. Руководит страной королева Маргрете Вторая. Государственный язык – датский, но многие жители хорошо владеют
- Химическая промышленность
Можно сказать, что химическая промышленность занимается изменением химического строения природных материалов, впоследствии получая весьма ценные продукты, предназначенные для использования в других отраслях промышленности.
- Клевер
Клевер – это род растений. Этот род включает в себя почти три сотни разновидностей по всему миру. Самым распространенным видом клевера считается клевер луговой – тот самый цветочек, который часто растет на клумбах как сорняк
Качественные и количественные характеристики информации 8 класс онлайн-подготовка на Ростелеком Лицей
Введение
Оценивать информацию можно по-разному. Качественные характеристики информации (ценность, понятность, актуальность, новизна, полнота, достоверность и т. д.) нам известны, поскольку мы постоянно их используем. Например, информация о расписании уроков на вчерашний день не обладает актуальностью. Если нам сообщили расписание на завтра, но только на первые четыре урока вместо шести, эта информация не обладает полнотой. Расписание могли также записать неразборчиво, так, что не всё удалось понять. И в первом, и во втором, и в третьем случае ценность информации снижается. Почти всегда качественные характеристики информации взаимосвязаны.
Качественные характеристики информации (ценность, понятность, актуальность, новизна, полнота, достоверность и т. д.) нам известны, поскольку мы постоянно их используем. Например, информация о расписании уроков на вчерашний день не обладает актуальностью. Если нам сообщили расписание на завтра, но только на первые четыре урока вместо шести, эта информация не обладает полнотой. Расписание могли также записать неразборчиво, так, что не всё удалось понять. И в первом, и во втором, и в третьем случае ценность информации снижается. Почти всегда качественные характеристики информации взаимосвязаны.
В обычном, бытовом понимании количество информации связано с ее смысловым содержанием: дважды повторенная в сообщении фраза не увеличивает количество информации вдвое.
Избыточность информации
Интересный факт установили ученые-лингвисты, занимающиеся изучением закономерностей, лежащих в основе большинства языков, проведя измерение информативной емкости разных языков. Компьютерная обработка большого количества текстов, сопоставление длин переводов одного текста на разные языки и многочисленные эксперименты по угадыванию букв текста продемонстрировали избыточность естественных языков – при равномерной нагрузке информацией тексты могли быть короче в 4–5 раз. Величина избыточности для разных языков примерно одинакова.
Компьютерная обработка большого количества текстов, сопоставление длин переводов одного текста на разные языки и многочисленные эксперименты по угадыванию букв текста продемонстрировали избыточность естественных языков – при равномерной нагрузке информацией тексты могли быть короче в 4–5 раз. Величина избыточности для разных языков примерно одинакова.
В вычислительной технике принят иной подход к измерению количества информации, основанный на подсчете количества символов в сообщении и не связанный с его содержанием.
В современных средствах вычислительной техники (компьютерах) числовая, текстовая, графическая информация хранится и обрабатывается в виде электрических сигналов, преобразуемых в аудио- и видеосигналы, воспринимаемые органами зрения и слуха.
Кодирование. Система счисления
Для представления в виде электрических сигналов информация кодируется с помощью двоичной системы счисления.
Кодированием называют представление символов одного алфавита символами другого.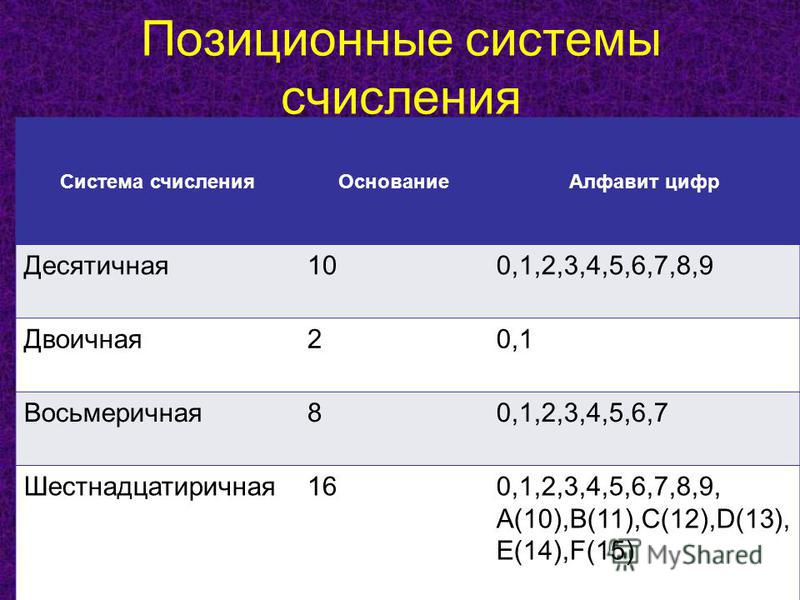
Система счисления – способ представления любого числа с помощью алфавита символов, называемых цифрами.
Количество символов в алфавите системы счисления называют ее основанием. Одной из систем счисления (десятичной) мы пользуемся постоянно. Системы счисления принято делить на непозиционные и позиционные.
Непозиционная и позиционная системы счисления
Непозиционная система счисления – это такая система, в которой вводится ряд символов для представления основных чисел, а остальные числа – результат их сложения и вычитания.
Пример этой системы – римская система счисления (Рис. 1). Основные символы римской системы счисления: I – один, X – десять, C – сто, M – тысяча; и их половины: V – пять, L – пятьдесят, D – пятьсот. Натуральные числа записываются при помощи повторения этих цифр (например, II – два, III – три, XX – двадцать, ССС – триста). Если большая цифра стоит перед меньшей, то они складываются, если наоборот – вычитаются (например, XII – двенадцать, IV – четыре).
Рис. 1. Представление чисел в римской системе счисления (Источник)
Позиционная система счисления – это такая система, в которой любое число представляется в виде последовательности цифр, количественное значение которых зависит от их места (позиции) в числе. Мы знаем, что эту позицию также называют разрядом.
Например, арабская десятичная система счисления. Алфавит этой системы счисления состоит из десяти символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), называемых арабскими цифрами. По правилам этой системы счисления символы располагаются начиная с нулевой позиции (разряда) и далее по возрастающей – слева направо. Чтобы представить число в этой системе счисления, нужно содержимое каждого разряда умножить на основание системы в степени, равной порядковому номеру разряда, а затем суммировать. Например, число 356 можно представить как сумму трех сотен, пяти десятков и шести единиц, т. е.:
356 = 3 х 102 + 5 х 101 + 6 х 100
Десятичная система счисления
Не случайно количество символов совпадает с количеством пальцев на обеих руках – свое начало она ведет от пальцевого счета.
Убежденным сторонником использования индо-арабской десятичной системы счисления в торговой практике был известный итальянский математик Леонардо Пизанский (Фибоначчи) (Рис. 2), получивший математическое образование в арабских странах. В своем сочинении Liber abaci (в 1202 году) он писал: «Девять индусских знаков – суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски zephirum, можно написать какое угодно число». Слово zephirum дало начало французскому и итальянскому слову zero (ноль).
Рис. 2. Леонардо Фибоначчи (Источник)
Двоичная система счисления
В алфавите двоичной системы счисления (как следует из ее названия) два символа: 0 и 1. С помощью последовательностей нулей и единиц (двоичных кодов), как в азбуке Морзе с помощью комбинаций точек и тире (Рис. 3), можно представить любую букву, цифру, символ.
Рис. 3. Азбука Морзе
Рождение двоичной системы исчисления
Официальное «рождение» двоичной системы счисления связывают с именем Готфрида Вильгельма Лейбница. В 1703 году была опубликована его статья, в которой рассматривались все правила выполнения арифметических действий над двоичными числами. Лейбниц, однако, не рекомендовал двоичную арифметику для практических вычислений вместо десятичной системы, но подчеркивал, что «вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот является для науки основным и порождает новые открытия …при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок».
В 1703 году была опубликована его статья, в которой рассматривались все правила выполнения арифметических действий над двоичными числами. Лейбниц, однако, не рекомендовал двоичную арифметику для практических вычислений вместо десятичной системы, но подчеркивал, что «вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот является для науки основным и порождает новые открытия …при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок».
Блестящие предсказания Лейбница сбылись через два с половиной столетия, когда выдающийся американский ученый, инженер Клод Шеннон, связал принципы двоичной системы счисления с работой релейных схем и заложил, тем самым, основы вычислительной техники, а физик и математик Джон фон Нейман использовал именно двоичную систему счисления в качестве универсального способа представления информации в вычислительных машинах.
Восьмеричная и шестнадцатеричная системы счисления
Восьмеричная система счисления – это система, в алфавите которой восемь символов: 0, 1, 2, 3, 4, 5, 6, 7.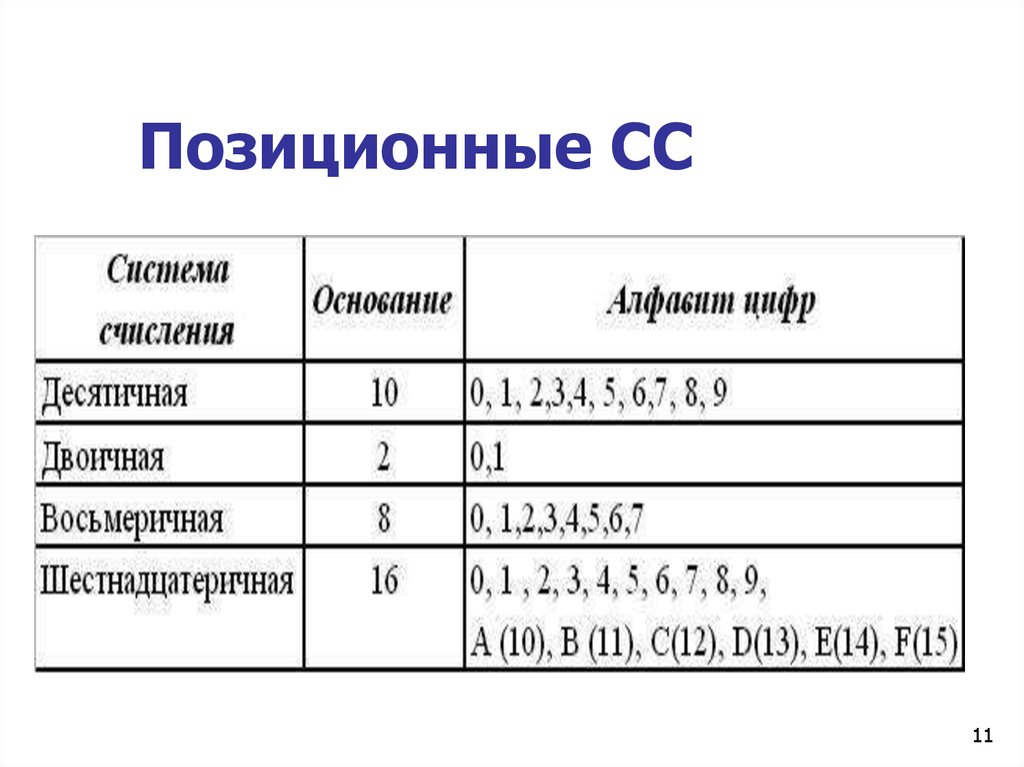 Она представляет собой компромисс между двоичной и десятичной системами, так как числа в этой системе читаются легко и переход от двоичного представления к восьмеричному очень прост. В восьмеричной системе после 7 для увеличения числа нужно выполнить сдвиг на один разряд влево, подобно тому, как в десятичной системе выполняем сдвиг на один разряд влево после 9 при увеличении числа на 1. Таким образом, получается, что 10 в восьмеричной системе равняется 8 в десятичной системе. Поскольку 8 = 23, следовательно, сдвиг на 1 разряд влево в восьмеричной системе соответствует сдвигу на 3 разряда влево в двоичной системе.
Она представляет собой компромисс между двоичной и десятичной системами, так как числа в этой системе читаются легко и переход от двоичного представления к восьмеричному очень прост. В восьмеричной системе после 7 для увеличения числа нужно выполнить сдвиг на один разряд влево, подобно тому, как в десятичной системе выполняем сдвиг на один разряд влево после 9 при увеличении числа на 1. Таким образом, получается, что 10 в восьмеричной системе равняется 8 в десятичной системе. Поскольку 8 = 23, следовательно, сдвиг на 1 разряд влево в восьмеричной системе соответствует сдвигу на 3 разряда влево в двоичной системе.
Алфавит шестнадцатеричной системы счисления состоит из десяти арабских цифр и шести букв латинского алфавита: A, B, C, D, E, F. Таким образом, например, десятичное число 10 в этой системе будет обозначаться буквой А, число 11 – буквой В и т. д.
Указать систему счисления, в которой представлено число x, можно одним из двух способов: цифрами или буквами. Если использовать первый способ, то
x10, x2, x8, x16 будут обозначениями числа в десятичной, двоичной, восьмеричной и шестнадцатеричной системе счисления соответственно.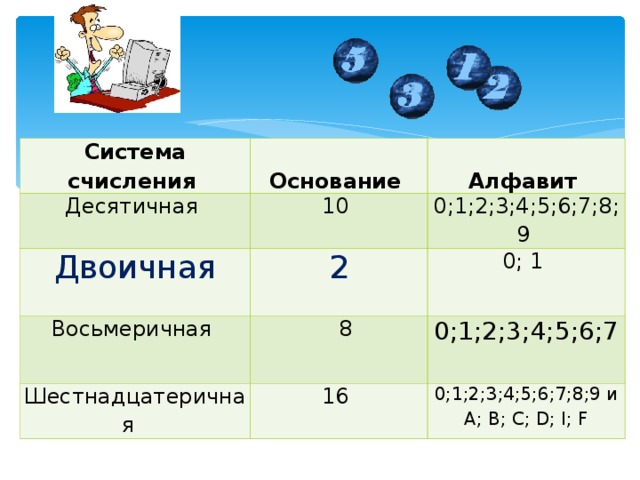 Введем теперь буквенные обозначения систем счисления.
Введем теперь буквенные обозначения систем счисления.
Тогда Dx, Bx, Ox, Hx также будут обозначениями числа в десятичной, двоичной, восьмеричной и шестнадцатеричной системе счисления соответственно. Именно буквенные обозначения используются в калькуляторе.
Исчезнувшие системы счисления
Некоторые народы пользовались пятеричной системой счисления, например, в Древнем Китае ее связывали с пятью стихиями (вода, огонь, дерево, металл и земля). В Древнем Вавилоне была распространена шестидесятеричная система, разработанная еще раньше шумерами, ее следы сохранились в делении часа и градуса на 60 минут и минуты на 60 секунд.
Перевод чисел из одной системы счисления в другую
Для перевода числа из любой системы счисления в десятичную нужно умножить содержимое каждого разряда на основание системы в степени, равной порядковому номеру разряда, и все сложить.
Например, 1568(O156) = 1 ´ 82 + 5 ´ 81 + 6 ´ 80 =64 + 40 + 6 = 11010 (D110)
10 0102 (B10 010)=1 ´ 24 + 0 ´ 23+ 0 ´ 22 + 1 ´ 21 + 0 ´ 20 = 16 + 2 = 1810 (D18)
A216 (HA2) = 10 ´ 161 + 2 ´ 160 = 160 + 2 = 16210 (D162)
Переход из двоичной системы счисления в восьмеричную осуществляется заменой справа налево каждой триады двоичных цифр на одну восьмеричную цифру.
Например, 2518 (O251) = 010 101 0012 (В010 101 001)
2 5 1
Для перевода числа из десятичной системы счисления в любую другую систему счисления нужно делить это число «до упора» (т. е. пока делится) на основание той системы, в которую переводим число, а потом прочесть остатки справа налево (как указывает стрелка).
Интересный факт
В рассказе известного американского фантаста Пола Андерсона «После судного дня» экипаж межпланетного космического корабля, возвращаясь из длительной экспедиции, на подлете к Земле обнаруживает вместо зелено-голубой планеты черный дымящийся шар. Придя в себя от ужасной картины, люди строят предположения о причинах и виновниках трагедии. На орбите вокруг Земли летает несколько ракет, препятствующих приближению к Земле. Две из них людям удается уничтожить, а третью – обезвредить и попасть внутрь нее. Обследуя ее, на перегородке приборной панели они обнаруживают нацарапанные «заметки для памяти. .., содержащие две системы символов». Зная, что обитатели ближайших галактик использовали в качестве базовых систем счисления такие системы, которые соответствуют количеству пальцев на их руках (например, шестеричную – трехпалые, восьмеричную – четырехпалые), земляне получают ключ к разгадке преступления.
.., содержащие две системы символов». Зная, что обитатели ближайших галактик использовали в качестве базовых систем счисления такие системы, которые соответствуют количеству пальцев на их руках (например, шестеричную – трехпалые, восьмеричную – четырехпалые), земляне получают ключ к разгадке преступления.
Список литературы
1. Босова Л.Л. Информатика и ИКТ: Учебник для 8 класса. – М.: БИНОМ. Лаборатория знаний, 2012.
2. Босова Л.Л. Информатика: Рабочая тетрадь для 8 класса. – М.: БИНОМ. Лаборатория знаний, 2010.
3. Астафьева Н.Е., Ракитина Е.А., Информатика в схемах. – М.: БИНОМ. Лаборатория знаний, 2010.
4. Г. А. Ковриженко, Системы счисления и двоичная арифметика. – М.: Радянська школа, 1984.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт 5byte.ru (Источник)
2. Интернет-сайт dic.academic.ru (Источник)
3. Интернет-библиотека Московского Центра непрерывного математического образования (Источник)
4. Энциклопедия Кругосвет (Источник)
Энциклопедия Кругосвет (Источник)
Домашнее задание
1. Раздел 1, Тема 1.1., стр. 19–30. Соловьева Л.Ф. Информатика и ИКТ. Учебник для 8 класса – СПб.: БХВ-Петербург, 2011. – 288 с.
2. Приведите примеры качественных характеристик информации.
3. Что называется кодированием?
4. Что такое система счисления?
5. Чем отличается позиционная система счисления от непозиционной?
6. По каким правилам осуществляется перевод чисел из одной системы счисления в другую?
Простая английская Википедия, бесплатная энциклопедия
Восьмеричная система счисления — это система счисления с основанием 8. В нем используются цифры от 0 до 7. Система аналогична двоичной (основание 2) и шестнадцатеричной (основание 16). Восьмеричные числительные записываются с использованием буквы или перед числительным, например, о04 или о1242. Восьмеричные числа также иногда записываются с маленькой восьмеркой справа внизу, например, 1242 8 .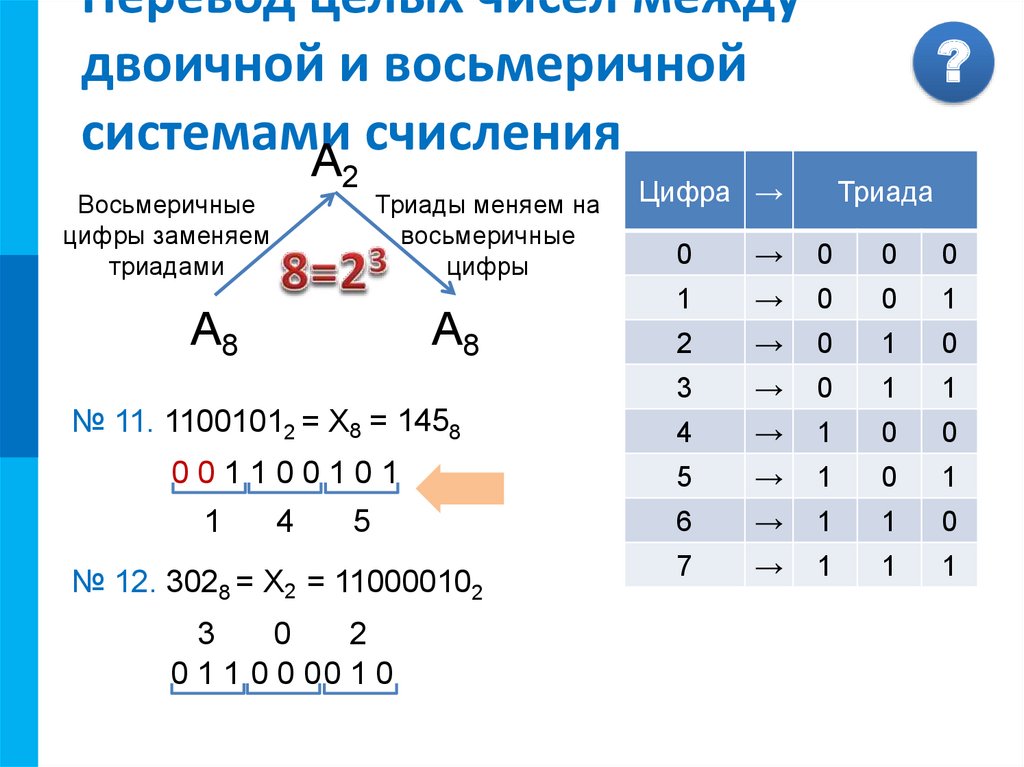
В свое время восьмеричная система использовалась в основном для работы с компьютерами. Это обеспечило более простой способ работы с двоичными числами. Поскольку компьютеры перешли от использования 24-битных систем к 32- и 64-битным системам, шестнадцатеричная система заменила восьмеричную для большинства применений. Некоторые группы, например, коренные американцы, использующие язык юки в Калифорнии и памейские языки [1] в Мексике, также используется восьмеричная система счисления. Они делают это потому, что при счете используют промежутки между пальцами, а не сами пальцы.
Содержимое
- 1 Восьмеричное и двоичное
- 2 Восьмеричный и десятичный
- 3 Восьмеричный и шестнадцатеричный
- 4 Связанные страницы
- 5 Каталожные номера
- 6 Другие сайты
Восьмеричная система счисления использует «трехбитное» двоичное кодирование. Каждая цифра восьмеричного числа соответствует трем цифрам двоичного числа. Группировка двоичных цифр выполняется справа налево. Первые три двоичных разряда справа группируются в последнюю часть восьмеричного числительного, затем следующие три разряда образуют предпоследнюю часть числительного.
Группировка двоичных цифр выполняется справа налево. Первые три двоичных разряда справа группируются в последнюю часть восьмеричного числительного, затем следующие три разряда образуют предпоследнюю часть числительного.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В десятичной системе (с основанием 10) каждая восьмеричная цифра равна той цифре, умноженной на показатель степени 8, который равен ее положению минус один.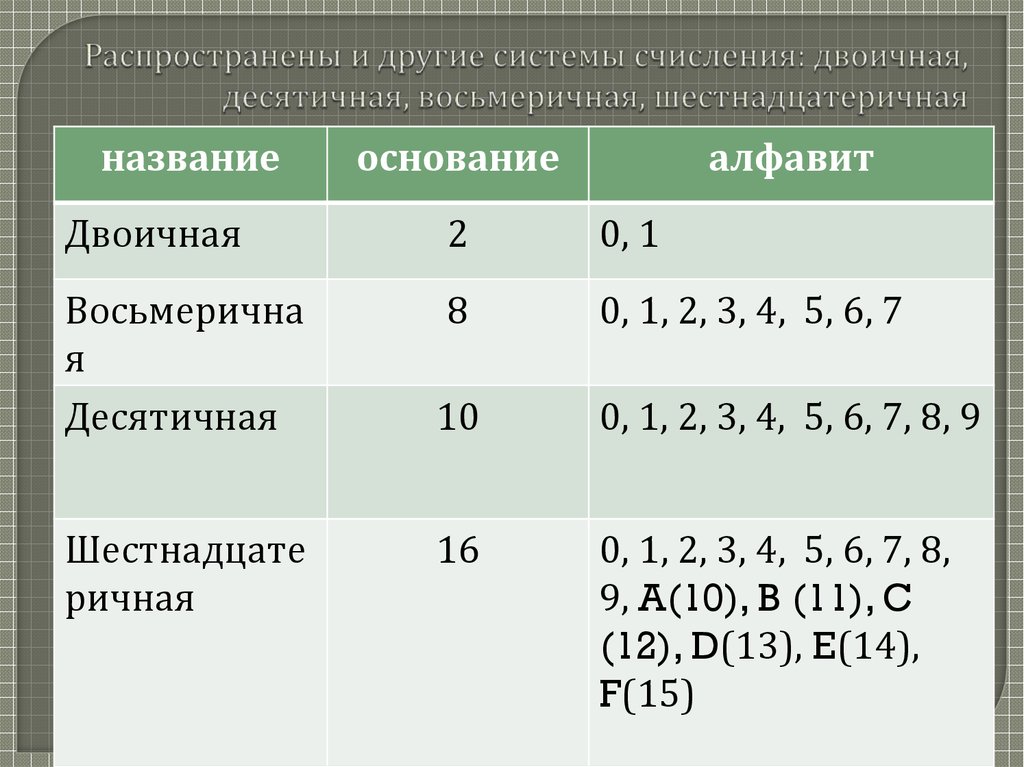
| Местоположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 32768 (8 5 ) | 4096 (8 4 ) | 512 (8 3 ) | 64 (8 2 ) | 8(8 1 ) | 1 (8 0 ) |
Пример: o3425 в десятичной системе
|
Восьмеричное похоже на шестнадцатеричное, поскольку оба они легко преобразуются в двоичные.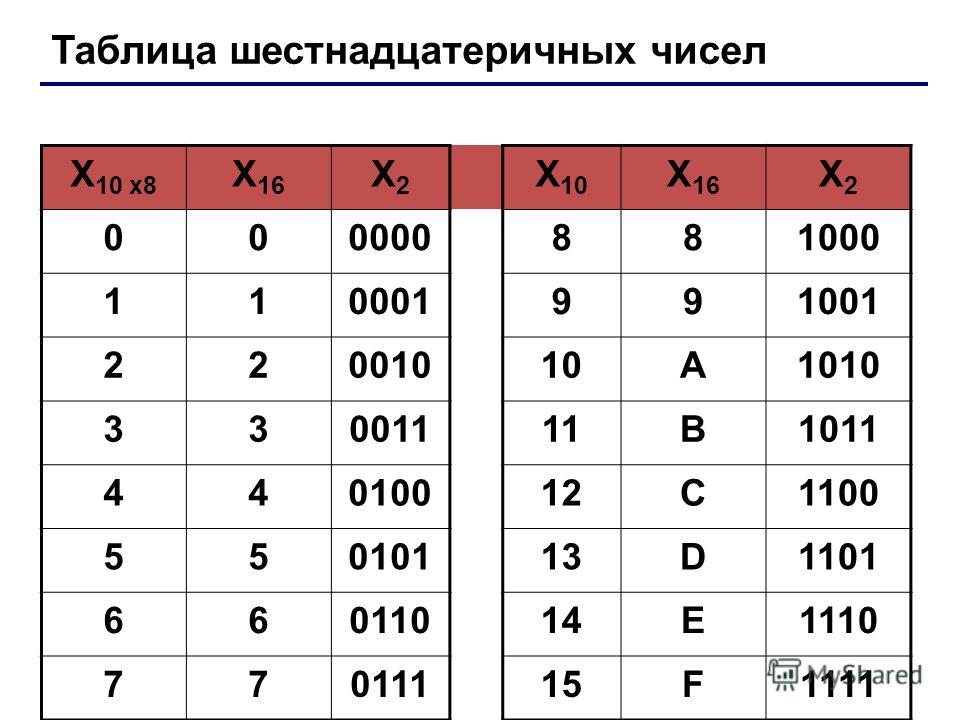 Где восьмеричное равно трехзначному двоичному, шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну систему в другую — преобразовать ее в двоичную, а затем в другую систему.
Где восьмеричное равно трехзначному двоичному, шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну систему в другую — преобразовать ее в двоичную, а затем в другую систему.
| Восьмеричный | Двоичный | Шестнадцатеричный | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| три цифры | четыре цифры | |||||||||
| о4 | 100 | 0100 | 04ч | |||||||
| о15 | 001 | 101 | 1101 | 0Дх | ||||||
| о306 | 011 | 000 | 110 | 1100 | 0110 | C6h | ||||
| о54253 | 101 | 100 | 010 | 101 | 011 | 0101 | 1000 | 1010 | 1011 | 58ABh |
- Двоичная система счисления
- Шестнадцатеричная система счисления
- Десятичная система счисления
- ↑ Авелино, Эриберто (2006), «Типология систем счисления Пейм и границы Мезоамерики как лингвистической области» (PDF), Linguistic Typology , 10 : 41–60, doi: 10.
 1515/LINGTY. 2006.002, S2CID 20412558
1515/LINGTY. 2006.002, S2CID 20412558
- Онлайн-конвертер. Архивировано 4 января 2007 г. на Wayback Machine для десятичных / восьмеричных чисел (JavaScript, GPL).
Восьмеричная система счисления — Electronics-Lab.com0476 — это еще одна цифровая система счисления, в которой используется система
Base-8 , аналогичная ранее обсуждавшейся шестнадцатеричной системе счисления с системой Base-16 . Oct- — это комбинированная форма, используемая в качестве префикса, означающего «восемь», и поэтому система с основанием 8 (восемь) называется восьмеричной системой счисления. Подобно шестнадцатеричному числу, восьмеричная система счисления уменьшает размер эквивалентного большого двоичного числа и упрощает чтение и запись исходного большого двоичного числа. Цифра системы счисления имеет диапазон чисел, которые она может использовать для выражения своего значения. Этот диапазон зависит от базового значения системы счисления, т. е. Системы с основанием 16 имеют диапазоны чисел «10» и «16» соответственно. Точно так же система счисления с основанием 8 (восьмеричная) имеет диапазон только «8» чисел от «0» до «7», то есть 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричные числа имеют только восемь (8) различных значений для каждой цифры, и каждая цифра имеет вес восемь (8), начиная с младшей значащей цифры (LSD). Для размещения и представления числа «8» в двоичном формате требуется всего три (3) бита. После этого восьмеричные значения (0, 1, 2, 3, 4, 5, 6 и 7) соответствуют двоичным эквивалентным значениям (000, 001, 010, 011, 100, 101, 110 и 111) соответственно.
е. Системы с основанием 16 имеют диапазоны чисел «10» и «16» соответственно. Точно так же система счисления с основанием 8 (восьмеричная) имеет диапазон только «8» чисел от «0» до «7», то есть 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричные числа имеют только восемь (8) различных значений для каждой цифры, и каждая цифра имеет вес восемь (8), начиная с младшей значащей цифры (LSD). Для размещения и представления числа «8» в двоичном формате требуется всего три (3) бита. После этого восьмеричные значения (0, 1, 2, 3, 4, 5, 6 и 7) соответствуют двоичным эквивалентным значениям (000, 001, 010, 011, 100, 101, 110 и 111) соответственно.
Восьмеричное число формируется путем группировки двоичных чисел в наборы по 3 бит. Это следует той же процедуре, которая использовалась ранее в шестнадцатеричном артикле. Однако в шестнадцатеричных числах двоичное число было разделено на группы по 4 бита (поскольку Base-16 использует диапазон от 0 до 15 и требует 4 бита). Восьмеричная система счисления проста по сравнению с шестнадцатеричной системой счисления, поскольку в ней используются только числа по сравнению с шестнадцатеричной системой, использующей числа и алфавиты. Более того, он имеет только восемь различных значений «8» по сравнению с шестнадцатью различными значениями «16» шестнадцатеричной системы счисления. В раннюю эру цифровых вычислений восьмеричная система счисления была очень известна, поскольку цифровые входы (от D0 до D7) и выходы (от Q0 до Q7) исчислялись восемью (8). Однако с увеличением количества цифровых входов и выходов, архитектуры системы и объема памяти и т. д. шестнадцатеричная система счисления стала более удобной для представления больших двоичных значений.
Более того, он имеет только восемь различных значений «8» по сравнению с шестнадцатью различными значениями «16» шестнадцатеричной системы счисления. В раннюю эру цифровых вычислений восьмеричная система счисления была очень известна, поскольку цифровые входы (от D0 до D7) и выходы (от Q0 до Q7) исчислялись восемью (8). Однако с увеличением количества цифровых входов и выходов, архитектуры системы и объема памяти и т. д. шестнадцатеричная система счисления стала более удобной для представления больших двоичных значений.
Представление восьмеричного числа
Восьмеричная система счисления использует систему с основанием 8, поэтому восьмеричное число представляется нижним индексом «8». Например, (142 8 ) идентифицируется как восьмеричное число, поскольку оно имеет нижний индекс «8». Кроме того, заметно, что каждая цифра восьмеричного числа имеет значение от 0 до 7. Например, восьмеричное число (128 8 ) неверно, поскольку его младшая значащая цифра (LSD) имеет значение «8». Который не относится к восьмеричному диапазону счисления, а относится к десятичной или шестнадцатеричной системе счисления. Таким образом, правильность числа можно определить, проверив его базовое значение и попадание числа каждой цифры в его базовый диапазон.
Который не относится к восьмеричному диапазону счисления, а относится к десятичной или шестнадцатеричной системе счисления. Таким образом, правильность числа можно определить, проверив его базовое значение и попадание числа каждой цифры в его базовый диапазон.
Восьмеричные числа
В следующей таблице перечислены десятичные числа от 0 до 7 и их эквиваленты в двоичных и восьмеричных числах.
Восьмеричный счет
Каждая цифра восьмеричного числа имеет вес восемь (8) , начиная с младшей значащей цифры. Вес каждой цифры увеличивается в степени восемь при переходе от младшей значащей цифры к старшей значащей цифре. Эквивалентный десятичный вес каждой восьмеричной цифры до 7 й цифра , дана.
Восьмеричная цифра имеет числовой диапазон от «0 до «7» , и для счета сверх этого диапазона слева добавляется еще одна восьмеричная цифра. Добавление второй цифры приводит к счету до (77 8 ) , что в десятичном виде эквивалентно ( 63 10 ). Таким образом, две восьмеричные цифры могут считать до 63. Точно так же трехзначное восьмеричное число может считать до (777 8 ) , который дает диапазон счета до (511 10 ) в десятичном виде.
Таким образом, две восьмеричные цифры могут считать до 63. Точно так же трехзначное восьмеричное число может считать до (777 8 ) , который дает диапазон счета до (511 10 ) в десятичном виде.
Добавление нулей к двоичному числу
Поскольку двоичное число разбивается на 3-битные группы для определения эквивалентного ему восьмеричного числа. Для этого требуется двоичное число, состоящее из битов, кратных трем (3), например. 3, 6, 9, 12 и 15 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 3 бита, начиная с младшего значащего бита (LSB). В случае, если биты двоичного числа не разделены поровну между 3-битными группами, у нас останется менее 3-бит в конце. Ведущие нули добавляются к оставшимся битам, чтобы увеличить их длину до 3 бит. Эта последняя группа из 3 битов составляет старшую значащую цифру (MSD) восьмеричного числа. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 101010) преобразуется в 15-битное (делится на 3) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное восьмеричное число.
В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 101010) преобразуется в 15-битное (делится на 3) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное восьмеричное число.
В приведенном выше примере к 13-битному числу необходимо добавить 2 бита с нулевыми значениями в крайнюю левую сторону, чтобы получить 15-битное двоичное число . Точно так же для 11-битного двоичного числа потребуется добавить один (1) нулевой бит. Использование восьмеричных чисел сокращает длину двоичных чисел в три (3) раза.
Преобразование восьмеричного числа в десятичное
Преобразование восьмеричного значения в десятичное достигается с помощью метода взвешенной суммы цифр, описанного в предыдущих статьях. В следующем примере восьмеричное число (4262 8 ) преобразуется в десятичное число.
Преобразование десятичного числа в восьмеричное
Преобразование десятичного числа в восьмеричное требует применения метода повторного деления на 8. Тот же метод использовался для преобразования десятичного числа в его эквивалентные двоичные и шестнадцатеричные значения в предыдущих статьях. Десятичное число (238 10 ) снова используется для получения эквивалентного восьмеричного числа в следующем примере.
Тот же метод использовался для преобразования десятичного числа в его эквивалентные двоичные и шестнадцатеричные значения в предыдущих статьях. Десятичное число (238 10 ) снова используется для получения эквивалентного восьмеричного числа в следующем примере.
Пример преобразования двоичного числа в восьмеричное
Преобразование 8-битного двоичного числа (11011001 2 ) в восьмеричное число показано ниже.
Пример преобразования восьмеричного числа в двоичное и десятичное
Преобразование ( 6271 8 ) в эквивалентное ему двоичное и десятичное число показано ниже в качестве примера.
Заключение
- Восьмеричное число использует систему с основанием 8, и значение каждой цифры находится в диапазоне от 0 до 7, т. е. восемь (8) чисел.
- В восьмеричном числе каждая цифра представляет собой группу или набор из 3 битов.
 Эквивалент восьмеричного двоичного числа получается путем разбиения двоичного числа на 3-битные группы, и каждой группе присваивается эквивалентное восьмеричное значение от «0» до «7».
Эквивалент восьмеричного двоичного числа получается путем разбиения двоичного числа на 3-битные группы, и каждой группе присваивается эквивалентное восьмеричное значение от «0» до «7». - Двоичные числа могут потребовать добавления начальных нулей в крайнюю левую (наиболее значащую) сторону для формирования 3-битных групп.
- Восьмеричное число представляется с помощью «8» в качестве нижнего индекса, например. 735 8 .
- Восьмеричное число можно преобразовать в десятичное число с помощью метода взвешенной суммы цифр.
- Преобразование десятичного числа в восьмеричное требует применения метода повторного деления на 8.
- Восьмеричное число уменьшает длину эквивалентного ему двоичного числа в три (3) раза. Однако сейчас восьмеричные числа используются редко, и, как обсуждалось ранее, их место заняла шестнадцатеричная система счисления.
Преобразователь случайных чисел | Преобразовать двоичную систему счисления с основанием 28 в восьмеричную Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 Как улучшить прием сотового телефона?Используйте контрольный список, чтобы улучшить его! Обзор Различные способы представления чисел Индуистские цифры Roman Системы в других культурах Unary Позиционная система Двоичный Классификация 0002 Negative Numbers Rational Numbers Natural Numbers Integers Complex Numbers Prime Numbers Interesting Facts about Numbers Anti-Fraud Numerals Modern Counting in Commerce Numeral Grouping Unlucky Numbers Изучайте технический английский с помощью этого видео! ОбзорПриложение-калькулятор для iPhone Число — это абстрактное математическое понятие, представляющее количество. Различные способы представления чиселНекоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания. Индийско-арабские цифры Индо-арабская система счисления сегодня является одной из наиболее широко используемых в мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках. Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). РимскиеРимские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Roman numerals are based on seven numbers written with the letters of the Latin alphabet:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее значение, что два необходимо, но это добавлено, но но, но нужно добавить, но но нужно добавить. меньшее число перед большим означает, что меньшее число вычитается из большего. Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, в которой есть только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»). Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Унарная система счисления. Метки счета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная системаПозиционная система работает с основанием. Например, в базе 10 у нас есть следующее:
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисленияДвоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу: Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» их. 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нуль, отрицательные и положительные числа, которые не являются дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательной единицы. Простые числаПростые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничества Для предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется 10-кратная система счисления, по-прежнему свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чисел И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это взято из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае число 7 также является несчастливым, потому что оно представляет собой духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Японии другое несчастливое число — 9.0003 9 , что имеет то же произношение, что и «страдание». В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «Я жил». Это подразумевает, что жизнь окончена, и относится к смерти. 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией. Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Ссылки Эта статья была написана Катериной Юрием Преобразование десятичного числа в основание 24 Преобразование основания 3 в десятичное Преобразование шестнадцатеричного в двоичное Преобразование двоичного в восьмеричное 4 Преобразование Преобразовать 32-ю систему счисления в десятичную Преобразовать двоичную в 36-ю Преобразовать десятичную в 20-ю Преобразовать десятичную в шестнадцатеричную Возможно, вас заинтересуют другие конвертеры из группы «Общие преобразователи единиц»:Длина и преобразователь расстояния массовый преобразователь Сухой объем и общие измерения приготовления пищи Преобразователь площади Объем и общий преобразователь измерения приготовления ТЕМПЕРАТУРС Преобразователь мощности Преобразователь силы Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Конвертер топливной экономичности, расхода топлива и экономии топлива Конвертер единиц хранения информации и данных Конвертер метрических префиксов Конвертер передачи данных Курсы обмена валют Размеры мужской одежды и обуви 9 Размеры Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков. |
6.
 0) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, поэтому 1010111 в двоичном формате равно десятичному числу 87.
0) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, поэтому 1010111 в двоичном формате равно десятичному числу 87. В приложении введите dec0b1010111 и убедитесь, что результат равен 87. Код «0b» используется для обозначения двоичного числа. Чтобы преобразовать 87 обратно в двоичный формат, введите bin87. Калькулятор должен отобразить 0b1010111. Число, следующее за кодом «0b», является двоичным эквивалентом 87.
Примеры
Преобразование каждого десятичного числа в двоичное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «bin» перед каждым числом.
1) корзина(105)
2) корзина(224)
3) корзина(100)
Примеры
Преобразование каждого двоичного числа в десятичное число.
1) 1101001
2) 11100000
3) 1100100
Решения калькулятора
Введите «dec» перед каждым аргументом и обозначьте двоичное число как «0b». 0).
0).
Чтобы увидеть это преобразование в приложении, введите oct8 и увидите, что на дисплее отображается 0o10, что означает, что десятичное число 8 эквивалентно 10 в восьмеричной системе счисления. Код «0o» означает, что следующее число является восьмеричным числом.
Чтобы преобразовать восьмеричное число 10 обратно в десятичное число, введите dec0o10. Результат 8.
Примеры
Преобразование каждого десятичного числа в восьмеричное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «oct» перед каждым аргументом.
1) окт(105)
2) окт(224)
3) окт(100)
Примеры
Преобразование каждого восьмеричного числа в десятичное.
1) 151
2) 340
3) 144
Решения с калькулятором
Введите «dec» перед каждым аргументом и обозначьте восьмеричное число «0o».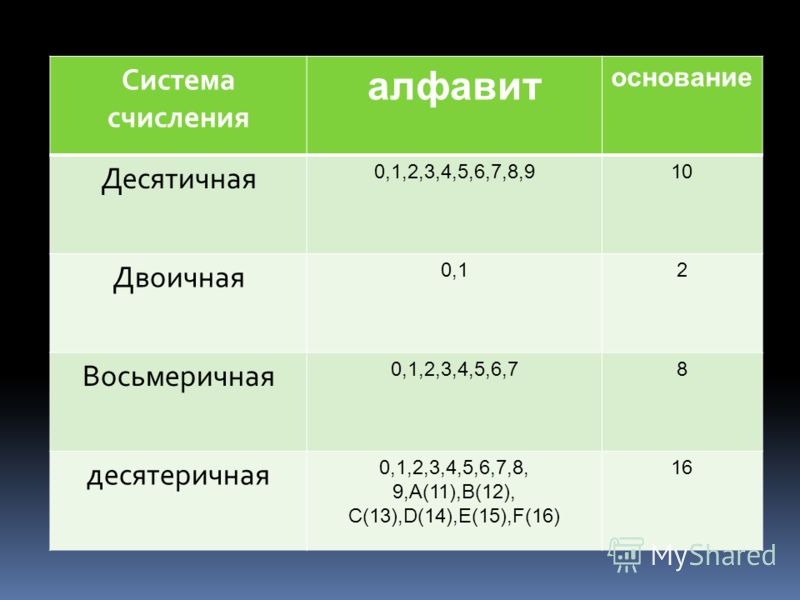
1) десят(0o151)
2) десят(0o340)
3) десят(0o144)
Преобразование десятичного числа в шестнадцатеричное и наоборот
Шестнадцатеричная система счисления – это система счисления с основанием 16. Он использует 16 символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F) для представления числа. В отличие от восьмеричной и двоичной систем, здесь используются первые шесть букв алфавита (A, B, C, D, E и F). Это означает, что после 9 система считает A для 10, B для 11, C для 12, D для 13, E для 14 и F для 15. Подсчет от 15 заменяет последнюю цифру.
Например, десятичное число 17 выражается как 11 в шестнадцатеричной системе. Чтобы увидеть его в приложении, введите hex17, и приложение отобразит 0x11. Первые два символа «0x» означают, что следующее число является шестнадцатеричным числом. Чтобы преобразовать шестнадцатеричное число 11 обратно в десятичное, введите dec0x11, и результатом будет 17.
Примеры
Преобразование каждого десятичного числа в шестнадцатеричное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «hex» перед каждым аргументом.
1) hex105
2) hex224
3) hex100
Примеры
Преобразование каждого шестнадцатеричного числа в десятичное.
1) 69
2) E0
3) 64
Решения для калькулятора
Введите «dec» перед каждым аргументом и обозначьте шестнадцатеричное число «0x».
1) десят (0x69)
2) десят (0xE0)
3) десят (0x64)
Преобразование между системами счисления
Не забудьте ввести код «0b» для преобразования двоичного числа, «0o» для преобразования восьмеричного числа и «0x» для преобразования шестнадцатеричного числа.
Примеры
1) Преобразовать 10011001 в шестнадцатеричное число.
2) Преобразовать 1234E в двоичный формат.
3) Преобразование A045 в восьмеричное.
4) Преобразовать 012576 в двоичный формат.
5) Преобразовать 101011 в восьмеричное.
Решения для калькулятора
1) Тип: hex(0b10011001)
Двоичный код 10011001 эквивалентен 99 в шестнадцатеричном формате.
2) Тип: bin(0x1234E)
Шестнадцатеричное число 1234E эквивалентно 10010001101001110.
4) Тип: bin0o012576
Восьмеричное число 012576 эквивалентно 1010101111110 в двоичном формате.
5) Тип: oct0b101011
Двоичное число 101011 эквивалентно восьмеричному числу 53.
СЛЕДУЮЩИЙ: 6.13. комплексные числа>
Список содержимого
Система счисления C — десятичная, двоичная, восьмеричная и шестнадцатеричная
Перейти к содержимомуСистема счисления C – десятичная, двоичная, восьмеричная и шестнадцатеричная
В этом уроке мы узнаем о различных системах счисления.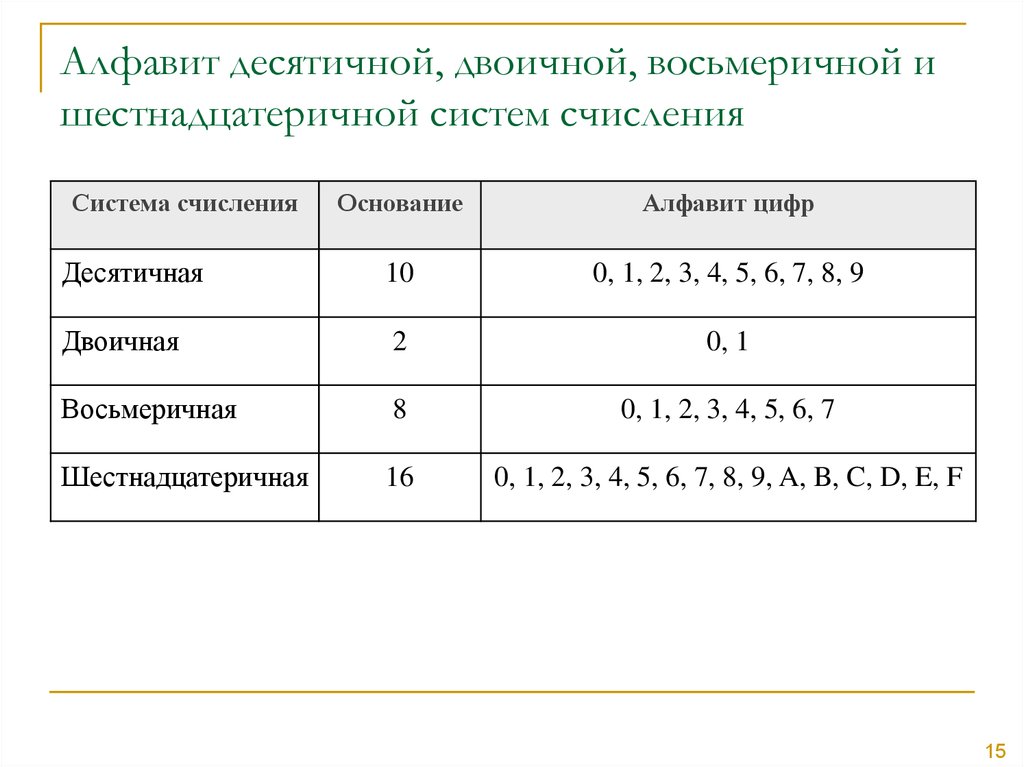
Введение:
В компьютерах мы обычно используем четыре различные системы счисления — Десятичная, Двоичная, Восьмеричная и Шестнадцатеричная.
десятичная система — это система счисления, которая используется в наших повседневных приложениях, таких как бизнес и т. д. В этой системе используются символы 0,1,2,3,4,5,6,7,8,9 для обозначения различных чисел.
В двоичной системе счисления , 0 и 1 являются единственными символами, которые используются для представления чисел всех величин. Например, обычное десятичное число 7 (семь) представляется в двоичном виде как 111 . Двоичная система в основном используется в компьютерах и других вычислительных устройствах.
Число в определенной системе счисления записывается как (Число) по базе . Например, (17) 10 — это десятичное число (семнадцать), а (10001) 2 — это двоичное число 10001, которое на самом деле представляет собой десятичное число, значение которого равно 17 .
Поскольку чаще используется десятичная система счисления, десятичное число (35) 10 записывается просто как 35. Однако, если одно и то же число должно быть представлено в двоичная система , записывается как (100011) 2 .
Точно так же восьмеричная система счисления использует 8 в качестве основы. Обычно он используется для отображения цифр и представления прав доступа к файлам в операционных системах UNIX/Linux.
Шестнадцатеричная система или Шестнадцатеричная — это система счисления, которая использует 16 в качестве основы для представления чисел.
1. Десятичные числа:
Числа, которые мы используем ежедневно, относятся к Десятичная система . Например, 0,1,2,3,4,…..,9999,…..и т.д. Его также называют основанием — 10 системой .
Она называется системой счисления с основанием – 10 , потому что она использует 10 уникальных цифр от 0 до 9 для представления любого числа.
Основание (также называемое основанием ) — это количество уникальных цифр или символов (, включая 0 ), которые используются для представления заданного числа.
В десятичной системе (где основание равно 10), всего 10 цифр (0,1,2,3,4,5,6,7,8 и 9) используются для представления числа любой величины. Например, сто тридцать пять представляется как 135 , где
135 = (1 * 10 2 ) + (3 * 10 1 ) + (5 * 10 0
1 )
135 = (1 * 100) + (3 * 10) + (5 * 1)
Подобным образом дроби представляются с основанием – 10, возведенным в отрицательную степень.
2. Двоичные числа:
Двоичная система счисления используется как в математике, так и в цифровой электронике. Двоичная система счисления или по основанию – 2 система счисления представляет числовые значения, используя только два символа – Ноль (0) и Единица (1) .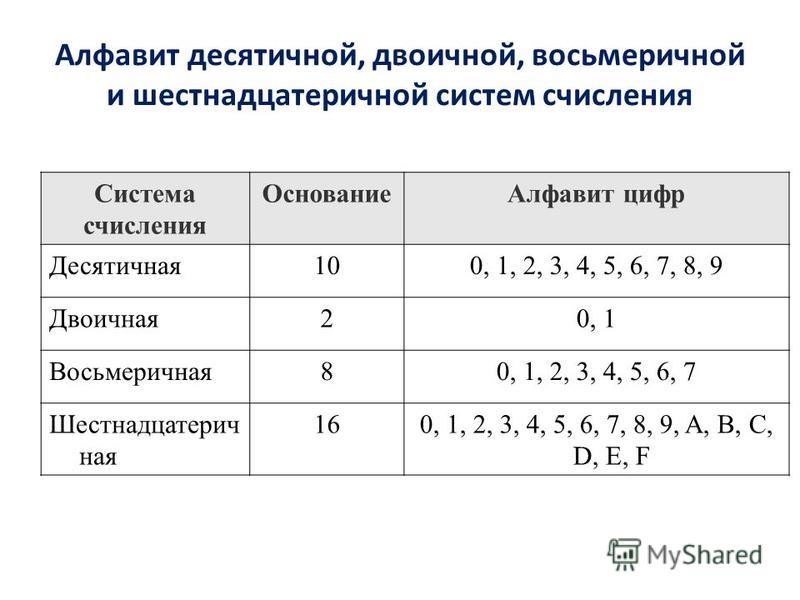
Компьютеры имеют схемы (логические вентили), которые могут находиться в одном из двух состояний: ВЫКЛ или ВКЛ . Эти два состояния представлены Zero (0) и Один (1) соответственно. Именно по этой причине вычисления в системах выполняются с использованием двоичной системы счисления (основание — 2), где все числа представлены с помощью 0 и 1.
Каждая двоичная цифра , то есть ноль ( 0 ) или единица ( 1 ), называется битом (известным как b 9085 inary dig ). Набор из 8 таких битов называется байт .
В компьютерной терминологии числа, кратные 9, получили разные названия.0475 2 10 (т. е. 1024 , умноженное на текущее значение), как показано в таблице ниже:
В компьютерном тексте изображения, музыка, видео или данные любого типа в конечном итоге сохраняются в двоичном формате.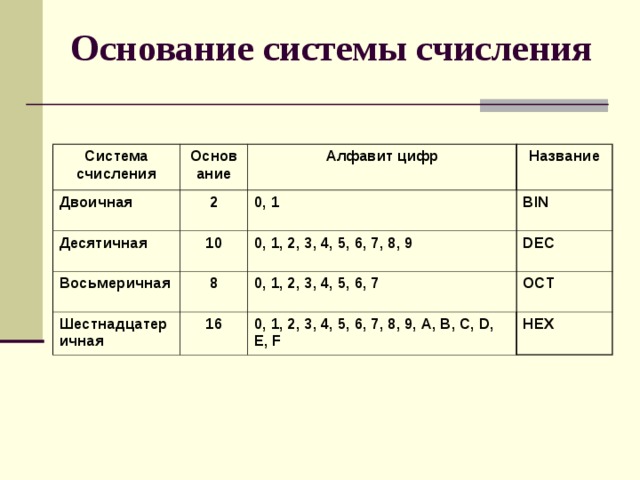 на диске.
на диске.
В двоичной системе всего 2 цифры (0 и 1) используются для представления числа любой величины.
Например, Ноль представлен как 0, где
0 = (0 * 2 0 ) = (0 * 1)
Аналогично, Один представлен как 1, где
1 = (1 * 2 0 ) = (1 * 1)
Теперь представим следующие числа в двоичном формате:
2 Два (2): поскольку 0 и 1 — единственные цифры, которые могут использоваться для представления 2, давайте разделим 2 на 2 и запишем частное и остаток следующим образом:[частное][остаток], т. е.: [1 ][0]
2 = (1 * 2 1 ) + (0 * 2 0 ) = (2) + (0)
Три (3): Поскольку 0 и 1 — единственные цифры, которые можно использовать для представления 3, давайте разделим 3 на 2 и напишем частное и остаток следующим образом:
[частное][остаток], т.
е. , : [1][1]
3 = (1 * 2 1 ) + (1 * 2 0 ) = (2) + (1)
Семнадцать (17): Поскольку 0 и 1 — единственные цифры, которые можно использовать чтобы представить 17, давайте разделим 17 на 2, напишем частное и остаток следующим образом:
[частное][остаток], т. е. :[8][1], повторив описанную выше логику для 8 (8 = [4][0]), 4(4 = [2][0]), 2( 2 = [1][0]) и 1(1 = [0][1]), мы окончательно получаем [1][0][0][0][1].
17 = (1 * 2 4 ) + (0 * 2 3 ) + (0 * 2 2 ) + (0 * 2 1 ) + (1 * 2 0 0 )
17 = (16) + (0) + (0) + (0) + (1)
В C перед двоичными числами стоит начальный префикс 0b (или 9 0B) 0476 (цифра ноль, за которой следует символ «b»). Например, чтобы сохранить двоичное значение четыре в переменной binary_Four, , мы пишем
int binary_Four = 0b100;
3.
 Восьмеричные числа:
Восьмеричные числа:Система нумерации, в которой используется основание – 8 , называется восьмеричной системой . Основание (также известное как основание) — это количество уникальных цифр или символов (включая 0), которые используются для представления заданного числа.
В восьмеричной системе (или системе с основанием – 8) всего 8 цифр (0, 1, 2, 3, 4, 5, 6 и 7) используются для представления числа любого размера (величины) .
. , и 7 представлены ниже:
1 = ( 1 * 8 0 ) = ( 1 * 1)
2 = ( 2 * 8 0 ) = ( 2 * 1)
……
7 = ( 7 * 8 0 ) = ( 7 * 1)
Теперь представим следующие числа в восьмеричной системе:
Восемнадцать (18): Поскольку от 0 до 7 — это только цифры, которые могут использоваться для представления 18, давайте разделим 18 на 8 и напишем частное и остаток следующим образом:
[частное][остаток], т.
е.: [2][2]
18 = ( 2 * 8 1 ) + ( 2 * 8 0 ) = (16) + (2)
Четыреста и двадцать один 40147: 7 — это только цифры, которые можно использовать для представления 421, давайте разделим 421 на 8 и запишем частное и остаток следующим образом:
[частное][остаток], т.е.: [52] [5] (делим 52 на 8, получаем [6][4] ), что равно [6][4][5 ]
421 = (6 * 8 2 ) + (4 * 8 1 ) + (5 * 8 0 ) = (384) + (32) + (5)
Чтобы отличить от десятичного числа цифры, восьмеричные числа имеют префикс 0 (ноль).
Например, чтобы сохранить восьмеричное значение семь в переменной octal_Seven , пишем
int octal_Seven = 07;
Аналогично, если мы хотим сохранить восьмеричное представление десятичного числа 9 в переменной число_Девять, , мы пишем
int число_Девять = 011;
Самая большая цифра в восьмеричной системе (7) 8 . Число (7) 8 в двоичном виде представляется как (111) 2 . В двоичной системе три двоичных разряда (бита) используются для представления старшего восьмеричного разряда. При преобразовании восьмеричное число в двоичное число , три бита используются для представления каждой восьмеричной цифры.
Число (7) 8 в двоичном виде представляется как (111) 2 . В двоичной системе три двоичных разряда (бита) используются для представления старшего восьмеричного разряда. При преобразовании восьмеричное число в двоичное число , три бита используются для представления каждой восьмеричной цифры.
В следующей таблице показано преобразование каждой восьмеричной цифры в соответствующие ей двоичные цифры.
Например, восьмеричное число 0246 преобразуется в соответствующую ему двоичную форму как
Восьмеричное число -> 2 4 6 Двоичный номер -> 010 100 110
Следовательно, 0246 равно (010100110) 2 .
Аналогично, при преобразовании двоичного числа в его восьмеричную форму, двоичное число делится на группы по 3 цифры в каждой, начиная с крайней правой части данного числа. Каждая из трех двоичных цифр заменяется соответствующими восьмеричными цифрами .
Каждая из трех двоичных цифр заменяется соответствующими восьмеричными цифрами .
Если в группе двоичных цифр в крайней левой части числа нет трех цифр, то в качестве префикса добавляется необходимое количество нулей для получения трех двоичных цифр. Например, давайте преобразуем двоичное число 1101100 в соответствующее ему восьмеричное число .
Двоичный номер -> 1 101 100 Двоичный номер -> 001 101 100 //После префикса нулей в крайней левой части группы Восьмеричное число -> 1 5 4
Следовательно, восьмеричный эквивалент данного двоичного числа 1101100 равен 0154 .
4. Шестнадцатеричные числа:
Система счисления с основанием – 16 называется в шестнадцатеричной системе или просто в шестнадцатеричной системе. Основание (также известное как основание) — это количество уникальных цифр или символов (включая 0), которые используются для представления заданного числа.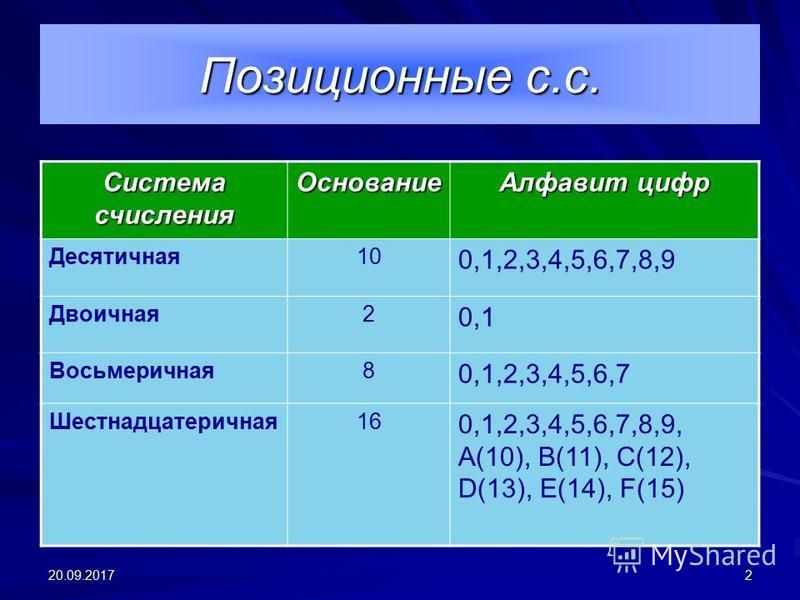
В шестнадцатеричной системе (или системе счисления по основанию – 16 ) всего используется 16 символов. Цифры от 0 (ноль) до 9 (девять) используются для представления значений от 0 до 9 соответственно и букв A , B , C , D , E и F (OR A , B , C , D , E и F F. F. F. F. соответственно.
Во многих языках программирования 0x используется в качестве префикса для обозначения шестнадцатеричного представления.
Например, в шестнадцатеричной системе счисления значение ноль представляется как 0x0 , где
0 = ( 0 * 16 0 ) = ( 0 * 1)
Аналогично,
1 = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 ) = ( 1 * 16 0 )
2 = ( 2 * 16 0 ) = ( 2 * 1)
….
.
15 = F = ( 15 * 16 0 ) = ( 15 * 1)
Теперь представим следующие числа в шестнадцатеричной системе счисления:
Десятичное число
0475 Eighteen (18) :Поскольку для представления 18 можно использовать только от 0 до 9 и алфавиты от A до F .
Разделим 18 на 16 и запишем частное и остаток следующим образом: частное][остаток], т. е. [1][2]
18 = 0x12 = ( 1 * 16 1 ) + ( 2 * 16 0 ) = (16) + (2)
Сотни и шестьдесят (1600).
Так как можно использовать только от 0 до 9 и алфавиты от A до F для представления 160.
Давайте разделим 160 на 16 и запишем частное и остаток следующим образом:
[частное][остаток], т.
е. [10][0] , [A][0] (поскольку 10 представлено буквой A)
160 = 0xa0 = ( 10 * 16 1 ) + ( 0 * 16 0 ) = (160) + (0)
. может использоваться при представлении шестнадцатеричных значений. Например,
int hex_Hundred_and_Sixty = 0xA0; // или 0Xa0, однако предпочтительнее 0xA0.
Старшая шестнадцатеричная цифра (F) 16 . Число (F) 16 в двоичном виде представлено как (1111)2 . Здесь четыре двоичных цифры (биты) используются для представления старшей шестнадцатеричной цифры. При преобразовании hex в двоичное четыре бита используются для представления каждой шестнадцатеричной цифры .
В следующей таблице показано преобразование каждого шестнадцатеричная цифра в соответствующие двоичные цифры .
Например, шестнадцатеричное число 0x5AF6 преобразуется в соответствующую ему двоичную форму следующим образом:
Шестнадцатеричный номер -> 5 A F 6 Двоичный номер -> 0101 1010 1111 0110
Следовательно, 0x5AF6 равно (0101101011110110) 2 .
Аналогичным образом при преобразовании двоичного числа в шестнадцатеричное двоичное число сначала делится на группы по 4 цифры, каждая из которых начинается с крайней правой стороны. Каждая из четырех двоичных цифр заменяется соответствующей ей шестнадцатеричной цифрой.
Если группа с крайней левой стороны двоичных цифр не содержит четырех цифр , необходимое количество нулей добавляется в качестве префикса для создания группы из четырех двоичных цифр.
Например, давайте преобразуем следующее двоичное число 1101100 в шестнадцатеричное.
Двоичный номер -> 110 1100 Двоичный номер -> 0110 1100 //После префикса нулей в самой левой группе Шестнадцатеричный номер -> 6 C
Следовательно, шестнадцатеричный эквивалент данного двоичного числа 1101100 это 0x6C .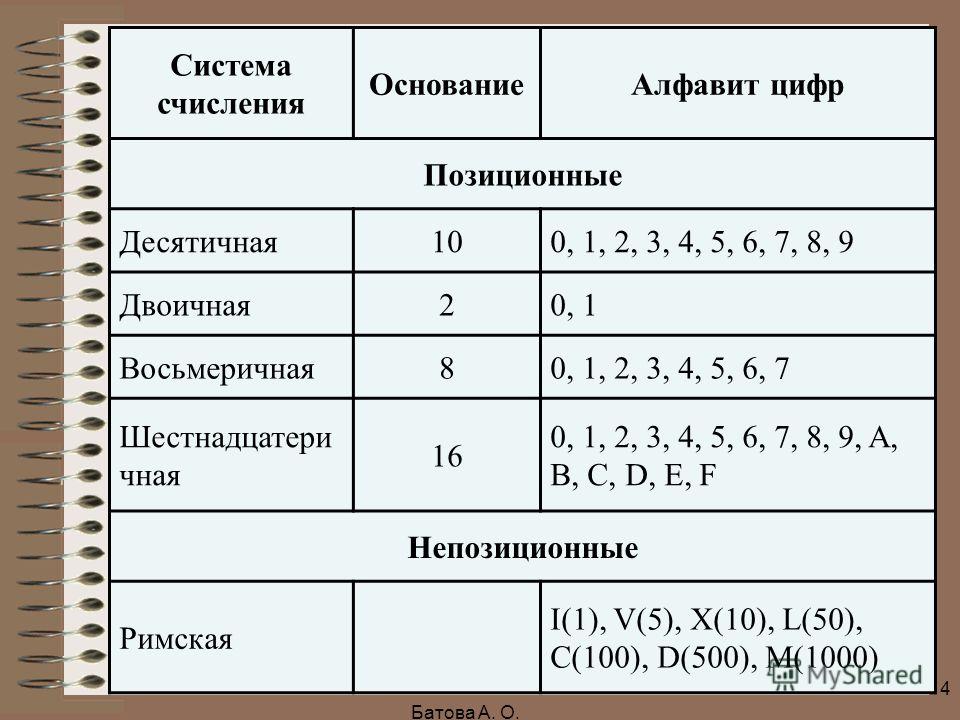
Каталожные номера:
- Wiki – Системы счисления
- Вики — Десятичная система счисления
- Вики — Двоичная система счисления
Приятного обучения 🙂
Учебники по C
| 128 | 200 | 80 | 1000 0000 | Ç | заглавная буква c с седилью |
| 129 | 201 | 81 | 1000 0001 | и | буква у с диэрезисом |
| 130 | 202 | 82 | 1000 0010 | и | буква е с остротой |
| 131 | 203 | 83 | 1000 0011 | — | буква а с циркумфлексом |
| 132 | 204 | 84 | 1000 0100 | и | буква а с диэрезисом |
| 133 | 205 | 85 | 1000 0101 | и | буква а с могилой |
| 134 | 206 | 86 | 1000 0110 | х | буква а с кольцом над |
| 135 | 207 | 87 | 1000 0111 | и | буква c с седилью |
| 136 | 210 | 88 | 1000 1000 | — | буква e с циркумфлексом |
| 137 | 211 | 89 | 1000 1001 | — | буква е с диэрезисом |
| 138 | 212 | 8А | 1000 1010 | и | буква е с гравировкой |
| 139 | 213 | 8Б | 1000 1011 | ï | буква i с диэрезисом |
| 140 | 214 | 8С | 1000 1100 | и | буква i с циркумфлексом |
| 141 | 215 | 8Д | 1000 1101 | х | буква i с могилой |
| 142 | 216 | 8Е | 1000 1110 | Ä | заглавная буква а с диэрезисом |
| 143 | 217 | 8Ф | 1000 1111 | Å | заглавная буква а с кольцом над |
| 144 | 220 | 90 | 1001 0000 | Э | заглавная буква е с острым знаком |
| 145 | 221 | 91 | 1001 0001 | æ | буква ае |
| 146 | 222 | 92 | 1001 0010 | Æ | заглавная буква ae |
| 147 | 223 | 93 | 1001 0011 | х | буква о с циркумфлексом |
| 148 | 224 | 94 | 1001 0100 | или | буква о с диэрезисом |
| 149 | 225 | 95 | 1001 0101 | х | буква о с могилой |
| 150 | 226 | 96 | 1001 0110 | х | буква u с циркумфлексом |
| 151 | 227 | 97 | 1001 0111 | х | буква у с могилой |
| 152 | 230 | 98 | 1001 1000 | ÿ | буква y с диэрезисом |
| 153 | 231 | 99 | 1001 1001 | . .. .. | заглавная буква о с диэрезисом |
| 154 | 232 | 9А | 1001 1010 | О | заглавная буква у с диэрезисом |
| 155 | 233 | 9Б | 1001 1011 | ¢ | буква о со штрихом |
| 156 | 234 | 9С | 1001 1100 | £ | знак фунта стерлингов |
| 157 | 235 | 9Д | 1001 1101 | ¥ | иен знак |
| 158 | 236 | 9Е | 1001 1110 | ₧ | знак песеты |
| 159 | 237 | 9Ф | 1001 1111 | ƒ | буква f с крючком |
| 160 | 240 | А0 | 1010 0000 | а | буква а с остротой |
| 161 | 241 | А1 | 1010 0001 | и | буква я с острым |
| 162 | 242 | А2 | 1010 0010 | — | буква о с остротой |
| 163 | 243 | А3 | 1010 0011 | по | буква у с острым |
| 164 | 244 | А4 | 1010 0100 | – | буква н с тильдой |
| 165 | 245 | А5 | 1010 0101 | С | заглавная буква н с тильдой |
| 166 | 246 | А6 | 1010 0110 | ª | женский порядковый номер |
| 167 | 247 | А7 | 1010 0111 | º | мужской порядковый номер |
| 168 | 250 | А8 | 1010 1000 | À | перевернутый вопросительный знак |
| 169 | 251 | А9 | 1010 1001 | ⌐ | наоборот не знак |
| 170 | 252 | АА | 1010 1010 | ¬ | не подписывать |
| 171 | 253 | АБ | 1010 1011 | ½ | одна половинка |
| 172 | 254 | АС | 1010 1100 | = | одна четверть |
| 173 | 255 | г.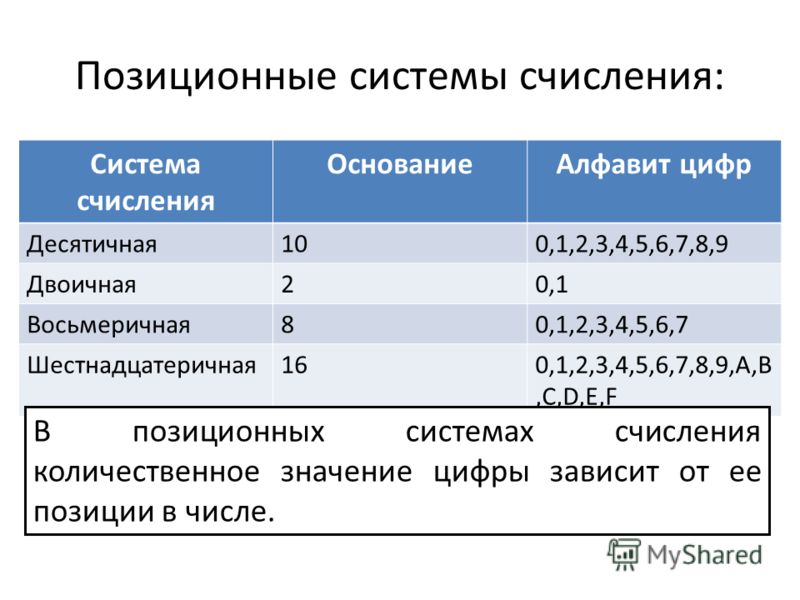 | г. н.э.1010 1101 | ¡ | перевернутый восклицательный знак |
| 174 | 256 | АЭ | 1010 1110 | « | левая двойная кавычка |
| 175 | 257 | АФ | 1010 1111 | » | правая двойная кавычка |
| 176 | 260 | В0 | 1011 0000 | ░ | светлый оттенок |
| 177 | 261 | В1 | 1011 0001 | ▒ | средний оттенок |
| 178 | 262 | В2 | 1011 0010 | ▓ | темный оттенок |
| 179 | 263 | В3 | 1011 0011 | │ | одинарная вертикальная |
| 180 | 264 | В4 | 1011 0100 | ┤ | одинарный вертикальный и левый |
| 181 | 265 | В5 | 1011 0101 | ╡ | одинарный вертикальный и двойной левый |
| 182 | 266 | В6 | 1011 0110 | ╢ | двойной вертикальный и одинарный левый |
| 183 | 267 | В7 | 1011 0111 | ╖ | удвоить вниз и один раз влево |
| 184 | 270 | В8 | 1011 1000 | ╕ | одинарный вниз и двойной влево |
| 185 | 271 | В9 | 1011 1001 | ╣ | двойной вертикальный и левый |
| 186 | 272 | ВА | 1011 1010 | ║ | двойной вертикальный |
| 187 | 273 | ББ | 1011 1011 | ╗ | удвоить ставку и оставить |
| 188 | 274 | г. до н.э. до н.э. | г. до н.э.1011 1100 | ╝ | удвоить и оставить |
| 189 | 275 | БД | 1011 1101 | ╜ | двойная вверх и одинарная левая |
| 190 | 276 | БЭ | 1011 1110 | ╛ | одинарная вверх и двойная влево |
| 191 | 277 | БФ | 1011 1111 | ┐ | в одиночку вниз и влево |
| 192 | 300 | С0 | 1100 0000 | └ | одинарный вверх и вправо |
| 193 | 301 | С1 | 1100 0001 | ┴ | одинарный и горизонтальный |
| 194 | 302 | С2 | 1100 0010 | ┬ | одинарный нижний и горизонтальный |
| 195 | 303 | С3 | 1100 0011 | ├ | одинарный вертикальный и правый |
| 196 | 304 | С4 | 1100 0100 | ─ | одинарный горизонтальный |
| 197 | 305 | С5 | 1100 0101 | ┼ | одинарная вертикальная и горизонтальная |
| 198 | 306 | С6 | 1100 0110 | ╞ | одинарный вертикальный и двойной правый |
| 199 | 307 | С7 | 1100 0111 | ╟ | двойной вертикальный и одинарный правый |
| 200 | 310 | С8 | 1100 1000 | ╚ | вдвое вверх и вправо |
| 201 | 311 | С9 | 1100 1001 | ╔ | двойной вниз и вправо |
| 202 | 312 | СА | 1100 1010 | ╩ | двойное и горизонтальное |
| 203 | 313 | КБ | 1100 1011 | ╦ | двойной вниз и горизонтальный |
| 204 | 314 | СС | 1100 1100 | ╠ | двойной вертикальный и правый |
| 205 | 315 | CD | 1100 1101 | ═ | двойной горизонтальный |
| 206 | 316 | СЕ | 1100 1110 | ╬ | двойной вертикальный и горизонтальный |
| 207 | 317 | КФ | 1100 1111 | ╧ | одинарный и двойной горизонтальный |
| 208 | 320 | Д0 | 1101 0000 | Æ | двойной вверх и одинарный горизонтальный |
| 209 | 321 | Д1 | 1101 0001 | ╤ | одинарный нижний и двойной горизонтальный |
| 210 | 322 | Д2 | 1101 0010 | ╥ | двойной нижний и одинарный горизонтальный |
| 211 | 323 | Д3 | 1101 0011 | ╙ | двойной вверх и одинарный вправо |
| 212 | 324 | Д4 | 1101 0100 | ╘ | одинарный и двойной правый |
| 213 | 325 | Д5 | 1101 0101 | ╒ | одинарный нижний и двойной правый |
| 214 | 326 | Д6 | 1101 0110 | ╓ | двойной вниз и одинарный правый |
| 215 | 327 | Д7 | 1101 0111 | ╫ | двойной вертикальный и одинарный горизонтальный |
| 216 | 330 | Д8 | 1101 1000 | ╪ | одинарная вертикальная и двойная горизонтальная |
| 217 | 331 | Д9 | 1101 1001 | ┘ | встал и ушел |
| 218 | 332 | ДА | 1101 1010 | ┌ | одинарный вниз и вправо |
| 219 | 333 | ДБ | 1101 1011 | █ | полный блок |
| 220 | 334 | DC | 1101 1100 | ▄ | нижний полублок |
| 221 | 335 | ДД | 1101 1101 | ▌ | левый полублок |
| 222 | 336 | ДЭ | 1101 1110 | ▐ | правый полублок |
| 223 | 337 | ДФ | 1101 1111 | ▀ | верхний полублок |
| 224 | 340 | Э0 | 1110 0000 | α | греческая буква альфа |
| 225 | 341 | Е1 | 1110 0001 | С | буква диез s |
| 226 | 342 | Е2 | 1110 0010 | Г | греческая заглавная буква гамма |
| 227 | 343 | Е3 | 1110 0011 | № | греческая буква пи |
| 228 | 344 | Е4 | 1110 0100 | Σ | греческая заглавная буква сигма |
| 229 | 345 | Е5 | 1110 0101 | о | греческая буква сигма |
| 230 | 346 | Е6 | 1110 0110 | мкм | микрознак |
| 231 | 347 | Е7 | 1110 0111 | т | греческая буква тау |
| 232 | 350 | Е8 | 1110 1000 | Ф | греческая заглавная буква фи |
| 233 | 351 | Е9 | 1110 1001 | Θ | греческая заглавная буква тета |
| 234 | 352 | ЕА | 1110 1010 | Ом | греческая заглавная буква омега |
| 235 | 353 | ЭБ | 1110 1011 | δ | греческая буква дельта |
| 236 | 354 | ЕС | 1110 1100 | ∞ | бесконечность |
| 237 | 355 | ЭД | 1110 1101 | ф | греческая буква фи |
| 238 | 356 | ЕЕ | 1110 1110 | ε | греческая буква эпсилон |
| 239 | 357 | ЭФ | 1110 1111 | ∩ | перекресток |
| 240 | 360 | Ф0 | 1111 0000 | ≡ | идентичен |
| 241 | 361 | Ф1 | 1111 0001 | ± | знак плюс-минус |
| 242 | 362 | Ф2 | 1111 0010 | ≥ | больше или равно |
| 243 | 363 | Ф3 | 1111 0011 | ≤ | меньше или равно |
| 244 | 364 | Ф4 | 1111 0100 | ⌠ | цельная верхняя половина |
| 245 | 365 | Ф5 | 1111 0101 | ⌡ | цельная нижняя половина |
| 246 | 366 | Ф6 | 1111 0110 | ÷ | знак деления |
| 247 | 367 | Ф7 | 1111 0111 | ≈ | почти равно |
| 248 | 370 | Ф8 | 1111 1000 | ° | знак градуса |
| 249 | 371 | Ф9 | 1111 1001 | ∙ | оператор пули |
| 250 | 372 | ФА | 1111 1010 | · | средняя точка |
| 251 | 373 | ФБ | 1111 1011 | √ | квадратный корень |
| 252 | 374 | ФК | 1111 1100 | ⁿ | верхний индекс сущ.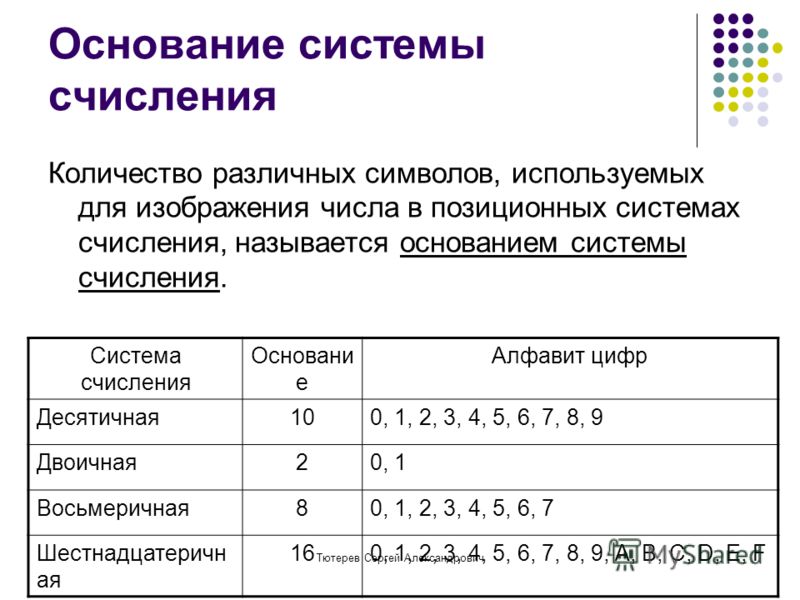 |


 Основные понятия. Виды систем счисления
Основные понятия. Виды систем счисления э.)
э.)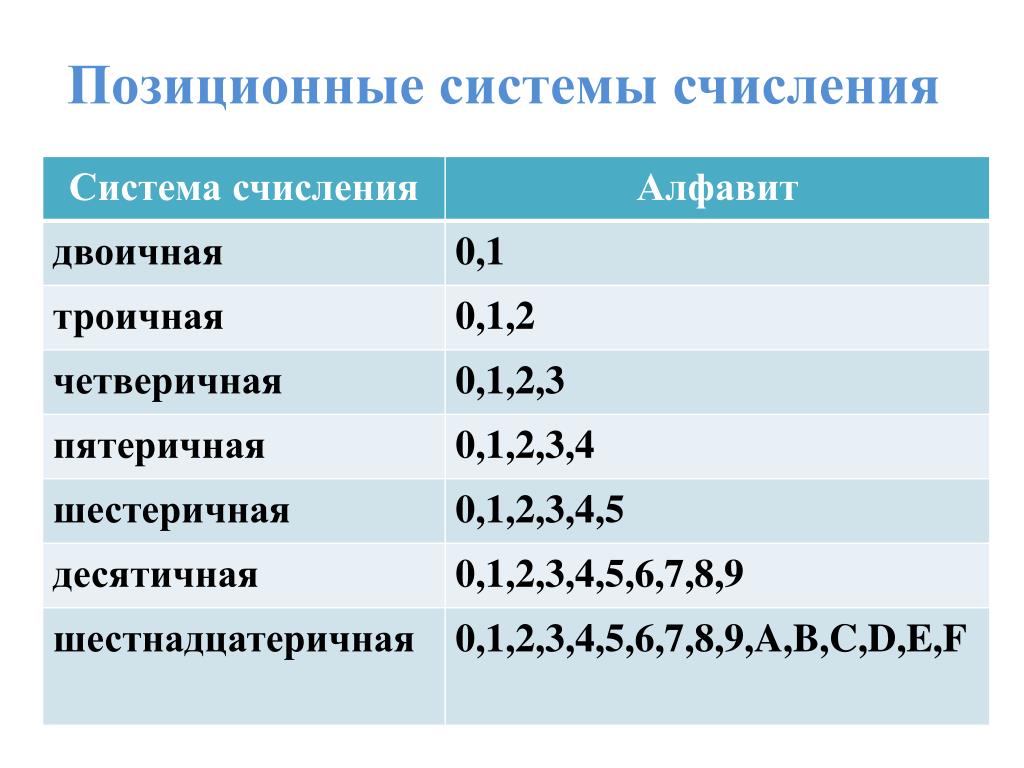 э.)
э.)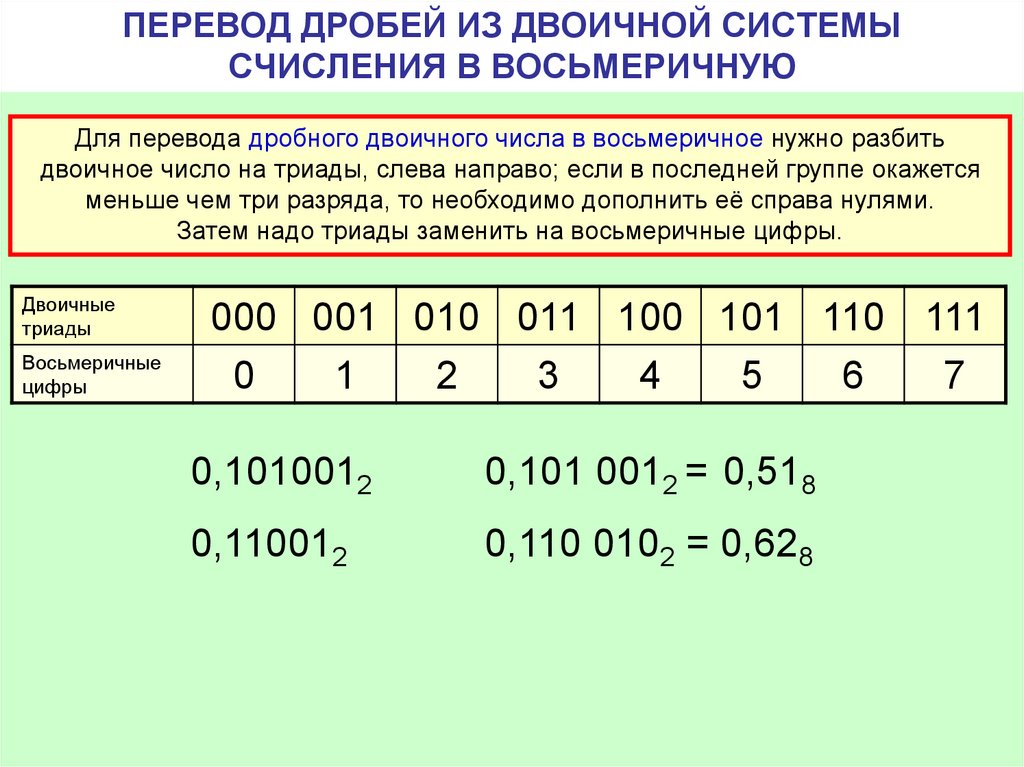 При р > 10 к десяти арабским цифрам добавляют латинские буквы.
При р > 10 к десяти арабским цифрам добавляют латинские буквы. Где сегодня используется римская система счисления для записи чисел?
Где сегодня используется римская система счисления для записи чисел? Используется двоичная система счисления.
Используется двоичная система счисления.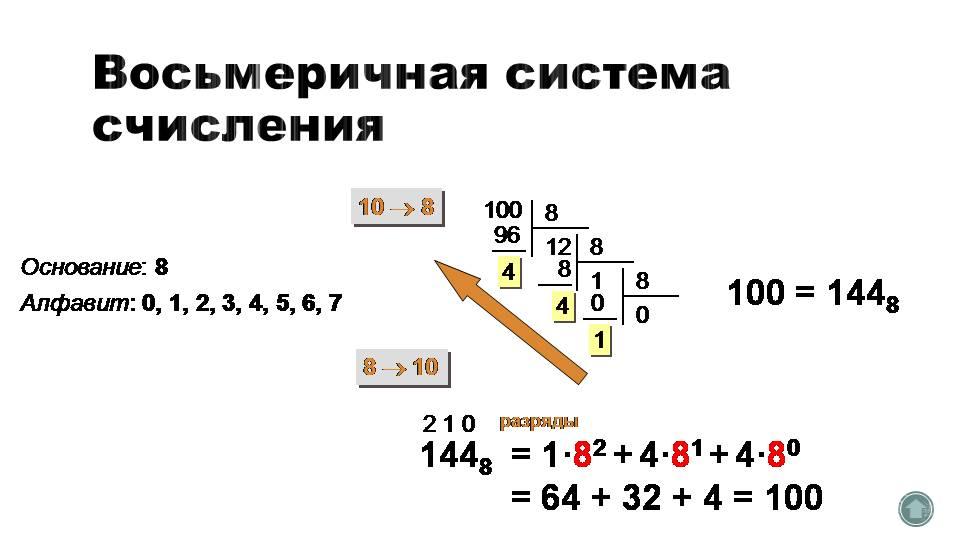



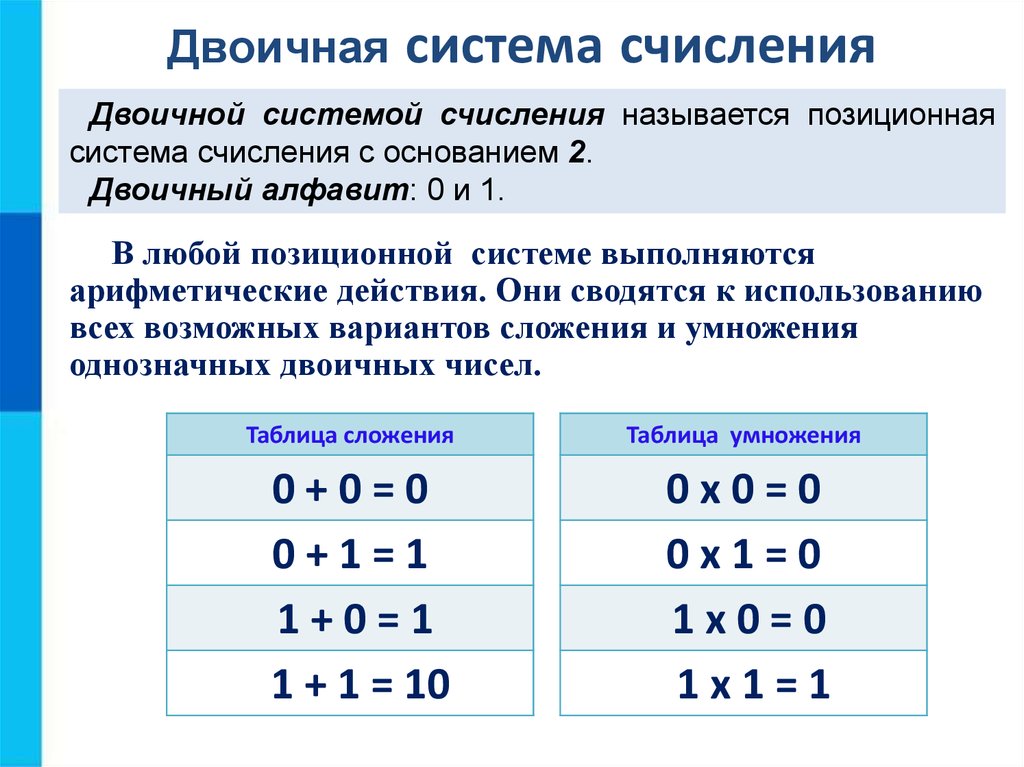 Почему же, по прошествии почти 650 лет, чехи помнят об этом человеке и считают его героем?
Почему же, по прошествии почти 650 лет, чехи помнят об этом человеке и считают его героем?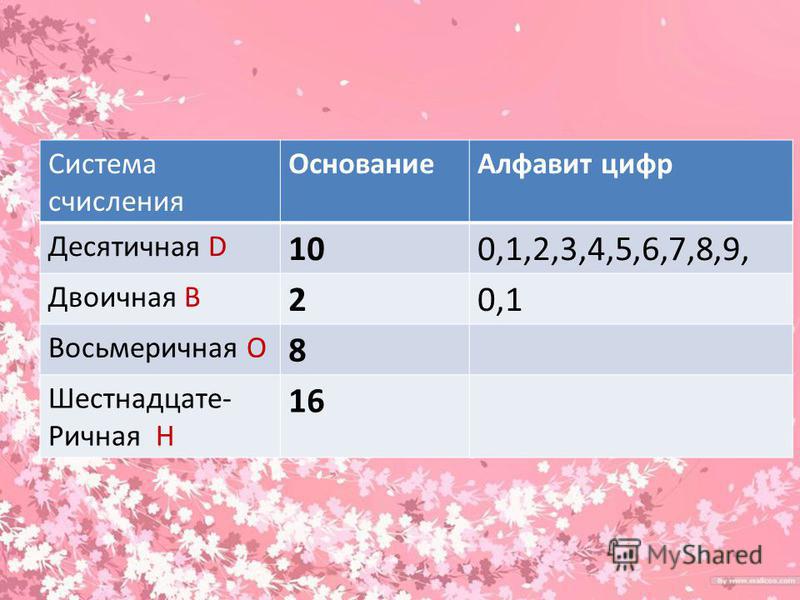 1515/LINGTY. 2006.002, S2CID 20412558
1515/LINGTY. 2006.002, S2CID 20412558 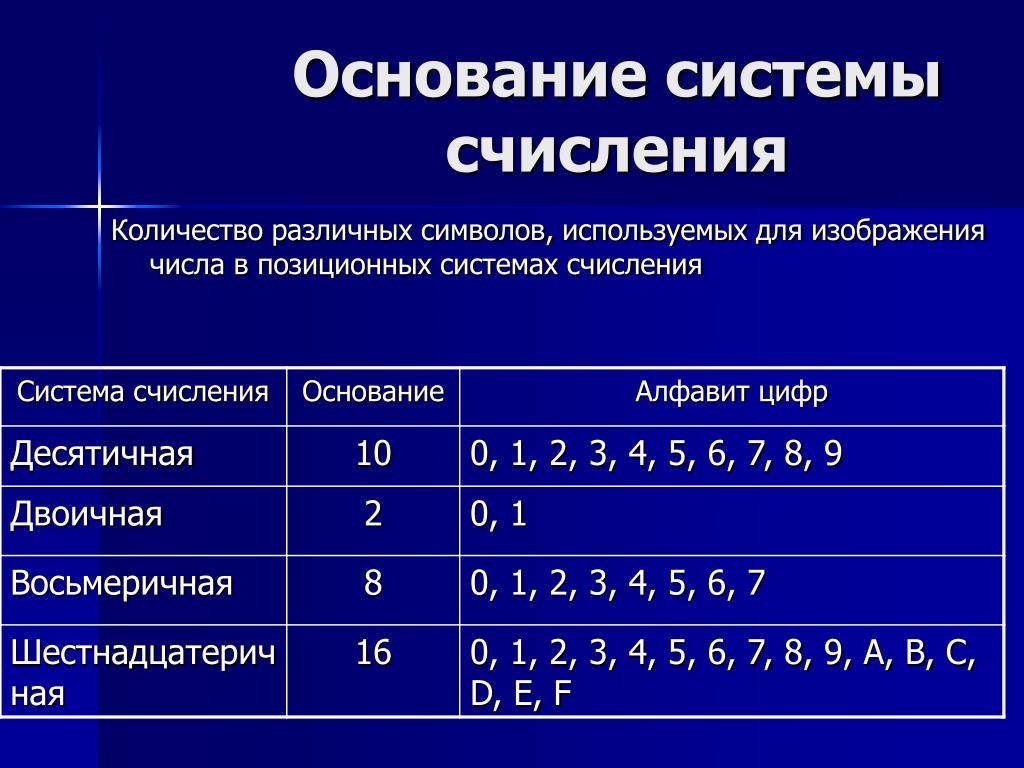 Эквивалент восьмеричного двоичного числа получается путем разбиения двоичного числа на 3-битные группы, и каждой группе присваивается эквивалентное восьмеричное значение от «0» до «7».
Эквивалент восьмеричного двоичного числа получается путем разбиения двоичного числа на 3-битные группы, и каждой группе присваивается эквивалентное восьмеричное значение от «0» до «7». Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.
Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.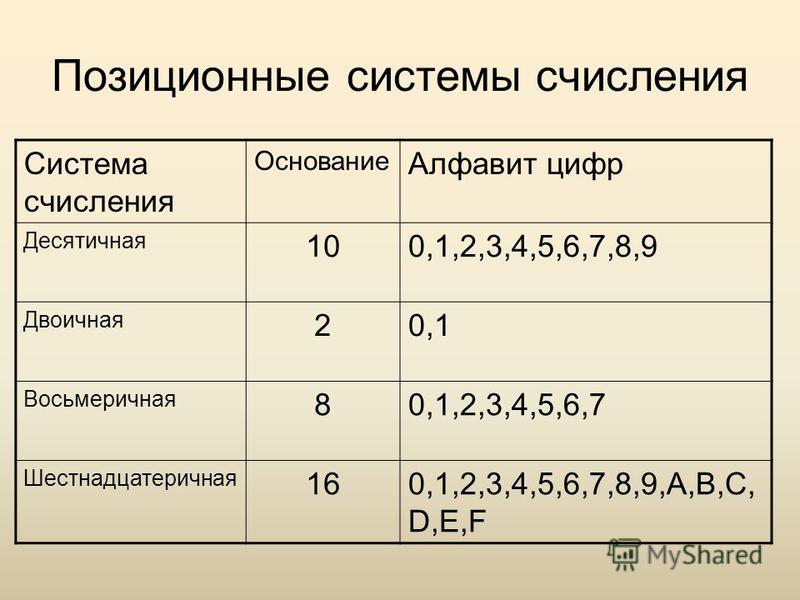 В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
 В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.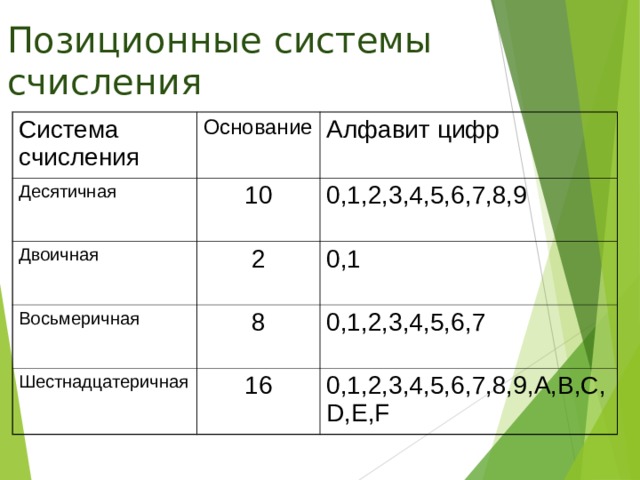 Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
 Здесь числа с основанием 10 используются в скобках для сравнения.
Здесь числа с основанием 10 используются в скобках для сравнения. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
 Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно оставляют на похороны.
Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно оставляют на похороны.
 Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.


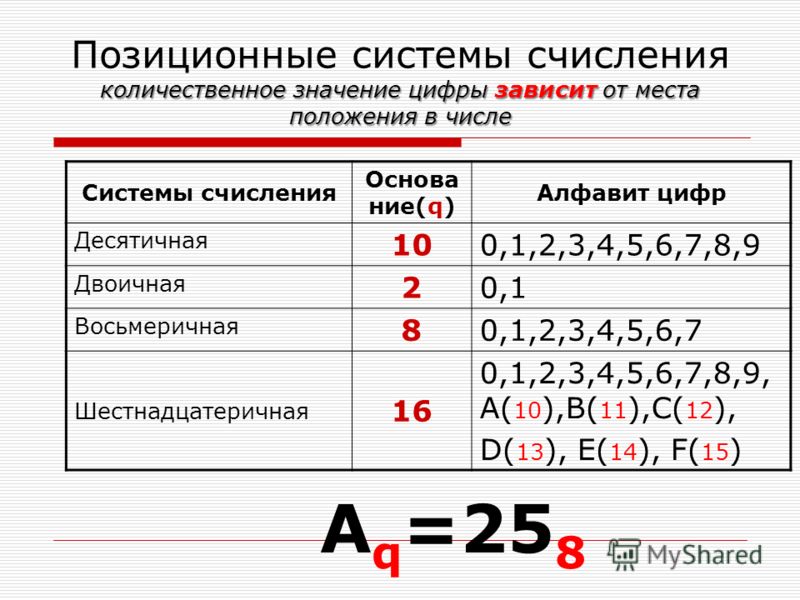
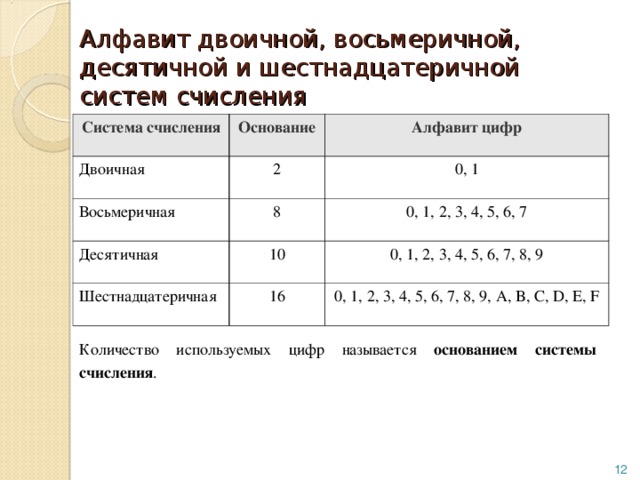 е. , : [1][1]
е. , : [1][1]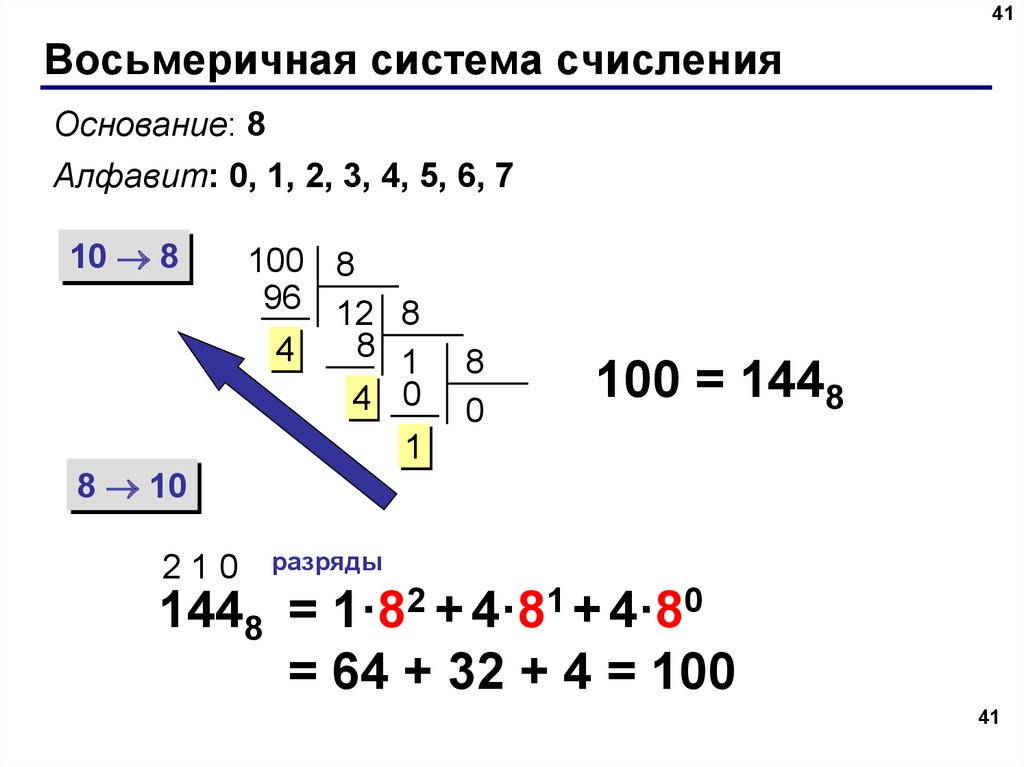 е.: [2][2]
е.: [2][2]  .
. е. [10][0] , [A][0] (поскольку 10 представлено буквой A)
е. [10][0] , [A][0] (поскольку 10 представлено буквой A)