Техническая механика. Теоретическая механика | ПроСопромат.ру
Часто в прикладных задачах механики приходится определять моменты сил, приложенных к телу, относительно его оси. Покажем, что в сечениях тела под действием внешних сил всегда возникают внутренние силы.
Рассмотрим устройство для подъема грузов, состоящее из вала ABC, на который насажены барабан АВ с радиусом r и зубчатое колесо С с радиусом R.
Вал приводится во вращение от электродвигателя D через зубчатую передачу. Вес поднимаемого груза Q передается через трос на обод барабана, а от шестерни K, насаженной на вал электродвигателя, передается движущая

При равномерном подъеме груза моменты внешних сил, приложенных к валу, должны уравновешиваться, т. е.
Реакции опор А и В не войдут в уравнение моментов, так как они пересекают ось z и, следовательно, не создают относительно этой оси моментов.
Из составленного уравнения равновесия следует, что PR = Qr или Мz (Р) = Мz (Q), т. е. на концы участка вала, расположенного между сечением приложения груза
Участок вала между сечениями приложения вращающих моментов, как уже отмечалось, находится в равновесии. Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.
Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.
Чтобы отсеченная часть
Использованный здесь метод установления внутренних сил в сечении вала называется методом сечений (более подробно о методе сечений — см. здесь).
Момент внутренних
 е. вращающих моментов, приложенных к отсеченной части вала:
е. вращающих моментов, приложенных к отсеченной части вала:,
где n — число вращающих моментов, приложенных к отсеченной части рассматриваемого вала.
Знак крутящего момента в поперечном сечении вала можно установить, исходя из направления внешних вращающих моментов. 
При возрастании веса поднимаемого груза соответственно увеличиваются вращающие моменты. Будут возрастать также крутящие моменты в сечениях вала. Очевидно, что при данных размерах вала нельзя допускать безграничного возрастания вращающего, а следовательно, и крутящего моментов, так как вал может разрушиться или сильно деформироваться. Поэтому определение крутящих моментов имеет очень большое практическое значение для расчетов на прочность.
Запись опубликована автором admin в рубрике Пара сил и моменты сил.Рычаг обладает способностью вращаться вокруг оси закрепления (рис. а).
а).
Равновесие рычага будет обеспечено только в том случае, когда алгебраическая сумма моментов всех действующих на рычаг сил относительно его неподвижной
Неподвижной точкой рычага, относительно которой мы будем составлять уравнение моментов, является точка пересечения оси вращения рычага с плоскостью чертежа (рис.а)
или
Рычаг можно использовать для подъема грузов, для создания больших давлений с помощью небольшого усилия и т. п. Рычаги двух видов показаны на рис.б и в.
Запись опубликована автором admin в рубрике Пара сил и моменты сил. 42).
42).На рисунке показаны две составляющие силы Р — это силы Р1 и Р2 . Составляющая Р2 параллельна оси Оz, поэтому ее момент относительно этой оси равен нулю. Составляющая Р1
Таким образом,
Запись опубликована автором admin в рубрике Задачи по механике.Когда момент силы относительно оси равен нулю?
Момент силы относительно оси равен нулю, когда сила и ось расположены в одной плоскости.
1) сила параллельна оси;
2) линия действия силы пересекает ось.
И в том, и в другом случае момент силы относительно оси равен нулю.
Запись опубликована автором admin в рубрике Вопросы по механике.Рассмотрим, как определяется момент силы относительно оси. Стремление силы вращать тело вокруг неподвижной оси зависит от величины силы, ее
Из опыта известно, что силы, проходящие через ось, и силы, параллельные оси, НЕ МОГУТ ВЫЗВАТЬ ВРАЩЕНИЯ ТЕЛА вокруг этой оси. Посмотрим на рисунок.
Ни сила Р1, линия действия которой пересекает ось Oz, ни сила Р2, параллельная оси, не смогут повернуть тело вокруг этой оси.
Для вращательного эффекта силы относительно закрепленной оси вводится понятие момента силы относительно оси Мz (Р). Вращательный эффект силы относительно оси и выражается ее моментом.
Пусть на тело в какой-то точке действует произвольная сила Р, не параллельная оси вращения Oz и не пересекающая эту ось. Проведем плоскость H, перпендикулярную оси Oz и проходящую через начало вектора силы. Разложим заданную силу Р на две составляющие: Р1, расположенную в плоскости H, и Р2, параллельную оси Oz.
Составляющая Р2, параллельная оси Oz момента относительно этой оси не создает. Составляющая Р1, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р1 измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.
Составляющая Р1, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р1 измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.
В выражение момента силы относительно оси входит не вся сила, а только ее составляющая, лежащая в плоскости, перпендикулярной оси вращения.
Знак момента по общему правилу определяется направлением вращения тела: (+) при движении по часовой стрелке, (—) при движении против часовой стрелки (правило условно). При определении знака момента наблюдатель должен непременно находиться со стороны положительного направления оси. На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
На рисунке внизу момент силы Р относительно оси Oz — величина отрицательная.
Рассмотрим частный случай.
В частном случае момент силы Р, расположенной в плоскости H, относительно оси Oz, перпендикулярной этой плоскости, определится произведением полной величины силы Р на ее плечо l относительно точки пересечения оси Oz и плоскости H
Итак, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы на плоскость относительно точки пересечения оси с этой плоскостью.
Зависят ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
Зависят. Момент силы относительно относительно точки определяется произведением модуля силы на плечо, поэтому величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Запись опубликована автором admin в рубрике Вопросы по механике.Какой из отрезков — ОВ, ОА или ОН — является плечом силы Р относительно точки О?
Плечом является отрезок ОН, так как плечо силы относительно точки- это длина перпендикуляра, опущенного из точки на линию действия силы.
Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а).
Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать тело вокруг этой точки. Точка О, относительно которой берется момент, называется центром
момента, а перпендикуляр а называется плечом силы относительно центра момента.
Таким образом,
М = сила×плечо.
Момент силы Р относительно О обозначается
М0(Р) = Ра.
Моменты сил измеряют в ньютонометрах (Нм) или килограммометрах (кГм) или в соответствующих кратных и дольных единицах, как и моменты пар.
Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б).
Установленное правило знаков для моментов сил, как и для моментов пар, условно.
Когда линия действия силы проходит через данную точку, ее момент относительно этой точки равен нулю, так как в рассматриваемом случае плечо равно нулю а = 0 (рис. в).
Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве.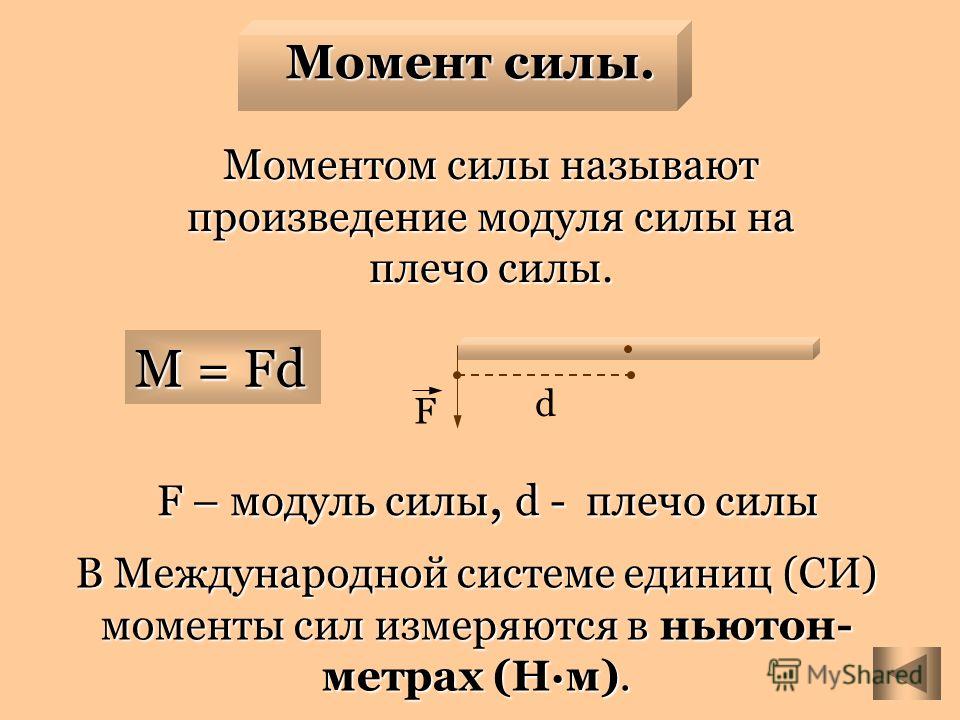 У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
К телу приложены две пары, лежащие в параллельных плоскостях. Первая пара образована силами по 4 кн, имеет плечо 0,5 м и ее момёнт вращает по часовой стрелке. Вторая пара образована силами 6 кн, имеет плечо 0,4 м и ее момент вращает против часовой стрелки. Определить величину и направление момента пары сил, которой можно уравновесить эти пары.
Определим сначала моменты каждой из пар сил. Момент первой пары М1 = 4· 0,5 =2 кН·м;
момент второй пары М2 = — 6· 0,4 = -2, 4 кН·м.
Таким образом, алгебраическая сумма моментов пар сил равна М=М1+М2= -0,4 кН·м.
Следовательно, величина и направление момента пары сил, которой можно уравновесить эти пары будет равна +0,4 кН·м.
Запись опубликована автором admin в рубрике Вопросы по механике.Будет ли тело находиться в равновесии, если на него действуют три пары сил, приложенных в одной плоскости, и моменты этих пар имеют следующие значения:
М1 = —600 Н·м; М2 = 320 Н·м и М3 = 280 Н· м.
Для того чтобы узнать — будет ли тело находиться в равновесии, следует определить алгебраическую сумму моментов пар сил. Если данная сумма будет равна нулю, то система пар уравновешена, и тело будет находиться в равновесии.
Определим алгебраическую сумму моментов пар сил
М = —600 + 320 + 280 =0.
Следовательно, тело будет находиться в равновесии.
Запись опубликована автором admin в рубрике Вопросы по механике.Группа А 21, 14.12.21 г., 2 пара и тесты по технической механике | Методическая разработка:
Тесты по технической механике
1. Что изучает статика?
1) статика изучает силы, их действия, сложение, разложение и равновесие их;
2) статика изучает статистические движения тел;
3) статика изучает механическое движение тел.
2. На какие разделы делится теоретическая механика?
1) статика, кибернетика, механика.
2) статика, кинематика, динамика.
3) кинематика, механика, кибернетика.
3. Когда расстояние между двумя точками тела остается неизменным его называют
1) абсолютно твердым телом
2) прочным телом
3) материальным телом.
4. Векторная величина, представляющая собой меру механического воздействия одних тел на другие – это
1) механическое воздействие;
2) сила;
3) удар.
5. Материальной точкой называется
1) абсолютно твердое тело, размерами которого можно пренебречь, сосредоточив всю массу тела в точке.
2) точка, сосредоточенная в центре тела.
3) точка, лежащая в центре тяжести фигуры.
6. Действия системы сил на одно и то же твердое тело, производя одинаковые воздействия называются:
1) эквивалентными;
2) внутренними;
3) внешними.
7. Если система сил эквивалентна одной силе, то эта сила называется
Если система сил эквивалентна одной силе, то эта сила называется
1) уравновешенной;
2) равнодействующей;
3) сосредоточенной.
8. На чем базируются все теоремы и уравнения статики?
1) на законах статики;
2) на наблюдениях;
3) на аксиомах.
9. Назовите единицу измерения силы?
1) Паскаль. 3) Ньютон.
2) Герц. 4) Джоуль
10. Что называется моментом силы относительно точки (центра)?
1) Произведение модуля этой силы на время её действия.
2) Произведение силы на квадрат расстояния до точки (центра).
3) Произведение силы на кратчайшее расстояние до этой точки (центра).
11. Когда момент силы считается положительным?
1) Когда под действием силы тело движется вперёд.
2) Когда под действием силы тело вращается по ходу часовой стрелки.
3) Когда под действием силы тело вращается против хода часовой стрелки
12. Трением скольжения называют:
1) сопротивление, возникающие при относительном перемещение одного тела по поверхности другого
2) сопротивление силе обратной коэффициенту трения.
13. Сила трения направлена в сторону, противоположную относительной скорости скольжения
1) это закон Кулона;
2) это свойство пары сил;
3) это закон статики.
14. Раздел механики, в котором изучается движение материальных тел под действием приложенных к ним сил – это
1) статика;
2) динамика;
3) кинематика.
15. Основной закон динамики
1) Устанавливает связь между ускорением и массой материальной точки и силой;
2) Масса является мерой инертности материальных тел в их поступательном движении;
3) Всякому действию соответствует равное и противоположно направленное противодействие.
16. Назовите единицу измерения силы?
1) Паскаль. 3) Ньютон.
2) Герц. 4) Джоуль
17. Что называется моментом силы относительно точки (центра)?
1) Произведение модуля этой силы на время её действия;
2) Отношение силы, действующей на тело, к промежутку времени, в течение которого эта сила действует;
3) Произведение силы на кратчайшее расстояние до этой точки (центра).
18. Когда момент силы считается положительным?
1) Когда под действием силы тело вращается по ходу часовой стрелки;
2) Когда под действием силы тело движется назад;
3) Когда под действием силы тело вращается против хода часовой стрелки.
19. Трением скольжения называют:
1) сопротивление, возникающие при относительном перемещение одного тела по поверхности другого;
2) сопротивление силе обратной коэффициенту трения;
3) скольжение фигурных коньков.
20. Сила трения направлена в сторону, противоположную относительной скорости скольжения
1) это закон Кулона;
2) это свойство пары сил;
3) это закон статики.
21. Раздел механики, в котором изучается движение материальных тел под действием приложенных к ним сил – это
1) статика;
2) динамика;
3) кинематика.
22. Основной закон динамики
1) устанавливает связь между ускорением и массой материальной точки и силой;
2) Масса является мерой инертности материальных тел в их поступательном движении;
3) Всякому действию соответствует равное и противоположно направленное противодействие.
23.Мера механического взаимодействия тел есть:
1) сила;
2) скорость;
3) ускорение.
24. Если вектор силы параллелен оси, то проекция силы на ось равна
1) самой силе;
2) нулю;
3) произведению силы на косинус угла между линией действия силы и осью.
25. Произведение модуля силы на ее плечо называется
1) моментом пары;
2) равнодействующей силой;
3) моментом силы относительно точки.
26. Уравнения равновесия пространственной системы сходящихся сил имеют вид
1)∑Х = 0 2)∑Х = 0 3)∑МА = 0
∑У = 0 ∑У = 0 ∑МВ = 0
∑Z = 0 ∑МС = 0
27. Система сил, линии действия которых не лежат в одной плоскости и пересекаются в одной точке , называется
1) плоской системой сходящихся сил;
2) плоской системой произвольно расположенных сил;
3) пространственной системой сходящихся сил;
28. Центр тяжести прямоугольника находится на пересечении
1) диаметров;
2) диагоналей;
3) медиан.
29. Линия, вдоль которой движется тело, называется
1) траектория движения;
2) путь;
3) Перемещение.
30. Скорость при равномерном движении определяется как
1) V = S/t;
2) V = ΔS/Δt ;
3) V = S′.
31. Угловая скорость при вращательном движении равна
1) ω =ϕ′;
2) ε =ω′;
3) V = ωR;
32. Движение точки относительно неподвижной системы координат называется
1) сложное движение точки;
2) простейшее движением точки;
3) вращательное движение.
33. Если вектор силы перпендикулярен оси, то проекция силы на ось равна
1) самой силе;
2) нулю;
3) произведению силы на косинус угла между линией действия силы и осью.
34. Произведение модуля одной из сил, составляющих пару, на ее плечо называется
1) моментом пары;
2) равнодействующей силой;
3) моментом силы относительно точки.
Читать книгу «Техническая механика. Шпаргалка» онлайн полностью📖 — Аурики Луковкиной — MyBook.
1. Аксиомы и понятие силы статики
Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).
Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Системой сил называют совокупность сил, действующих на тело.
Эквивалентная система сил – система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.
Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.
Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).
Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.
2. Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки).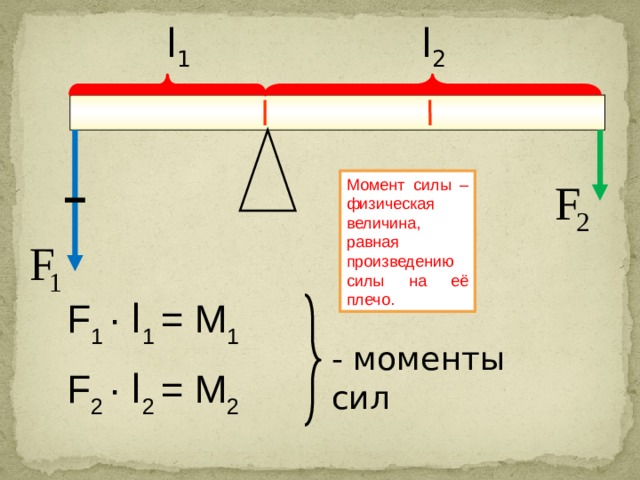 Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Защемление, или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
R = Rx+ Ry.
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе.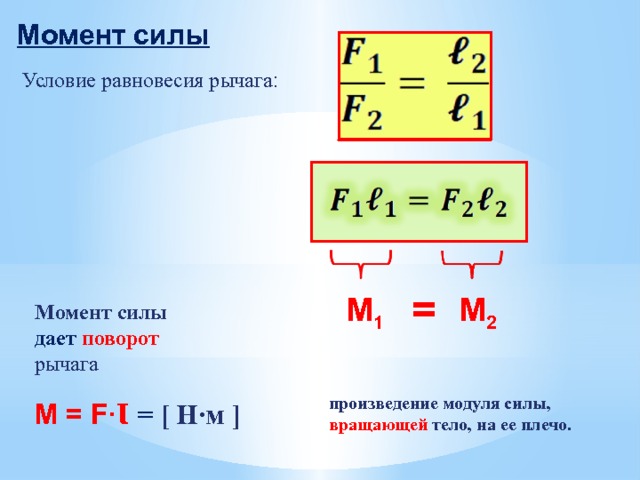 (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
(Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Билеты к экзамену по теоретической механике ФАЛТ — Кафедра теоретической механики
Осенний семестр
1. Скорость и ускорение точки. Векторный способ. Базис Дарбу (естественный трехгранник). Разложение скорости и ускорения по осям естественного трехгранника.
2. Скорость и ускорение точки в полярных координатах.
3. Криволинейные системы координат, коэффициенты Ляме. Скорость и ускорение в криволинейной системе координат.
4. Ортогональные криволинейные системы координат (полярная, цилиндрическая и сферическая).
5. Скорость и ускорение твердого тела при поступательном движении. Разложение движения твердого тела на поступательное и вращательное.
Разложение движения твердого тела на поступательное и вращательное.
6. Частные случаи вращения: вокруг точки и оси. Плоскопараллельное движение твердого тела.
7. Задание ориентации твердого тела: углы, матрицы поворота, кватернионы.
8. Угловая скорость твердого тела. Распределение скоростей точек твердого тела (формула Эйлера). Распределение ускорений точек твердого тела (формула Ривальса).
9. Кинематические уравнения Эйлера.
10. Сложное движение точки. Переносное и относительное движение. Сложение скоростей и ускорений при сложном движении точки. Теорема Кориолиса, переносное, относительное и кориолисово ускорения.
11. Сложное движение твердого тела. Сложение угловых скоростей и угловых ускорений при сложном движении твердого тела.
12. Теория скользящих векторов. Главный вектор и главный момент системы скользящих векторов. Изменение главного момента системы при изменении полюса. Центр давления и фокус аэродинамических сил, действующих на профиль крыла в однородном стационарном потоке.
13. Инварианты системы скользящих векторов. Элементарные преобразования. Эквивалентные системы скользящих векторов.
14. Простейшие системы скользящих векторов: вектор, пара, винт, векторный нуль. Приведение системы скользящих векторов к простейшему виду. Кинематические аналогии.
15. Динамика точки и системы материальных точек. Инерциальные и неинерциальные системы отсчета. Законы Ньютона.
16. Количество движения, момент количества движения (кинетический момент), кинетическая энергия точки и системы материальных точек. Изменение кинетического момента при изменении полюса.
17. Центр масс. Кёнигова система, ее применение для подсчета кинетического момента и кинетической энергии системы материальных точек (теоремы Кёнига). Внешние и внутренние силы. Момент силы, работа силы.
18. Теоремы об изменении количества движения, кинетического момента, кинетической энергии для точки и системы материальных точек. Законы сохранения.
19. Потенциальные, гироскопические, диссипативные силы. Потенциальная энергия. Консервативные системы, закон сохранения полной энергии.
20. Теоремы динамики в неинерциальных системах отсчета. Переносные и кориолисовы силы инерции. Вид основных теорем динамики в кёниговыхнеинерциальных системах отсчета.
21. Применение законов динамики к системам переменного состава. Уравнение Мещерского. Формула Циолковского.
22. Движение материальной точки в центральном поле. Законы сохранения. Интегрирование уравнений движения в квадратурах, случаи аналитической интегрируемости (степенная зависимость потенциальной энергии от радиуса).
23. Общие свойства движения в центральном поле. Законы Кеплера. Интеграл Лапласа.
24. Переменные, формула и уравнение Бине.
25. Задача двух тел. Задача многих тел. Понятие о космических перелетах. Эллипс Гомана.
26. Динамика твердого тела. Кинетическая энергия и кинетический момент при движении твердого тела около неподвижной точки.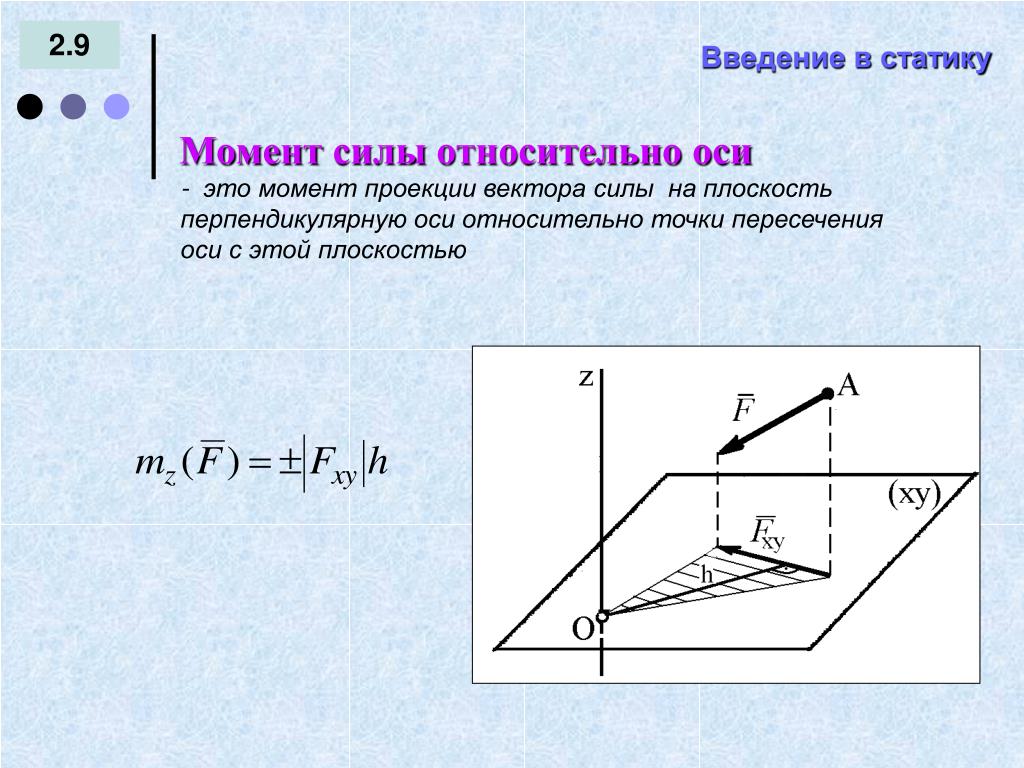
27. Геометрия масс. Моменты инерции. Тензор инерции и эллипсоид инерции. Преобразование тензора инерции при повороте осей; главные оси инерции. Преобразование тензора инерции при параллельном переносе осей; теорема Гюйгенса–Штейнера.
28. Динамические уравнения Эйлера. Случай Эйлера. Первые интегралы. Движение динамически симметричного твердого тела в случае Эйлера, параметры свободной регулярной прецессии в случае Эйлера. Интерпретация Пуансо. Интерпретация Мак-Каллога.
29. Момент сил, поддерживающий регулярную прецессию динамически симметричного твердого тела. Движение твердого тела с динамической симметрией в наблюдаемых переменных.
30. Случай Лагранжа–Пуассона. Вынужденная регулярная прецессия. Интегрирование уравнений движения в случае малых углов нутации. Элементарная теория гироскопов. Применение гироскопов в аэрокосмической технике.
31. Уравнения Лагранжа. Основные определения. Основные понятия о связях. Классификация связей. Возможные и виртуальные перемещения. Число степеней свободы. Гипотеза идеальных связей. Голономные системы.
Классификация связей. Возможные и виртуальные перемещения. Число степеней свободы. Гипотеза идеальных связей. Голономные системы.
32. Обобщенные координаты. Обобщенные силы.
33. Уравнения Лагранжа второго рода. Уравнения Лагранжа в случае потенциальных сил, лагранжиан.
34. Свойства уравнений Лагранжа: ковариантность, разрешимость. Структура кинетической энергии.
35. Понятие первого интеграла динамической системы. Теорема об изменении полной энергии. Консервативные системы.
36. Обобщенный интеграл энергии (интеграл Якоби–Пенлеве). Циклические координаты и циклические интегралы.
37. Гироскопические и диссипативные обобщенные силы. Обобщенный потенциал.
Отмеченное курсивом – не обязательно для групп ПМИ.
Весенний семестр
1. Определение положения равновесия. Условия равновесия системы с идеальными связями (принцип виртуальных перемещений). Условия равновесия голономных систем (в терминах обобщенных сил).
2. Устойчивость по Ляпунову положения равновесия. Теорема Лагранжа об устойчивости равновесия консервативных систем. Условия неустойчивости консервативных систем.
3. Асимптотическая устойчивость положения равновесия. Теорема Ляпунова об устойчивости по линейному приближению (без доказательства). Критерий Рауса–Гурвица (без доказательства) асимптотической устойчивости положения равновесия линейный стационарной системы.
4. Влияние гироскопических и диссипативных сил на устойчивость равновесия.
5. Малые колебания консервативных систем вблизи устойчивого положения равновесия. Уравнение частот. Главные (нормальные) координаты. Общее решение. Случай кратных корней.
6. Основные типы бифуркаций в динамических системах. Два сценария потери устойчивости: дивергенция и флаттер.
7. Вынужденные колебания линейной стационарной системы под действием гармонических сил. Частотные характеристики.
8. Явление резонанса. Реакция линейной стационарной системы на негармоническое воздействие.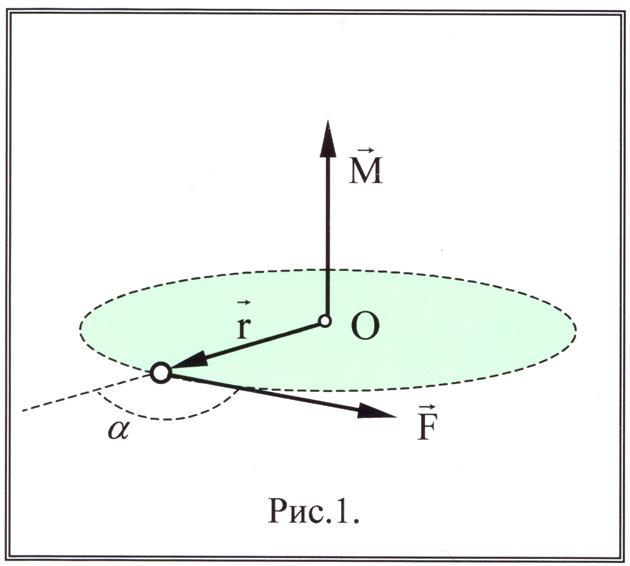
9. Переменные Гамильтона. Функция Гамильтона. Канонические уравнения Гамильтона.
10. Преобразование уравнений Лагранжа в уравнения Гамильтона. Функция Гамильтона для консервативной системы.
11. Первые интегралы гамильтоновых систем. Скобки Пуассона. Теорема Якоби–Пуассона. Циклические первые интегралы.
12. Понижение порядка уравнений Гамильтона в случае циклических координат и для обобщенно консервативных систем.
13. Преобразование лагранжиана при замене координат и времени. Теорема Эмми Нетер.
14. Действие по Гамильтону. Вариация действия по Гамильтону. Вариационный принцип Гамильтона.
15. Интегральные инварианты Пуанкаре–Картана и Пуанкаре.
16. Обратные теоремы теории интегральных инвариантов.
17. Теорема Лиувилля об инвариантности фазового объема гамильтоновой системы.
18. Теорема Ли Хуа Чжуна об интегральных инвариантах первого порядка гамильтоновых систем.
19. Канонические преобразования. Локальный критерий каноничности.
Локальный критерий каноничности.
20. Производящая функция и валентность канонического преобразования. Критерий каноничности в терминах производящих функций.
21. Свободное каноническое преобразование и его производящая функция. Правила преобразования гамильтонианов при канонических преобразованиях.
22. Фазовый поток гамильтоновых систем как однопараметрическое семейство канонических преобразований.
23. Уравнение Гамильтона–Якоби. Полный интеграл уравнения Гамильтона–Якоби и его использование в задаче интегрирования уравнений движения гамильтоновой системы.
24. Случаи разделения переменных в уравнении Гамильтона-Якоби.
|
Random converter |
Конвертер момента силыКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Исходная величина ньютон-метркилоньютон-метрмиллиньютон-метрмикроньютон-метртонна-сила (короткая)-метртонна-сила (длинная)-метртонна-сила (метрическая)-метркилограмм-сила-метрграмм-сила-сантиметрфунт-сила-футпаундаль-футпаундаль-дюйм Преобразованная величина ньютон-метркилоньютон-метрмиллиньютон-метрмикроньютон-метртонна-сила (короткая)-метртонна-сила (длинная)-метртонна-сила (метрическая)-метркилограмм-сила-метрграмм-сила-сантиметрфунт-сила-футпаундаль-футпаундаль-дюйм Ферромагнитные жидкостиЗнаете ли вы, что ферромагнитные жидкости используются в громкоговорителях для отвода тепла от катушки? Подробнее… Двутавровые балки в конструкции здания Общие сведения Терминология в английском языке Примеры момента силы Заключение Общие сведенияМомент силы — это физическая величина, характеризующая насколько сила, приложенная к телу, вызывает вращение тела вокруг оси. Вращающий момент (torque в английской терминологии) — результат приложения двух сил, которые рука прилагает к отвертке, а отвертка, в свою очередь — к головке винта Как уже упоминалось выше, в этой статье мы уделяем много внимания контексту, в котором используется тот или иной английский термин. Наша задача — объяснить разницу, чтобы помочь читателю, если он в будущем столкнется с этими терминами в английском тексте. Самое главное, что следует помнить — оба термина, момент силы и torque, используют для одной и той же физической величины, но в разных контекстах. Во многих языках, как и в русском, используют только один термин. Ниже рассмотрим в каком же контексте используют каждый из этих терминов. Терминология в английском языкеКак мы уже упоминали выше, английские термины «момент силы» и «torque» используют для одного и того же понятия, но в разных контекстах. Ниже рассмотрим несколько примеров. Стоит еще раз напомнить, что разница в использовании этих двух терминов зависит от контекста, но используют их для одного и того же физического явления. Нередко оба эти термина используют попеременно. На вороток действует пара сил от рук, в результате чего возникает вращающий момент, (по-английски torque). Чтобы понять, что такое момент силы, рассмотрим вначале, что такое момент в общем. Момент — это интенсивность, с которой сила действует на тело на определенном расстоянии относительно тела. Момент силы пропорционален силе и радиусу. Это значит, что если сила приложена к телу на определенном расстоянии от оси вращения, то вращательное действие этой силы умножается на радиус, то есть чем дальше от оси вращения приложена сила, тем более вращающее действие она оказывает на тело. Это принцип используется в системах рычагов, шестерней и блоков, чтобы получить выигрыш в силе. В этом контексте чаще всего говорят о моменте силы и о его использовании в различных системах, например в системах рычагов. Примеры работы рычагов показаны в статье «Подробнее о вращающем моменте». Стоит заметить, что в этой статье мы в основном обсуждаем вращающий момент, что соответствует английскому термину «torque». Изгибающий момент. В данной ситуации нет кручения, поэтому здесь лучше говорить о моменте силы, а не о вращающем моменте. Иногда понятия момент силы и вращающий момент различают с помощью понятия «пары сил». Пара сил — это две силы одинаковой величины, действующие в противоположном направлении. Эти силы вызывают вращение тела, и их векторная сумма равна нулю. То есть, термин «момент силы» используют в более общем контексте, чем вращающий момент. В некоторых случаях термин «вращающий момент» используют, когда тело вращается, в то время как термин «момент силы» используют, когда тело не вращается, например, если речь идет об опорных балках и других конструктивных элементах зданий в строительстве. В таких системах концы балки либо жестко закреплены (жесткая заделка), либо крепление позволяет балке вращаться. Во втором случае говорят, что эта балка закреплена на шарнирной опоре. Если на эту балку действует сила, например, перпендикулярно ее поверхности, то в результате образуется момент силы. Если балка не фиксирована, а прикреплена на шарнирной опоре, то она свободно движется в ответ на действующие на нее силы. Примеры момента силыЗдесь момент силы каждого ребенка равен весу этого ребенка, умноженному на его расстояние от оси вращения. Девочка сидит ближе к точке опоры, но прилагает больше силы к качелям, чем мальчик, поэтому качели — в равновесии. Хороший пример момента силы в быту — это действие на тело одновременно момента силы и изгибающего момента, о котором мы говорили выше. Момент силы часто используют в строительстве и в проектировании строительных конструкций, так как, зная момент силы, можно определить нагрузку, которую должна выдержать эта конструкция. Нагрузка включает нагрузку от собственного веса, нагрузку, вызванную внешними воздействиями (ветром, снегом, дождем, и так далее), нагрузку от мебели и нагрузку, вызванную посетителями и обитателями здания (их вес). При постройке в 1900 году моста Александры через реку Оттава использовано много двутавровых балок Если на балку или другой конструктивный элемент действует сила, то в ответ на эту силу возникает изгибающий момент, под действием которого некоторые части этой балки сжимаются, в то время как другие, наоборот, растягиваются. Представим, к примеру, балку, на которую действует сила, направленная вниз и приложенная по центру. Под воздействием этой силы балка принимает вогнутую форму. Верхняя часть балки, на которую действует сила, сжимается под воздействием этой силы, в то время как нижняя, наоборот, растягивается. Если нагрузка больше, чем этот материал может выдержать, то балка разрушается. Наибольшая нагрузка — на самый верхний и самый нижний слои балки, поэтому в строительстве и при проектировании сооружений эти слои часто укрепляют. Если на конструкцию действует изгибающий момент, то двутавровые балки — решение проблем, связанных с прочностью. Турбовинтовые двигатели с воздушными винтами создают крутящий момент, который действует на фюзеляж этого турбовинтового самолета; по-английски в данном случае могут говорить о моменте силы (moment of force) или о возникновении напряжения при кручении (torsional stress), так как вращение отсутствует ЗаключениеВ это статье мы рассмотрели, чем отличаются термины «момент силы» и «вращающий момент», а также английские термины «moment of force» и «torque», и увидели несколько примеров момента силы. Литература Автор статьи: Kateryna Yuri Вас могут заинтересовать и другие конвертеры из группы «Механика»:Плоский угол Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер площади Конвертер плотности Конвертер энергии и работы Конвертер силы Конвертер длины и расстояния Конвертер массы Конвертер момента инерции Конвертер мощности Конвертер давления, механического напряжения, модуля Юнга Конвертер удельного объема Конвертер вращающего момента Конвертер объема и единиц измерения в кулинарных рецептах Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер линейной скорости Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. |
Теоретическая механика
Лекция (1-5). Введение. Момент силы.
Лекция (6-10). Аксиомы
Лекция (11). Аксиома отвердевания
Лекция (12). Системы сил
Лекция (13). Сила — скользящий вектор
Лекция (14-15). Элементарные операции
Лекция (16). Приведение к 2-м силам
Лекция (17). Пара сил
Лекция (20). Теорема Пуансо
Лекция (21). Условие равновесия
Лекция (22). Варианты систем уравнений равновесия плоской системы
Лекция (23). Условие равновесия плоской системы
Лекция (24). Формула Пуансо
Лекция (25-26). Динама
Лекция (27). Случаи приведения
Лекция (28). Трение скольжения
Лекция (29). Трение качения
Лекция (30).
 Ферма
ФермаЛекция (30) eng. Truss
Лекция eng. Constraints and Their Reactions
Задача. Фигура из стержней
Задача. Самолет
Задача. Плоская фигура. Способ 1 (разбиение)
Задача. Плоская фигура. Способ 2 (метод отрицательных площадей)
Задача. Плоская фигура. Способ 4 (формула Грина)
Задача. Плоская фигура. Способ 5 (эксперимент)
Лекция. Сложение параллельных сил. Свойство пары.Лекция в Н202. 9.2.2016
Лекция. Часть 1. Приведение системы сил к центру. Изменение центра приведения.
Лекция. Часть 2. Скалярный инвариант.
Лекция. Часть 3. Уравнение центральной винтовой оси. Динама.
Лекция. Часть 4. Минимальный момент приведения.
Лекция. Часть 5. Уравнение центральной винтовой оси.
 Пример.
Пример.Решение задачи на равновесие одного тела (2015)
Решение задачи на равновесии рамы (2016). Три реакции. ТФ-04-15
Рама. Одно тело, скользящая заделка, подвижная опора (1A)
Рама. Одно тело, скользящая заделка, подвижная опора (1B)
Рама. Одно тело, скользящая заделка, подвижная опора (1С)
Рама. Составная конструкция (2)
Рама. Составная конструкция (2a). Заделка-шарнир-подвижный шарнир. Анимация и графика П.Горшкова.
Составная трехшарнирная конструкция.
Рама. Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.
Цепь . Определяем положение равновесия. Анимация и графика П.Горшкова.
Задача на теорему о трех силах. . Определяем реакции опор. Анимация и графика П.Горшкова.
Составная конструкция (3 тела, шарнир) .
 Определяем реакции опор. Анимация и графика П.Горшкова.
Определяем реакции опор. Анимация и графика П.Горшкова.Составная конструкция (3 тела, шарнир, стержень) . Определяем реакции опор. Анимация и графика П.Горшкова.
Рама. Составная конструкция (3)
Рама. Составная конструкция. (4)
Рама. Составная конструкция. Три тела (5)
Рама. Составная конструкция. Три тела (6)
Плоская стержневая система (6 стержней). Вырезание узлов. Анимация Петра Горшкова. Задача из Решебника (с.15)
Составная конструкция. Решение задачи в системе Maple.
Составная конструкция. Линейно распределенная нагрузка. (1-я часть)
Составная конструкция. Линейно распределенная нагрузка. Maple (2-я часть)
Составная конструкция. Распределенная нагрузка.
Составная конструкция. Линейно распределенная нагрузка. Съемка на практических занятиях в гр. ТФ-06-13
Составная конструкция.
 Нагрузка, распределенная по дуге. + решение в Maple
Нагрузка, распределенная по дуге. + решение в MapleСоставная конструкция.Нагрузка, распределенная по дуге. ТФ-05-13, 21.2.2014.
Составная конструкция с цилиндром и нитями. + решение в Maple
Составная конструкция. Две пластины. + решение в Maxima
Две пластины.
Составная конструкция.Пластина и уголок
Ферма. Программа
Диаграмма Максвелла-Кремоны
Ферма/Диаграмма-Максвелла-Кремоны
Ферма (8)
Трение качения (7)
Трение качения. Механизм
Задача на трение качения (3 тела) . Определяем условие равновесия системы. Анимация и графика П.Горшкова.
Задача на трение скольжения. Определяем условие равновесия рамы. Анимация и графика П.Горшкова.
Задача на трение скольжения .
 Определяем условие равновесия рамы + некоторые рассуждения на общие темы…
Определяем условие равновесия рамы + некоторые рассуждения на общие темы…Пространственная стержневая система (6 стержней). Вырезание узлов. Анимация Петра Горшкова. Задача из Решебника (с.86)
Полка (9)
Инварианты (10)
Плита на 6 стержнях
Текст программы для MaximaОдносторонняя связь в раме
Центр тяжести
СТАТИКА
Плоская система сил. Задачи
Ферма
Трение
Пространственная система сил. Задачи
Полярные координаты. Лекция.
Радиус кривизны. ТФ-05-13.
Многозвенный механизм. Метод кинематических графов. МЦС. Все в общем виде.
Многозвенный механизм. Скорости и ускорения. МЦС. МЦУ.
Пятизвенник. Уравнение трех угловых скоростей и ускорений
Метод кинематических графов. Многозвенный механизм. Угловые скорости. Решение в Maple
Многозвенный механизм.
 МЦС
МЦСЧетырехзвенник. Уравнение трех угловых скоростей (1)
Четырехзвенник. Уравнение трех угловых скоростей (2)
Четырехзвенник. Теорема трапеции
План скоростей.
Ускорение точки тела при плоском движении.
Ускорения. Механизм
Планетарный механизм. Метод графов и метод МЦС
Планетарный механизм (1). Метод Виллиса и метод МЦС
Планетарный механизм (2). Метод Виллиса и метод МЦС
Угловые скорости многозвенного механизма. Эффективное решение с помощью уравнения трех угловых скоростей
Сложное движениеСложное движение точки. Ускорение Кориолиса. Вывод формулы
Сложное движение точки. Ускорение Кориолиса. Правило Жуковского
Сложное движение точки. Ускорение Кориолиса. Пример
Сложное движение точки.
 Абсолютное ускорение. Задача
Абсолютное ускорение. ЗадачаСложное движение точки. Задача о муфте (К13,1)
Сложное движение точки. Задача о муфте/Ускорение (ТФ-05-13)
Сложное движение точки. Задача о муфте (К13,2)
Сложное движение точки. Задача о качающейся муфте (К13,3). Программа для Maple
Сферическое движение. Кинематические уравнения Эйлера в проекции на подвижные оси
3D кинематика. Решение задачи о треугольнике
3D кинематика. Параллелепипед с шарнирной крышкой
3D кинематика. Передача вращений
Редуктор (на занятиях ЭР-16-11)
Формула поворота Родрига (на лекции)
КИНЕМАТИКА
ТочкаПлоское движение
-
ДИНАМИКА
Кинетическая энергия. Решение задачи Д2 (приведенные массы)
Решение задачи на теорему об изменении кинетической энергии. Maple
Решение задачи на теорему о движении центра масс.
 Maple
MapleРешение задачи на теорему о движении центра масс. ТФ-05-13, практические занятия в МЭИ
Теорема Эйлера о движении жидкости . Лекция 1.4.2014
Решение задачи динамики для механизма с двумя степенями свободы (D11) (Уравнение Лагранжа 2-го рода)
Задача о механизме с двумя степенями свободы. Уравнение Лагранжа. Лекция 22.4.2014
Динамика кулисы. Лекция 15.12.2014
Maple-программа к лекции, Текст задачи из лекции.Потенциальное силовое поле (Лекция в МЭИ, 22.4.2014)
Решение задачи с помощью принципа возможных перемещений(Определение реакций опор)
Решение задачи с помощью принципа возможных перемещений(Определение условия равновесия механизма, Р-16-11, 24 марта)
Три способа решения простой задачи динамики (Катушка на нити, определяем ускорение)
Динамика механизма с неизвестным параметром (Д7)
Вывод уравнения Лагранжа 2-го рода
Кинетическая энергия тела в пространстве
Кинетическая энергия тела в простейших случаях движения
Кинетическая энергия системы (стержни, блок).
 Приведенная масса
Приведенная массаЗадачи на принцип возможных перемещений
Регулярная прецессия гироскопа.
Задачи о гироскопе. Гироскопический момент
Динамические уравнения Эйлера.
Теорема Карно
Прямой удар. Точка. Коэффициент восстановления
Косой удар.
Центр удара.
Удар по пластине
Удар в зубчатой передаче. (Лекция 15 мая 2015 г. ИТАЭ, МЭИ)
Два груза на балке Лекция 11.9.2015 в гр. С-12-11
Стабильность Лекция 5 мая 2015 в гр. ЭР-16-12
Момент инерции тела относительно произвольной оси.
Несвободное движение точки. Уравнение Лагранжа
Динамическая балансировка
Уравнение Лагранжа в форме Лагранжа
Устойчивость по Ляпунову
Уравнение Мещерского.
 Формула Циолковского
Формула ЦиолковскогоСиловое поле. Условие потенциальности
Колебания механической системы
Колебания системы с 2 степенями свободы. Задача 1.
Колебания системы с 2 степенями свободы. Задача 2.
Колебания узла фермы
Предельные частоты и предельные массы
Колебания точки
Задача о двойном маятнике (лекция 27 мая 2014, МЭИ)
Законы Кеплера
Теория удара
Колебания, устойчивость и др.
1. Два цилиндра, пластина, стержни.
2. Брусок, цилиндр сверху, шток и стержень. Простая задача.
3. Используем теорему о сложении скоростей.
4.
 Задача с муфтой. Используем метод прямого дифференцирования.
Задача с муфтой. Используем метод прямого дифференцирования.5. Задача с линейной обобщенной координатой. Цилиндр, клин и муфта.
6. Задача с параллелограммом.
7. Кривошип, два цилиндра, наклонный стержень, муфта
8. Цилиндр, закрепленный шарнирно на ободе, брусок и пластина между ними
9. Цилиндр, наклонная плоскость, пресс и пластина между ними. Линейная обобщенная координата
10. Невесомый прямоугольный уголок, скользящий по ребрам неподвижного бруска.
11. Блок из колес с неподвижной осью, груз на наклонной плоскости. Повернутые оси координат. Линейная обобщенная координата.
12. Блок из колес с неподвижной осью и цилиндр с подвижной осью.
 Линейная обобщенная координата.
Линейная обобщенная координата.13. Два цилиндра и груз. Один цилиндр катится по неподвижной поверхности, другой закреплен на ободе первого и катится по грузу.
14. Два цилиндра и соединяющий их стержень
15. Два цилиндра, сверху балка и вертикальный шток
Экзаменационная задача в МЭИ. Решение задачи на составление уравнения Лагранжа 2-го рода
|
19.09.2017 18:55
Карта механики — Моменты
Момент (также иногда называемый крутящим моментом) определяется как «стремление силы вращать тело». Там, где силы вызывают линейные ускорения, моменты вызывают угловых ускорений . Таким образом, моменты можно рассматривать как скручивающие силы.
Представьте два ящика на ледяной поверхности. Сила, действующая на коробку А, просто заставит коробку начать ускоряться, а сила, действующая на коробку В, заставит коробку и ускориться, и начать вращаться. Сила, действующая на коробку B, действует на момент, а сила на коробку A — нет.
Сила, действующая на коробку B, действует на момент, а сила на коробку A — нет.Векторное представление момента:
Моменты, как и силы, могут быть представлены в виде векторов и иметь величину, направление и «точку приложения». Однако для некоторых моментов лучшим названием точки приложения будет ось вращения . Это будет точка или ось, относительно которой мы будем определять все моменты.
Величина:
Величина момента — это степень, в которой момент вызывает угловое ускорение тела, на которое он действует. Он представлен скаляром (одним числом). Величину момента можно представить как силу скручивающей силы, действующей на тело. Когда момент представлен в виде вектора, величина момента обычно указывается явно. хотя длина вектора момента также часто соответствует относительной величине момента.
Величина момента измеряется в единицах силы, умноженной на расстояние. Стандартными метрическими единицами величины момента являются ньютон-метры, а стандартными английскими единицами измерения момента являются футо-фунты.
| \[М=Ж*д\] |
| \[Метрика: Н*м\] |
| \[английский: lb*ft\] |
Направление:
В двумерной задаче направление можно рассматривать как скалярную величину, соответствующую направлению вращения, которое вызовет момент. Момент, вызывающий вращение против часовой стрелки, является положительным моментом, а момент, вызывающий вращение по часовой стрелке, является отрицательным моментом.
Чтобы использовать правило правой руки, выровняйте правую руку, как показано, так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы в данный момент указывали в направлении вращения. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента. Однако в трехмерной задаче тело может вращаться вокруг оси в любом направлении. Если это так, нам нужен вектор для представления направления момента. Направление вектора момента будет совпадать с осью вращения, которую вызовет этот момент, но чтобы определить, какое из двух направлений, которые мы можем использовать вдоль этой оси, мы используем правило правой руки. Чтобы использовать правило правой руки, выровняйте правую руку, как показано, так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы в данный момент указывали в направлении вращения. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Направление вектора момента будет совпадать с осью вращения, которую вызовет этот момент, но чтобы определить, какое из двух направлений, которые мы можем использовать вдоль этой оси, мы используем правило правой руки. Чтобы использовать правило правой руки, выровняйте правую руку, как показано, так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы в данный момент указывали в направлении вращения. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Если мы вернемся к двумерным задачам, то увидим, что все повороты происходят вокруг оси, указывающей прямо внутрь или наружу страницы (ось z). Используя правило правой руки, вращение против часовой стрелки представлено вектором в положительном направлении z, а вращение по часовой стрелке представлено вектором в отрицательном направлении z.
Ось вращения:
В задачах инженерной статики мы можем выбрать любую точку/ось в качестве оси вращения.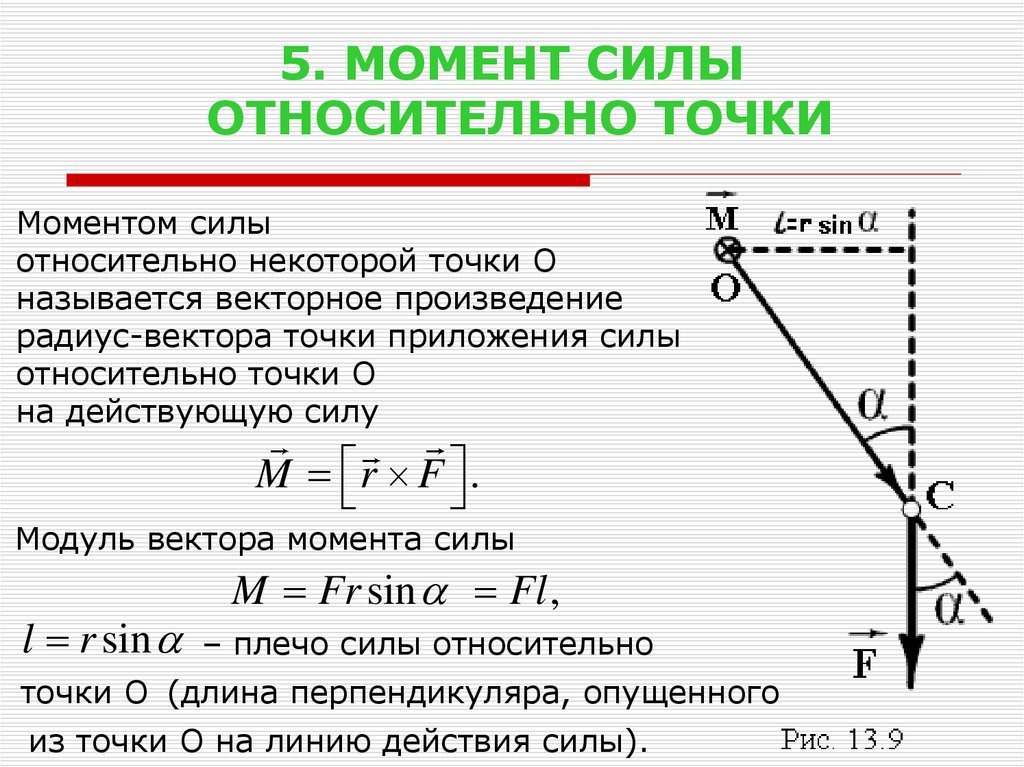 Однако выбор этой точки повлияет на величину и направление результирующего момента, а момент действителен только относительно этой точки.
Однако выбор этой точки повлияет на величину и направление результирующего момента, а момент действителен только относительно этой точки.
Хотя мы можем взять момент относительно любой точки в задаче статики, если мы складываем вместе моменты от нескольких сил, все моменты должны быть взяты вокруг общей оси вращения . Моменты, снятые в разных точках, не могут быть сложены вместе, чтобы найти «чистый момент»
Кроме того, если мы перейдем к предмету динамики, когда тела движутся, мы захотим связать моменты с угловыми ускорениями. Чтобы это работало, нам нужно будет взять моменты либо относительно одной точки, которая не движется (например, петля на двери), либо нам нужно будет взять моменты относительно центра масс тела. Суммирование моментов относительно других осей вращения не приведет к правильным расчетам.
Суммирование моментов относительно других осей вращения не приведет к правильным расчетам.
Расчет моментов:
Для расчета момента, действующего на тело, у нас будет два основных варианта: скалярные методы и векторные методы . Скалярные методы обычно быстрее для двухмерных задач, когда тело может вращаться только по часовой стрелке или против часовой стрелки, тогда как векторные методы обычно быстрее для трехмерных задач, где ось вращения более сложная.
1.6 Крутящий момент/момент – инженерная механика: статика
Глава 1: Основные понятия
Моменты создаются силой, действующей на расстоянии от центра вращения. Существует три способа вычисления моментов: скалярный, векторный и с использованием правила правой руки. Первые два метода будут представлены в этом разделе, а третий будет обсуждаться в разделе 3.1.3 о правиле правой руки.
Момент (иногда называемый крутящим моментом) определяется как «стремление силы вращать тело». Там, где силы вызывают линейные ускорения, моменты вызывают угловых ускорений . Таким образом, моменты можно рассматривать как скручивающие силы.
Там, где силы вызывают линейные ускорения, моменты вызывают угловых ускорений . Таким образом, моменты можно рассматривать как скручивающие силы.
Векторное представление момента:
Моменты, как и силы, могут быть представлены в виде векторов и иметь величину, направление и «точку приложения». Однако на некоторые моменты точка приложения лучше называется 9.0003 ось вращения . Это будет точка или ось, относительно которой мы будем определять все моменты.
Величина:
Величина момента — это степень, в которой момент вызывает угловое ускорение тела, на которое он действует. Он представлен скаляром (одним числом). Величину момента можно представить как силу скручивающей силы, действующей на тело. Когда момент представлен в виде вектора, величина момента обычно указывается явно. хотя длина вектора момента также часто соответствует относительной величине момента.
Величина момента измеряется в единицах силы, умноженной на расстояние.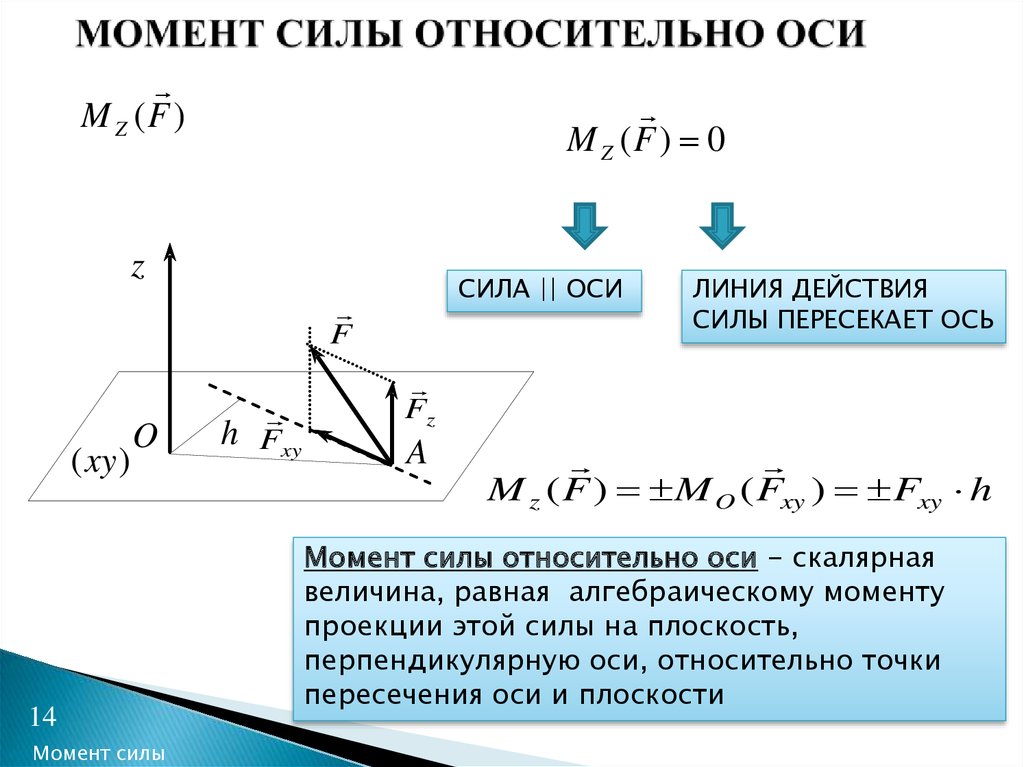 Стандартными метрическими единицами величины момента являются ньютон-метры, а стандартными английскими единицами измерения момента являются футо-фунты.
Стандартными метрическими единицами величины момента являются ньютон-метры, а стандартными английскими единицами измерения момента являются футо-фунты.
[латекс]M= F\ast d\\Метрика: N\ast m\\Английский: lb \ast ft[/latex] .
Направление:
В двумерной задаче направление можно рассматривать как скалярную величину, соответствующую направлению вращения, которое вызовет момент. Момент, вызывающий вращение против часовой стрелки, является положительным моментом, а момент, вызывающий вращение по часовой стрелке, является отрицательным моментом.
Однако в трехмерной задаче тело может вращаться вокруг оси в любом направлении. Если это так, нам нужен вектор для представления направления момента. Направление вектора момента будет совпадать с осью вращения, которую вызовет этот момент, но чтобы определить, какое из двух направлений, которые мы можем использовать вдоль этой оси, мы используем правило правой руки. Чтобы использовать правило правой руки, выровняйте правую руку, как показано, так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы в данный момент указывали в направлении вращения. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Если мы вернемся к двухмерным задачам, то увидим, что все повороты происходят вокруг оси, указывающей прямо внутрь или наружу страницы (ось z). Используя правило правой руки, вращение против часовой стрелки представлено вектором в положительном направлении z, а вращение по часовой стрелке представлено вектором в отрицательном направлении z.
Ось вращения:
В задачах инженерной статики мы можем выбрать любую точку/ось в качестве оси вращения. Однако выбор этой точки повлияет на величину и направление результирующего момента, а момент действителен только относительно этой точки.
Хотя мы можем взять момент относительно любой точки в задаче статики, если мы складываем моменты от нескольких сил, все моменты должны быть взяты вокруг общей оси вращения . Моменты, полученные относительно разных точек, не могут быть сложены вместе, чтобы найти «чистый момент»
Кроме того, если мы перейдем к предмету динамики, где движутся тела, мы захотим связать моменты с угловыми ускорениями. Чтобы это работало, нам нужно будет взять моменты либо относительно одной точки, которая не движется (например, петля на двери), либо нам нужно будет взять моменты относительно центра масс тела. Суммирование моментов относительно других осей вращения не приведет к правильным расчетам.
Чтобы это работало, нам нужно будет взять моменты либо относительно одной точки, которая не движется (например, петля на двери), либо нам нужно будет взять моменты относительно центра масс тела. Суммирование моментов относительно других осей вращения не приведет к правильным расчетам.
Расчет моментов:
Для расчета момента силы, действующей на тело, у нас будет два основных варианта: скалярный метод и векторный метод . Скалярные методы обычно быстрее для двухмерных задач, когда тело может вращаться только по часовой стрелке или против часовой стрелки, тогда как векторные методы обычно быстрее для трехмерных задач, где ось вращения более сложная.
Для любой точки протяженного тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент относительно этой точки. Как обсуждалось на странице моментов, момент — это склонность силы вызывать вращение.
Источник: Engineering Mechanics, Джейкоб Мур и др. , http://mechanicsmap.psu.edu/websites/1_mechanics_basics/1-5_moments/moments.html
, http://mechanicsmap.psu.edu/websites/1_mechanics_basics/1-5_moments/moments.html
Обсуждая, как вычислить момент силы относительно точки с помощью скалярных величин, мы начнем с примера силы, действующей на простой рычаг, как показано ниже. В этом простом рычаге действует сила на конце рычага, на расстоянии d от центра вращения рычага (точка А), где сила имеет величину F.
При использовании скалярных величин величина момента будет равна расстоянию по перпендикуляру между линией действия силы и точкой, относительно которой мы измеряем момент.
$$M=F\ast d$$Чтобы определить знак момента, мы определяем, какой тип вращения вызовет сила. В этом случае мы можем видеть, что сила заставила бы рычаг вращаться против часовой стрелки вокруг точки A. Вращения против часовой стрелки вызываются положительными моментами, а вращения по часовой стрелке вызываются отрицательными моментами.
Другим важным фактором, который следует помнить, является то, что значение d является перпендикулярным расстоянием от силы до точки, относительно которой мы измеряем момент. Мы могли бы измерить расстояние от точки A до начала вектора силы, или хвоста вектора силы, или действительно любой точки вдоль линии действия силы F. Однако расстояние, которое нам нужно использовать для расчета скалярного момента, равно кратчайшее расстояние между точкой и линией действия силы. Это всегда будет линия, перпендикулярная линии действия силы, идущая к точке, о которой мы берем момент.
Мы могли бы измерить расстояние от точки A до начала вектора силы, или хвоста вектора силы, или действительно любой точки вдоль линии действия силы F. Однако расстояние, которое нам нужно использовать для расчета скалярного момента, равно кратчайшее расстояние между точкой и линией действия силы. Это всегда будет линия, перпендикулярная линии действия силы, идущая к точке, о которой мы берем момент.
Источник: Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/3_equance_rigid_body/3-1_moment_scalar/moment_scalar.html
Если вектор положения и сила не точно равны 90 градусам, уравнение T = | р | | Ф | sin Θ может быть полезным и по-прежнему дает скалярное число для момента или крутящего момента. Это хорошо, если бы у нас были действительно простые системы, такие как открытие двери или вращение волчка. Что происходит, когда у вас есть вращающаяся дверь, и несколько человек пытаются пройти через нее? Или сила, которая не точно по двум осям? Чтобы решить эту проблему, мы будем использовать векторы, как показано в следующем разделе.
Альтернативой вычислению момента через скалярные величины является использование векторного метода или метода векторного произведения . Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод векторного произведения. Метод векторного произведения для вычисления моментов гласит, что вектор момента силы относительно точки будет равен векторному произведению вектора r от точки до любого места на линии действия силы и самого вектора силы.
$$\vec M=\vec r\times\vec F$$
Большим преимуществом этого метода является то, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от указать на любую часть линии действия. Для любой задачи существует множество возможных r векторов, хотя из-за того, как работает векторное произведение, все они должны в конце концов давать один и тот же вектор момента.
Здесь важно отметить, что все количества ( р , F и M ) являются векторами. Прежде чем вы сможете вычислить векторное произведение, вам нужно будет записать r и F в виде компонент вектора. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента векторов r и F . Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для расчетов.
Полученный вектор момента совпадет с осью вращения для данного момента, где вы можете использовать правило правой руки, чтобы определить, движется ли момент по часовой стрелке или против часовой стрелки вокруг этой оси.
Наконец, также важно отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным. Это означает, что порядок векторов имеет значение, и r крест F не будет таким же, как F крест r .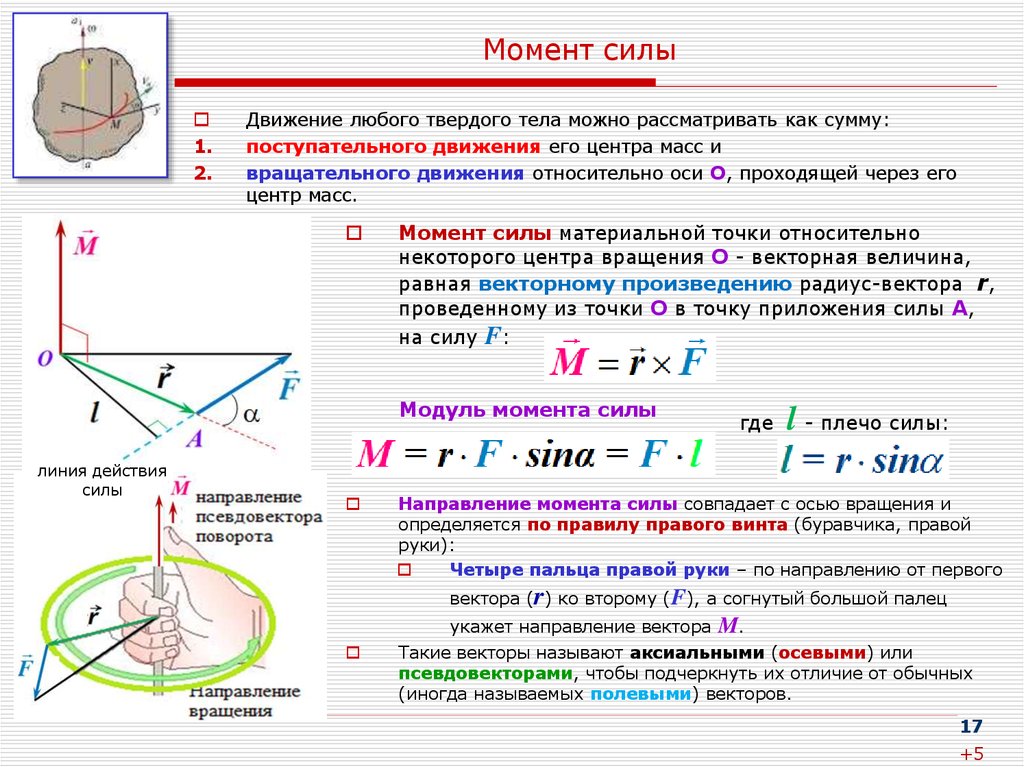 Важно всегда использовать r крест F при расчете моментов.
Важно всегда использовать r крест F при расчете моментов.
Источник: Инженерная механика, Джейкоб Мур и др., http://mechanicsmap.psu.edu/websites/3_equance_rigid_body/moment_vector/momentvector.html
Используете ли вы скаляры: M = |r| |Ф| sinΘ или векторы: M = r x F вы можете решить большую часть проблемы момента / крутящего момента. Скалярный метод быстрее для двумерных задач, особенно если векторы расположены под углом 90 градусов друг к другу (sin 90º = 1). Векторный метод более надежен, особенно если используются дополнительные углы. Существует вероятность ошибок, поэтому рекомендуется использовать этап «Проверка шага 6», чтобы попробовать несколько методов, чтобы убедиться, что ваш ответ правильный.
См. примеры в разделе 1.8, так как многие из них касаются моментов.
В основном: Существует три метода расчета моментов, два из которых обсуждались здесь. Моменты или крутящий момент создаются силой, действующей на некотором расстоянии от оси вращения.
Применение: Когда вы открываете тяжелую дверь, вы толкаете ее. Если вы подтолкнете ближе к оси вращения, вам понадобится большая сила, чтобы заставить его двигаться. Если вы толкаете дальше от оси (поэтому r больше), сила может быть меньше, чтобы совершить такое же движение.
Забегая вперед: Моменты применяются, когда задействованы твердые тела, поэтому мы снова рассмотрим моменты в главе 3.1.3, когда вы изучите третий способ расчета моментов (крутящий момент).
ПРИКЛАДНАЯ МЕХАНИКА — Момент — УЧЕБНЫЕ МАТЕРИАЛЫ
МОМЕНТ:
Стремление сил состоит не только в перемещении тела, но и во вращении тела. Эта вращательная тенденция силы известна как МОМЕНТ.
МОМЕНТ – вращательное действие силы, действующей на тело вокруг шарнирной точки.
Произведение силы на перпендикулярное расстояние от точки до линии действия силы называется моментом силы относительно этой точки. Таким образом, момент силы зависит от следующего:
Таким образом, момент силы зависит от следующего:
- Величина силы.
- Перпендикулярное расстояние от шарнирной точки до линии действия силы.
Рассмотрим тело, прибитое гвоздем в точке O и действующее под действием силы F. Эта сила F стремится повернуть тело вокруг точки O. Это вращательное действие силы F называется моментом силы. Однако если сила такова, что она проходит через точку О, то она не будет стремиться вращать тело, а будет стремиться сдвинуть тело по прямой линии.
Величина момента в точке O, M o = F x d
, где d — расстояние по перпендикуляру от точки O до линии действия силы.
Момент силы является векторной величиной
Направление M o будет получено с помощью правила правой руки. Для этого пальцы правой руки складывают таким образом, чтобы они следовали направлению вращения.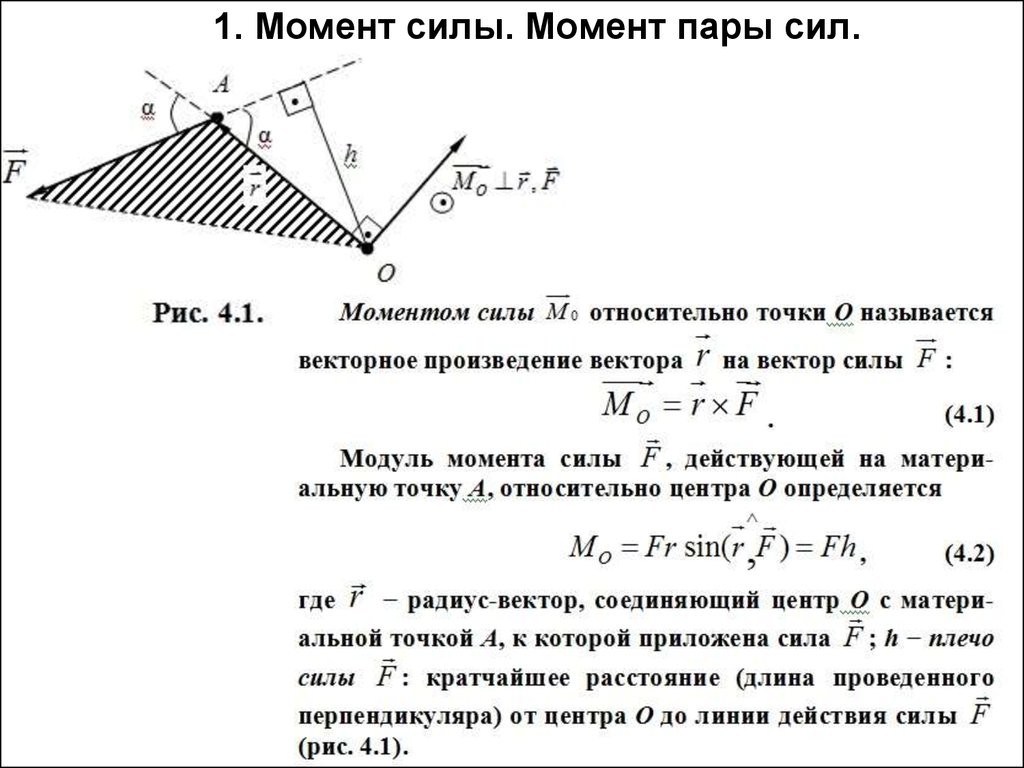 Затем большой палец указывает вдоль оси момента, которая дает направление и ощущение момента.
Затем большой палец указывает вдоль оси момента, которая дает направление и ощущение момента.
ЕДИНИЦЫ МОМЕНТА:
В единицах МКС = кг-м
В единицах СИ = Н-м
ПО ЧАСОВОЙ И ПРОТИВ ЧАСОВОЙ СТР. точка или линия, моменты классифицируются как моменты по часовой стрелке и против часовой стрелки.
МОМЕНТ ПО ЧАСОВОЙ СТРЕЛКЕ
Если сила, действующая на тело, стремится повернуть тело по часовой стрелке, то момент, возникающий при этом, называется МОМЕНТ ПО ЧАСОВОЙ СТРЕЛКЕ .
Момент в точке поворота = F x d (по часовой стрелке)
МОМЕНТ ПРОТИВ ЧАСОВОЙ СТРЕЛКИ .
Момент в точке опоры = F x d (против часовой стрелки)
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МОМЕНТА:
Рассмотрим силу F, действующую на тело и представленную вектором AB. Пусть О — точка, относительно которой нужно вычислить момент силы. Опустите ОС перпендикулярно АВ. Присоединяйтесь к ОА и ОБ.
Опустите ОС перпендикулярно АВ. Присоединяйтесь к ОА и ОБ.
Момент силы около O, Mo = F x OC
Mo = AB x OC
Mo = 2 x (1/2 x AB x OC)
Mo = 2 x Площадь △OAB
Следовательно, момент силы относительно точки равен удвоенной площади треугольника, образованного таким образом, если взять точку в качестве вершины треугольника и линию в качестве основания треугольника.
ПРИНЦИП МОМЕНТА:
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов всех сил относительно точки в их плоскости равна нулю.
или
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов сил относительно точки по часовой стрелке равна сумме моментов сил относительно точки против часовой стрелки. та же самая точка.
Рассмотрим четыре копланарные силы F1, F2, F3 и F4, действующие на тело, и тело находится в равновесии.
Пусть О — точка, вокруг которой может вращаться тело. Пусть d1, d2, d3 и d4 — перпендикулярное расстояние точки O, образующей линию действия сил F1, F2, F3 и F4 соответственно. Момент сил F1, F2, F3 и F4 относительно точки О равен:
Момент силы F1 = F1 x d1 (против часовой стрелки)
Момент силы F2 = F2 x d2 (против часовой стрелки)
Момент силы F3 = F3 x d3 (по часовой стрелке)
Момент силы F4 = F4 x d4 (по часовой стрелке)
Равнодействующая этих моментов будет равна алгебраической сумме всех моментов относительно O.
Результирующий момент ∑M = F1d1 + F2d2 – F3d3 – F4d4
Так как тело находится во вращательном равновесии, согласно принципу моментов , результирующий момент, т.е. алгебраическая сумма всех моментов, должен быть равен нулю.
∑M = 0
F1d1 + F2d2 – F3d3 – F4d4
F1d1 + F2d2 = F3d3 + F4d4
Sum of anticlockwise moments = sum of clockwise moments
VARIGNON’S THEOREM:
It states that if a number of coplanar на тело действуют силы, то алгебраическая сумма их моментов относительно точки равна моменту их равнодействующей относительно этой же точки.
Пусть F1 и F2 — две силы, действующие на тело, равнодействующая F, тогда
Mo = r x F1 + r x F2
Mo = r(F1 + F2)
Mo = r x F
Пусть F1 и F2 — две силы, представленные линиями AB и AD. Пусть O будет точкой, относительно которой нужно взять момент. Из O проведите линию OC, параллельную AB, с пересечением AD в точке D. Соедините BC, чтобы завершить параллелограмм. Теперь соедините диагональ AC, которая дает результирующую R двух сил. Присоединяйтесь к ОА и ОБ.
Из рисунка
площадь △ ABC = площадь △ ADC = площадь △ AOB
(∵ Эти треугольники лежат на одном основании и между двумя одинаковыми параллельными прямыми)
Сейчас,
Момент силы F1 относительно O = 2 x площадь △OAB
Момент силы F2 относительно O = 2 x площадь △OAD
Момент равнодействующей силы R относительно O = 2 x площадь △OAC
Сумма моментов двух сил относительно O = 2 x площадь △OAB + 2 x площадь △OAD
= 2 x площадь △ADC + 2 x площадь △OAD
= 2 x (площадь △OAB + площадь △ OAD)
= 2 x площадь △OAC
= момент равнодействующей силы R о O
СВЯЗАННЫЕ ВИДЕО:
youtube.com/embed/V1mMPS-701A» frameborder=»0″ allowfullscreen=»allowfullscreen»>
youtube.com/embed/kRS-NmZjfeo» frameborder=»0″ allowfullscreen=»allowfullscreen» data-mce-fragment=»1″>
Преобразователь случайных чисел | Преобразователь момента силы Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: ньютон-метркилоньютон-метрмиллиньютон-метрмикроньютон метртонна-сила (короткий) метртон-сила (длинный) метртон-сила (метрическая) метр-килограмм-сила метрграмм-сила сантиметрфунт-сила фут-фунт фут-фунт дюйм метркилоньютон-метрмиллиньютон-метрмикроньютон метртон-сила (короткий) метртон-сила (длинный) метртон-сила (метрическая) метркилограмм-сила метрграмм-сила сантиметрфунт-сила фут-фунт-фут-фунт-дюйм Электрическая проводимость и проводимостьЗнаете ли вы, что обычный диэлектрический материал, такой как стекло, может хорошо проводить электричество при определенных условиях? Нажмите или коснитесь, чтобы узнать больше об электрической проводимости! Двутавровые балки в строительстве Обзор Терминология Использование на английском языке Примеры момента силы Заключение Обзор крутящий момент. Две силы, которые рука прикладывает к отвертке, а отвертка прикладывает к головке винта, создают крутящий момент В этой статье мы подробно обсуждаем разницу между моментом силы и крутящим моментом, но следует отметить, что в большинстве случаев и крутящий момент, и момент силы в английском языке относятся к одному и тому же понятию и используются взаимозаменяемо. В употреблении этих слов есть очень незначительные нюансы, и это часто вызывает путаницу. Терминология Использование на английском языкеКак мы уже упоминали выше, и момент силы, и крутящий момент используются для описания одного и того же явления, но иногда используются в разных контекстах. В этом разделе мы рассмотрим контексты, в которых «момент силы» используется чаще, чем «крутящий момент». Крутящий момент часто определяют как явление, вызывающее изменение углового момента. С другой стороны, момент силы не должен вызывать это изменение. Это означает, что крутящий момент является частным случаем момента силы. Мы также можем сказать, что крутящий момент — это момент силы, но момент силы не обязательно является крутящим моментом. Ниже мы рассмотрим некоторые примеры этого. Однако мы должны еще раз повторить, что эта разница между моментом силы и крутящим моментом различается в некоторых контекстах, но в других ситуациях крутящий момент и момент силы используются взаимозаменяемо. Две руки воздействуют на вороток, создавая две силы, и это создает крутящий момент Чтобы понять, что такое момент силы, нам нужно понять, что такое момент в физике вообще. Момент указывает величину, с которой данная сила действует на объект с данного расстояния. Эта величина зависит как от величины действительной силы, действующей на предмет, так и от расстояния от точки приложения силы до некоторой точки предмета. Как мы видели в определении выше, для момента силы эта точка находится на оси вращения. Момент силы пропорционален силе и радиусу. Это означает, что если к объекту приложена данная сила на данном расстоянии от оси вращения, то величина этой силы увеличивается на радиус, и действие силы на объект больше фактической величины сама сила. Этот принцип используется при создании механического преимущества с помощью систем рычагов, шестерен и шкивов. Когда мы рассматриваем момент силы в этом контексте, мы часто рассматриваем, например, приложение силы к плечу рычага. Изгибающий момент. В этой конструкции нет вращения и, следовательно, нет крутящего момента, а присутствует только момент силы Крутящий момент и момент силы также иногда различают по-другому. Крутящий момент иногда относится к моменту «пары». Здесь пара — это две силы одинаковой величины, действующие в противоположных направлениях и заставляющие объект вращаться. Сумма этих векторов равна нулю. Таким образом, момент силы является более общим термином, а крутящий момент — частным случаем. В некоторых контекстах крутящий момент используется, когда объект движется или вращается, тогда как момент силы используется, когда движение не происходит, например, в таких системах, как опорные балки и другие конструктивные элементы. В этих системах края балки или конструкции могут быть закреплены или вращаться. В последнем случае говорят, что балки свободно оперты. Когда на балку действует сила, например, в направлении, перпендикулярном ее поверхности, создается момент силы. Примеры момента силыЗдесь момент силы равен весу, который каждый ребенок прикладывает к качелям, умноженному на расстояние до точки опоры. Девочка находится ближе к точке опоры, но прикладывает больше усилий, чем мальчик, и это помогает удерживать качели почти в равновесии. Момент силы в сочетании с изгибающим моментом, который мы обсуждали выше, является одним из примеров момента силы в реальной жизни. Момент силы — полезная концепция в строительстве и проектировании конструкций, поскольку знание момента силы, действующей на элемент конструкции, позволяет нам определить величину нагрузки, которую должна выдерживать система. Двутавровые балки широко использовались при строительстве Королевского моста Александры через реку Оттава в 1900 г. растяжение других частей. Например, представьте себе балку, на которую действует сила, направленная вниз и приложенная к середине этой балки. Из-за этой силы луч принимает форму «смайлика». Его верхняя часть сжимается, особенно посередине, где прикладывается сила. Нижняя часть, особенно вокруг центра, растягивается. Если момент слишком велик для материала, чтобы выдержать, то балка ломается. Максимальное напряжение приходится на самый верхний и самый нижний слои, поэтому при проектировании строительных конструкций принято усиливать эти участки. Хорошим примером является I -луч . Его поперечное сечение имеет форму заглавной буквы « I » с засечками вверху и внизу. Иногда это больше похоже на заглавную букву «Н». Это очень эффективная конструкция, так как участки, испытывающие наибольшую нагрузку, усилены, но использование материала минимально. Часто двутавровые балки делают из стали, но можно использовать и другие материалы для изготовления прочных балок, выдерживающих большие нагрузки. На YouTube можно найти примеры экспериментов по проверке прочности двутавровых балок из менее прочных, чем сталь, материалов, таких как фанера и пенопласт. Двутавровые балки часто выбирают, когда на конструкцию воздействует изгибающий момент. Они также полезны при работе с напряжением сдвига , которое представляет собой напряжение, действующее параллельно поверхности конструкции. Крутящий момент двигателя создает скручивающую нагрузку на фюзеляж этого турбовинтового самолета Заключение В этой статье мы рассмотрели разницу между крутящим моментом и моментом силы в англоязычной терминологии и рассмотрели некоторые примеры момента силы. Здесь мы в основном рассматривали помехи, создаваемые моментом силы, но есть много ситуаций, когда момент силы полезен. В статье о крутящем моменте подробно рассматриваются эти примеры. Различие в терминологии, которое мы обсуждали, в основном относится к машиностроению США и Великобритании, но в физике США и Великобритании термины крутящий момент и момент силы обычно используются взаимозаменяемо. Список литературы Эта статья была написана Kateryna Yuri . Вы можете быть заинтересованы в других преобразователях в группе механиков:Угловой преобразователь Англосная скорость и конвертер с частотой вращения Преобразователь Преобразователь плотности Преобразователь энергии и работы Преобразователь силы Преобразователь длины и расстояния массовый преобразователь Moment of Inertia Converter Power Converter Давление, напряжение, преобразователь модуля Young Специфический объемный преобразователь Преобразование крутящего момента Общие и общие измерения приготовления. Преобразователь линейной скорости и скорости Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут получите ответ от опытных технических переводчиков. |
Законы баланса массы, сил и моментов | Механика сплошных сред твердого тела
Фильтр поиска панели навигации Oxford AcademicContinuum Mechanics of SolidsPhysics Continuum MaterialsBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicContinuum Mechanics of SolidsPhysics Continuum MaterialsBooksJournals Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Еще
Cite
Anand, Lallit, and Sanjay Govindjee,
«Законы равновесия масс, сил и моментов»
,
Механика континуумов твердых веществ
(
Оксфорд,
2020;
онлайн EDN,
Oxford Academic
, 17 сентября 2020
), HTTPS://doi. org/10993/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093. oso/9780198864721.003.0004,
org/10993/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093/1093. oso/9780198864721.003.0004,
, по состоянию на 4 октября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
закрыть
Фильтр поиска панели навигации Oxford AcademicContinuum Mechanics of SolidsPhysics Continuum MaterialsBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicContinuum Mechanics of SolidsPhysics Continuum MaterialsBooksJournals Термин поиска на микросайте
Расширенный поиск
Реферат
В этой главе рассматривается закон баланса масс, а также законы баланса сил и моментов.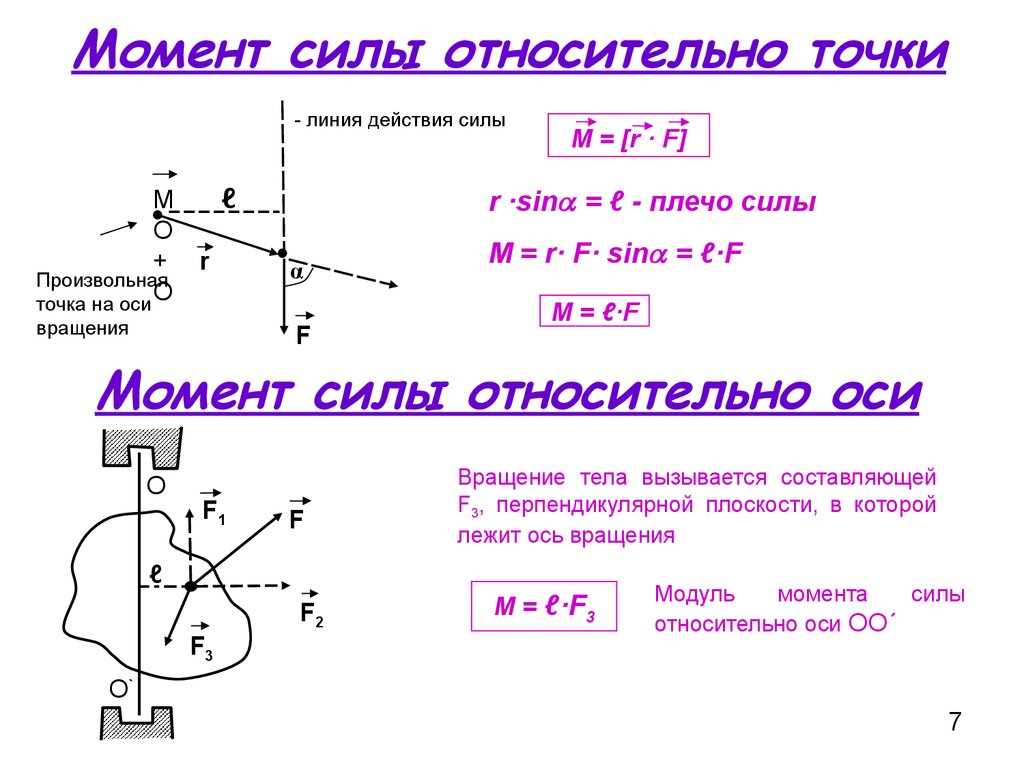 Важное родственное понятие напряжения состоит в том, что оно затем представлено как формализованное Коши в терминах центральной теоремы механики сплошных сред, которая утверждает, что соблюдение глобального баланса сил и моментов эквивалентно существованию симметричного тензорного поля в деформированном теле, называемом напряжение Коши, так что вектор тяги, действующий на каждый ориентированный элемент поверхности в точке тела, задается тензором напряжения Коши, линейно действующим на внешнюю единицу, перпендикулярную поверхности в этой точке. Кроме того, тензор напряжений должен удовлетворять дифференциальному уравнению в частных производных, известному как уравнение движения, которое утверждает, что дивергенция тензора напряжений плюс объемная сила на единицу объема равна плотности массы, умноженной на ускорение.
Важное родственное понятие напряжения состоит в том, что оно затем представлено как формализованное Коши в терминах центральной теоремы механики сплошных сред, которая утверждает, что соблюдение глобального баланса сил и моментов эквивалентно существованию симметричного тензорного поля в деформированном теле, называемом напряжение Коши, так что вектор тяги, действующий на каждый ориентированный элемент поверхности в точке тела, задается тензором напряжения Коши, линейно действующим на внешнюю единицу, перпендикулярную поверхности в этой точке. Кроме того, тензор напряжений должен удовлетворять дифференциальному уравнению в частных производных, известному как уравнение движения, которое утверждает, что дивергенция тензора напряжений плюс объемная сила на единицу объема равна плотности массы, умноженной на ускорение.
Ключевые слова: Баланс массы, Плотность массы, Баланс сил, Баланс моментов, Вектор тяги, Объемная сила, Напряжение Коши, Уравнение движения
Предмет
Физика конденсированного состояния
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.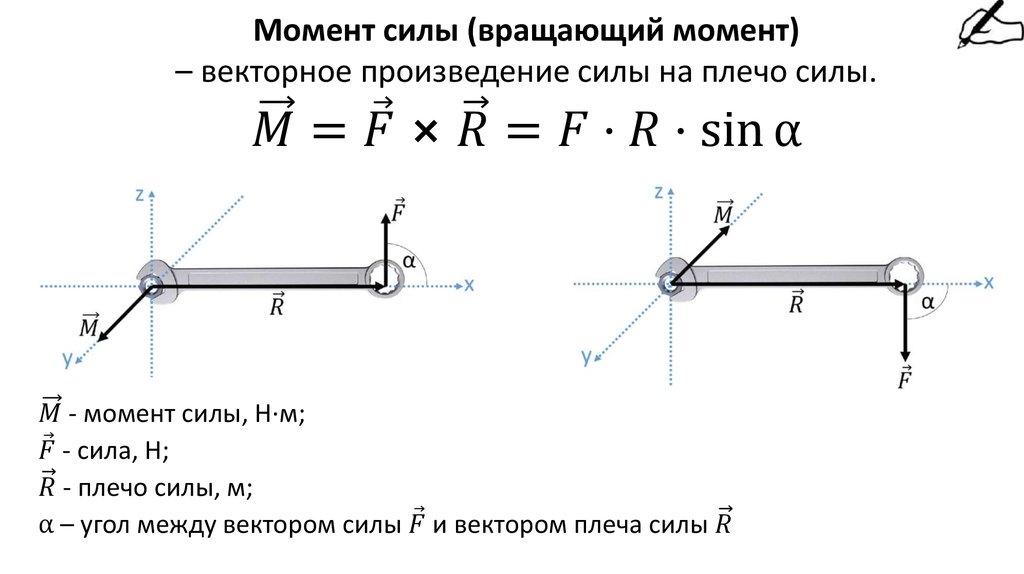


 Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева В английском и некоторых других языках это явление называют разными словами, в зависимости от контекста. Поскольку эта статья написана для сайта переводчиков, мы немного поговорим о терминологии в других языках. Величина момента силы равна векторному произведению силы, приложенной к телу на вычисленное по перпендикуляру расстояние между осью вращения и точкой приложения силы, которая вызывает вращение. В английском языке для момента силы используют два термина, момент силы (moment of force) и отдельный термин, torque. Английский термин torque используют для обозначения физической величины, которую измеряют так же, как и момент силы (в английском), но только в контексте, в котором сила, ответственная за это свойство, обязательно вызывает вращение тела. Эту величину также измеряют, умножив силу на расстояние между осью вращения и точкой приложения силы. В русском языке термину «torque» соответствуют термины «вращающий момент» и «вращательный момент», которые являются синонимами.
В английском и некоторых других языках это явление называют разными словами, в зависимости от контекста. Поскольку эта статья написана для сайта переводчиков, мы немного поговорим о терминологии в других языках. Величина момента силы равна векторному произведению силы, приложенной к телу на вычисленное по перпендикуляру расстояние между осью вращения и точкой приложения силы, которая вызывает вращение. В английском языке для момента силы используют два термина, момент силы (moment of force) и отдельный термин, torque. Английский термин torque используют для обозначения физической величины, которую измеряют так же, как и момент силы (в английском), но только в контексте, в котором сила, ответственная за это свойство, обязательно вызывает вращение тела. Эту величину также измеряют, умножив силу на расстояние между осью вращения и точкой приложения силы. В русском языке термину «torque» соответствуют термины «вращающий момент» и «вращательный момент», которые являются синонимами. Русский термин «крутящий момент» относится к внутренним усилиям, возникающим в объектах под действием приложенных к ним нагрузок. Этому термину соответствуют английские термины «torsional movement», «torque effect», «torsional shear» и некоторые другие.
Русский термин «крутящий момент» относится к внутренним усилиям, возникающим в объектах под действием приложенных к ним нагрузок. Этому термину соответствуют английские термины «torsional movement», «torque effect», «torsional shear» и некоторые другие.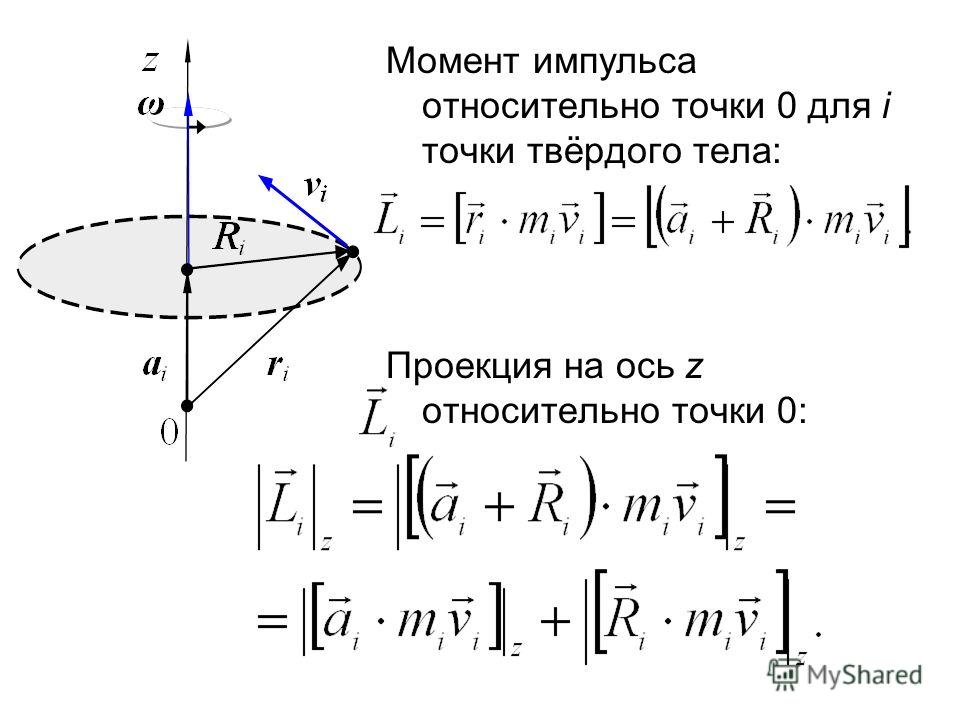 В этом разделе обсудим, когда в английском наиболее часто используют термин «момент силы» и почти не используют «torque». Часто о понятии «torque» говорят в контексте, когда сила, действующая на тело вызывает изменение углового ускорения тела. С другой стороны, когда в английском языке говорят о моменте силы, то сила, действующая на тело не обязательно вызывает такое ускорение. То есть, «torque» — это частный пример момента силы, но не наоборот. Можно также сказать, что «torque» — это момент силы, но момент силы — не «torque».
В этом разделе обсудим, когда в английском наиболее часто используют термин «момент силы» и почти не используют «torque». Часто о понятии «torque» говорят в контексте, когда сила, действующая на тело вызывает изменение углового ускорения тела. С другой стороны, когда в английском языке говорят о моменте силы, то сила, действующая на тело не обязательно вызывает такое ускорение. То есть, «torque» — это частный пример момента силы, но не наоборот. Можно также сказать, что «torque» — это момент силы, но момент силы — не «torque». Величина момента силы зависит от величины силы, которая действует на тело, и от расстояния от точки приложения силы до точки на теле. Как мы увидели из определения выше, эта точка часто находится на оси вращения.
Величина момента силы зависит от величины силы, которая действует на тело, и от расстояния от точки приложения силы до точки на теле. Как мы увидели из определения выше, эта точка часто находится на оси вращения.
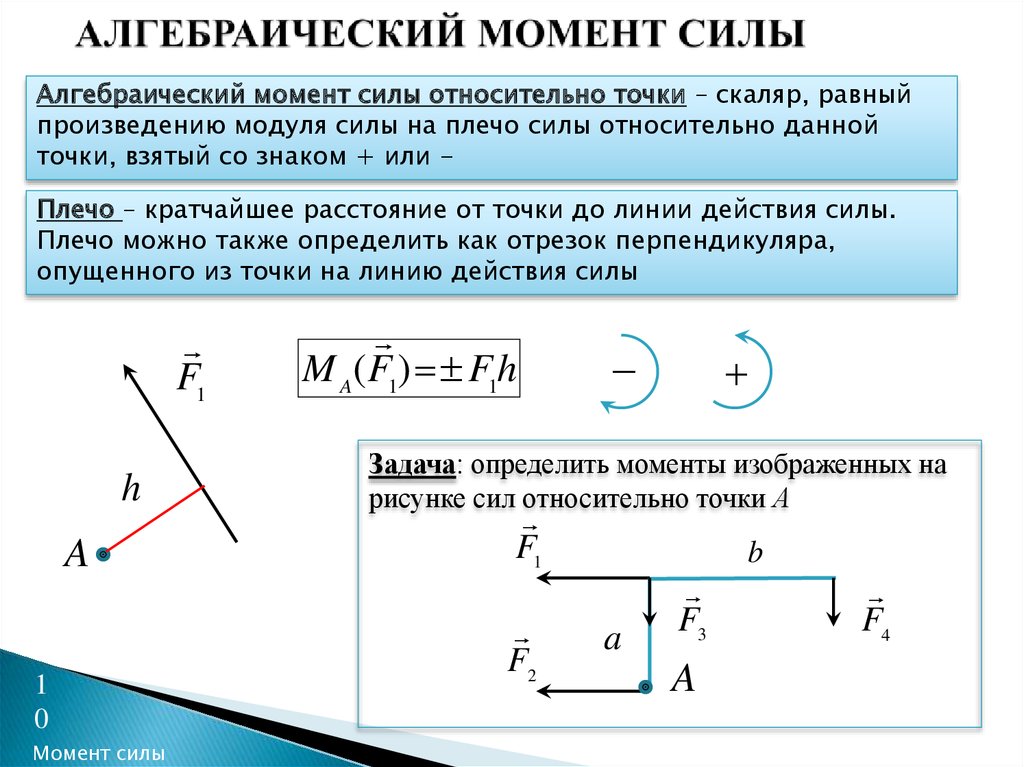 Если же балка фиксирована, то в противодействие моменту силы образуется другой момент, известный как изгибающий момент. Как видно из этого примера, термины момент силы и вращающий момент различаются тем, что момент силы не обязательно изменяет угловое ускорение. В этом примере угловое ускорение не изменяется потому, что силам извне, действующим на балку, противодействуют внутренние силы.
Если же балка фиксирована, то в противодействие моменту силы образуется другой момент, известный как изгибающий момент. Как видно из этого примера, термины момент силы и вращающий момент различаются тем, что момент силы не обязательно изменяет угловое ускорение. В этом примере угловое ускорение не изменяется потому, что силам извне, действующим на балку, противодействуют внутренние силы.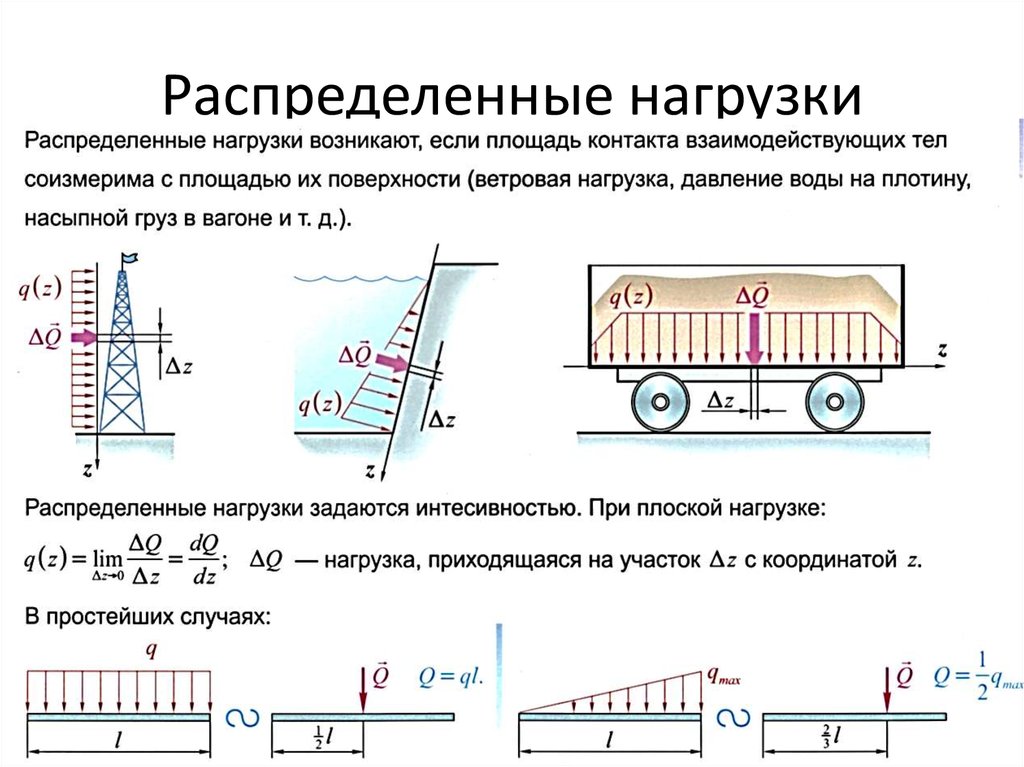 Нагрузка, вызванная людьми и интерьером, называется в строительстве полезной нагрузкой, а нагрузка, вызванная весом самого здания и окружающей средой называется статической или постоянной нагрузкой.
Нагрузка, вызванная людьми и интерьером, называется в строительстве полезной нагрузкой, а нагрузка, вызванная весом самого здания и окружающей средой называется статической или постоянной нагрузкой.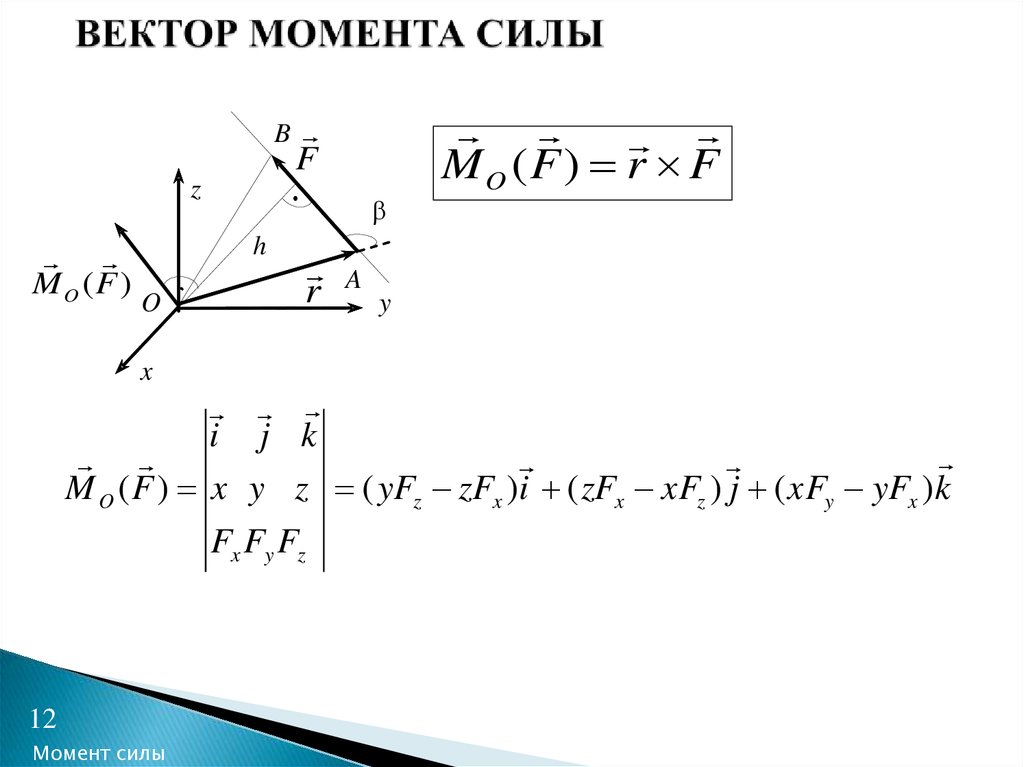 Хороший пример — использование двутавровых конструкций. Двутавр — конструктивный элемент с поперечным сечением в форме буквы Н или латинской буквы “I” с верхней и нижней засечками (поэтому английском языке используют термин I-beam, Такая форма очень экономична, так как она позволяет упрочнить самые слабые части балки, используя при этом наименьшее количество материала. Чаще всего двутавровые балки сделаны из стали, но для прочной балки двутавровой конструкции вполне можно использовать и другие материалы. На YouTube можно найти видеосюжеты испытания двутавровых балок, сделанных из материалов, менее прочных, чем сталь, например из пенопласта и фанеры (нужно искать plywood beam test). Двутавровые балки из фанеры и древесностружечных плит появились на российском рынке стройматериалов относительно недавно, хотя они давно и очень широко применяются при строительстве каркасных домов в Северной Америке.
Хороший пример — использование двутавровых конструкций. Двутавр — конструктивный элемент с поперечным сечением в форме буквы Н или латинской буквы “I” с верхней и нижней засечками (поэтому английском языке используют термин I-beam, Такая форма очень экономична, так как она позволяет упрочнить самые слабые части балки, используя при этом наименьшее количество материала. Чаще всего двутавровые балки сделаны из стали, но для прочной балки двутавровой конструкции вполне можно использовать и другие материалы. На YouTube можно найти видеосюжеты испытания двутавровых балок, сделанных из материалов, менее прочных, чем сталь, например из пенопласта и фанеры (нужно искать plywood beam test). Двутавровые балки из фанеры и древесностружечных плит появились на российском рынке стройматериалов относительно недавно, хотя они давно и очень широко применяются при строительстве каркасных домов в Северной Америке.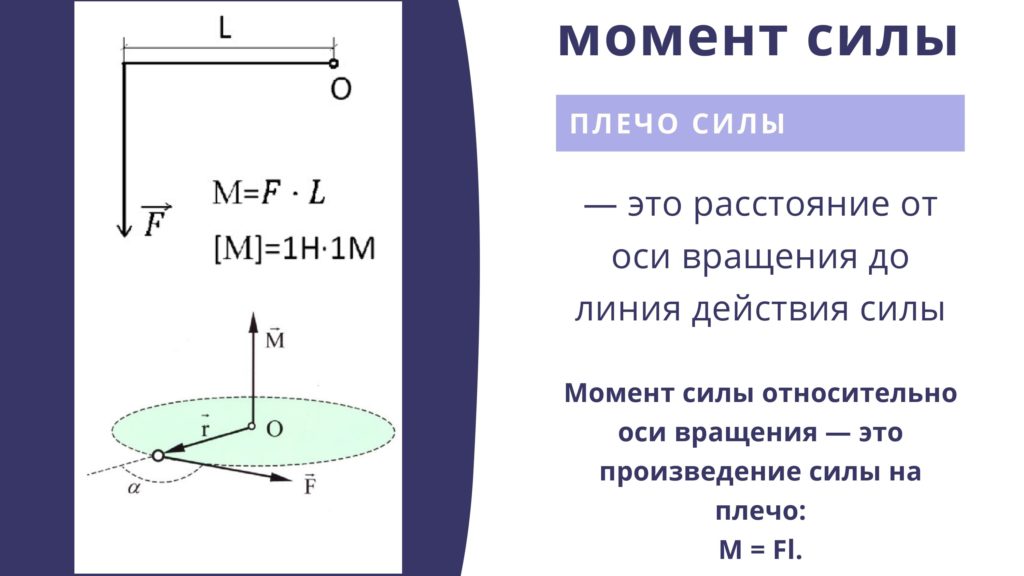 Двутавровые балки также используют в конструкциях, которые подвергаются напряжению сдвига. Края двутавровой балки противодействуют изгибающему моменту, в то время как центральная опора противостоит напряжению сдвига. Несмотря на ее достоинства, двутавровая балка не может противостоять крутящим нагрузкам. Чтобы уменьшить эту нагрузку на поверхность конструкции, ее делают круглой и полируют поверхность, чтобы предотвратить скопление нагрузки в точках с неровной поверхностью. Увеличение диаметра и изготовление такой конструкции полой внутри может помочь уменьшить ее вес.
Двутавровые балки также используют в конструкциях, которые подвергаются напряжению сдвига. Края двутавровой балки противодействуют изгибающему моменту, в то время как центральная опора противостоит напряжению сдвига. Несмотря на ее достоинства, двутавровая балка не может противостоять крутящим нагрузкам. Чтобы уменьшить эту нагрузку на поверхность конструкции, ее делают круглой и полируют поверхность, чтобы предотвратить скопление нагрузки в точках с неровной поверхностью. Увеличение диаметра и изготовление такой конструкции полой внутри может помочь уменьшить ее вес.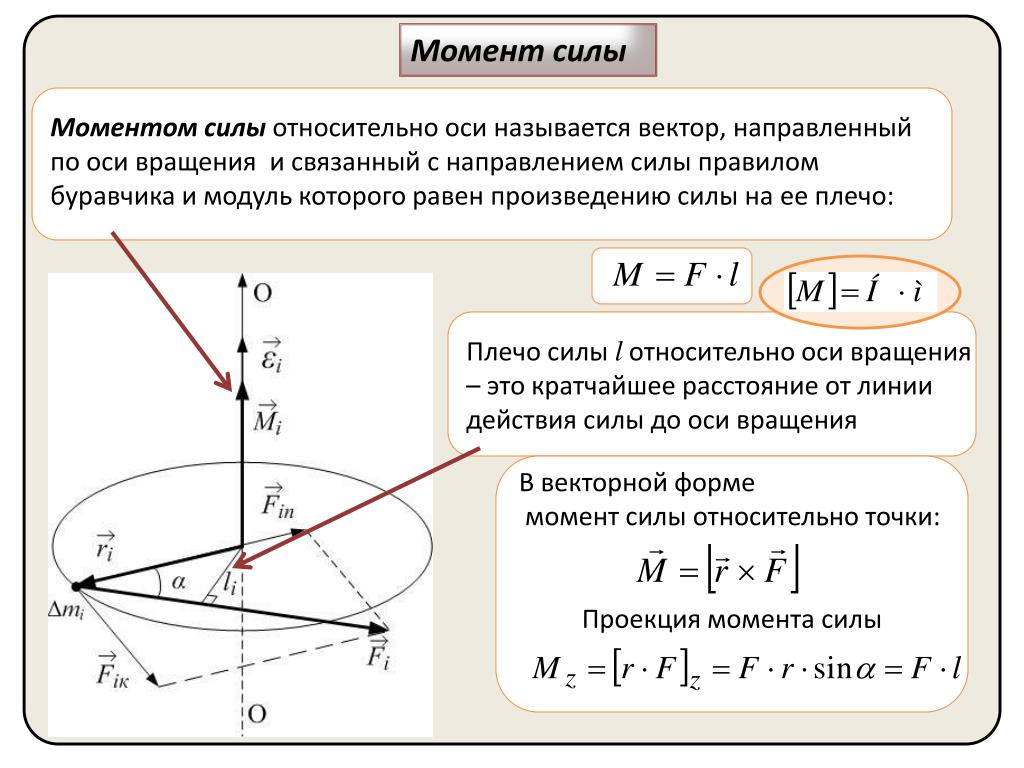 В основном мы говорили о случаях, когда момент силы создает проблемы в строительстве, но часто бывает наоборот и момент силы приносит пользу. Примеры использования момента силы на практике — в статье «Подробнее о вращающем моменте». Стоит также упомянуть, что разница в терминологии в английском языке чаще всего значительна в американском и британском машиностроении и строительстве, в то время как в физике эти термины часто взаимозаменяемы.
В основном мы говорили о случаях, когда момент силы создает проблемы в строительстве, но часто бывает наоборот и момент силы приносит пользу. Примеры использования момента силы на практике — в статье «Подробнее о вращающем моменте». Стоит также упомянуть, что разница в терминологии в английском языке чаще всего значительна в американском и британском машиностроении и строительстве, в то время как в физике эти термины часто взаимозаменяемы. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.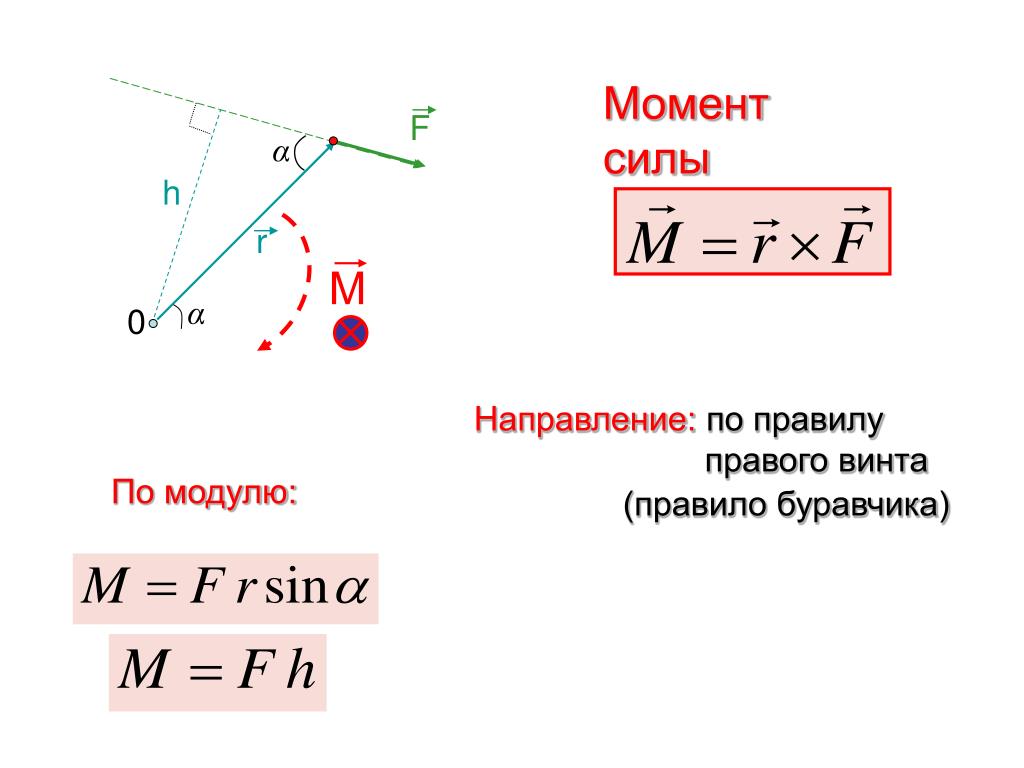 Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения. », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube Ферма
Ферма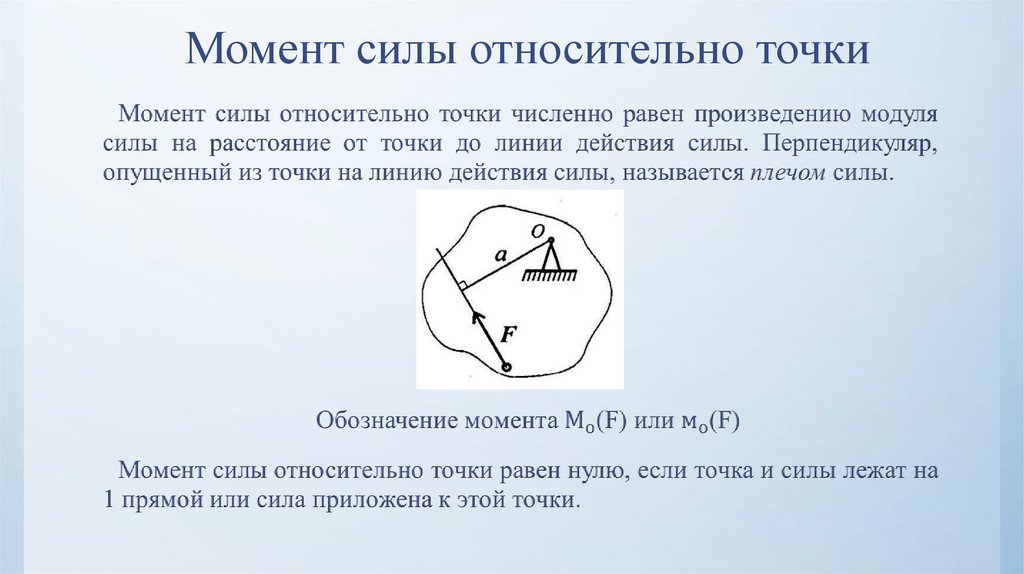 Пример.
Пример.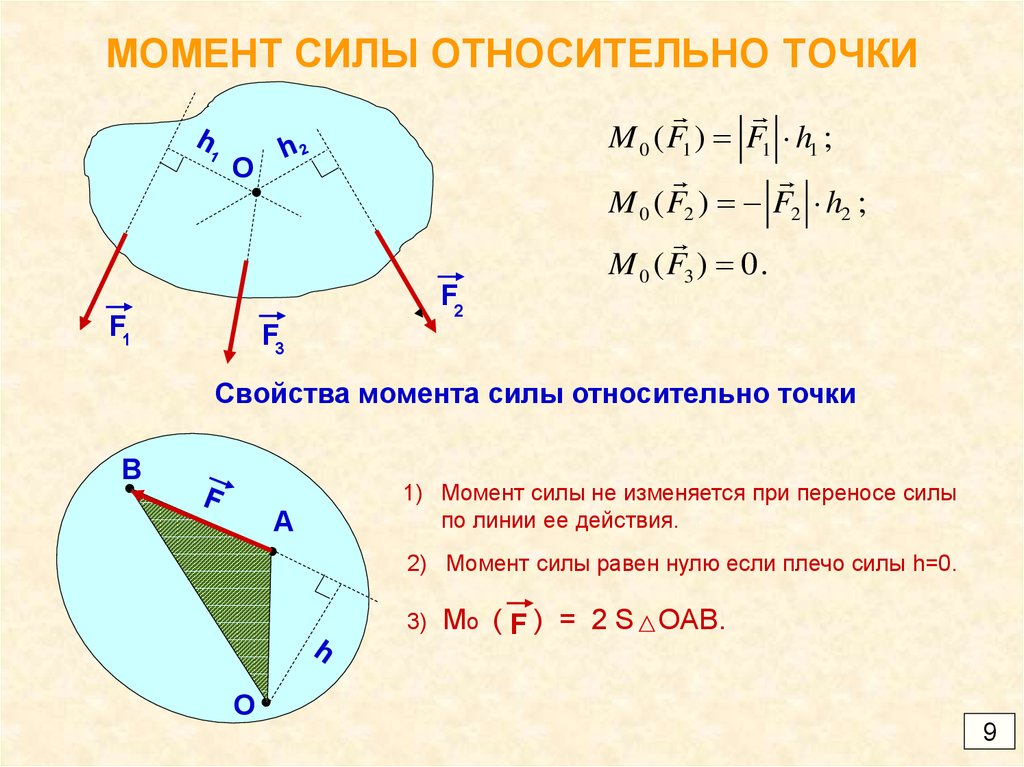 Определяем реакции опор. Анимация и графика П.Горшкова.
Определяем реакции опор. Анимация и графика П.Горшкова. Нагрузка, распределенная по дуге. + решение в Maple
Нагрузка, распределенная по дуге. + решение в Maple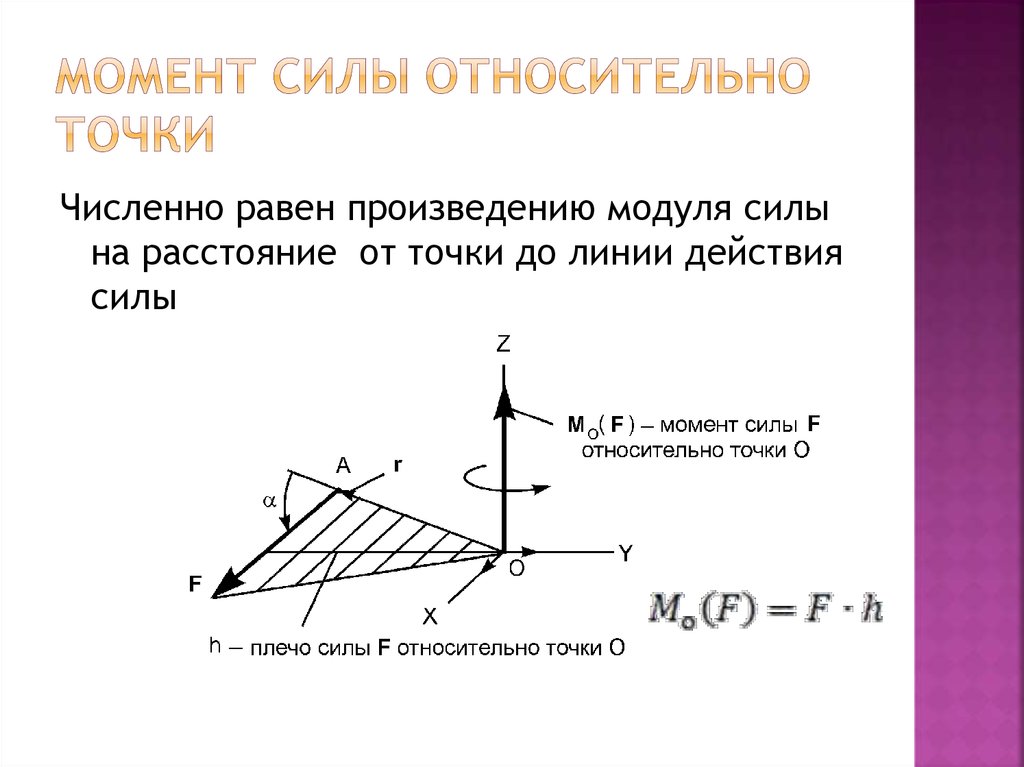 Определяем условие равновесия рамы + некоторые рассуждения на общие темы…
Определяем условие равновесия рамы + некоторые рассуждения на общие темы… МЦС
МЦС Абсолютное ускорение. Задача
Абсолютное ускорение. Задача Maple
Maple Приведенная масса
Приведенная масса Формула Циолковского
Формула Циолковского Задача с муфтой. Используем метод прямого дифференцирования.
Задача с муфтой. Используем метод прямого дифференцирования. Линейная обобщенная координата.
Линейная обобщенная координата. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица Момент силы — это мера способности силы вызывать вращательное или крутящее движение тела вокруг оси. Его величина равна векторному произведению вектора силы, приложенной к объекту, и перпендикулярного расстояния от оси до линии действия силы, вызывающей вращение. Крутящий момент является родственным понятием и измеряется так же, как и момент силы, но определяется как стремление объекта вращаться при приложении к нему силы. Она также измеряется как произведение силы на расстояние между точкой приложения и осью вращения.
Момент силы — это мера способности силы вызывать вращательное или крутящее движение тела вокруг оси. Его величина равна векторному произведению вектора силы, приложенной к объекту, и перпендикулярного расстояния от оси до линии действия силы, вызывающей вращение. Крутящий момент является родственным понятием и измеряется так же, как и момент силы, но определяется как стремление объекта вращаться при приложении к нему силы. Она также измеряется как произведение силы на расстояние между точкой приложения и осью вращения.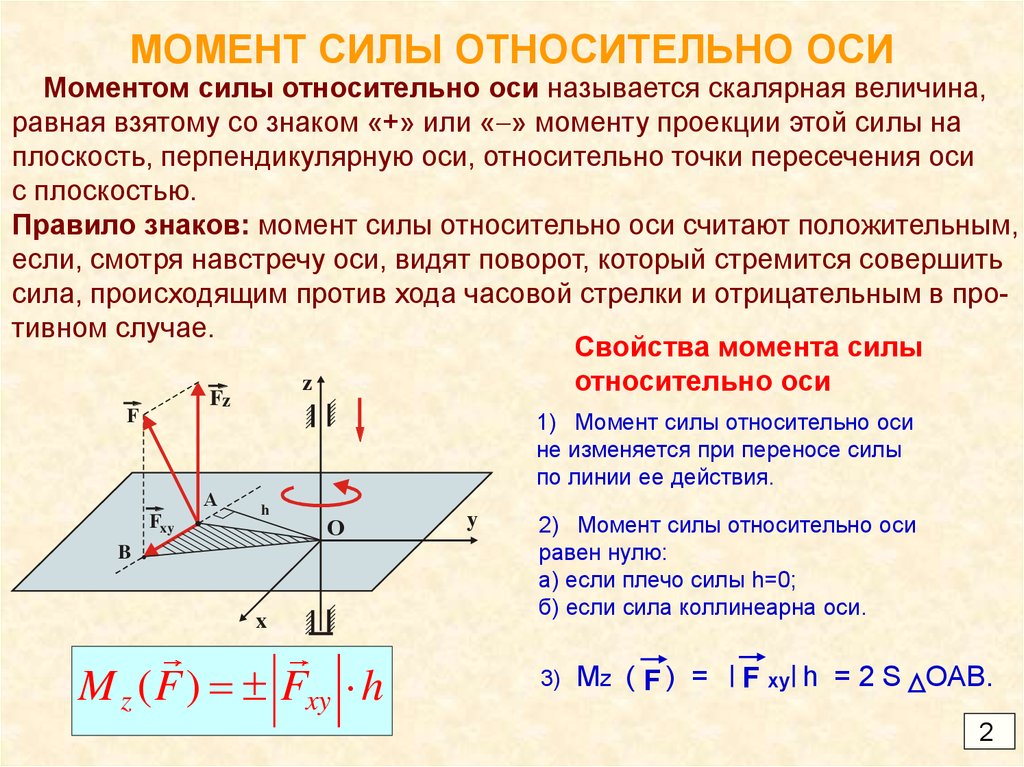 Кроме того, английский — один из немногих языков, в которых используются два отдельных термина. Во многих других языках используется только один термин. Здесь мы подробно обсудим нюансы, чтобы помочь устранить путаницу в использовании этих двух терминов.
Кроме того, английский — один из немногих языков, в которых используются два отдельных термина. Во многих других языках используется только один термин. Здесь мы подробно обсудим нюансы, чтобы помочь устранить путаницу в использовании этих двух терминов.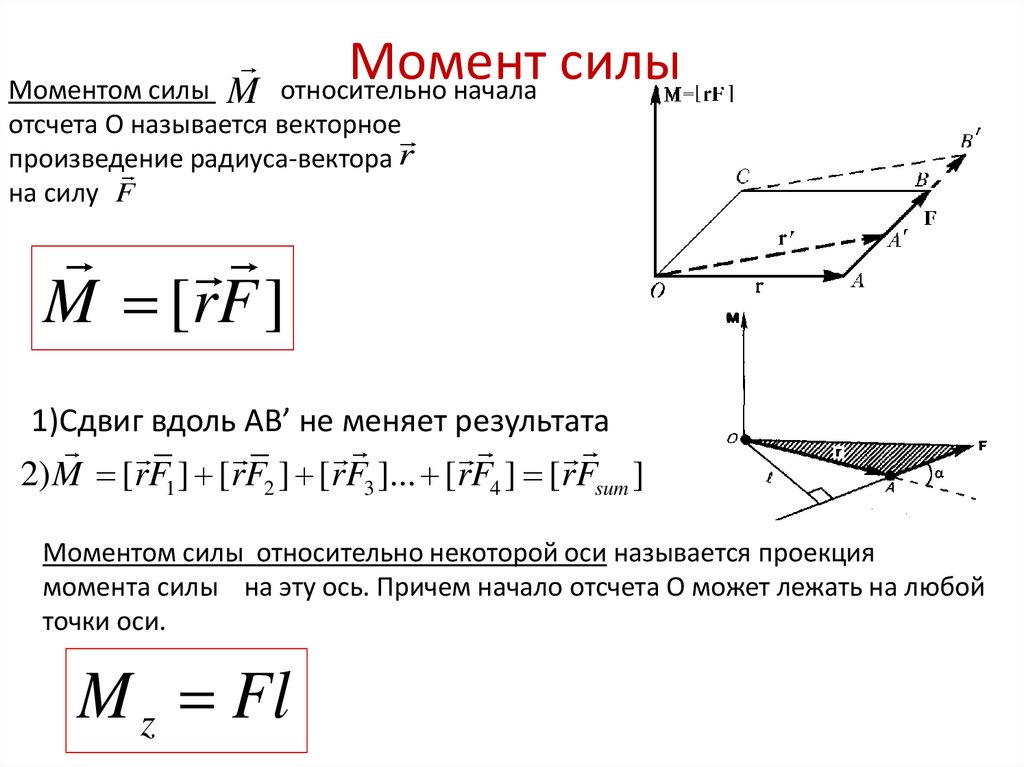
 Вы можете увидеть примеры того, как работают рычаги, в статье о крутящем моменте.
Вы можете увидеть примеры того, как работают рычаги, в статье о крутящем моменте. Если движение балки не стеснено, то она будет вращаться свободно, а если стеснена, то возникнет внутренний момент, противодействующий моменту силы. В результате кузов деформируется. Этот внутренний момент, противодействующий моменту силы, известен как 9.0525 изгибающий момент . Как вы видите в этом примере, момент силы не совпадает с крутящим моментом, потому что он не вызывает изменения углового момента. Это отсутствие изменения количества движения обусловлено внутренним противодействием тела этим внешним силам.
Если движение балки не стеснено, то она будет вращаться свободно, а если стеснена, то возникнет внутренний момент, противодействующий моменту силы. В результате кузов деформируется. Этот внутренний момент, противодействующий моменту силы, известен как 9.0525 изгибающий момент . Как вы видите в этом примере, момент силы не совпадает с крутящим моментом, потому что он не вызывает изменения углового момента. Это отсутствие изменения количества движения обусловлено внутренним противодействием тела этим внешним силам. Это напряжение включает в себя деформацию, вызванную самой конструкцией, например, деформацию, вызванную ее весом, а также нагрузку, вызванную внешними элементами, такими как ветер, снег, дождь, предметы, хранящиеся в здании, такие как как мебель, так и люди, которые входят в здание. В проектировании конструкций нагрузка, включающая людей и предметы, хранящиеся в здании, называется 9.0525 постоянная нагрузка , а нагрузка, вызванная весом конструкции, называется статической нагрузкой .
Это напряжение включает в себя деформацию, вызванную самой конструкцией, например, деформацию, вызванную ее весом, а также нагрузку, вызванную внешними элементами, такими как ветер, снег, дождь, предметы, хранящиеся в здании, такие как как мебель, так и люди, которые входят в здание. В проектировании конструкций нагрузка, включающая людей и предметы, хранящиеся в здании, называется 9.0525 постоянная нагрузка , а нагрузка, вызванная весом конструкции, называется статической нагрузкой .
 Участок корпуса, известный как «паутина», отвечает за устойчивость к касательному напряжению. Однако двутавровые балки не рассчитаны на сопротивление скручиванию. Напряжение кручения создается крутящим движением. Чтобы его минимизировать, конструкции делают круглыми, полыми и с большим диаметром, что позволяет уменьшить их вес. Их поверхности отполированы, чтобы гарантировать отсутствие участков с сосредоточенным напряжением.
Участок корпуса, известный как «паутина», отвечает за устойчивость к касательному напряжению. Однако двутавровые балки не рассчитаны на сопротивление скручиванию. Напряжение кручения создается крутящим движением. Чтобы его минимизировать, конструкции делают круглыми, полыми и с большим диаметром, что позволяет уменьшить их вес. Их поверхности отполированы, чтобы гарантировать отсутствие участков с сосредоточенным напряжением.

 Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах.
Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах.
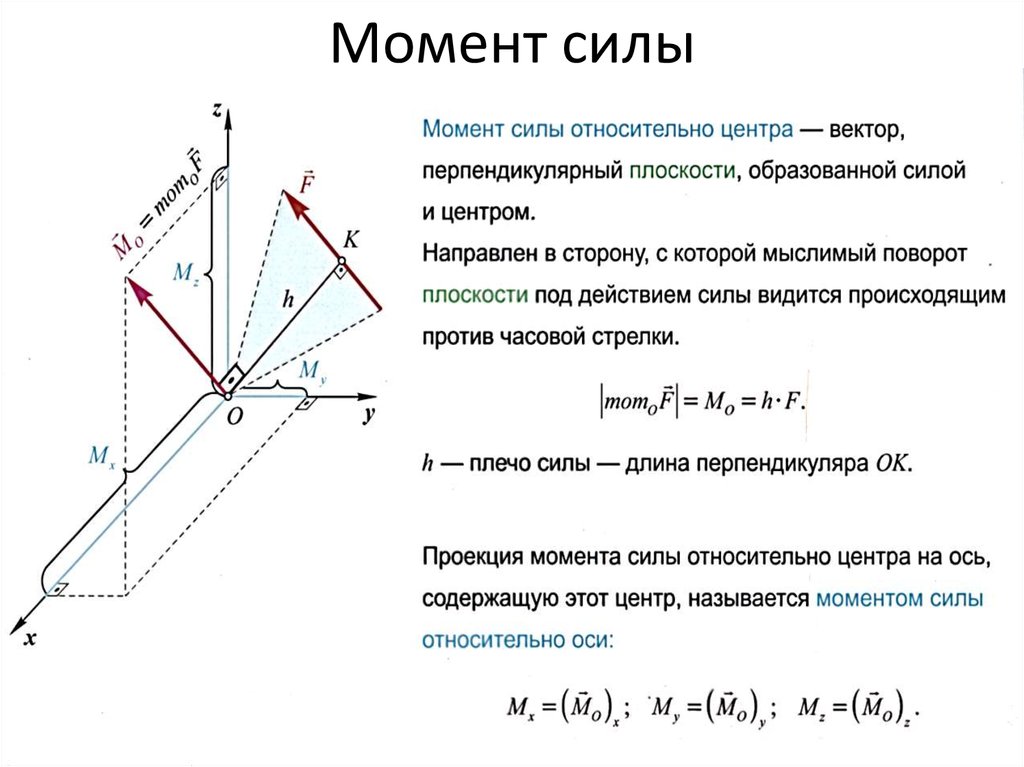 com Канал Unit Converter на YouTube
com Канал Unit Converter на YouTube