Восьмеричная система счисления – как переводить, таблица
4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
Числа можно представлять не только в десятичном формате, но и в системе счисления с основанием 8, которая использует для обозначения символы 0, 1, 2, 3, 4, 5, 6, 7. О том, как переводить в восьмеричную систему счисления числа из десятичной и двоичной системы и обратно, рассказано в данной статье.
Восьмеричная система счисления
Восьмеричная система счисления имеет вспомогательный характер, ее удобно использовать для сокращенной записи бинарных комбинаций чисел. Она более удобна в работе чем двоичная, так как использует меньшее количество разрядов. Восьмеричная система применялась в свое время для программирования на машинном языке, а также в устройствах подготовки данных, вышедших из употребления с появлением персональных компьютеров.
Алфавит восьмеричной системы составляют восемь цифр от 0 до 7, соответственно основание равно 8.
Следует обратить внимание, что после 7 в числовом ряду идет 10, а после 17 число 20.
Число 8 имеет символический смысл, является первым кубом двойки и отождествляется с трехмерным измерением. Для многих древних народов восьмёрка сакральное число. Внешне выглядит как символ бесконечности. В информатике один байт равен 8 битам.
Рис. 1. Символ бесконечности.Перевод 8 – 2
Перенос восьмеричного числа в двоичный формат – это самый простой способ перевода чисел. Каждой восьмеричной цифре ставится в соответствие группа двоичных цифр в количестве трех. Эта группа называется триадой.
И, наоборот, при переводе двоичного числа в восьмеричный формат производится замена трех двоичных цифр одной восьмеричной. Разбивка целого двоичного числа на трехзначные звенья производится справа налево. Когда крайняя триада получается неполной, то ее дополняют нулями.
Для более быстрого перевода чисел используется таблица записи восьмеричных чисел двоичным форматом.
Например, 348 = 0111002. Ноль впереди числа отбрасываем и получаем в итоге 111002.
И обратный перевод, например: 1101101
Перевод 8 – 10
Преобразование чисел из восьмеричного формата в десятичную форму выполняется с использованием правила перевода: целая часть числа последовательно делится на основание новой системы счисления, то есть 8, и остатки от деления записываются начиная с последнего частного в обратном направлении. Например:
246 / 8 = 30 и в остатке 6
30 / 8 = 3 и в остатке 6
3 меньше 8, деление завершено.
Таким образом, 24610 = 3668.
Обратный перевод выполняется путем разложения числа в развернутую форму:
3668 = 3*82 + 6*81 + 6*80 = 3*64 + 6*8 + 6*1 = 192 + 48 + 6 = 24610
Арифметические действия
Арифметические действия в системе счисления с основанием 8 выполняются также как и в десятичной.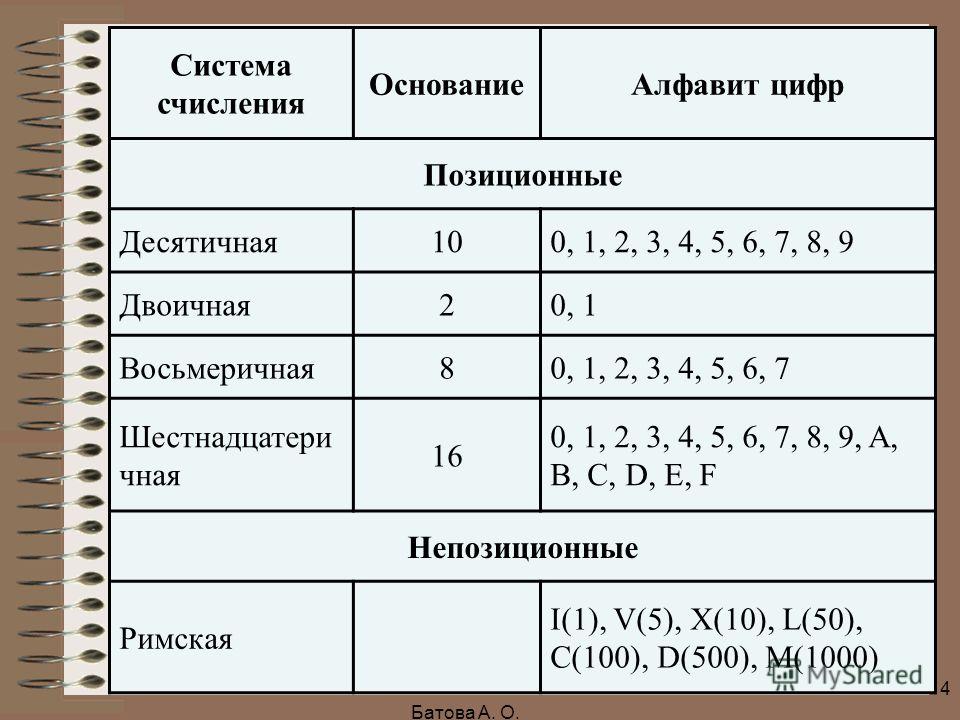 Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.
Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.
Например, сумма 34 + 25 = 61. Это получилось следующим образом. Сначала складываются младшие разряды 4 + 5 = 11 (смотрят по таблице). Единица остается в младшем разряде, а вторая единица переносится в старший разряд и добавляется к сумме чисел 3 + 2 = 5. Итого получилось 61.
Что мы узнали?
Восьмеричная система счисления удобна для представления бинарных кодов и записи машинных команд в программировании. Основание этой системы равно 8. Для перевода чисел из двоичной системы счисления в восьмеричную и обратно используются триады. Перевод восьмеричных чисел в десятичную систему выполняется путем поочередного деления частного числа и записи остатков от деления. Обратный перевод выполняется через раскрытие числа в развернутую форму.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Елена Кетросан
10/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
А какая ваша оценка?
§ 1.1. Системы счисления
§ 1.1. Системы счисления
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- система счисления
- цифра
- алфавит
- позиционная система счисления
- основание
- развёрнутая форма записи числа
- свёрнутая форма записи числа
- двоичная система счисления
- восьмеричная система счисления
- шестнадцатеричная система счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.
Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
- 1) унарная система;
- 2) непозиционные системы;
- 3) позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
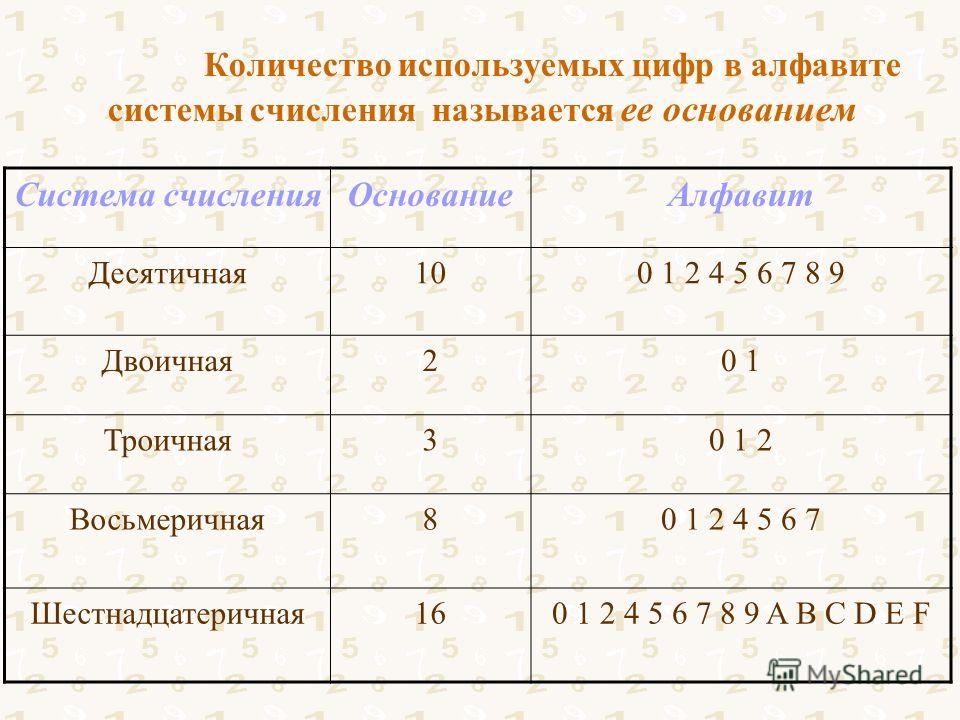
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».
Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.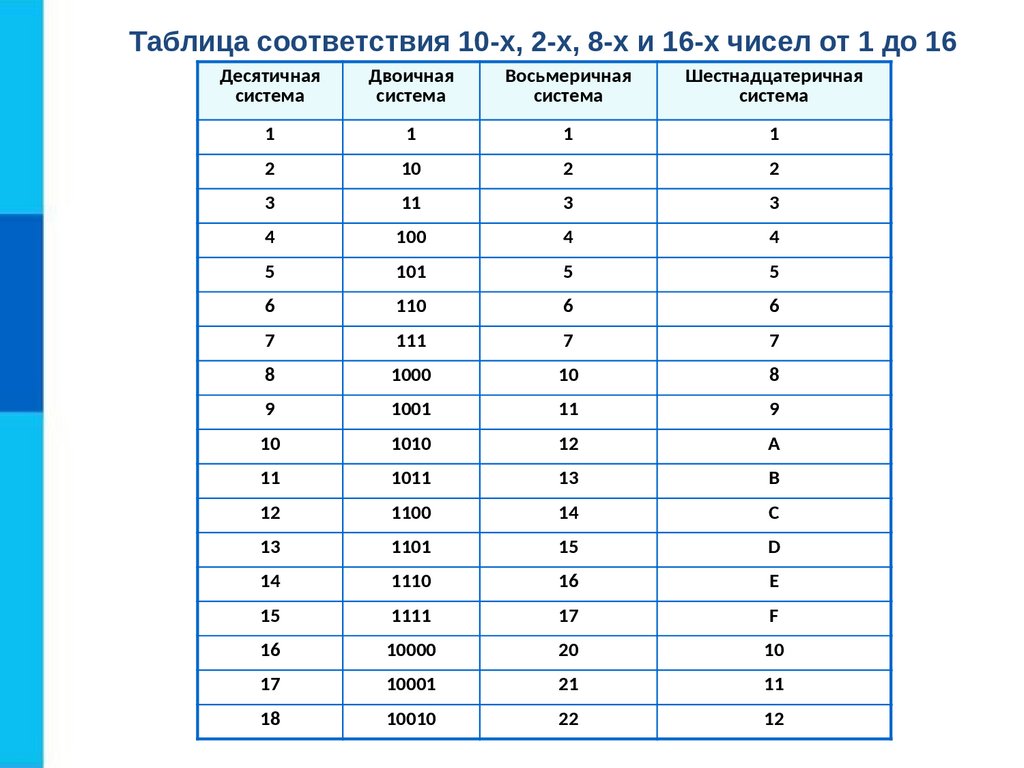
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде1 ± an-1an-2…a1a0,a-1…a-m. 1 Далее будут рассматриваться только положительные целые числа.
1 Далее будут рассматриваться только положительные целые числа.
Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
- 1 • 104 + 4 • 103 + 3 • 102 + 5 • 101 + 1 • 100 + 1 • 10-1.
Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
На основании формулы (1) для целых двоичных чисел можно записать:
- аn-1аn-2…а1а0 = an-1 • 2n-1 + аn-2 • 2n-2 +…+ а0 • 20.
 (1′)
(1′)
Например:
- 100112 = 1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 1 • 20 = 24 + 21 + 20 = 1910.
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1′).
Разделим аn-1 • 2n-1 + аn-2 • 2n-2 + … + а0 • 20 на 2. Частное будет равно аn-1 • 2n-2 + … + а1, а остаток будет равен а0.
Полученное частное опять разделим на 2, остаток от деления будет равен а1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:
- а0, а1, а2, … аn-1,.

которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.
Пример 5. Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
- 36310 = 1011010112
 1.3. Восьмеричная система счисления
1.3. Восьмеричная система счисленияВосьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1,2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
- аn-1аn-2…а1а0 = аn-1 • 8n-1 + аn-2 • 8n-2 + … + а0 • 80. (1″)
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
10310 = 1478
1.1.4. Шестнадцатеричная система счисленияОснование: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
- 3AF16 = 3 • 162 + 10 • 161 + 15 • 160 = 768 + 160 + 15 = 94310.
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
15410 = 9А16
1. 1.5. Правило перевода целых десятичных чисел в систему счисления с основанием q
1.5. Правило перевода целых десятичных чисел в систему счисления с основанием qДля перевода целого десятичного числа в систему счисления с основанием q следует:
- 1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
- 2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
- 3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 2010.
В Единой коллекции цифровых образовательных ресурсов (http://sc.edu.ru/) размещена интерактивная анимация «Преобразование десятичного числа в другую систему счисления» (135050). С её помощью можно понаблюдать за переводом произвольного целого числа от 0 до 512 в позиционную систему счисления, основание которой не превышает 16.
В размещённой там же виртуальной лаборатории «Цифровые весы» (135009) вы сможете освоить ещё один способ перевода целых десятичных чисел в другие системы счисления — метод разностей.
1.1.6. Двоичная арифметикаАрифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
Пример 8. Таблица двоичного сложения предельно проста. Так как 1 + 1 = 10, то 0 остаётся в младшем разряде, а 1 переносится в старший разряд.
Пример 9. Операция умножения двоичных чисел выполняется по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Таким образом, в двоичной системе счисления умножение сводится к сдвигам множимого и сложениям.
1.1.7. «Компьютерные» системы счисленияВ компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ по сравнению с другими системами счисления:
- двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
- представление информации посредством только двух состояний надёжно и помехоустойчиво;
- двоичная арифметика наиболее проста;
- существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
С помощью ресурса «Интерактивный задачник, раздел “Системы счисления»» (128659), размещённого в Единой коллекции цифровых образовательных ресурсов, можно проверить, насколько прочно вы усвоили изученный в этом параграфе материал.
Самое главное о системе счисленияСистема счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.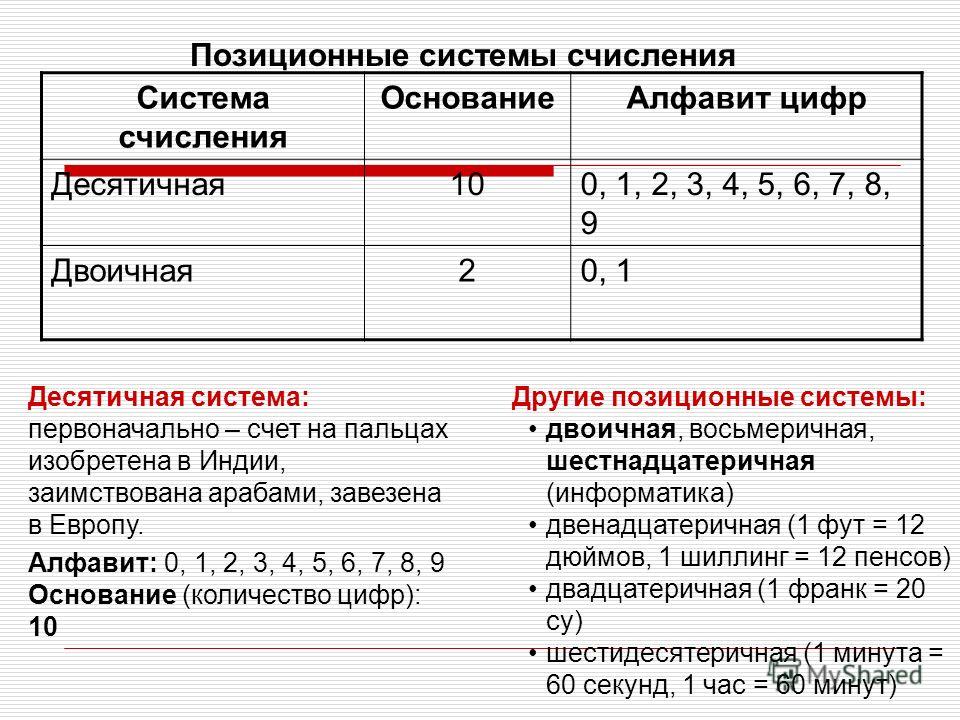
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
3. Цифры каких систем счисления приведены на рис. 1.1?
4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
5. Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
6. Запишите в развёрнутой форме числа
7. Вычислите десятичные эквиваленты следующих чисел 172? 2EA??
8. Укажите какое из чисел 1100112, 1114, 358 и 1В16 является
9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
10. Верны ли следующие равенства? а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если: а) 14х = 910;
б) 2002х = 13010.
12. Переведите целые числа из десятичной системы счисления в двоичную: а) 89; б) 600; в) 2010
13. Переведите целые числа из десятичной системы счисления в восьмеричную: а) 513; б) 600; в) 2010.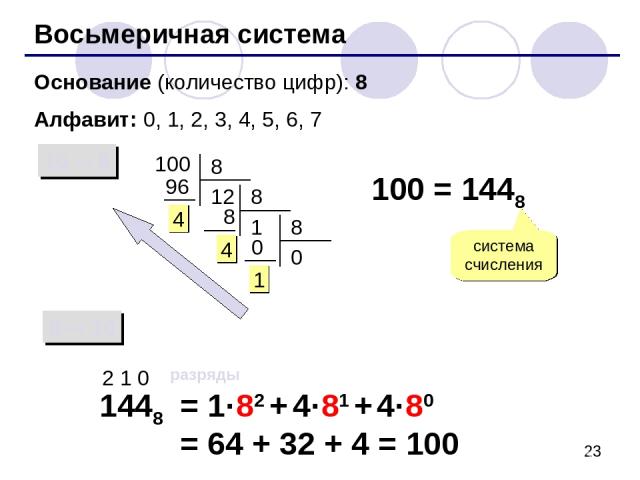
14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную: а) 513; б) 600; в) 2010.
15. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
16. Выполните операцию сложения над двоичными числами: а) 101010 + 1101; б) 1010 + 1010; в) 10101 + 111.
17. Выполните операцию умножения над двоичными числами: а) 1010 · 11; б) 111 · 101; в) 1010 · 111.
18. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе: а) 1100 ? 11 ? 100 = 100000; б) 1100 ? 10 ? 10 = 100; в) 1100 ? 11 ? 100 = 0.
19. Вычислите выражения: а) (11111012 + AF16) : 368; б) 1258 + 1012 ? 2A16 ? 1418. Ответ дайте в десятичной системе счисления.
Ответ дайте в десятичной системе счисления.
20. Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?
21. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.
22. Постройте граф, отражающий разновидности систем счисления.
23. Подготовьте небольшое сообщение об одной из систем счисления (когда и где применялась, какие символы использовались и т. д.).
Оглавление
§ 1.1. Системы счисления
§ 1.2. Представление чисел в компьютере
Простая английская Википедия, бесплатная энциклопедия
Переключить оглавлениеИз простой английской Википедии, бесплатной энциклопедии
Восьмеричная система счисления — это система счисления с основанием 8. В нем используются цифры от 0 до 7. Система аналогична двоичной (основание 2) и шестнадцатеричной (основание 16).
В свое время восьмеричная система использовалась в основном для работы с компьютерами. Это обеспечило более простой способ работы с двоичными числами. Поскольку компьютеры перешли от использования 24-битных систем к 32- и 64-битным системам, шестнадцатеричная система заменила восьмеричную для большинства применений. Некоторые группы, например, коренные американцы, использующие язык юки в Калифорнии и памейские языки
Восьмеричная система счисления использует «трехбитное» двоичное кодирование. Каждая цифра восьмеричного числа соответствует трем цифрам двоичного числа. Группировка двоичных цифр выполняется справа налево. Первые три двоичных разряда справа группируются в последнюю часть восьмеричного числительного, затем следующие три разряда образуют предпоследнюю часть числительного.
Первые три двоичных разряда справа группируются в последнюю часть восьмеричного числительного, затем следующие три разряда образуют предпоследнюю часть числительного.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В десятичной системе (с основанием 10) каждая восьмеричная цифра равна той цифре, умноженной на показатель степени числа 8, который равен ее положению минус один.
| Местоположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 32768 (8 5 ) | 4096 (8 4 ) | 512 (8 3 ) | 64 (8 2 | 8(8 1 ) | 1 (8 0 ) |
Пример: o3425 в десятичной системе
|
Восьмеричное похоже на шестнадцатеричное, поскольку оба они легко преобразуются в двоичные. Где восьмеричное равно трехзначному двоичному, шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну систему в другую — преобразовать ее в двоичную, а затем в другую систему.
Где восьмеричное равно трехзначному двоичному, шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну систему в другую — преобразовать ее в двоичную, а затем в другую систему.
| Восьмеричный | Двоичный | Шестнадцатеричный | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| три цифры | четыре цифры | |||||||||
| о4 | 100 | 0100 | 04ч | |||||||
| о15 | 001 | 101 | 1101 | 0Дх | ||||||
| о306 | 011 | 000 | 110 | 1100 | 0110 | C6h | ||||
| о54253 | 101 | 100 | 010 | 101 | 011 | 0101 | 1000 | 1010 | 1011 | 58ABh |
- Двоичная система счисления
- Шестнадцатеричная система счисления
- Десятичная система счисления
- ↑ Авелино, Эриберто (2006), «Типология систем счисления Пейм и границы Мезоамерики как лингвистической области» (PDF), Лингвистическая типология , 10 : 41–60, doi: 10.
 1515/LINGTY.2006.002, S2CID 20412558
1515/LINGTY.2006.002, S2CID 20412558
- Онлайн-конвертер. Архивировано 4 января 2007 г. на Wayback Machine для десятичных и восьмеричных чисел (JavaScript, GPL)
Восьмеричная система счисления (определение, таблица, восьмеричная в двоичную)
Восьмеричная система счисления имеет основание восемь и использует числа от 0 до 7. Восьмеричные числа в системе счисления обычно представляются двоичными числами, когда они сгруппированы парами по три. Например, восьмеричное число 12 8 выражается как 001010 2 в двоичной системе, где 1 эквивалентно 001, а 2 эквивалентно 010.
| Восьмеричная система счисления |
| Основание – 8 |
| Восьмеричный символ – 0, 1, 2, 3, 4, 5, 6 и 7 |
Содержание:
|
Помимо восьмеричной системы счисления в математике существуют и другие системы счисления, например:
- Двоичная система счисления
- Шестнадцатеричная система счисления
- Десятичная система счисления
Определение
Система счисления, в основе которой лежит «восемь», называется восьмеричной системой счисления. Он использует числа от 0 до 7. Давайте возьмем пример, чтобы понять концепцию. Как мы уже говорили, любое число с основанием 8 является восьмеричным числом, например 24 8 , 109 8 , 55 8 и т. д.
Он использует числа от 0 до 7. Давайте возьмем пример, чтобы понять концепцию. Как мы уже говорили, любое число с основанием 8 является восьмеричным числом, например 24 8 , 109 8 , 55 8 и т. д.
Подобно тому, как восьмеричное число представляется с основанием 8, точно так же двоичное число представляется с основанием 2, десятичное число — с основанием 10, а шестнадцатеричное число — с основанием 16.
Примеры этих систем счисления:
- 22 2 — двоичное число
- 100 10 — десятичное число
- 40 16 — шестнадцатеричное число .
Если мы решим восьмеричное число, то каждый разряд будет степенью числа восемь.
- 124 8 = 1 × 8 2 + 2 × 8 1 + 4 × 8 0
Системная таблица восьмеричных чисел
Мы используем только 3 бита для представления восьмеричных чисел. Каждая группа будет иметь отдельное значение от 000 до 111.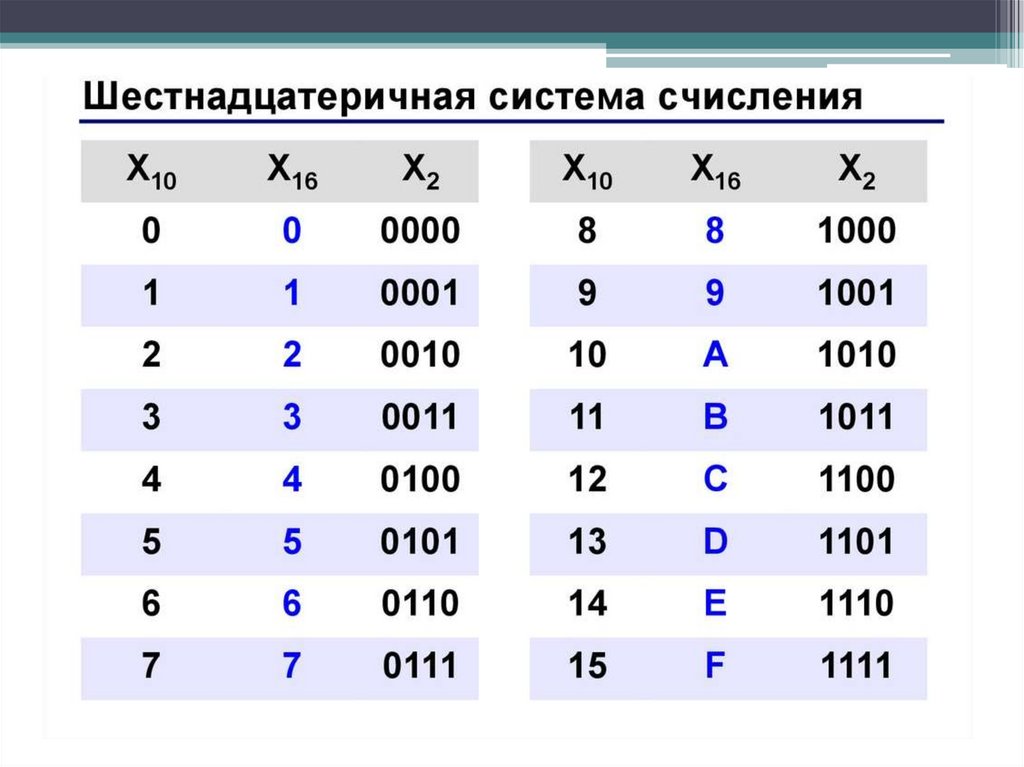
Восьмеричное цифровое значение | Двоичный эквивалент |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Примечание. Восьмеричная система счисления поддерживает цифры от 0 до 7. После 7, например, 8 и 9, восьмеричные цифры не используются. Например, 19 не является восьмеричным числом.
Преобразование десятичного числа в восьмеричное
Для преобразования десятичных чисел в восьмеричные используется восьмеричный метод dabble. В этом методе десятичное число каждый раз делится на 8, это дает или дает остаток. Первый остаток, который мы получаем, — это младшая значащая цифра (LSD), а последний остаток — это старшая значащая цифра (MSD). Давайте разберемся с преобразованием на примере справки.
Давайте разберемся с преобразованием на примере справки.
Пример десятичного преобразования в восьмеричное
Проблема : Предположим, что 560 — десятичное число, преобразовать его в восьмеричное число.
Решение : Если 560 — десятичное число, то
560/8 = 70 и остаток 0
70/8 = 8 и остаток равен 6
8/8 = 1 и остаток 0
А 1/8 = 0 и остаток 1
Таким образом, восьмеричное число начинается с MSD до LSD, то есть 1060
Следовательно, 560 10 = 1060 8
Проблема: Преобразовать 0,52 в восьмеричное число.
Решение: Дробную часть десятичного числа нужно умножить на 8.
0,52 × 8 = 0,16 с переносом 4
0,16 × 8 = 0,28 с переносом 1
0,28 × 8 = 0,24 с переносом 2
0,24 × 8 = 0,92 с переносом 1
Итак, для дробного восьмеричного числа мы читаем сгенерированный перенос сверху вниз.
Следовательно, 4121 — восьмеричное число.
Восьмеричный в десятичный
Чтобы преобразовать восьмеричное число в десятичное, нам нужно умножить каждую цифру данного восьмеричного числа на 8 в уменьшающей степени.
Давайте узнаем здесь, преобразование восьмеричного числа в десятичное число или основание 8 в основание 10.
Примеры преобразования восьмеричного в десятичный
Пример 1: Предположим, что 215 8 — восьмеричное число, тогда его десятичная форма будет
.215 8 = 2 × 8 2 + 1 × 8 1 + 5 × 8 0
= 2 × 64+ 1 × 8 + 5 × 1 = 128 + 8 + 5
= 141 10
Пример 2: Пусть 125 — восьмеричное число, обозначаемое как 125 8 . Найдите десятичное число.
125 8 = 1× 8 2 + 2 × 8 1 + 5 × 8 0
= 1 × 64 + 2 × 8 + 5 × 1 = 64+16+5
=85 10
Двоичное число в восьмеричное число
Двоичное число можно преобразовать в восьмеричное с помощью приведенной ниже таблицы.
Восьмеричный номер | Эквивалентный двоичный номер |
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Пример преобразования двоичного кода в восьмеричный
Пример: Преобразование (100010) 2 в восьмеричное число.
Решение: С помощью таблицы запишем
100→4
и 010→2
Следовательно, (100010) 2 = 42
Точно так же мы можем преобразовать восьмеричное число в двоичное с помощью таблицы.
Восьмеричный код в шестнадцатеричный
Шестнадцатеричные числа состоят из цифр и букв. Оно представляется с основанием 16. Числа от 0 до 9 представляются в обычном виде, а от 10 до 15 обозначаются как A, B, C, D, E, F. Преобразование восьмеричного числа в шестнадцатеричное требует два шага.
Оно представляется с основанием 16. Числа от 0 до 9 представляются в обычном виде, а от 10 до 15 обозначаются как A, B, C, D, E, F. Преобразование восьмеричного числа в шестнадцатеричное требует два шага.
- Сначала преобразуйте восьмеричные числа в десятичные.
- Затем преобразуйте десятичные числа в шестнадцатеричные числа.
Пример
Разберемся на примере. Возьмем тот же пример, где мы преобразовали восьмеричные числа в десятичные, например;
(55) 8 = (45) 10
Теперь преобразуйте (45) 10 в шестнадцатеричное число, разделив 45 на 16, пока не получите остаток меньше 16.
Следовательно, мы можем написать, (45) 10 = (2D) 16
или (55) 8 = (2D) 16
Восьмеричная таблица умножения
| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
приложений
Восьмеричная система счисления широко используется в компьютерных приложениях, а также в авиации для использования числа в форме кода.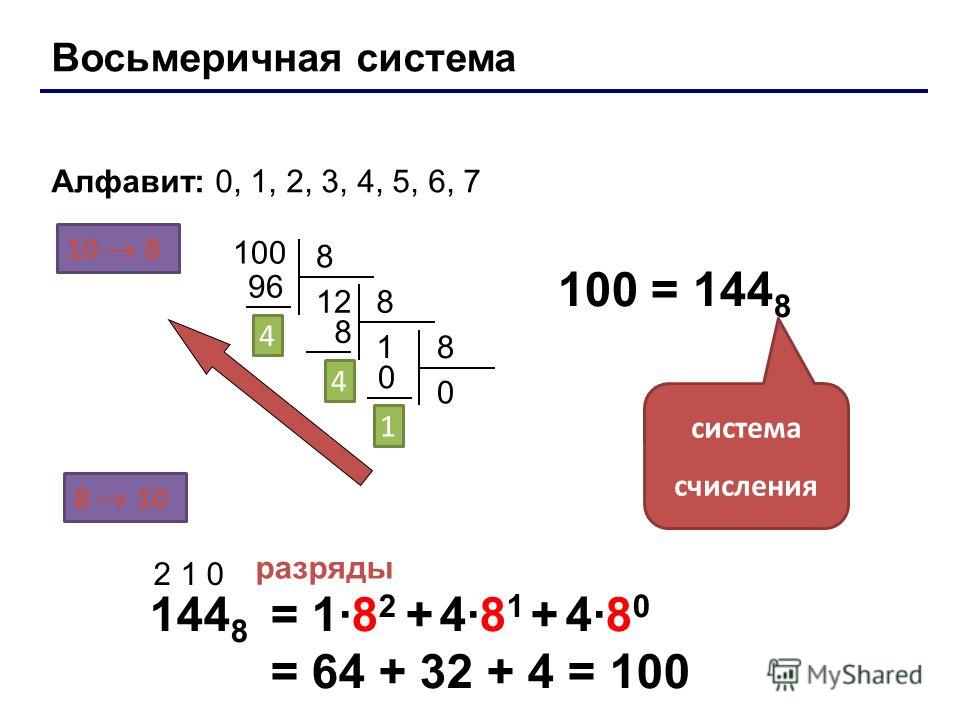
На основе приложений восьмеричной системы счисления разработано несколько вычислительных систем. Все вычислительные системы современного поколения используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова. Точно так же для различных языков программирования восьмеричные числа используются для кодирования или написания зашифрованного языка, который понимает только вычислительная машина.
Также в авиационном секторе или области или, скажем, в авиационной промышленности транспондеры, используемые в самолетах, передают код, который выражается в виде четырех восьмеричных цифр. Эти коды запрашиваются наземным радаром.
Важность
В восьмеричной системе счисления используется меньше цифр (3 бита), чем в шестнадцатеричной (4 бита), что является одним из ее преимуществ. Следовательно, вычислений будет меньше, а возможность возникновения ошибки ухудшится.
Из-за меньшего количества цифр также легко преобразовать восьмеричную систему счисления в любую другую систему счисления и наоборот.
Одним из недостатков является то, что компьютеры не воспринимают восьмеричные числа напрямую, поэтому их необходимо сначала преобразовать в двоичные числа.
Проблемы и решения
Q.1: Преобразуйте 275 8 в десятичное число.
Решение: 2 x 8 2 + 7 x 8 1 + 5 x 8 0
= 64×2 + 8×7 + 1×5
= 128 + 56 + 5
= 189
Следовательно, 275 8 = 189 10
Q.2: Преобразование десятичного числа 139 в эквивалентное восьмеричное число.
Решение: Нам нужно многократно делить 139 на 8, пока частное не станет равным 0.
| 8 | 139 | Остаток |
| 8 | 17 | 3 |
| 8 | 2 | 1 |
| 0 | 2 |
Теперь возьмите остатки снизу вверх, чтобы получить эквивалентное восьмеричное число.
139 10 = 213 8
Q.3: Преобразование восьмеричного числа 540 в двоичное число .
Решение: Дано, 540 — это восьмеричное число
.По таблице восьмеричных чисел мы можем получить двоичный эквивалент каждой цифры.
5 → 101
4 → 100
0 → 000
Следовательно,
540 8 = 101100000 2
Практические вопросы
Преобразуйте следующие восьмеричные числа в эквивалентные им десятичные числа.
- 23 8 (Ответ: 19 10 )
- 770 8 (Ответ: 504 10 )
- 152 8 (Ответ: 106 10 )
Преобразуйте следующие восьмеричные числа в шестнадцатеричные числа.
- 23 8 (Ответ: 13 16 )
- 770 8 (Ответ: 1F8 16 )
- 152 8 (Ответ: 6A 16 )
Кроме того, изучите темы, связанные с системами счисления, загрузив BYJU’S — The Learning App.
Часто задаваемые вопросы – Часто задаваемые вопросы
Что такое восьмеричная система счисления?
Система счисления, выраженная с основанием 8 и диапазоном только от 0 до 8, называется восьмеричной системой счисления. Он представлен как N8.
Для чего используются восьмеричные числа?
Восьмеричная система счисления широко используется в компьютерных приложениях. Все вычислительные системы современного поколения используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова. Также в авиационном секторе восьмеричные числа используются в виде кода.
Какое значение имеет восьмеричная система счисления?
Поскольку в восьмеричных числах используется меньшее количество цифр по сравнению с десятичными и шестнадцатеричными числами, поэтому проще выполнять вычисления за меньшее количество шагов, а также меньше вероятность возникновения ошибки.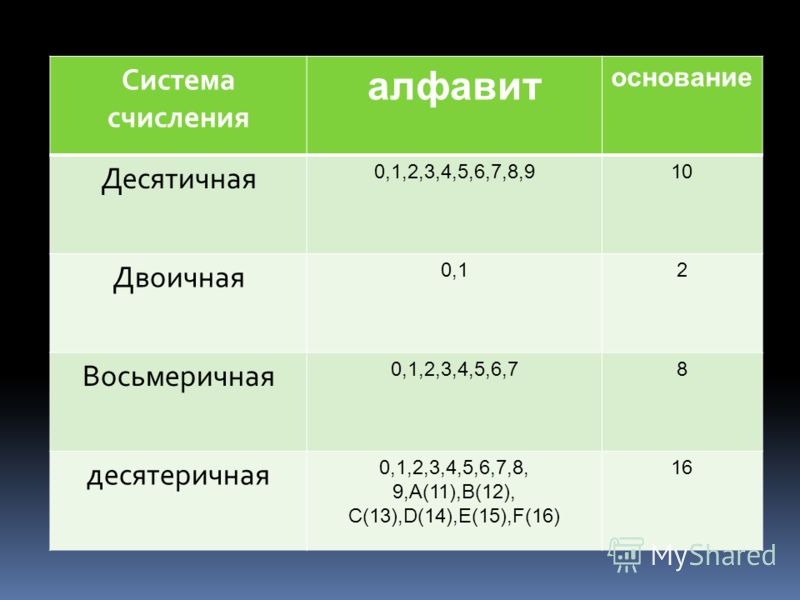


 (1′)
(1′)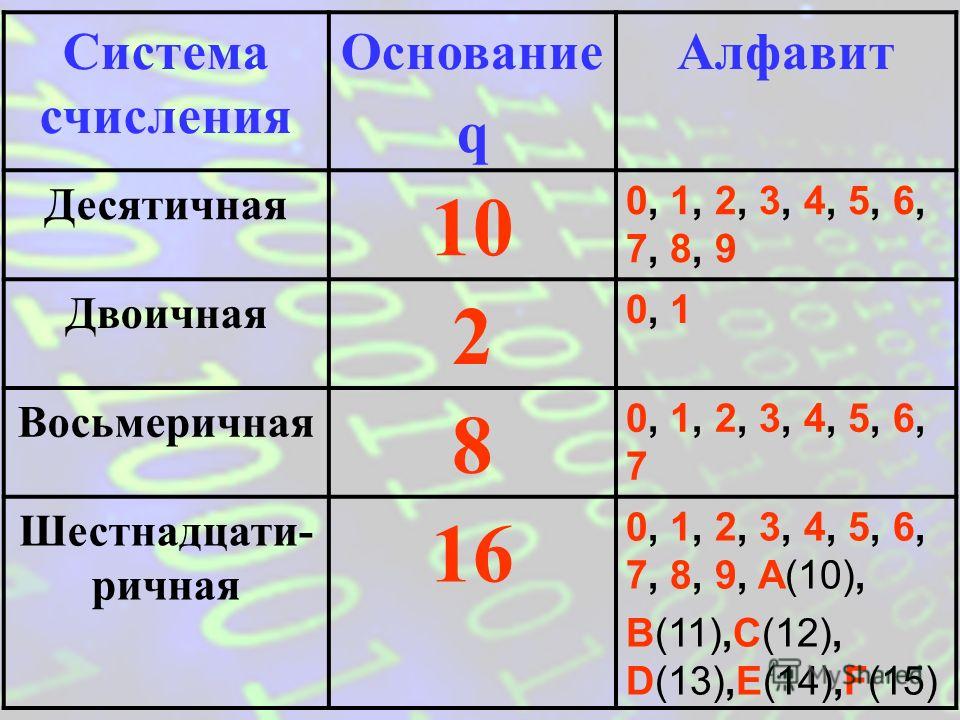

 1515/LINGTY.2006.002, S2CID 20412558
1515/LINGTY.2006.002, S2CID 20412558