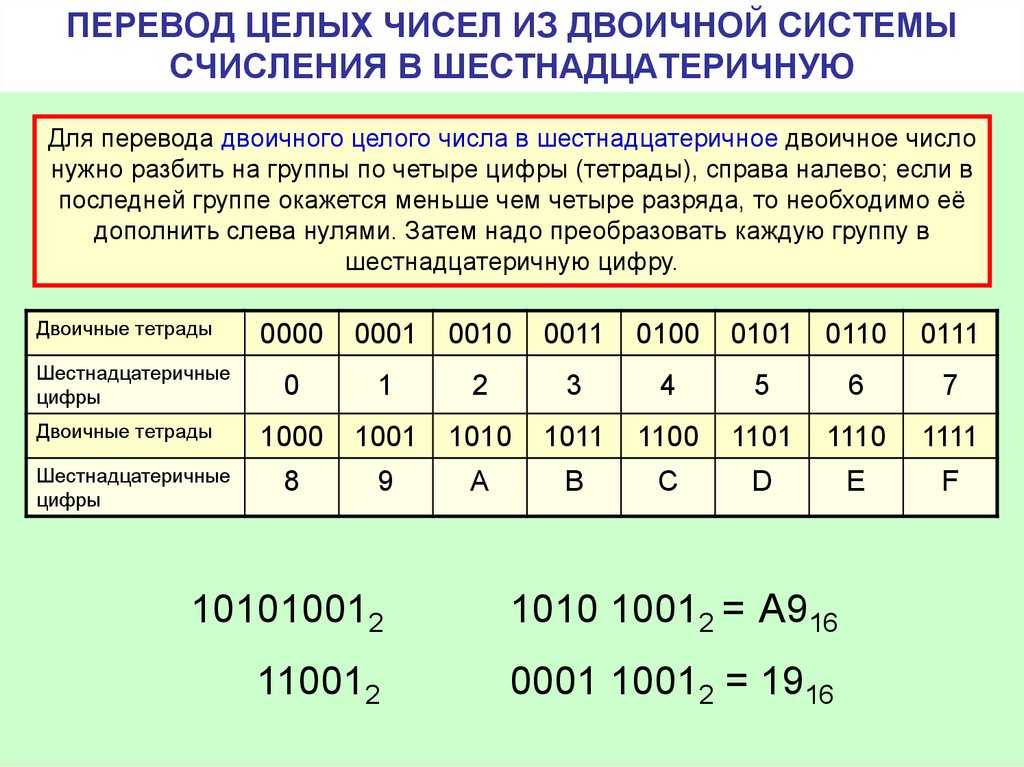
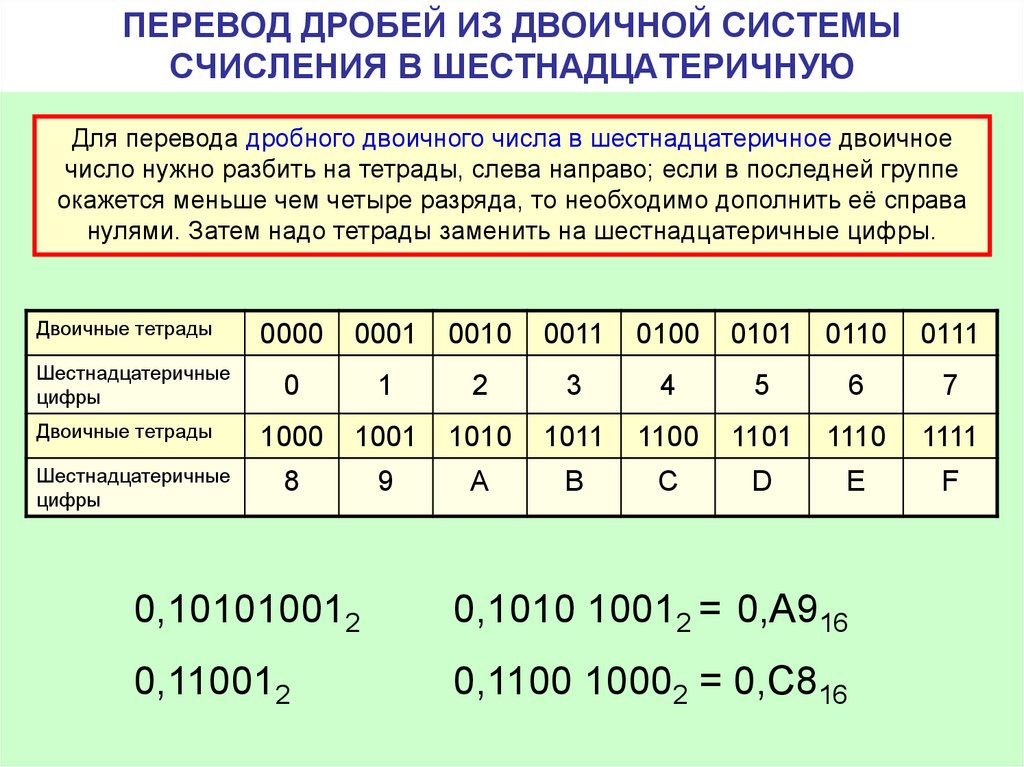
Восьмеричная и шестнадцатеричная системы счисления. «Компьютерные» системы счисления
Технологическая карта урока
Учитель: Чупров Димитрий Иванович
Предмет: Информатика
Класс: 8
УМК:
Учебник для 8 класса Информатика
Автор: Л.Л. Босова. М.: БИНОМ Лаборатория знаний, 2016
Тип урока: урок освоения новых знаний
Тема урока: «Восьмеричная и шестнадцатеричная системы счисления. «Компьютерные» системы счисления »
Цель урока: знакомство с системами счисления, показать практическую значимость различных видов систем счисления.
Задачи:
Обучающие:
познакомить учащихся с понятием «системы счисления», с позиционными и непозиционными системами счисления;
сформировать навыки счета в восьмеричной и шестнадцатеричной системах счисления;
Развивающие:
способствовать развитию логического и алгоритмического мышления;
воздействие на психологические процессы: внимание, восприятие, память.
Воспитательные:
формировать познавательную и творческую активность учащихся, воспитывать у них чувство ответственности, коммуникативность, толерантность, волю и настойчивость.
Планируемые результаты:
Предметные:
— учащиеся узнают: понятия «системы счисления», «позиционные системы счисления», «непозиционные системы счисления», правила записи чисел в различных системах счисления;
— учащиеся научатся: применять правила записи и счета чисел в различных системах счисления.
Личностные:
Будут сформированы: умения слушать и слышать собеседника, высказывать свое мнение, анализировать свои возможности в достижении планируемых результатов. Доносить свою позицию до других, владея приёмами монологической и диалогической речи. Понимать другие позиции (взгляды, интересы), осознание смысла учения и понимание личной ответственности за будущий результат;
Понимать другие позиции (взгляды, интересы), осознание смысла учения и понимание личной ответственности за будущий результат;
Метапредметные:
— регулятивные: должны уметь определять цель своей деятельности, составлять план действий и вносить в случае необходимости дополнения и коррективы в план и способ действия для достижения цели, контролировать свою деятельность в процессе достижения результата;
— коммуникативные: умение вступать в диалог, умение строить устные высказывания с использованием математического языка.
— познавательные: умение формулировать проблему и решать ее, умение строить логическую цепь размышлений, умение структурировать найденную информацию в нужной форме, умение устанавливать причинно-следственные связи, умение делать выводы.
Методы обучения: частично-поисковый.
Средства обучения: компьютер, проектор, учебник, карточки.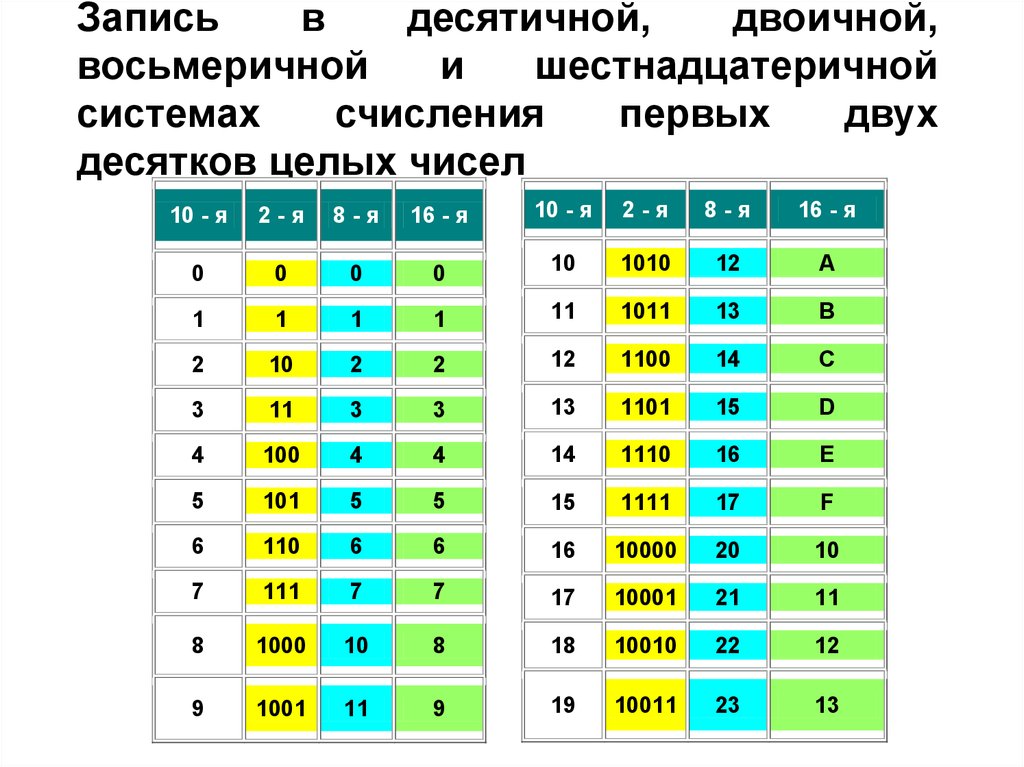
Формы организации познавательной деятельности: фронтальная, индивидуальная, работа в парах.
Дидактическая структура урока | Деятельность учителя | Деятельность учеников | Формируемые УУД |
1. Мотивация к учебной деятельности (3 мин) Цель: включение в учебную деятельность на личностно-значимом уровне(«надо-хочу-могу») | Вход в урок: Здравствуйте, ребята. − Как вы думаете, сколько будет два плюс два? — Совершенно верно, каждый из вас прав. Сегодня у нас урок открытия новых знаний. Вспомните, как происходит познание нового — Именно так. − И я желаю вам удачи в поиске новых знаний, в этом вам обязательно помогут ранее изученные знания! | Дети отвечают «4» , некоторые задумываются, и ещё некоторые отвечают 11 или 10. Задают вопрос, в какой системе счисления (для этого нам необходимо повторить уже известное; правильно определить то, что мы не знаем; найти способ преодоления затруднения, сформулировав новый способ (алгоритм, формулу, правило), и научиться его применять.) | Личностные: − самоопределение − смыслообразование Коммуникативные: − планирование учебного сотрудничества с учителем и сверстниками |
2. Актуализация знаний и пробное учебное действие(6 мин) Цель: готовность мышления и осознание потребности к построению нового способа действия | Подводящий диалог: Ребята, у меня в руках несколько карандашей, сколько их? Запишите это значение на доске. Как еще можно представить данную информацию? К какому типу информации относится информация, записанная на доске? Что вы использовали для представления числовой информации? Затруднение: Назовите число, показанное на доске(XLCCIV) Как вы думаете, есть ли другие виды представления числовой информации? Сколько будет 4*4 ? Как еще можно представить данную информацию? Как вы думаете, есть ли другие виды представления числовой информации? | Ответы учащихся: — восемь — 8 — VIII, ||||||||| и др. — к числовой — Арабские цифры, римские цифры, палочки и др. Не могут назвать число — Не знаем, наверное есть и др. -16 -XVI -шестнадцать | Познавательные: − Умение анализировать, сравнивать, обобщать, − умение использовать знаково−символических средства Регулятивные: −осознание того, что уже усвоено и что еще подлежит усвоению − фиксирование индивидуального затруднения в пробном действии − волевая саморегуляция в ситуации затруднения |
3. Цель: определение причины и места затруднения | Почему вы не можете однозначно ответить на последние два вопроса? | — Нам не хватает имеющихся знаний о способах записи числовой информации | Познавательные: − постановка и формулирование проблемы − структурирование знаний самостоятельное выделение и формулирование познавательной цели − выбор наиболее эффективных способов решения задач Регулятивные: − умение планировать, прогнозировать |
4. Построение проекта выхода из затруднения (2 мин) Цель: постановка цели учебной деятельности, выбор способа и средств ее реализации | Сформулируйте цель вашей деятельности, которую вы могли бы поставить перед собой сегодня на уроке. Сформулируйте тему урока Корректирует формулировку темы: «Восьмеричная и шестнадцатеричная системы счисления» | — узнать какие есть способы записи чисел, как их правильно записывать и читать ««Восьмеричная и шестнадцатеричная системы счисления» | Познавательные: − структурирование знаний самостоятельное выделение и формулирование познавательной цели − выбор наиболее эффективных способов решения задач Регулятивные: − умение планировать, прогнозировать |
5. Изучение нового материала (15 минут) Цель: Построение и фиксация нового знания Физкультминутка | Что необходимо знать для записи числа? Вы абсолютно правы. Давайте обратимся к учебнику и выясним, как называются знаковые системы для записи числовой информации. Вывешивает определение на доске. Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения. Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310. Физкультминутка | — Какие знаковые системы можно использовать. Знакомятся с определением «Системы счисления». Проговаривают во внешней речи. 8*8*8 = 512 8*8 = 64 * 0 = 0 6*8 = 48 Получают 563 Физкультминутка | Познавательные: − выдвижение гипотез и их обоснование − установление причинно−следственных связей − самостоятельное создание способов решения проблем творческого и поискового характера на основе метода рефлексивной самоорганизации − построение логической цепи рассуждений, доказательство Регулятивные: − познавательная инициатива Личностные: − осознание ответственности за общее дело Коммуникативные: − выражение своих мыслей с достаточной полнотой и точностью − формулирование и аргументация своего мнения и позиции в коммуникации − достижение договорённостей и согласование общего решения |
6. (7 минут) | Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…,9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита. Как будут называться цифры? 3AF16 = 3 • 162 + 10 • 161 + 15 • 160 = 768 + 160 + 15 = 94310. | A , B , C, D, E, F 16*16=256 Получают 943 | Познавательные: − использование знаково−символических средств − выполнение действий по алгоритму − осознание и произвольное построение речевого высказывания − построение логической цепи рассуждений, доказательство Коммуникативные: − использование критериев для обоснования своего суждения − управление поведением партнёра − выражение своих мыслей с достаточной полнотой и точностью Личностные: − осознание ответственности за общее дело |
6. | Работа по группам. Класс делится на 2 группы. От каждой группы один человек решает за доской. Остальные решают коллективно. Какая группа выполнит задание быстрее и верно, та получает 5 баллов. Задания 14 на странице 15 | Выполняют задание самостоятельно в тетради. Выполняют самопроверку по образцу. Называют место своего затруднения, причину исправляют ошибки. Выполняют самооценку | Познавательные: − анализ, синтез, сравнение, обобщение, аналогия, классификация − использование знаково−символических средств − выполнение действий по алгоритму − доказательство Регулятивные: − контроль − коррекция − оценка − волевая саморегуляция в ситуации затруднения |
7. | А сейчас проверим, как вы усвоили правила выполнения арифметических действий в двоичной системе счисления. Будем решать задания на листочках, а затем, используя программу Калькулятор, проверять правильность выполнения. Заданий всего пять. За верный результат на листочках ставите себе 1, за неверный – 0. Подсчитав полученные баллы, вы поставите себе оценку за урок. | Учащиеся решают задания на листочках, затем проверяют правильность решения, используя программу Калькулятор. Выставляют себе оценку. Листочки сдают учителю. | Познавательные: − анализ, синтез, сравнение, обобщение, аналогия, классификация − моделирование, преобразование модели − установление причинно−следственных связей − выведение следствий − выполнение действий по алгоритму Личностные: − нравственно−этическое оценивание усваиваемого содержания Коммуникативные: − постановка вопросов |
8. | Сегодня на уроке мы научились выполнять арифметические действия в двоичной системе счисления. Что было для вас необычно? Что вы узнали нового и интересного? Какие вопросы и трудности у вас возникали? Выставление оценок за урок. Домашнее задание: вопросы к параграфу 1.1 и решить задания №13,14 стр 15 | Учащиеся отвечают на вопросы, дают оценку урока, записывают домашнее задание. | Познавательные: − рефлексия способов и условий действия − контроль и оценка процесса и результатов деятельности Личностные: − самооценка на основе критерия успешности − адекватное понимание причин успеха/неуспеха в учебной деятельности |
Восьмеричная и шестнадцатеричные системы счисления.
 Компьютерные системы — презентация на Slide-Share.ru 🎓
Компьютерные системы — презентация на Slide-Share.ru 🎓1
Первый слайд презентации
Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления. Правило перевода целых десятичных чисел в систему счисления с основанием q.
Изображение слайда
2
Слайд 2
Цели урока :
образовательные – выяснить, почему именно двоичная система счисления используется в компьютере, показать связь между двоичной, восьмеричной и шестнадцатеричной системами счисления; сформировать знания и умения перевода небольших десятичных и двоичных чисел в восьмеричную и шестнадцатеричную системы счисления.
развивающие – умение анализировать любую позиционную систему счисления как знаковую систему;
воспитательные – понимание роли фундаментальных знаний как основы современных информационных технологий.
Изображение слайда
3
Слайд 3
Задачи: 1) рассмотрение восьмеричной системы счисления как знаковой системы; 2) рассмотрение правила перевода целых десятичных чисел в восьмеричную систему счисления 3) рассмотрение шестнадцатеричной системы счисления как знаковой системы; 4) рассмотрение правила перевода целых десятичных чисел в шестнадцатеричную систему счисления; 5) рассмотрение правила перевода двоичных чисел в шестнадцатеричную и восьмеричную системы счисления; 6) характеристика двоичной, восьмеричной и шестнадцатеричной систем счисления с точки зрения их использования в компьютерной технике.
Изображение слайда
4
Слайд 4
a n–1 a n–2 …a 1 a 0 = a n–1 8 n–1 +a n–2 8 n–2 +…+a 0 8 0
Пример : 1063 8 =1 8 3 +0 8 2 +6 8 1 +3 8 0 =563 10.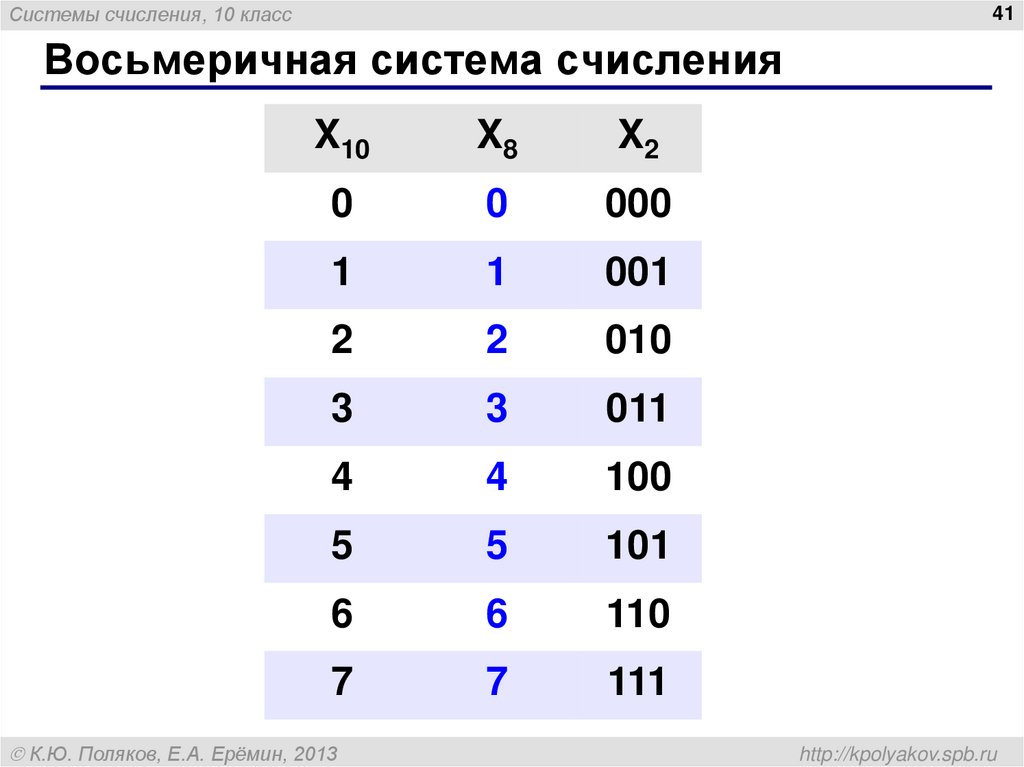 Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Изображение слайда
5
Слайд 5
Основание : q = 16.
Алфавит : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система счисления
Переведём десятичное число 154 в шестнадцатеричную систему счисления:
154 10 = 9А 16
154
16
9
-144
10
(А)
9
16
0
3АF 16 =3 16 2 +10 16 1 +15 16 0 =768+160+15=943 10.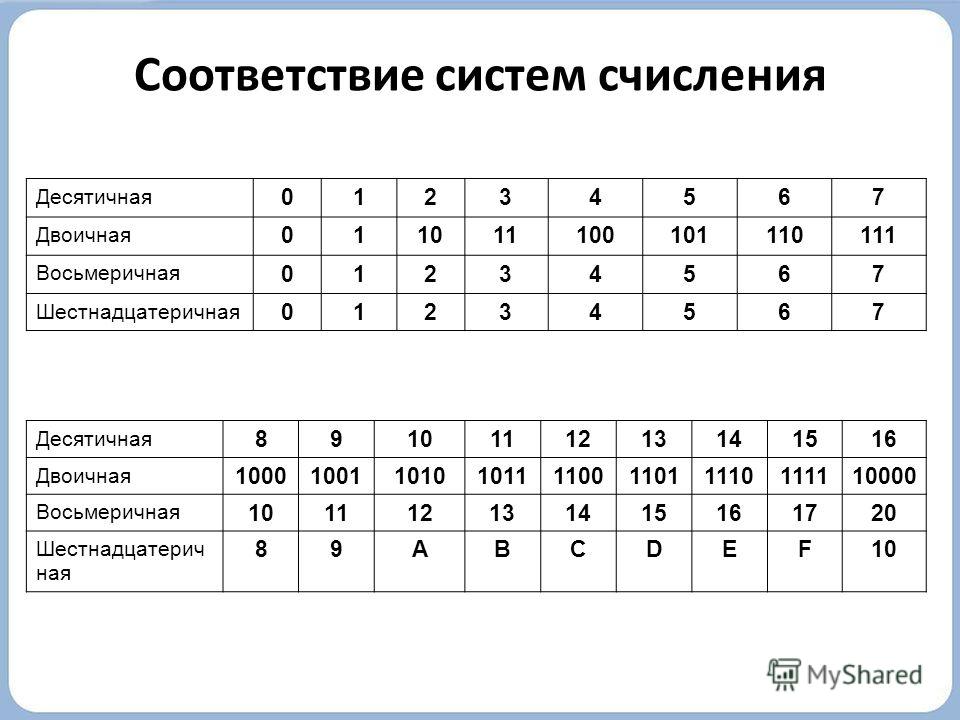
Изображение слайда
6
Слайд 6
1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю; 2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления; 3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка. Цифровые весы Правило перевода целых десятичных чисел в систему счисления с основанием q
Изображение слайда
7
Слайд 7
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16 Десятичная система Двоичная система Восьмеричная система Шестнадцатеричная система 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 17 10001 21 11 18 10010 22 12
Изображение слайда
8
Слайд 8
Двоичная арифметика Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения: + 0 1 0 0 1 1 1 10 0 1 0 0 0 1 0 1
Изображение слайда
9
Слайд 9
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике, так как:
двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями;
представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных. Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.
Изображение слайда
10
Последний слайд презентации: Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы
Задание Написать конспект к данным темам презентации, фото отправить в беседу в ВК (просьба нумеровать страницы тетради и на первой странице на полях оставлять свою фамилию). Читать с. 9-12 учебника.
Изображение слайда
Презентация по информатике на тему Компьютерные системы счисления доклад, проект
«Компьютерные» системы счисления
От системы счисления, используемой в компьютере, зависят объем памяти, скорость вычислений и сложность выполнения алгоритмов. В компьютерах используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
В компьютерах используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
В жизни мы в основном пользуемся десятичной системой счис- ления (арабская нумерация).
Начало этой системе счисления было положено в Вавилоне и Древнем Египте. Цифры 1234567890 сложились в Индии около 400 г. н.э. Арабы стали пользоваться подобной нумерацией около 800 г. н.э. после перевода работ математика Мухаммеда Аль Хорезми. Цифры арабской нумерации уже были немного похожи на наши:
Примерно в 1200 г. н.э. европейцы, заимствовав нумерацию у арабов, называли ее арабской. Это исторически неправильное название удерживается и поныне.
Форма индийских цифр претерпевала многообразные изменения, форма, которой мы пользуемся сейчас, установилась в XVI в.
Карл 12
В компьютерах десятичная система счисления используется для ввода и вывода информации.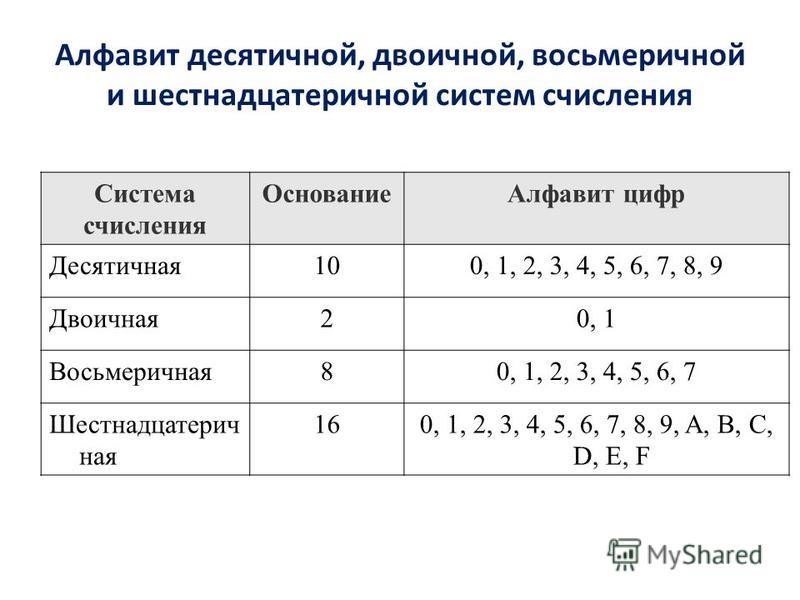
В 1703 г. немецкий математик Лейбниц (1646—1716) ввел двоичную систему счисления 1936 г. американский инженер и математик предложил использовать ее для конструирования электронных схем.
В настоящее время двоичная система счисления является стандартной при создании компьютеров, т.к. в ней наиболее просто выполняются арифметические и логические операции.
Восьмеричная и шестнадцатеричная системы счисления используются в компьютере для составления программ на языке машинных кодов. Шведский король Карл XII в 1717 г. увлекся восьмеричной системой и собирался ввести ее как общегосударственную.
Шестнадцатеричная система счисления используется и сейчас: столовые сервизы на 12 персон, в пачке 12 фломастеров, в году 12 месяцев и прочее.
В компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ перед другими системами:
• двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
• представление информации посредством только двух состояний надёжно и помехоустойчиво;
• двоичная арифметика наиболее проста;
• существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Оперативная память компьютера состоит из ячеек, в каждой из которых может храниться 8 битов информации, т. е. в каждой ячейке может храниться 8 разрядов двоичного числа. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот нее разряд числа, а запятая находится справа после младшего разряда, т. е. вне разрядной сетки. Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов).
Пример: Число А2 = 111100002 будет храниться в ячейке памяти следующим образом:
111100000
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целого неотрицательного числа. Минимальное число соответствует восьми нулям, хранящимся в восьми ячейках памяти, и равно 0. Максимальное число соответствует восьми единицам, хранящимся в ячейках памяти, и равно 255. Таким образом, диапазон изменения целых неотрицательных чисел от 0 до 255.
Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное, записывается 1), а остальные 15 позиций само число.
Пример: Отрицательное число — 200210 = -111110100102 будет записано в 16-разрядном представлении следующим образом:
1000011111010010
Максимальное положительное число (с учетом выделения одного разряда на знак) для данного формата представления равно:
А=215-1=32767
Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций.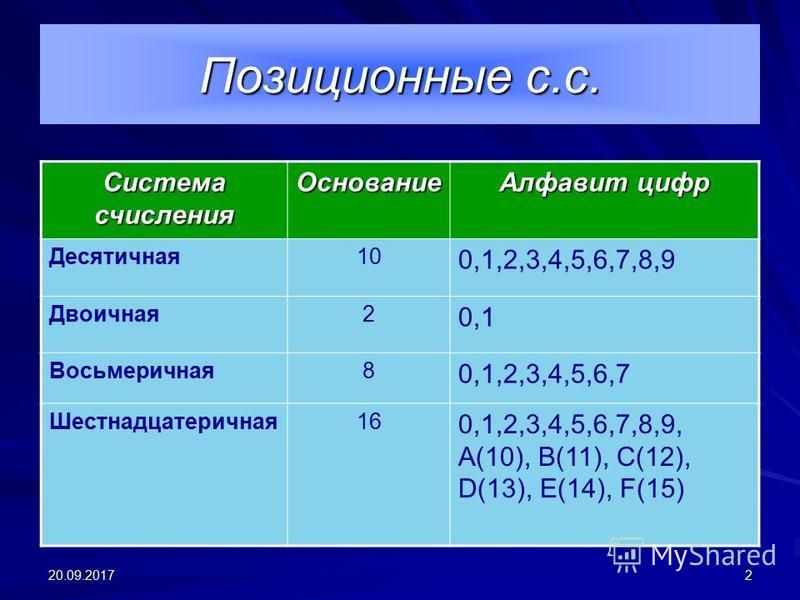 Недостатком является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые дробные, так и очень большие числа.
Недостатком является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые дробные, так и очень большие числа.
Для представления чисел в диапазоне от очень маленьких дробей до очень больших чисел с высокой точностью используется формат с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Число в форме с плавающей запятой занимает в памяти компьютера четыре (число обычной точности) или восемь (число двойной точности) байтов.
Скачать презентацию
Компьютерные системы счисления 101: Двоичные и шестнадцатеричные преобразования
Главная/Блог/Компьютерные системы счисления 101: Двоичные и шестнадцатеричные преобразования
01 октября 2020 г. — 9 мин чтения
Аманда Фосетт
Когда мы печатаем слова на компьютере переведет их в числа. На самом деле для компьютера вся информация записывается в виде последовательности единиц и нулей. Компьютерные системы счисления — это то, как мы представляем числа в архитектуре компьютерной системы.
На самом деле для компьютера вся информация записывается в виде последовательности единиц и нулей. Компьютерные системы счисления — это то, как мы представляем числа в архитектуре компьютерной системы.
Системы счисления — одна из самых фундаментальных концепций, которую должны изучить специалисты по информатике. Это важный шаг для всех, кто хочет стать компьютерщиком или программистом.
Сегодня мы познакомим вас с системами счисления, необходимыми для компьютерного ученого. Мы углубимся в двоичную и шестнадцатеричную системы счисления.
Сегодня мы узнаем:
- Что такое система счисления в информатике?
- Что такое двоичная система счисления?
- Что такое шестнадцатеричная система счисления?
- Как преобразовать между двоичным и шестнадцатеричным
- Что такое восьмеричная система счисления?
- Что узнать дальше
Сделайте первый шаг к тому, чтобы стать компьютерщиком
Узнайте, как представлять числа в двоичном формате, и поймите, как числа хранятся и представляются в компьютерах. Никаких знаний в области программирования не требуется!
Никаких знаний в области программирования не требуется!
Системы счисления для компьютерных ученых
Что такое система счисления в информатике?
Люди давно умеют считать. Для этого мы используем системы, которые связывают уникальные символы с конкретными значениями. это называется система счисления , и это метод, который мы используем для представления и обработки чисел
Система счисления должна иметь уникальные символы для каждого значения, быть последовательной, предоставлять сопоставимые значения и быть легко воспроизводимой.
Вероятно, вы лучше всего знакомы с десятичной системой , которая лежит в основе того, как люди считают. Десятичная система имеет основание 10 , потому что она предоставляет 10 символов для представления всех чисел:
Люди используют десятичную систему, потому что у нас есть 10 пальцев, чтобы считать, но у машин нет такой роскоши. Итак, мы создали другие системы счисления, выполняющие те же функции. Компьютеры представляют информацию не так, как люди, поэтому нам нужны разные системы для представления чисел.
Итак, мы создали другие системы счисления, выполняющие те же функции. Компьютеры представляют информацию не так, как люди, поэтому нам нужны разные системы для представления чисел.
Компьютеры поддерживают следующие системы счисления:
- Двоичная
- Окталь
- Десятичный
- Шестнадцатеричный
Знакомство с двоичной системой счисления
Компьютер использует бит для представления информации. Бит — это самая основная единица хранения данных в компьютере. Важный компонент компьютеров называется транзистором . Подобно выключателю света, транзистор либо позволяет, либо предотвращает протекание тока. Итак, у него всего два состояния: на и на .
Каждое число в компьютере представляет собой электрический сигнал. На заре компьютеров электрические сигналы представлялись в состоянии «включено» (отрицательный заряд) и в состоянии «выключено» (положительный заряд). Это формирует своего рода двоичный переключатель.
Это формирует своего рода двоичный переключатель.
Эти два состояния могут быть представлены одним из двух символов: 1 и 0 . Это означает, что двоичная система счисления имеет основание 2. Для представления каждого числа нужны только символы.
Базовые цифры для двоичной системы просты: 0 соответствует низкому уровню, а 1 соответствует высокому уровню.
Вместо того, чтобы представлять числа как отдельные единицы (например, число 10 или 400), мы используем группы единиц и нулей. Например, вот как это выглядит, когда компьютер считает от 0 до 10:
Это называется двоичной системой счисления. Каждая двоичная цифра обозначается как бит . Например, 011001100110 состоит из 4 битов: 000, 111, 111 и 000. Когда дело доходит до размещения значений битов (то есть цифр) в этой системе, мы размещаем значения, соответствующие возрастающим степеням числа 2, справа налево. оставил.
Крайний правый бит называется младшим битом (LSB) , а крайний левый бит — старшим значащим битом (MSB) .
Вы можете манипулировать битами слева и справа с помощью побитовых операторов для эффективного изменения значения числа на уровне машинного кода.
Преобразование из десятичной в двоичную
Теперь, когда мы знаем основы двоичной системы, давайте узнаем, как мы будем преобразовывать десятичную в двоичную. Начнем с преобразования двоичного кода в десятичный.
Мы знаем, что в двоичной системе есть разрядные значения степеней двойки. Эти значения являются весами цифр (0 или 1) в этих разрядах. Вот как это работает:
- Мы умножаем каждую цифру на ее вес (ее положение умножается на 2)
- Суммируем их все, чтобы получить десятичное число
Итак, возьмем двоичное число 11111010 и переведем его в десятичную систему счисления.
1 из 4
1 из 4
1 из 4
1 из 4
А теперь попробуем наоборот. Как преобразовать десятичное число в двоичное? Одним из способов сделать это является повторное деление, которое является удобным сокращением.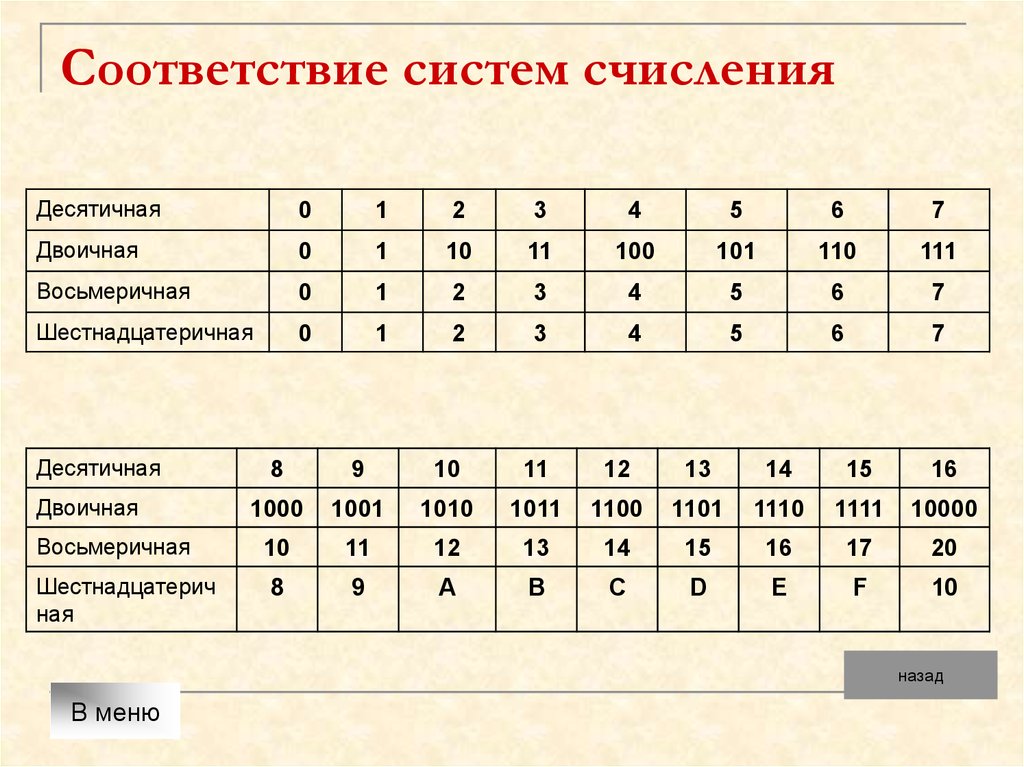
Итак, возьмем число 19. Начнем с деления его на два и записи остатка. Когда мы делим 19 на 2, мы получаем 9 с остатком 1.
Затем мы берем 9 и делим его на 2, что дает нам результат 4 с остатком 1. Этот процесс продолжается до тех пор, пока мы не достигнем нуля. Остатки, которые мы собрали, образуют наше двоичное число!
Многократное деление на 2 и отслеживание остатков — это быстрый способ преобразования десятичного числа в двоичное!
Попробуйте сами!
Каково двоичное представление числа 94?
A)
1001110
B)
0111101
C)
101110
Вопрос
1
из
из
из
20 0003
. 0047
0047
Теперь, когда мы немного узнали о двоичной системе, давайте узнаем о другой распространенной системе, используемой компьютерами: , шестнадцатеричной системе счисления .
Двоичные числа просты для компьютеров, но не так просты для понимания людьми. А когда вы работаете с большими числами, становится трудно писать без ошибок. Итак, чтобы решить эту проблему, мы можем организовать двоичные числа в группы по четыре бита, образуя шестнадцатеричную систему счисления.
Шестнадцатеричная система представляет собой более компактный способ представления чисел на компьютере, поскольку для представления значения цифры требуется всего 4 бита.
Шестнадцатеричная система (часто называемая «шестнадцатеричной») состоит из 16 символов , поэтому ее основание равно 16. Шестнадцатеричная система использует 10 чисел десятичной системы и шесть дополнительных символов, A, B, C, D , E и F.
Значения разрядов в шестнадцатеричном формате представляют собой степени 16. Давайте посмотрим, каким будет шестнадцатеричное число XYZ в десятичном виде. Как вы можете видеть ниже, шестнадцатеричным числам предшествует #, чтобы указать, что они имеют основание 16.
Давайте посмотрим, каким будет шестнадцатеричное число XYZ в десятичном виде. Как вы можете видеть ниже, шестнадцатеричным числам предшествует #, чтобы указать, что они имеют основание 16.
Изучите основы информатики.
Познакомьтесь с системами счисления, не просматривая видео или документацию. Текстовые курсы Educative легко просматриваются и включают живую среду кодирования, что делает обучение быстрым и эффективным.
Системы счисления для компьютерных ученых
Преобразование между двоичной и шестнадцатеричной системами счисления
Теперь, когда мы понимаем как двоичную, так и шестнадцатеричную системы счисления, давайте узнаем, как преобразовать двоичное число в шестнадцатеричное число. Начнем с двоичного в шестнадцатеричный.
Мы сгруппируем двоичные цифры в наборы по четыре (начиная справа). Затем мы заменяем каждый квартет соответствующим шестнадцатеричным представлением.
1 из 4
1 из 4
1 из 4
1 из 4
9 1
из 4 для двоичного числа! Давайте рассмотрим пример.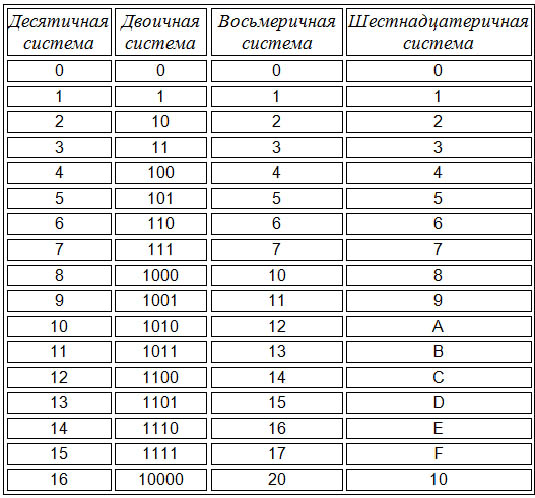 Ниже мы расширяем каждую шестнадцатеричную цифру, заменяя ее эквивалентным двоичным квартетом.
Ниже мы расширяем каждую шестнадцатеричную цифру, заменяя ее эквивалентным двоичным квартетом.
1 из 3 93 = 823=8.
Мы используем восемь основных символов для восьмеричной системы, которые заимствованы из десятичной системы. Двоичные триплеты могут иметь значения в диапазоне от 0–70 до 70–7.
Итак, значения разрядов будут возрастать в степенях числа 888 справа налево.
Чтобы преобразовать из двоичного числа в восьмеричное , мы следуем этой базовой методике:
- Группируем двоичное число в наборы по три (аналогично тому, что мы делали с шестнадцатеричным)
- Довести каждую группу цифр до числа, кратного трем, путем добавления нулей
- Напишите соответствующий восьмеричный символ под каждой группой
- Теперь у вас будет восьмеричное число .
Преобразование восьмеричного числа в двоичное аналогично, но немного проще:
- Напишите двоичное представление для каждой восьмеричной цифры
- Соедините эти числа вместе
- У вас не будет двоичного числа
Что узнать дальше
Поздравляем! Теперь у вас есть основательное введение в системы счисления для информатики.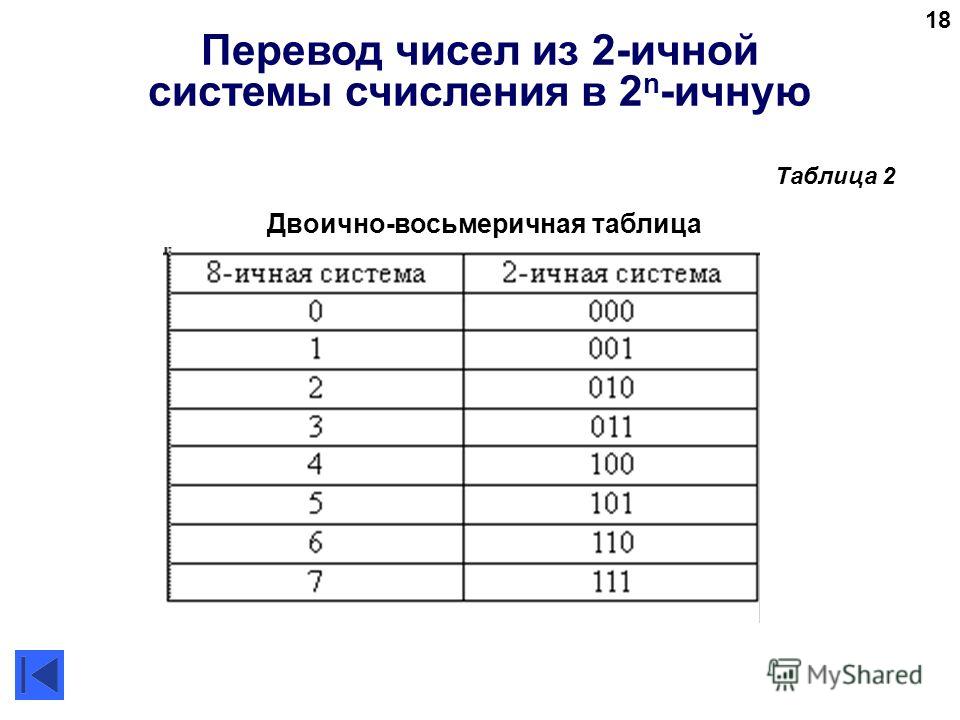 Вы сделали свой первый фундаментальный шаг в мир компьютерного программирования. Однако предстоит еще многому научиться. Ваши следующие шаги — научиться:
Вы сделали свой первый фундаментальный шаг в мир компьютерного программирования. Однако предстоит еще многому научиться. Ваши следующие шаги — научиться:
- Как создать свою систему счисления
- Двоичные операции
- Двоичные числа со знаком
- Представление с фиксированной точкой
- Основы битов и байтов
- ASCII-код
- Юникод
- Основы компьютерной памяти
Как только вы изучите эти темы, вы станете на путь понимания компьютеров! Чтобы начать работу с этими понятиями и более подробно изучить двоичные, шестнадцатеричные и восьмеричные числа, ознакомьтесь с курсом 9 Educative.0009 Системы счисления для компьютерных ученых , который охватывает все это и многое другое.
Вы познакомитесь с основными системами счисления и узнаете, как представлять и обрабатывать положительные, отрицательные и дробные числа в двоичном формате. Никаких знаний в области программирования не требуется, так что начните сегодня и начните свою карьеру в качестве компьютерного ученого.
Приятного обучения!
Продолжить чтение по информатике
- Руководство для начинающих по компьютерам и программированию
- Научитесь программировать: руководство для начинающих по программированию и синтаксису
- Руководство для начинающих по 5 самым популярным языкам программирования
НАПИСАЛ Аманда Фосетт
Присоединяйтесь к сообществу, насчитывающему более 1,4 миллиона читателей. Бесплатное электронное письмо раз в два месяца с обзором лучших статей и советов по программированию на сайте Educative.
Десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления, двоичная арифметика
Когда мы набираем буквы или слова, компьютер переводит их в числа, поскольку компьютеры могут понимать только числа. Компьютер может понять позиционную систему счисления, в которой есть только несколько символов, называемых цифрами, и эти символы представляют разные значения в зависимости от позиции, которую они занимают в числе.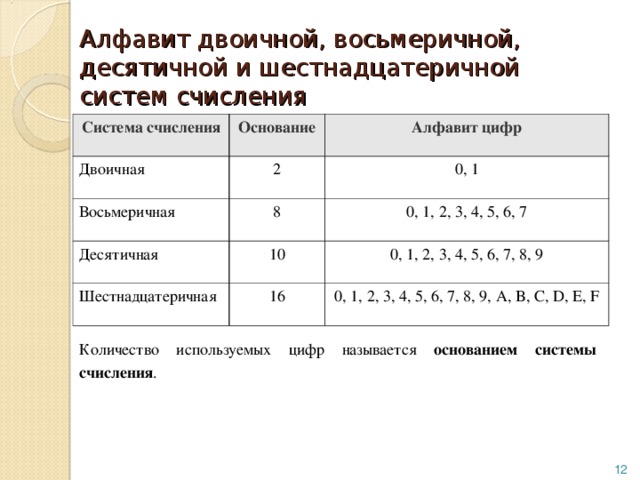
Значение каждой цифры в числе можно определить с помощью –
- Цифра
- Позиция цифры в числе
- Основание системы счисления (где основание определяется как общее количество цифр, доступных в системе счисления)
Десятичная система счисления
В повседневной жизни мы используем десятичную систему счисления. Десятичная система счисления имеет основание 10, так как использует 10 цифр от 0 до 9. В десятичной системе счисления последовательные позиции слева от десятичной точки представляют единицы, десятки, сотни, тысячи и т. д.
Каждая позиция представляет определенную силу основания (10). Например, десятичное число 1234 состоит из цифры 4 в позиции единиц, 3 в позиции десятков, 2 в позиции сотен и 1 в позиции тысяч. Его значение можно записать как
(1 x 1000)+ (2 x 100)+ (3 x 10)+ (4 x l)
(1 x 10 3 )+ (2 x 10 2 )+ (3 x 10 1 )+ (4 x l0 0 )
1000 + 200 + 30 + 4
1234
Как программист или ИТ-специалист, вы должны понимать следующие системы счисления, которые часто используется в компьютерах.
| С.№. | Система счисления и описание |
| 1 | Двоичная система счисления
Основание 2. Используемые цифры: 0, 1 |
| 2 | Восьмеричная система счисления
Основание 8. Используемые цифры: от 0 до 7 |
| 3 | Шестнадцатеричная система счисления
База 16. Используемые цифры: от 0 до 9, Используемые буквы: A-F |
Двоичная система счисления
Характеристики двоичной системы счисления следующие: −
- Используются две цифры, 0 и 1
- Также называется системой счисления с основанием 2
- Каждая позиция в двоичном числе представляет собой 0 степень основания (2). Пример 2 0
- Последняя позиция в двоичном числе представляет собой степень основания (2) x .
 Пример 2 x где x представляет последнюю позицию — 1.
Пример 2 x где x представляет последнюю позицию — 1.
Пример
Двоичный номер: 10101 2
Расчет десятичного эквивалента −
| Шаг | Двоичный номер | Десятичное число |
| Этап 1 | 10101 2 | ((1 x 2 4 ) + (0 x 2 3 ) + (1 x 2 2 ) + (0 x 2 1 ) + (1 x 2 0 )) 10 |
| Этап 2 | 10101 2 | (16 + 0 + 4 + 0 + 1) 10 |
| Этап 3 | 10101 2 | 21 10 |
Примечание − 10101 2 обычно записывается как 10101.
Восьмеричная система счисления
4,5,6,7 Пример 8 0
Пример 8 0 Пример
Восьмеричное число: 12570 8
Вычисление десятичного эквивалента −
| Шаг | Восьмеричный номер | Десятичное число |
| Этап 1 | 12570 8 | ((1 x 8 4 ) + (2 x 8 3 ) + (5 x 8 2 ) + (7 x 8 1 ) + (0 x 8 0 )) 67 10 |
| Этап 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Этап 3 | 12570 8 | 5496 10 |
Note − 12570 8 is normally written as 12570.
Hexadecimal Number System
Characteristics of hexadecimal number system are as follows −
- Uses 10 digits and 6 letters, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, Б, В, Г, Е, Ж
- Буквы обозначают числа, начинающиеся с 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15
- Также называется системой счисления с основанием 16 .
- Каждая позиция в шестнадцатеричном числе представляет собой 0 степень основания (16). Например, 16 0
- Последняя позиция в шестнадцатеричном числе представляет собой степень основания (16) x . Пример 16 x где x представляет последнюю позицию – 1
Пример
Шестнадцатеричный номер: 19FDE 16
Вычисление десятичного эквивалента −
| Шаг | Двоичный номер | Десятичное число | |
| Этап 1 | 19FDE 16 | ((1 x 16 4 ) + (9 x 16 3 ) + (F x 16 2 ) + (D x 16 1 ) + (E x 16 0 )) 6 7 7 | 6 |
| Этап 2 | 19FDE 16 | ((1 х 16 4 ) + (9 х 16 3 ) + (15 х 16 2 ) + (13 х 16 1 ) + (14 х 16 0 )) 10 | |
| Этап 3 | 19FDE 16 | (65536+ 36864 + 3840 + 208 + 14) 10 | |
| Этап 4 | 19FDE 16 | 106462 10 |
Примечание − 19FDE 16 обычно записывается как 19FDE.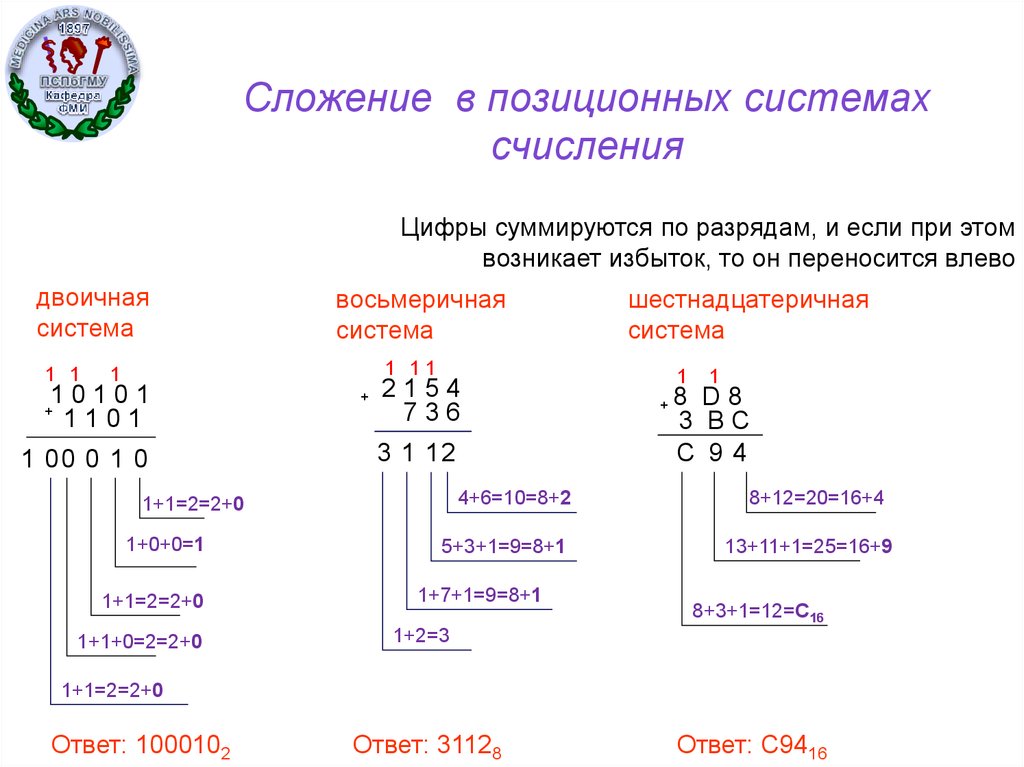
Существует множество методов и приемов, которые можно использовать для преобразования чисел из одной системы счисления в другую. В этой главе мы продемонстрируем следующее —
- Десятичная система счисления в другую базовую систему
- Другая базовая система для десятичной системы счисления
- Другая базовая система для недесятичной системы счисления
- Метод быстрого доступа — двоичный код в восьмеричный
- Метод быстрого доступа — восьмеричное преобразование в двоичное
- Метод быстрого доступа — двоичный код в шестнадцатеричный
- Метод быстрого доступа — шестнадцатеричный код в двоичный
Десятичная система счисления в другую систему счисления
Шаг 1 – Разделите десятичное число, которое необходимо преобразовать, на значение новой системы счисления.
Шаг 2 – Получите остаток от шага 1 как крайнюю правую цифру (наименее значащую цифру) нового основного числа.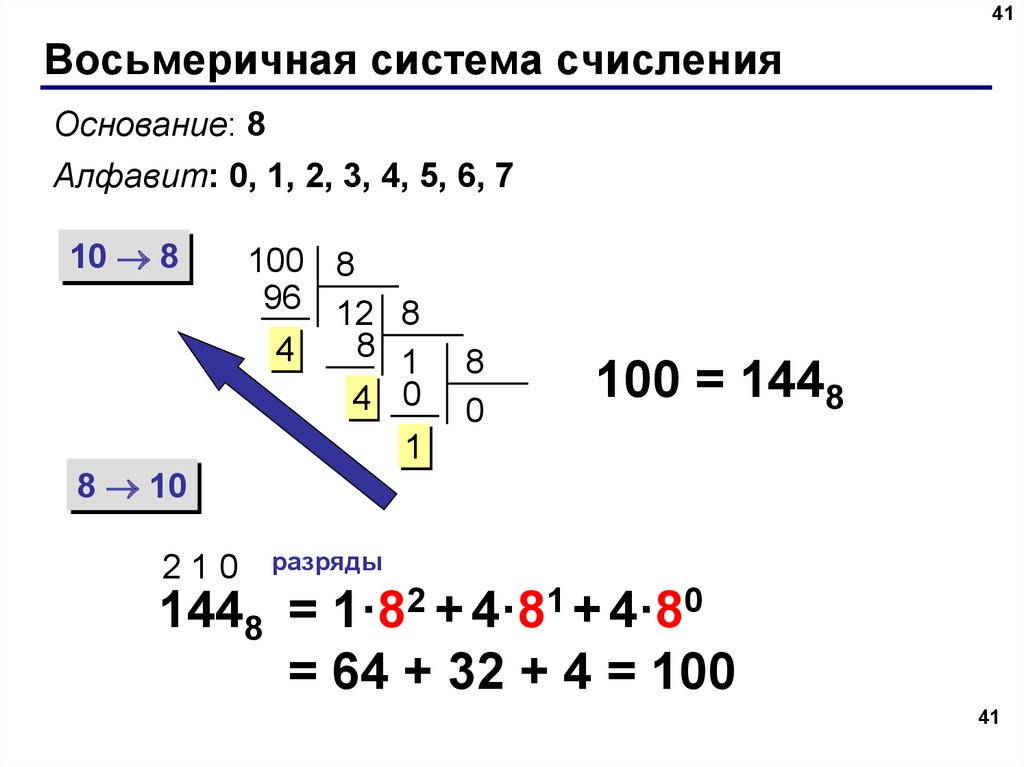
Шаг 3 – Разделите частное предыдущего деления на новое основание.
Шаг 4 − Запишите остаток от шага 3 как следующую цифру (слева) нового основного числа.
Повторяйте шаги 3 и 4, получая остаток справа налево, пока частное не станет равным нулю на шаге 3.
Последний остаток, полученный таким образом, будет старшей значащей цифрой (MSD) нового основного числа.
Пример
Десятичное число: 29 10
Вычисление двоичного эквивалента −
| Шаг | Эксплуатация | Результат | Остаток |
| Этап 1 | 29/2 | 14 | 1 |
| Этап 2 | 14/2 | 7 | 0 |
| Этап 3 | 7 / 2 | 3 | 1 |
| Этап 4 | 3 / 2 | 1 | 1 |
| Этап 5 | 1 / 2 | 0 | 1 |
Как упоминалось в шагах 2 и 4, остатки должны быть расположены в обратном порядке, чтобы первый остаток стал наименее значащей цифрой (LSD), а последний остаток стал старшей значащей цифрой (MSD).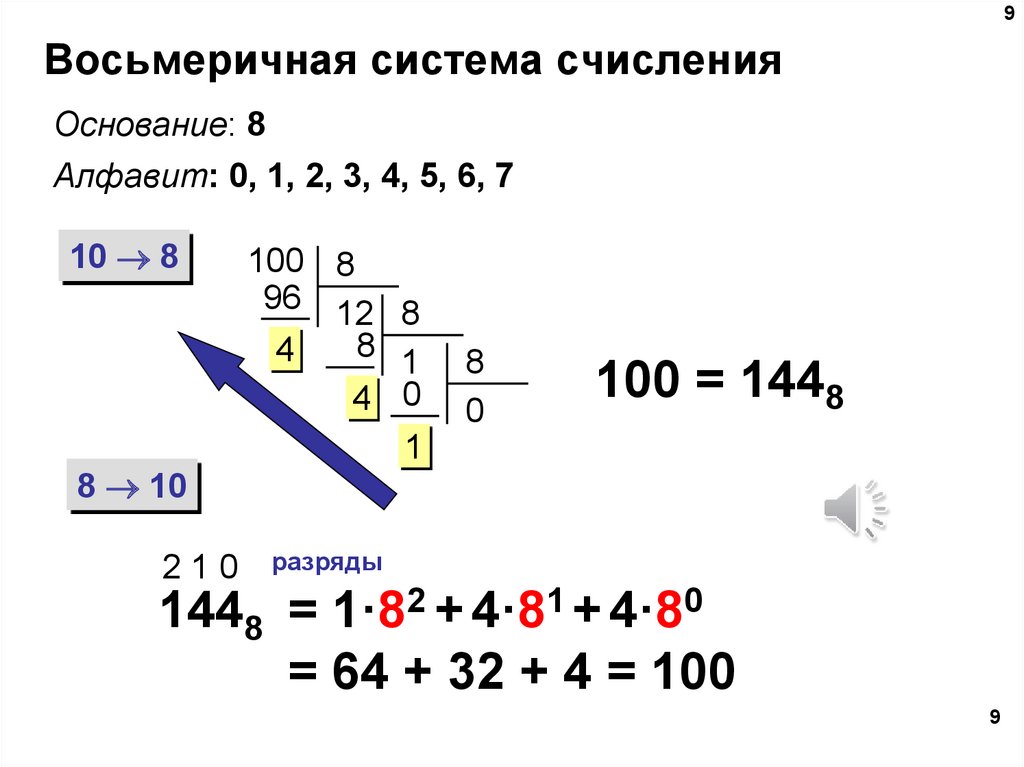
Десятичное число: 29 10 = Двоичный номер: 11101 2.
Другая базовая система в десятичную систему система счисления).
Шаг 2 – Умножьте полученные значения столбца (на шаге 1) на цифры в соответствующих столбцах.
Шаг 3 − Суммируйте произведения, рассчитанные на шаге 2. Сумма представляет собой эквивалентное десятичное значение.
Пример
Двоичный номер: 11101 2
Расчет десятичного эквивалента −
| Шаг | Двоичный номер | Десятичное число |
| Этап 1 | 11101 2 | ((1 x 2 4 ) + (1 x 2 3 ) + (1 x 2 2 ) + (0 x 2 1 ) + (1 x 2 0 )) 67 10 |
| Этап 2 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| Этап 3 | 11101 2 | 29 10 |
Двоичное число : 11101 2 = Десятичное число : 29 10
Другая базовая система в недесятичную систему
Шаг 1: преобразование исходного числа в десятичное.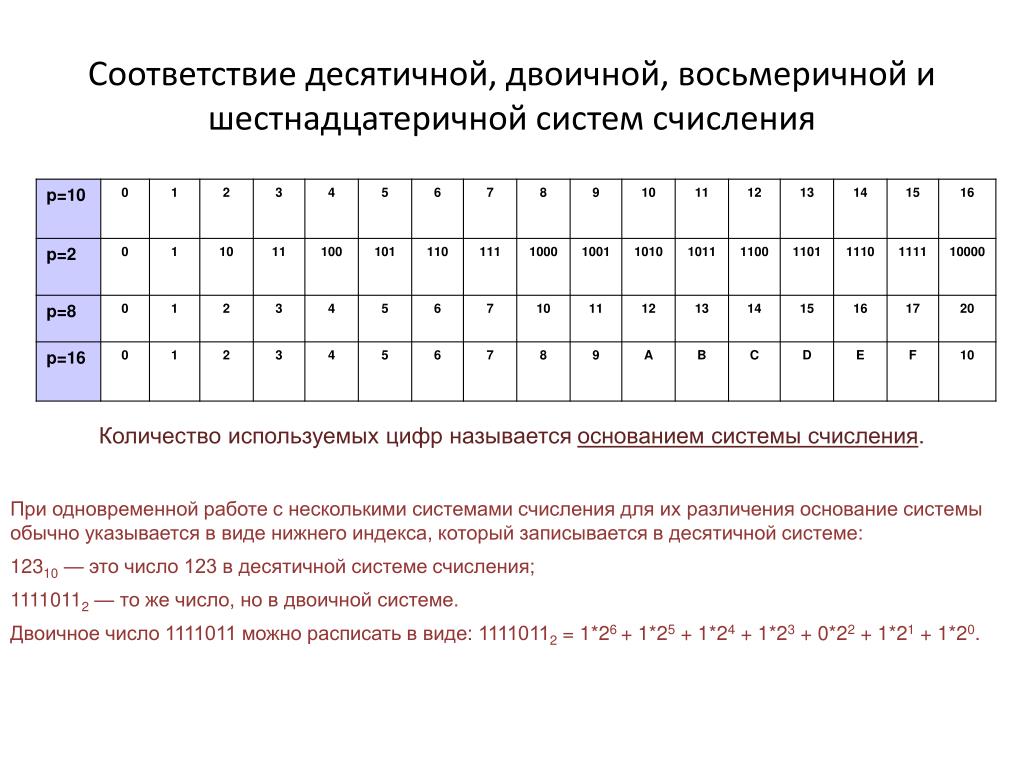
Шаг 2 – Преобразуйте полученное таким образом десятичное число в новое базовое число.
Пример
Восьмеричное число: 25 8
Вычисление двоичного эквивалента −
Шаг 1 – Преобразование в десятичное число
| 0 Шаг0 | Восьмеричный номер | Десятичное число |
| Этап 1 | 25 8 | ((2 x 8 1 ) + (5 x 8 0 )) 10 |
| Этап 2 | 25 8 | (16 + 5) 10 |
| Этап 3 | 25 8 | 21 10 |
Восьмеричное число: 25 8 = Десятичное число: 21 10
Шаг 2. Преобразование десятичного числа в двоичное
Десятичное число: 21 10 = Двоичное число: 10101 2
Восьмеричное число: 25 8 = Двоичное число: 10101 2
Метод быстрого доступа ─ Двоичный в восьмеричный
Шаг 1 – Разделите двоичные числа, начиная с трех правых, на группы по три цифры).
Шаг 2 – Преобразуйте каждую группу из трех двоичных цифр в одну восьмеричную цифру.
Пример
Двоичный номер: 10101 2
Расчет восьмеричного эквивалента −
| Шаг | Двоичный номер | Восьмеричный номер |
| Этап 1 | 10101 2 | 010 101 |
| Этап 2 | 10101 2 | 2 8 5 8 |
| Этап 3 | 10101 2 | 25 8 |
Двоичный номер: 10101 2 = Восьмеричный номер: 25 8
Сокращенный метод ─ Восьмеричное в двоичное
Шаг 1 – Преобразование каждой восьмеричной цифры в 3-значное двоичное число (для этого преобразования восьмеричные цифры могут рассматриваться как десятичные).
Шаг 2 – Объедините все полученные двоичные группы (по 3 цифры в каждой) в одно двоичное число.
Пример
Восьмеричное число: 25 8
Вычисление двоичного эквивалента −
| Шаг | Восьмеричный номер | Двоичный номер |
| Этап 1 | 25 8 | 2 10 5 10 |
| Этап 2 | 25 8 | 010 2 101 2 |
| Этап 3 | 25 8 | 010101 2 |
Восьмеричное число: 25 8 = Двоичное число: 10101 2
Сокращенный метод ─ Двоичный в шестнадцатеричный
Шаг 1 − Разделите двоичные цифры на группы по четыре (начиная справа).
Шаг 2 – Преобразуйте каждую группу из четырех двоичных цифр в один шестнадцатеричный символ.
Пример
Двоичный номер: 10101 2
Вычисление шестнадцатеричного эквивалента −
| Шаг | Двоичный номер | Шестнадцатеричный номер |
| Этап 1 | 10101 2 | 0001 0101 |
| Этап 2 | 10101 2 | 1 10 5 10 |
| Этап 3 | 10101 2 | 15 16 |
Двоичный номер: 10101 2 = Шестнадцатеричный номер: 15 16
Метод быстрого доступа — шестнадцатеричный код в двоичный
Шаг 1 – Преобразуйте каждую шестнадцатеричную цифру в 4-значное двоичное число (для этого преобразования шестнадцатеричные цифры могут рассматриваться как десятичные).
Шаг 2 – Объедините все полученные двоичные группы (по 4 цифры в каждой) в одно двоичное число.
Пример
Шестнадцатеричное число: 15 16
Вычисление двоичного эквивалента −
| Шаг | Шестнадцатеричный номер | Двоичный номер |
| Этап 1 | 15 16 | 1 10 5 10 |
| Этап 2 | 15 16 | 0001 2 0101 2 |
| Этап 3 | 15 16 | 00010101 2 |
Шестнадцатеричное число: 15 16 = Двоичное число: 10101 2
Нравится:
Нравится Загрузка…
Что такое система счисления?
Система счисления важна с точки зрения понимания того, как представляются данные, прежде чем они смогут быть обработаны любой цифровой системой, включая цифровой компьютер. есть два основных способа представления числовых значений различных физических величин, с которыми мы постоянно имеем дело в нашей повседневной жизни. Арифметическое значение, которое используется для представления количества и используется в расчетах, определяется как ЧИСЛА. Такой символ, как «4, 5, 6», который представляет число, известен как 9.0009 цифры . Без чисел невозможен подсчет вещей, даты, времени, денег и т. д. Эти числа также используются для измерения и используются для маркировки. Свойства чисел делают их полезными при выполнении над ними арифметических операций. Эти числа могут быть записаны в числовой форме, а также в словах.
Арифметическое значение, которое используется для представления количества и используется в расчетах, определяется как ЧИСЛА. Такой символ, как «4, 5, 6», который представляет число, известен как 9.0009 цифры . Без чисел невозможен подсчет вещей, даты, времени, денег и т. д. Эти числа также используются для измерения и используются для маркировки. Свойства чисел делают их полезными при выполнении над ними арифметических операций. Эти числа могут быть записаны в числовой форме, а также в словах.
Например, 3 записывается словами как три, 35 записывается словами как тридцать пять и т. д. Учащиеся могут писать числа от 1 до 100 словами, чтобы узнать больше. Существуют различные типы чисел, которые мы можем выучить. Это целые и натуральные числа, нечетные и четные числа, рациональные и иррациональные числа и т. д.
Число и его типы
Числа, используемые в математике, в основном представляют собой десятичные системы счисления. В десятичной системе счисления используются цифры от 0 до 9 с основанием 10. Существует много типов чисел в десятичной системе счисления, ниже приведены некоторые из упомянутых типов чисел,
Существует много типов чисел в десятичной системе счисления, ниже приведены некоторые из упомянутых типов чисел,
- Числа, которые представлены справа от нуля, называются положительными числами . Значение этих чисел увеличивается при движении вправо. Положительные числа используются для сложения между числами. Пример: 1, 2, 3, 4.
- Числа, которые представлены слева от нуля, называются Отрицательными Числами . Значение этих чисел уменьшается при движении влево. Отрицательные числа используются для вычитания между числами. Пример: -1, -2, -3, -4.
- Натуральные числа — это самый простой тип чисел, которые варьируются от 1 до бесконечности. Эти числа также называются положительными числами или счетными числами. Натуральные числа представлены символом N.
- Целые числа — это в основном натуральные числа, но они также включают «ноль». Целые числа представлены символом W.
- Целые числа представляют собой совокупность целых чисел плюс отрицательные значения натуральных чисел.
 Целые числа не включают дробные числа, т.е. они не могут быть записаны в форме a/b . Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом Z.
Целые числа не включают дробные числа, т.е. они не могут быть записаны в форме a/b . Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом Z. - Рациональные числа — это числа, которые можно представить в виде дроби, т. е. a/b. Здесь a и b оба являются целыми числами и b ≠ 0. Все дроби — рациональные числа, но не все рациональные числа — дроби.
- Иррациональные числа – это числа, которые нельзя представить в виде дробей, т.е. их нельзя записать в виде a/b.
- Числа, у которых нет других делителей, кроме 1, и само число называются Простые числа. Все числа, кроме простых чисел, называются составными числами , кроме 0. Ноль не является ни простым, ни составным числом.
Что такое система счисления?
Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом. Система записи для обозначения чисел с использованием цифр или символов в логическом порядке определяется как Система счисления. Система счисления Представляет полезный набор чисел, отражает арифметическую и алгебраическую структуру числа и обеспечивает стандартное представление. Из цифр от 0 до 9 можно составить все числа. С помощью этих цифр любой может составить бесконечное число. Например, 156,3907, 3456, 1298, 784859 и т. д.
Система записи для обозначения чисел с использованием цифр или символов в логическом порядке определяется как Система счисления. Система счисления Представляет полезный набор чисел, отражает арифметическую и алгебраическую структуру числа и обеспечивает стандартное представление. Из цифр от 0 до 9 можно составить все числа. С помощью этих цифр любой может составить бесконечное число. Например, 156,3907, 3456, 1298, 784859 и т. д.
Типы систем счисления
В зависимости от базового значения и количества разрешенных цифр существует множество типов систем счисления. Четыре распространенных типа системы счисления:
- Система десятичных чисел
- Система двоичных номеров
- Система октальных номеров
- Система гексадецима
. Десятичная система счисления. Он использует 10 цифр, т.е. 0-9 для создания чисел. Здесь каждая цифра в числе находится в определенном месте, а разрядное значение является произведением различных степеней 10. Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Например, 10264 имеет следующие разрядные значения:
(1 × 10 4 ) + (0 × 10 3 ) + (2 × 10 2 ) + (6 × 10 1 ) (4 × 10 0 )
= 1 × 10000 + 0 × 1000 + 2 × 100 + 6 × 10 + 4 × 1
= 10000 + 0 + 200 + 60 + 4
= 10264
+ 4
= 10264. Двоичная система счисления
Система счисления с базовым значением 2 называется двоичной системой счисления. Он использует 2 цифры, то есть 0 и 1 для создания чисел. Числа, образованные из этих двух цифр, называются двоичными числами. Двоичная система счисления очень полезна в электронных устройствах и компьютерных системах, потому что ее можно легко реализовать, используя всего два состояния ВКЛ и ВЫКЛ, то есть 0 и 1.
Десятичные числа 0-9 представлены в двоичном виде как: 0, 1, 10, 11, 100, 101, 110, 111, 1000 и 1001
Например, 14 можно записать как 1110, 19 можно записать как 10011, 50 может быть написано как 110010.
Пример 19 в Бинарная система
Здесь 19 можно записать как 10011
Преимущества
любой цифровой компьютер, хотя решение задачи на компьютере также может включать арифметическую операцию. Введение математики логики Джорджем Булем заложило основу для современного цифрового компьютера. Он свел математику логики к двоичной записи «0» и «1».
Другим преимуществом этой системы счисления было то, что все виды данных можно было удобно представить с помощью нулей и единиц.
Кроме того, основные электронные устройства, используемые для аппаратной реализации, могут удобно и эффективно работать в двух совершенно разных режимах.
схемы, необходимые для выполнения арифметических операций.
Восьмеричная система счисления
Восьмеричная система счисления — это система, в которой базовое значение равно 8. В ней используются 8 цифр, т. е. 0–7, для создания восьмеричных чисел. Восьмеричные числа можно преобразовать в десятичные значения, умножив каждую цифру на разрядное значение, а затем сложив результат. Здесь значения мест равны 80, 81 и 82. Восьмеричные числа полезны для представления чисел UTF8. Пример,
(135) 10 можно записать как (207) 8
(215) 10 можно записать как (327) 8
HexAdeCamal System. базовое значение 16 называется шестнадцатеричной системой счисления. Он использует 16 цифр для создания своих номеров. Цифры от 0 до 9 воспринимаются как цифры в десятичной системе счисления, но цифры от 10 до 15 представлены как A-F, т.е. 10 представлен как A, 11 как B, 12 как C, 13 как D, 14 как E и 15 как F. Шестнадцатеричные числа полезны для обработки адресов памяти. Шестнадцатеричная система счисления обеспечивает сжатый способ представления больших двоичных чисел, хранящихся и обрабатываемых. Примеры,
Шестнадцатеричные числа полезны для обработки адресов памяти. Шестнадцатеричная система счисления обеспечивает сжатый способ представления больших двоичных чисел, хранящихся и обрабатываемых. Примеры,
(255) 10 можно записать как (FF) 16
(1096) 10 можно записать как (448) 16
(4090) 667. FFA) 16
HEXADECIMAL 0 1 2 3 4 5 6 7 8 9 A B C D E F DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Примеры задач
Вопрос 1. Преобразовать (18) 10 в двоичное число?
Преобразовать (18) 10 в двоичное число?
Решение:
Поэтому (18) 10 = (1001) 2
Вопрос 2: Преобразовать 325 8 в десятичную дробь?
Решение:
325 8 = 3 × 8 2 + 2 × 8 1 + 5 × 8 0
= 3 × 64 + 2 × 2 + 5 + 5 5 + 5 5 + 5 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 0 1 × 8 0
= 192 + 16 + 5
= 213 10
Вопрос 3: Преобразовать (2056) 16 в восьмеричное число?
Решение:
Здесь (2056) 16 в шестнадцатеричной форме
Сначала мы преобразуем в десятичную форму из шестнадцатеричной.
(2056) 16 = 2 × 16 3 + 0 × 16 2 + 5 × 16 1 + 6 × 16 0
= 2 × 4096 + 0 + 60374 0
75= 2 × 4096 + 0 + 60374 9000 3
= 2 × 4096 + 0 + 60374 0
= 2 × 4096. = 8192 + 0 + 80 + 6
= (8278) 10
Теперь преобразуйте это десятичное число в восьмеричное, разделив его на 8
Итак, возьмем значение остатка от 20126
(8278) 10 = (20126) 8
Следовательно, (2056) 16 = (20126) 8
ВОПРОС 4: CONVERT (101110) 2 9055.
Solution:
Given (101110) 2 a binary number, to convert it into octal number
OCTAL NUMBER BINARY NUMBER 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 Используя приведенную выше таблицу, мы можем записать данное число как
101 110, т.


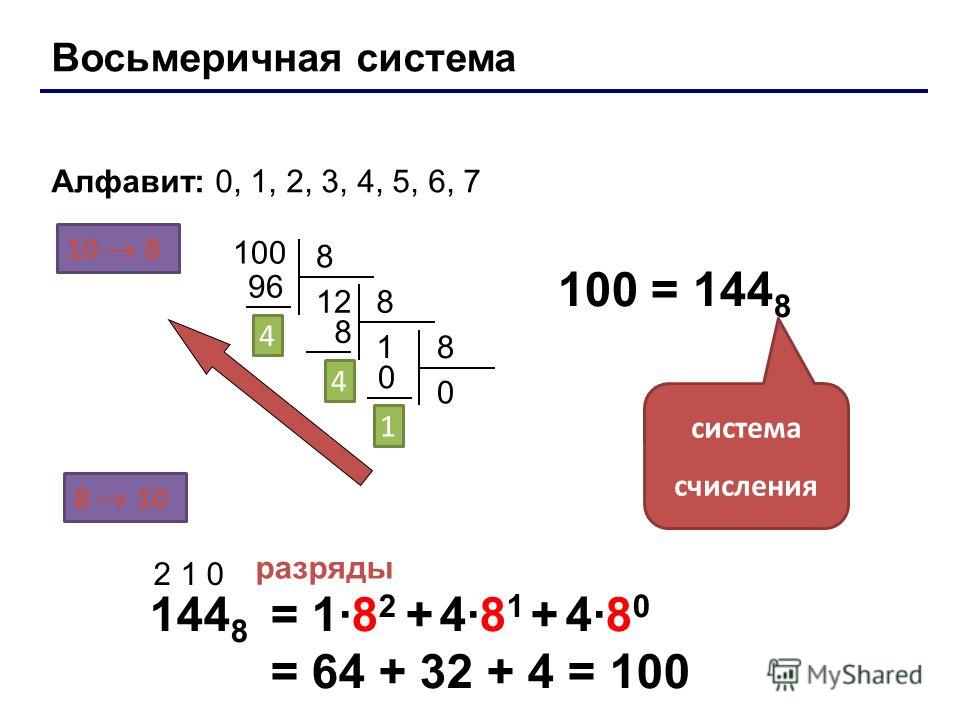
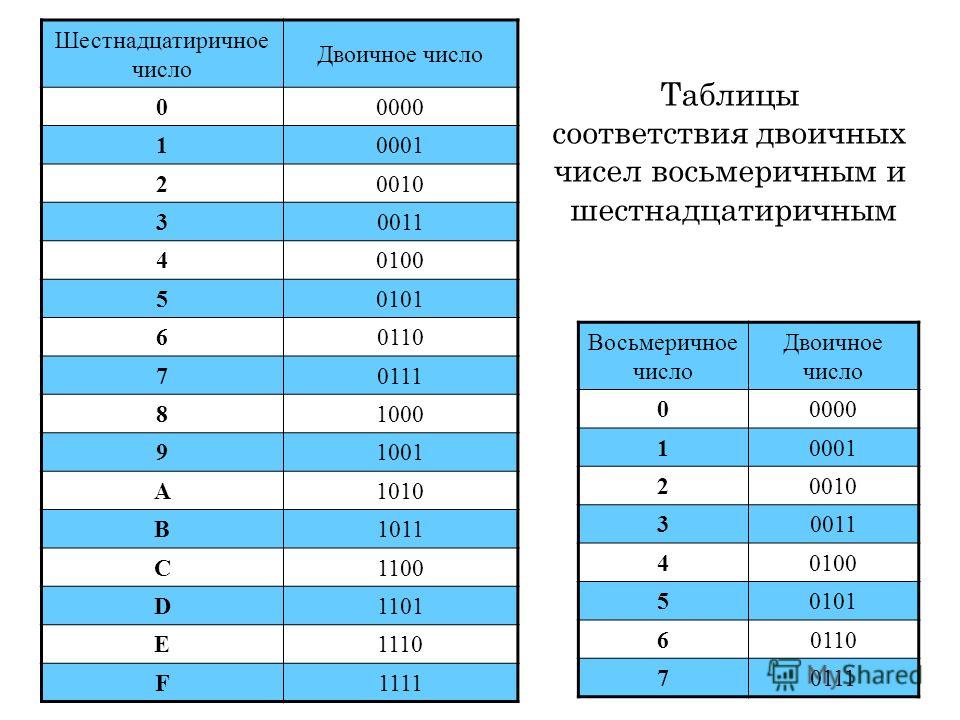 Выявление места и причины затруднения (1 мин).
Выявление места и причины затруднения (1 мин).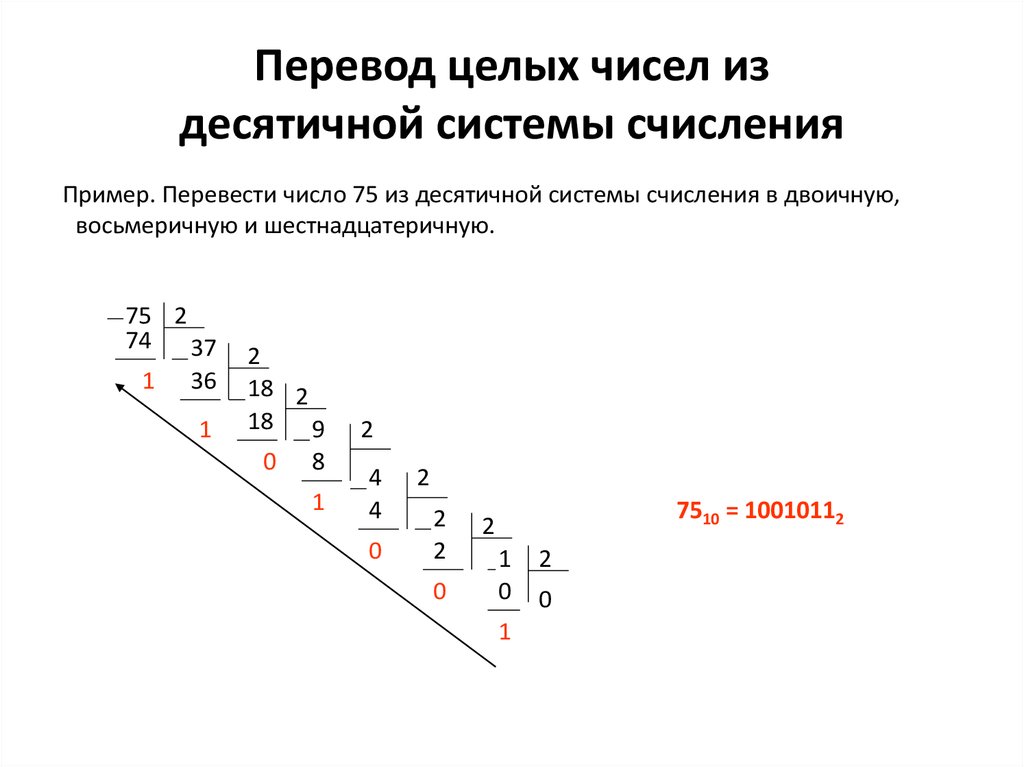
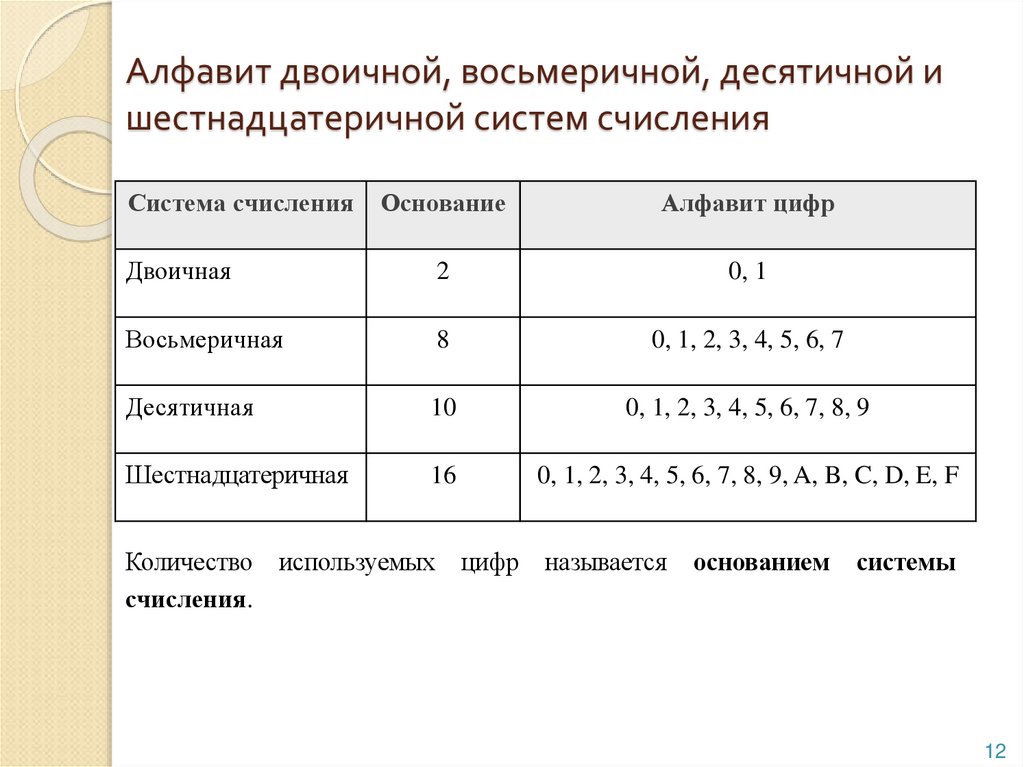
 Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего. Первичное закрепление нового материала с комментированием во внешней речи
Первичное закрепление нового материала с комментированием во внешней речи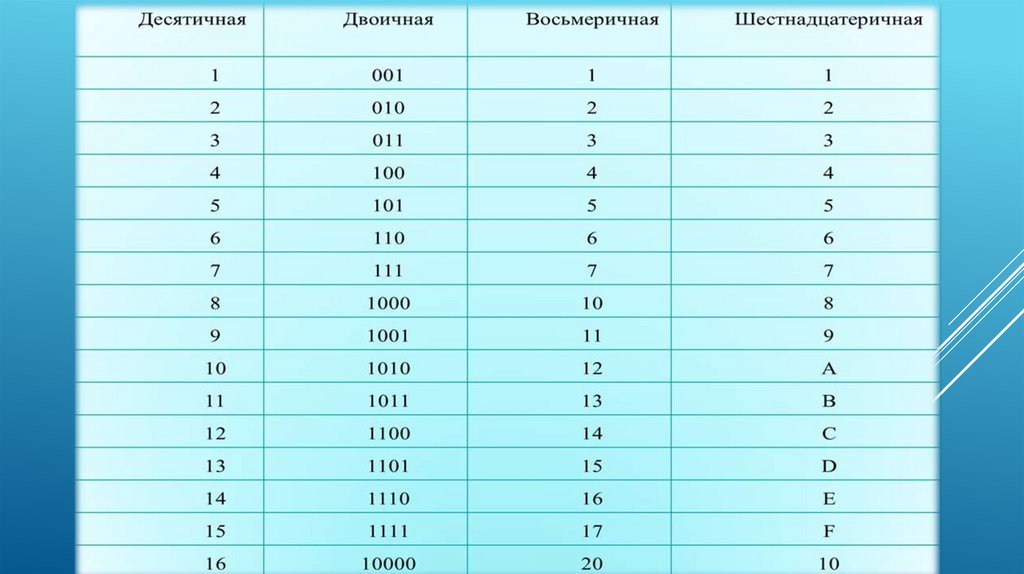 Самостоятельная работа с самопроверкой по эталону (7 мин)
Самостоятельная работа с самопроверкой по эталону (7 мин)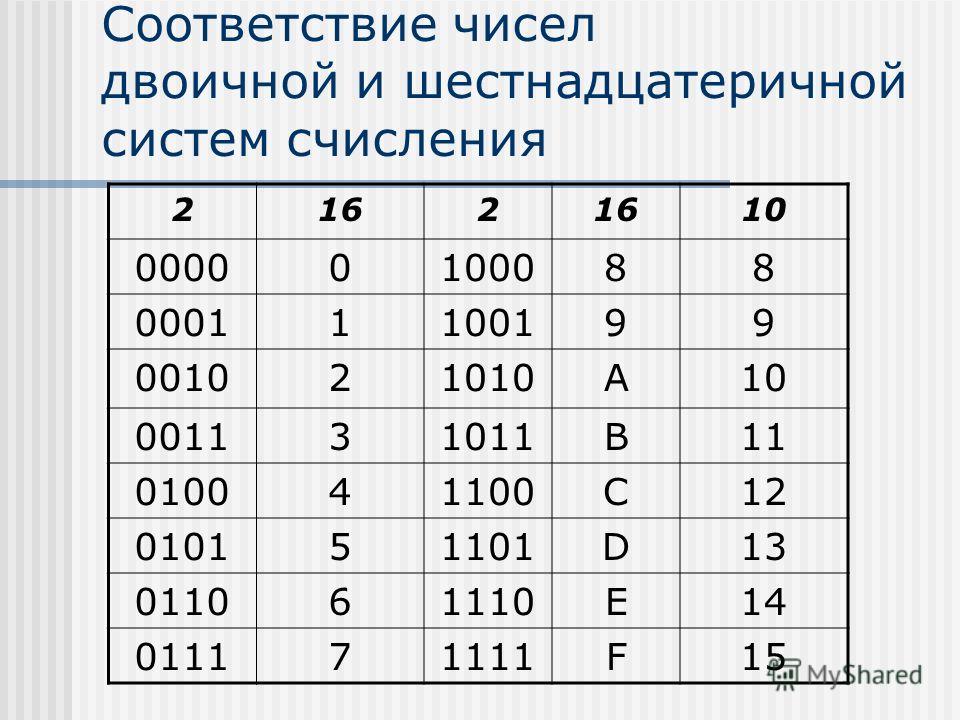 Включение в систему знаний и повторение (10 мин)
Включение в систему знаний и повторение (10 мин) Рефлексия учебной деятельности (2 мин)
Рефлексия учебной деятельности (2 мин) Пример 2 x где x представляет последнюю позицию — 1.
Пример 2 x где x представляет последнюю позицию — 1.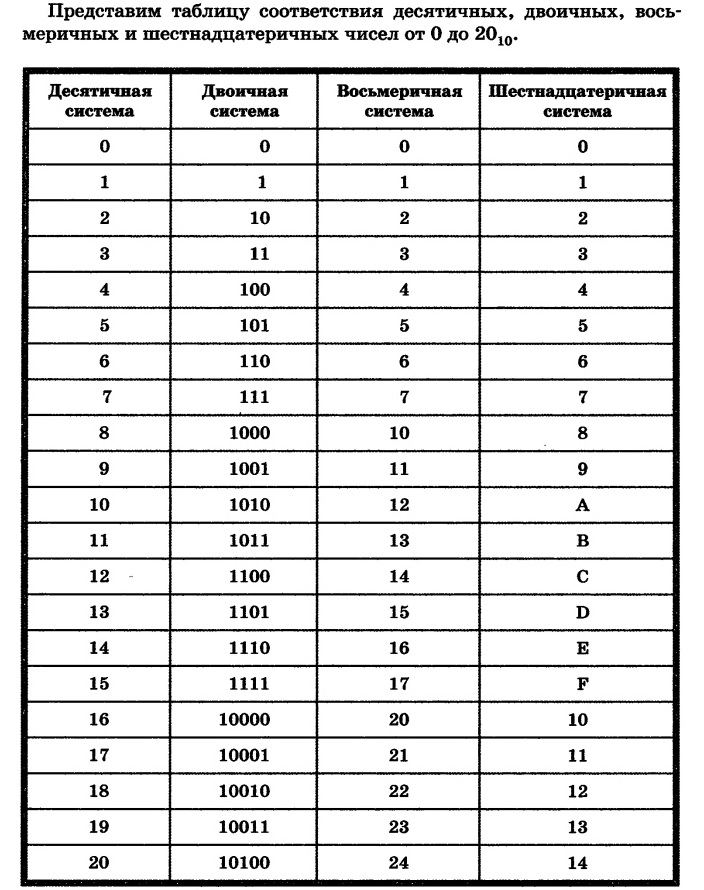 Целые числа не включают дробные числа, т.е. они не могут быть записаны в форме a/b . Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом Z.
Целые числа не включают дробные числа, т.е. они не могут быть записаны в форме a/b . Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом Z.