Coil32 — Последовательный колебательный контур
Здесь будет немного теории колебательного контура с отступлениями и комментариями. Надеюсь, что эта информация будет полезна не только студентам и школьникам, но и поможет радиолюбителям, дополнив практику теорией, может быть забытой кем-то, может для кого-то новой.
Последовательный колебательный контур – это цепь, составленная из последовательно соединенных индуктивности и ёмкости.(рис1)  рис 1
рис 1
R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах. При этом сами L и C, можно представить как идеальные без потерь.
È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов
Ζ = R + (jωL + 1 / jωC) = R + jωX
Или, что тоже самое:
Ζ = ¦Ζ¦ejφ,
где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC)
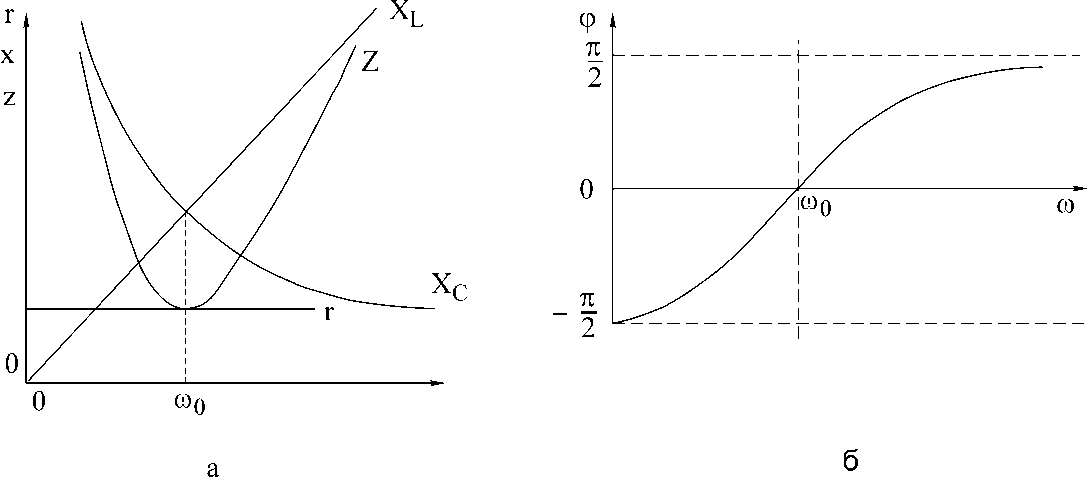
Активную составляющую входного сопротивления R можно приближенно считать не зависящей от частоты генератора, хотя реально это совсем не так. Здесь работают факторы скин-эффекта, эффекта близости другие эффекты от которых зависит добротность. Но для получения представления как меняется реактивное сопротивление контура от частоты пока этими тонкостями можно пренебречь. Реактивная составляющая является функцией частоты и в зависимости от величины L, C, и ω изменяется по величине и знаку (рис2).
 рис 2
рис 2
В точке ω0 контур попадает в режим, при котором
XC= — XL, X=0. Этот режим называется резонансом напряжений, при этом ω0L — 1/ω0C = 0, откуда
ω0 = 1/√LC или ƒ0 = 1/(2π√LC),
формула резонансной частоты контура, впервые выведенная сэром Вильямом Томсоном (1824 – 1907), великим английским физиком, более известным как лорд Кельвин, в честь которого названа шкала абсолютных температур.
В точке резонанса Ζ = R. Ток в цепи: Ì
UC = UL = ω0LÌ0 = (1/ω0C)Ì0
При этом
UL/Ì0 = UC/Ì0 = ω0L = 1/ω0C = √L/C = ρ
ρ–характеристическое или волновое сопротивление контура.
Очевидно, что ρ » R, поэтому UC = UL » E, откуда и произошло название – резонанс напряжений. Т.е. амплитуда напряжения на реактивных элементах на резонансной частоте в десятки и сотни раз превышает амплитуду напряжения источника. Подобное явление наблюдается в механике, например маятник в часах, качели и носит общее название явление резонанса.
Это возрастание амплитуды характеризуется следующими соотношениями
UL/E = UC/E = ρ/R = Q
Q – безразмерная величина, носящая название добротности контура.
Обратим внимание на выражение Q = ρ/R = √L/C/R, из которого следует, что добротность должна расти при увеличении соотношения L/C. Однако, это не совсем так. Дело в том, что при увеличении L одновременно растет и R, ведь число витков и размеры катушки увеличиваются и, грубо говоря, увеличивается длина провода катушки и его омическое сопротивление. Поэтому зависимость величины добротности контура от соотношения индуктивности и емкости носит более сложный характер и простыми формулами не описывается. В начале мы пренебрегли «тонкостями» зависимости активного сопротивления контура от частоты, но здесь уже так легкомысленно поступать нельзя.
Вообще, конструкция контура для разных областей его применения разрабатывалась в основном энтузиастами радиолюбителями с паяльником в руках, интуицией и минимумом расчетов. Так было на заре развития радио. Тогда в результате экспериментов было установлено, что добиться хорошей чувствительности и избирательности приемника, например, можно применив контур с катушкой внушительных размеров. Потом уже с появлением малошумящих полупроводников и высокочастотных ферритов размеры перестали играть такое значение. Но и сегодня практический опыт нельзя оставлять без внимания, советую ознакомится с ним на этом форуме
Амплитудно-частотая характеристика тока в цепи колебательного контура описывается уравнением:
I/I0 = 1/√1+Q2(ƒ/ƒ0-ƒ0/ƒ)2
Фазочастотная характеристика определяется выражением:
φ = arctg[Q(ƒ/ƒ0-ƒ0/ƒ)]
Эти характеристики относительно нормированной частоты ω/ω0 приведены на следующем рисунке: Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазо-сдвигаюшую цепь.
Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазо-сдвигаюшую цепь.
Основные параметры контура
Если предварительно зарядить конденсатор и подключить его к индуктивности (рис. 4.2.7.1), то будет происходить обмен энергией между электрическим полем конденсатора и магнитным полем катушки. В этой цепи будут происходить колебания, поэтому этот контур называется колебательным.
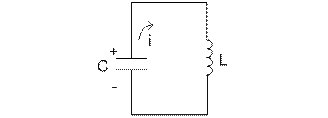
Рис.4.2.7.1.
Так как колебания происходят без воздействия внешнего источника, а за счет заранее занесенной энергии, то они называются свободными.
Колебания происходят с определенной частотой 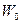 , называемой частотой свободных колебаний.
, называемой частотой свободных колебаний.
Из условия равенства энергий 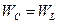
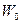 =
= 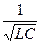 ;
; 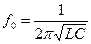 ;
;
Основными параметрами колебательного контура, кроме частоты свободных колебаний, являются:
— период свободных колебаний:
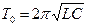 ;
;
— характеристическое (волновое) сопротивление:
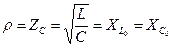
Характеристическим сопротивлением называется индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний.
Так как в контуре отсутствуют потери, то контур называется идеальным.
В реальном колебательном контуре (рис. 4.2.7.2) имеются потери, поэтому при возникновении в контуре свободных колебаний энергия предварительно заряженного конденсатора тратится безвозвратно, преобразуясь в тепло. В результате затраты энергии постепенно уменьшается её запас и амплитуда контура уменьшается до нуля. Следовательно, колебания в контуре будут затухающими.(рис 4.2.7.3)
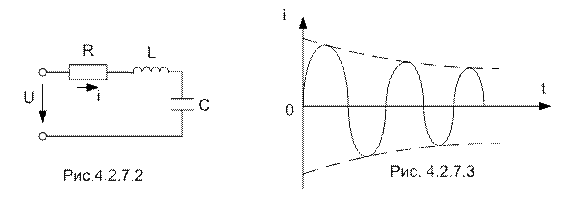
Для характеристики интенсивности затухания свободных колебаний введено понятие «затухание контура». Затуханием называется отношение активного сопротивления контура к его характеристическому сопротивлению.
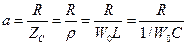
Величина, обратная затуханию, называется добротностью контура.
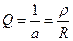
Добротность характеризует качество контура.
Рассмотрим различные варианты последовательного соединения элементов в цепях переменного тока.
4.2.7. Гармонические колебания в цепи при параллельном соединении элементов R,L,C.
К цепи, содержащей параллельное соединение R,L,C
(рис. 4.2.8.1 а) приложено напряжение u= 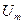 sin
sin 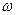 t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
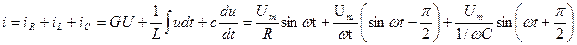 ,
,
где, 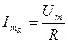 =G
=G 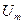 ,
,
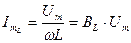 ,
,
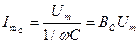 .
.
Полная проводимость цепи будет равна: 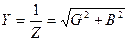
Активная проводимость: 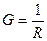
Реактивная проводимость: 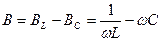
При параллельном соединении элементов строят треугольники токов и проводимостей (рис.4.2.8.1.б,в)
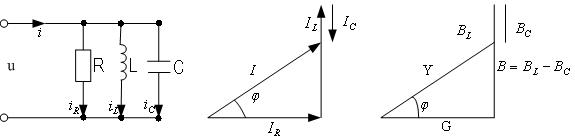
а) б) в)
Рис. 4.2.8.1.
4.2.8. Резонанс в электрических цепях переменного тока.
В радиотехнике и электросвязи большое значение имеет явление резонанса. Такое явление возникает в цепях, содержащих участки, с емкостным и индуктивным характером. Если цепь содержит последовательно соединенные с генератором элементы, то она называется последовательным колебательным контуром.(рис. 4.2.9.1а). Если элементы соединены параллельно с генератором, то цепь носит название – параллельный колебательный контур. (рис. 4.2.9.1б).
Среди многообразия частот имеется частота, на которой в цепи происходит обмен энергией между магнитными и электрическими полями. К генератору энергия не возвращается. От генератора поступает в контур столько энергии, сколько её тратится на активном сопротивлении цепи, тем самым обеспечиваются незатухающие колебания в контуре.
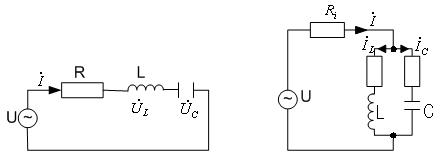
а) б)
рис. 4.2.9.1
· Частоту, на которой наблюдается явление резонанса, называют резонансной и определяют по формуле:
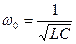 ;
; 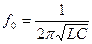
· Характеристическим сопротивлением контура называют реактивные сопротивления на резонансной частоте и определяют как:
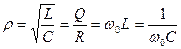 [Ом]
[Ом]
· Резонансные свойства контура характеризуются добротностью контура, которая равна:

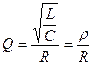
Добротность контура зависит от внутреннего сопротивления генератора 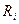 .
.
В последовательном колебательном контуре, (рис.4.2.9.1а) чем больше 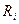 , тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
, тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
В параллельном колебательном контуре, (рис. 4.2.9.1б) если 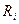 будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
Различают два типа резонансов. В последовательном колебательном контуре возникает резонанс напряжений, а в параллельном – резонанс токов. Свойства цепей при резонансе рассматриваются в следующей таблице:
Важной характеристикой колебательного контура является полоса пропускания – это полоса частот, в пределах которой величина не меньше 0,707 от своего максимального значения. Полосу пропускания можно определить по формуле:
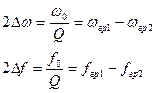
Где: 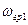 ;
; 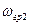 ;
; 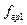 ;
; 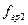 — граничные частоты, на которых величина равна 0,707 от своего максимального значения.
— граничные частоты, на которых величина равна 0,707 от своего максимального значения.
Колебательные контуры и явление резонанса широко используются в радиотехнике и электросвязи. В радиоприемниках и усилителях они являются избирательными цепями, в автогенераторах, электрических фильтрах, в корректорах и других устройствах являются частотно-зависимыми элементами.
Пример:
Электрическая цепь состоит из последовательно соединенных резистора R=15 Ом, катушки индуктивности L=636 мкГн и конденсатора C=600 пФ.
Определить резонансную частоту 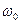 , характеристическое сопротивление
, характеристическое сопротивление 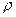 , добротностьQ, затухание d. Чему равны ток
, добротностьQ, затухание d. Чему равны ток 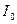 , расходуемая в цепи мощность
, расходуемая в цепи мощность 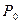 , напряжения на индуктивности
, напряжения на индуктивности 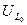 , и емкости
, и емкости 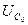 , если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на
, если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на 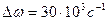 ?
?
Рассчитать и построить зависимости:
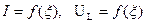
для значений обобщенной расстройки 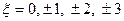 . Показать на графике полосу пропускания контура.
. Показать на графике полосу пропускания контура.
Решение:
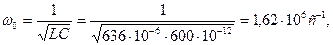
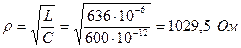 ,
,
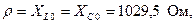
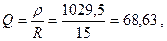
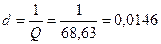 ,
,

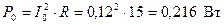 ,
,
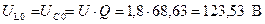 ,
,
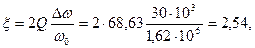
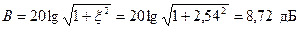 .
.
Рассчитаем и построим заданные зависимости:
1. 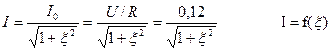
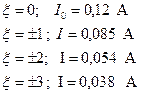

2. 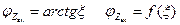
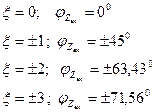

Вопросы для самоконтроля:
1. Что называется колебательным контуром?
2. Какие колебания называются свободными, вынужденными?
3. Что называется «резонансом напряжений»?
4. Что называется «резонансом токов»?
5. Условия возникновения резонансов
6. Что характеризует добротность контура?
7. Как определяется резонансная частота?
4.3. Расчет цепей символическим методом
Символический метод основан на использовании комплексных чисел.
Комплексное число состоит из вещественной А’ и мнимой А» частей. А = А’ + jА».
Комплексное число можно представить вектором на комплексно-числовой плоскости. (рис. 4.3.1.) Проекция вектора на вещественную ось (ось абцисс) соответствует вещественной части комплексного числа А’, проекция вектора на мнимую ось (ось ординат) соответствует коэффициенту при мнимой единице А»,
j-мнимая единица представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки.
Комплексным числам А=3+ j4 и В= 5-j2
Соответствуют векторы А и В, изображенные на рис. 4.3.1.
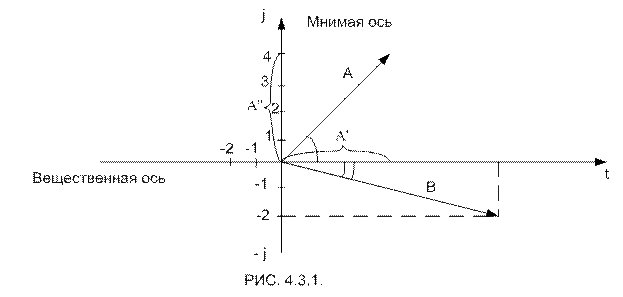
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Модуль комплексного числа:
|А|= 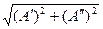 ;
;
Т.е. |А|= 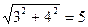 ;
; 
 |В|=
|В|= 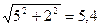
Углы 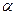 и
и 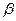 , образованные векторами А и В, называются аргументами комплексного числа
, образованные векторами А и В, называются аргументами комплексного числа
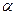 = arctg
= arctg 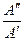
Для приведенных примеров
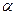 = arctg
= arctg 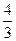 =53°10′
=53°10′
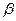 = arctg
= arctg 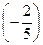 =-21°40′
=-21°40′
Существует 3 формы записи количественного числа:
1. Алгебраическая А = А’ + jА»
2. Тригонометрическая А=|А|cos 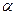 +j|А|sin
+j|А|sin 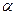 ,
,
Так как А’=|А| cos 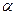
А»=|А| sin 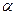
3. Показательная А=|А|е 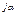 =5е
=5е 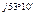
В=|В|е 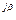 =5,4е
=5,4е 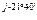
Для перевода из показательной формы в алгебраическую пользуются тригонометрической формой записи комплексного числа.
Для перевода из алгебраической в показательную форму определяют модуль и аргумент.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производят в алгебраической форме, а умножение и деление удобнее и проще производить в показательной форме.
При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:
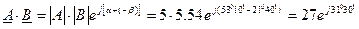
При делении комплексных чисел в показательной форме этих чисел делятся, а аргументы вычитаются
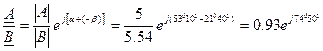
Если ток и напряжение изменяется по синусоидальному закону
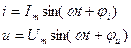
То их можно изобразить векторами и записать комплексными числами
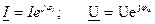
Комплекс полного сопротивления цепи:

Алгебраическая форма записи комплекса полного сопротивления
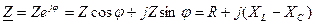
Любую цепь переменного тока можно рассчитывать по закону постоянного тока, если все величины представить в комплексной форме.
Комплекс полной мощности цепи 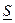 определяется произведением комплекса напряжения
определяется произведением комплекса напряжения 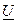 и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
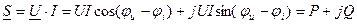
где Р- активная мощность
Q- реактивная мощность
Пример
Определить полное сопротивление цепи (рис.4.3.2) напряжение на зажимах, мощности (активную, реактивную, полную) если
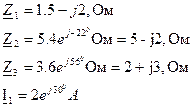
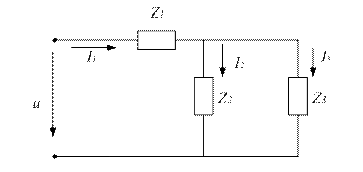
Решение
1. Полное сопротивление цепи
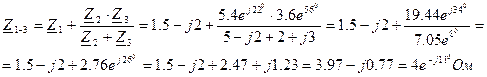
2. Напряжения на зажимах цепи
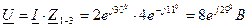
3. Полная мощность цепи
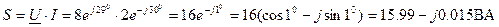
где Р=15.99 = 16 Вт – активная мощность
Q= -0.015 Вт – реактивная мощность
Вопросы для самоконтроля.
1 . Какие формы записи комплексных чисел вы знаете?
2. Сложите два числа
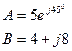
3. Перемножить два числа
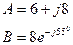
4. Выражаем токи через потенциалы, ЭДС и сопротивления.
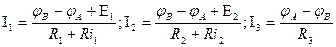 ,
,
5. Примем 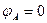
6. Подставляем полученные выражения токов в уравнение 1.

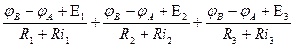
7. Подставим числовые значения и решаем полученное уравнение.
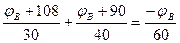
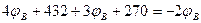
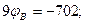
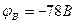
8. Определяем токи в ветвях.
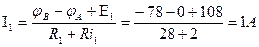

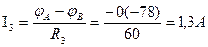
Действительные направления токов совпадают с выбранными.
Тема №3: Трехфазные цепи. [Электротехника Электронное пособие для студентов очной и заочной форм обучения всех технических специальностей]
Основными приемниками электрической энергии являются электрические двигатели, применяемые для приведения в движение рабочих машин. Наиболее простые из них трехфазные асинхронные двигатели. Для производства, распределения и передачи электрической энергии применяют трехфазные генераторы.
Система, состоящая из трех цепей, в которой действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые одним источником – называется трехфазной.
Система будет симметричной, если будут равны амплитуды фаз и углы сдвига фаз между каждой парой ЭДС.
На рисунке 4.14а, изображены временные диаграммы ЭДС , на рисунке 4.14б, векторная диаграмма, а на 4.14в, иллюстрируется принцип получения трехфазной системы ЭДС . В равномерном магнитном поле с постоянной угловой скоростью 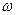 вращаются три одинаковых жёстко скрепленных друг с другом катушки.
вращаются три одинаковых жёстко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве относительно друг друга на 120°. В каждой катушке находится синусоидальная ЭДС одинаковой амплитуды. Уравнения ЭДС записывают в следующем виде:
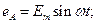
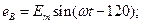
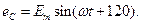

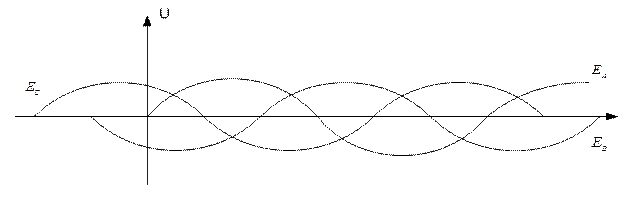 а)
а)
ЕА
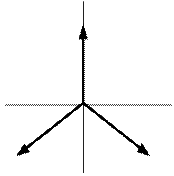
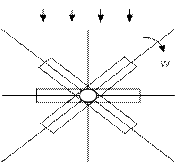
ЕС ЕВ
б) в)
Рисунок 5.11
Векторы вращающиеся против часовой стрелки и фазы чередуются А, В, С, что называют прямой последовательностью фаз.
Дата добавления: 2016-11-29; просмотров: 14745;
Похожие статьи:
Coil32 — Параллельный колебательный контур
Параллельный колебательный контур в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного. Реальные элементы контура обладают потерями и при анализе цепи используется реалистичная модель из идеальных сосредоточенных элементов в которой потери учитываются с помощью «виртуальных» последовательных активных сопротивлений RL и RC.
Собственная паразитная емкость катушки обычно не учитывается, т. к. она просто суммируется с контурной. Программа Coil32 рассчитывает потери в проводе катушке RL без учета потерь в каркасе, экране, сердечнике и во всех предметах, с которыми взаимодействует окружающая катушку электромагнитная волна. Однако, учитывается скин-эффект и эффект близости. Эти же потери учитывает параметр «конструктивная добротность катушки» — QL. Это не добротность всего контура, а добротность катушки, которая связана с ее сопротивлением потерь следующим соотношением:
 |
[1] |
Потери в контурном конденсаторе на порядок меньше и характеризуются добротностью конденсатора. Поскольку потери конденсатора сосредоточены в основном в диэлектрике, можно считать, что его добротность QC и сопротивление потерь RC связаны с параметром, учитывающем потери в диэлектрике tgδ, следующим образом:
 |
[2] |
При анализе цепи часто ее преобразуют в эквивалентную параллельную RLC-цепь. В этом случае, заменяя сопротивления проводимостями, мы упрощаем анализ и получаем формулы идентичные формулам последовательного контура. Многие радиолюбители полагают, что последовательные RL и RC просто преобразуются в параллельное R. Это не так:
Как видим активные сопротивления и реактивности при таком преобразовании «перепутались», поэтому для наглядности проведем анализ без использования проводимостей, прямо по исходной схеме. Входное сопротивление двухполюсника получается следующим:
Активная и реактивная (мнимая) составляющие:

При резонансе токи в реактивных элементах (IL, IC) в Q раз больше общего тока цепи (I), поэтому для параллельного контура явление носит название резонанса токов.
Резонансная частота параллельного колебательного контура — это частота, при которой реактивная составляющая входного сопротивления равна нулю, входное сопротивление чисто активно, и, соответственно, фазовый сдвиг между током и напряжением на входных зажимах цепи тоже равен нулю. Приравняв Xвх к нулю и проведя соответствующие преобразования получим следующую формулу для резонансной частоты параллельного колебательного контура:
 |
[3] |
Один из важнейших параметров контура — его характеристическое сопротивление:
Формулу резонансной частоты можно представить иначе:
 |
[5] |
ω0 — резонансная частота последовательного колебательного контура.
Как видим резонансная частота параллельного колебательного контура равна резонансной частоте последовательного колебательного контура, составленного из тех же элементов, с добавкой поправочного коэффициента √[(L/C — RL^2)/(L/C — RC^2)]. На практике этот коэффициент всегда близок к единице и равен единице если RL=RC или RL=RC=0.
Пример:
Имеем контур с индуктивностью 3μГн и емкостью 42пФ, сопротивление потерь катушки — RL=2 Ом, конденсатора — RC=0.1 Ом. По формуле Томпсона резонансная частота контура равна 14.178649 МГц, точно вычисляем по формуле [1] — 14.178253 МГц. Как видим, активные сопротивления потерь вносят в идеальный контур дополнительную реактивность и уводят его частоту вниз, в данном случае почти на 400 Гц.
Это совсем небольшое отклонение нужно иметь ввиду, но оно намного меньше отклонений, вносимых неучтенными паразитными емкостями. Поэтому при выполнении условий: RL<< ρ, RC<< ρ, что обычно бывает на практике, можно считать, что условия резонанса токов совпадают с условиями резонанса напряжений в последовательном контуре, составленном из тех же элементов L и C,
ω0 = 1/√LC или ƒ0 = 1/(2π√LC)
На этом «родственная схожесть» последовательного и параллельного контуров не заканчивается.
При выполнении тех же условий: RL<< ρ, RC<< ρ
где Zвх.посл = (RL + RC) + j(ωL — 1 ⁄ ωC) – входное сопротивление последовательного контура, составленного из тех же элементов.
Как видим, можно считать, что сопротивления потерь катушки и конденсатора суммируются, поэтому общую добротность контура Q можно определить следующим выражением:
 |
[6] |
На резонансной частоте ω0:
 |
[7] |
Поскольку реактивные сопротивления взаимно компенсируются, контур на резонансной частоте имеет чисто активное сопротивление равное Rэ (эквивалентное или эффективное сопротивление контура).
Из последней формулы следует, что:
 |
[8] |
Т.е. добротность контура равна отношению его характеристического сопротивления к сопротивлению потерь. Иначе говоря, на данной частоте более добротным будет контур с меньшей емкостью и большей индуктивностью. Как же тогда соотносится добротность контура с конструктивной добротностью катушки? Чтобы понять это, следует иметь ввиду, что характеристическое сопротивление контура численно равно модулю реактивного сопротивления индуктивности или емкости на резонансной частоте. Последние, как известно, в этом случае равны и отличаются лишь знаком. Если мы пренебрежем потерями в конденсаторе, тогда формула [8] сводится к формуле [1]. Ведь на резонансной частоте ρ = |XL|, а в сумме RΣ = RL + RC, последнее слагаемое мы не учитываем. Другими словами, если пренебречь потерями в конденсаторе, то добротность контура равна конструктивной добротности катушки. В итоге мы приходим к выводу, что формулы [1] и [8] в этом случае эквивалентны. Если же нам необходимо учесть потери в конденсаторе, то следует использовать формулу [6].
Необходимо отметить два важных момента:
- Coil32 рассчитывает конструктивную добротность для «голой катушки в вакууме». Наличие экрана увеличивает распределенную емкость и уменьшает индуктивность. Характеристическое сопротивление контура падает, добротность уменьшается. Кроме этого добавляются потери на вихревые токи в экране. Каркас катушки также снижает ее добротность и добротность контура соответственно.
- Добротность катушки растет с ростом частоты только на «низких» частотах, далеких от частоты собственного резонанса катушки. При приближении к собственному резонансу добротность достигает максимума на частотах 60-85% от Fsrf и затем плавно снижается. Это происходит от того, что на этих частотах начинает проявлятся зависимость индуктивности и собственной емкости катушки от частоты.
Амплитудно-частотная характеристика имеет такой же вид, как и резонансная кривая последовательного контура; ФЧХ представляет собой зеркальное отображение ФЧХ последовательного контура.
Важно понятие полоса пропускания контура Это частотный интервал в пределах которого импеданс Zвх не ниже 1 ⁄ √2 (или 0,707) от максимального на резонансной частоте. Справедлива следующая формула, которую можно использовать для измерения добротности:
В практике представляет интерес величина ослабления контуром нежелательных частот:
 |
[10] |
Для расстроек более трех полос пропускания формула упрощается:
где знак не учитывается.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность. Эквивалентная добротность Q параллельного колебательного контура:
Q = Q0·Ri ⁄ (Rэ + Ri)
- Q0 — добротность ненагруженного контура
- Ri — входное сопротивление источника
- Rэ — эквивалентное сопротивление ненагруженного котура
Эту формулу можно использовать для учета влияния любых подключенных к контуру сопротивлений (например, нагрузки) на его добротность.
Для уменьшения влияния внешних цепей, а также для трансформации сопротивлений применяют частичное включение нагрузки в контур
Как видно из рисунка это можно сделать различными способами, отводом от катушки, с помощью катушки связи, емкстным делителем. Тогда выходное сопротивление контура:
Rвых = p2Rэ
где p – коэффициент связи. Для емкостного делителя:
p = C1 ⁄ (C1 + C2)
Для индуктивной связи:
p = M ⁄ L
где M — полная взаимоиндуктивность между Lc и L (это относится как к случаю с отводом катушки так и к случаю с катушкой связи). Следует отметить, что коэффициент связи не равен отношению числа витков, как в трансформаторе, поскольку каждый виток катушки Lc пересекается не всеми силовыми линиями катушки контура вследствие рассеяния магнитного поля.
При подключении внешней нагрузки к контуру с помощью частичного включения, результирующая добротность определяется:
Q = Q0·Ru ⁄ (Rэ + Ru)
Ru = p2Ri (Ri – внешняя нагрузка)
Следует отметить, что для максимального коэффициента передачи электромагнитной энергии, выходное сопротивление контура должно быть равно сопротивлению нагрузки. Все вышесказанное справедливо и в случае согласования контура с источником сигнала.
Резонансная частота и волновое сопротивление последовательного контура
 Рассмотрим работу последовательного колебательного контура (рис. 11.1) при воздействии на него идеального источника гармонической э.д.с.
Рассмотрим работу последовательного колебательного контура (рис. 11.1) при воздействии на него идеального источника гармонической э.д.с. 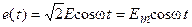 .
.
Определим комплексное сопротивление контура
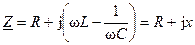 ,
,
где 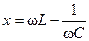 — мнимая составляющая сопротивления
— мнимая составляющая сопротивления
Поскольку при резонансе напряжений мнимая составляющая сопротивления контура равна нулю 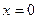 , то на резонансной частоте
, то на резонансной частоте 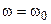 получаем следующее уравнение
получаем следующее уравнение
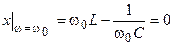 ,
,
решая которое находим угловую резонансную частоту
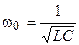 .
.
Угловой частоте 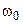 соответствует обычная частота
соответствует обычная частота
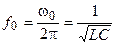 .
.
Из полученного выражения следует, что резонансная частота колебательного контура зависит только от параметров реактивных элементов контура 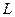 ,
, 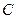 и её можно изменять с помощью перестраиваемых индуктивностей и ёмкостей.
и её можно изменять с помощью перестраиваемых индуктивностей и ёмкостей.
Если частота э.д.с. источника напряжения, действующего в контуре, совпадает с резонансной частотой контура, то такой контур называют настроенным. В противном случае контур называется расстроенным.
Используя выражение для резонансной частоты контура, можно индуктивность контура выразить через ёмкость и наоборот:
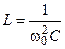 ,
, 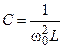 .
.
Из условия резонанса 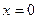 следует, что на резонансной частоте реактивное сопротивление емкости равно реактивному сопротивлению индуктивности. Данное значение сопротивления называется волновым (характеристическим) сопротивление контура, которое можно определить в следующем виде
следует, что на резонансной частоте реактивное сопротивление емкости равно реактивному сопротивлению индуктивности. Данное значение сопротивления называется волновым (характеристическим) сопротивление контура, которое можно определить в следующем виде
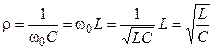 .
.
Таким образом, на резонансной частоте сопротивление последовательного контура является активным 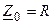 . При этом комплексная и вещественная амплитуды тока контура будут иметь вид
. При этом комплексная и вещественная амплитуды тока контура будут иметь вид
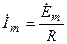 ,
, 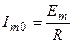
и ток в вещественной форме
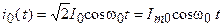 .
.
где 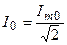 — действующее значение тока контура при резонансе.
— действующее значение тока контура при резонансе.
При расстройке контура модуль его сопротивления 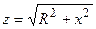 увеличивается, что вызывает уменьшение амплитуды тока
увеличивается, что вызывает уменьшение амплитуды тока
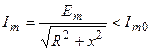 .
.
Поскольку на резонансной частоте сопротивления реактивных элементов контура равны и через них проходит один и тот же ток, то амплитуды напряжения на этих элементах будут также равны:
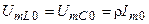 .
.
Дата добавления: 2017-09-01; просмотров: 2215;
Похожие статьи:
Параметры последовательного резонансного контура
Резонансом называется такой режим пассивной электрической схемы, содержащей индуктивности и емкости, при котором входное реактивное сопротивление или входная реактивная проводимость схемы равны нулю, следовательно, равна нулю реактивная мощность на входе схемы, а напряжение и ток на входе совпадают по фазе.
Рассмотрим пассивный двухполюсник, подключенный к источнику гармонического сигнала (рис. 3.47).
Рис. 3.47
Входное сопротивление двухполюсника – это эквивалентное сопротивление схемы, содержащейся в пассивном двухполюснике, относительно полюсов
1 – 2. Любое комплексное сопротивление можно представить в алгебраической форме:
= RВХ + jХВХ,
где RВХ и jХВХ – соответственно активное и реактивное сопротивление входа.
Комплексная входная проводимость может быть представлена в виде:
= gВХ + jbВХ ,
где gВХ и jbВХ – соответственно активная и реактивная составляющие входной
проводимости.
По определению резонанс наступит в схеме, если ХВХ = 0 или bВХ = 0. Следовательно, сопротивление и проводимость при резонансе носят активный характер.
Различают два типа резонанса.
Резонанс напряжений наблюдается в схеме с последовательным соединением участков, содержащих индуктивности и емкости. При резонансе напряжений индуктивное сопротивление одной части схемы компенсируется емкостным сопротивлением другой части схемы:
XL = XC.
Резонанс токов наблюдается в схеме с параллельным соединением участков, содержащих индуктивности и емкости. При резонансе токов индуктивная проводимость одной части схемы компенсируется емкостной проводимостью другой части схемы, параллельно соединенной с первой:
bL = bC.
Рассмотрим подробно резонансный контур при последовательном соединении R, L, C элементов (рис. 3.48):
Рис. 3.48
Такой контур называется последовательным колебательным контуром, потому что идет перекачка магнитной и электрической энергий.
Комплексная схема замещения имеет вид (рис. 3.49):
Рис. 3.49
Существует пять параметров резонансного контура:
– частота резонанса ω0 или f0 ;
– волновое или характеристическое сопротивление ρ ;
– добротность контура Q;
– затухание контура d;
– полоса пропускания контура Δω0 или Δf0 .
Резонансная частота ω0 определяется из основного соотношения:
XL(ω0) = XC(ω0) или XL(ω0) – XC(ω0) = 0.
Можно записать:
ω0L = (ω0С)–1 или ω0 = .
Таким образом, резонансная частота не зависит от активного сопротивления R контура.
Круговая ω0 и линейная f0 частоты связаны соотношением:
ω0 = 2πf0 .
В общем случае пассивного двухполюсника для определения резонансной частоты необходимо определить входное комплексное сопротивление , выделить его реактивную составляющую и приравнять её к нулю. Таким образом,
ХВХ(ω0) = 0– это уравнение для определения частот резонанса в любом пассивном двухполюснике.
Волновое (характеристическое) сопротивление ρ резонансного контура – это сопротивление индуктивности или емкости на резонансной частоте:
ρ = XL(ω0) = XC(ω0) = ω0L = (ω0С)–1.
С учетом формулы для расчета ω0 можно записать:
ρ = .
Добротность Q – это отношение волнового сопротивления к активному сопротивлению контура или, что то же самое, отношение напряжения на реактивном элементе к приложенному:
Q = ρ · R–1 , но поскольку ρ = XL(ω0)
Q = R–1 · .
При последовательном соединении ток один и тот же во всех элементах, следовательно UL = I·XL , UC = I·ХС, UR = I·R = UВХ, так как ZВХ = R при
XВХ = 0.
Таким образом, Q = UL(ω0)· (ω0) = I·XL(ω0)· (I·R)-1 = UС(ω0)· (ω0).
При увеличении активного сопротивления R контура его добротность Q уменьшается.
Добротность Q показывает, во сколько раз напряжение на реактивном элементе (индуктивности или емкости) превышает напряжение на входе контура.
Добротностью QК катушки индуктивности называется отношение:
QК = ХK·R ,
где ХK и RК – сопротивления последовательно включенных индуктивного и
активного элементов в схеме замещения катушки индуктивности.
Добротностью QС конденсатора называется отношение
QС = XС·R ,
где XС и Rс – сопротивления последовательно включенных емкостного и
активного элементов в схеме замещения конденсатора.
Затухание d контура – величина, обратная добротности.
d = R·ρ-1 = R · .
Полоса пропускания Δω0 резонансного контура – это полоса частот вблизи резонансной частоты ω0, на границах которой ток снижается до 0,707 резонансного тока Imax.
Рассмотрим зависимости I(ω), UL(ω) и UС(ω). Построим их в одних координатах (рис. 3.50). Для последовательного контура модуль тока I связан с модулями сопротивлений R, ωL и (ωС)-1 соотношением:
.
Рис. 3.50
Рассмотрим зависимость I(ω) при трех значениях частоты ω.
Пусть ω = 0. Это режим постоянного тока. С позиции физики индуктивность превращается в коротко замкнутое соединение, а емкость – в обрыв. Схема замещения контура примет вид (рис. 3.51):
Рис. 3.51
При ω → ∞ сопротивление индуктивности ωL→ ∞, а емкости (ωС)-1 → 0, то есть индуктивность становится обрывом, а емкость – коротко замкнутым соединением (рис. 3.52). Схема замещения примет вид:
Рис. 3.52
Рассмотрим режим, когда ω = ω0. В этом случае ωL = (ωС)-1, то есть
Z == Zmin = R, следовательно на резонансной частоте ток имеет максимальное значение i(ω0) = Imax.
Рассмотрим зависимости UL(ω) и UС(ω) при постоянных R , L, С.
Зависимость UL(ω)
UL = I·XL = .
При ω = 0 ХL = 0, следовательно UL = 0.
При ω → ∞ UL → Е, так как на индуктивности обрыв и напряжение Е прикладывается к полюсам индуктивности.
При 0 < ω < ω0 растет ток I, растет ХL, следовательно растет и UL.
При ω0 < ω < ∞ ток I уменьшается, растет ХL, следовательно, в этом диапазоне частот наступает максимум UL(ω) при ωLmax > ω0. Можно показать, что ωLmax связана с ω0 соотношением:
.
Зависимость UС(ω)
UС = I·XС = .
При ω = 0 емкость представляет собой разрыв, и э.д.с. прикладывается к её полюсам, то есть UС(0) = Е.
При ω → ∞ сопротивление емкости ХС → 0, следовательно и UС(∞) = 0.
При 0 < ω < ω0 ток I растет, a ХC уменьшается с ростом ω, следовательно, при ωСmax < ω0 наступает максимум функции UС(ω). Можно показать, что ωСmax связана с ω0 соотношением:
Чем больше затухание d, то есть чем больше активное сопротивление R,
тем больше расхождение частот . Чем меньше R, тем ближе
частоты к частоте ω0 и друг к другу.
Рассмотрим зависимость φ(ω)
Для последовательного контура из треугольника сопротивлений следует соотношение (рис. 3.53):
Рис. 3.53
φ = arctg (X·R-1) = arctg {R-1·[ωL – (ωC)-1]}
Исследуем эту зависимость и построим её график (рис. 3.54).
Рис. 3.54
При ω → 0 arctg (−∞) → − 0,5π. Нельзя рассматривать режим ω = 0, так как при постоянном токе угол сдвига фаз φ не имеет смысла.
При ω → ∞ arctg (∞)→ 0,5π.
При ω = ω0 arctg0 = 0.
Если R2 > R1 , то Q2 < Q1 и φ2 < φ1.
Построим зависимость Z(ω) при R = Var.
Построим зависимости XL = ωL, XC = (ωC)-1, (XL – XC), Z(ω) в одних координатах (рис. 3.55).
Рис. 3.55
На графиках (рис. 3.55) приведены зависимости XL(ω), XC(ω), их разность
XL(ω) − XC(ω) и две зависимости Z1(ω) и Z2(ω) для модуля комплексного сопротивления Z(ω), рассчитанные по формуле:
.
Зависимость Z1(ω) соответствует R = R1, а зависимость Z2(ω) соответствует R = R2, при этом R2 > R1 .
Нетрудно видеть, что модуль Z комплексного сопротивления имеет минимум, равный активному сопротивлению R контура на резонансной частоте ω0. Модуль Z возрастает с отклонением частоты ω от резонансной и с уменьшением добротности Q контура.
В заключение несколько слов о влиянии резонансных явлений. Напряжения на индуктивности и емкости в режиме резонанса напряжений могут быть очень большими, а в сумме дают ноль. Это явление называется перенапряжением, оно отрицательно сказывается на изоляции, иногда ведет к пробою − повреждению изоляции.
Пример 25. Дана схема (рис. 3.56).
Рис. 3.56
Резонансная частота ω0 определится:
ω0 = = 103∙( )-1 = 447,2 рад/с;
f0 = ω0∙(2π)-1 = 447,2∙(2∙3,14)-1 = 71,2 Гц;
Q = XL(ω0)∙R-1 = ω0LR-1 = 447,2∙0,1∙10-1 = 4,472;
ρ = XL(ω0) = ω0L = 447,2∙0,1 = 44,72 Ом ;
d = Q-1 = (4,472)-1 = 0,2236.
МЕТОДЫ РАСЧЕТА СЛОЖНЫХ СХЕМ
Схема называется сложной, если она включает несколько источников и (или) соединение элементов типа «звезда» (рис. 4.1,а) или «треугольник»
(рис. 4.1,б):
а) б)
Рис. 4.1
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
3.4. КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ | Политех в Сети
Другой разновидностью линейных цепей являются колебательные контуры. С их помощью решается одна из важнейших задач радиотехники – осуществление частотной селекции (избирательности). Из множества несущих частот различных радиостанций, поступающих в антенну радиоприемника, необходимо выбрать узкую полосу частот интересующей нас радиостанции. Для решения этой задачи нужны частотно–избирательные цепи в виде колебательных контуров. Колебательный контур – это линейная электрическая цепь, составленная из конденсатора  и катушки индуктивности
и катушки индуктивности 
3.4.1.Свободные колебания в идеальном контуре
Рассмотрим вначале колебательный контур, в котором отсутствуют потери электрической энергии, то есть контур из идеальной катушки индуктивности и идеального конденсатора. Зарядим однократно конденсатор от внешней батареи до напряжения  . При этом электрическая энергия, запасенная конденсатором, будет равна
. При этом электрическая энергия, запасенная конденсатором, будет равна
 (3.45)
(3.45)
За счет разряда конденсатора через катушку индуктивности происходит преобразование электрической энергии в магнитную энергию. При этом магнитная энергия, запасенная катушкой индуктивности, становится равной
 . (3.46)
. (3.46)
Затем происходит обратное преобразование магнитной энергии в электрическую энергию. В результате в контуре происходит колебательный процесс на некоторой частоте  , Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:
, Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:
 . (3.47)
. (3.47)
Учитывая, что  , подставим значение
, подставим значение  В предыдущее выражение:
В предыдущее выражение:
 (3.48)
(3.48)
Отсюда резонансная частота колебаний
 , (3.49)
, (3.49)
А период колебаний
 . (3.50)
. (3.50)
Из равенства энергий найдем волновое (характеристическое) сопротивление контура  :
:
 . (3.51)
. (3.51)
На резонансной частоте модуль реактивного сопротивления катушки индуктивности равен модулю реактивного сопротивления конденсатора:
 (3.52)
(3.52)
Подставляя значение резонансной частоты в выражения для модулей реактивных сопротивлений, получим:
 , (3.53)
, (3.53)
 =
= (3.54)
(3.54)
Таким образом, на резонансной частоте сопротивления реактивных элементов контура равны волновому сопротивлению. В идеальном контуре колебания будут незатухающими.
3.4.2.Свободные колебания в реальном контуре
Рассмотрим физические процессы в реальном контуре, состоящем из последовательно соединенных катушки индуктивности, конденсатора и некоторого активного сопротивления потерь  . Сопротивление
. Сопротивление  эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.
эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.

Рис. 3.11. Последовательный колебательный контур
Если зарядить однократно от внешней батареи конденсатор, то в контуре возникнет колебательный процесс. На основе второго закона Кирхгофа можно записать:
 . (3.55)
. (3.55)
Или:
 (3.56)
(3.56)
Продифференцируем все слагаемые уравнения (2.55) по времени и разделим на  :
:
 (3.57)
(3.57)
Обозначим  , Где
, Где  — коэффициент затухания.
— коэффициент затухания.
Учитывая, что  , перепишем уравнение в следующем виде:
, перепишем уравнение в следующем виде:
 (3.58)
(3.58)
Ищем решение этого уравнения в виде: 
 .
.
Подставим это решение в уравнение:
 (3.59)
(3.59)
Или:
 , (3.60)
, (3.60)
Где:  .
.
 — резонансная частота реального контура.
— резонансная частота реального контура.
Решение последнего уравнения имеет вид:
 (3.61)
(3.61)
Отсюда ток в контуре равен:
 . (3.62)
. (3.62)
Полагая начальную фазу j=0, ток в контуре будет равен:
 (3.63)
(3.63)
Если a=0, то колебания не затухают. При этом:
 (3.64)
(3.64)
 (3.65)
(3.65)
В реальном контуре  , поэтому колебания на частоте
, поэтому колебания на частоте  Будут затухающими.
Будут затухающими.


Рис. 3.12. Затухающие колебания в контуре с потерями
Период колебаний реального контура:


 (3.66)
(3.66)
Если  , то период колебаний
, то период колебаний  . При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.
. При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.
Колебательный процесс возможен только, когда  или
или  .
.
Отсюда:  или
или  .
.
У радиотехнических контуров волновое сопротивление  .
.
Поэтому с большой степенью точности можно считать, что период колебаний и резонансная частота в реальном контуре определяются следующими выражениями:
 (3.67)
(3.67)
 (3.68)
(3.68)
По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается добротностью:
 (3.69)
(3.69)
Для радиотехнических контуров добротность 
Добротность контура равна отношению напряжения на индуктивности  или на емкости
или на емкости  к напряжению на активном сопротивлении при резонансе:
к напряжению на активном сопротивлении при резонансе:
 (3.70)
(3.70)
В этом выражении  — Ток в контуре на резонансной частоте.
— Ток в контуре на резонансной частоте.
Умножим числитель и знаменатель на  :
:

 . (3.71)
. (3.71)
Добротность равна умноженному на 2 отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.
отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.
Величина обратная добротности называется затуханием контура:
 . (3.72)
. (3.72)
3.4.3.Последовательный контур. Вынужденные колебания.
На рис. 3.13 представлен последовательный колебательный контур, к которому подключен генератор гармонических сигналов  , внутреннее сопротивление которого равно нулю.
, внутреннее сопротивление которого равно нулю.

Рис3.13. Последовательный контур с внешним генератором
На основании второго закона Кирхгофа запишем:
 . (3.73)
. (3.73)
Ток в контуре будет равен:
 (3.74)
(3.74)
Входное сопротивление

 . (3.75)
. (3.75)
Реактивная составляющая входного сопротивления
 . (3.76)
. (3.76)
В зависимости от расстройки контура относительно резонансной частоты возможны три случая:
 — При этом реактивная составляющая входного сопротивления
— При этом реактивная составляющая входного сопротивления  носит индуктивный характер;
носит индуктивный характер;
 При этом реактивная составляющая входного сопротивления
При этом реактивная составляющая входного сопротивления  носит емкостный характер;
носит емкостный характер;
 при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.
при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.
На резонансной частоте входное сопротивление контура равно активному сопротивлению и ток в контуре равен значению  .
.
Эквивалентная схема контура при резонансе приведена на рисунке.

Рис. 3.14. Эквивалентная схема последовательного контура на
Резонансной частоте.
Амплитуды напряжений на реактивных элементах на резонансной частоте равны по величине и противоположны по фазе.
 . (3.77)
. (3.77)
Из этого выражения найдем резонансную частоту:
 . (3.78)
. (3.78)
Оценим величину отношения напряжений на реактивных элементах на резонансной частоте к напряжению внешнего генератора:
 , (3.79)
, (3.79)
 . (3.80)
. (3.80)
Таким образом, на резонансной частоте в последовательном контуре напряжения на реактивных элементах равны по абсолютной величине и в Q раз превышают напряжение внешнего генератора. Такой резонанс называется резонансом напряжений.
3.4.4.Амплитудно-частотная характеристика последовательного контура.
Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.
Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, представленного на рис. 2.14, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:
 =
= . (3.81)
. (3.81)
Реактивная составляющая входного сопротивления контура равна:
 (3.82)
(3.82)
Здесь
 (3.83)
(3.83)
— относительная расстройка контура.
Для небольших абсолютных расстроек контура  (в пределах полосы пропускания)
(в пределах полосы пропускания)
 (3.84)
(3.84)
С учетом этого амплитудно-частотная характеристика контура
 , (3.85)
, (3.85)
Где:  — обобщенная расстройка контура.
— обобщенная расстройка контура.
Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:
 . (3.86)
. (3.86)
Фазовая характеристика контура
 (3.87)
(3.87)
При настройке контура в резонанс  , обобщенная расстройка
, обобщенная расстройка  , реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно
, реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно  . Характер зависимости
. Характер зависимости  свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности
свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности  , который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров
, который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров 
 . АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.
. АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.
Рис.2.15 АЧХ последовательного контура
Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в  раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:
раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:
 . (3.88)
. (3.88)
Отсюда полоса пропускания контура на уровне  Будет равна:
Будет равна:
 (3.89)
(3.89)
Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:
 (3.90)
(3.90)
Фазовая характеристика последовательного контура, построенная по выражению (2.98), приведена на рис. 3.16.
 (3.91)
(3.91)

Рис.3.16. Фазовая характеристика последовательного контура
3.4.5. Параллельный колебательный контур.
Параллельный колебательный контур состоит из параллельно включенных катушки индуктивности и конденсатора, как показано на рис. 3.17. Активное сопротивление катушки индуктивности равно  , а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению
, а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению  . Контур питается идеальным генератором тока.
. Контур питается идеальным генератором тока.

Рис. 3.17. Параллельный колебательный контур.
Входное сопротивление контура равно:
 . (3.92)
. (3.92)
Для высокодобротных контуров в области резонансной частоты  и
и  . Учитывая это, можно записать:
. Учитывая это, можно записать:
 (3.93)
(3.93)
Где:  ;
;  .
.
Таким образом, входное сопротивление зависит от частоты. Токи в ветвях контура также зависят от частоты. На резонансной частоте  сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток
сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток
 . (3.94)
. (3.94)
Входное сопротивление контура при резонансе становится активным и равно:
 (3.95)
(3.95)
Следовательно, ток в контуре на резонансной частоте равен:
 (3.96)
(3.96)
Таким образом, токи в ветвях контура при резонансе в  раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.
раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.
Зависимость отношения амплитуды напряжения на контуре  на текущей частоте к амплитуде напряжения на контуре на резонансной частоте
на текущей частоте к амплитуде напряжения на контуре на резонансной частоте  от частоты называют амплитудно-частотной характеристикой параллельного контура.
от частоты называют амплитудно-частотной характеристикой параллельного контура.
Запишем выражение для амплитудно-частотной характеристики параллельного контура:
 (3.97)
(3.97)
Входное сопротивление контура равно:
 (3.98) Умножим числитель и знаменатель этого выражения на (
(3.98) Умножим числитель и знаменатель этого выражения на ( ):
):
 . (3.99)
. (3.99)
Найдем модуль входного сопротивления:
 . (3.100)
. (3.100)
Подставив модуль входного сопротивления в выражение (3.97), окончательно получим:
 . (3.101)
. (3.101)
Таким образом, АЧХ параллельного и последовательного контуров описываются одним и тем же выражением.
Фазовая характеристика параллельного контура (рис. 2.18) построена на основании выражения
 (3.102)
(3.102)

Рис. 3.18. Фазовая характеристика параллельного контура
3.4.6. Методы измерения добротности колебательных контуров
Существует несколько методов измерения добротности колебательных контуров.
Если подключить к контуру генератор гармонических сигналов и, изменяя частоту генератора, снять резонансную кривую контура, то добротность можно рассчитать по формуле:
 , (3.103)
, (3.103)
Где:  — резонансная частота;
— резонансная частота;
 — полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.
— полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.
Добротность контура можно также измерить по затухающим колебаниям в контуре, если подключить к контуру генератор прямоугольных импульсов. При этом прямоугольные импульсы должны быть достаточно короткими и с большим периодом, чтобы к моменту прихода следующего импульса колебания в контуре уже успели закончится (рис. 3.19).

Рис. 3.19. Определение добротности по затухающим колебаниям
Если обозначить начальную амплитуду затухающих колебаний  , то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в
, то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в  раз, можно рассчитать добротность, исходя из следующих выражений:
раз, можно рассчитать добротность, исходя из следующих выражений:
 , (3.104)
, (3.104)
 , (3.105)
, (3.105)
 . (3.106)
. (3.106)
Таким образом, добротность равна умноженному на  числу периодов, в течение которых начальная амплитуда колебаний уменьшается в
числу периодов, в течение которых начальная амплитуда колебаний уменьшается в  Раз.
Раз.
Кроме названных методов измерения добротности существуют специальные приборы — измерители добротности колебательных контуров.
3.4.7. Связанные контуры.
Недостатком одиночных колебательных контуров является их плохая избирательность. Количественно избирательность оценивается коэффициентом прямоугольности, который равен отношению ширины полосы пропускания на уровне 0,7 к ширине полосы пропускания на уровне 0,1 (иногда на уровне 0,01):
 . (3.107)
. (3.107)
Чем ближе значение коэффициента прямоугольности к 1, тем лучше избирательность контура.
Коэффициент прямоугольности одиночного контура  = 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.
= 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.
Ценным свойством связанных контуров является возможность осуществить АЧХ по форме, близкую к прямоугольной. Связанные контуры взаимно влияют друг на друга. Степень влияния зависит от сопротивления связи. В качестве элементов связи используют конденсаторы и индуктивности. Чаще всего используют индуктивную (трансформаторную) связь. В этом случае степень связи определяется коэффициентом взаимной индукции  . В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где
. В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где  — коэффициент взаимной индукции,
— коэффициент взаимной индукции,  – сопротивление связи.
– сопротивление связи.


Рис. 3.20. Связанные контуры и их эквивалентная схема
Коэффициент взаимной индукции равен:
 , (3.108)
, (3.108)
Где:  — магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;
— магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;
 — магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.
— магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.
Для неферромагнитной среды  .
.
Эдс, индуцируемая во втором контуре, равна:

 (3.109)
(3.109)
Сопротивление связи равно
 . (3.110)
. (3.110)
Степень связи между контурами оценивается коэффициентом связи  , который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.
, который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.
Коэффициент передачи напряжения из первого контура во второй равен:

 (3.111)
(3.111)
Если включить генератор во второй контур, то получим коэффициент передачи напряжения из второго контура в первый:
 . (3.112)
. (3.112)
Коэффициент связи между контурами равен среднему геометрическому из коэффициентов передачи:
 (3.113)
(3.113)
Коэффициент связи выражает отношение общего магнитного потока, пронизывающего обе катушки индуктивности, к полному магнитному потоку. Величина ( ) характеризует поток рассеяния.
) характеризует поток рассеяния.
Выясним характер и форму амплитудно-частотной характеристики системы из двух индуктивно связанных контуров, представленных на рис.2.20. Для упрощения предположим, что контуры состоят из одинаковых элементов  и поэтому имеют одинаковую резонансную частоту
и поэтому имеют одинаковую резонансную частоту  . АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте
. АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте  . Две другие соответствуют максимуму коэффициента передачи и будут на частотах
. Две другие соответствуют максимуму коэффициента передачи и будут на частотах
 , (3.114)
, (3.114)
 . (3.115) .
. (3.115) .
Частоты  зависят от коэффициента связи
зависят от коэффициента связи  и величины затухания контуров
и величины затухания контуров  и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи.
и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи.  — быстрая частота связи, а
— быстрая частота связи, а  — медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.
— медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.

Рис. 3.21. Зависимость частот связи от коэффициента связи
При критической связи  и на резонансной кривой будет один максимум на частоте
и на резонансной кривой будет один максимум на частоте  .
.
При связи меньше критической  формулы для частот связи
формулы для частот связи  и
и  не имеют смысла и на АЧХ будет только один максимум на частоте
не имеют смысла и на АЧХ будет только один максимум на частоте  .
.
При связи больше критической ( ) на АЧХ появляются два максимума на частотах
) на АЧХ появляются два максимума на частотах  и
и  .
.

Рис. 3.22. АЧХ одиночного и двух связанных контуров ( ).
).
Полоса пропускания связанных контуров определяется, как ширина АЧХ на уровне 0,7 от максимальной ординаты при этом минимум АЧХ также должен быть на уровне 0,7. Можно показать, что при одинаковом затухании и  Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности
Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности  = 0,6 , а для трёх – 0,65.
= 0,6 , а для трёх – 0,65.
В серийно выпускаемой радиоаппаратуре в качестве элементов, обеспечивающих высокую избирательность используют пъезофильтры, созданные на основе пьезоэлектриков. Пьезоэлектрики – кристаллические вещества, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация (прямой пьезоэффект). Следствием прямого пьезоэффекта является обратный пьезоэффект – появление механической деформации под действием электрического поля. Пьезофильтр состоит из отдельных, объединенных в группы пьезоэлементов (стержней, пластинок) с нанесенными на определенные поверхности электродами, к которым подводится электрическое напряжение, для создания деформации в результате обратного пьезоэффекта. Пьезофильтр обеспечивает хорошую прямоугольность АЧХ. Добротность керамических пьезофильтров составляет несколько тысяч, а затухание вне полосы составляет -60дБ.
42. Определение резонанса, понятие последовательного и параллельного колебательных контуров.
Последовательный
колебательный контур – это цепь,
составленная из последовательно
соединенных индуктивности и
ёмкости.(рис1)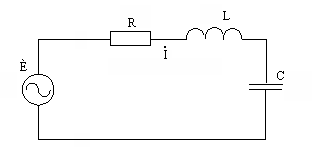 рис
1
рис
1
R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах. При этом сами L и C, можно представить как идеальные без потерь.
È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов
Ζ = R + (jωL + 1 / jωC) = R + jωX
Или, что тоже самое:
Ζ = ¦Ζ¦ejφ, где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC)
Параллельным
колебательным контуром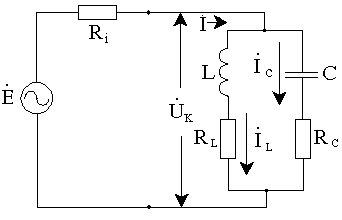 называется
цепь, составленная из катушки индуктивности
и конденсатора, подключенных параллельно
выходным зажимам источника. RL и
RC –
это внутренние сопротивления потерь
конденсатора и катушки, представленные
в виде «виртуальных» элементов.
Ri –
это внутреннее сопротивление источника.
называется
цепь, составленная из катушки индуктивности
и конденсатора, подключенных параллельно
выходным зажимам источника. RL и
RC –
это внутренние сопротивления потерь
конденсатора и катушки, представленные
в виде «виртуальных» элементов.
Ri –
это внутреннее сопротивление источника.
43.Условие и способы получения резонанса. Резонансная частота
Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
44. Резонанс в последовательном колебательном контуре. Добротность, векторная диаграмма. Характеристическое сопротивление, затухание контура.
Резонанс напряжений – явление, при котором цепь содержащая активные и реактивные сопротивления, будет только активное сопротивление (XL — XC = 0). При этом ток в цепи совпадает по фазе с напряжением. Условие возникновение резонанса напряжений – равенство нулю реактивного сопротивления.
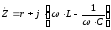
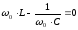
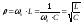 — характеристическое
сопротивление контура.
— характеристическое
сопротивление контура.
Таким
образом: 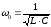 – резонансная
частота
– резонансная
частота
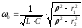 -резонансная
для парралельного
-резонансная
для парралельного
При
резонансе напряжений ток максимален,
так как сопротивление минимально, а 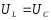
Добротностью контура называется отношение модуля реактивной составляющей напряжения в цепи к модулю входного напряжения в момент резонанса.
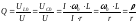
Полосу
частот вблизи резонанса, на границах
которой ток снижается до величины 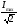 принято называтьполосой
пропускания резонансного тока.
принято называтьполосой
пропускания резонансного тока.
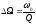
Чем больше добротность, тем острее кривая и уже полоса пропускания