Простая волновая обмотка

Дата публикации: 26 мая 2014.
Категория: Машины постоянного тока.

Общие положения

Рисунок 1. Секции неперекрещенной (а) и перекрещенной (б) простой волновой обмотки

Мысленно обходя последовательно соединенные секции простой волновой обмотки, мы совершаем волнообразный обход якоря, причем каждый обход включает p секций и заканчивается на коллекторной пластине, которая находится слева или справа рядом с исходной (рисунок 1). В первом случае (рисунок 1, а), получается неперекрещенная обмотка, а во втором (рисунок 1, б) – перекрещенная. Во втором случае расход меди будет несколько больше. Рассматриваемую обмотку называют также простой последовательной обмоткой.

В соответствии со сказанным между шагом по коллектору y_к (рисунок 1) и числом коллекторных пластин K простой волновой обмотки существует зависимость

p × y_к ± 1 = K ,

откуда

(1)

Знак минус относится к неперекрещенной  обмотке, а знак плюс – к перекрещенной. Поскольку шаг y_к = y должен быть целым числом, то K не может принимать произвольных значений.

Шаг y₁ определяется по формуле (1), представленной в статье «Электродвижущая сила секций», и выражению

Шаги y₁ и y₂ близки к τ, а y = y_к — к 2×τ.

Симметричная волновая обмотка

Ознакомимся со свойствами простой волновой обмотки на примере обмотки с 2×p = 4 и Z = Z_э = S = K = 17. Возьмем при этом

и

y₂ = y – y₁ = 8 – 4 = 4 .

Порядок соединений секционных сторон обмотки определяется таблицей на рисунке 2, а схема обмотки имеет вид, показанный на рисунке 3. Ряд секций, выделенных на рисунке 3 жирными линиями, в отличие от секций петлевых обмоток замыкается накоротко через две щетки одной полярности и соединительные провода между ними. Короткозамкнутые секции обведены рамкой также и на рисунке 2

Рисунок 2. Таблица соединений секционных сторон простой волновой обмотки, показанной на рисунке 3

На рисунке 4 построены звезда электродвижущих сил секций и векторная диаграмма электродвижущих сил обмотки, представленной на рисунке 3. Масштаб звезды электродвижущих сил в два раза больше масштаба многоугольника электродвижущих сил.

Рисунок 3. Схема простой волновой обмотки с 2×p = 4, Z = Z_э = S = K = 17, y₁ = 4, y₂ = 4, y_к = 8

Как следует из рисунка 2, 3 и 4, обмотка имеет две параллельные ветви. Одна из них содержит секции 17, 8, 16, 7, 15, 6, присоединена своими концами к коллекторным пластинам 17, 14 и расположена, таким образом, между щетками А2, В2. Другая ветвь содержит секции 13, 4, 12, 3, 11, 2, присоединена концами к пластинам 13, 10 и расположена между щетками В2, А1.

Полученный вывод носит общий характер: всякая простая волновая обмотка имеет число параллельных ветвей

и векторная диаграмма электродвижущих сил такой обмотки всегда состоит из одного многоугольника.

Поскольку каждая из ветвей простой волновой обмотки проходит под всеми полюсами, то неравенство потоков полюсов не вызывает неравенства электродвижущих сил и токов параллельных ветвей. Поэтому такая обмотка не нуждается в уравнительных соединениях.

Рисунок 4. Векторная диаграмма электродвижущих сил обмотки, изображенной на рисунке 3

Более того, согласно выражению (5), представленному в статье «Простая петлевая обмотка», и выражению (1), данной статьи, шаг y_п в простой волновой обмотке является нецелым числом, и поэтому равнопотенциальных точек не имеется, что видно также из рисунка 4.

При волновой обмотке на коллекторе можно установить только два щеточных пальца, например А1 и В2 на рисунке 3, так как все щетки данной полярности соединены короткозамкнутыми секциями, через которые ток нагрузки распределяется по параллельно работающим щеткам каждой полярности. Два щеточных пальца примут на себя весь ток нагрузки. Эта возможность иногда используется в машинах мощностью до 0,5 кВт, если доступ для ухода за щетками по всей окружности коллектора затруднен. Однако условия коммутации при этом ухудшаются. Кроме того, в более мощных машинах возникает необходимость удлинять коллектор. Поэтому обычно ставится полный комплект (2×p) щеточных пальцев.

При а = 1 условия симметрии, описанные выражениями (5), (6) и (7) в статье «Общие сведения о якорных обмотках машин постоянного тока», удовлетворяются при любых p, Z, u_п и K. Однако возможности выбора этих величин ограничиваются соотношением (1), настоящей статьи, которое при подстановке K = u_п × Z принимает вид

(4)

Поскольку шаг y_к должен быть целым числом, то отсюда видно, что, например, при четных p как Z, так и u_п должны быть нечетными (u_п = 1, 3, 5…).

Простая волновая обмотка с мертвой секцией

Трудности в соблюдении равенства (1) или (4) в ряде случаев обходят, используя несимметричные обмотки. Например, при четных p и Z_э = u_п × Z можно применить обмотку с K = Z_э – 1 и оставить одну секцию неиспользованной, или «мертвой». У этой секции обрезаются концы, и она не присоединяется к коллектору (секция оставляется на якоре, чтобы не нарушать балансировки).

Схема такой обмотки для 2×p = 4, Z_э = 16 и K = 15 показана на рисунке 5, причем принято, что

При обходе обмотки и счете шагов стороны мертвой секции исключаются.

Рисунок 5. Схема простой волновой обмотки с мертвой секцией с 2×p = 4, Z = Z_э = 16, K = 15, y₁ = 4, y₂ = 4, y_к = 8

Искусственно замкнутая простая волновая обмотка

Предположим, что Z_э = S = K = 16 и 2×p = 4. Шаги обмотки выберем из предположения, что Z_э, S и K на единицу больше, то есть Z_э = S = K = 17. При этом, согласно выражению (1), можно взять

Исходя из таких значений шагов, составляем схему обмотки (рисунок 6), начиная, например, с пластины 1. При первом обходе вокруг якоря проходим секции 1 и 1 + 8 = 9 и должны были бы прийти к пластине 9 + 8 = 17. Второй обход должен был бы включать в себя секции 17 и 8. Однако, поскольку секции 17 и пластины 17 нет, то после завершения первого обхода конец секции 9 с помощью обходной перемычки непосредственно соединяем с пластиной 8 и началом секции 8. После этого ход обмотки следует по обычным правилам с тем лишь отличием, что каждый второй результирующий шаг сокращается на единицу.

Рисунок 6. Схема искусственно замкнутой простой волновой обмотки с 2×p = 4, Z = Z_э = S = K = 16, y₁ = 4, y₂ = 4, y_к = 8

Рассмотренные несимметричные волновые обмотки находят применение в машинах мощностью до нескольких десятков киловатт и работают вполне удовлетворительно.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

Простая волновая обмотка машин (двигателей) постоянного тока

Простой волновой обмоткой называется обмотка, в которой пос­ледовательно соединяются секции, находящиеся под разными парами полюсов. При этом расстояние между коллекторными пластинами, к которым присоединяются концы секции (рисунок 1), примерно равно двойному полюсному делению

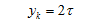
т.е. за один обход по якорю укладывается столько секций, сколько пар полюсов имеет машина. При этом конец последней по обходу сек­ции присоединяют к коллекторной пластине, расположенной рядом с исходной слева или справа. В зависимости от этого обмотку назы­вают левоходовой или правоходовой. Обычно применяют левоходовую обмотку.

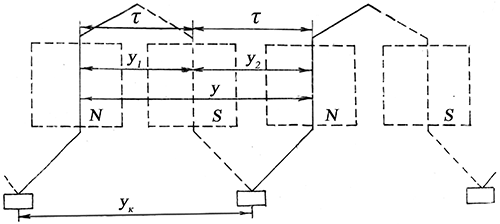
Рисунок 1 — Простая волновая обмотка

За один обход перемещаются по коллектору на  p·y_к  кол­лекторных делений. Следовательно,

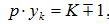
( – ) – для левоходовой обмотки;

( + ) – для правоходовой обмотки.

Отсюда определяется шаг обмотки по коллектору

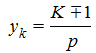
Продолжая в том же порядке укладывать секции, мы замкнем обмотку на исходной коллекторной пластине. Исходя из принципа соответствия хода обмотки по якорю и коллектору, результирующий шаг обмотки

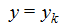
Первый частичный шаг определяется по известной формуле

Определяем второй частичный шаг. Из рисунка 1

На рисунке 2 и 3 представлены развернутая и электрическая схема простой волновой обмотки с данными

Порядок построения: 1-й верхний проводник соединяется с 4-м нижним (у₁=3), затем с 7-м верхним (у₂=3) с 10 нижним 13 верхним и т. д.Соединия между секциями припаиваются к ближайшим коллекторным плас­тинам. Шаг по коллектору при этом получается у_к=6. Как видим из схемы, ток в обмотке якоря разветвляется только по двум параллель­ным ветвям: первая ветвь – 12, 5, 11, 4 секции, вторая ветвь – I, 8, 2, 9 секции.

Рисунок 2 — развернута, схема простой волновой обмотки

 

Параллельная ветвь в волновых обмотках обра­зуется из последовательно соединенных секций, лежащих под всеми полюсами машины. Число параллельных ветвей 2а у простой волновой обмотки независимо от числа полюсов машины равно 2, т.е. 2а=2.

 Рисунок 3 — Электрическая схема простой волновой обмотки

Секции 6, 13, 7 и 10, 3 не участвуют в наведении ЭДС, так как они оказываются короткозамкнутыми (коммутируемыми) при данном положе­нии якоря.

Простая волновая обмотка может быть выполнена только при опреде­ленном сочетании S и р. Например, при четном  S  и  р  ре­зультирующий шаг y не получается в виде целого числа. Для обра­зования волновой обмотки в этом случае одну секцию, оставляя ее на якоре, не включают в общую схему. Такую обмотку называют волновой с «мёртвой» секцией.

Обмотки якоря | Электрикам

Элементом обмотки якоря является секция, которая своими концами присоединена к двум пластинам коллектора. Секции могут быть одновитковыми и многовитковыми. Пазовые стороны секций расположены в пазах сердечника якоря. Расстояние между пазовыми сторонами секции приблизитеьно равно полюсному делению.

где D_a — диаметр сердечника якоря.

Обычно обмотки якоря выполняют двухслойными. В зависимости от порядка присоединения секций к пластинам коллектора обмотки разделяют на волновые и петлевые, простые, сложные и комбинированные.

Простая волновая обмотка

В простой волновой обмотке концы каждой секции присоединены к пластинам коллектора, находящимся на расстоянии, называемом шагом обмотки по коллектору,

где К — число коллекторных пластин в коллекторе.

На рис. 13.5 показана схема простой волновой обмотки якоря. Секции обмотки образуют две параллельные ветви (2а = 2). Число параллельных ветвей в обмотке и число секций в каждой ветви определяют ток I_а и ЭДС Е_а обмотки якоря:

где S — количество секций в обмотке якоря; е_с — ЭДС одной секции; I_с — допустимое значение тока в секции.

Сложная волновая обмотка

Применяется в машинах постоянного тока, рассчитанных на большие токи. Сложная волновая обмотка состоит из двух простых волновых обмоток, соединяемых щетками параллельно (рис. 13.6). Такая обмотка содержит четыре параллельные ветви, следовательно, ток в ней может быть увеличен в два раза, а ЭДС при этом остается прежней.

Простая петлевая обмотка

В машинах постоянного тока низкого напряжения (значительного тока) необходима обмотка якоря с большим числом параллельных ветвей. Таким свойством обладают петлевые обмотки. В простой петлевой обмотке якоря (рис. 13.7) каждая секция присоединена к двум рядом лежащим коллекторным пластинам, а число параллельных ветвей равно числу полюсов, т.е. 2а = 2р.

Сложная петлевая обмотка

При необходимости получить еще большее число параллельных ветвей применяют сложную петлевую обмотку якоря (рис. 13.8). Такая обмотка содержит две простые петлевые обмотки (m = 2), поэтому у нее число параллельных ветвей удвоено, т.е. 2а =  2 * 2р = 4р. Такие обмотки необходимы в машинах значительной мощности при низком напряжении сети: 12; 24; 48 В.

Для того чтобы распределение токов в параллельных ветвях обмотки якоря было одинаковым, необходимо, чтобы электрическое сопротивление этих ветвей не отличалось друг от друга и чтобы ЭДС, наводимые в секциях, составляющих каждую параллельную ветвь, были одинаковыми. При несоблюдении этих условий между параллельными ветвями появляются уравнительные токи, нарушающие работу щеточно-коллекторного контакта.

Исключение составляет простая волновая обмотка, секции которой равномерно распределены под всеми полюсами машины, поэтому магнитная не симметрия машины не вызывает появления в этой обмотке уравнительных токов. Что же касается простой петлевой и всех видов сложных обмоток якоря, то в них всегда имеются причины к появлению уравнительных токов. Это приводит к необходимости применения в указанных обмотках так называемых уравнительных соединений, по которым замыкаются уравнительные токи, разгружая щеточно-коллекторный контакт от перегрузки. Уравнительные соединения усложняют изготовление обмотки якоря и ведут к дополнительному расходу обмоточной меди.

Комбинированная обмотка

 В электрических машинах со значи­тельным током в обмотке якоря простые волновые обмотки неприменимы, так как в этих обмотках число параллельных ветвей не может быть более двух. Чтобы увеличить число параллельных ветвей и избежать нежелательного применения уравнительных соединений в машинах с большой токовой нагрузкой, используют комбинированную обмотку. Такая обмотка состоит из секций волновой и петлевой обмоток, а число параллельных ветвей в ней равно сумме параллельных ветвей петлевой и волновой обмоток. Необходимо, чтобы число параллельных ветвей волновой обмотки было равно числу ветвей петлевой обмотки. Поэтому в четырехполюсной машине комбинированную обмотку выполняют из простой петлевой (2а = 2р = 4) и сложной волновой (m = 2) обмоток. В этом случае число параллельных ветвей комбинированной обмотки равно 2а_комб = 4 + 4 = 8. В такой обмотке ветви одной из составляющих обмоток служат уравнительными соединениями для другой. В итоге комбинированная обмотка с таким числом параллельных ветвей оказывается проще сложной петлевой обмотки.

§ 25.2. Волновые обмотки якоря

Простая волновая обмотка. Простую волновую обмотку получают при последовательном соединении секций, находящихся под разными парами полюсов (рис. 25.7). Концы секций простой волновой обмотки присоединены к коллекторным пластинам, уда­ленным друг от друга на расстояние шага обмотки по коллектору

у_к =у. За один обход по якорю укладывают столько секций, сколь­ко пар полюсов имеет машина, при этом конец последней по об­ходу секции присоединяют к пластине, расположенной радом с исходной.

Простую волновую обмотку называют левоходовой, если ко­нец последней по обходу секций присоединяется к пластине, на­ходящейся слева от исходной (рис. 25.7, а). Если же эта пластина находится справа от исходной, то обмотку называют правоходовой (рис. 25.7, б).

Секции волновой обмотки могут быть одновитковыми и многовитковыми. Шаг простой волновой обмотки по кол­лектору

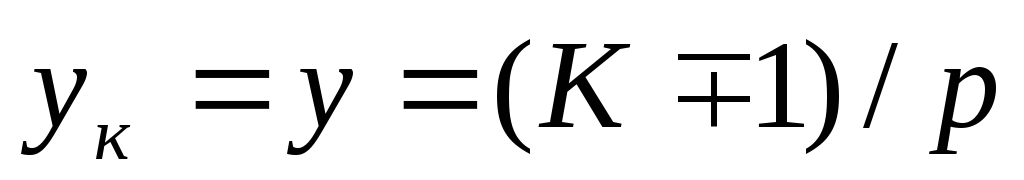(25.6)

Знак минус соответствует левоходовой обмотке, а знак плюс — правоходовой. Правоходовая обмотка не получила практического применения, так как ее выполнение связано с дополнительным расходом меди на перекрещивание лобовых частей.

Первый частичный шаг обмотки определяют по (25.3), а вто­рой частичный шаг

.

Пример 25.4. Четырехполюсная машина постоянного тока имеет простую волновую обмотку якоря из 13 секций. Построить развернутую схему и схему параллельных ветвей этой обмотки.

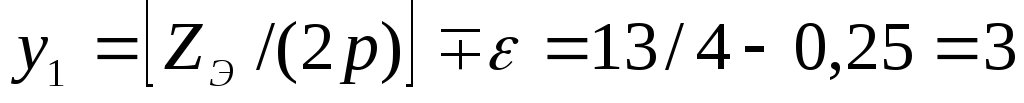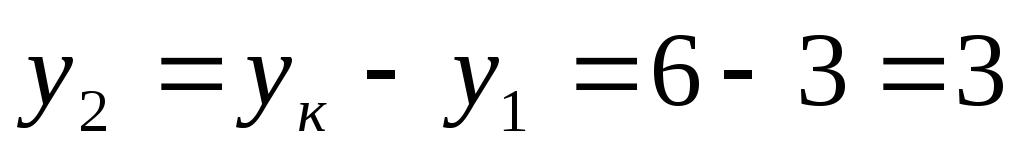Решение. Шаги обмотки: пазов; паза; паза.

При первом обходе по якорю укладываем секции 1 и 7 (рис. 25.7,

в). При втором обходе укладываем секции 13 и 6 и т. д., пока не будут уложены все 13 секций и обмотка не окажется замкнутой. Секции 3, 6 и 9 в рассматриваемый момент времени замкнуты на коротко через щетки одинаковой полярности и провода, соеди­няющие их.

Рис. 25.7. Простая волновая обмотка: а — правоходовая, б — левоходовая; в — развернутая схема

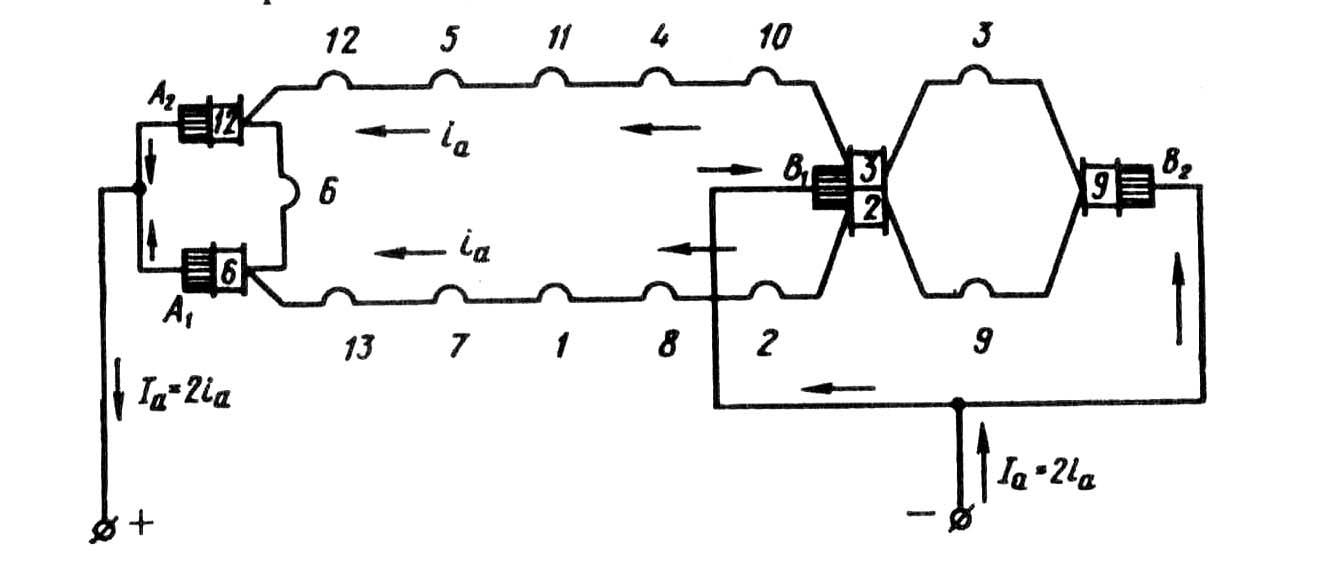
Рис. 25.8. Электрическая схема обмотки рис. 25.7, в

Затем определяем полярность щеток. Далее выполня­ем электрическую схему (схему параллельных ветвей), из которой видно (рис. 25.8), что обмотка состоит из двух параллельных вет­вей (2

=2). Это является характерным для простых волновых об­моток, у которых число параллельных ветвей не зависит от числа полюсов и всегда равно двум.

Из рассмотренных схем видно, что секции, входящие в одну параллельную ветвь, равномерно распределены под всеми полю­сами машины. Следует также отметить, что в простой волновой обмотке можно было бы обойтись двумя щетками, например щет­ками и

. Но в этом случае нарушилась бы симметрия обмотки, и число секций в параллельных ветвях стало бы неодинаковым: в одной ветви семь секций, а в другой — шесть. Поэтому в ма­шинах с простыми волновыми обмотками устанавливают пол­ный комплект щеток, столько же, сколько главных полюсов, тем более что это позволяет уменьшить значение тока, прихо­дящегося на каждую щетку, а следовательно, уменьшить раз­меры коллектора.

Сложная волновая обмотка (рис. 25.9). Несколько простых волновых обмоток (обычно две), уложенных на одном якоре, образуют сложную волновую обмотку.

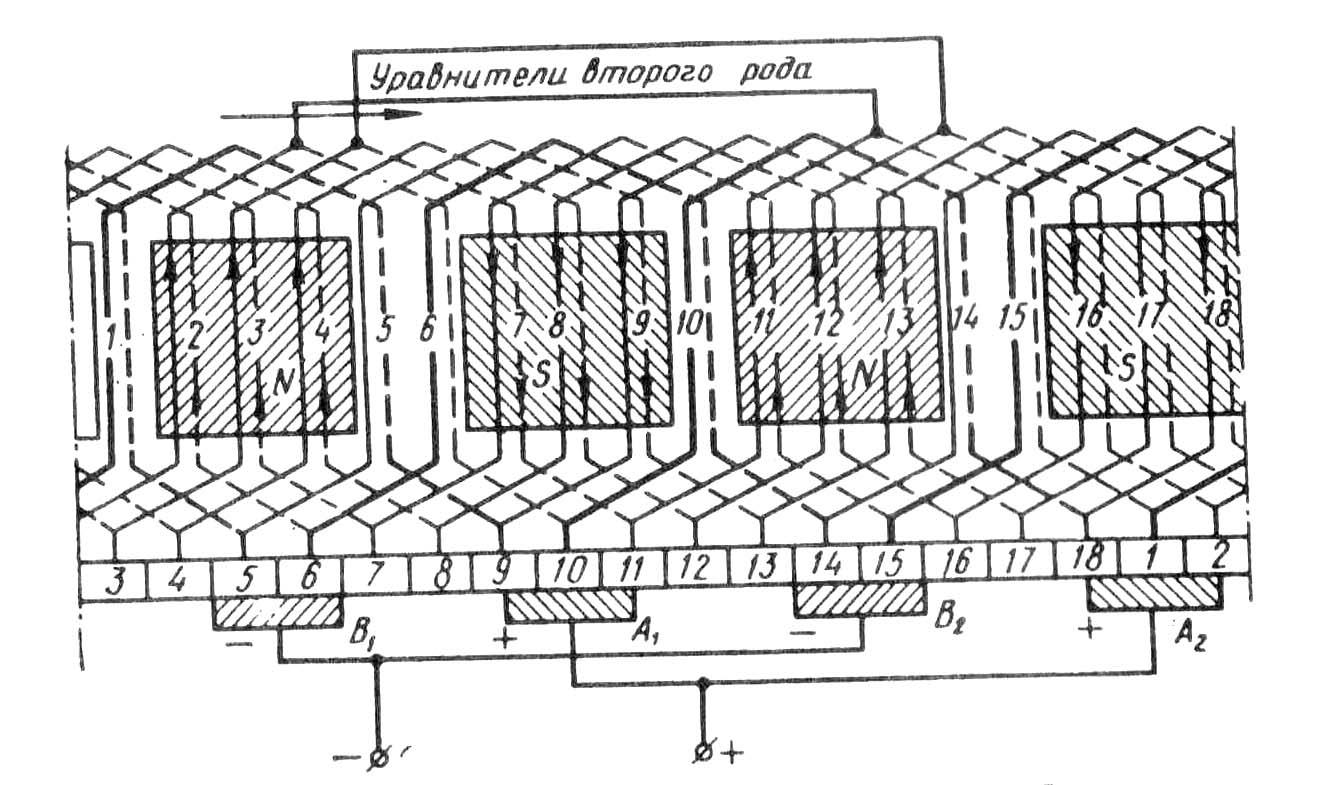
Рис. 25.9. Развернутая схема сложной волновой обмотки

Число параллельных ветвей в сложной волновой обмотке 2=2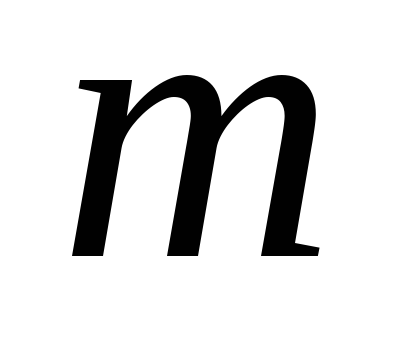(обычно 2= 4), гдет — чис­ло простых обмоток в сложной (обычно т = 2). Простые обмотки, входящие в сложную, соединяют параллельно посредством щеток. Шаг по коллектору, а следовательно, и результирующий шаг по якорю

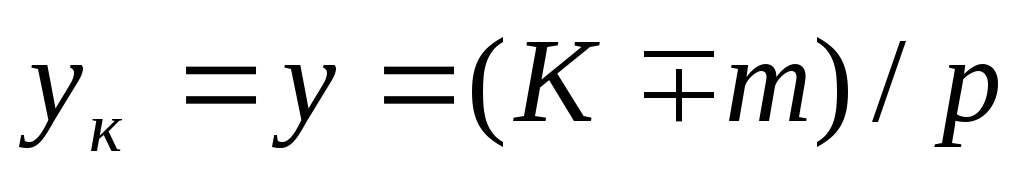. (25.7)

Первый частичный шаг по якорю определяют по (25.3).

Пример 25.5. Сложная волновая обмотка с 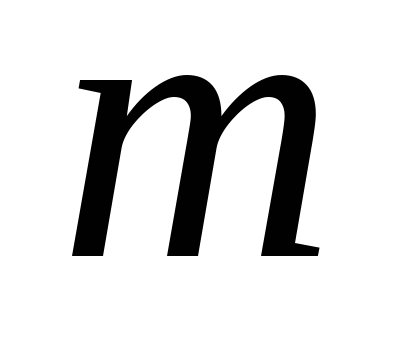= 2 состоит из 18 секций.

Выполнить развернутую схему этой обмотки, если 2=4.

Решение. Шаги обмотки: 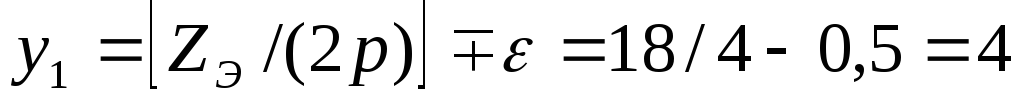паза,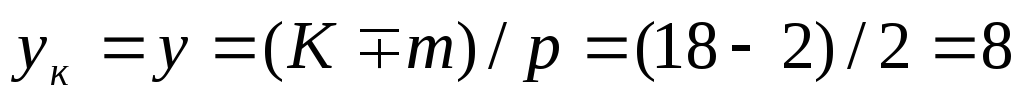 пазов; 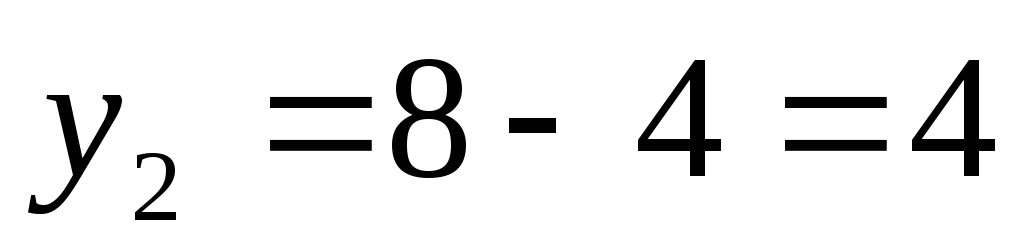паза.

Порядок выполнения схемы обмотки такой же, как и при сложной петлевой обмотке: сначала укладывают в пазы якоря одну простую обмотку, состоящую из нечетных секций, а затем другую, состоящую из четных секций (рис. 25.9) Число параллельных ветвей в обмотке 2 = 4.

Сложная волновая обмотка

Дата публикации: 01 июня 2014.
Категория: Машины постоянного тока.

Общие положения

Сложную волновую обмотку можно рассматривать как сочетание m простых волновых обмоток, которые включаются на параллельную работу с помощью щеток. Число параллельных ветвей такой обмотки соответственно в m раз больше числа ветвей простой волновой обмотки:

Рассматриваемую обмотку называют также сложной последовательной обмоткой.

Согласно соотношению (7), представленному в статье «Общие сведения о якорных обмотках машин постоянного тока» и выражению (1), данной статьи, выполнение симметричных m-ходовых волновых обмоток возможно при условии

2 × p / m = целое число

(2)

Максимально возможное число ходов при этом

m = 2 × p

и максимальное число ветвей

2 × a = 4 × p ,

то есть такое же, как и у двухходовой петлевой обмотки. Секции и коллекторные пластины m ходов обмотки по окружности чередуются. Поэтому после одного обхода p последовательно соединенных секций вокруг якоря мы должны выйти не к соседней с исходной пластине коллектора, как при простой волновой обмотке, а со сдвигом на m делений влево или в право. В соответствии с этим

p × y_к ± m = K

и

(3)

Шаги y₁ и y₂ = y – y₁ определяются обычным образом. Кратность замыкания обмотки равна общему наибольшему делителю чисел m и K.

Рассмотрим двухходовую двукратнозамкнутую обмотку со следующими данными: 2×p = 4, m = 2, 2×a = 4, Z = Z_э = S = K = 18. Условия симметрии, описанные выражениями (5) – (7), в статье «Общие сведения о якорных обмотках машин постоянного тока», при этом удовлетворяются.

Выберем шаги:

Рисунок 1. Таблица соединений секционных сторон сложной волновой обмотки, изображенной на рисунке 2

На основании этих данных составлены таблица соединения секционных сторон обмотки (рисунок 1) и схема обмотки (рисунок 2). Обмотка состоит из не связанных между собой двух простых волновых обмоток, из которых одна охватывает нечетные секции и пластины, а другая – четные. На основании рисунка 1 и схемы рисунка 2 на рисунке 3 изображены звезда пазовых электродвижущих сил и векторная диаграмма электродвижущих сил обмотки. Диаграмма состоит из двух накладывающихся друг на друга многоугольников.

Уравнительные соединения

Для равномерной нагрузки отдельных ходов сложной волновой обмотки ее нужно снабдить уравнителями второго рода.

Рисунок 2. Схема двухходовой двукратнозамкнутой волновой обмотки с 2×p = 4, m = 2, Z = Z_э = S = K = 18, y₁ = 5, y₂ = 3, y = y_к = 8

Рисунок 3. Векторная диаграмма электродвижущих сил обмотки, изображенной на рисунке 2

В рассмотренных выше случаях равнопотенциальный шаг

y_п = K / p

соответствует сдвигу по коллектору на два полюсных деления. Однако в сложных волновых обмотках K/p, согласно соотношению (3), может не равняться целому числу коллекторных делений. Поэтому в общем случае сложной волновой обмотки ближайшие равнопотенциальные коллекторные пластины могут отстоять друг от друга на n = 1, 2, 3… пар полюсных делений. При этом

где n – такое целое число, при котором y_п также является целым числом.

Умножив выражение (3) на n, можно заметить, что y_п [смотрите формулу (4)] может быть целым числом при таком наименьшем n когда

a × n / p = 1 ,

откуда

(5)

Согласно формуле (4), при соблюдении условия (5) равнопотенциальный шаг сложной волновой обмотки

Расположение уравнителей второго рода на одной стороне машины возможно только при соблюдении условия (5). При u_п > 1 требуется также соблюдение условия

В случае, изображенном на рисунке 2,

y_п = K / a = 18 / 2 = 9 ,

что следует также из диаграммы электродвижущих сил на рисунке 3.

На рисунке 2 показан один уравнитель второго рода.

Применяются также обмотки с p = 3 и a = 2, для которых условие (5) не соблюдается. В этом случае уравнители второго рода располагаются своими концами на разных сторонах якоря и проходят между валом и сердечником якоря.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

§ 25.2. Волновые обмотки якоря

Простая волновая обмотка. Простую волновую обмотку получают при последовательном соединении секций, находящихся под разными парами полюсов (рис. 25.7). Концы секций простой волновой обмотки присоединены к коллекторным пластинам, уда­ленным друг от друга на расстояние шага обмотки по коллектору у_к =у. За один обход по якорю укладывают столько секций, сколь­ко пар полюсов имеет машина, при этом конец последней по об­ходу секции присоединяют к пластине, расположенной радом с исходной.

Простую волновую обмотку называют левоходовой, если ко­нец последней по обходу секций присоединяется к пластине, на­ходящейся слева от исходной (рис. 25.7, а). Если же эта пластина находится справа от исходной, то обмотку называют правоходовой (рис. 25.7, б). Секции волновой обмотки могут быть одновитковыми и многовитковыми. Шаг простой волновой обмотки по кол­лектору

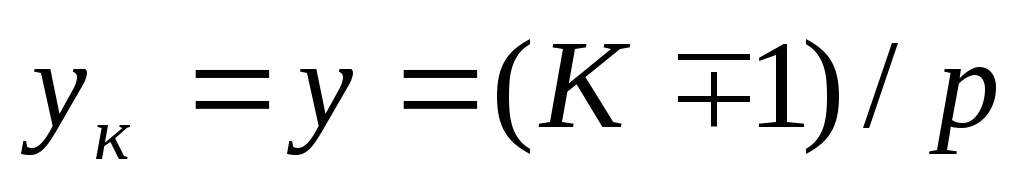(25.6)

Знак минус соответствует левоходовой обмотке, а знак плюс — правоходовой. Правоходовая обмотка не получила практического применения, так как ее выполнение связано с дополнительным расходом меди на перекрещивание лобовых частей.

Первый частичный шаг обмотки определяют по (25.3), а вто­рой частичный шаг .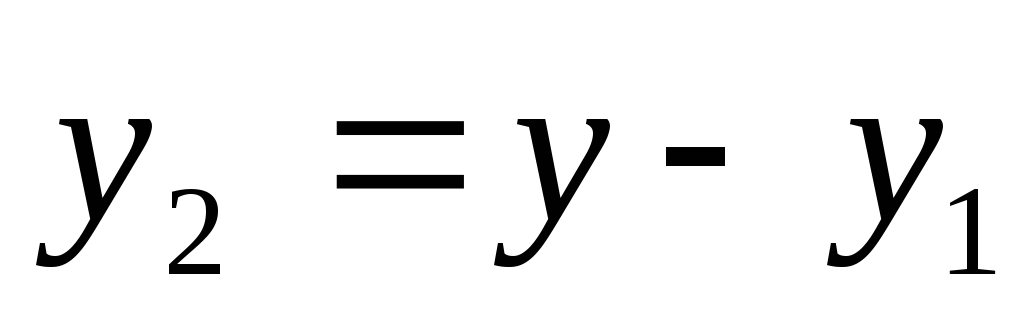

Пример 25.4. Четырехполюсная машина постоянного тока имеет простую волновую обмотку якоря из 13 секций. Построить развернутую схему и схему параллельных ветвей этой обмотки.

Решение. Шаги обмотки: 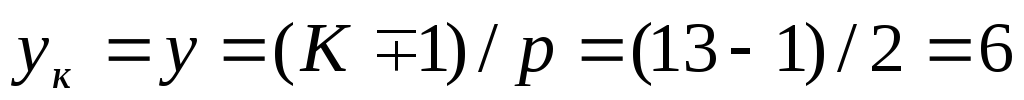пазов; 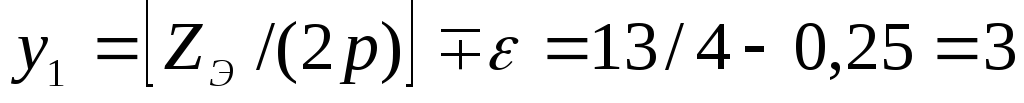паза; паза.

При первом обходе по якорю укладываем секции 1 и 7 (рис. 25.7, в). При втором обходе укладываем секции 13 и 6 и т. д., пока не будут уложены все 13 секций и обмотка не окажется замкнутой. Секции 3, 6 и 9 в рассматриваемый момент времени замкнуты на коротко через щетки одинаковой полярности и провода, соеди­няющие их.

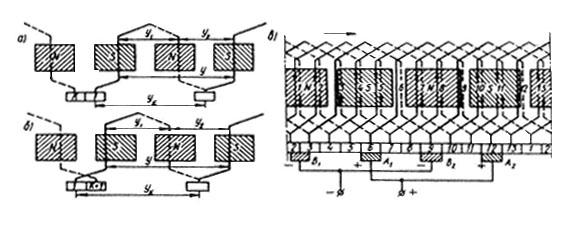
Рис. 25.7. Простая волновая обмотка: а — правоходовая, б — левоходовая; в — развернутая схема

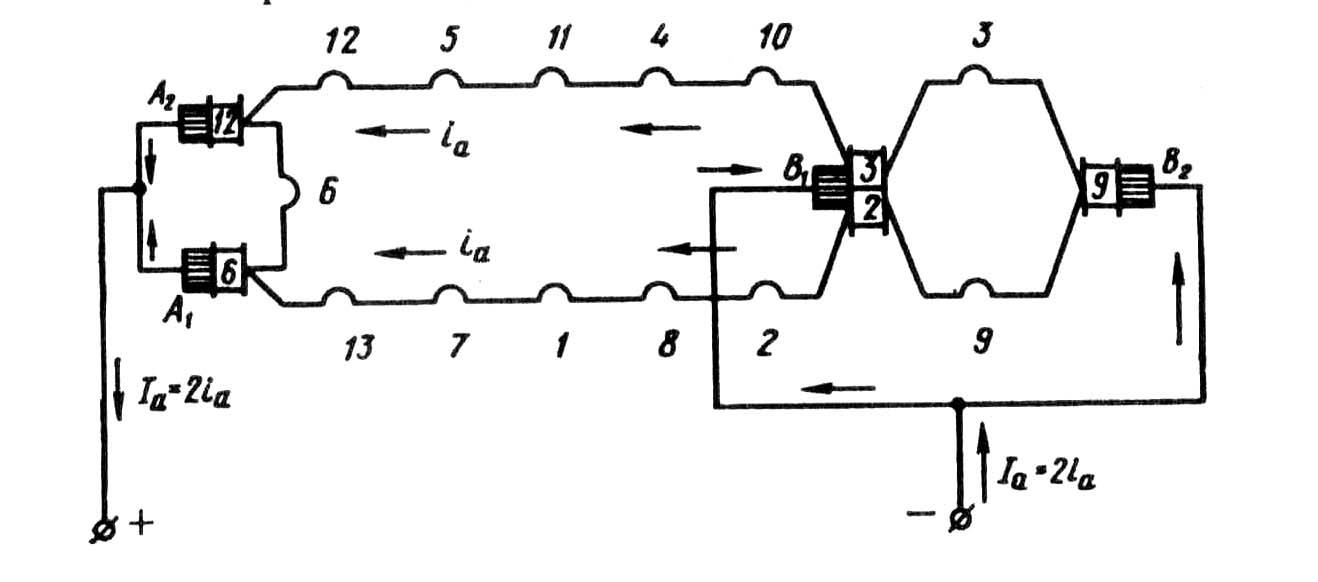
Рис. 25.8. Электрическая схема обмотки рис. 25.7, в

Затем определяем полярность щеток. Далее выполня­ем электрическую схему (схему параллельных ветвей), из которой видно (рис. 25.8), что обмотка состоит из двух параллельных вет­вей (2=2). Это является характерным для простых волновых об­моток, у которых число параллельных ветвей не зависит от числа полюсов и всегда равно двум.

Из рассмотренных схем видно, что секции, входящие в одну параллельную ветвь, равномерно распределены под всеми полю­сами машины. Следует также отметить, что в простой волновой обмотке можно было бы обойтись двумя щетками, например щет­кам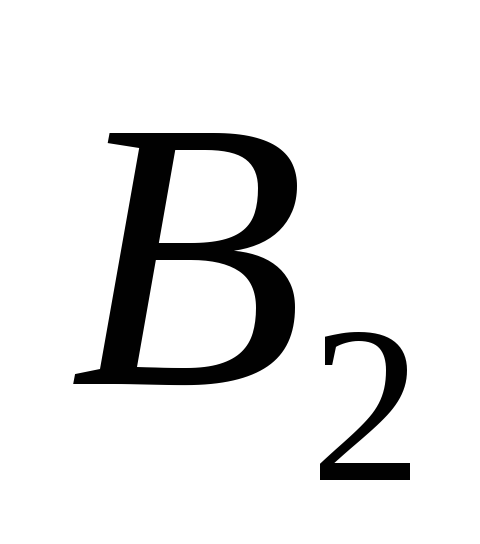и и. Но в этом случае нарушилась бы симметрия обмотки, и число секций в параллельных ветвях стало бы неодинаковым: в одной ветви семь секций, а в другой — шесть. Поэтому в ма­шинах с простыми волновыми обмотками устанавливают пол­ный комплект щеток, столько же, сколько главных полюсов, тем более что это позволяет уменьшить значение тока, прихо­дящегося на каждую щетку, а следовательно, уменьшить раз­меры коллектора.

Сложная волновая обмотка (рис. 25.9). Несколько простых волновых обмоток (обычно две), уложенных на одном якоре, образуют сложную волновую обмотку.

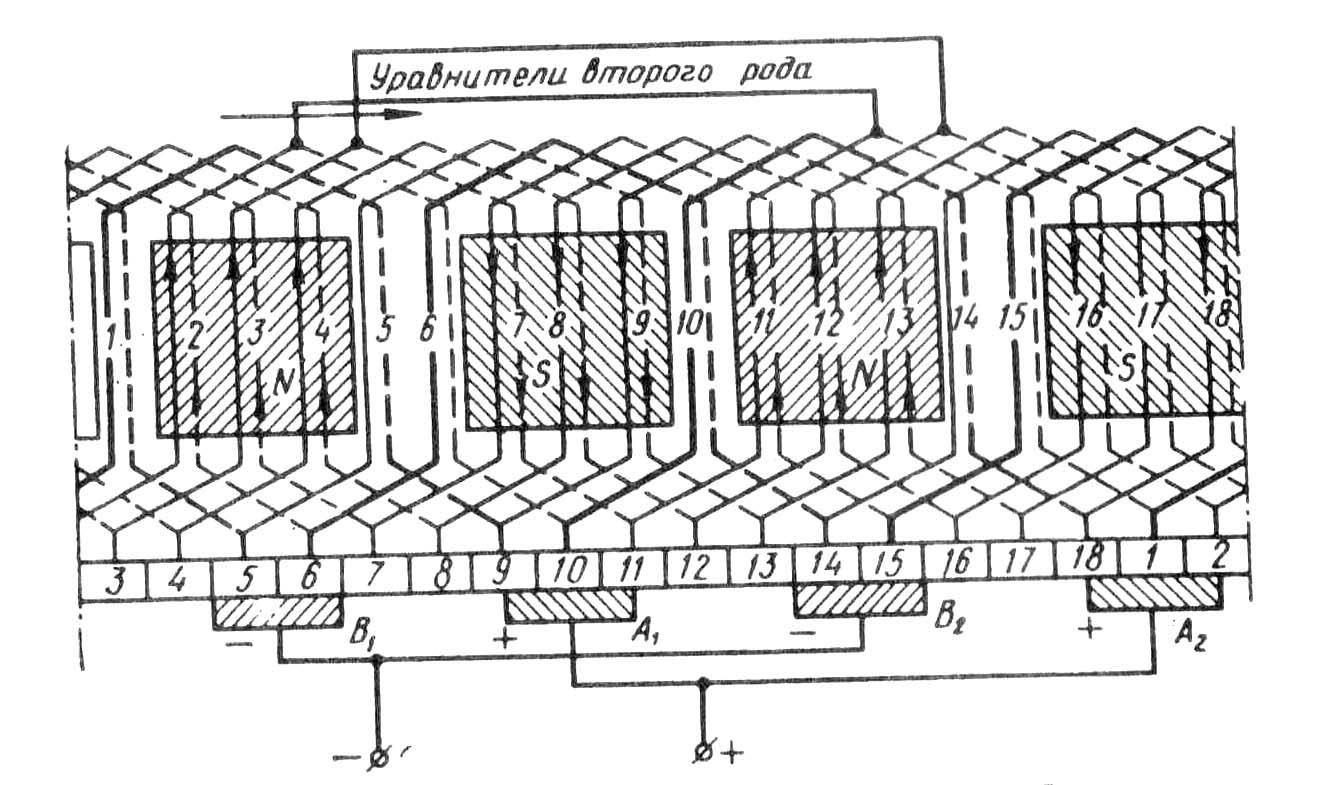
Рис. 25.9. Развернутая схема сложной волновой обмотки

Число параллельных ветвей в сложной волновой обмотке 2=2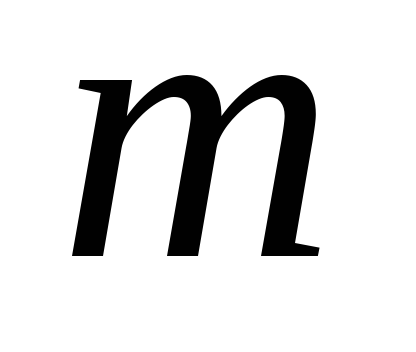(обычно 2= 4), гдет — чис­ло простых обмоток в сложной (обычно т = 2). Простые обмотки, входящие в сложную, соединяют параллельно посредством щеток. Шаг по коллектору, а следовательно, и результирующий шаг по якорю

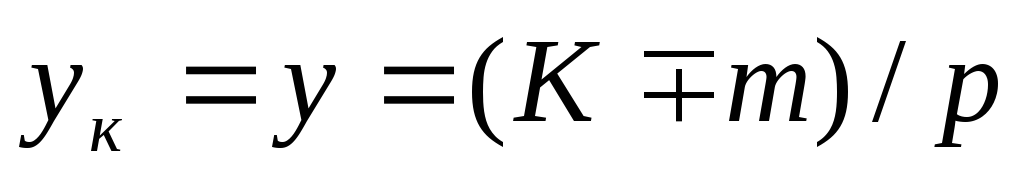. (25.7)

Первый частичный шаг по якорю определяют по (25.3).

Пример 25.5. Сложная волновая обмотка с 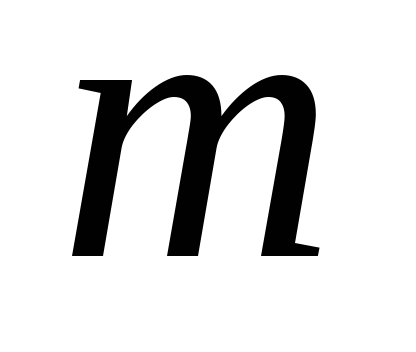= 2 состоит из 18 секций.

Выполнить развернутую схему этой обмотки, если 2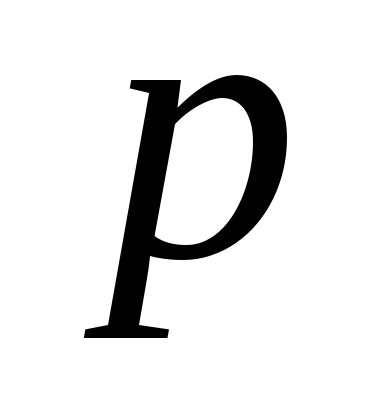=4.

Решение. Шаги обмотки: паза,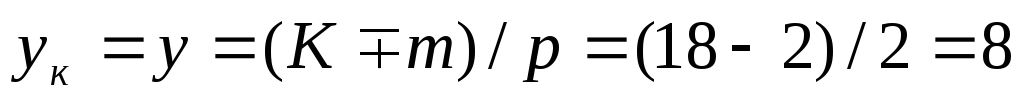 пазов; паза.

Порядок выполнения схемы обмотки такой же, как и при сложной петлевой обмотке: сначала укладывают в пазы якоря одну простую обмотку, состоящую из нечетных секций, а затем другую, состоящую из четных секций (рис. 25.9) Число параллельных ветвей в обмотке 2 = 4.

Простые волновые обмотки машин постоянного тока | Обмотчик электрических машин

Страница 44 из 84

Ширина секции волновой обмотки примерно равна полюсному делению, так же как и в петлевых обмотках, но их лобовые части соединяются не с соседними пластинами коллектора, а с пластинами, расположенными друг от друга на расстоянии, близком к двойному полюсному делению. Поэтому лобовые части секции волновой обмотки отогнуты в разные стороны от оси секции (рис. 123). Результирующий шаг обмотки по элементарным пазам равен шагу по коллектору у = уК, т. е. тоже близок к двойному полюсному делению. Напомним, что двойное полюсное деление, выраженное в коллекторных делениях, равно 2τк=К/р. Но в простой волновой обмотке шаг ук не может быть равен 2τк, он должен быть или немного больше, или немного меньше, чем двойное полюсное деление.
Если принять ук=2τк, то при построении обмотки, сделав р шагов, т. е. столько шагов, сколько пар полюсов в машине, мы завершим полный обход по окружности якоря и коллектора, и конец последней секции попадет опять на ту же пластину коллектора, с которой соединено начало первой секции, так как

Рис. 123. Элементы схемы и обозначения шагов волновой обмотки якоря: а — двухвитковые секции обмотки, б — часть схемы

2τкр = К и уложенные секции будут замкнуты сами на себя. Чтобы уложить все секции в пазы, их шаг по коллектору уменьшают или увеличивают так, чтобы после одного обхода (после р шагов) конец секции соединялся с пластиной коллектора, находящейся рядом с первоначальной, т. е. укр= К-+l. Из этого условия шаг простой волновой обмотки по коллектору должен быть ук= (К+- 1)/р. Знак минус в этой формуле ставится как основной, так как при знаке плюс после каждого полного обхода по окружности якоря (после каждых р шагов) концы секций соединятся с пластинами коллектора, следующими за первоначальными, так как рук=К+1. Лобовые части секций перекрестятся между собой (рис. 124, а) и обмотка получится перекрещивающейся, так же как и петлевая обмотка с шагом по коллектору, равным ук=—1.
При знаке минус конец последней в обходе секции соединяется с пластиной коллектора, предшествующей первоначальной, и лобовые части секций располагаются без перекрещиваний (рис. 124, б). Такая обмотка более удобна в технологическом отношении и более распространена в практике электромашиностроения.
В простой волновой обмотке число параллельных ветвей всегда равно двум и не зависит от числа полюсов в машине: 2 а = 2.
На рис. 125 изображена схема простой волновой обмотки, в которой для большей наглядности принято малое число пазов и коллекторных пластин Z = К = 19; uп — 1; 2р = 4. Выводные

Рис. 124. Волновая обмотка:
а — перекрещивающаяся, б — неперекрещивающаяся
концы каждой секции обмотки соединяются в определенные моменты со щетками на коллекторе. Расстояние между одноименными щетками по поверхности коллектора такое же, как между началом и концом секции, поэтому при установке щеток обмотка соединяется в две параллельные ветви. На рис. 126, а показано, как образуются параллельные ветви простой волновой обмотки машины с 2р = 4, а на рис. 126,б — с 2р = 6. И в том и другом случае число параллельных ветвей в обмотке не меняется. Оно останется также равным двум и при других числах полюсов. Это является одной из Основных особенностей простой волновой обмотки. В обмотке с 2а=2 нет точек с постоянными одинаковыми потенциалами, уравнительные токи не возникают и не требуется установки уравнительных соединений.

Рис. 125. Схема простой волновой обмотки якоря с Z=19, uп=1, K=19

Поэтому простая волновая обмотка в технологическом отношении проще, чем петлевая, и ее применяют почти во всех машинах малой и средней мощности, в которых ток не превышает 500—600 А, т. е. в каждой параллельной ветви остается меньше, чем 250—300 А.
Машина с волновой обмоткой якоря в отличие от машин с петлевой обмоткой может работать с неполным числом щеточных болтов. Если на схеме (см. рис. 126) удалить по одной из щеток разной полярности, то направление токов в каждой ветви не изменится. Это свойство волновых обмоток используют на практике в тех случаях, когда габариты машины не позволяют расположить на коллекторе полное число щеточных болтов, например, в ряде конструкций тяговых двигателей.