Внутреннее сопротивление — Википедия
 Двухполюсник и его эквивалентная схема
Двухполюсник и его эквивалентная схемаВну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).
В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.
Эквивалентная схема активного двухполюсника
Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.
В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.
Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.
Сопротивление и внутреннее сопротивление
Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:
- Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход
- Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
- В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
- Внутреннее сопротивление невозможно убрать из двухполюсника[5]
- Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:
| I = E r + R , U R = E r + R R , P R = E 2 ( r + R ) 2 R . {\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.} |
Нахождение внутреннего сопротивления
Расчёт
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| U o u t 1 = U − r I 1 U o u t 2 = U − r I 2 {\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}} | (Напряжения) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
| r = U o u t 1 − U o u t 2 I 2 − I 1 , U = U o u t 1 + I 1 U o u t 1 − U o u t 2 I 2 − I 1 = U o u t 1 + I 1 r {\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r} | (ОбщийСлучай) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:
| U o c = U − 0 0 = U − r I s c {\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}} |
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| r = U o c I s c , U = U o c {\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}} | (ВнутрСопр) |
Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Рассчитать выходное напряжение двухполюсника в режиме холостого хода
- Рассчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (ВнутрСопр).
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Измерение сопротивления петли фаза-нуль
Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросетиЧастным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:
- активная составляющая: 0,49 Ом
- реактивная составляющая: 0,09 Ом
- модуль полного сопротивления: 0,5 Ом
- ожидаемый ток короткого замыкания: 440 А
Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I1=0.
Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.
Применение
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:
- Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E
- Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен Imax=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной Pmax=E²/(4r)[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.
Примеры
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).
Большое внутреннее сопротивление
Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).
- Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
- Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
- Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.
Отрицательное внутреннее сопротивление
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.
См. также
Входной импеданс антенны
Ссылки
Литература
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.
Примечания
- ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
- ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣUint, где ΣUint — алгебраическая сумма ЭДС внутренних источников.
- ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
- ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
- ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
- ↑ То же самое, что и напряжение
- ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА. Проверено 6 апреля 2014.
- ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
- ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
- ↑ В рабочем диапазоне частот
 Двухполюсник и его эквивалентная схема
Двухполюсник и его эквивалентная схемаВну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).
В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.
Эквивалентная схема активного двухполюсника
Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.
Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.
В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.
Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.
Сопротивление и внутреннее сопротивление
Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется[2].
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:
- Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы [4]
- Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
- В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
- Внутреннее сопротивление невозможно убрать из двухполюсника[5]
- Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:
| I = E r + R , U R = E r + R R , P R = E 2 ( r + R ) 2 R . {\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.} |
Нахождение внутреннего сопротивления
Расчёт
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| U o u t 1 = U − r I 1 U o u t 2 = U − r I 2 {\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}} | (Напряжения) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
| r = U o u t 1 − U o u t 2 I 2 − I 1 , U = U o u t 1 + I 1 U o u t 1 − U o u t 2 I 2 − I 1 = U o u t 1 + I 1 r {\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r} | (ОбщийСлучай) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:
| U o c = U − 0 0 = U − r I s c {\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}} |
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| r = U o c I s c , U = U o c {\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}} | (ВнутрСопр) |
Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Рассчитать выходное напряжение двухполюсника в режиме холостого хода
- Рассчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (ВнутрСопр).
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Измерение сопротивления петли фаза-нуль
Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросетиЧастным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:
- активная составляющая: 0,49 Ом
- реактивная составляющая: 0,09 Ом
- модуль полного сопротивления: 0,5 Ом
- ожидаемый ток короткого замыкания: 440 А
Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I1=0.
Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.
Применение
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:
- Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
- Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен Imax=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной Pmax=E²/(4r)[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.
Примеры
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).
Большое внутреннее сопротивление
Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).
- Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
- Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
- Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.
Отрицательное внутреннее сопротивление
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.
См. также
Входной импеданс антенны
Ссылки
Литература
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.
Примечания
- ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
- ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣUint, где ΣUint — алгебраическая сумма ЭДС внутренних источников.
- ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
- ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
- ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
- ↑ То же самое, что и напряжение
- ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА. Проверено 6 апреля 2014.
- ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
- ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
- ↑ В рабочем диапазоне частот
 Двухполюсник и его эквивалентная схема
Двухполюсник и его эквивалентная схемаВну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).
В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.
Эквивалентная схема активного двухполюсника
Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.
Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.
В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.
Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.
Сопротивление и внутреннее сопротивление
Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется[2].
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:
- Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы [4]
- Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
- В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
- Внутреннее сопротивление невозможно убрать из двухполюсника[5]
- Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:
| I = E r + R , U R = E r + R R , P R = E 2 ( r + R ) 2 R . {\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.} |
Нахождение внутреннего сопротивления
Расчёт
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| U o u t 1 = U − r I 1 U o u t 2 = U − r I 2 {\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}} | (Напряжения) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
| r = U o u t 1 − U o u t 2 I 2 − I 1 , U = U o u t 1 + I 1 U o u t 1 − U o u t 2 I 2 − I 1 = U o u t 1 + I 1 r {\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r} | (ОбщийСлучай) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:
| U o c = U − 0 0 = U − r I s c {\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}} |
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| r = U o c I s c , U = U o c {\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}} | (ВнутрСопр) |
Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Рассчитать выходное напряжение двухполюсника в режиме холостого хода
- Рассчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (ВнутрСопр).
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Измерение сопротивления петли фаза-нуль
Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросетиЧастным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:
- активная составляющая: 0,49 Ом
- реактивная составляющая: 0,09 Ом
- модуль полного сопротивления: 0,5 Ом
- ожидаемый ток короткого замыкания: 440 А
Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I1=0.
Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.
Применение
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:
- Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
- Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен Imax=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной Pmax=E²/(4r)[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.
Примеры
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).
Большое внутреннее сопротивление
Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).
- Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
- Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
- Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.
Отрицательное внутреннее сопротивление
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.
См. также
Входной импеданс антенны
Ссылки
Литература
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.
Примечания
- ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
- ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣUint, где ΣUint — алгебраическая сумма ЭДС внутренних источников.
- ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
- ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
- ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
- ↑ То же самое, что и напряжение
- ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА. Проверено 6 апреля 2014.
- ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
- ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
- ↑ В рабочем диапазоне частот
Что такое внутреннее сопротивление цепи
Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.
В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для гальванического элемента или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.
Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.
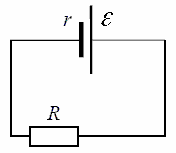
На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены ЭДС источника, его внутреннее сопротивление, а также сопротивление нагрузки. Согласно закону Ома для замкнутой цепи, ток в данной цепи будет равен:
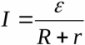
Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:
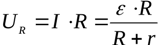
Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:
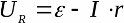
В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.
График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:
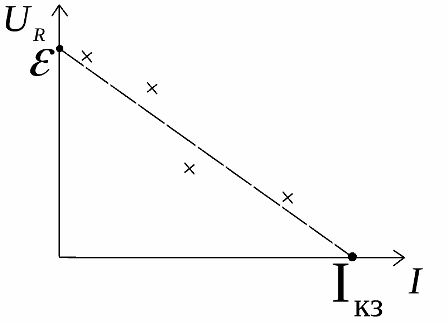
Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен току короткого замыкания. Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.
Экспериментальное нахождение внутреннего сопротивления
Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.
В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:
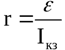
Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.
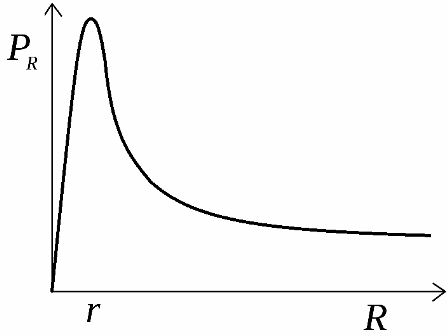
Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:
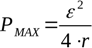
Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.
КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает источник:
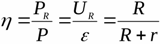
Ясно, что если источник развивает такую мощность, что на нагрузке получается максимум возможной мощности для данного источника, то КПД источника окажется равным 50%.
Закон Ома для полной цепи, определение которого касается значения электрического тока в реальных цепях, находится в зависимости от источника тока и от сопротивления нагрузки. Этот закон носит и другое название – закон Ома для замкнутых цепей. Принцип действия данного закона заключается в следующем.
В качестве самого простого примера, электрическая лампа, являющаяся потребителем электрического тока, совместно с источником тока есть не что иное, как замкнутая электрическая цепь. Данная электрическая цепь наглядно показана на рисунке.
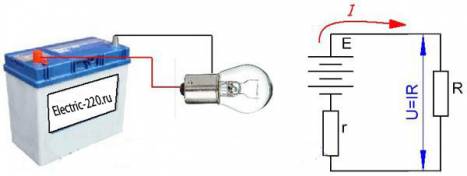
Электроток, проходя через лампочку, также проходит и через сам источник тока. Таким образом, во время прохождения по цепи, ток испытает сопротивление не только проводника, но и сопротивление, непосредственно, самого источника тока. В источнике сопротивление создается электролитом, находящимся между пластинами и пограничными слоями пластин и электролита. Отсюда следует, что в замкнутой цепи, ее общее сопротивление будет состоять из суммы сопротивлений лампочки и источника тока.
Внешнее и внутреннее сопротивление
Сопротивление нагрузки, в данном случае лампочки, соединенной с источником тока, носит название внешнего сопротивления. Непосредственное сопротивление источника тока называется внутренним сопротивлением. Для более наглядного изображения процесса, все значения необходимо условно обозначить. I – сила тока, R – внешнее сопротивление, r – внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR. Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.
Электродвижущая сила аккумулятора
Аккумулятор должен иметь следующее значение электродвижущей силы, способной поддерживать необходимый ток в цепи: Е=IхR+Iхr . Из формулы видно, что электродвижущая сила аккумулятора составляет сумму внешнего и внутреннего напряжения. Значение тока нужно вынести за скобки: Е=I(r+R) . Иначе можно представить: I=Е/(r+R) . Двумя последними формулами выражается закон Ома для полной цепи, определение которого звучит следующим образом: в замкнутой цепи сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений этой цепи.
Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.
У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.
Измерение сопротивления петли фаза-нуль
Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).
Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.
Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.
На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:
- заменяются участки провода, не отвечающие требованиям по диаметру сечения;
- перекручиваются болтовые соединения с обязательной установкой врезных шайб;
- вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
- при необходимости в контур защитного заземления добавляются дополнительные элементы;
- исключается последовательное подключение корпусов устройств к общей шине заземления.
После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление
Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.
Реактивное внутреннее сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Большое внутреннее сопротивление
Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.
Внутреннее сопротивление и импеданс
Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема
Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:
- цепи, содержащие источник тока или напряжения;
- двухполюсники, не являющиеся источниками.
Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.
Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.
Влияние внутреннего сопротивления на свойства двухполюсника
Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:
где:
- E – напряжение ЭДС;
- R – сопротивление нагрузки;
- r – активное внутреннее сопротивление двухполюсника.
Формула применима к двухполюсникам, не отдающим энергию.
К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Видео
Внутреннее сопротивление источника-2
Эта статья поможет разобраться с источниками: что такое короткое замыкание, напряжение на зажимах, как найти внутреннее сопротивление источника.
Задача 1. При подключении лампочки к источнику тока с  В напряжение на лампочке
В напряжение на лампочке  В, а ток в ней
В, а ток в ней  А. Каково внутреннее сопротивление источника?
А. Каково внутреннее сопротивление источника?
Падение напряжения на лампочке равно 4 В, следовательно,  В падает на внутреннем сопротивлении источника. Тогда, зная ток, можем найти это сопротивление:
В падает на внутреннем сопротивлении источника. Тогда, зная ток, можем найти это сопротивление:
![Rendered by QuickLaTeX.com \[r=\frac{E-U}{I}=\frac{0,5}{0,25}=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2651cf4bddf462b594e7c6931bcbcfe4_l3.png)
Ответ: 2 Ом.
Задача 2. Источник с ЭДС  В и внутренним сопротивлением
В и внутренним сопротивлением  Ом замкнут никелиновой проволокой длиной
Ом замкнут никелиновой проволокой длиной  м и площадью поперечного сечения
м и площадью поперечного сечения  мм
мм . Каково напряжение на зажимах источника?
. Каково напряжение на зажимах источника?
Определим сопротивление проволоки:
![Rendered by QuickLaTeX.com \[R=\frac{\rho l}{S}=\frac{0,42\cdot2,1}{0,21}=4,2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-17782e0884956913d92b63a8c17b18f8_l3.png)
Таким образом, ток в цепи будет равен:
![Rendered by QuickLaTeX.com \[I=\frac{E}{r+R}=\frac{2}{4,2+0,8}=0,4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6d64cbd9cf2aedbef97176e45b16ce00_l3.png)
Тогда на внутреннем сопротивлении при таком токе упадет
![Rendered by QuickLaTeX.com \[U_r=Ir=0,4\cdot0,8=0,32\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d32cf57d9ed1c78e6bae426676de036c_l3.png)
И на зажимах источника будет
![Rendered by QuickLaTeX.com \[U=E-U_r=2-0,32=1,68\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-60cf37354d8ac7b3a887d7b2c2efbae0_l3.png)
Можно было найти это напряжение иначе, как напряжение на проволоке:
![Rendered by QuickLaTeX.com \[U=IR=0,4\cdot4,2=1,68\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a08fbc1a4426c73d88268f7b15986b0d_l3.png)
Ответ:  В.
В.
Задача 3. Какого диаметра был выбран железный провод длиной  м,
м,
если после замыкания им источника тока с ЭДС  В и внутренним сопротивлением
В и внутренним сопротивлением  Ом сила тока в нем
Ом сила тока в нем  А?
А?
Падение напряжения на внутреннем сопротивлении равно  В, на проволоке, следовательно, падает
В, на проволоке, следовательно, падает  В. При данном токе сопротивление проволоки равно:
В. При данном токе сопротивление проволоки равно:
![Rendered by QuickLaTeX.com \[R=\frac{U}{I}=2,3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-31bcf2bfc6344ddd5187a06a9e2f85f4_l3.png)
Тогда ее сечение равно:
![Rendered by QuickLaTeX.com \[S=\frac{\rho l}{R}=\frac{0,098\cdot5}{2,3}=0,213\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0b52c683e47f8c98cf74fc403482c34_l3.png)
Сечение получено в мм ! Поэтому диаметр получится в мм.
! Поэтому диаметр получится в мм.
Так как  , то
, то
![Rendered by QuickLaTeX.com \[d=\sqrt{\frac{4S}{\pi}}=\sqrt{\frac{4\cdot0,213}{3,14}}=0,52\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-06105e86b1895c803192b56a9c9c78e3_l3.png)
Ответ:  мм
мм
Задача 4. В проводнике сопротивлением  Ом, подключенном к элементу с
Ом, подключенном к элементу с  В, сила тока
В, сила тока  А. Какова сила тока при коротком замыкании элемента?
А. Какова сила тока при коротком замыкании элемента?
Падение напряжения на внешнем сопротивлении равно  В. Следовательно, на внутреннем падает
В. Следовательно, на внутреннем падает  В. Значит, его сопротивление в 10 раз меньше
В. Значит, его сопротивление в 10 раз меньше  и равно
и равно  Ом. Тогда при коротком замыкании
Ом. Тогда при коротком замыкании
![Rendered by QuickLaTeX.com \[I_{kz}=\frac{E}{r}=\frac{1,1}{0,2}=5,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cbb73fb4a5f8eb344372918d88c5151d_l3.png)
Ответ:  А.
А.
Задача 5. При сопротивлении внешней цепи  Ом напряжение на зажимах источника
Ом напряжение на зажимах источника  В, а при сопротивлении
В, а при сопротивлении  Ом напряжение
Ом напряжение  В. Найти ЭДС и внутреннее сопротивление источника.
В. Найти ЭДС и внутреннее сопротивление источника.
Запишем систему уравнений:
![Rendered by QuickLaTeX.com \[U_1=E-U_r=E-Ir=E-\frac{Er}{r+R_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4797ab8fe8c474aaa186fdcabc9e1b9d_l3.png)
![Rendered by QuickLaTeX.com \[U_2=E-\frac{Er}{r+R_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-eaa86b751f5706502a1f6d339d59ce70_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[E=\frac{U_1}{1-\frac{r}{r+R_1}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5dfdb2b910dbd1ea2829dfeae244dcac_l3.png)
![Rendered by QuickLaTeX.com \[E=\frac{U_2}{1-\frac{r}{r+R_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e66c39ee28cd62a7f924d2c4422da914_l3.png)
Приравнивая, получим:
![Rendered by QuickLaTeX.com \[U_2+\frac{U_2 r}{R_2}= U_1+\frac{U_1 r}{R_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-803ab317cdff174ad276443bd8098d23_l3.png)
![Rendered by QuickLaTeX.com \[r\left(\frac{U_2}{R_2}-\frac{U_1}{R_1}\right)=U_1-U_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-31d661dcff41b7beb60f061dc517a830_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[r=\frac{(U_1-U_2)R_1R_2}{U_2R_1-U_1R_2}=\frac{(U_2-U_1)R_1R_2}{U_1R_2-U_2R_1}=\frac{(0,5)\cdot2}{3-2}=1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-431d1acbd54b226b572d232bc0b9b879_l3.png)
Ответ:  Ом.
Ом.
Задача 6. При подключении к источнику тока сопротивления  Ом сила тока в цепи
Ом сила тока в цепи  А, а при подключении сопротивления
А, а при подключении сопротивления  Ом -сила тока
Ом -сила тока  А. Найти внутреннее сопротивление и ЭДС батареи.
А. Найти внутреннее сопротивление и ЭДС батареи.
Ток в цепи:
![Rendered by QuickLaTeX.com \[I =\frac{E}{r+R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d3ac9280514453c6e43cf0543b2e461c_l3.png)
![Rendered by QuickLaTeX.com \[E=I(r+R)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-121d22443686a7cc884780a0859bf3ff_l3.png)
Тогда запишем:
![Rendered by QuickLaTeX.com \[E=I_1(r+R_1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5e8f9fa307a0de4d889aa0d631daf5ac_l3.png)
![Rendered by QuickLaTeX.com \[E=I_2(r+R_2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0985c05c6cfac1b021daa0e8f6ac838b_l3.png)
Разделив уравнения друг на друга, получим:
![Rendered by QuickLaTeX.com \[\frac{I_1}{I_2}=\frac{ r+R_2}{ r+R_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-732641bf1b95502cef5749c540bb0979_l3.png)
![Rendered by QuickLaTeX.com \[r (I_1- I_2)= I_2R_2 -I_1R_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-05b7bcde8680bd1da6b2cb7214c43822_l3.png)
![Rendered by QuickLaTeX.com \[r=\frac{ I_2R_2 -I_1R_1}{ I_1- I_2}=\frac{16- 1,8\cdot8}{ 1,8-1}=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6bfd622cdccb4a73cf3a683e37fdfd20_l3.png)
Ответ:  Ом.
Ом.
Задача 7. В замкнутой цепи при уменьшении внешнего сопротивления на  % ток увеличился на
% ток увеличился на  % . На сколько процентов
% . На сколько процентов  увеличился бы ток, если бы внешнее сопротивление уменьшили на
увеличился бы ток, если бы внешнее сопротивление уменьшили на  % ?
% ?
До всевозможных изменений в цепи протекал ток, определяемый выражением:
![Rendered by QuickLaTeX.com \[I=\frac{E}{r+R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-389552afb74928f35029a561a0ee0fb9_l3.png)
Затем внешнее сопротивление уменьшили на 20 процентов, и оно стало равно  . При этом ток равен
. При этом ток равен  :
:
![Rendered by QuickLaTeX.com \[1,2I=\frac{E}{r+0,8R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-52e873973c2b3d335340272ee0d9d124_l3.png)
Теперь запишем, каким будет ток, если внешнее сопротивление уменьшить на 40% ( ):
):
![Rendered by QuickLaTeX.com \[I_x=\frac{E}{r+0,6R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-68a82cd1196150f03a8b19480f6bf7d2_l3.png)
Пользуясь первыми двумя уравнениями, определим соотношением между  и
и  :
:
![Rendered by QuickLaTeX.com \[E=I(r+R)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-121d22443686a7cc884780a0859bf3ff_l3.png)
![Rendered by QuickLaTeX.com \[E=1,2I(r+0,8R)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-24f1430c9429f9c14a988eccd2eb1b1c_l3.png)
Приравняем правые части:
![Rendered by QuickLaTeX.com \[I(r+R)= 1,2I(r+0,8R)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-38e29b48afe4f55c7bfa7b0b9ad729cb_l3.png)
![Rendered by QuickLaTeX.com \[R-1,2\cdot0,8R=0,2r\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-846a8372c1bb76d4de5a0ea187f205f1_l3.png)
![Rendered by QuickLaTeX.com \[0,04R=0,2r\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3d6a9aad684652c3a0c870af8b2d13d1_l3.png)
Или
![Rendered by QuickLaTeX.com \[R=5r\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-001fce43644d07242bd2b3e504fd11f2_l3.png)
Теперь разделим друг на друга второе и третье уравнения (третье будем делить на второе):
![Rendered by QuickLaTeX.com \[\frac{I_x}{1,2I}=\frac{ r+0,8R }{ r+0,6R }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dc11075356767b3cf4452ad7f42201ee_l3.png)
Подставляя  , получим:
, получим:
![Rendered by QuickLaTeX.com \[\frac{I_x}{I}=\frac{1,2( r+4r) }{ r+3r }=1,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9861f48e7ae54b86ad1d77ae6d7f3489_l3.png)
Ответ: ток увеличится на 50%.
Внутреннее сопротивление — Википедия
 Двухполюсник и его эквивалентная схема
Двухполюсник и его эквивалентная схемаВну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).
В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.
Эквивалентная схема активного двухполюсника
Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.
Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.
В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.
Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.
Сопротивление и внутреннее сопротивление
Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется[2].
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:
- Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы [4]
- Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
- В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
- Внутреннее сопротивление невозможно убрать из двухполюсника[5]
- Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:
| I = E r + R , U R = E r + R R , P R = E 2 ( r + R ) 2 R . {\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.} |
Нахождение внутреннего сопротивления
Расчёт
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| U o u t 1 = U − r I 1 U o u t 2 = U − r I 2 {\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}} | (Напряжения) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
| r = U o u t 1 − U o u t 2 I 2 − I 1 , U = U o u t 1 + I 1 U o u t 1 − U o u t 2 I 2 − I 1 = U o u t 1 + I 1 r {\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r} | (ОбщийСлучай) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:
| U o c = U − 0 0 = U − r I s c {\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}} |
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| r = U o c I s c , U = U o c {\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}} | (ВнутрСопр) |
Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Рассчитать выходное напряжение двухполюсника в режиме холостого хода
- Рассчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (ВнутрСопр).
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Измерение сопротивления петли фаза-нуль
Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросетиЧастным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:
- активная составляющая: 0,49 Ом
- реактивная составляющая: 0,09 Ом
- модуль полного сопротивления: 0,5 Ом
- ожидаемый ток короткого замыкания: 440 А
Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I1=0.
Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.
Применение
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:
- Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
- Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен Imax=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной Pmax=E²/(4r)[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.
Примеры
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).
Большое внутреннее сопротивление
Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).
- Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
- Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
- Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.
Отрицательное внутреннее сопротивление
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.
См. также
Входной импеданс антенны
Ссылки
Литература
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.
Примечания
- ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
- ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣUint, где ΣUint — алгебраическая сумма ЭДС внутренних источников.
- ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
- ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
- ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
- ↑ То же самое, что и напряжение
- ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА. Проверено 6 апреля 2014.
- ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
- ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
- ↑ В рабочем диапазоне частот
Внутреннее сопротивление и его физический смысл
Каждый источник тока имеет собственное внутреннее сопротивление. Электрическая цепь – это замкнутый контур с потребителями, к которому прикладывается напряжение. Каждый такой контур имеет внешнее сопротивление и внутреннее.
Внешним называется сопротивление всей цепи с потребителями и проводниками, а внутреннее сопротивление исходит от самого источника.
Если в качестве источника тока используется электрическая машина, то её внутреннее сопротивление делится на активное, индуктивное и ёмкостное. Активное зависит от длины проводника и его толщины, а также материала, из которого выполнен проводник, и его состояния. Индуктивное зависит от индуктивности катушки (величины её противоЭДС), а емкостное возникает между витками обмотки. Оно является довольно малым. Если в качестве источника используется обычная батарея, то в ней тоже создаётся сопротивление за счёт электролита.
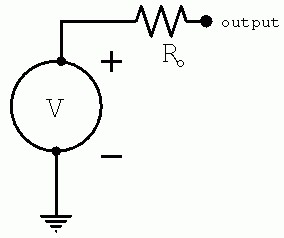
Ток – это направленное движение частиц, а сопротивление – это создаваемое препятствие на пути его движения. Такие препятствия встречаются и в электролите, и в свинцовых пластинах аккумуляторных батарей, словом, везде, где возникает ток.
Из-за того, что существует внутреннее сопротивление в источнике, нельзя полагать, что напряжение в цепи – это и есть полная электродвижущая сила источника. Конечно, падением напряжения в самом источнике можно пренебречь, однако только в том случае, если оно ничтожно мало.
Если в цепи источника создаются большие токи, то напряжение на зажимах нельзя считать истинной электродвижущей силой. Ток в источнике – это признак падения напряжения в нём. В этом случае действует закон Кирхгофа, который гласит, что истинная ЭДС цепи – это сумма падений напряжений на всех участках, в том числе и в самом источнике. А записывается формула так:
E = ∑U + Ir r
Где:
E – общая электродвижущая сила цепи;
U – падение напряжения на участках цепи;
Ir – внутренний ток, создаваемый в источнике;
r – внутреннее сопротивление источника.
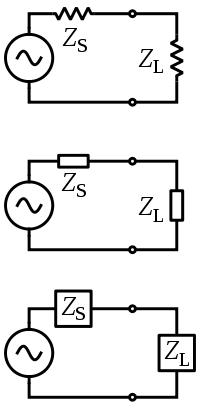 Чтобы понять физический смысл внутреннего сопротивления источника, следует провести небольшой опыт. Первоначально измеряется электродвижущая сила источника. Это делается путём подключения вольтметра к батарее, которая не находится под нагрузкой. После этого необходимо подключить небольшое сопротивление и последовательно установить амперметр. Таким образом, будет известен ток, при этом надо измерить также напряжение под нагрузкой.
Чтобы понять физический смысл внутреннего сопротивления источника, следует провести небольшой опыт. Первоначально измеряется электродвижущая сила источника. Это делается путём подключения вольтметра к батарее, которая не находится под нагрузкой. После этого необходимо подключить небольшое сопротивление и последовательно установить амперметр. Таким образом, будет известен ток, при этом надо измерить также напряжение под нагрузкой.Записав все значения величин, легко определить внутреннее сопротивление. Для этого в первую очередь определяется падение напряжения в батарее. С помощью формулы
Ur = E-U
производим вычисление.
В этой формуле:
Ur – падение напряжения внутреннего сопротивления источника;
E – напряжение (ЭДС), измеренное на источнике без потребителя;
U – напряжение, измеренное непосредственно на сопротивлении.
Таким образом, внутренне сопротивление вычисляется по следующей формуле:
r=Ur/I
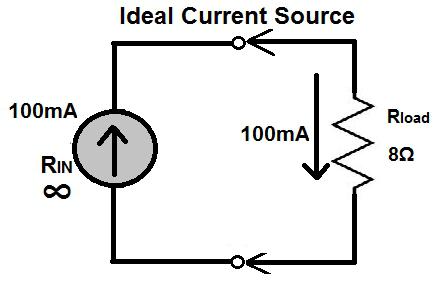
Некоторые специалисты пренебрегают этой величиной, считая, что её можно не учитывать ввиду малого значения. Однако практика показывает, что при сложных расчетах внутреннее сопротивление сильно влияет на конечный результат.
10.3 Батареи и внутреннее сопротивление (ESCPV)
До сих пор мы имели дело с идеальными батареями в том, что они не затрагиваются цепью или током в любом случае и обеспечить точное напряжение, пока они не станут плоскими.
Если вы измеряете разность потенциалов на клеммах батарея сама по себе вы будете получить значение, отличное от того, что вы измеряете, когда оно находится в полной цепи.Значение будет меньше, когда батарея включена в полную цепь. Иногда разница называется потерянных вольт . Ничего не имеет на самом деле был потерян, но энергия была передана.
Настоящие батареи сделаны из материалов, которые имеют сопротивление. Это означает, что реальные батареи — это не просто источники разности потенциалов (напряжения), но они также обладают внутренним сопротивлением. Если источником полной разности потенциалов является называется ЭДС, \ (\ mathcal {E} \), то реальная батарея может быть представлена как ЭДС, соединенная последовательно с резистором \ (r \).внутренний Сопротивление батареи обозначается символом \ (r \).
- Груз
Внешнее сопротивление в цепи называется нагрузкой.
Предположим, что батарея с ЭДС \ (\ mathcal {E} \) и внутренним сопротивлением \ (r \) подает ток \ (I \) через внешний нагрузочный резистор \ (R \). Тогда разность потенциалов на нагрузочном резисторе равна той, которую обеспечивает аккумулятор:
\ [V _ {\ text {load}} = I \ cdot R \]Аналогично, из закона Ома, разность потенциалов по внутреннему сопротивлению равна:
\ [{V} _ {\ text {внутреннее сопротивление}} = I \ cdot r \]Разность потенциалов \ (V \) батареи связана с ее ЭДС \ (\ mathcal {E} \) и внутренним сопротивлением \ (r \):
\ Начать {*} Align \ mathcal {E} & = V + Ir \\ & \ Текст {или} \\ V & = \ mathcal {E} -Ir \ Конец {*} выравниваниеБатарея является источником энергии и энергии, передаваемой за единицу заряда (эдс) через батарею равна общей проделанной работе (разности потенциалов) через компоненты в цепи.Это можно проиллюстрировать, показывая энергию на единицу заряда как функция положения в цепи. Заряд получает энергию при движении через батарея и теряет энергию при движении через резисторы.
- Положительная работа выполняется за единицу заряда от батареи, передающей энергию, равную ЭДС.
- Зарядка работает, чтобы преодолеть внутреннее сопротивление батареи. Выполнение работы требует, чтобы заряд теряет энергию. Работа по преодолению внутреннего сопротивления \ (V _ {\ text {внутреннее сопротивление}} = Ir \).
- Когда заряд батареи покидает аккумулятор, он потребляет меньше энергии, чем исходная ЭДС. Теперь это общее энергия, которую он может использовать для выполнения работы, проходящей через схему, \ (V _ {\ text {load}} = \ mathcal {E} -Ir \).
- Когда заряд движется по цепи, он работает, проходя через каждый компонент, который равен к \ (ИК \).
ЭДС батареи по существу постоянна, потому что она зависит только от химическая реакция (которая преобразует химическую энергию в электрическую энергию) происходит внутри батареи.Таким образом, мы видим, что разность потенциалов через Клеммы батареи зависят от тока, потребляемого нагрузкой. чем выше ток, тем ниже разность потенциалов на клеммах, потому что ЭДС постоянна. По той же причине, разность потенциалов равняется эдс только тогда, когда ток очень мал.
Ток, который можно получить от батареи, ограничен критическим, максимальным значением \ ({I} _ {c} \). Чем больше сопротивление в цепи, тем меньше будет ток.Представьте, что у вас есть провод без сопротивления, который вы используете для подключения клемм аккумулятора. Цепь завершена, ток будет течь, и добавление любого сопротивления в цепь уменьшит ток. Ток без внешнего сопротивления будет \ ({I} _ {c} \). При токе \ ({I} _ {c} \), \ (V = \ text {0} \ text {V} \), поскольку в цепи нет нагрузки. Тогда уравнение становится:
\ Начать {*} Align \ text {0} & = \ mathcal {E} — {I} _ {c} r \\ {I} _ {c} r & = \ mathcal {E} \\ {I} _ {c} & = \ frac {\ mathcal {E}} {r} \ Конец {*} выравниваниеМаксимальный ток, который может потребляться от батареи, меньше \ (\ frac {\ mathcal {E}} {r} \).
Рабочий пример 6: внутреннее сопротивление
Определите внутреннее сопротивление батареи, которая имеет ЭДС \ (\ text {12,00} \) \ (\ text {V} \) и имеет разность потенциалов на его клеммах \ (\ text {10,00} \) \ (\ text {V} \), когда текущий из \ (\ text {4,00} \) \ (\ text {A} \) протекает через батарею при подключении в цепи.
Определите, как подойти к проблеме
Это проблема внутреннего сопротивления.Итак, мы используем уравнение:
\ Начать {*} Align \ mathcal {E} & = V + Ir \ end {align *}Решить проблему
\ Начать {*} Align \ mathcal {E} & = V + Ir \\ \ text {12} & = \ text {10} + \ text {4} \ left (r \ right) \\ r & = \ text {0,5} \ text {Ω} \ end {align *}Написать окончательный ответ
Внутреннее сопротивление аккумулятора равно \ (\ text {0,50} \) \ (\ text {Ω} \).
Нахождение внутреннего сопротивления батареи
Цель
Для определения внутреннего сопротивления батареи.
Аппарат
Для этого эксперимента вам понадобятся следующие предметы:
Метод
Мы настроим схему, которая содержит батарею, которую мы хотим изучать последовательно с резистором. Тогда мы будем измерять разность потенциалов через нагрузку а также ток для ряда различных резисторов / реостата в цепи. Неважно, если это каждый раз другой резистор резисторы последовательно или параллельно.Важно то, что общее сопротивление схема меняется так, что ток каждый раз меняется. Причина что делать это может рассказать нам о внутреннем сопротивлении батареи потому что разность потенциалов через внутреннее сопротивление \ (V _ {\ text {внутреннее сопротивление}} = I \ cdot r \) и мы можем изменить I, изменив сопротивление цепи. Если разность потенциалов через внутреннее сопротивление меняется, и мы складываем все потенциальные различия, \ (\ mathcal {E} = V _ {\ text {load}} + V _ {\ text {внутреннее сопротивление}} \) мы можем определить внутреннее сопротивление.
Для этого мы на самом деле построим график зависимости \ (V _ {\ text {load}} \) от \ (I \) и затем воспользуемся функциями графика для определения \ (\ mathcal {E} \) и \ (р\). Чтобы понять, почему построение графика поможет нам, мы начнем с уравнения для величины \ (\ mathcal {E} \) и заменим закон Ома и перегруппируем его следующим образом: \ Начать {*} Align \ mathcal {E} & = V _ {\ text {load}} + V _ {\ text {внутреннее сопротивление}} \\ \ mathcal {E} & = V _ {\ text {load}} + I \ cdot r \\ V _ {\ text {load}} & = \ mathcal {E} -I \ cdot r \\ V _ {\ text {load}} & = -r \ cdot I + \ mathcal {E} \\ \ underbrace {V _ {\ text {load}}} _ {y} & = \ underbrace {-r} _ {m} \ cdot \ underbrace {I} _x + \ underbrace {\ mathcal {E}} _ {c} \ Конец {*} выравнивание Если мы построим график \ (V _ {\ text {load}} \) против \ (I \), мы будем отображать данные, которые регулируются этим отношением.Это позволяет нам сделать вывод, что наклон графа \ (m \) будет \ (- r \), а вертикальная ось перехвата \ (c \) будет ЭДС \ (\ mathcal {E} \ ).
результатов
Запишите результаты в таблицу, подобную приведенной ниже. Вы можете взять больше чтений, если хотите.
| Настройка | \ (V _ {\ text {load}} \) (\ (\ text {V} \)) | \ (I \) (\ (\ text {A} \)) |
| Сопротивление 1 | ||
| Сопротивление 2 | ||
| Сопротивление 3 | ||
| Сопротивление 4 | ||
| Сопротивление 5 |
Обсуждение и заключение
Нанесите свои данные на набор осей, аналогичный этому примеру.Синий крестики представляют измеренные точки данных, серая пунктирная линия — нарисовал прямую линию через данные точки. Лучшая линия, которую вы рисуете, не должна проходить через все точки данных, это в общем случае должно иметь как можно больше точек над и под линией. Наклон линии можно измерить и приравнять к \ (- r \), а перехват с вертикальной осью даст вам \ (\ mathcal {E} \). перехват с горизонтальной осью даст вам максимально возможный ток батарея может доставить.
- Ваши данные образуют совершенно прямую линию?
- Какие ошибки были внесены?
Рабочий пример 7: Внутреннее сопротивление в цепи с резисторами в серии
Для следующей схемы рассчитайте:
разности потенциалов \ (V_ \ text {1} \), \ (V_ \ text {2} \) и \ (V_ \ text {3} \) по резисторам \ (R_ \ text {1} \), \ (R_ \ text {2} \) и \ (R_ \ text {3} \)
,сопротивление \ (R_ \ text {3} \).
сопротивление \ (R_ \ text {3} \).
Если внутреннее сопротивление равно \ (\ text {0,1} \) \ (\ text {Ω} \), какова ЭДС батареи и какая мощность рассеивается внутренним сопротивлением батареи?
Примечание
Это очень похожий вопрос на то, что вы видели ранее. Это чтобы выделить Дело в том, что подход при работе с внутренним сопротивлением все же строится на принципы, с которыми вы уже работали.
Определите, как подойти к проблеме
Нам даны разность потенциалов на элементе и ток в цепи, а также сопротивления двух из трех резисторов.Мы можем использовать закон Ома для расчета разности потенциалов по известным резисторам. Поскольку резисторы находятся в последовательной цепи, разность потенциалов равна \ (V = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \), и мы можем вычислить \ (V_ \ text {3} \). Теперь мы можем использовать эту информацию, чтобы найти разность потенциалов на неизвестном резисторе \ (R_ \ text {3} \).
Рассчитать разность потенциалов по \ (R_ \ text {1} \)
Используя закон Ома: \ Начать {*} Align R_ \ text {1} & = \ frac {V_ \ text {1}} {I} \\ I \ cdot R_ \ text {1} & = I \ cdot \ frac {V_ \ text {1}} {I} \\ V_ \ text {1} & = {I} \ cdot {R_ \ text {1}} \\ & = 2 \ cdot 1 \\ V_ \ text {1} & = \ text {2} \ text {V} \ end {align *}
Рассчитать разность потенциалов по \ (R_ \ text {2} \)
Снова используя закон Ома: \ Начать {*} Align R_ \ text {2} & = \ frac {V_ \ text {2}} {I} \\ I \ cdot R_ \ text {2} & = I \ cdot \ frac {V_ \ text {2}} {I} \\ V_ \ text {2} & = {I} \ cdot {R_ \ text {2}} \\ & = 2 \ cdot 3 \\ V_ \ text {2} & = \ text {6} \ text {V} \ end {align *}
Рассчитать разность потенциалов по \ (R_ \ text {3} \)
Поскольку разность потенциалов на всех объединенных резисторах должна быть такой же, как разность потенциалов на ячейке в последовательной цепи, мы можем найти \ (V_ \ text {3} \), используя: \ Начать {*} Align V & = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \\ V_ \ text {3} & = V — V_ \ text {1} — V_ \ text {2} \\ & = 23 — 2 — 6 \\ V_ \ text {3} & = \ text {15} \ text {V} \ end {align *}
Найти сопротивление \ (R_ \ text {3} \)
Мы знаем разность потенциалов через \ (R_ \ text {3} \) и ток через него, поэтому мы можем использовать закон Ома для расчета значения сопротивления: \ Начать {*} Align R_ \ text {3} & = \ frac {V_ \ text {3}} {I} \\ & = \ frac {\ text {15}} {\ text {2}} \\ R_ \ text {3} & = \ text {7,5} ~ \ Omega \ end {align *}
Разность потенциалов на внутреннем сопротивлении батареи
Значение эдс может быть рассчитано из разности потенциалов нагрузки и разности потенциалов по внутреннему сопротивлению.2} {R} \) и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов через него, поэтому мы можем использовать любую форму уравнения для мощности:
\ Начать {*} Align P_r & = V_rI_r \\ & = (\ text {0,2}) (\ text {2}) \\ & = \ text {0,4} \ text {W} \ end {align *}Написать окончательный ответ
- \ (V_ \ text {1} = \ text {2,0} \ text {V} \)
- \ (V_ \ text {2} = \ text {6,0} \ text {V} \)
- \ (V_ \ text {3} = \ text {10,0} \ text {V} \)
- \ (R_ \ text {3} = \ text {7,5} \ Omega \)
- \ (\ mathcal {E} = \ text {23,2} \ text {V} \)
- \ (P_r = \ text {0,4} \ text {W} \)
Рабочий пример 8: внутреннее сопротивление и резисторы параллельно
Разность потенциалов в батарее составляет 18 В, когда она подключена к двум параллельным резисторам \ (\ text {4,00} \) \ (\ Omega \) и \ (\ text {12,00} \) \ ( \ Омега \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов. Если внутреннее сопротивление батареи равно \ (\ text {0,375} \) \ (\ text {Ω} \), какова ЭДС батареи?
Сначала нарисуйте схему, прежде чем делать какие-либо вычисления. Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на элементе и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалентное сопротивление остальной цепи. Резисторы расположены параллельно и поэтому:
\ Начать {*} Align
\ frac {\ text {1}} {R} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2}} \ \
& = \ frac {\ text {1}} {\ text {4}} + \ frac {\ text {1}} {\ text {12}} \\
& = \ frac {3 + 1} {\ text {12}} \\
& = \ frac {\ text {4}} {\ text {12}} \\
R & = \ frac {\ text {12}} {\ text {4}} = \ text {3,00} \ \ Omega
\ Конец {*} выравнивание
Теперь используя закон Ома, чтобы найти ток через ячейку:
\ Начать {*} Align
R & = \ frac {V} {I} \\
Я & = \ frac {V} {R} \\
& = \ frac {\ text {18}} {\ text {3}} \\
Я & = \ text {6,00} \ text {A}
\ end {align *}
Теперь определим ток через один из параллельных резисторов
Мы знаем, что для конфигурации с чисто параллельными резисторами разность потенциалов на элементе такая же, как на разности потенциалов на каждом из параллельных резисторов.Для этой схемы:
\ Начать {*} Align
V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V}
\ Конец {*} выравнивание
Давайте начнем с вычисления тока через \ (R_ \ text {1} \) с использованием закона Ома:
\ Начать {*} Align
R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\
I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\
& = \ frac {\ text {18}} {\ text {4}} \\
I_ \ text {1} & = \ text {4,50} \ text {A}
\ end {align *}
Рассчитать ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_ \ text {2} \):
\ Начать {*} Align
R_ \ text {2} & = \ frac {V_ \ text {2}} {I_ \ text {2}} \\
I_ \ text {2} & = \ frac {V_ \ text {2}} {R_ \ text {2}} \\
& = \ frac {\ text {18}} {\ text {12}} \\
I_ \ text {2} & = \ text {1,50} \ text {A}
\ Конец {*} выравнивание Альтернативный метод расчета \ (I_ \ text {2} \) мог бы использовать тот факт, что токи через каждый из параллельных резисторов должны составлять общий ток через ячейку: \ Начать {*} Align
Я & = I_ \ text {1} + I_ \ text {2} \\
I_ \ text {2} & = I — I_ \ text {1} \\
& = 6 — 4.5 \\
I_ \ text {2} & = \ text {1,5} \ text {A}
\ end {align *}
Определить ЭДС
Этот общий ток через батарею является током через внутреннее сопротивление батареи. Знание тока и сопротивления позволяет нам использовать закон Ома для определения разности потенциалов во внутреннем сопротивлении и, следовательно, в эдс батареи.
Используя закон Ома, мы можем определить разность потенциалов через внутреннее сопротивление:
\ Начать {*} Align
V & = I \ cdot r \\
& = \ text {6} \ cdot \ text {0,375} \\
& = \ text {2,25} \ text {V}
\ Конец {*} выравнивание Мы знаем, что ЭДС батареи — это разность потенциалов на клемме, суммированная с разностью потенциалов на внутреннем сопротивлении, так:
\ Начать {*} Align
\ mathcal {E} & = V + Ir \\
& = \ text {18} + \ text {2,25} \\
& = \ text {20,25} \ text {V}
\ end {align *} Написать окончательный ответ
Ток через ячейку: \ (\ text {6,00} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4,00} \) \ (\ Omega \) составляет \ (\ text {4,50} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12,00} \) \ (\ Omega \) составляет \ (\ text {1,50} \) \ (\ text {A} \).
ЭДС батареи — \ (\ text {20,25} \) \ (\ text {V} \).
Рабочий пример 9: Мощность в последовательных и параллельных сетях резисторов
Учитывая следующую схему:
Ток, выходящий из батареи, равен \ (\ text {1,07} \) \ (\ text {A} \), общая мощность, рассеиваемая во внешней цепи, равна \ (\ text {6,42} \) \ ( \ text {W} \), отношение общих сопротивлений двух параллельных сетей \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, отношение \ (R_ \ text {1}: R_ \ text {2} \) — 3: 5 и \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \).
Определите:
- Разность потенциалов батареи,
- мощность рассеивается в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \), и
- , если батарея помечена как имеющая эдс \ (\ text {6,50} \) \ (\ text {V} \), каково значение сопротивления каждого резистора и мощности, рассеиваемой в каждом из них.
Что требуется
В этом вопросе вам дают различную информацию и просят определить мощность, рассеиваемую в каждом резисторе и каждой комбинации резисторов.Обратите внимание, что информация в основном относится к общей схеме. Это подсказка, что вы должны начать с общей схемы и перейти к более конкретным элементам схемы.
Расчет разности потенциалов батареи
Сначала мы сосредоточимся на батарее. Нам дают мощность для всей цепи, а также ток, выходящий из батареи. Мы знаем, что разность потенциалов на клеммах батареи — это разность потенциалов в цепи в целом.
Мы можем использовать соотношение \ (P = VI \) для всей цепи, потому что разность потенциалов такая же, как разность потенциалов на клеммах батареи:
\ Начать {*} Align
P & = VI \\
V & = \ frac {P} {I} \\
& = \ frac {\ text {6,42}} {\ text {1,07}} \\
& = \ text {6,00} \ text {V}
\ end {align *}
Разность потенциалов на батарее равна \ (\ text {6,00} \) \ (\ text {V} \).
Мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \)
Помните, что мы работаем от общих деталей схемы до деталей для отдельных элементов, это противоположно тому, как вы рассматривали эту схему ранее.
Мы можем рассматривать параллельные сети как эквивалентные резисторы, поэтому схема, с которой мы сейчас имеем дело, выглядит следующим образом:
Мы знаем, что ток через два элемента цепи будет одинаковым, потому что это последовательная цепь, и что сопротивление для всей цепи должно быть: \ (R_ {Ext} = R_ {P \ text {1}} + R_ {P \ текст {2}} \). Мы можем определить полное сопротивление из закона Ома для цепи в целом:
\ Начать {*} Align
V_ {батарея} & = IR_ {Ext} \\
R_ {Ext} & = \ frac {V_ {battery}} {I} \\
& = \ Гидроразрыва {\ текст {6,00}} {\ текст {1,07}} \\
& = \ text {5,61} \ text {Ω}
\ end {align *}
Мы знаем, что соотношение между \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, что означает, что мы знаем:
\ Начать {*} Align
R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \ \ \ text {и} \\
R_T & = R_ {P \ text {1}} + R_ {P \ text {2}} \\
& = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} + R_ {P \ text {2}} \\
& = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\
(\ text {5,61}) & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\
R_ {P \ text {2}} & = \ frac {\ text {2}} {\ text {3}} (\ text {5,61}) \\
R_ {P \ text {2}} & = \ text {3,74} \ text {Ω}
\ Конец {*} выравнивание
и поэтому:
\ Начать {*} Align
R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \\
& = \ Гидроразрыва {\ текст {1}} {\ текст {2}} (3.2 (\ text {3,74}) \\
& = \ text {4,28} \ text {W}
\ Конец {*} выравнивание
Эти значения добавят к исходному значению мощности, которое мы имели для внешней цепи. Если они этого не сделали
мы бы сделали ошибку в расчетах.
Параллельная сеть 1 расчеты
Теперь мы можем начать делать подробный расчет для первого набора параллельных резисторов.
Мы знаем, что соотношение между \ (R _ {\ text {1}}: R _ {\ text {2}} \) равно 3: 5, что означает, что мы знаем \ (R _ {\ text {1}} = \ frac {\ текст {3}} {\ текст {5}} R _ {\ текст {2}} \).Мы также знаем общее сопротивление для двух параллельных резисторов в этой сети.
is \ (\ text {1,87} \) \ (\ text {Ω} \). Мы можем использовать
соотношение между значениями двух резисторов, а также формула для общего
сопротивление (\ (\ frac {\ text {1}} {R_PT} = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2 }} \))
чтобы найти значения резистора:
\ Начать {*} Align
\ Гидроразрыва {\ текст {1}} {R_ {Р \ текст {1}}} & = \ гидроразрыва {\ текст {1}} {R_ \ текст {1}} + \ гидроразрыва {\ текст {1}} { R_ \ text {2}} \\
\ Гидроразрыва {\ текст {1}} {R_ {Р \ текст {1}}} & = \ гидроразрыва {\ текст {5}} {3R_ \ текст {2}} + \ гидроразрыва {\ текст {1}} { R_ \ text {2}} \\
\ Гидроразрыва {\ текст {1}} {R_ {Р \ текст {1}}} & = \ гидроразрыва {\ текст {1}} {R_ \ текст {2}} (\ гидроразрыва {\ текст {5}} { \ text {3}} + 1) \\
\ Гидроразрыва {\ текст {1}} {R_ {Р \ текст {1}}} & = \ гидроразрыва {\ текст {1}} {R_ \ текст {2}} (\ гидроразрыва {\ текст {5}} { \ text {3}} + \ frac {\ text {3}} {\ text {3}}) \\
\ Гидроразрыва {\ текст {1}} {R_ {Р \ текст {1}}} & = \ гидроразрыва {\ текст {1}} {R_ \ текст {2}} \ гидроразрыва {\ текст {8}} {\ текст {3}} \\
R_ \ text {2} & = R_ {P \ text {1}} \ frac {\ text {8}} {\ text {3}} \\
& = (\ text {1,87}) \ frac {\ text {8}} {\ text {3}} \\
& = \ text {4,99} \ text {Ω}
\ Конец {*} выравнивание
Мы также можем вычислить \ (R _ {\ text {1}} \):
\ Начать {*} Align
R _ {\ text {1}} & = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \\
& = \ frac {\ text {3}} {\ text {5}} (\ text {4,99}) \\
& = \ text {2,99} \ text {Ω}
\ end {align *}
Для определения мощности нам нужно рассчитанное нами сопротивление и либо разность потенциалов, либо ток.Два резистора расположены параллельно, поэтому разность потенциалов на них такая же, как и разность потенциалов на параллельной сети. Мы можем использовать закон Ома, чтобы определить разность потенциалов в сети параллельных резисторов, так как мы знаем общее сопротивление и ток:
\ Начать {*} Align
V & = I R \\
& = (\ text {1,07}) (\ text {1,87}) \\
& = \ text {2,00} \ text {V}
\ end {align *}
Теперь у нас есть информация, необходимая для определения мощности через каждый резистор:
\ Начать {*} Align
P_ \ text {1} & = \ frac {V ^ 2} {R_ \ text {1}} \\
& = \ frac {(\ text {2,00}) ^ 2} {\ text {2,99}} \\
& = \ text {1,34} \ text {W}
\ Конец {*} выравнивание \ Начать {*} Align
P_ \ text {2} & = \ frac {V ^ 2} {R_ \ text {2}} \\
& = \ frac {(\ text {2,00}) ^ 2} {\ text {4,99}} \\
& = \ text {0,80} \ text {W}
\ end {align *}
Параллельная сеть 2 вычисления
Теперь мы можем начать делать подробный расчет для второго набора параллельных резисторов.
Нам дано \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \), и мы знаем \ (R_ {P \ text {2}} \), поэтому мы можем вычислить \ (R_ \ text {4} \) из:
\ Начать {*} Align
\ frac {\ text {1}} {R_ {P \ text {2}}} & = \ frac {\ text {1}} {R_ \ text {3}} + \ frac {\ text {1}} { R_ \ text {4}} \\
\ frac {\ text {1}} {\ text {3,74}} & = \ frac {\ text {1}} {\ text {7,00}} + \ frac {\ text {1}} {R_ \ text {4}} \\
R_ \ text {4} & = \ text {8,03} \ text {Ω}
\ end {align *}
Мы можем вычислить разность потенциалов во второй параллельной сети, вычитая разность потенциалов первой параллельной сети из разности потенциалов батареи, \ (V_ {P \ text {2}} = \ text {6,00} — \ text {2,00} = \ text {4,00} \ text {V} \).2} {\ text {8,03}} \\
& = \ text {1,99} \ text {W}
\ end {align *}
Внутреннее сопротивление
Мы знаем, что ЭДС батареи — это \ (\ text {6,5} \) \ (\ text {V} \), но разность потенциалов, измеренная на клеммах, составляет всего \ (\ text {6} \) \ (\ текст {V}, \). Разница представляет собой разность потенциалов во внутреннем сопротивлении батареи, и мы можем использовать известный ток и закон Ома для определения внутреннего сопротивления:
\ Начать {*} Align
V & = I \ cdot R \\
R & = \ frac {V} {I} \\
& = \ frac {\ text {0,5}} {\ text {1,07}} \\
& = \ text {0,4672897} \\
& = \ text {0,47} \ text {Ω}
\ Конец {*} выравнивание Мощность, рассеиваемая внутренним сопротивлением батареи:
\ Начать {*} Align
P & = VI \\
& = \ text {0,5} \ cdot \ text {1,07} \\
& = \ text {0,535} \ text {W}
\ end {align *} Рабочий пример 10: внутреннее сопротивление и фары [NSC 2011 Paper 1]
Фара и две задние лампы IDENTICAL скутера подключены параллельно к батарее с неизвестным внутренним сопротивлением, как показано на упрощенной принципиальной схеме ниже.Фара имеет сопротивление \ (\ text {2,4} \) \ (\ text {Ω} \) и управляется переключателем \ (\ textbf {S} _1 \). Задние фонари управляются переключателем \ (\ textbf {S} _2 \). Сопротивление соединительных проводов можно игнорировать.
График рядом показывает разницу потенциалов между клеммами батареи до и после того, как переключатель \ (\ textbf {S} _1 \) замкнут (пока переключатель \ (\ textbf {S} _2 \) разомкнут). Переключатель \ (\ textbf {S} _1 \) закрыт в момент времени \ (\ textbf {t} _1 \).
Используйте график, чтобы определить ЭДС батареи.
(1 оценка)
ЗАКРЫТО ТОЛЬКО ПЕРЕКЛЮЧАТЕЛЕМ \ (\ textbf {S} _1 \), рассчитайте следующее:
Ток через фару
(3 оценки)
Внутреннее сопротивление батареи
(3 оценки)
ОБА ВЫКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) сейчас закрыты.Батарея выдает ток \ (\ text {6} \) \ (\ text {A} \) в течение этого периода.
Рассчитайте сопротивление каждой задней лампы.
(5 баллов)
Как повлияет показание вольтметра, если фара перегорела? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) по-прежнему замкнуты.)
Запишите только УВЕЛИЧЕНИЯ, УМЕНЬШЕНИЯ или ОСТАЕТСЯ ЖЕ.
Дайте объяснение.
(3 оценки)
Вопрос 1
\ (\ text {12} \) \ (\ text {V} \)
(1 оценка)
Вопрос 2.1
Вариант 1:
\ Начать {*} Align
Я & = \ frac {V} {R} \\
& = \ frac {\ text {9,6}} {\ text {2,4}} \\
& = \ text {4 A}
\ Конец {*} выравнивание Вариант 2:
\ Начать {*} Align
\ text {emf} & = IR + Ir \\
12 & = I (\ text {2,4}) + \ text {2,4} \\
\ следовательно я & = \ text {4 A}
\ Конец {*} выравнивание (3 оценки)
Вопрос 2.2
Вариант 1:
\ Начать {*} Align
\ text {emf} & = IR + Ir \\
12 & = \ text {9,4} + 4r \\
r & = \ text {0,6} \ \ Omega
\ Конец {*} выравнивание Вариант 2:
\ Начать {*} Align
V_ {потерянный} & = Ir \\
\ text {2,4} & = \ text {4} r \\
\ следовательно r & = \ text {0,6} \ \ Omega
\ Конец {*} выравнивание Вариант 3:
\ Начать {*} Align
\ text {emf} & = I (R + r) \\
\ text {12} & = \ text {4} (\ text {2,4} + r) \\
\ следовательно r & = \ text {0,6} \ \ Omega
\ Конец {*} выравнивание (3 оценки)
Вопрос 3
Вариант 1:
\ Начать {*} Align
\ text {emf} & = IR + Ir \\
\ text {12} & = \ text {6} (R + \ text {0,6}) \\
R _ {\ text {ext}} & = \ text {1,4} \ \ Omega
\ Конец {выравнивание *} \ BEGIN {*} выравнивания
\ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\
R & = \ text {3,36} \ \ Omega
\ Конец {*} выравнивание Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 2:
\ Начать {*} Align
\ text {Emf} & = V _ {\ text {терминал}} + Ir \\
12 & = V _ {\ text {терминал}} + 6 (\ text {0,6}) \\
\ следовательно V _ {\ text {терминал}} & = \ text {8,4} \ text {V}
\ Конец {выравнивание *} \ BEGIN {*} выравнивания
Я _ {\ text {2,4} \ \ Omega} & = \ frac {V} {R} \\
& = \ frac {\ text {8,4}} {\ text {2,4}} \\
& = \ text {3,5 A}
\ Конец {выравнивание *} \ BEGIN {*} выравнивания
Я _ {\ text {задние фонари}} & = 6 — \ text {3,5} \\
& = \ text {2,5} \ text {A} \\
R _ {\ text {задние фонари}} & = \ frac {V} {I} \\
& = \ frac {\ text {8,4}} {\ text {2,5}} \\
& = \ text {3,36} \ \ Omega \\
R _ {\ text {tail lamp}} & = \ text {1,68} \ \ Omega
\ Конец {*} выравнивание Вариант 3:
\ Начать {*} Align
V & = IR \\
\ text {12} & = \ text {6} (R) \\
R _ {\ text {ext}} & = 2 \ \ Omega
\ Конец {выравнивание *} \ BEGIN {*} выравнивания
R _ {\ text {параллельный}} & = 2 — \ text {0,6} \\
& = \ text {1,4} \ \ Omega \\
\ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\
R & = \ text {3,36} \ \ Omega
\ Конец {*} выравнивание Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 4:
Для параллельной комбинации: \ (I_ {1} + I_ {2} = 6 \ text {A} \)
\ Начать {*} Align
\ следовательно \ frac {V} {\ text {2,4}} + \ frac {V} {R _ {\ text {задние фонари}}} & = \ text {6} \\
\ text {8,4} \ left (\ frac {1} {\ text {2,4}} + \ frac {1} {R _ {\ text {tail lights}}} \ right) & = \ text {6 } \\
\ следовательно R _ {\ text {задние фонари}} & = \ text {3,36} \ \ Omega \\
R _ {\ text {tail lamp}} & = \ text {1,68} \ \ Omega
\ Конец {*} выравнивание (5 баллов)
Вопрос 4
Увеличивает
Сопротивление увеличивается, а ток уменьшается.Таким образом, \ (Ir \) (потерянное напряжение) должно уменьшиться, что приводит к увеличению напряжения.
(3 оценки)
[ИТОГО: 15 баллов]
, Влияет ли внутреннее сопротивление на производительность? С переходом от аналогового к цифровому, новые требования предъявляются к батарее. В отличие от портативных аналоговых устройств, которые потребляют постоянный ток, цифровое оборудование заряжает аккумулятор короткими сильными импульсами тока.
Одним из неотложных требований к батарее для цифровых приложений является низкое внутреннее сопротивление. Измеренное в миллиомах внутреннее сопротивление является привратником, который в значительной степени определяет время работы.Чем ниже сопротивление, тем меньше соприкасается батарея при подаче необходимых пиков мощности. Высокое показание в МОм может вызвать раннюю индикацию «низкого заряда батареи» на казалось бы хорошей батарее, поскольку доступная энергия не может быть доставлена требуемым образом и остается в батарее.
На рисунке 1 показана сигнатура напряжения и соответствующее время работы батареи с низким уровнем заряда. , среднее и высокое внутреннее сопротивление при подключении к цифровой нагрузке. Подобно мягкому шарику, который легко деформируется при сжатии, напряжение батареи с высоким внутренним сопротивлением модулирует напряжение питания и оставляет провалы, отражая импульсы нагрузки.Эти импульсы толкают напряжение к линии конца разряда, что приводит к преждевременному отключению. Как видно на графике, внутреннее сопротивление определяет большую часть времени работы.
Рисунок 1: Кривая разряда на импульсной нагрузке с различным внутренним сопротивлением. Эта диаграмма демонстрирует время работы 3 батарей с одинаковой емкостью, но с разными уровнями внутреннего сопротивления.
Время разговора как функция внутреннего сопротивления
В рамках продолжающегося исследования по измерению времени работы батарей с различными уровнями внутреннего сопротивления, Cadex Electronics проверила несколько батарей для сотовых телефонов, которые некоторое время находились в эксплуатации. Все батареи были одинакового размера и дали хорошие показатели емкости при проверке с помощью анализатора батареи при постоянной нагрузке разряда. Никель-кадмиевая упаковка дала 113% -ную емкость, никель-металлогидридная проверка — 107%, а литий-ионный — 94%.Внутреннее сопротивление варьировалось в широких пределах и составило низкое 155 мОм для никель-кадмиевого, высокое 778 мОм для никель-металлогидридного и умеренное 320 мОм для литий-ионного. Эти показания внутреннего сопротивления типичны для стареющих батарей с этими химическими составами.
Давайте теперь проверим, как тестовые батареи работают на мобильном телефоне. Максимальный импульсный ток сотовых телефонов GSM (Глобальная система мобильной связи) составляет 2,5 А. Это представляет собой большой ток относительно небольшой батареи, около 800 миллиампер (мАч) часов.Например, импульс тока 2,4 А от батареи емкостью 800 мАч соответствует частоте C 3C. Это в три раза превышает текущий рейтинг батареи. Такие сильные импульсы тока могут подаваться только при низком внутреннем сопротивлении батареи.
На рисунках 2, 3 и 4 показано время разговора трех батарей при моделируемом токе GSM 1C, 2C и 3C. Можно увидеть прямую связь между внутренним сопротивлением батареи и временем разговора. никель-кадмий показал лучшие результаты в данных условиях и обеспечил время разговора 120 минут при разряде 3C (оранжевая линия).никель-металл-гидридный тест выполнялся только при 1 ° С (синяя линия) и провал при 3 ° С. литий-ионный позволил умеренное время разговора 50 минут при 3C.
Рисунок 2: Разряд и результирующее время разговора никель-кадмия при 1С, 2С и 3С в соответствии с графиком нагрузки GSM.Тестируемая батарея имеет емкость 113%, внутреннее сопротивление — низкое 155 мОм.
Рисунок 3: Разряд и результирующее время разговора гидрида никеля с металлом при 1C, 2C и 3C в соответствии с графиком нагрузки GSM.Тестируемая батарея имеет емкость 107%, внутреннее сопротивление — 778 мОм.
Рисунок 4: Разрядка и результирующее время разговора литий-ионной батареи при 1C, 2C и 3C в соответствии с графиком нагрузки GSM. Тестируемая батарея имеет емкость 94%, внутреннее сопротивление составляет 320 МОм. Внутреннее сопротивление как функция состояния заряда
Внутреннее сопротивление зависит от уровня заряда батареи. Наибольшие изменения заметны на никелевых батареях.На рисунке 5 мы наблюдаем внутреннее сопротивление никель-металлогидрида, когда он пустой, во время зарядки, при полной зарядке и после 4-часового периода отдыха.
Уровни сопротивления самые высокие при низком уровне заряда и сразу после зарядки. Вопреки распространенному мнению, лучшая производительность батареи достигается не сразу после полной зарядки, а после нескольких часов отдыха. Во время разряда внутреннее сопротивление батареи уменьшается, достигает минимальной точки при половинном заряде и снова начинает ползти вверх (пунктирная линия).
Рисунок 5: Внутреннее сопротивление в никель-металл-гидриде. Обратите внимание на более высокие показания сразу после полной разрядки и полной зарядки. Отдых батареи перед использованием дает лучшие результаты.
Ссылки: Shukla et al. 1998. Rodrigues et al. 1999.
Внутреннее сопротивление литий-ионного аккумулятора довольно плоское: от пустого до полного заряда.Батарея уменьшается асимптотически с 270 мВт при 0% до 250 мВт при 70% -ном уровне заряда. Самые большие изменения происходят между 0% и 30% SoC.
Сопротивление свинцовой кислоты увеличивается с разрядом. Это изменение вызвано уменьшением удельного веса, истощением электролита, так как он становится более водянистым. Увеличение сопротивления почти линейно с уменьшением удельного веса. Оставшиеся несколько часов частично восстановят батарею, так как сульфат-ионы могут пополняться.Изменение сопротивления между полной зарядкой и разрядкой составляет около 40%. Холодная температура увеличивает внутреннее сопротивление всех батарей и добавляет примерно 50% между + 30 ° C и -18 ° C для свинцово-кислотных батарей. На рисунке 6 показано увеличение внутреннего сопротивления свинцово-кислотной батареи в гелеобразном состоянии, используемой для инвалидных колясок.
Рисунок 6: Типичные показания внутреннего сопротивления свинцово-кислотной батареи для инвалидных колясок.Аккумулятор разряжен от полной зарядки до 10.50V. Показания были получены при напряжении холостого хода (OCV).
аккумуляторных лабораторий Cadex.
*** Пожалуйста, ознакомьтесь с комментариями ***
Комментарии предназначены для «комментирования», открытого обсуждения среди посетителей сайта. Battery University следит за комментариями и понимает важность выражения взглядов и мнений на общем форуме. Однако все общение должно осуществляться с использованием соответствующего языка и предотвращения спама и дискриминации.
Если у вас есть предложение или вы хотите сообщить об ошибке, воспользуйтесь формой «свяжитесь с нами» или напишите нам по адресу: [email protected]. Мы хотели бы услышать от вас, но мы не можем ответить на все вопросы. Мы рекомендуем опубликовать ваш вопрос в разделах комментариев для Battery University Group (BUG), чтобы поделиться.
или перейти в другой архив
, Измерение внутреннего сопротивления батарей
Избранные
любимец
6 Внутреннее сопротивление
При разработке схемы с аккумулятором мы часто предполагаем, что аккумулятор является идеальным источником напряжения. Это означает, что независимо от того, какую нагрузку мы прилагаем к батарее или мало, напряжение на клеммах источника всегда будет оставаться неизменным.
Если мы моделируем эту батарею как идеальный источник напряжения, изменение значения R L не влияет на напряжение между клеммами батареи
В действительности, несколько факторов могут ограничивать способность батареи действовать как идеальный источник напряжения.Размер батареи, химические свойства, возраст и температура влияют на величину тока, который может выдавать батарея. В результате мы можем создать лучшую модель батареи с идеальным источником напряжения и резистором серии .
Батареи могут быть смоделированы как идеальный источник напряжения с последовательным резистором (с маркировкой R I )
Мы можем измерить напряжение аккумулятора на его клеммах без подключения нагрузки. Это известно как напряжение холостого хода (V OC ).
Измерение напряжения щелочного элемента АА без нагрузки
Обратите внимание, что из-за отсутствия тока через внутренний резистор падение напряжения на нем равно 0 В. Поэтому можно предположить, что V OC равно напряжению идеального источника напряжения в батарее.
Если подключить нагрузку к батарее, напряжение на клеммах падает.
Здесь мы измеряем падение напряжения на резисторе 4 Ом
Это падение напряжения вызвано внутренним сопротивлением батареи.Мы можем рассчитать внутреннее сопротивление, если взять показания напряжения холостого хода и напряжения на клеммах батареи с подключенной нагрузкой.
Для начала мы создадим диаграмму, показывающую нашу схему.
Вот наша схема. Мы хотим рассчитать R I .
Мы можем подключить измеренное нами нагруженное напряжение (V L ) и значение резистора (R L ) в закон Ома, чтобы ток протекал через цепь (I).
Нам также нужно получить напряжение на внутреннем резисторе. Мы можем сделать это, используя закон напряжения Кирхгофа. Упрощенно для этой схемы, мы можем сказать, что падение напряжения на обоих резисторах должно складываться с напряжением идеального источника напряжения.
Теперь, когда мы знаем падение напряжения на внутреннем резисторе и ток через него, мы можем снова использовать закон Ома, чтобы найти его сопротивление.
Отсюда видно, что внутреннее сопротивление (на данный момент) элемента AA составляет 0.273 Ом .
ПРИМЕЧАНИЕ : с помощью этого метода мы можем сделать только снимок внутреннего сопротивления. Внутреннее сопротивление может варьироваться в зависимости от времени работы батареи и температуры. Через 10 минут значение сопротивления может быть другим! Обычная щелочная батарея типа АА может иметь внутреннее сопротивление от 0,1 до 0,9 Ом.
← Предыдущая страница
Введение ,
Используйте график, чтобы определить ЭДС батареи.
(1 оценка)
ЗАКРЫТО ТОЛЬКО ПЕРЕКЛЮЧАТЕЛЕМ \ (\ textbf {S} _1 \), рассчитайте следующее:
Ток через фару
(3 оценки)
Внутреннее сопротивление батареи
(3 оценки)
ОБА ВЫКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) сейчас закрыты.Батарея выдает ток \ (\ text {6} \) \ (\ text {A} \) в течение этого периода.
Рассчитайте сопротивление каждой задней лампы.
(5 баллов)
Как повлияет показание вольтметра, если фара перегорела? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) по-прежнему замкнуты.)
Запишите только УВЕЛИЧЕНИЯ, УМЕНЬШЕНИЯ или ОСТАЕТСЯ ЖЕ.
Дайте объяснение.
(3 оценки)
С переходом от аналогового к цифровому, новые требования предъявляются к батарее. В отличие от портативных аналоговых устройств, которые потребляют постоянный ток, цифровое оборудование заряжает аккумулятор короткими сильными импульсами тока.
Одним из неотложных требований к батарее для цифровых приложений является низкое внутреннее сопротивление. Измеренное в миллиомах внутреннее сопротивление является привратником, который в значительной степени определяет время работы.Чем ниже сопротивление, тем меньше соприкасается батарея при подаче необходимых пиков мощности. Высокое показание в МОм может вызвать раннюю индикацию «низкого заряда батареи» на казалось бы хорошей батарее, поскольку доступная энергия не может быть доставлена требуемым образом и остается в батарее.
На рисунке 1 показана сигнатура напряжения и соответствующее время работы батареи с низким уровнем заряда. , среднее и высокое внутреннее сопротивление при подключении к цифровой нагрузке. Подобно мягкому шарику, который легко деформируется при сжатии, напряжение батареи с высоким внутренним сопротивлением модулирует напряжение питания и оставляет провалы, отражая импульсы нагрузки.Эти импульсы толкают напряжение к линии конца разряда, что приводит к преждевременному отключению. Как видно на графике, внутреннее сопротивление определяет большую часть времени работы.
| | Рисунок 1: Кривая разряда на импульсной нагрузке с различным внутренним сопротивлением. Эта диаграмма демонстрирует время работы 3 батарей с одинаковой емкостью, но с разными уровнями внутреннего сопротивления. |
Время разговора как функция внутреннего сопротивления
В рамках продолжающегося исследования по измерению времени работы батарей с различными уровнями внутреннего сопротивления, Cadex Electronics проверила несколько батарей для сотовых телефонов, которые некоторое время находились в эксплуатации. Все батареи были одинакового размера и дали хорошие показатели емкости при проверке с помощью анализатора батареи при постоянной нагрузке разряда. Никель-кадмиевая упаковка дала 113% -ную емкость, никель-металлогидридная проверка — 107%, а литий-ионный — 94%.Внутреннее сопротивление варьировалось в широких пределах и составило низкое 155 мОм для никель-кадмиевого, высокое 778 мОм для никель-металлогидридного и умеренное 320 мОм для литий-ионного. Эти показания внутреннего сопротивления типичны для стареющих батарей с этими химическими составами.
Давайте теперь проверим, как тестовые батареи работают на мобильном телефоне. Максимальный импульсный ток сотовых телефонов GSM (Глобальная система мобильной связи) составляет 2,5 А. Это представляет собой большой ток относительно небольшой батареи, около 800 миллиампер (мАч) часов.Например, импульс тока 2,4 А от батареи емкостью 800 мАч соответствует частоте C 3C. Это в три раза превышает текущий рейтинг батареи. Такие сильные импульсы тока могут подаваться только при низком внутреннем сопротивлении батареи.
На рисунках 2, 3 и 4 показано время разговора трех батарей при моделируемом токе GSM 1C, 2C и 3C. Можно увидеть прямую связь между внутренним сопротивлением батареи и временем разговора. никель-кадмий показал лучшие результаты в данных условиях и обеспечил время разговора 120 минут при разряде 3C (оранжевая линия).никель-металл-гидридный тест выполнялся только при 1 ° С (синяя линия) и провал при 3 ° С. литий-ионный позволил умеренное время разговора 50 минут при 3C.
Рисунок 2: Разряд и результирующее время разговора никель-кадмия при 1С, 2С и 3С в соответствии с графиком нагрузки GSM.Тестируемая батарея имеет емкость 113%, внутреннее сопротивление — низкое 155 мОм.
Рисунок 3: Разряд и результирующее время разговора гидрида никеля с металлом при 1C, 2C и 3C в соответствии с графиком нагрузки GSM.Тестируемая батарея имеет емкость 107%, внутреннее сопротивление — 778 мОм.
Рисунок 4: Разрядка и результирующее время разговора литий-ионной батареи при 1C, 2C и 3C в соответствии с графиком нагрузки GSM. Тестируемая батарея имеет емкость 94%, внутреннее сопротивление составляет 320 МОм.
Внутреннее сопротивление как функция состояния заряда
Внутреннее сопротивление зависит от уровня заряда батареи. Наибольшие изменения заметны на никелевых батареях.На рисунке 5 мы наблюдаем внутреннее сопротивление никель-металлогидрида, когда он пустой, во время зарядки, при полной зарядке и после 4-часового периода отдыха.Уровни сопротивления самые высокие при низком уровне заряда и сразу после зарядки. Вопреки распространенному мнению, лучшая производительность батареи достигается не сразу после полной зарядки, а после нескольких часов отдыха. Во время разряда внутреннее сопротивление батареи уменьшается, достигает минимальной точки при половинном заряде и снова начинает ползти вверх (пунктирная линия).
| Рисунок 5: Внутреннее сопротивление в никель-металл-гидриде. Обратите внимание на более высокие показания сразу после полной разрядки и полной зарядки. Отдых батареи перед использованием дает лучшие результаты. Ссылки: Shukla et al. 1998. Rodrigues et al. 1999. |
Внутреннее сопротивление литий-ионного аккумулятора довольно плоское: от пустого до полного заряда.Батарея уменьшается асимптотически с 270 мВт при 0% до 250 мВт при 70% -ном уровне заряда. Самые большие изменения происходят между 0% и 30% SoC.
Сопротивление свинцовой кислоты увеличивается с разрядом. Это изменение вызвано уменьшением удельного веса, истощением электролита, так как он становится более водянистым. Увеличение сопротивления почти линейно с уменьшением удельного веса. Оставшиеся несколько часов частично восстановят батарею, так как сульфат-ионы могут пополняться.Изменение сопротивления между полной зарядкой и разрядкой составляет около 40%. Холодная температура увеличивает внутреннее сопротивление всех батарей и добавляет примерно 50% между + 30 ° C и -18 ° C для свинцово-кислотных батарей. На рисунке 6 показано увеличение внутреннего сопротивления свинцово-кислотной батареи в гелеобразном состоянии, используемой для инвалидных колясок.
| | Рисунок 6: Типичные показания внутреннего сопротивления свинцово-кислотной батареи для инвалидных колясок.Аккумулятор разряжен от полной зарядки до 10.50V. Показания были получены при напряжении холостого хода (OCV). аккумуляторных лабораторий Cadex. |
*** Пожалуйста, ознакомьтесь с комментариями ***
Комментарии предназначены для «комментирования», открытого обсуждения среди посетителей сайта. Battery University следит за комментариями и понимает важность выражения взглядов и мнений на общем форуме. Однако все общение должно осуществляться с использованием соответствующего языка и предотвращения спама и дискриминации.
Если у вас есть предложение или вы хотите сообщить об ошибке, воспользуйтесь формой «свяжитесь с нами» или напишите нам по адресу: [email protected]. Мы хотели бы услышать от вас, но мы не можем ответить на все вопросы. Мы рекомендуем опубликовать ваш вопрос в разделах комментариев для Battery University Group (BUG), чтобы поделиться.
или перейти в другой архив
,Измерение внутреннего сопротивления батарей
Избранные любимец 6Внутреннее сопротивление
При разработке схемы с аккумулятором мы часто предполагаем, что аккумулятор является идеальным источником напряжения. Это означает, что независимо от того, какую нагрузку мы прилагаем к батарее или мало, напряжение на клеммах источника всегда будет оставаться неизменным.
Если мы моделируем эту батарею как идеальный источник напряжения, изменение значения R L не влияет на напряжение между клеммами батареи
В действительности, несколько факторов могут ограничивать способность батареи действовать как идеальный источник напряжения.Размер батареи, химические свойства, возраст и температура влияют на величину тока, который может выдавать батарея. В результате мы можем создать лучшую модель батареи с идеальным источником напряжения и резистором серии .
Батареи могут быть смоделированы как идеальный источник напряжения с последовательным резистором (с маркировкой R I )
Мы можем измерить напряжение аккумулятора на его клеммах без подключения нагрузки. Это известно как напряжение холостого хода (V OC ).
Измерение напряжения щелочного элемента АА без нагрузки
Обратите внимание, что из-за отсутствия тока через внутренний резистор падение напряжения на нем равно 0 В. Поэтому можно предположить, что V OC равно напряжению идеального источника напряжения в батарее.
Если подключить нагрузку к батарее, напряжение на клеммах падает.
Здесь мы измеряем падение напряжения на резисторе 4 Ом
Это падение напряжения вызвано внутренним сопротивлением батареи.Мы можем рассчитать внутреннее сопротивление, если взять показания напряжения холостого хода и напряжения на клеммах батареи с подключенной нагрузкой.
Для начала мы создадим диаграмму, показывающую нашу схему.
Вот наша схема. Мы хотим рассчитать R I .
Мы можем подключить измеренное нами нагруженное напряжение (V L ) и значение резистора (R L ) в закон Ома, чтобы ток протекал через цепь (I).
Нам также нужно получить напряжение на внутреннем резисторе. Мы можем сделать это, используя закон напряжения Кирхгофа. Упрощенно для этой схемы, мы можем сказать, что падение напряжения на обоих резисторах должно складываться с напряжением идеального источника напряжения.
Теперь, когда мы знаем падение напряжения на внутреннем резисторе и ток через него, мы можем снова использовать закон Ома, чтобы найти его сопротивление.
Отсюда видно, что внутреннее сопротивление (на данный момент) элемента AA составляет 0.273 Ом .
ПРИМЕЧАНИЕ : с помощью этого метода мы можем сделать только снимок внутреннего сопротивления. Внутреннее сопротивление может варьироваться в зависимости от времени работы батареи и температуры. Через 10 минут значение сопротивления может быть другим! Обычная щелочная батарея типа АА может иметь внутреннее сопротивление от 0,1 до 0,9 Ом.
← Предыдущая страница
Введение ,

