Википедия электромагнетизм: Категория:Электромагнетизм — Википедия – Electromagnetism — Wikipedia — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Электромагнетизм — Традиция

Молния-это электростатический разряд , который движется между двумя заряженными областями. Его принцип основан на действии электромагнитной силы^[1]

Электромагнетизм — область изучения электромагнитной силы , которая является типом физического взаимодействия, которое происходит между электрически заряженными частицами en:Electric_charge. Электромагнитные силы, как правило, проявляются в виде электромагнитного поля, например, электрического поля, магнитного поля и света. Электромагнитные силыэто одно из четырех фундаментальных взаимодействий en:Fundamental_interaction в природе. Три другие — сильного взаимодействия en:Strong_interaction, слабого взаимодействияи en:Weak_interaction гравитации en:Gravitation.^[2]

Слово электромагнетизм является соединением двух греческих en:Greek_language терминов, ἢλεκτρον, ēlektron, «Янтарь», и μαγνήτης, магнитные, из «magnítis líthos» (μαγνήτης λίθος), что означает «магнезиальный камень», вид железной руды en:Iron_ore. В науке электромагнитных явлений электромагнетизм определяется с точки зрения электромагнитной силы, иногда называемая силой Лоренца, которая включает в себя как электричество и магнетизм en:Magnetism как элементы одного явления.

Электромагнитные силы играют главную роль в определении внутренних свойств большинства объектов, возникающих в повседневной жизни. Обычная материя на молекулярном уровне, в том числе его плотность определяет баланс между электромагнитной силы и силой, порожденной обменом импульсов, переносимых электронами, которая обретает форму, в результате межмолекулярных сил между отдельными молекулами в веществе. Электроны связаны электромагнитной волновой механикой в орбитах вокруг атомных ядер , образуя атомы, которые являются строительным материалом для молекул. Она регулирует процессы в химии, которые возникают от взаимодействия между электронами соседних атомов, которые, в свою очередь, определяются взаимодействием между электромагнитной силы и импульса электронов.

Существуют многочисленные математические описания электромагнитного поля. В классической электродинамике, электрические поля описаны как электрический потенциал и электрический ток в закон Ома en:Ohm’s_law, магнитные поля, связанные с электромагнитной индукцией и магнетизмом en:Magnetism, уравнениями Максвелла описывают электрические и магнитные поля, создают и изменяют друг друга, заряды и токи.

Теоретическое значение электромагнетизма, в частности, создание скорости света на основе свойств «среднего» распространения (проницаемость en:Permeability_(electromagnetism) и диэлектрической проницаемости en:Permittivity), привело к разработке специальной теории относительности Альберта Эйнштейна в 1905 году.

Хотя электромагнетизм считается одной из четырех фундаментальных сил при высокой энергии электрослабой силой, а электромагнетизм с ними объединяется. В истории Вселенной, в quark эпохе en:Quark_epoch, электрослабая сила разделяется на электромагнитные и слабые силы.

История из электромагнитной теории[править]

См. также: История из электромагнитной теории

Ганс Кристиан Эрстед

Первоначально электричество и магнетизм рассматривали как две отдельные силы. Это представление изменилось, однако, с публикацией Джеймса Клерка Максвелла EN:James_Clerk_Maxwell 1873 г. Трактат об электричестве и Магнетизме en:A_Treatise_on_Electricity_and_Magnetism, в котором взаимодействие положительных и отрицательных зарядов было показано, что оно регулируется одной силой. Существует четыре основных эффектов, возникающих в результате этих взаимодействий, все из которых были наглядно продемонстрированы экспериментами:

Электрические заряды притягиваются или отталкиваются с силой, обратно пропорциональной квадрату расстояния между ними: разноименные заряды притягивают, как и те (одноимённые), что отталкивают.

Магнитные полюса (или состояние поляризации в отдельных точках) привлекают или отталкивают друг друга подобным образом и всегда идут парами: каждый Северный полюс запряженных в Южном полюсе.
Электрический ток в проводе создает круговое магнитное поле вокруг провода, его направление (по часовой стрелке или против часовой стрелки) в зависимости от направления текущего тока.
В проводе индуцируется ток в петле из проволоки, когда она перемещается в направлении или в сторону от магнитного поля, или магнит перемещается в направлении или от него, в направлении тока, в зависимости от движения.

Готовясь к вечерней лекции на 21 апреля 1820, Hans Christian Ørsted сделал удивительное наблюдение. Когда он занимался со своими материалами (предметами), он заметил, что стрелка компаса отклоняется от магнитного Севера , когда электрический ток от батареи он был включен и выключен. Этот прогиб убедил его, что магнитные поля излучают со всех сторон провода, несущие электрический ток en:Ampère’s_force_law, en:Ampère’s_circuital_law, подобно тому, как свет и тепло делать, и что это подтвердили прямую связь между электричеством и магнетизмом.

Майкл Фарадей

На момент открытия Эрстеда не предполагают какого-либо удовлетворительного объяснения этого явления, не пытается представлять явления в математические рамки. Однако, три месяца спустя он начал более интенсивные исследования. Вскоре после этого он опубликовал свои выводы, доказывая, что электрический ток создает магнитное поле, как она течет через провод. В CGS единица магнитной индукции (эрстед) назван в честь его заслуг в области электромагнетизма.

Джеймс Клерк Максвелл[править]

Выводы Джеймс Клерк Максвелла en:James_Clerk_Maxwell в результате интенсивных исследований на протяжении всей научной открытой и закрытой деятельности (большую часть научной деятельности учёный проводил в королевской лаборатори скрыто) в

электродинамике повлияли на французского физика Андре-Мари Ампера’s в разработках единой математической форме представление магнитных сил между токоведущими жилами. Открытие Эрстеда также представляет собой большой шаг в направлении единой концепции энергии.

Это объединение, которое наблюдалось у Майкла Фарадея, продленное Джеймс клерк Максвеллом, и частично переформулировнное Оливером Хевисайдом и Генрихом Герцем, является одним из ключевых достижений 19-го века математической физики. Это имело далеко идущие последствия, одним из которых было понимание природы света. В отличие от всего, что предлагалось в Электромагнетизме, свет и другие электромагнитные волны являются в настоящее время, рассматриваются и принимаются как форма квантованных, самораспространяющийся колебательных возмущений электромагнитного поля, которые были названы фотонами. Разные частоты колебания порождают различные формы электромагнитного излучения, от радиоволн низких частот видимого света как промежуточные частоты, гамма-излучение на высоких частотах.

Эрстед был не единственным человеком, который рассмотрел взаимосвязь между электричеством и магнетизмом. В 1802 году Джан Доменико Romagnosi, Итальянский ученый — правовед, отклонил магнитную стрелку, с помощью электростатических зарядов. На самом деле, без гальванического тока это существовало в настройке и, следовательно, не присутствовал электромагнетизм. Стоимость открытия была опубликована в 1802 году в итальянской газете, но это в значительной степени забывается современным научным сообществом.

[3]

Фундаментальные силы[править]

Представление вектора электрического поля волны циркулярно поляризованного электромагнитного излучения.

Электромагнитные силы является одним из четырех известных фундаментальных сил.

Условно принято четыре фундаментальных сил:

Гравитационные взаимодействия,
Электромагнитные силы,
Сильная ядерная и слабая ядерная сила (надо понимать как динамика поля).
Гравитационная сила, которая моделируется в виде непрерывной классической области. Каждый из трех других моделируется в виде дискретного квантового поля, экспонаты измеряемой единицы или элементарных частиц.

Другие фундаментальные силы:

Все другие силы (например, трения) являются в конечном счете производными от этих основных сил и импульса осуществляемые движение частиц.

Электромагнитные силы — это единственные, которые отвечает практически за все явления, с которыми человек сталкивается в повседневной жизни в ядерной шкале, за исключением гравитации. Грубо говоря, все силы, участвующие во взаимодействиях между атомами могут быть объяснены с помощью электромагнитной силы, действующей на электрически заряженные атомные ядра и электроны внутри и вокруг атомов, вместе с тем, как эти частицы вносят импульс в их движения. Это включает в себя силы, которые мы испытываем в «толкании» или «движении» обычных материальных объектов, которые приходят от межмолекулярных сил между отдельными молекулами в наших телах и сил в объектах. Она также включает в себя все виды химических явлений.

Необходимой частью понимания внутриатомных для межмолекулярных сил — эффективная сила, генерируемых импульсов электронов движения и, что электроны движутся между взаимодействующими атомами, несущие импульсы с ними. Как совокупность электронов становится более ограниченной, их минимальные обороты обязательно увеличивается из-за запрета принципа Паули. Поведение материи на молекулярном уровне, в том числе его плотность определяет баланс между электромагнитной силы и силой, порожденной обменом импульсов, переносимых электронами.

Классическая электродинамика[править]

Квантовая механика[править]

Фотоэлектрический эффект[править]

Электрослабые взаимодействия[править]

Величины и единицы[править]

Единицы СИ[править]

Дополнительная литература[править]

Веб-источники[править]

Внешние ссылки[править]

Электродинамика — Википедия

Электродина́мика — раздел физики, изучающий электромагнитное поле в наиболее общем случае (то есть, рассматриваются переменные поля, зависящие от времени) и его взаимодействие с телами, имеющими электрический заряд (электромагнитное взаимодействие)^[1]. Предмет электродинамики включает связь электрических и магнитных явлений, электромагнитное излучение (в разных условиях, как свободное, так и в разнообразных случаях взаимодействия с веществом), электрический ток (вообще говоря, переменный) и его взаимодействие с электромагнитным полем (электрический ток может быть рассмотрен при этом как совокупность движущихся заряженных частиц). Любое электрическое и магнитное взаимодействие между заряженными телами рассматривается в современной физике как осуществляющееся посредством электромагнитного поля, и, следовательно, также является предметом электродинамики.

Чаще всего под термином электродинамика по умолчанию понимается классическая электродинамика, описывающая только непрерывные свойства электромагнитного поля посредством системы уравнений Максвелла; для обозначения современной квантовой теории электромагнитного поля и его взаимодействия с заряженными частицами обычно используется устойчивый термин квантовая электродинамика. Термин «электродинамика» ввёл Андре-Мари Ампер, опубликовавший в 1823 году работу «Конспект теории электродинамических явлений».

Основные понятия, которыми оперирует электродинамика, включают в себя:

Электромагнитное поле — это основной предмет изучения электродинамики, вид материи, проявляющийся при взаимодействии с заряженными телами. Исторически разделяется на два поля:
- Электрическое поле — создаётся любым заряженным телом или переменным магнитным полем, оказывает воздействие на любое заряженное тело.
- Магнитное поле — создаётся движущимися заряженными телами, заряженными частицами, имеющими спин, и переменными электрическими полями, оказывает воздействие на движущиеся заряды и заряженные тела, имеющие спин. (Понятие спина в обменном взаимодействии тождественных частиц учитывается в квантовой механике и представляет собой чисто квантовый эффект, исчезающий при предельном переходе к классической механике.)
Электрический заряд — это свойство тел, позволяющее им взаимодействовать с электромагнитными полями: создавать эти поля, будучи их источниками, и подвергаться (силовому) действию этих полей.
Электромагнитный потенциал — 4-векторная физическая величина, полностью определяющая распределение электромагнитного поля в пространстве. В трехмерной формулировке электродинамики из него выделяют:
Вектор Пойнтинга — векторная физическая величина, имеющая смысл плотности потока энергии электромагнитного поля.

Основными уравнениями, описывающими поведение электромагнитного поля и его взаимодействие с заряженными телами являются:

Уравнения Максвелла, определяющие поведение свободного электромагнитного поля в вакууме и среде, а также генерацию поля источниками. Среди этих уравнений можно выделить:
Выражение для силы Лоренца, определяющее силу, действующую на заряд, находящийся в электромагнитном поле.
Закон Джоуля — Ленца, определяющий величину тепловых потерь в проводящей среде с конечной проводимостью, при наличии в ней электрического поля.

Частными уравнениями, имеющими особое значение являются:

Основным содержанием классической электродинамики является описание свойств электромагнитного поля и его взаимодействия с заряженными телами (заряженные тела «порождают» электромагнитное поле, являются его «источниками», а электромагнитное поле в свою очередь действует на заряженные тела, создавая электромагнитные силы). Это описание, кроме определения основных объектов и величин, таких как электрический заряд, электрическое поле, магнитное поле, электромагнитный потенциал, сводится к уравнениям Максвелла в той или иной форме и формуле силы Лоренца, а также затрагивает некоторые смежные вопросы (относящиеся к математической физике, приложениям, вспомогательным величинам и вспомогательным формулам, важным для приложений, как например вектор плотности тока или эмпирический закона Ома). Также это описание включает вопросы сохранения и переноса энергии, импульса, момента импульса электромагнитным полем, включая формулы для плотности энергии, вектора Пойнтинга и т. п.

Иногда под электродинамическими эффектами (в противоположность электростатике) понимают те существенные отличия общего случая поведения электромагнитного поля (например, динамическую взаимосвязь между меняющимися электрическим и магнитным полем) от статического случая, которые делают частный статический случай гораздо более простым для описания, понимания и расчётов.

Специальные разделы электродинамики[править | править код]

Электростатика описывает свойства статического (не меняющегося со временем или меняющегося достаточно медленно, чтобы «электродинамическими» эффектами можно было пренебречь, то есть, когда в уравнениях Максвелла можно отбросить, из-за их малости, члены с производными по времени) электрического поля и его взаимодействия с электрически заряженными телами (электрическими зарядами), которые также неподвижны или движутся с достаточно малыми скоростями (или, быть может, если есть и быстро движущиеся заряды, но они достаточно малы по величине), чтобы создаваемые ими поля можно было приближенно рассматривать как статические. Обычно при этом подразумевается и отсутствие (или пренебрежимая малость) магнитных полей.^[2]
Магнитостатика исследует постоянные токи (и постоянные магниты) и постоянные магнитные поля (поля не меняются во времени или меняются настолько медленно, что быстротой этих изменений в расчёте можно пренебречь), а также их взаимодействие.
Электродинамика сплошных сред рассматривает поведение электромагнитных полей в сплошных средах.
Релятивистская электродинамика рассматривает электромагнитные поля в движущихся средах.

Электродинамика лежит в основе физической оптики, физики распространения радиоволн, а также пронизывает практически всю физику, так как почти во всех разделах физики приходится иметь дело с электрическими полями и зарядами, а часто и с их нетривиальными быстрыми изменениями и движениями. Кроме того, электродинамика является образцовой физической теорией (и в классическом и в квантовом своём варианте), сочетающей очень большую точность расчётов и предсказаний с влиянием теоретических идей, родившихся в её области, на другие области теоретической физики.

Электродинамика имеет огромное значение в технике и лежит в основе: радиотехники, электротехники, различных отраслей связи и радио.

Первым доказательством связи электрических и магнитных явлений стало экспериментальное открытие Эрстедом в 1819—1820 порождения магнитного поля электрическим током. Он же высказал идею о некотором взаимодействии электрических и магнитных процессов в пространстве, окружающем проводник, однако в довольно неясной форме.

В 1831 году Майкл Фарадей экспериментально открыл явление и закон электромагнитной индукции, ставшие первым ясным свидетельством непосредственной динамической взаимосвязи электрического и магнитного полей. Он же разработал (применительно к электрическому и магнитному полям) основы концепции физического поля и некоторые базисные теоретические представления, позволяющие описывать физические поля, а также 1832 году предсказал существование электромагнитных волн.

В 1864 году Дж. К. Максвелл впервые опубликовал полную систему уравнений «классической электродинамики», описывающую эволюцию электромагнитного поля и его взаимодействие с зарядами и токами. Он высказал теоретически обоснованное предположение о том, что свет является электромагнитной волной, то есть объектом электродинамики.

В 1895 году Лоренц внёс существенный вклад в построение классической электродинамики, описав взаимодействие электромагнитного поля с (движущимися) точечными заряженными частицами. Это позволило ему вывести преобразования Лоренца. Он же первым заметил, что уравнения электродинамики противоречат ньютоновской физике.

В 1905 году А. Эйнштейн публикует работу «К электродинамике движущихся тел», в которой формулирует специальную теорию относительности. Теория относительности, в отличие от ньютоновской физики, находится в полном согласии с классической электродинамикой и логически завершает её построение, позволив создать её ковариантную формулировку в пространстве Минковского через 4-потенциал и 4-тензор электромагнитного поля.

В середине XX века была создана квантовая электродинамика — одна из наиболее точных физических теорий, служащая фундаментом и образцом для всех современных теоретических построений в физике элементарных частиц.

↑ Баумгарт К. К.,. Электродинамика // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Хотя можно считать, что это делается в целом скорее лишь для упрощения изложения, так как сочетание электростатики и магнитостатики (их совместное применение в рамках одной задачи) в принципе достаточно тривиально чтобы не представлять трудностей, сохраняя почти все преимущества того и другого приближения. Задачи же, когда это актуально, достаточно нередки.

ЭСБЕ/Электромагнетизм — Викитека

Электромагнетизм. — Начало учению об электромагнитных явлениях положено открытием Эрстеда. В 1820 г. Эрстед показал, что проволока, по которой течет электрический ток, вызывает отклонение магнитной стрелки. Он подробно исследовал это отклонение с качественной стороны, но не дал общего правила, по которому можно было бы определять направление отклонения в каждом отдельном случае. Вслед за Эрстедом открытия пошли одно за другим. Ампер (1820) опубликовал свои работы о действии тока на ток или тока на магнит. Амперу принадлежит общее правило для действия тока на магнитную стрелку: если вообразить себя расположенным в проводнике лицом к магнитной стрелке и притом так, чтобы ток имел направление от ног к голове, то северный полюс отклоняется влево. Далее мы увидим, что Ампер свел явления электромагнитные к явлениям электродинамическим (1823). К 1820 г. относятся также работы Араго, который заметил, что проволока, по которой течет электрический ток, притягивает к себе железные опилки. Он же намагнитил впервые железные и стальные проволоки, помещая их внутрь катушки медных проволок, по которым проходил ток. Ему же удалось намагнитить иглу, поместив ее в катушку и разрядив лейденскую банку через катушку. Независимо от Араго намагничивание стали и железа током было открыто Дэви.

Первые количественные определения действия тока на магнит точно так же относятся к 1820 г. и принадлежат Био и Савару. Эти ученые из своих опытов вывели следующее:

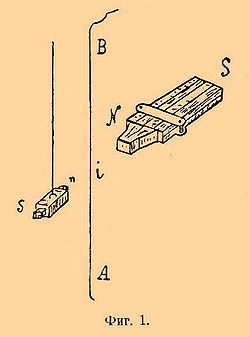
Если укрепить маленькую магнитную стрелку sn вблизи длинного вертикального проводника AB и астазировать земное поле магнитом NS (фиг. 1), то можно обнаружить следующее:

1. При прохождении тока через проводник магнитная стрелка устанавливается своей длиной под прямым углом к перпендикуляру, опущенному из центра стрелки на проводник.

2. Сила, действующая на тот или другой полюс n и s перпендикулярна к плоскости, проведенной через проводник и данный полюс

3. Сила, с которой действует на магнитную стрелку данный ток, проходящий по очень длинному прямолинейному проводнику, обратно пропорциональна расстоянию от проводника до магнитной стрелки.

Все эти наблюдения и другие могут быть выведены из следующего элементарного количественного закона, известного под именем закона Лапласа-Био-Савара:

dF = k(imSinθds)/r², (1),

где dF — действие элемента тока на магнитный полюс; i — сила тока; m — количество магнетизма, θ — угол, составляемый направлением тока в элементе с линией, соединяющей полюс с элементом тока; ds — длина элемента тока; r —расстояние рассматриваемого элемента от полюса; k — коэффициент пропорциональности.

На основании закона действие равно противодействию, Ампер заключил, что магнитный полюс должен действовать на элемент тока с такой же силой

dФ = k(imSinθds)/r², (2)

прямо противоположной по направлению силе dF, точно также действующей по направлению, составляющему прямой угол с плоскостью, проходящей через полюс и данный элемент. Хотя выражения (1) и (2) хорошо согласуются с опытами, тем не менее на них приходится смотреть не как на закон природы, а как на удобное средство описывать количественную сторону процессов. Главная причина этого в том, что мы не знаем никаких токов, кроме замкнутых, и, следовательно, допущение элемента тока в сущности неправильно. Далее, если мы прибавим к выражениям (1) и (2) какие-нибудь функции, ограниченные только условием, что интеграл их по замкнутому контуру равен нулю, то согласие с опытами будет не менее полное.

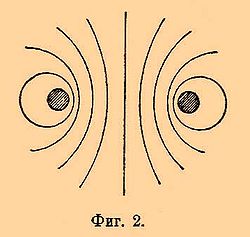
Все факты вышеуказанные приводят к выводу, что электрический ток вызывает вокруг себя магнитное поле. Для магнитной силы этого поля должны быть справедливы все законы, справедливые для магнитного поля вообще. В частности, вполне уместно введением понятия о силовых линиях магнитного поля, вызываемого электрическим током. Направление силовых линий в этом случае может быть обнаружено обычным способом при посредстве железных опилок. Если пропустить вертикальную проволоку с током через горизонтальный лист картона и насыпать на картон опилок, то при легком постукивании опилки расположатся концентрическими кругами, если только проводник достаточно длинен. Если проводник имеет форму замкнутого вертикального круга, то на горизонтальном сечении опилки расположатся приблизительно так, как показано на фиг. 2.

Так как силовые линии вокруг проволоки замыкаются и так как силовая линия определяет путь, по которому двигалась бы единица магнетизма в данном поле, то ясно, что можно вызвать вращение магнитного полюса вокруг тока. Первый прибор, в котором подобное вращение было осуществлено, был построен Фарадеем. Очевидно, что по силе магнитного поля можно судить о силе тока. К этому вопросу мы сейчас и подойдем.

Рассматривая магнитный потенциал очень длинного прямолинейного тока, мы легко можем доказать, что этот потенциал многозначен. В данной точке он может иметь бесконечно большое число различных значений, разнящихся одно от другого на 4 kmiπ, где k — коэффициент, остальные буквы известны. Этим и объясняется возможность непрерывного вращения магнитного полюса вокруг тока. 4kmiπ и есть работа, совершаемая при одном обороте полюса; она берется за счет энергии источника тока. Особый интерес представляет случай замкнутого тока. Замкнутый ток мы можем себе представить в виде петли, сделанной на проволоке, по которой течет ток. Петля имеет произвольную форму. Два конца петли свернуты в жгут (шнур) и идут к далеко поставленному элементу. Опыт показывает, что жгут, составленный из двух проводников, по которым ток течет в противоположных направлениях и которые навиты один на другой, не производит магнитного поля. Элемент предполагается далеко расположенным. Следовательно, остается только петля, которую можно рассматривать, как замкнутый ток. Рассматривая магнитный потенциал такого замкнутого тока в какой-нибудь точке P и сравнивая его с потенциалом в той же точке двойного магнитного слоя, ограниченного тем же контуром, что и наш ток, мы придем к такому выводу (как известно, двойным магнитным слоем называется бесконечно тонкий листок, ограниченный данным контуром и намагниченный перпендикулярно к своей поверхности; произведение σε — поверхностной плотности намагничивания на толщину слоя — называется магнитной силой листка; обозначим ее через ф).

Если сила двойного магнитного слоя численно равна ki и если двойной магнитный слой расположен на поверхности S (фиг. 3) таким образом, что его положительная сторона (сев. магнетизм) приходится с той стороны, откуда ток представляется идущим обратно часовой стрелке, то потенциал в каких-либо точках P и Р′ от двойного магнитного слоя и от замкнутого тока отличается только на величину постоянную, т. е. не зависящую от координат.

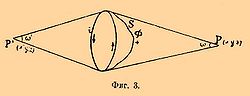
Обозначим потенциалы от замкнутого тока через Ω и Ω′, а от двойного магнитного слоя через V и V′; телесный угол, под которым из точек P и P′ виден контур, обозначим через ω и ω′.

Тогда мы будем иметь

Ω = kiω + С, Ω′ = kiω′ + C, (3)

V = фω, W′ = фω′

Итак, силы, с которыми действуют на данное количество магнетизма замкнутый ток и двойной магнитный слой, ограниченный тем же контуром, что и ток, и удовлетворяющий указанным выше двум условиям, равны и по величине и по направлению. Следовательно, любой замкнутый ток можно заменить эквивалентным ему двойным магнитным слоем. Такой способ рассмотрения замкнутых токов приводит к установлению электромагнитной единицы силы тока.

Условие эквивалентности есть ф = ki приняв k = 1, получим i = 1, если ф = 1. Это и есть электромагнитная единица. Словами эта теорема может быть выражена так.

Электромагнитная единица силы тока есть сила такого тока, которые, проходя по замкнутому контуру, оказывает на данное внешнее количество магнетизма то же действие, что и двойной магнитный слой, ограниченный тем же контуром и обладающий силой ф = 1. Отсюда сейчас получаются измерения электромагнитной единицы силы тока.

[i] = [ф] = [m] ε / S = [L^3/2M ^½T^—¹] / [L] = [L^½M ^½T^—¹] (4)

Рассматривая работу, совершаемую при передвижении единицы количества северного магнетизма в магнитном поле замкнутого тока по замкнутой кривой из данной точки снова в первоначальное положение, можно убедиться в том, что эта работа равна 0, когда кривая движения единицы магнетизма не охватывает собой линии тока (фиг. 4, кривые РР₁P₂Р, РР₁′Р₂′Р) и равна ± 4πi, когда кривая движения охватывает собой линию тока (кривая QQ′Q₂Q₁Q).

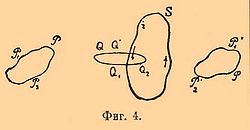
Это происходит от того, что, переходя через двойной магнитный слой, потенциал меняется не непрерывно, а скачком на ± 4πi. Следовательно, если единица количества магнетизма n раз обернется вокруг тока, то работа будет ± 4πni. Мы видим, что и потенциал замкнутого тока есть функция многозначная с периодом ± 4πi. Общее выражением для потенциала замкнутого тока, т. е. для величины работы, необходимой для переведения единицы северного магнетизма из бесконечности в данную точку, равно

Ω = ± iω + n4πi. (5)

Прежде, чем пойти дальше в рассмотрении электромагнитных явлений, нам надо установить понятие о магнитном потоке.

Пусть H есть нормальная к элементу поверхности dS слагающая магнитной силы поля. Тогда через элемент поверхности dS проходит, как говорят, магнитный силовой поток HdS.

Выражение это требует введения еще одного множителя, если мы примем во внимание магнитную проницаемость среды и если нам надо обобщить вывод на случай нескольких сред. В таком случае его пишут так: μHdS, и называют потоком магнитной индукции, или просто магнитным потоком через элемент поверхности. Если мы от элемента поверхности перейдем к определенной площади, то надо взять двойной интеграл от выражения μHdS. Условимся говорить, что из данной поверхности исходит одна силовая трубка, если

∫∫μHdS = 1.

Тогда вообще μHdS = dN

∫∫μHdS = N (6)

прямо дают число силовых трубок N, проходящих через данную поверхность. Выражение μHdS не теряет свойства непрерывности при переходе из одной среды в другую.

Далее, в данном магнитном потоке для любого сечения S справедливо соотношение ∫∫μH_ndS = const, где H_n— нормальная производящая магнитной силы. Это свойство уподобляет магнитный поток потоку несжимаемой жидкости. О силовых трубках магнитного потока прежде всего предполагают, что они не начинаются у одного полюса и кончаются у другого; а что они внутри магнита идут от второго полюса к первому и, следовательно, замкнуты сами на себя (фиг. 5). Следовательно, мы имеем замкнутую магнитную цепь.

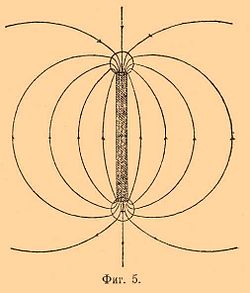
Рассмотрим одну силовую трубку этой цепи. Пусть её сечение dq. Возьмем элемент силовой линии dl в этой трубке. Работа необходимая, чтобы обвести вокруг по этой силовой линии единицу количества магнетизма пусть будет равна А. Она называется магнитодвижущей силой.

Очевидно,

А = ∫Hdl. (7)

С другой стороны, магнитный поток равняется

N = μHdq или H = N/μdq, (8)

отсюда

A = N∫(dl/μdq),

или

N = А/(∫dl/μdq) = [∫Hdl] /[ ∫(1/μ )(dl/ dq)]. (9)

Формула полученная весьма похожа на формулу Ома. Магнитный поток играет роль силы тока ∫Hdl — магнитодвижущая сила, аналогичная электродвижущей силе в формуле Ома ∫(1/μ)(dl/ dq), играет роль магнитного сопротивления. Оно, подобно электрическому, прямо пропорционально длине и обратно пропорционально поперечному сечению. 1/μ — удельное магнитное сопротивление.

Хевисайд предложил называть величину ∫(1/μ)(dl/ dq) магнитной неподатливостью. Обозначая ее одной буквой W, мы получаем известное соотношение A = NW,т. е. магнитодвижущая сила равна произведению магнитного потока на магнитное сопротивление.

Перейдем теперь снова к Э. Определим магнитную силу внутри соленоида. Вообразим себе тонкостенную трубку сечения q и длины l; q предполагается малым сравнительно с l. В стенках течет ток; направление токовых линий перпендикулярно к направлению оси трубки. Осуществить этот случай можно, свив проволоку в спираль и пропуская через нее ток (соленоид, фиг. 6).

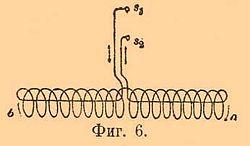
Если у соленоида на длину l приходится n витков и по нему течет ток i, то это равносильно тому, как если бы обороты соленоида не были изолированы один от другого и если бы в образованной при этом сплошной металлической трубке протекал ток равный ni. Внутри соленоида магнитные силовые линии будут параллельны оси соленоида. Применим к магнитному потоку соленоида только что полученное выражение для магнитной цепи. Мы видели, что если провести единицу магнетизма по замкнутой кривой вокруг проволоки с током i, то производится работа 4πi. Следовательно, магнитодвижущая сила соленоида из n оборотов и с силой тока i будет равна 4πni.

Что касается сопротивления магнитной цепи, то трубки магнитной индукции, выйдя из соленоида, где они параллельны оси соленоида, замкнутся через внешнее пространство. При этом сечение сильно возрастет и, следовательно, сопротивление будет мало по сравнению с сопротивлением внутри соленоида. Мы можем пренебречь первым сравнительно со вторым. Тогда выражение для магнитного потока напишется так: N = A/W, A = 4πni,

W = l/q, N = 4πniq/l.

Магнитная сила внутри соленоида

H = N/q = 4πni/l. (10)

Если оба конца соленоида свести и устроить замкнутый соленоид, то силовые линии вовсе не выйдут наружу, и вышенаписанные формулы становятся строго верными. Внешнего действия такой соленоид не обнаружит, так как для каждой внешней замкнутой кривой магнитодвижущая сила = 0.

Если оба конца свободны, то соленоид должен действовать как магниты. Количество магнетизма полюса может быть измерено таким образом m = N/4π = niq/l.

Эти формулы есть следствие формулы (2). Число силовых линий значительно возрастет, если ввести в соленоид железный сердечник, так как тогда уменьшится сопротивление магнитной цепи.

Соответственно этому получатся и более мощные магниты. На этом основано устройство электромагнитов. Внутри катушки из изолированной проволоки (соленоида) помещается сердечник из мягкого железа.

Число линий сил внутри соленоида будет

4πni /(1/μ) (l/q). (11)

Заметим, что только что написанная формула в несколько более общем виде

N = (Σ4πni)/ [Σ1/((μ) ( l /q)] играет большую роль в электротехнике. Она известна под именем формулы Каппа и братьев Гопкинсонов. Итак, соленоид с железным сердечником есть электромагнит. Э. придается самая разнообразная форма. Фиг. 7 изображает прямой электромагнит, фиг. 8 обыкновенный большой подковообразный магнит; на таблице Электромагнит, фиг. 5 представлен горизонтальный электромагнит Румкорфа, особенно удобный для исследования магнитооптических явлений; фиг. 9 — электромагнит Джоуля, очень большой подъемной силы, так как в нем сердечник очень широкий и очень короткий, т. е. очень малого сопротивления.

Электромагниты значительно превосходят все другие магниты по силе, и только благодаря им и стало возможно исследование многих свойств и явлений в магнитном поле, напр., магнитных свойств всех тел (пара- и диамагнетизм), магнитного вращения плоскости поляризации, магнитострикция, явления Керра, Зеемана, Холля, гистерезис etc.

Магнитные свойства соленоида привели Ампера к выводу, что все электромагнитные явления в сущности суть электродинамические и что всякий магнит есть соленоид. Именно Ампер предположил, что можно каждый кусок железа или стали представлять себе состоящим из маленьких молекулярных магнитов, которые суть не что иное как частицы того же железа или стали, но вокруг которых течет ток в определенном направлении. Явление намагничивания и состоит в ориентировке всех этих магнитиков параллельно друг другу. Тогда внутри магнита токи никакого действия не окажут, так как рядом с каждым током, текущим справа налево, непременно будет ток обратного направления. Токи же на поверхности сложатся в один соленоидальный. Следовательно, магнит есть соленоид. Многие, хотя не все, явления магнетизма хорошо объясняются теорией Ампера. Однако мы видели, что удобен и вполне возможен и обратный путь, когда замкнутые токи рассматриваются как двойные магнитные слои, следовательно, явления электродинамические сводятся к электромагнитным. Таким образом, можно выяснить все явления электромагнетизма, не прибегая к действию на расстояние. Выводится и правило Ампера и его же закон элементарного действия магнитного поля на элемент тока. В заключение укажу на выражение потенциальной энергии двойного магнитного слоя или замкнутого тока.

P = — фN для двойного магнитного слоя.

P = — iN для замкнутого тока. Именно из этого выражения исходя и выводится увеличение параметра тока в магнитном поле и элементарный закон действия магнитного ноля на ток.

К. Баумгарт.

Электромагнетизм* — это… Что такое Электромагнетизм*?

— Начало учению об электромагнитных явлениях положено открытием Эрстеда. В 1820 г. Эрстед показал, что проволока, по которой течет электрический ток, вызывает отклонение магнитной стрелки. Он подробно исследовал это отклонение с качественной стороны, но не дал общего правила, по которому можно было бы определять направление отклонения в каждом отдельном случае. Вслед за Эрстедом открытия пошли одно за другим. Ампер (1820) опубликовал свои работы о действии тока на ток или тока на магнит. Амперу принадлежит общее правило для действия тока на магнитную стрелку: если вообразить себя расположенным в проводнике лицом к магнитной стрелке и притом так, чтобы ток имел направление от ног к голове, то северный полюс отклоняется влево. Далее мы увидим, что Ампер свел явления электромагнитные к явлениям электродинамическим (1823). К 1820 г. относятся также работы Араго, который заметил, что проволока, по которой течет электрический ток, притягивает к себе железные опилки. Он же намагнитил впервые железные и стальные проволоки, помещая их внутрь катушки медных проволок, по которым проходил ток. Ему же удалось намагнитить иглу, поместив ее в катушку и разрядив лейденскую банку через катушку. Независимо от Араго намагничивание стали и железа током было открыто Дэви.

= k(imSin θ ds)/r2, (1),

На основании закона действие равно противодействию, Ампер заключил, что магнитный полюс должен действовать на элемент тока с такой же силой

dФ

= k(imSin θ ds)/r2, (2)

прямо противоположной по направлению силе dF, точно также действующей по направлению, составляющему прямой угол с плоскостью, проходящей через полюс и данный элемент. Хотя выражения (1) и (2) хорошо согласуются с опытами, тем не менее на них приходится смотреть не как на закон природы, а как на удобное средство описывать количественную сторону процессов. Главная причина этого в том, что мы не знаем никаких токов, кроме замкнутых, и, следовательно, допущение элемента тока в сущности неправильно. Далее, если мы прибавим к выражениям (1) и (2) какие-нибудь функции, ограниченные только условием, что интеграл их по замкнутому контуру равен нулю, то согласие с опытами будет не менее полное.

Рассматривая магнитный потенциал очень длинного прямолинейного тока, мы легко можем доказать, что этот потенциал многозначен. В данной точке он может иметь бесконечно большое число различных значений, разнящихся одно от другого на 4 kmi π , где k — коэффициент, остальные буквы известны. Этим и объясняется возможность непрерывного вращения магнитного полюса вокруг тока. 4 kmi π и есть работа, совершаемая при одном обороте полюса; она берется за счет энергии источника тока. Особый интерес представляет случай замкнутого тока. Замкнутый ток мы можем себе представить в виде петли, сделанной на проволоке, по которой течет ток. Петля имеет произвольную форму. Два конца петли свернуты в жгут (шнур) и идут к далеко поставленному элементу. Опыт показывает, что жгут, составленный из двух проводников, по которым ток течет в противоположных направлениях и которые навиты один на другой, не производит магнитного поля. Элемент предполагается далеко расположенным. Следовательно, остается только петля, которую можно рассматривать, как замкнутый ток. Рассматривая магнитный потенциал такого замкнутого тока в какой-нибудь точке P и сравнивая его с потенциалом в той же точке двойного магнитного слоя, ограниченного тем же контуром, что и наш ток, мы придем к такому выводу (как известно, двойным магнитным слоем называется бесконечно тонкий листок, ограниченный данным контуром и намагниченный перпендикулярно к своей поверхности; произведение σε — поверхностной плотности намагничивания на толщину слоя — называется магнитной силой листка; обозначим ее через ф).

Если сила двойного магнитного слоя численно равна ki и если двойной магнитный слой расположен на поверхности S (фиг. 3) таким образом, что его положительная сторона (сев. магнетизм) приходится с той стороны, откуда ток представляется идущим обратно часовой стрелке, то потенциал в каких-либо точках P и Р’ от двойного магнитного слоя и от замкнутого тока отличается только на величину постоянную, т. е. не зависящую от координат.

Обозначим потенциалы от замкнутого тока через Ω и Ω’, а от двойного магнитного слоя через V и V’; телесный угол, под которым из точек P и P’ виден контур, обозначим через ω и ω ‘.

Тогда мы будем иметь

Ω = ki ω + С, Ω ‘ = ki ω ‘ + C, (3)

= фω, W’ = фω ‘

[i] = [ ф ] = [m] ε / S = [L3/2M ½T—1] / [L] = [L½M ½T—1] (4)

Рассматривая работу, совершаемую при передвижении единицы количества северного магнетизма в магнитном поле замкнутого тока по замкнутой кривой из данной точки снова в первоначальное положение, можно убедиться в том, что эта работа равна 0, когда кривая движения единицы магнетизма не охватывает собой линии тока (фиг. 4, кривые РР 1P2 Р , РР 1′ Р 2 ‘Р ) и равна ╠ 4 π i, когда кривая движения охватывает собой линию тока (кривая QQ’Q2Q1Q).

Это происходит от того, что, переходя через двойной магнитный слой, потенциал меняется не непрерывно, а скачком на ╠ 4 π i. Следовательно, если единица количества магнетизма n раз обернется вокруг тока, то работа будет ╠ 4π ni. Мы видим, что и потенциал замкнутого тока есть функция многозначная с периодом ╠ 4 π i . Общее выражением для потенциала замкнутого тока, т. е. для величины работы, необходимой для переведения единицы северного магнетизма из бесконечности в данную точку, равно

Ω = ╠ i ω + п4π i. (5)

Пусть H есть нормальная к элементу поверхности dS слагающая магнитной силы поля. Тогда через элемент поверхности dS проходит, как говорят, магнитный силовой поток HdS.

Выражение это требует введения еще одного множителя, если мы примем во внимание магнитную проницаемость среды и если нам надо обобщить вывод на случай нескольких сред. В таком случае его пишут так: μ HdS, и называют потоком магнитной индукции, или просто магнитным потоком через элемент поверхности. Если мы от элемента поверхности перейдем к определенной площади, то надо взять двойной интеграл от выражения μ HdS. Условимся говорить, что из данной поверхности исходит одна силовая трубка, если

∫∫ μ HdS = 1.

Тогда вообще μ HdS = dN

∫∫ μ HdS = N (6)

прямо дают число силовых трубок N, проходящих через данную поверхность. Выражение μ HdS не теряет свойства непрерывности при переходе из одной среды в другую.

Далее, в данном магнитном потоке для любого сечения S справедливо соотношение ∫∫ μ HndS = const, где Hn — нормальная производящая магнитной силы. Это свойство уподобляет магнитный поток потоку несжимаемой жидкости. О силовых трубках магнитного потока прежде всего предполагают, что они не начинаются у одного полюса и кончаются у другого; а что они внутри магнита идут от второго полюса к первому и, следовательно, замкнуты сами на себя (фиг. 5). Следовательно, мы имеем замкнутую магнитную цепь.

Рассмотрим одну силовую трубку этой цепи. Пусть её сечение dq. Возьмем элемент силовой линии dl в этой трубке. Работа необходимая, чтобы обвести вокруг по этой силовой линии единицу количества магнетизма пусть будет равна А. Она называется магнитодвижущей силой.

Очевидно,

= ∫Hdl. (7)

С другой стороны, магнитный поток равняется

= μ Hdq или H = N/ μ dq, (8)

отсюда

= N∫(dl/ μ dq),

или

= А/(∫dl/μ dq) = [∫Hdl] /[ ∫(1/ μ )(dl/ dq)]. (9)

Формула полученная весьма похожа на формулу Ома. Магнитный поток играет роль силы тока ∫ Hdl — магнитодвижущая сила, аналогичная электродвижущей силе в формуле Ома ∫(1/μ)(dl/ dq), играет роль магнитного сопротивления. Оно, подобно электрическому, прямо пропорционально длине и обратно пропорционально поперечному сечению. 1/μ — удельное магнитное сопротивление.

Хевисайд предложил называть величину ∫(1/μ)(dl/ dq) магнитной неподатливостью. Обозначая ее одной буквой W, мы получаем известное соотношение A = NW,т. е. магнитодвижущая сила равна произведению магнитного потока на магнитное сопротивление.

Перейдем теперь снова к Э. Определим магнитную силу внутри соленоида. Вообразим себе тонкостенную трубку сечения q и длины l; q предполагается малым сравнительно с l. В стенках течет ток; направление токовых линий перпендикулярно к направлению оси трубки. Осуществить этот случай можно, свив проволоку в спираль и пропуская через нее ток (соленоид, фиг. 6).

Если у соленоида на длину l приходится n витков и по нему течет ток i, то это равносильно тому, как если бы обороты соленоида не были изолированы один от другого и если бы в образованной при этом сплошной металлической трубке протекал ток равный ni. Внутри соленоида магнитные силовые линии будут параллельны оси соленоида. Применим к магнитному потоку соленоида только что полученное выражение для магнитной цепи. Мы видели, что если провести единицу магнетизма по замкнутой кривой вокруг проволоки с током i, то производится работа 4π i. Следовательно, магнитодвижущая сила соленоида из n оборотов и с силой тока i будет равна 4π ni.

= l/q, N = 4 π niq/l.

Магнитная сила внутри соленоида

= N/q = 4 π ni/l. (10)

Если оба конца свободны, то соленоид должен действовать как магниты. Количество магнетизма полюса может быть измерено таким образом m = N/4 π = niq/l.

Число линий сил внутри соленоида будет

4 π ni /(1/ μ) (l/q). (11)

Заметим, что только что написанная формула в несколько более общем виде

= (Σ 4 π ni)/ [ Σ (1/ μ) (l /q)] играет большую роль в электротехнике. Она известна под именем формулы Каппа и братьев Гопкинсонов. Итак, соленоид с железным сердечником есть электромагнит. Э. придается самая разнообразная форма. Фиг. 7 изображает прямой электромагнит, фиг. 8 обыкновенный большой подковообразный магнит; на таблице Электромагнит, фиг. 5 представлен горизонтальный электромагнит Румкорфа, особенно удобный для исследования магнитооптических явлений; фиг. 9 — электромагнит Джоуля, очень большой подъемной силы, так как в нем сердечник очень широкий и очень короткий, т. е. очень малого сопротивления.

= — фN для двойного магнитного слоя.

= — iN для замкнутого тока. Именно из этого выражения исходя и выводится увеличение параметра тока в магнитном поле и элементарный закон действия магнитного ноля на ток.

К. Баумгарт.

Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.

Электромагнетизм — это… Что такое Электромагнетизм?

Электродина́мика — раздел физики, изучающий электромагнитное поле в наиболее общем случае (то есть, рассматриваются переменные поля, зависящие от времени) и его взаимодействие с телами, имеющими электрический заряд (электромагнитное взаимодействие). Предмет электродинамики включает связь электрических и магнитных явлений, электромагнитное излучение (в разных условиях, как свободное, так и в разнообразных случаях взаимодействии с веществом), электрический ток (вообще говоря, переменный) и его взаимодействие с электромагнитным полем (электрический ток может быть рассмотрен при этом как совокупность движущихся заряженных частиц). Любое электрическое и магнитное взаимодействие между заряженными телами рассматривается в современной физике как осуществляющееся через посредство электромагнитного поля, и, следовательно, также является предметом электродинамики.

Чаще всего под термином электродинамика по умолчанию понимается классическая (не затрагивающая квантовых эффектов) электродинамика; для обозначения современной квантовой теории электромагнитного поля и его взаимодействия с заряженными частицами обычно используется устойчивый термин квантовая электродинамика.

Свойства статического (не меняющегося со временем или меняющегося достаточно медленно, чтобы «электродинамическими эффектами» в описанном выше смысле можно было пренебречь) электрического поля и его взаимодействия с электрически заряженными телами (электрическими зарядами) описывает отдельный раздел физики — электростатика, хотя являющийся в принципе частным разделом электродинамики, но имеющий самостоятельное значение из-за сильного упрощения всех расчётов в этом случае.

Еще одним сходным частным случаем электродинамики является магнитостатика, исследующая постоянные токи и постоянные магнитные поля (поля не меняются во времени или меняются настолько медленно, что быстротой этих изменений в расчете можно пренебречь).

Электродинамика лежит в основе физической оптики, физики распространения радиоволн, а также пронизывает практически всю физику, так как почти во всех разделах физики приходится иметь дело с электрическими полями и зарядами, а часто и с их нетривиальными быстрыми изменениями и движениями. Кроме того, электродинамика является образцовой физической теорией (и в классическом и в квантовом своем варианте), сочетающей очень большую точность расчетов и предсказаний с влиянием теоретических идей, родившихся в ее области, на другие области теоретической физики.

История

В 1832 году английский физик Майкл Фарадей теоретически предсказал существование электромагнитного излучения.

В 1864 году Дж. К. Максвелл впервые опубликовал полную основных уравнений «классической электродинамики», описывающие эволюцию электромагнитного поля и его взаимодействие с зарядами и токами.

В ? году Лоренц завершил построение классической электродинамики, описав взаимодействие электромагнитного поля с (движущимися) точечными заряженными частицами.

В середине XX века была создана квантовая электродинамика — одна из наиболее точных физических теорий.

См. также

Ссылки

Wikimedia Foundation. 2010.

Электромагнитные теории сознания — Википедия

Электромагнитная теория сознания — теория, утверждающая что электромагнитное поле, производимое мозгом, есть фактический носитель сознательного опыта.

Первоначально была предложена Джонджо Макфадденом, Сьюзен Покетт и E. Рой Джоном. Отправной точкой теории является тот факт, что всякий раз, когда нейрон возбуждается, чтобы произвести потенциал действия, он также производит возмущение в окружающем электромагнитном поле (ЭМП).

Информация, закодированная в паттернах возбужденных нейронов, таким образом, отражается в ЭМП мозга.

Размещение сознания в ЭМП мозга, а не в нейронах, имеет преимущество четкого объяснения того, как информация, размещенная в миллионах нейронов рассеянных всюду в мозгу, может быть объединена в единый сознательный опыт (иногда называемый проблемой объединения): информация объединена в ЭМП.

Таким образом, ЭМП сознания, можно полагать, является «объединителем информации». Эта теория иначе объясняет несколько озадачивающих фактов, например, как выяснилось, внимание и понимание имеют тенденцию быть коррелированными с синхронным возбуждением множества нейронов, а не с возбуждением индивидуальных нейронов.

Когда нейроны возбуждаются вместе, их ЭМП производят более сильные возмущения общего ЭМ поля мозга; таким образом, синхронное нейронное возбуждение будет иметь тенденцию большего воздействия на ЭМП мозга (и таким образом на сознание), чем возбуждение индивидуальных нейронов.

Различные ЭМП-теории расходятся относительно влияния предложенного ЭМП сознания на функции мозга.

В CEMI полевой теории Макфаддена, глобальное ЭМП мозга влияет на перемещение электрических зарядов через нейронные мембраны и, таким образом, влияет на вероятность того, что отдельные нейроны будут возбуждаться, обеспечивая петлю обратной связи, которая управляет свободной волей.

Однако в теориях Сьюзен Покетт и E. Рой Джона нет никакой причинной связи между ЭМП сознания и нашими сознательно желаемыми действиями.

Если теория верна, то это имеет первостепенное значение для усилий по воплощению сознания в машинах с искусственным интеллектом, поскольку существующие микропроцессорные технологии созданы таким образом, чтобы передавать информацию линейно по электрическим каналам, а более общие электромагнитные эффекты рассматриваются как помехи и подавляются.

Первые эксперименты по физическому воплощению электромагнитной теории сознания проведены российской исследовательской группой. Исследователи сообщили о создании необходимых компонентов аппаратных средств ЭВМ для реализации «электромагнитного сознания», основанного на CEMI теории Джонджо МакФаддена. В частности, сотрудниками кафедры Экспериментальной физики Уральского государственного технического университета — УПИ, К. Н. Шевченко, Н. В. Шевченко, Б. В. Шульгиным создана модель нейронной сети на нейронах (ЭМ-нейронах) с дополнительными каналами обмена информации посредством электромагнитного поля (ЭМП). Разработка защищена патентом (Патент RU 2309457 C1, МПК G06N 3/06, G06G 7/60. Модель нейронной сети. Заявлено 06.05.2006; Опубликовано 27.10.2007; Бюллетень № 30).

Дополнительные каналы взаимодействия посредством ЭМП технически реализованы особой конструкцией аксона искусственного нейрона в виде цепочки последовательно включенных радиоимпульсных автогенераторов со схемами самогашения и схем выделения огибающей радиоимпульса. Идеология работы сети из ЭМ-нейронов во многом совпадает с CEMI теорией Джонджо Макфаддена, отличие заключается в механизме конкретной реализации процесса обмена информации между нейронами посредством ЭМП.

ЭМ-нейрон имеет большее функциональное сходство с биологическим прототипом по сравнению с известными моделями и выполняет функции обработки информации, свойственные биологическому нейрону. За исключением факта излучения и приема электромагнитных колебаний (новизна изобретения), работа ЭМ-нейрона не противоречит известным моделям биоподобных искусственных нейронов и соответствует наблюдаемым процессам в нейрофизиологии.

Исследования малоразмерной сети из 3-х ЭМ-нейронов показали, что ЭМ-нейроны способны конкурировать друг с другом за источники питания. В результате конкуренции происходит самоорганизация нейронной сети — хаотические режимы сменяются синхронными, демонстрируя паттерны со сложными временными кодами.

Вопрос о самозарождении сознания в сети с такой архитектурой остается открытым, поскольку исследования продолжаются.

Квантовая электродинамика — Википедия

Ква́нтовая электродина́мика (КЭД) — квантовополевая теория электромагнитных взаимодействий; наиболее разработанная часть квантовой теории поля. Классическая электродинамика учитывает только непрерывные свойства электромагнитного поля, в основе же квантовой электродинамики лежит представление о том, что электромагнитное поле обладает также и прерывными (дискретными) свойствами, носителями которых являются кванты поля — фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание частицами фотонов.

Квантовая электродинамика количественно объясняет эффекты взаимодействия излучения с веществом (испускание, поглощение и рассеяние), а также последовательно описывает электромагнитные взаимодействия между заряженными частицами. К числу важнейших проблем, которые не нашли объяснения в классической электродинамике, но успешно разрешаются квантовой электродинамикой, относятся тепловое излучение тел, рассеяние рентгеновских лучей на свободных (точнее, слабо связанных) электронах (эффект Комптона), излучение и поглощение фотонов атомами и более сложными системами, испускание фотонов при рассеянии быстрых электронов во внешних полях (тормозное излучение) и другие процессы взаимодействия электронов, позитронов и фотонов. Меньший успех теории при рассмотрении процессов с участием других частиц обусловлен тем, что в этих процессах, кроме электромагнитных взаимодействий, играют важную роль и другие фундаментальные взаимодействия (сильное и слабое).

Квантовая электродинамика как последовательная квантовая теория поля была создана в 1940-х годах в работах Фейнмана, Швингера, Томонаги, Дайсона. Это была первая перенормируемая теория поля.

Каждому событию квантовой электродинамики (например, перемещению фотона или электрона из одной точки пространства-времени в другую или испусканию или поглощению фотона электроном) соответствует комплексное число — амплитуда вероятности события. Вероятность события равна квадрату модуля амплитуды вероятности события.
Если событие может произойти взаимоисключающими способами, амплитуды вероятностей событий складываются. Если событие происходит поэтапно, или в результате ряда независимых событий, амплитуды вероятностей событий перемножаются.

Математически, КЭД — это абелева калибровочная теория поля с группой симметрии U(1). Калибровочное поле, которое переносит взаимодействие между заряженными полями спина 1/2, является электромагнитным полем. Лагранжиан КЭД для поля спина 1/2 (электронно-позитронного поля), взаимодействующего с электромагнитным полем, равен сумме лагранжианов электрон-позитронного поля (первый член суммы), фотонного поля (второй член суммы) и слагаемого, описывающего взаимодействие электромагнитного поля с электронно-позитронным полем (излучение фотона электроном и рождение фотоном электронно-позитронных пар) (третий член суммы):

L=ψ¯(iγμDμ−m)ψ−12∂kAi(x)∂kAi(x)−eAμψ¯γμψ,{\displaystyle {\mathcal {L}}={\bar {\psi }}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{2}}\partial _{k}A^{i}(x)\partial ^{k}A_{i}(x)-eA_{\mu }{\bar {\psi }}\gamma ^{\mu }\psi ,}

где

γμ{\displaystyle \gamma ^{\mu }} — матрицы Дирака,

ψ{\displaystyle \psi } — оператор биспинорного поля спина 1/2 (то есть электрон-позитронного поля),

ψ¯≡ψ†γ0{\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma _{0}}, дираковски сопряжённая ψ{\displaystyle \psi },

Dμ≡∂μ+ieAμ+ieBμ{\displaystyle D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }} — ковариантная производная,

m{\displaystyle m} — масса фермиона,

e{\displaystyle e} — заряд фермиона,

Aμ{\displaystyle A_{\mu }} — оператор фотонного поля (ковариантный 4-потенциал в классической теории поля),

Bμ{\displaystyle B_{\mu }} — внешнее поле,

Операторы электронного ψ{\displaystyle \psi } и фотонного A{\displaystyle A} полей удовлетворяют системе уравнений (уравнения Дирака-Максвелла):^[2]

(γk(i∂k−eAk(x)−eBk)−m)ψ(x)=0{\displaystyle (\gamma ^{k}(i\partial _{k}-eA_{k}(x)-eB_{k})-m)\psi (x)=0}

◻2Ak(x)=eψ¯(x)γkψ(x){\displaystyle \square ^{2}A_{k}(x)=e{\bar {\psi }}(x)\gamma _{k}\psi (x)}

Эти уравнения дополняются калибровочным условием Лоренца:

A,kk|0⟩=0{\displaystyle A_{,k}^{k}\vert 0\rangle =0}

Вычислительные методы квантовой электродинамики[править | править код]

Метод возмущений[править | править код]

Основным вычислительным методом квантовой электродинамики является метод возмущений. В нулевом приближении электромагнитным взаимодействием пренебрегают и частицы считаются невзаимодействующими. В первом, втором и т. д. приближениях учитываются однократные, двукратные и т. д. акты взаимодействия между частицами. Вероятность каждого акта взаимодействия пропорциональна заряду частицы e{\displaystyle e}. Чем больше актов взаимодействия рассматривается, тем в более высокой степени входит заряд в выражение для амплитуды вероятности процесса.^[3] Вычисления в квантовой электродинамике заключаются в нахождении из лагранжиана, описывающего взаимодействие элементарных частиц, эффективных сечений реакций и скоростей распада частиц. Для вычислений по методу возмущений используется метод диаграмм Фейнмана, при помощи которых вычисляются матричные элементы, входящие в выражения для вероятностей переходов.^[4]

Современные направления исследований в КЭД[править | править код]

Нелинейная КЭД
КЭД во внешних полях
Некоммутативная КЭД

Опыты по проверке квантовой электродинамики[править | править код]

Дифференциальное и полное сечения рассеяния комптон-эффекта, процесса рассеяния электрона на электроне и позитроне, процессов взаимодействия γ{\displaystyle \gamma } — квантов с атомами и ядрами, аномальный магнитный момент и лэмбовский сдвиг электрона с высокой точностью совпадают с расчетами квантовой электродинамики.^[5]^[6]^[7]

Нерешенные проблемы квантовой электродинамики[править | править код]

Энергия вакуума[править | править код]

Вакуумом в квантовой электродинамике называется состояние, в котором у всех осцилляторов n=0{\displaystyle n=0}, следовательно энергия каждого осциллятора равна ℏω2{\displaystyle {\frac {\hbar \omega }{2}}}, где ω{\displaystyle \omega } — собственная частота осциллятора. Сумма всех мод осцилляторов с частотами от нуля до бесконечности равна бесконечности. На практике этой расходимостью пренебрегают и энергию вакуумного состояния принимают равной нулю. Остается открытым вопрос: не образует ли вакуум гравитационного поля, подобно массе, распределенной с постоянной плотностью? По «правилу обрезания» моды с очень большими частотами исключаются из рассмотрения. Плотность энергии вакуумного состояния EV=2ℏc2(2π)3∫0kmaxk⋅4πk2dk=ℏckmax48π2{\displaystyle {\frac {E}{V}}=2{\frac {\hbar c}{2{(2\pi )}^{3}}}\int \limits _{0}^{k_{max}}k\cdot 4\pi k^{2}dk={\frac {\hbar ck_{max}^{4}}{8\pi ^{2}}}}. Подставляя значение kmax=Mcℏ{\displaystyle k_{max}={\frac {Mc}{\hbar }}}, где M{\displaystyle M} — масса протона, получаем значение плотности массы, эквивалентное этой энергии: mvak=EVc2=2⋅1015{\displaystyle m_{vak}={\frac {E}{Vc^{2}}}=2\cdot 10^{15}} грамм на кубический сантиметр пространства. Гравитационные эффекты, соответствующие этой энергии вакуума, не обнаружены.^[8] Не удается вычислить энергию вакуума как собственное значение для гамильтониана вакуумного состояния, а при применении методов теории возмущений к расчету вероятности перехода из вакуумного состояния в состояние с фотоном и электронно-позитронной парой получаются расходящиеся интегралы.^[9]

Расходимость рядов[править | править код]

При расчете вероятностей процессов в квантовой электродинамике методом возмущений к выражению для амплитуды процесса последовательно добавляются слагаемые вида n!αn{\displaystyle n!\alpha ^{n}}, где α{\displaystyle \alpha } — постоянная тонкой структуры, n{\displaystyle n} — число вершин на диаграммах Фейнмана в данном приближении. Ряды вида ∑n=1∞n!αn{\displaystyle \sum _{n=1}^{\infty }n!\alpha ^{n}}, являются расходящимися. В опытах данная расходимость не проявляется, поскольку предельная точность вычислений при помощи таких рядов составляет 10−57%{\displaystyle 10^{-57}\%}^[3]

Расходимость интегралов[править | править код]

Требование локальности взаимодействия между частицами в квантовой электродинамике приводит к тому, что интегралы по пространству, описывающие процессы взаимодействия частиц, оказываются расходящимися за счет больших импульсов виртуальных частиц. Это свидетельствует о неприменимости принятых в квантовой электродинамике методов описания взаимодействий на малых расстояниях.^[10]

↑ Фейнман Р. КЭД — странная теория света и вещества. М.: Наука.— 1988.— 144 с. Серия Библиотечка «Квант», выпуск 66.
↑ Тирринг, 1964, с. 136.
↑ ¹ ² Физика микромира, под ред. Д. В. Ширкова, М.:Наука.— 1980.— 528 с., тир. 50000 экз.
↑ Кейн, 1990, с. 15.
↑ Широков Ю. М., Юдин Н. П. Ядерная физика.— М.: Наука.— 1972.
↑ Смондырев М. А. Квантовая электродинамика на малых расстояниях// Природа.— 1980.— № 9.
↑ Электромагнитные взаимодействия и структура элементарных частиц / ред. А. М. Балдин. — М: Мир.— 1969.— 327 с.
↑ Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям.— М.: Мир.— 1968.
↑ Дирак П. А. М. Принципы квантовой механики.— М.: Наука.— 1979.
↑ Мигдал А. Б. Качественные методы в квантовой теории.— М.: Наука.— 1975.