2.2. Входное сопротивление

Входное сопротивление ЭП определяется как отношение малого приращения входного напряжения к изменению входного тока. Предположим, что в схеме на рис.2.1 в качестве сопротивления нагрузки выступает сопротивление R₁. Для рассматриваемой схемы входное напряжение — это напряжение на базе транзистора, а входной ток — ток базы. Входное сопротивление ЭП может быть определено по формуле

r_{вх =} dU_вх/dI_вх= (dU_бэ+dU_вых)/dI_б=dU_бэ/dI_б+dU_вых/dI_б=r_бэ+R₁dIэ/dI_б=r_бэ+ (β+1)R₁, где- коэффициент усиления транзистора по току.

Итак входное сопротивление эмиттерного повторителя равно

r_вх=r_бэ+ (β+1)R₁.

Пример. Найдем входное сопротивление эмиттерного повторителя при следующих исходных данных: ток коллектораI

к= 1 мА,R₁= 3 кОм, β = 100.

r_вх=r_бэ+ (β+1)R₁= βu_т /I_к+(β+1)R₁=

=100 25,5мВ/ 1 мА + 101 3 кОм = 2,55 кОм + 303 кОм = 305,6 кОм.

Из расчета видно, что в общем входном сопротивлении доля первого слагаемого (r_бэ) незначительная, поэтому часто использую более приближенную формулу для определения выходного сопротивления эмиттерного повторителя

rвх= βR1

(2.2)

2.3. Выходное сопротивление

ЭП определяется, как отношение изменения выходного напряжения к изменению выходного тока r_вых= —dU_вых/dI_выхпри условии, что входное напряжение не изменяется, т.е.U_вх=const, аdU_вх= 0.

Для определения выходного сопротивления рассмотрим схему на рис.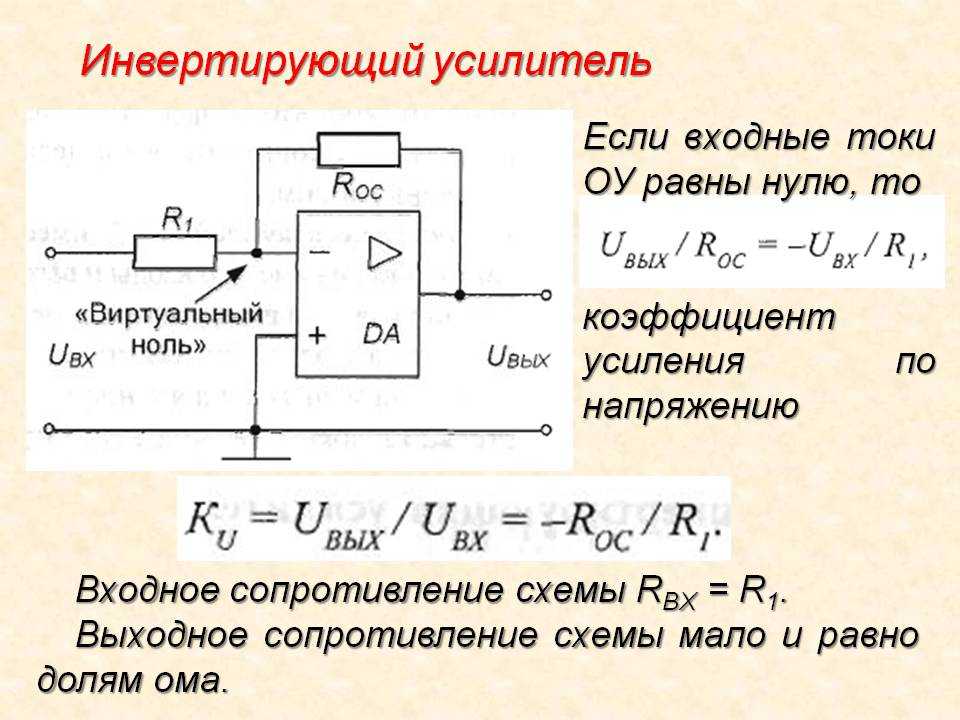 2.3. здесь R_ист– сопротивление источника входного сигнала.

rвых= —dUвых/dIвых = —dUвых/dIэ.

(2.3)

dU_вх =dU_Rист+dU_бэ+dU_вых.

Учитывая, что dU_вх= 0, и пренебрегаяdU_бэполучим

dU_вых= -dU_Rист= -dI_бR_ист= -dI_эR_ист /(β+1).

Подставим, найденное значение dU_выхв формулу (2.3) и найдем выходное сопротивление усилителя

r_вых= R_ист/(1+).

Из формулы видно, что выходное (внутреннее) сопротивление источника входного сигнала уменьшается в (+1) раз при подключении ЭП.

2.4. Смещение в эмиттерном повторителе

Схема на рис. 2.1 пропускает на выход сигнал, который больше, чем 0.6В (U_бэоткрытого транзистора). Для того, чтобы схема могла усиливать разнополярные сигналы необходимо создатьсмещение, которое обеспечивает протекание коллекторного тока в течение полного периода сигнала. Смещение обеспечивается путем подачи положительного постоянного напряжения на базу транзистора. Переменный входной сигнал складывается с постоянным напряжением смещения. Величина напряжения смещения должна быть такой величины, чтобы при отрицательной амплитуде входного сигнала напряжение на базе было больше 0,6 В, т.е. транзистор был открыт.

Смещение в усилителе можно задавать с помощью делителя напряжения R₁, R₂, как показано на рис.2.4. R₁и R₂выбраны так, чтобы на выходе формировался максимальный симметричный сигнал. Это можно обеспечить, если напряжение на эмиттере транзистора при отсутствии входного сигнала будет равно примерно половине напряжения питания U_п. При подаче на вход переменного напряжения на эмиттере сигнал будет изменяться относительно напряжения U

п / 2. Процесс выбора рабочих напряжений в схеме при отсутствии входного сигнала называетсяустановкой рабочей точки. Сопротивления R₁и R₂выбираются из условия, что ток протекающий через делитель (ток через сопротивление R₂) должен быть намного больше ( по крайней мере в 10 раз) тока базы транзистора, чтобы изменение тока базы при изменении входного сигнала оказывало малое влияние на изменение постоянной составляющей тока делителя.

Разделительная емкость С₁не пропускает постоянное напряжение смещения на вход источника сигнала, а емкость С₂пропускает в нагрузку только переменный полезный сигнал.

Разделительные емкости С₁и С₂образуют фильтры верхних частот, нижняя граничная частота которых должна быть выбрана так, чтобы полностью пропускались нижние частоты сигнала. Величины емкости могут быть определены по формуле

С 1/ 2fR_экв, где R_эквдля вычисления С1 равно параллельному соединению сопротивлений R1,R2 и r_вх. Для определения С2 предполагаем, что сопротивление нагрузки ЭП будет не меньше R3. Поэтому R_эквв этом случае выбирают равным R3.

Результаты моделирования схемы, показанной на рис.2.4 представлены на рис.2.5.

Из рисунка видно, что выходное напряжение v(5) практически полностью повторяет входное напряжение v(3). Переменное напряжение на базе v(1), по амплитуде равное входному напряжению, изменяется относительно постоянного напряжения смещения, примерно равное 7,5 В. Напряжение на эмиттере v(4) меньше напряжения на базе на U_бэ ≈ 0

Определение входного сопротивления. OrCAD PSpice. Анализ электрических цепей

Определение входного сопротивления. OrCAD PSpice. Анализ электрических цепей

ВикиЧтение

OrCAD PSpice.

Анализ электрических цепей
Кеоун Дж.

Содержание

Определение входного сопротивления

Желательно, кроме того, найти входное сопротивление со стороны источника входного напряжения. Если мы просто используем команду

.TF V(4) vs

результаты будут некорректными. Вы можете это сделать и посмотреть, что получится. Удаление конденсатора С₁ из схемы также не сработает, так как это приведет к изменению условий смещения.

Правильный подход показан на рис. 10.15, где во входную цепь включен источник с напряжением и внутренним сопротивлением, определенными по теореме Тевенина. При этом поддерживаются соответствующие напряжения и токи смещения, и можно использовать функцию преобразования .TF.

Рис. 10.15. Схема для определения входного сопротивления усилителя ОЭ

Из выходного файла на рис. 10.16 (содержащего также листинг входного файла) можно видеть, что напряжения смещения не изменились. Эта распечатка показывает входное сопротивление как 13,16 Ом. Сопротивление в цепи базы транзистора R_i=13,16–4,444=8,7 кОм. Расчетное значение 9,2 кОм отличается от этого немногим больше, чем на 5%, из чего мы заключаем, что оба метода адекватны.

Find Input Resistance of CE Amplifier Circuit with RE

VCC 4 0 12V

VTh 1 1a 1.33333V

RC 4 2 1k

RE 3 0 100

Rs 5 1a 4.4444k

Q1 2 1 3 BJT

.MODEL BJT NPH(BF=80)

.TF v(2) vs

.OP

.opt nopage

vs 5 0 ac 10mV

.ac LIN 1 5kHz 5kHz

.PRINT ac i(Rs) i(RC) v(1) v(2) v(3)

. END

NODE VOLTAGE NODE  VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 1.1464  ( 2)  8.6345  ( 3) .3408   ( 4) 12.0000

( 5) 0.0000  ( 1a) -.1870

VOLTAGE SOURCE CURRENTS

NAME CURRENT

VCC -3.366E-03

VTh -4.207E-05

vs  -4.207E-05

TOTAL POWER DISSIPATION 4.04E-02 WATTS

**** SMALL-SIGNAL CHARACTERISTICS

V(2)/vs = -6.079Е+00

INPUT RESISTANCE AT vs. = 1.316E+04

OUTPUT RESISTANCE AT V(2) = 1.000E+03

FREQ      I(Rs)     I(RC)     V(1)      V(2)      V(3)

5.000E+03 7.599E-07 6.079E-05 6.623E-03 6.0791-02 6.155E-03

Рис. 10.16. Выходной файл с результатами анализа схемы на рис. 10.15

Данный текст является ознакомительным фрагментом.

Определение

Определение Инструменты компонентного тестирования в большей степени, чем какие-либо другие инструменты, выражают наше представление о том, что понимать под «выполненной» работой. Когда бизнес-аналитики и специалисты по контролю качества создают спецификацию,

4.1.1 Определение

4.1.1 Определение Индексы существуют на диске в статической форме и ядро считывает их в память прежде, чем начать с ними работать. Дисковые индексы включают в себя следующие поля:• Идентификатор владельца файла. Права собственности разделены между индивидуальным

Определение IP по ICQ

Определение IP по ICQ Чтобы определить IP того, кто общается с вами посредством ICQ, достаточно воспользоваться программой UIN2IP (http://neptunix.narod.ru/uin.htm).Вот список некоторых функций UIN2IP:– автоматическое обновление листа;– автоматическое копирование IP-адреса в буфер при двойном

3.6.1. Определение ограничений

3.6.1. Определение ограничений Для определения (задания) ограничений используется команда edquota. Ограничение дискового пространства пользователя производится командой edquota с параметром –u (см. рис. 3.7), а определение квот для группы — с параметром –g. После выполнения этой

2.

2.1. Определение

2.2.1. Определение В общем смысле, контекстная реклама – это вид интернет-рекламы, демонстрируемой человеку в зависимости от содержимого интернет-страницы, на которой она расположена. Например, объявление о продаже автомобиля на сайте об автомобилях, реклама сотовых

Создание входного файла

Создание входного файла Откройте программу pspice.exe (рис. В.3) и выберите позиции меню File, New, Text File, как показано на рис. В.4. Рис. B.3. Пиктограммы на рабочем столе PSpice Рис. В.4. Создание текстового файла на PSpiceПоявится пустое окно с мигающим курсором, позволяющее ввести текст.

Изменение входного файла

Изменение входного файла Чтобы извлечь больше информации из анализа на PSpice, изменим входной файл (с расширением *.cir), добавив две следующие строки.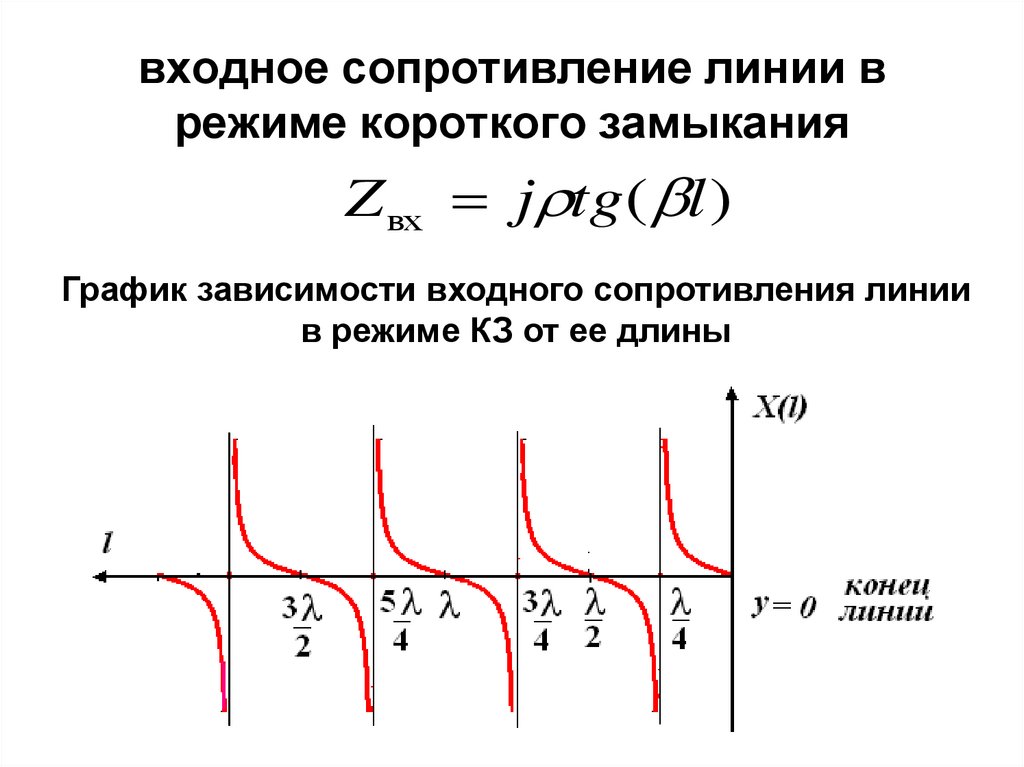 .DC VS 24V 24V 24V.PRINT DC I(R1) I(R2) I(R3)и снова запустим процесс моделирования. **** 09/08/99 10:48:54 ******* Evaluation PSpice (Nov 1998) *******First Circuit for PSpice**** CIRCUIT

Влияние изменения сопротивления катушки

Влияние изменения сопротивления катушки На рис. 2.13 одна из параллельных ветвей содержит R=10 Ом и L=100 мГн. Эта цепь может служить моделью реальной катушки с малым сопротивлением. Интересно, как влияет сопротивление катушки на поведение схемы? Изменим входной файл,

Определение полного входного сопротивления в цепях переменного тока

Определение полного входного сопротивления в цепях переменного тока Рассмотрим «черный ящик», содержащий цепь с неизвестным полным сопротивлением, показанный на рис. 2.16. С помощью команды .PRINT вы можете вывести и V(I), и I(R). Однако эта команда не позволяет вывести значение

Выбор сопротивления нагрузочного резистора для максимальной передаваемой мощности

Выбор сопротивления нагрузочного резистора для максимальной передаваемой мощности Мы рассмотрели теорему о максимальной мощности для схем постоянного и переменного тока. В обоих случаях устанавливалась нагрузка и затем проводился анализ. Если мы изменяли значение

Полные сопротивления в режиме холостого хода

Полные сопротивления в режиме холостого хода Если в качестве независимых переменных выбрать токи четырехполюсника, можно записать следующие уравнения:V1 = z11I1 + z12I2;V2 = z21V1 + z22I2;из которых следует, что Чтобы показать, как в этом случае используется PSpice, рассмотрим простую

7.5. Значение сопротивления в качестве изменяемой переменной

7.5. Значение сопротивления в качестве изменяемой переменной Теперь вы научитесь проводить анализ цепи постоянного тока DC Sweep, при котором в качестве изменяемой переменой будет использоваться значение сопротивления. В таких случаях значение сопротивления называется

10.

1.2. Упражнение на определение наименьшего сопротивления

10.1.2. Упражнение на определение наименьшего сопротивления Допустимый ток коллектора BC548B составляет ICmax=200 мА. Определите, какое наименьшее сопротивление должна иметь лампочка при таком токе коллектора, чтобы ее можно было приводить в действие с помощью схемы,

Итератор входного потока (Istream Iterator)

Итератор входного потока (Istream Iterator) istream_iterator‹T› читает (используя operator››) последовательные элементы из входного потока, для которого он был создан. После своего создания итератор каждый раз при использовании ++ читает и сохраняет значение T. Если достигнут конец потока

Определение нотации

Определение нотации С точки зрения физической модели, XML-документы являются не более чем текстом. Содержимое документов и их разметка имеет исключительно текстовый вид. Вместе с тем, во многих случаях документы должны включать данные других форматов, например,

11.5.4. Чтение данных и» стандартного входного потока

11.5.4. Чтение данных и» стандартного входного потока Команда paste имеет удобную опцию — (дефис), которая позволяет принимать данные из стандартного входного потока. Каждый дефис в командной строке соответствует одной колонке выходных данных. Например, список файлов

Входное и выходное сопротивление — Вики курса

Из Вики курса

Перейти к: навигация, поиск

20.309: Биологические приборы и измерения

Что происходит, когда мы соединяем один компонент схемы с другим? Иногда компонент схемы ведет себя по-разному, когда он сам по себе, и когда он подключен к другому компоненту. Чтобы понять, как будет вести себя схема, мы должны рассмотреть входное и выходное сопротивление различных частей. 9Выходной импеданс 0007 относится к импедансу или противодействию протеканию тока компонента, который часто имеет источник электричества для «приведения в действие» компонента нагрузки. Между тем, входной импеданс относится к сопротивлению компонента нагрузки току, протекающему от источника электрического тока. Во многих случаях вам понадобится высокое входное сопротивление по сравнению с выходным сопротивлением, и в следующих разделах вы поймете, почему.

Компонент источника имеет выходной импеданс, а компонент нагрузки — входной импеданс. Что происходит, когда мы соединяем вещь 1 с вещью 2?

Давайте рассмотрим пример подключения батареи к резистору. Когда мы видим батарею на 9 В, мы часто думаем, что она должна выдавать 9 В на своих клеммах. Это действительно так, но только тогда, когда он не получает никакого тока. Оказывается, внутри батареи есть некоторый внутренний импеданс, который не позволяет выходному напряжению оставаться на уровне 9 В, когда начинает течь ток. Таким образом, мы можем смоделировать батарею как источник чистого напряжения, соединенный последовательно с резистором, где значение сопротивления $ R_{out} $ равно выходному сопротивлению батареи. Вот пример 9ВАХ батареи V (соотношение ток-напряжение).

Модель батареи 9 В, показывающая внутреннее сопротивление в виде резистора со значением $ R_{out} $. $ I_{SC} $ относится к току короткого замыкания (если провод был помещен между выходными клеммами), а $ V_{OC} $ относится к напряжению холостого хода (напряжение, измеренное между выходными клеммами при отсутствии тока). течет)

Теперь подключим к этому источнику нагрузку. Для простоты подключим резистор сопротивлением $R_{in}$. Следовательно, входное сопротивление этой нагрузки равно $R_{in}$. Когда мы строим ВАХ нагрузки с источником, пересечение двух линий является рабочей точкой.

Выходное сопротивление нагрузки равно $ R_{out} $. Когда нагрузка подключена к источнику, рабочая точка определяется пересечением двух линий на графике ВАХ. Рабочая точка дает напряжение, приложенное к нагрузке, а также количество тока, протекающего через нее.

Здесь мы видим, что после подключения нагрузки к источнику выходное напряжение больше не равно 9 В; скорее это задается рабочей точкой. В приведенном выше примере показана батарея 9 В, имеющая выходное сопротивление 1,5 Ом, и нагрузка, имеющая входное сопротивление 3 Ом. Если вы используете соотношения делителя напряжения для расчета напряжения, приложенного к нагрузке, и тока, протекающего через нее, вы обнаружите, что оно составляет 6 В и 2 Ом соответственно, как указано в рабочей точке графически. Это показывает нам, что хотя 9Батарея V выдает 9 В, когда ток отсутствует, как только мы применяем нагрузку, выходное напряжение падает до 6 В, чтобы учесть увеличенный ток.

Что произошло бы, если бы сопротивление нагрузки было очень высоким? Подумайте, как изменение наклона ВАХ для нагрузки повлияет на рабочую точку.

Изучив предыдущий пример, вы можете увидеть, что нагрузка на источник, входной импеданс которого по величине аналогичен выходному импедансу источника, приводит к падению выходного напряжения. Как можно нагрузить источник таким образом, чтобы поддерживать выходное напряжение?

Если $ Z_{in} >> Z_{out} $ (входной импеданс нагрузки >> выходной импеданс источника), , то выходное напряжение источника может быть достаточно близко к его напряжению холостого хода, что мы можем игнорировать изменения, вызванные Загрузка. Один из способов думать об этом состоит в том, что если входное сопротивление нагрузки очень велико по сравнению с выходным сопротивлением источника, то он не будет потреблять большой ток от источника, и напряжение в точке подключения будет поддерживаться. Это хороший принцип, которому следует следовать при соединении различных компонентов вместе.

1. Каково выходное сопротивление $ Z_{out} $ следующей цепи? Мы хотим подключить еще один контур к синим узлам.

Решение: При нахождении выходного импеданса мы «заглядываем» в синие выходные узлы схемы. Помните из показанной ранее кривой ВАХ, что $ Z_{out} = {V_{oc} \over I_{sc}} $, где $ V_{oc} $ — напряжение холостого хода (когда синие узлы остаются открытыми). , $V_{oc}=V_{in}{Z_2 \over Z_1 + Z_2}$) и $I_{sc}$ — ток короткого замыкания (при замыкании синих узлов $I_{sc}={V_ {in}\over Z_1}$). Другими словами, выходное сопротивление аналогично эквивалентному сопротивлению Thevenin. Кратчайший способ найти $Z_{out}$ — заменить источник напряжения проводом и найти эквивалентное сопротивление или импеданс. Здесь, если мы заменим источник напряжения проводом, схема будет выглядеть как параллельные резистор и конденсатор, где $ Z_{out} = {Z_1 Z_2 \over Z_1 + Z_2} $ .

2. Если мы хотим подключить еще один фильтр нижних частот (контур 2) последовательно со схемой из вопроса 1 (контур 1), какой критерий должен соблюдаться, чтобы мы могли игнорировать влияние нагрузки второго контура? Запишите ответ в виде $Z_1, Z_2, Z_3, Z_4$.

Решение: Мы знаем, что для игнорирования нагрузки нам нужно $ Z_{out} << Z_{in} $. Поскольку мы уже нашли $ Z_{out} $ в вопросе 1, теперь нам нужно найти $ Z_{in} $. Глядя на узлы схемы 2, она выглядит как последовательно соединенные резистор и конденсатор. Здесь нет источников напряжения, которые можно заменить проводами, у нас есть просто разомкнутая цепь с резистором, подключенным к конденсатору. Таким образом, $ Z_{in} = Z_3 + Z_4 $. Заменяя $ Z_{out} $ и $ Z_{in} $, критерием для нас, чтобы игнорировать эффекты загрузки схемы 2, является, если: $ {Z_1 Z_2 \over Z_1 + Z_2} << Z_3 + Z_4 $ .

3. Если мы обнаружим, что критерий из вопроса 2 не выполняется, и контур 2 загружает контур 1, что мы можем поместить между двумя контурами, чтобы изолировать их эффекты?

Решение: Буфер, состоящий из операционного усилителя. Мы моделируем операционный усилитель как имеющий очень низкий или пренебрежимо малый выходной импеданс и очень высокий или бесконечный входной импеданс. Таким образом, он может буферизовать эффекты между двумя цепями, как показано ниже.

Входное и выходное сопротивление | Advanced Teaching Labs

ВВЕДЕНИЕ

Многие из вас видели эквивалентную схему Thevenin — как превратить сложную схему в простую. Даже простой операционный усилитель состоит из множества компонентов:

Источник изображения: Texas Instruments.

Из-за его сложности более распространенным подходом является рассмотрение его как черного ящика с входом/выходом:

Однако сам черный ящик должен иметь некоторое сопротивление/импеданс, и это влияет на то, как мы интегрируем этот ящик в практическое использование — будет ли эта коробка потреблять слишком много тока, поскольку у нее очень низкое сопротивление, или эта коробка будет потреблять большую часть падения напряжения, поскольку у нее высокое сопротивление?

==================================

ВХОДНОЕ СОПРОТИВЛЕНИЕ

Определение входного сопротивления : «Сколько импеданса (сопротивления) с точки зрения ВХОДА »

— Определяет, какой ток вам нужно получить от входа (просто закон Ома)

— Определяет, какое напряжение будет общим черным ящиком (помните, что вход также имеет внутреннее сопротивление)

— Не имеет НИЧЕГО общего с выходом.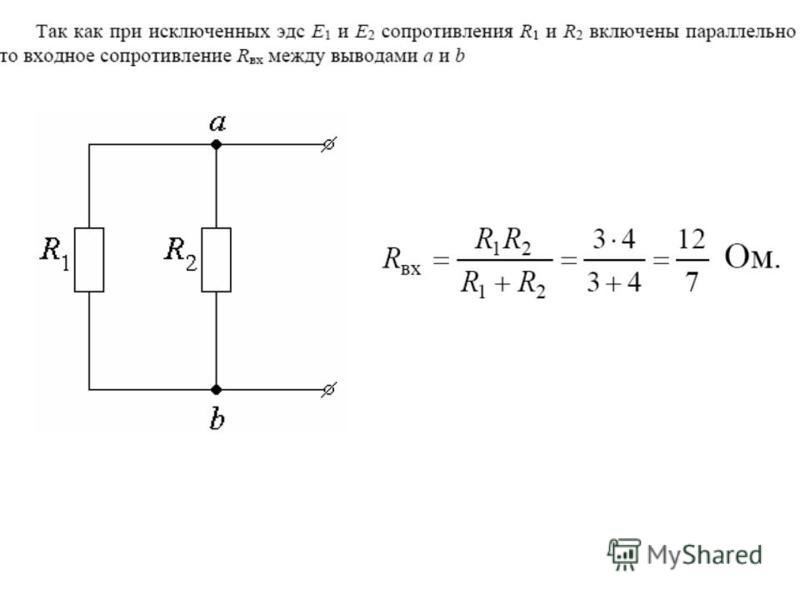 (Не пытайтесь смотреть на выход, чтобы определить входное сопротивление)

Поместим генератор функций на вход черного ящика:

Но нет ничего идеального, все устройства ввода имеют некоторое внутреннее сопротивление, поэтому:

Для упрощения будем рассматривать черный ящик как один большой резистор, сопротивление которого является входным импедансом (Zin):

Давайте задумаемся на мгновение:

• Если Zin мал:
  • Функциональный генератор будет потреблять много тока из-за низкого сопротивления, что может даже повредить устройство
  • Много напряжения уходит на внутреннее сопротивление, расходуется много энергии, и очень мало сигналов достигает черного ящика.
  • Приходится повышать входное напряжение для компенсации потерь — неэкономично.
• Если Зин большой:
  • По закону Ома большое сопротивление означает малый ток.
  • Большая часть напряжения пойдет в черный ящик, так как внутреннее сопротивление невелико и не вызовет большого падения напряжения.
  • Не нужно беспокоиться о счетах за электричество

Итак… как тогда определить входное сопротивление? Поскольку теперь в схеме нет ничего, кроме последовательно соединенных резисторов, мы можем добавить тестовый резистор на вход:

По сравнению с тестовым резистором 20 кОм, внутреннее сопротивление 5 Ом почти ничто — мы можем с уверенностью предположить, что тестовый резистор и Зин возьмет на себя большую часть перепадов напряжения.

Теперь это выглядит так:

Это не что иное, как два последовательных резистора — простой делитель напряжения.

Для расчета Zin можно:

1. Измерить амплитуду напряжения в точках A и B и использовать соотношение для расчета Zin, или:
2. Установите другой тестовый резистор до тех пор, пока амплитуда напряжения на B не составит ПОЛОВИНА напряжения на A — подразумевает, что значение нового тестового резистора равно ТО ЖЕ , что и Zin

 

Поздравляем, вы только что измерили входное сопротивление!

*Хорошая схема должна иметь высокое входное сопротивление.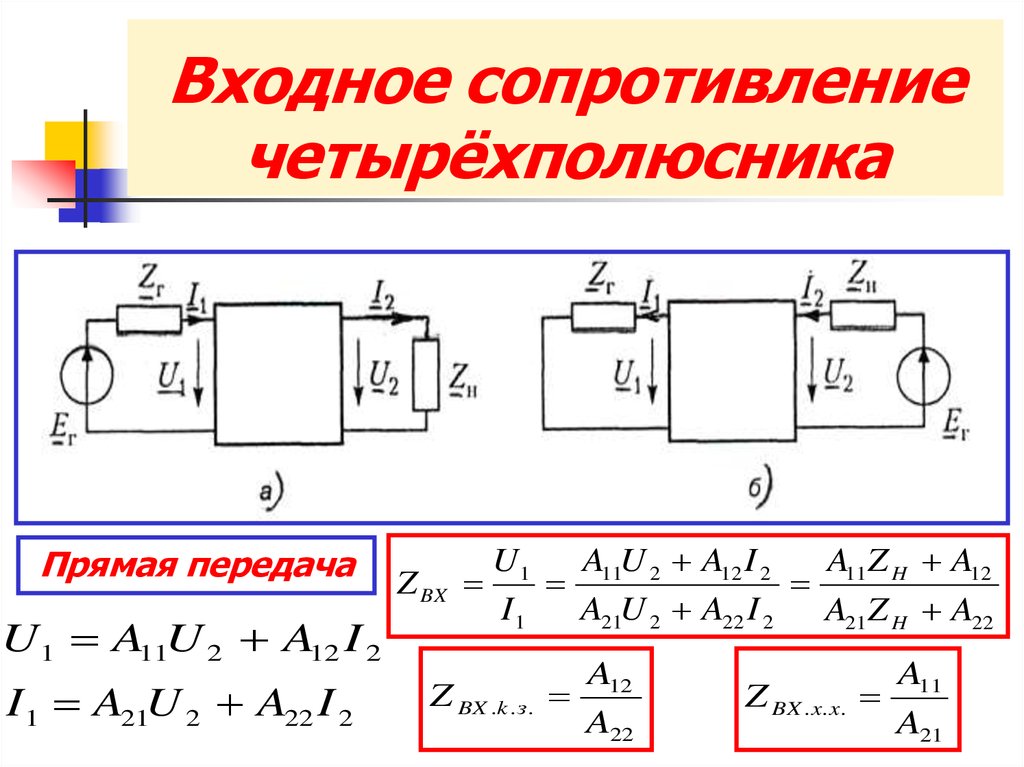

*Некоторые специальные устройства чувствительны к входной частоте (например, конденсаторы). Если вы не уверены, измените входную частоту и снова измерьте входное сопротивление.

============================================== ==========================

ВЫХОДНОЕ СОПРОТИВЛЕНИЕ

Определение выходного сопротивления: «Сколько импеданса (сопротивления) с точки зрения ВЫХОД »

— Определяет, сколько напряжения будет распределено между черным ящиком и выходной нагрузкой

— Входная амплитуда НЕ ЗНАЧИТ . (Не пытайтесь смотреть на вход, чтобы определить выходной импеданс, так как ваш черный ящик все равно может преобразовать ваш входной сигнал) ничего не увидит):

Поскольку мы смотрим на черный ящик с точки зрения вывода, входной сигнал мог быть преобразован черным ящиком и иметь другую форму волны, поэтому мы можем превратить его в Эквивалентная схема Thevenin:

И Rth будет выходным импедансом. Мы также можем назвать его Zout.

Давайте задумаемся:

• Если Zout маленький:
  • При малом сопротивлении Zout не будет иметь слишком большого падения напряжения, поэтому большая часть сигнала от Vth может пройти в следующий каскад.
• Если Зин большой:
  • К сожалению, к Zout будет приложено много напряжения от Vth, и только часть Vth может пройти в следующую стадию.

 

Теперь, чтобы рассчитать Rth, нам нужно знать напряжение Vth — его можно просто измерить с помощью осциллографа в точке C. Поскольку идеальный осциллограф имеет ~бесконечное сопротивление (или ~10 МОм в реальности), поэтому большинство Vth могут быть загружены в прицел.

Теперь мы можем добавить в цепь нагрузочный резистор:

С добавленным нагрузочным резистором измерьте амплитуду напряжения в точке C, и вы должны увидеть меньшую амплитуду, чем Vth. Теперь, когда мы знаем амплитуду Vth (общее напряжение), амплитуду напряжения на нагрузочном резисторе и сопротивление нагрузки, вычислить значение Zout не составит труда.