Лекция на тему: «Векторы».
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
Длина вектора
Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные
одной прямой или лежащие на одной прямой называют коллинеарными
векторами (рис. 2).
Вектора, параллельные
одной прямой или лежащие на одной прямой называют коллинеарными
векторами (рис. 2).
рис. 2 | |||||||||
Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b Условия коллинеарности векторов 2. Два вектора коллинеарны N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю. Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных
(пространственных) задач. Ответ: вектора a и b коллинеарны при n = 6 и m = 4. Сонаправленные вектора Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
Противоположно направленные вектора Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4). Компланарные вектора Определение.
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные. Условия компланарности векторов
Равные вектора Определение.
|
Условие равенства векторов. Вектора равны, если их координаты равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторовПример 1.
Решение:
a = b — так как их координаты равны,
a ≠ c —
так как их координаты не равны,
b ≠ c —
так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = {1; 8;}
и b = {1; 2n}
равны.
Решение:
Проверим равенство компонентов векторов
ax = bx =
1
ay = by =>
8 = 2n => n =
8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторовПример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.
Решение:
a = c — так как их координаты равны,
a ≠ b —
так как их координаты не равны,
b ≠ c —
так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx =
1
ay = by =
2
az = bz =>
4 = 2n => n =
4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Определение. Единичным вектором или ортом —
называется вектор, длина которого равна единице.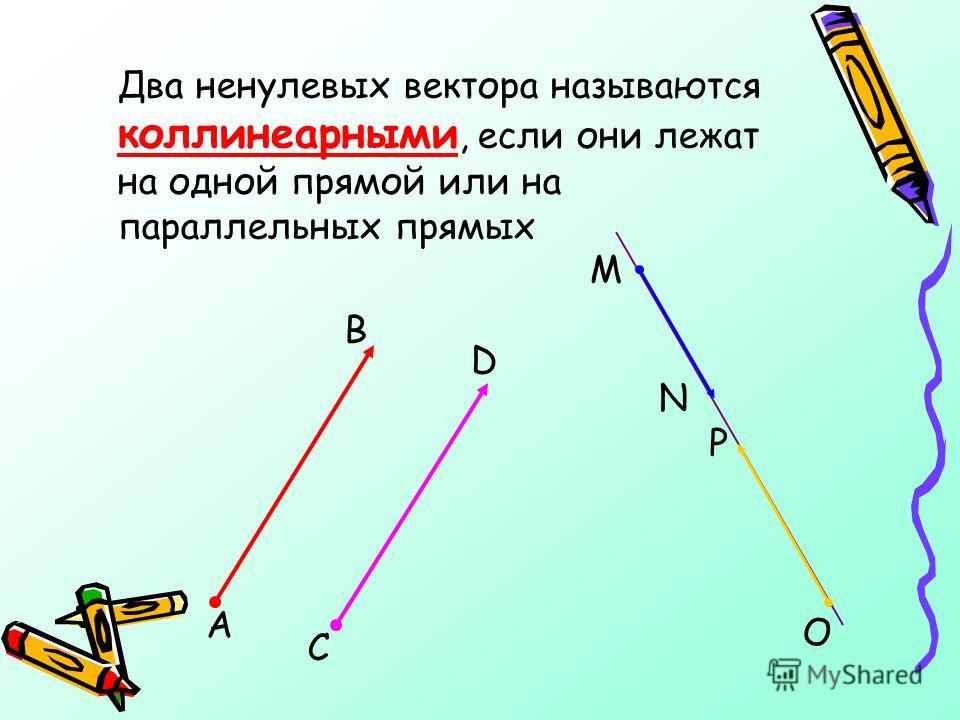
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Ортогональность векторов
Определение.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
рис. 1 |
Условие ортогональности векторов.Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
a · b = 0
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задачВ случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — A
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В
случае n-мерного пространства
вектор AB заданный координатами точек A(A1 ; A2 ; .
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры для плоских задачПример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).
Решение:
ABx = Bx —
Ax => B
ABy = By —
Ay => By = ABy +
Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx —
Ax => Ax = Bx —
ABx => Ax = 3 — 5 = -2
ABy = By —
Ay => Ay = By —
ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).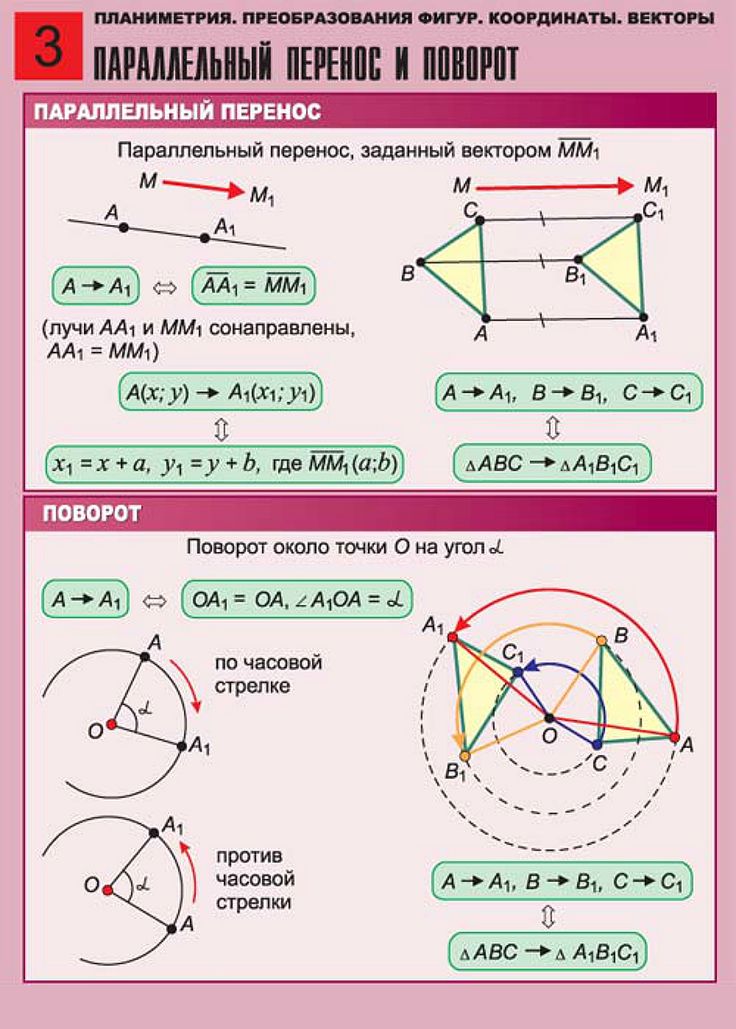
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).
Решение:
ABx = Bx —
Ax => Bx = ABx +
Ax => Bx = 5 + 3 = 8
ABy = By —
Ay => By = ABy +
Ay => By = 1 + (-4) = -3
ABz = Bz —
Az => Bz = ABz +
Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).
Решение:
ABx = Bx —
Ax => Ax = Bx —
ABx => Ax = 3 — 5 = -2
ABy = By —
Ay => Ay = By —
ABy => Ay = -4 — 1 = -5
ABz = Bz —
Az => Az = Bz —
ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).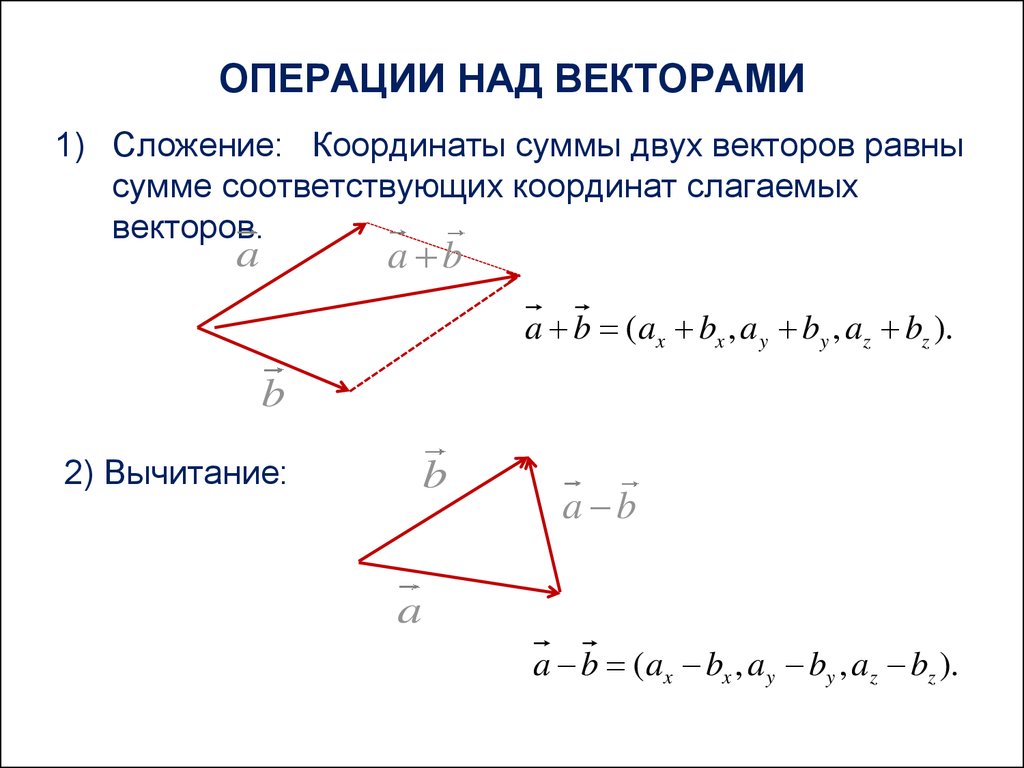
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).
Решение:
AB1 =
B1 — A1 => B1 =
AB1 + A1 => B1 =
5 + 3 = 8
AB2 = B2 — A2 => B2 =
AB2 + A2 => B2 =
1 + (-4) = -3
AB3 = B3 — A3 => B3 =
AB3 + A3 => B3 =
2 + 3 = 5
AB4 = B4 — A4 => B4 =
AB4 + A4 => B4 =
1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).
Решение:
AB1 =
B1 — A1 => A1 =
B1 — AB1 => A1 =
3 — 5 = -2
AB2 = B2 — A2 => A2 =
B2 — AB2 => A2 =
-4 — 1 = -5
AB3 = B3 — A3 => A3 =
B3 — AB3 => A3 =
1 — 4 = -3
AB4 = B4 — A4 => A4 =
B4 — AB4 => A4 =
8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Определение длины вектора
Определение.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две
вертикальные линии слева и справа |AB|.
Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Формулы длины вектора
Формула длины вектора для плоских задачВ случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2
Формула длины вектора для пространственных задачВ случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2 + az2
Примеры вычисления длины вектора для плоских задачиПример 1. Найти длину вектора a = {2; 4}.
Решение: |a| = √22 + 42 = √4 + 16 = √20 = 2√5.
Пример 2. Найти длину вектора a = {3; -4}.
Решение: |a| = √32 + (-4)2 = √9 + 16 = √25 = 5.
Примеры вычисления длины вектора для пространственных задачиПример 3. Найти длину вектора a = {2; 4; 4}.
Решение: |a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Пример 4. Найти длину вектора a = {-1; 0; -3}.
Решение: |a| = √(-1)2 + 02 + (-3)2 = √1 + 0 + 9 = √10.
Примеры вычисления длины вектора для пространств с размерностью большей 3Пример 5. Найти длину вектора a = {1; -3; 3; -1}.
Решение: |a| = √12 + (-3)2 + 32 + (-1)2 = √1 + 9 + 9 + 1 = √20 = 2√5
Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.
Решение: |a| = √22 +
42 + 42 + 62 + 22 =
√4 + 16
+ 16 + 36 + 4 = √76 = 2√19.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задачВ случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задачВ случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторовВ
случае n-мерного пространства скалярное произведение
векторов a = {a1 ; a2 ; . .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей
формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей
формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Определение. Проекцией
вектора AB на ось l называется
число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются
проекциями точек A и B на ось l. (рис. 1).
(рис. 1).
рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Пр ba = | a · b |
|b| |
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
Пр ba = | a · b | = | 11 | =
2. |
|b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачиПример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
Пр ba = | a · b | = | 12 | = 2 |
|b| | 6 |
Ответ: Пр ba =
2.
Кафедра математики Физического факультета МГУ им. М.В.Ломоносова
Аналитическая геометрия является одним из базовых курсов высшей математики, лежащих в основе физико-математического образования.
Общая трудоемкость курса — 108 часов. Курс включает 36 часов лекций, 18 часов семинарских занятий, требует 54 часов самостоятельной работы студентов.
В курсе рассматриваются следующие вопросы: системы координат, векторы и операции над ними, скалярное, векторное и смешанное произведения векторов, теория прямых и плоскостей, элементы теории кривых и поверхностей второго порядка, комплексные числа, матрицы и операции над ними, теория определителей, теория систем линейных алгебраических уравнений, элементы теории линейных пространств. На примерах геометрических объектов малой размерности курс знакомит студентов с основными идеями метода координат и даёт общие навыки работы с простейшими алгебраическими системами.
Лекторы
- Голубцов Петр Викторович
- Колыбасова Валентина Викторовна
- Овчинников Алексей Витальевич
Отчётность
зачет и экзамен
Содержание курса
- Комплексные числа и операции над ними.
 Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.
Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел. - Алгебра матриц. Матрицы и операции над ними. Умножение матриц. Линейная зависимость и независимость. Теория определителей. Ранг матрицы. Теорема о базисном миноре. Системы линейных уравнений.
- Алгебра векторов. Системы координат. Понятие вектора. Линейные операции над векторами. Базис и координаты. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Двойное векторное произведение.
- Линейные образы. Прямые на плоскости. Прямые и плоскости в пространстве.
- Кривые и поверхности второго порядка.
- Элементы теории линейных пространств. Понятие линейного пространства. Основные примеры. Базис и размерность линейного пространства. Основные свойства линейных пространств. Изоморфизмы линейных пространств.
Основная литература
- Ильин В.А., Позняк Э.
 Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999.
Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999. - Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, Физматлит, 1999.
- Овчинников А.В. Алгебра и геометрия в вопросах и задачах. Кн.1. Основы алгебры и аналитической геометрии. — М.: ЛЕНАНД, 2016.
- Клетеник Д.В. Сборник задач по аналитической геометрии. — М.: Наука, Физматлит, 1998.
Дополнительная литература
- Александров П.С. Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979.
- Александров П.С. Лекции по аналитической геометрии. — Наука, 1968.
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Физматлит, 2005.
- Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. — М.: Физматлит, 2003.
- Овчинников А.В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009.
- Федорчук В.В. Курс аналитической геометрии и лин. алгебры. — М.
 : МГУ, 1990.
: МГУ, 1990. - Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. — Спб, 2003.
Материалы по курсу
Вопросы и задачи к экзамену
1 поток. Лектор: ст.н.с. В.В. Колыбасова
- Лекция 1. Формулы Крамера. Определители 1-го, 2-го и 3-го порядка
- Лекция 2. Простейшие операции с векторами
- Лекция 3. Базис, координаты, системы координат
- Лекция 4. Скалярное, векторное, смешанное произведения. Преобразование прямоугольных координат на плоскости
- Лекция 5. Комплексные числа
- Лекция 6. Прямая на плоскости
http://sites.google.com/site/vkolybasova
2 поток. Лектор: доц. А.В. Овчинников
Курс лекций
Контрольные задания
Полярная сетка
3 поток. Лектор: проф. П.В. Голубцов
Дополнительно
Лекции доц. А.В. Бадьина
- План лекций
- Лекция 1. Логико-математическая символика
- Лекция 2.
 Векторы в пространствах E1, E2, E3
Векторы в пространствах E1, E2, E3 - Лекция 3. Матричная алгебра. Определители порядков 1, 2, 3
- Лекция 4. Скалярное, смешанное, векторное произведения
- Лекция 5. Прямые в пространстве E2. Прямые и плоскости в пространстве E3
- Лекция 7. Линейное пространство
- Лекция 8. Базис линейного пространства
- Лекция 9. Определитель матрицы
- Лекция 10. Размерность линейного пространства. Ранг матрицы
- Лекция 11. Линейные операторы. Изоморфизмы линейных пространств
- Лекция 12. Система линейных алгебраических уравнений
- Лекция 13. Кривые второго порядка
Векторная теория изменений — теория изменений для сложных систем
Если вы хотите сократить путь, этот блог запускает объяснение векторной теории изменений — теории изменений для сложных систем.
***
Представьте, что вы стоите у подножия горы. Когда вы смотрите вверх, туман превращается в густой туман, скрывающий местность перед вами. Вы держите карту в руках. Деталей мало; он показывает только ключевые ориентиры / вехи по пути, почти не указывая тип местности. На ней показана одна тропа, ведущая прямо в гору, и не так-то просто понять, где именно вы находитесь. Есть инструкции, которые сопровождают карту, но они описывают путь так, как будто вы стоите на вершине пика. Эта карта, возможно, была бы полезна без тумана, но туман делает ее непредсказуемой.
Когда вы смотрите вверх, туман превращается в густой туман, скрывающий местность перед вами. Вы держите карту в руках. Деталей мало; он показывает только ключевые ориентиры / вехи по пути, почти не указывая тип местности. На ней показана одна тропа, ведущая прямо в гору, и не так-то просто понять, где именно вы находитесь. Есть инструкции, которые сопровождают карту, но они описывают путь так, как будто вы стоите на вершине пика. Эта карта, возможно, была бы полезна без тумана, но туман делает ее непредсказуемой.
—Хм… на данный момент, если вы похожи на меня, вы не так уверены в этой экспедиции.
К счастью, мимо проходит местный пешеход, знакомый с местностью, и вы просите его о помощи.
Они показывают вам свою карту, которая намного более подробная и актуальная. Это показывает, что на самом деле есть несколько путей, ведущих к вершине, и уровень сложности каждого из них. Эта подробная карта показывает, что единственная тропа, отмеченная на вашей собственной карте, которая ведет прямо в гору, на самом деле очень крутая с рыхлой осыпью.
— Хороший. Здорово, что мимо прошел местный житель и вы попросили о помощи. Иначе можно было бы побеспокоиться.
Местный житель показывает на карте, где вы находитесь, и описывает несколько хороших маршрутов, которыми можно пройти по лесам, озерам и оврагам. И они также расскажут вам о некоторых представителях флоры и фауны в этом районе. По их карте легко сказать, где вы находитесь и какие маршруты начинаются отсюда.
Однако на картах не указано «здесь водятся странные звери», поэтому местный житель подсказывает вам некоторые участки леса, чтобы не ходить после наступления темноты. Они дают вам компас, чтобы вы могли отправиться в нужном направлении.
Во время прогулки вам нужно внимательно следить за тем, что вас окружает, чтобы не пропустить ни одной из достопримечательностей, описанных местным бродягой. Оглядевшись, вы замечаете трутовики — лекарственные грибы, из которых можно приготовить прекрасный чай.
— Отлично! Иначе вы бы никогда этого не заметили!
В конце концов вы доберетесь до точки обзора.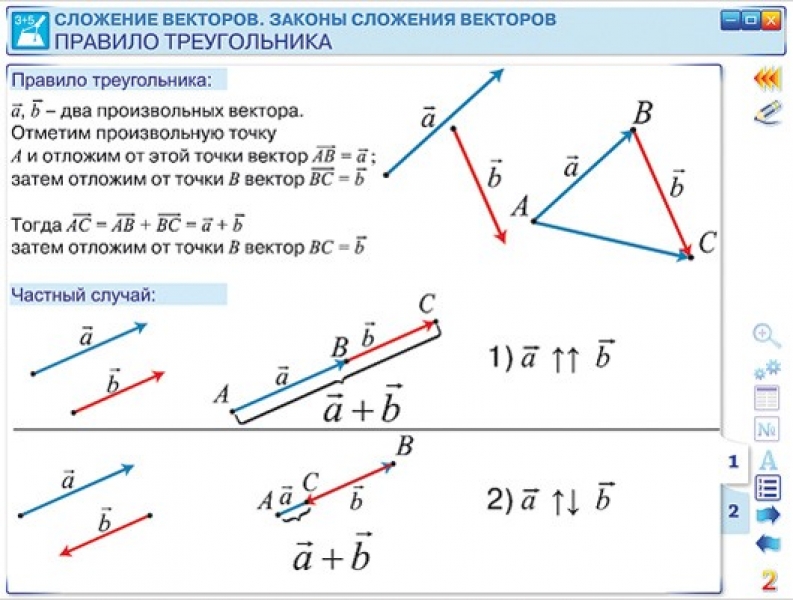 Туман немного рассеялся. Вы вдыхаете свежий воздух и дикий пейзаж. Вы встречаете другого местного жителя, который рекомендует маршрут, особенно живописный в это время года, к ближайшей вершине. На эту вершину на самом деле легче добраться, чем на первоначальную вершину, на которую вы намеревались подняться, поэтому вы решаете идти туда. Когда вы достигаете вершины, сцена захватывает дух.
Туман немного рассеялся. Вы вдыхаете свежий воздух и дикий пейзаж. Вы встречаете другого местного жителя, который рекомендует маршрут, особенно живописный в это время года, к ближайшей вершине. На эту вершину на самом деле легче добраться, чем на первоначальную вершину, на которую вы намеревались подняться, поэтому вы решаете идти туда. Когда вы достигаете вершины, сцена захватывает дух.
—Красота оставаться открытым для возможностей, а?
***
Первая карта представляет собой попытку использовать традиционную теорию изменений в сложной среде. Традиционные теории изменений обычно включают в себя представление конечной точки, а затем работу в обратном направлении, чтобы определить каждый шаг, который должен быть достигнут, чтобы реализовать конечную цель, с обоснованиями и предположениями, идентифицированными на каждом этапе (Taplin & Clark, 2012; Weiss, 1995). Это полезный подход при работе в упорядоченных системах, где связь между причиной и следствием ясна и предсказуема (см.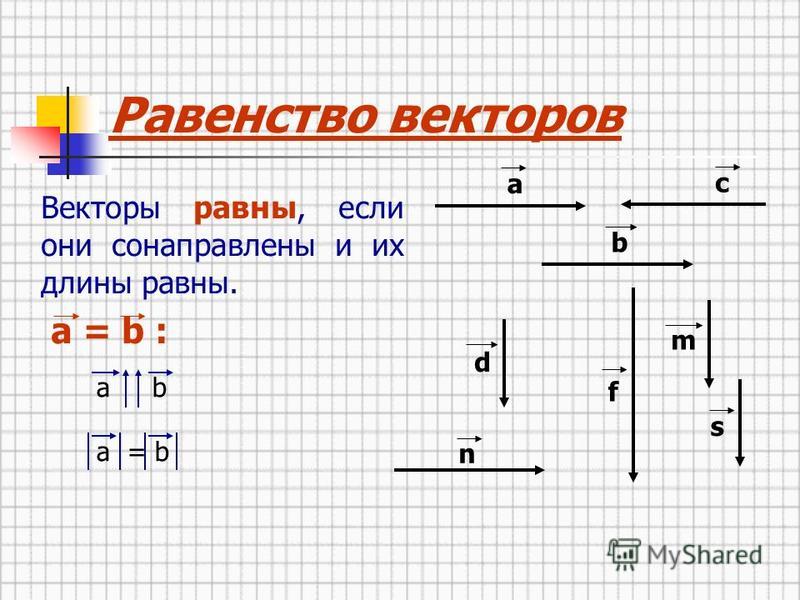 структуру Cynefin).
структуру Cynefin).
Однако сценарий, с которым мы имеем дело, представляет собой сложную неизвестную территорию. Момент встречи с бегущим по холмам и далее представляет собой векторную теорию изменений — теорию изменений для сложных систем — более подходящую.
Я рад, что вы прошли весь путь через чащу моего творческого письма, потому что здесь лежит сокровище! Я написал краткое пояснение по векторной теории изменений, в котором описывается, почему подходы к теории изменений до сих пор не подходили для сложных систем и как векторная теория изменений помогает исправить эти проблемы. Он шаг за шагом проведет вас через векторную теорию изменений: начиная с того места, где вы находитесь, определяя направление и находя ступени, разрабатывая вмешательства и отслеживая непрерывную обратную связь, а не безрассудно стремясь к фиксированной конечной точке любой ценой.
Заглавное изображение: Джеймс Армс на Uunsplash
Скалярная, векторная и матричная математика
С момента первой публикации эта книга стала незаменимым справочником для пользователей матриц во всех областях техники, естественных наук и прикладной математики.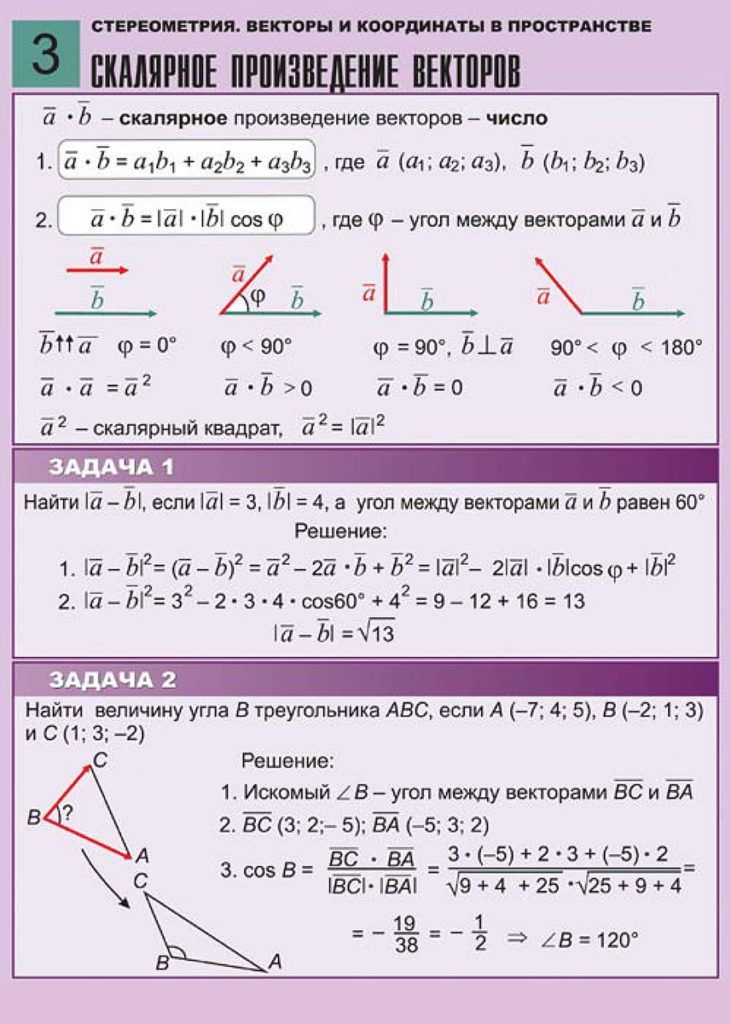 В этом исправленном и дополненном издании Деннис Бернштейн сочетает обширный материал по скалярной и векторной математике с последними результатами теории матриц, что делает эту книгу наиболее полной, современной и простой в использовании книгой по этому предмету.
В этом исправленном и дополненном издании Деннис Бернштейн сочетает обширный материал по скалярной и векторной математике с последними результатами теории матриц, что делает эту книгу наиболее полной, современной и простой в использовании книгой по этому предмету.
В каждой главе описываются соответствующие теоретические основы, за которыми следуют специализированные результаты. Сотни тождеств, неравенств и фактов изложены ясно и строго, с перекрестными ссылками, ссылками на литературу и полезными комментариями. Этот уникальный сборник, начиная с предварительных сведений о множествах, логике, отношениях и функциях, охватывает все основные темы теории матриц, такие как преобразования и разложения, полиномиальные матрицы, обобщенные инверсии и нормы. Дополнительные темы включают графы, группы, выпуклые функции, многочлены и линейные системы. Книга также содержит множество новых материалов по скалярным неравенствам, геометрии, комбинаторике, рядам, интегралам и многому другому.
Теперь более полный, чем когда-либо, Скалярная, векторная и матричная математика включает подробный список символов, сводку обозначений и условных обозначений, обширную библиографию и указатель авторов со ссылками на страницы, а также исчерпывающий предметный указатель.
- Полностью обновлен и дополнен новыми материалами по скалярной и векторной математике
- Охватывает последние результаты по теории матриц
- Содержит список символов и сводку соглашений для простого и точного использования
- Включает обширную библиографию с обратными ссылками, а также указатель авторов
Деннис С. Бернштейн — профессор аэрокосмической техники Мичиганского университета.
«Эта книга является прорывом… Это одновременно и вводный и полностью самостоятельный учебник для студентов, и пособие для исследователей, и справочник, и исследовательская монография… Я не знаю ни одной близкой сравнение этой книги и в последующие годы книга Бернстайна всегда будет стоять на полке в моем кабинете». — Джайдеб Саркар, Zentralblatt MATH
«Похвала предыдущим выпускам: «Когда мне задают вопрос о матрице, я теперь отсылаю своих корреспондентов. . . к справочнику Бернстайна».» —Филип Дж. Дэвис, SIAM News
Дэвис, SIAM News
«Похвала предыдущим изданиям: «Количество охватываемого материала впечатляет и хорошо структурировано. . . . Я настоятельно рекомендую эту книгу как источник для получения или проверки матричных результатов, которые в противном случае пришлось бы искать в обширной литературе по теории матриц».0060 — Пол Ван Доурен, Журнал IEEE Control Systems
«Похвала предыдущим изданиям: «Автору очень удалось собрать огромное количество результатов по матричной теории в одном источнике. . . . Прекрасная работа и превосходное исполнение!»» — Monatshefte für Mathematik
«Похвала предыдущим изданиям: «Замечательный источник матричных результатов. Я положу его на полку рядом со своим столом, чтобы иметь к нему быстрый доступ. Книга — впечатляющее достижение.»» — Гельмут Люткеполь, Изображение
«Похвала предыдущим изданиям: «Хорошо организованная сокровищница информации для всех, кто интересуется матрицами и их приложениями».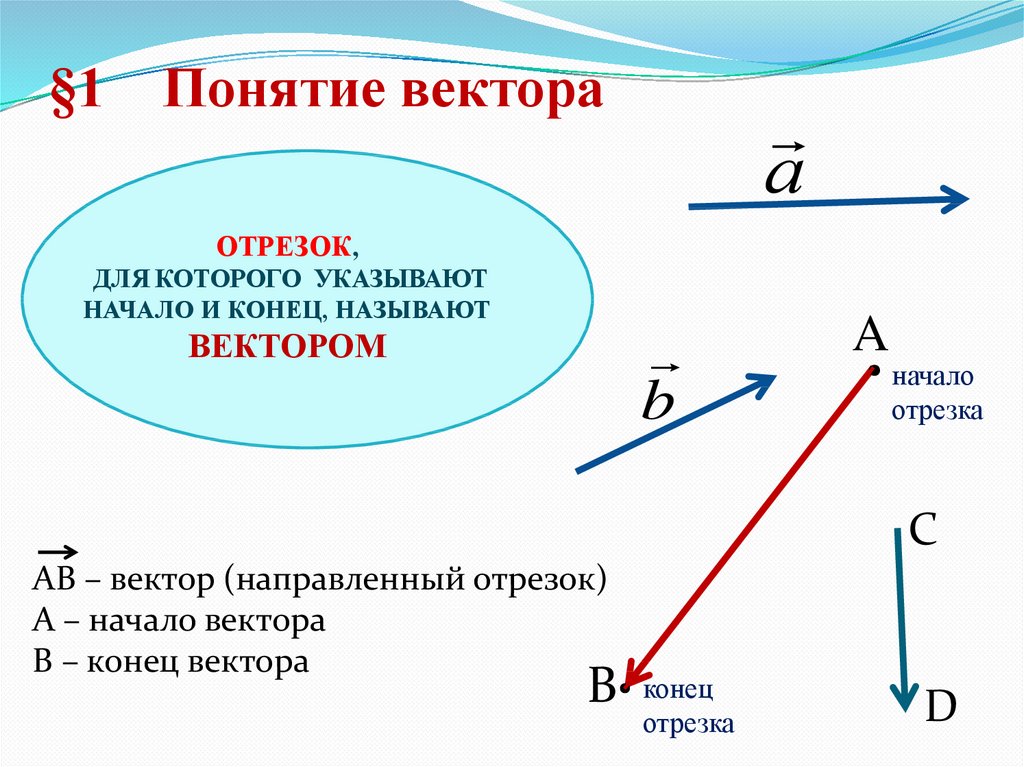 «Эта книга содержит огромное количество разнообразных результатов по матричной и линейной алгебре, тщательно собранных из многочисленных источников. Уже ставшая основным справочником для всех, кто интересуется теорией и практикой матриц, это новое издание включает в себя множество дополнительных материалов. Если вы Если у вас есть какие-либо вопросы о множествах, графиках и функциях, производных и интегралах, последовательностях и пределах и даже о геометрии, вы почти наверняка найдете здесь ответ». — Гётц Тренклер, Технический университет Дортмунда, Германия
«Эта книга содержит огромное количество разнообразных результатов по матричной и линейной алгебре, тщательно собранных из многочисленных источников. Уже ставшая основным справочником для всех, кто интересуется теорией и практикой матриц, это новое издание включает в себя множество дополнительных материалов. Если вы Если у вас есть какие-либо вопросы о множествах, графиках и функциях, производных и интегралах, последовательностях и пределах и даже о геометрии, вы почти наверняка найдете здесь ответ». — Гётц Тренклер, Технический университет Дортмунда, Германия
«Книга Бернштейна унаследовала все достоинства своих ценных предшественников и предлагает гораздо больше, чем просто обновление. Были затронуты новые темы и включено много новых результатов, и автор приложил огромные усилия, чтобы представить их в ясной, краткой, и логическим путем. Эта книга останется основным справочником для инженеров, математиков, физиков, статистиков и других ученых, интересующихся чистым и прикладным матричным анализом и смежными темами».



 Вектора, параллельные
одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Вектора, параллельные
одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
 2
2 Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.
Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел. Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999.
Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999. : МГУ, 1990.
: МГУ, 1990.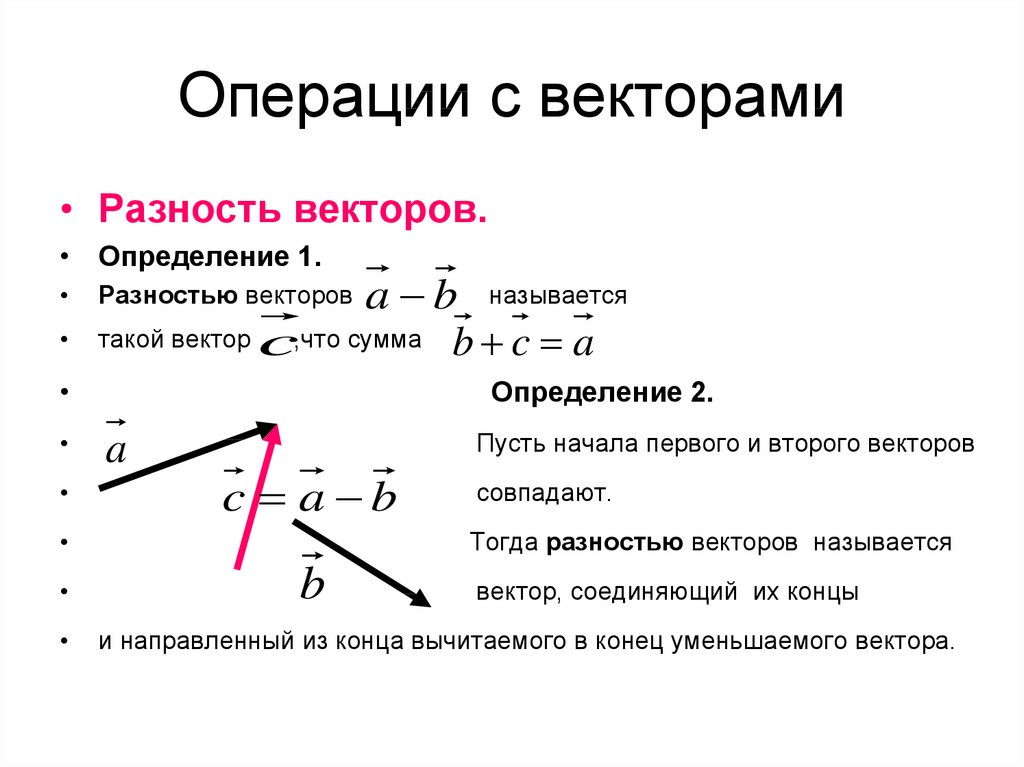 Векторы в пространствах E1, E2, E3
Векторы в пространствах E1, E2, E3