1.3. Основные действия с векторами – кратко, с чертежами



В школьном курсе геометрии рассматривается ряд действий и правил с векторами, и для начала мы повторим наиболее важные из них:

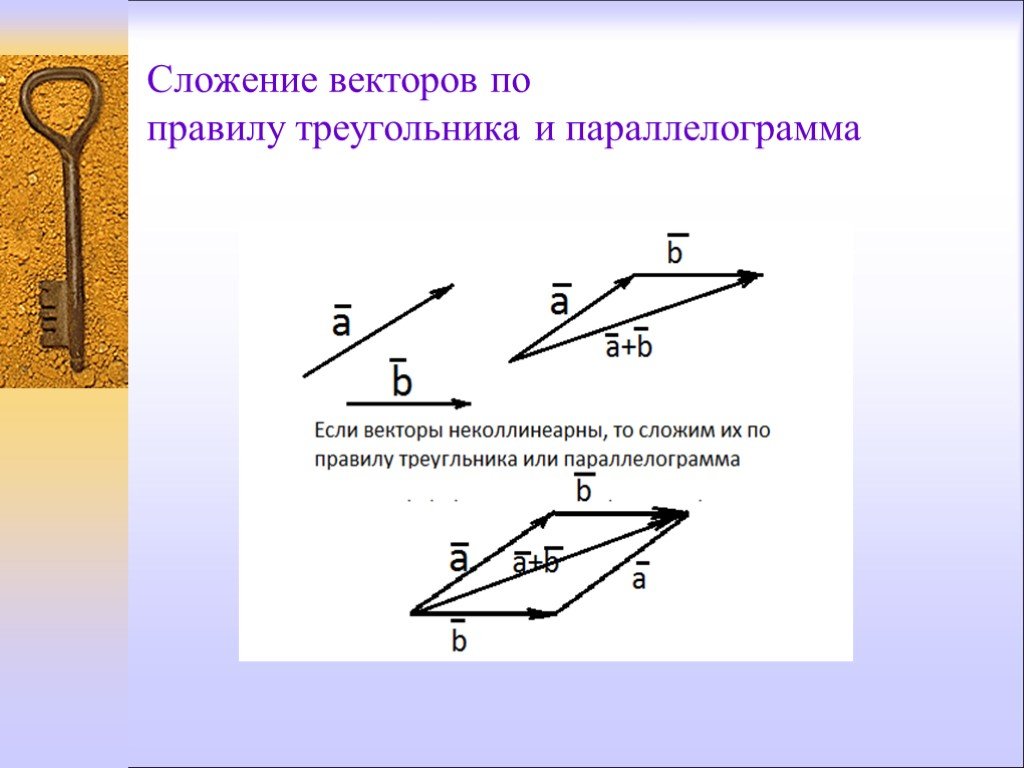
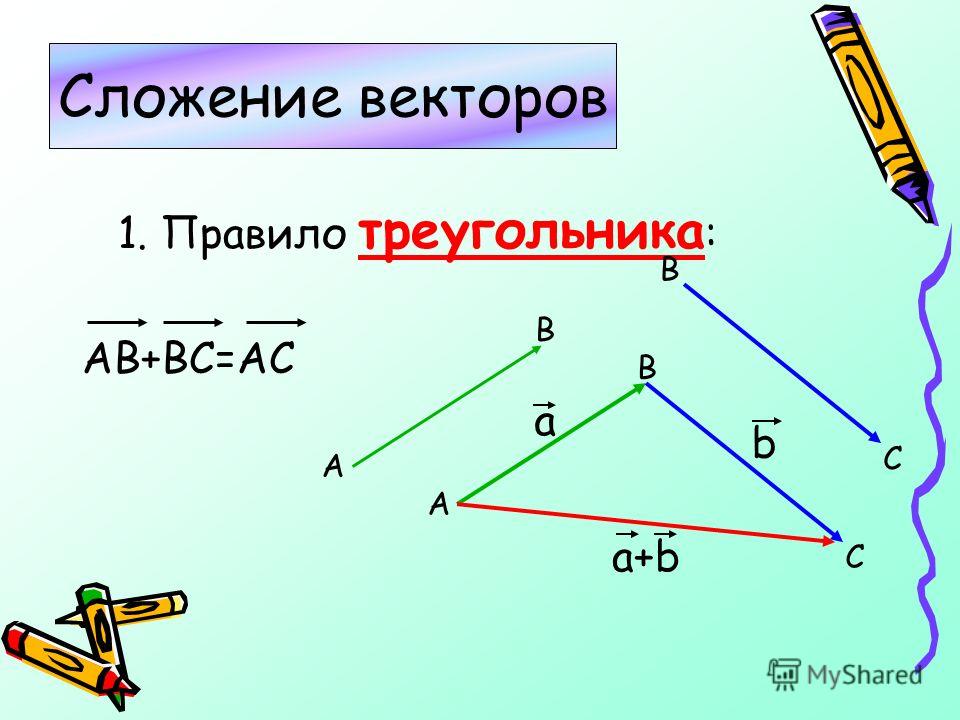
Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора  и :

Требуется найти их сумму. В силу того, что все векторы свободны, отложим вектор  от конца вектора :

Суммой векторов  и  является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов  представляет собой вектор результирующего пути  с началом в точке отправления и концом в точке прибытия.

Векторы перестановочны:  – мысленно отложите вектор  от конца вектора  (см. рисунок выше), и вы поймёте, что получится тот же самый вектор .

Аналогичное правило справедливо для суммы любого количества векторов. Как говорится, тело может пройти свой путь по зигзагу, а может и на автопилоте по результирующему вектору суммы.

Кстати, если вектор  отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Произведением ненулевого вектора  на число  является такой вектор , длина которого равна , причём при  векторы   и  сонаправлены, а при  направлены противоположно.

Правило умножения вектора на число легче понять с помощью рисунка:

Разбираемся более детально:

1) Направление. Если множитель  отрицательный,  то полученный вектор будет направлен в противоположную сторону – смотрим на векторы  и .

2) Длина. Если множитель заключен в пределах , то длина вектора соразмерно уменьшается. Так, длина вектора  в два раза меньше длины вектора . Если множитель  по модулю больше единицы, то длина вектора увеличивается в  раз. Так, длина вектора  в два раза больше длины вектора .

3) Очевидно, что все векторы коллинеарны, при этом один вектор

линейно* выражен через другой, например, . Обратное тоже справедливо: если один вектор можно линейно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

* Справка: линейно – это значит, через множитель-константу.

4) Векторы  сонаправлены. Векторы  и  тоже сонаправлены.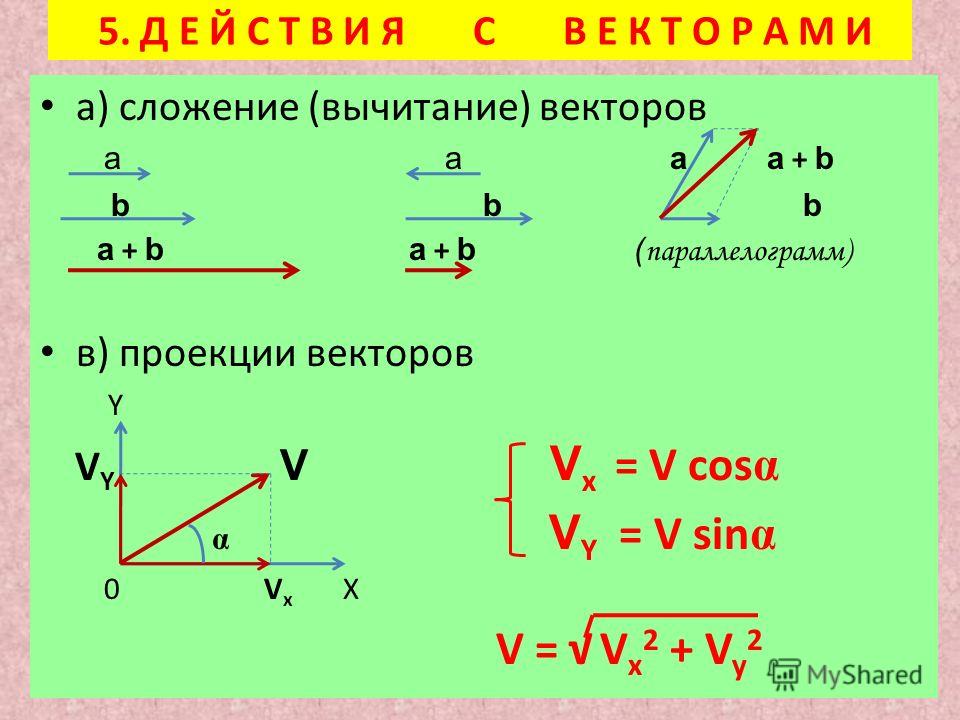 Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

1.4. Координаты вектора на плоскости и в пространстве

1.2. Коллинеарность векторов

| Оглавление |



Автор: Aлeксaндр Eмeлин

Аналитическая геометрия

Аналитическая геометрия

Привалов И.И. Аналитическая геометрия. М.: Наука, 1966. — 272 с. Учебник для студентов высших технических заведений. Содержит разделы: Аналитическая геометрия на плоскости, Аналитическая геометрия в пространстве. Много решенных примеров и задач. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. 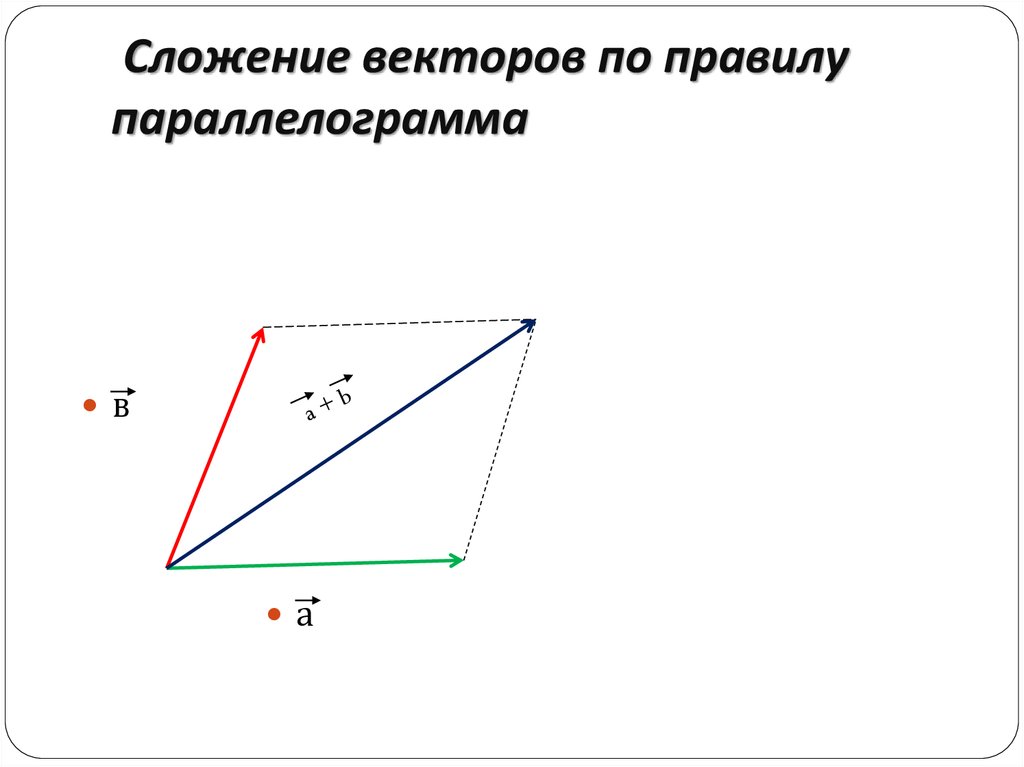Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. 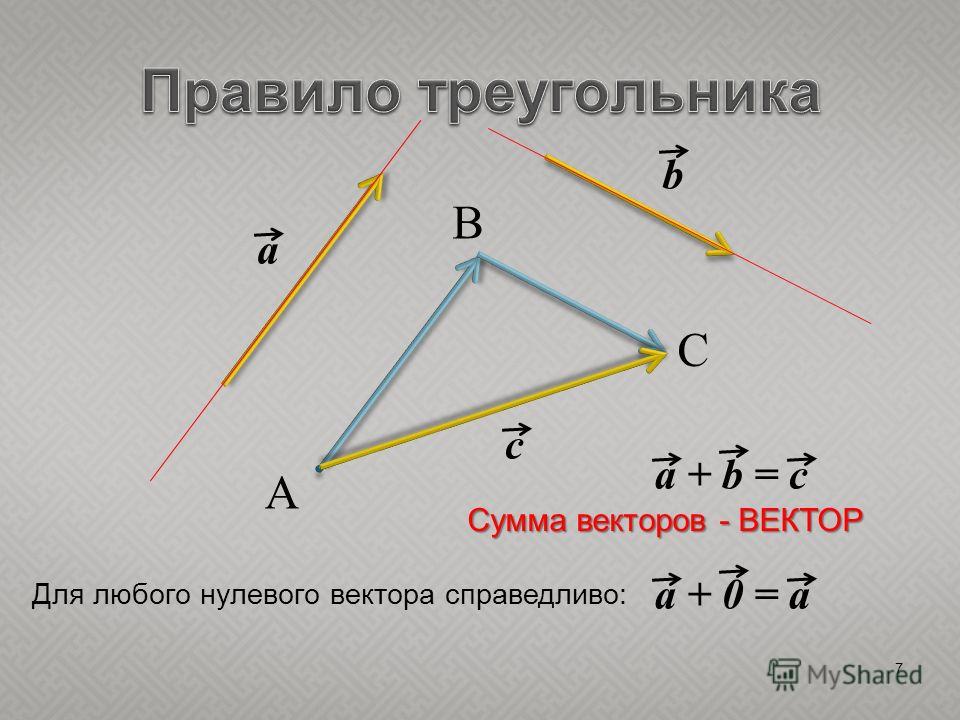§ 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. 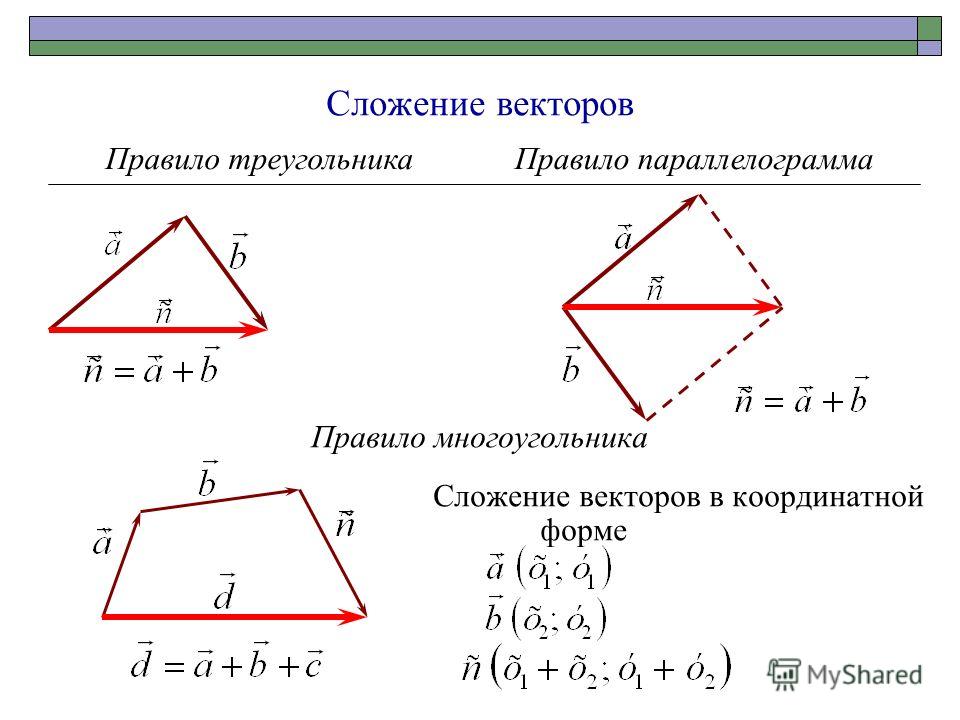Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. 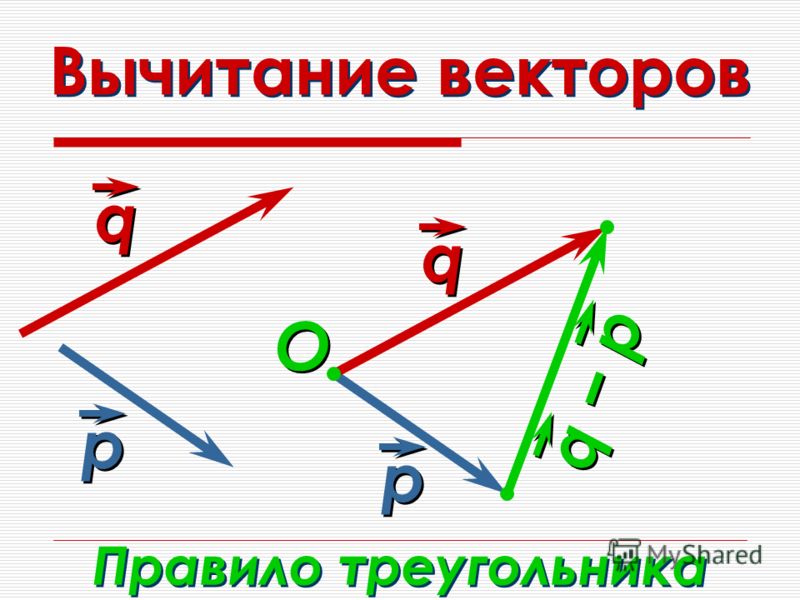§ 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова. Упражнения Ответы

Объяснение урока: Графические операции над векторами

В этом объяснении мы научимся выполнять операции над векторами графически используя правила треугольника и параллелограмма.

Векторы — это объекты, полностью определяемые своей величиной и направлением. Мы помним, что мы можем представлять векторы в виде направленного отрезка в подходящем виде. пространство, где длина отрезка говорит нам величину вектора а направление указывается начальной и конечной точками направленного отрезок. В этом пространстве мы можем думать о векторах как о представлениях смещения, от начальной точки до конечной точки.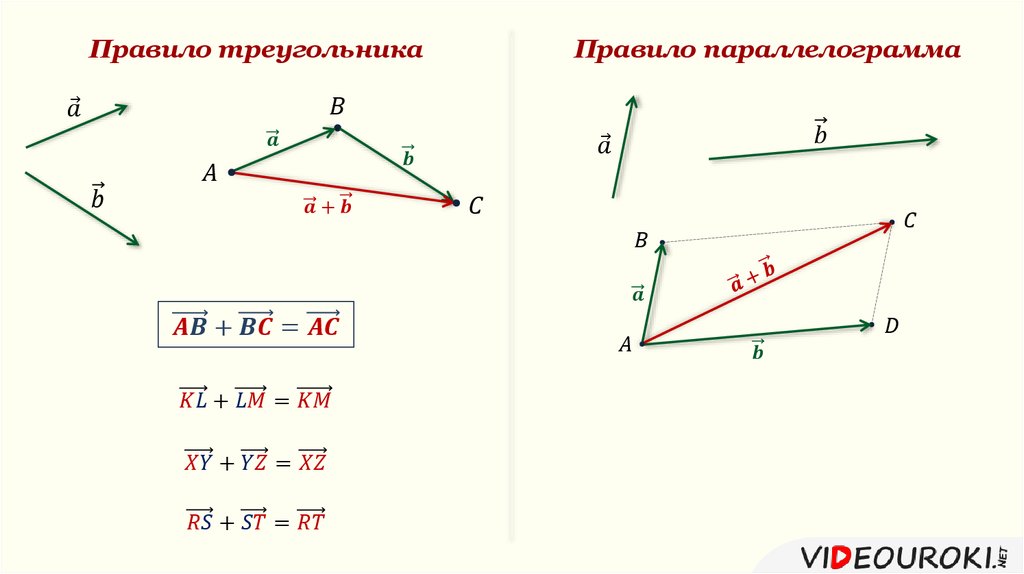

Например, вектор от 𝐴 до 𝐵 можно представить в виде направленного отрезка от 𝐴 до 𝐵.

Длина этого отрезка равна величине 𝐴𝐵, написано ‖‖𝐴𝐵‖‖, и направление показано стрелкой. Стоит повторить, что вектор полностью определяется его величина и направление, поэтому любые два вектора с одинаковыми величинами и направление будет равно. В частности, мы можем нарисовать вектор в любом месте 𝑥𝑦-плоскость; это не изменит его величины или направления, и, следовательно, это будет все тот же вектор.

Мы также можем представить этот вектор изменением по горизонтали и по вертикали. Если 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦), то из диаграммы (или координаты) мы можем найти горизонтальные и вертикальные изменения при движении от 𝐴 до 𝐵.

Изменение горизонтальной координаты равно 𝑥−𝑥 а изменение вертикальной координаты равно 𝑦−𝑦. Мы пишем это как 𝐴𝐵=(𝑥−𝑥,𝑦−𝑦). Первая компонента говорит нам о горизонтальном смещении вектора, а вторая Компонент сообщает нам вертикальное смещение вектора.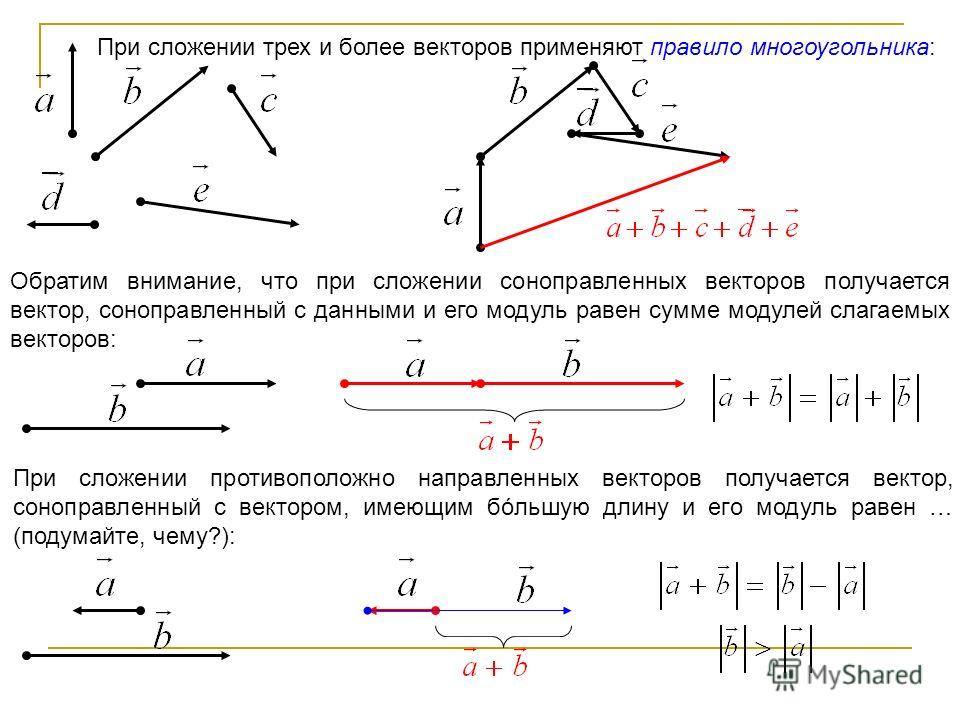

Это позволяет нам складывать векторы вместе. С точки зрения смещения, сумма два вектора будут суммарным смещением обоих векторов. С точки зрения компонентов, напомним, что это означает, что если мы имеем ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦); мы добавляем горизонтальные и вертикальные компоненты отдельно. Затем это позволяет нам добавлять векторы вместе графически.

Например, если у нас есть вектор 𝐴𝐵, то в этом пространстве это смещение от точки 𝐴 указать 𝐵. Сходным образом, 𝐵𝐶 — смещение от точки 𝐵 указать 𝐶. Их сумма, 𝐴𝐵+𝐵𝐶, должно быть общее смещение обоих векторов, то есть смещение от 𝐴 до 𝐵 и затем от 𝐵 до 𝐶. Это вектор 𝐴𝐶, и мы можем показать это графически.

Мы видим, что смещение от 𝐴 к 𝐶 совпадает со смещением от 𝐴 в 𝐵 и затем из 𝐵 до 𝐶, так как их начальная и конечная точки такие же. Это часто называют правилом треугольника для векторов.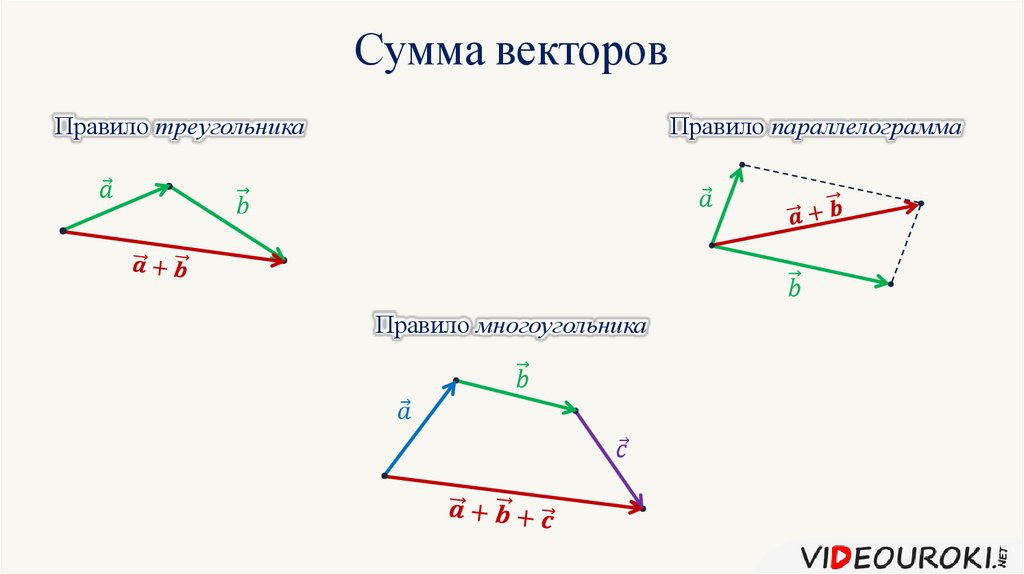 Мы можем констатировать это следующим образом.

Правило: Правило треугольника для векторов

Для любых трех точек 𝐴, 𝐵 и 𝐶, у нас есть 𝐴𝐵+𝐵𝐶=𝐴𝐶 как показано на диаграмме.

В результате правила треугольника, если у нас есть два вектора ⃑𝑢 и ⃑𝑣 представлены графически, то мы можем сложить эти векторы вместе, зарисовав конечная точка ⃑𝑢 должна быть начальной точкой ⃑𝑣, как показано.

Прежде чем мы увидим, как применить это к задачам, связанным с векторами, есть еще один правило мы можем показать. Рассмотрим параллелограмм 𝐴𝐵𝐶𝐷.

В параллелограмме противоположные стороны параллельны и имеют одинаковую длину; следовательно, 𝐴𝐷=𝐵𝐶𝐴𝐵=𝐷𝐶.and

Мы можем применить правило треугольника для векторов к этой диаграмме, учитывая стороны как векторы и добавление вектора 𝐴𝐶 к диаграмме, как показано.

Применение правила треугольника для векторов к точкам 𝐴, 𝐵 и 𝐶 имеем 𝐴𝐵+𝐵𝐶=𝐴𝐶.

Мы знаем, что 𝐴𝐷=𝐵𝐶 так как они имеют одинаковую величину и направление. Мы можем увидеть это графически как мы можем перевести векторы друг на друга. Подставив это в уравнение дает 𝐴𝐵+𝐴𝐷=𝐴𝐶.

Это известно как правило параллелограмма для векторов. следующее.

Правило: Правило параллелограмма для векторов

Для векторов 𝐴𝐵 и 𝐴𝐷 с той же начальной точкой, 𝐴, 𝐴𝐵+𝐴𝐷=𝐴𝐶, где 𝐶 — точка, из которой 𝐴𝐵𝐶𝐷 параллелограмм, как показано на следующем рисунке.

Поскольку векторы имеют ряд применений, например, в качестве инструмента для оценки равнодействующая сил или для решения геометрических задач треугольник и параллелограмм правила можно рассматривать исключительно с точки зрения области, в которой мы работаем. Однако обычно проще преобразовать проблему в векторы.

Давайте начнем с нескольких примеров сложения векторов. графически.

Пример 1. Нахождение компонентов суммы сквозных векторов на Диаграмма

На сетке единичных квадратов показаны векторы ⃑𝑢 и ⃑𝑣.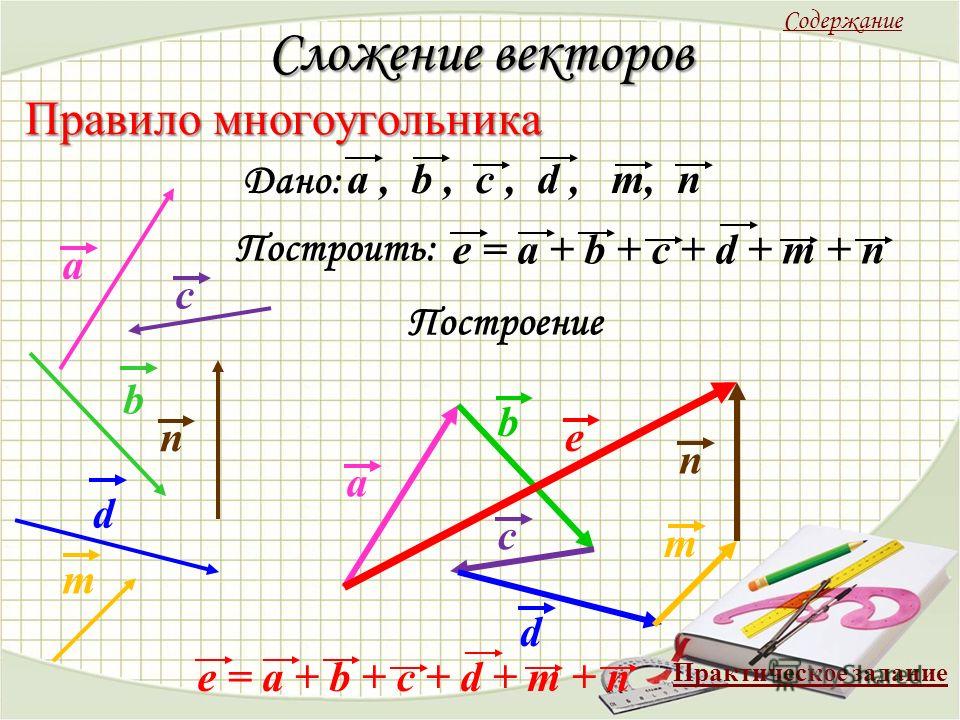

1. Из каких компонентов состоит ⃑𝑢?
2. Из каких компонентов состоит ⃑𝑣?
3. Из каких компонентов состоит ⃑𝑢+⃑𝑣?

Ответ

Часть 1

Напомним, что компоненты вектора, представленного графически, это горизонтальные и вертикальные смещения вектора в этом пространстве. Особенно, для вектора из 𝐴(𝑥,𝑦) к 𝐵(𝑥,𝑦), его компонентами будут разница в координатах: 𝐴𝐵=(𝑥−𝑥,𝑦−𝑦).

Есть несколько способов использовать это для определения компонентов вектора ⃑𝑢. Например, мы могли бы ввести координату систему на сетку единичных квадратов. Однако в этом нет необходимости. Вместо, нам нужно знать только горизонтальные и вертикальные перемещения при движении от начальной точки ⃑𝑢 до конечной точки из ⃑𝑢. Начнем с горизонтального смещение.

Переход от хвоста к вершине вектора ⃑𝑢, мы путешествуем по трем квадратам. Так как это единичные квадраты и мы двигаться вправо, мы можем записать это как смещение +3 единицы.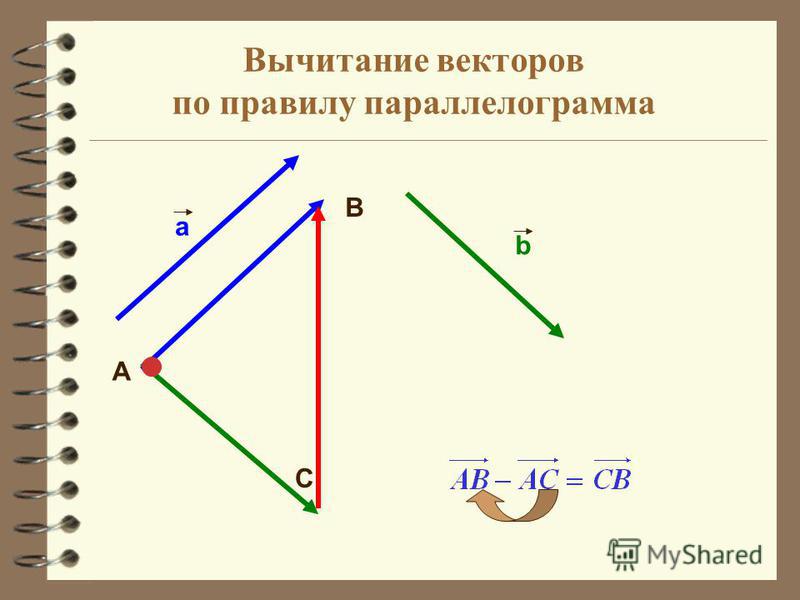

То же самое можно сделать и по вертикали.

Мы перемещаемся на две единицы вверх, поэтому смещение равно +2 единицам. Это дает нам обе компоненты нашего вектора. Помните, нам не нужно включить положительный символ; это дает нам ⃑𝑢=(3,2).

Часть 2

Мы можем выполнить ту же процедуру для вектора ⃑𝑣.

Во-первых, мы видим, что сдвинулись на две единицы вправо, поэтому первый компонент вектор будет равен 2. Мы должны быть осторожны при проверке вертикального смещения вектор; так как мы движемся вниз, значение будет отрицательным.

Путешествие от хвоста к вершине вектора ⃑𝑣, мы перемещаемся на три единицы вниз. Поэтому вертикальная составляющая ⃑𝑣 будет −3. Следовательно, ⃑𝑣=(2,−3).

Часть 3

Есть два метода, которые мы можем использовать для сложения векторов.

Во-первых, мы можем вспомнить, что мы складываем векторы вместе по компонентам, а затем используем наши ответы в первых двух частях вопроса; это дает ⃑𝑢+⃑𝑣=(3,2)+(2,−3)=(3+2,2+(−3))=(5,−1).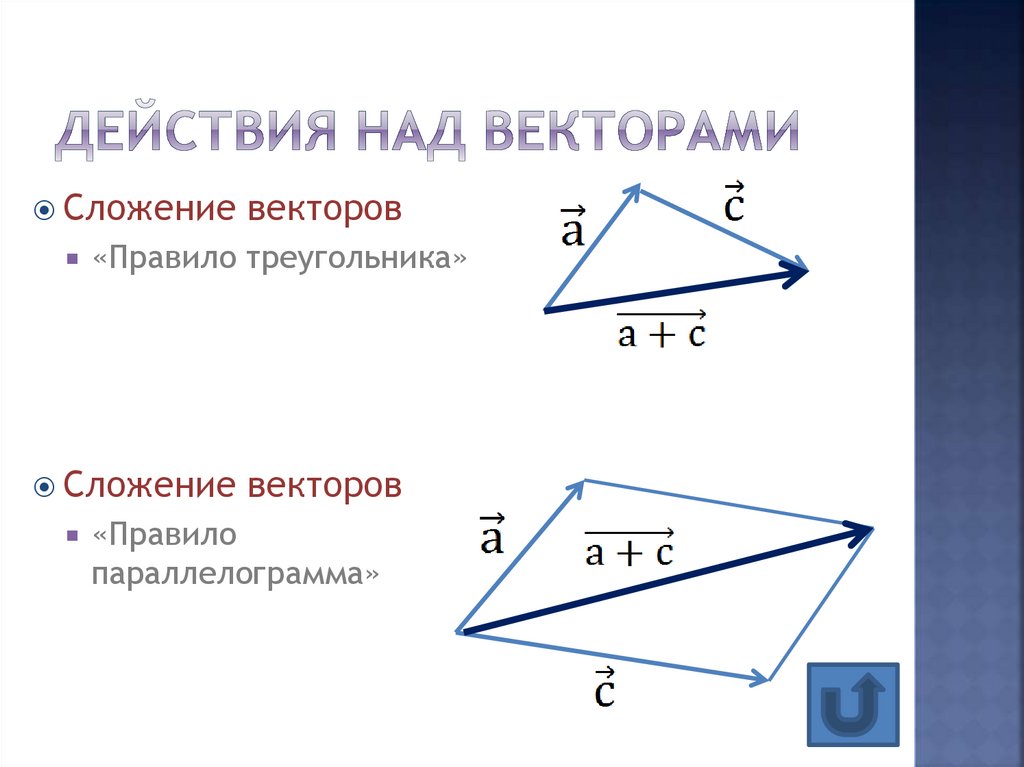

Однако этот результат зависит от того, найдем ли мы компоненты обоих векторов правильно, а затем не допуская ошибок в расчетах. Это становится более проблема, чем больше векторов нас просят сложить вместе. Вместо этого мы также можем добавить два вектора вместе графически.

Поскольку мы складываем компоненты каждого вектора по отдельности, мы можем складывать векторы вместе методом «кончик к хвосту». Нарисуем векторы так, чтобы вершина одного вектора совмещена с хвостом следующего, поэтому сумма векторов — это вектор из начальной точки первого вектора в конечная точка конечного вектора. Так как векторы уже нарисованы в этом образом, мы имеем следующее.

Вектор ⃑𝑢+⃑𝑣 представлена ​​третьей стороной в треугольнике, так как направления ⃑𝑢 и ⃑𝑣 совпадают. Затем мы можем найти компоненты ⃑𝑢+⃑𝑣 используя схему.

По вектору ⃑𝑢+⃑𝑣, мы перемещаемся на 5 единиц вправо и на 1 единицу вниз, поэтому горизонтальная составляющая равна 5, а вертикальная составляющая равна −1, что дает нам ⃑𝑢+⃑𝑣=(5,−1).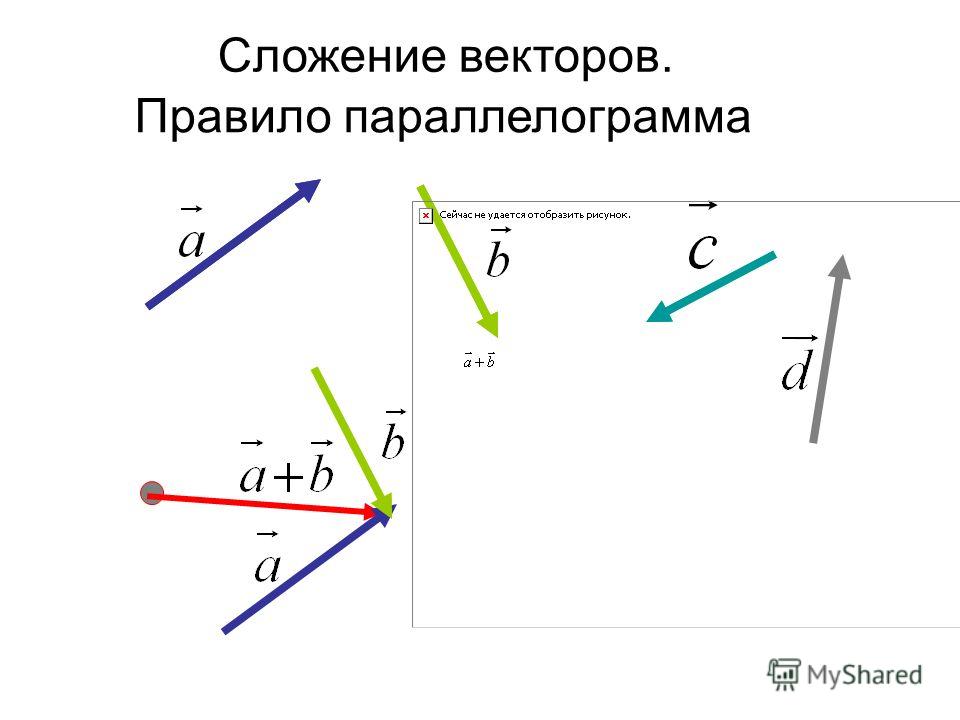

Мы видим, что это согласуется с прямым вычислением, которое мы сделали выше.

Пример 2. Нахождение суммы двух векторов, заданных графически

Какой график представляет ⃑𝐴+⃑𝐵, где ⃑𝐴=(3,4) и ⃑𝐵=(4,1)?

Ответ

Так как нам даны компоненты ⃑𝐴 и ⃑𝐵, мы можем складывать векторы покомпонентно получить ⃑𝐴+⃑𝐵=(3,4)+(4,1)=(3+4,4+1)=(7,5).

Глядя на варианты, мы видим, что единственный вариант A имеет ⃑𝐴=(3,4), ⃑𝐵=(4,1), и ⃑𝐴+⃑𝐵=(7,5), так что это правильный ответ. Проблема с таким ответом на вопрос состоит в том, что мы часто просят сложить векторы вместе графически, не давая вариантов, поэтому схему тоже построим сами.

Мы можем начать с рисования векторов ⃑𝐴=(3,4) и ⃑𝐵=(4,1) на диаграмму, где мы помним, что первая компонента сообщает нам горизонтальное смещение, а второй компонент говорит нам о вертикальном смещение.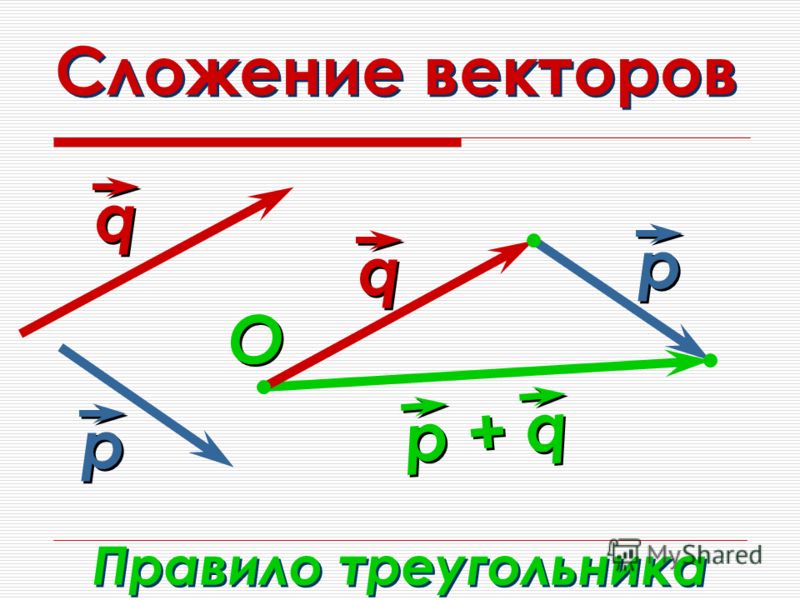 Также стоит отметить, что мы можем зарисовывать векторы в любом месте. на самолете. Однако для простоты мы начнем оба вектора с источник. Во-первых, ⃑𝐴=(3,4) переместится на 3 единицы вправо и на 4 единицы вверх, чтобы дать нам следующее.

То же самое можно сделать с вектором ⃑𝐵=(4,1), который переместится на 4 единицы вправо и на 1 единицу вверх, как показано на рисунке.

Стоит отметить, что поскольку мы начали наши векторы с начала координат, координаты конечных точек будут равны соответствующим компоненты вектора; их часто называют векторами положения.

Чтобы сложить эти два вектора вместе графически, мы начнем с их эскиза. так что конечная точка одного вектора является начальной точкой другого. Мы переместим ⃑𝐵 так, чтобы его начальная точка находилась в (3,4); он все равно переместится на 4 единицы вправо и 1 единицу вверх, что дает нам следующее.

Наконец, правило треугольника для векторов говорит нам, что сумма этих двух векторами будет вектор, имеющий начальную точку ⃑𝐴 и конечная точка ⃑𝐵 так как эти векторы нарисованы хвост, что дает нам следующее.

На диаграмме видно, что ⃑𝐴+⃑𝐵 перемещается на 7 единиц вправо и на 5 единиц вверх, поэтому ⃑𝐴+⃑𝐵=(7,5), и это показано в варианте A.

В наших предыдущих примерах мы использовали графические представления наряду с их компоненты для решения проблем. В нашем следующем примере мы будем использовать только графический представление векторов для решения геометрической задачи.

Пример 3. Определение правильной диагонали в законе параллелограмма

Какой вектор эквивалентен ⃑𝑢+⃑𝑣?

Ответ

Четырехугольник 𝐴𝐶𝐷𝐵 имеет противоположные стороны как равные векторы. Поскольку равные векторы имеют одинаковую величину и направление, мы можем сделать вывод что 𝐴𝐶𝐷𝐵 является параллелограммом. Мы хотим применить правило параллелограмма для векторов, чтобы сложить эти векторы. Для этого замечаем что ⃑𝑣 — это вектор из 𝐴 в 𝐶, поэтому ⃑𝑣=𝐴𝐶.

Аналогично, ⃑𝑢=𝐴𝐵.

Правило параллелограмма для сложения векторов говорит нам, что если 𝐴𝐶 и 𝐴𝐵 имеют одинаковую начальную точку, 𝐴, тогда 𝐴𝐶+𝐴𝐵=𝐴𝐷, где 𝐷 — точка, которая делает 𝐴𝐶𝐷𝐵 параллелограмм. Вектор 𝐴𝐷 — диагональ параллелограмма показано.

Следовательно, ⃑𝑢+⃑𝑣=𝐴𝐷.

Используя приведенный выше пример, мы можем показать полезный результат для параллелограмма, который мы построен.

Применяя правило треугольника для векторов в точках 𝐴, 𝐶 и 𝐷 имеем 𝐴𝐶+𝐶𝐷=𝐴𝐷.

В пересчете на ⃑𝑢 и ⃑𝑣, это говорит о том, что ⃑𝑣+⃑𝑢=⃑𝑢+⃑𝑣.

Другими словами, это геометрическая демонстрация коммутативности вектора добавление.

До сих пор мы рассматривали только совместное сложение векторов. Мы сейчас рассмотрим пример, где нас просят найти разность двух векторов.

Пример 4. Определение правильного графического представления разности двух Векторы

Какой из следующих параллелограммов показывает допустимый способ получения ⃑𝐴−⃑𝐵?

Ответ

Чтобы вычесть два вектора графически, мы будем использовать два результата. Во-первых, мы можем перепишем выражение в виде суммы двух векторов: ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵.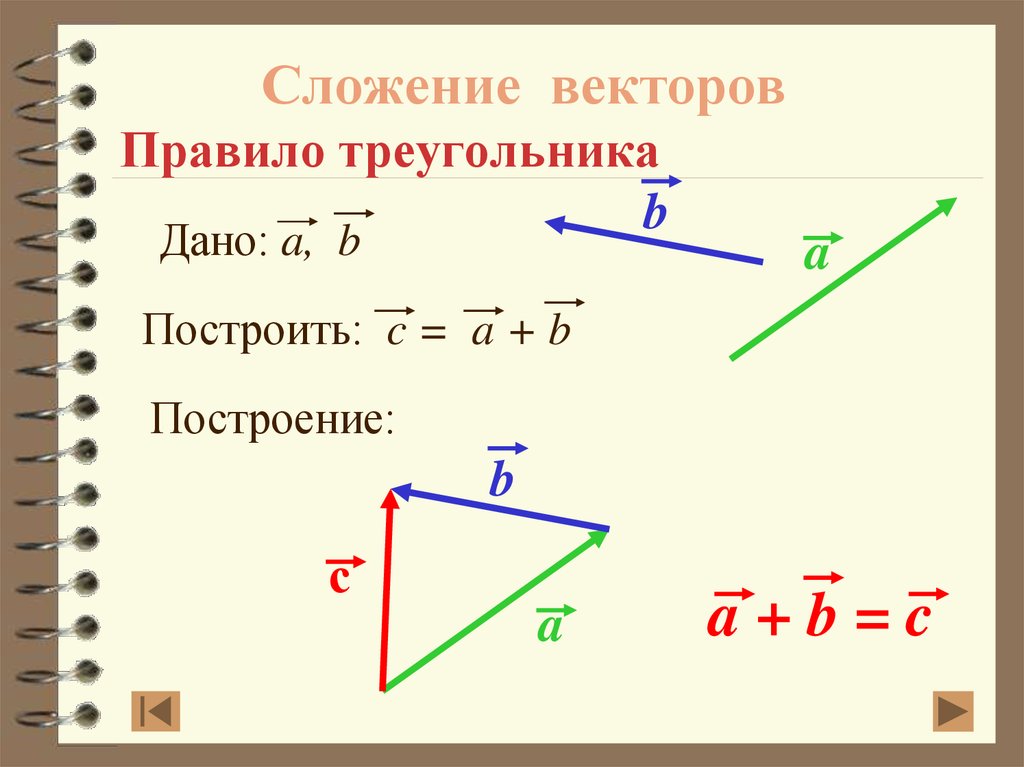

Это говорит нам о разнице между ⃑𝐴 и ⃑𝐵 равно сумме ⃑𝐴 и −⃑𝐵, и мы знаем, как графически складывать векторы, используя оба треугольника и правила параллелограмма. Поскольку в опции включены параллелограммы, мы будем использовать правило параллелограмма.

Правило параллелограмма для сложения векторов говорит нам, что если 𝑃𝑄 и 𝑃𝑆 — векторы с одинаковой начальной точкой, 𝑃, тогда 𝑃𝑄+𝑃𝑆=𝑃𝑅, где 𝑅 — точка, из которой 𝑃𝑄𝑅𝑆 параллелограмм, как показано на следующем рисунке.

Если обозначить векторы, являющиеся сторонами параллелограмма, ⃑𝐴 и −⃑𝐵 имеем следующее.

Тогда, поскольку ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵, мы можем заменить вектор на диагонали с ⃑𝐴−⃑𝐵, то же, что вариант C.

Тогда мы можем задать следующий вопрос: даны два вектора ⃑𝐴 и ⃑𝐵, графически, как мы можем найти ⃑𝐴−⃑𝐵? Сделать это, мы начнем с наброска ⃑𝐴 и ⃑𝐵 иметь одну и ту же начальную точку, скажем 𝑃; мы также пометим конечные точки векторов 𝑄 и 𝑅, как показано.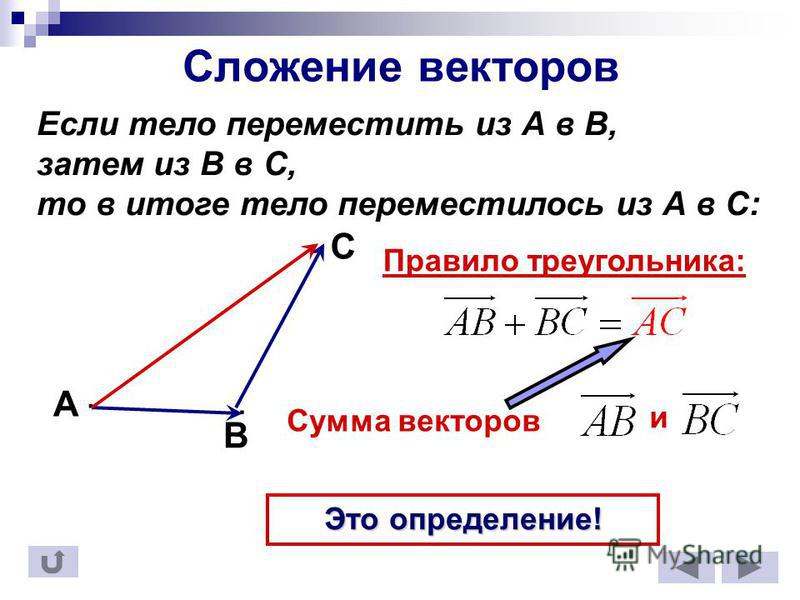

Мы хотим определить ⃑𝐴−⃑𝐵=𝑃𝑅−𝑃𝑄. Напомним, что ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵 и что умножение вектора на -1 меняет его направление и делает не изменить свою величину. На нашей диаграмме это означает −⃑𝐵 это вектор от 𝑄 до 𝑃, как показано.

Тогда мы можем видеть, что конечная точка −⃑𝐵 является начальной точкой ⃑𝐴, поэтому мы можем добавить эти векторов с использованием правила треугольника для сложения векторов; имеем следующее.

Затем мы можем использовать коммутативность сложения векторов для записи −⃑𝐵+⃑𝐴=⃑𝐴−⃑𝐵. Это означает 𝑃𝑅−𝑃𝑄=𝑄𝑅.

Затем мы можем представить это графически, как показано на рисунке.

Давайте теперь посмотрим на несколько примеров применения этого рассуждения для вычитания двух вектора заданы графически.

Пример 5. Нахождение разности двух векторов, представленных графически

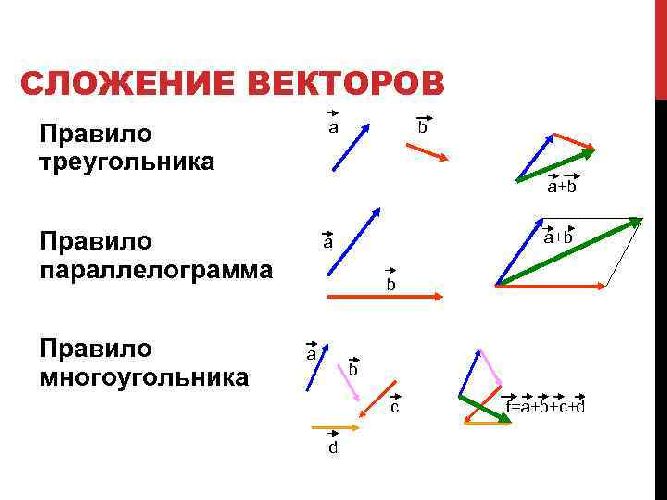
Что из следующего эквивалентно 𝐴𝐵−𝐷𝐵?

1.  40052
2.  𝐷𝐶
3.  40052
4.  40052
5. 𝐵𝐶

Ответ

. Мы просят найти разницу двух векторов. Для этого начнем с отметив, что умножение вектора на -1 меняет его направление но оставляет величину неизменной, поэтому −𝐷𝐵=𝐵𝐷.

Следовательно, 𝐴𝐵−𝐷𝐵=𝐴𝐵+𝐵𝐷.

Мы можем нарисовать оба этих вектора на диаграмме.

Поскольку конечная точка 𝐴𝐵 является начальной точки 𝐵𝐷, мы можем сложить эти векторы, используя правило треугольника для сложения векторов, которое говорит нам 𝐴𝐵+𝐵𝐷=𝐴𝐷, что мы можем показать на схеме.

Однако это не один из предложенных вариантов. Нам также необходимо использовать факт что 𝐴𝐵𝐶𝐷 — параллелограмм, у которого противоположные стороны одинакового размера и параллельны. Следовательно, 𝐴𝐷=𝐵𝐶.

Следовательно, ответ — вариант E, 𝐵𝐶.

Пример 6. Решение геометрической задачи с использованием векторов в качестве сторон параллелограмма

Что из следующего эквивалентно 12𝐶𝐵−𝐷𝐶?

1.  40052
2. 𝐶𝐸
3. 𝐵𝐸
4.  40052
5. 𝐸𝐶

Ответ

Мы хотим определить вектор эквивалент к данному выражению с помощью использования с использованием с помощью диаграмма.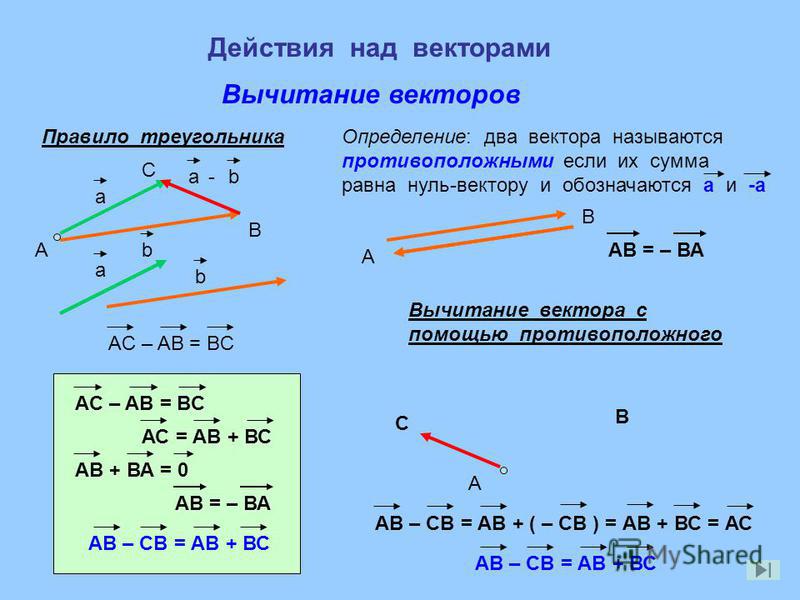 Для этого сначала заметим, что для вектора ⃑𝑢, 12⃑𝑢 будет иметь то же направление, но вдвое меньше. Итак, мы начнем с нахождение вектора, эквивалентного 𝐶𝐵−𝐷𝐶. Мы можем сделать это, сначала вспомнив, что −𝐷𝐶=𝐶𝐷, поэтому 𝐶𝐵−𝐷𝐶=𝐶𝐵+𝐶𝐷.

Мы можем добавить эти векторы на диаграмму.

Чтобы сложить векторы вместе графически, мы можем использовать правило параллелограмма для векторы. Поскольку начальные точки обоих векторов одинаковы, их сумма будет диагональю параллелограмма.

Следовательно, 𝐶𝐵−𝐷𝐶=𝐶𝐵+𝐶𝐷=𝐶𝐴.

Мы хотим найти 12 таких векторов, поэтому нам нужен вектор в том же направлении, что и 𝐶𝐴 но с половинной величиной. Так как 𝐸 является серединой 𝐶𝐴, для этого есть два варианта; как 𝐶𝐸, так и 𝐸𝐴 будет иметь то же направление, что и 𝐶𝐴, но вдвое меньше.

Следовательно, 12𝐶𝐵−𝐷𝐶=12𝐶𝐵+𝐶𝐷=12𝐶𝐴=𝐶𝐸.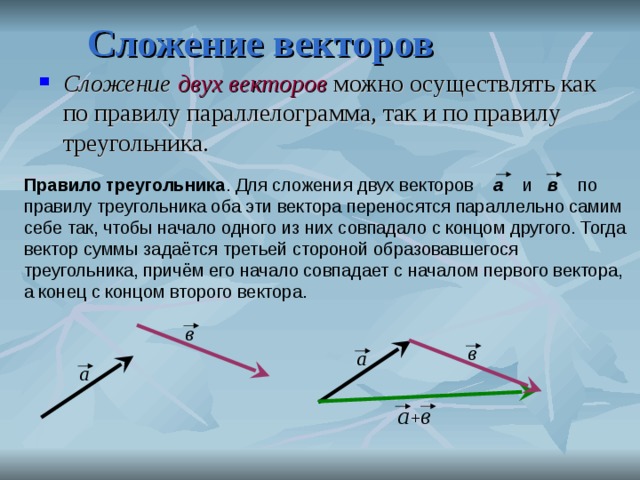

Итак, ответ вариант Б, 𝐶𝐸.

Стоит отметить, что мы можем применить эти правила для кратного сложения векторов раз. Например, рассмотрим следующую схему.

Если мы хотим найти 𝐴𝐵+𝐵𝐶+𝐶𝐷, мы можем сделать это, применив треугольник правило сложения векторов дважды. Во-первых, у нас есть 𝐴𝐵+𝐵𝐶=𝐴𝐶, как показано на следующей диаграмме.

Затем мы можем добавить 𝐴𝐶 и 𝐶𝐷 с правилом треугольника для сложения векторов. У нас есть 𝐴𝐶+𝐶𝐷=𝐴𝐷, как показано.

Следовательно, 𝐴𝐵+𝐵𝐶+𝐶𝐷=𝐴𝐷.

Графически мы можем представить это как три вектора 𝐴𝐵, 𝐵𝐶, и 𝐶𝐷 все нарисованы от кончика к хвосту, поэтому их сумма равна вектор, который имеет начальную точку 𝐴 и конечную точку 𝐷. Мы можем применить те же рассуждения к еще более сложным формы, как мы увидим в нашем последнем примере.

Пример 7. Упрощение суммы векторов, являющихся сторонами многоугольника

Завершено: На следующем рисунке 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=.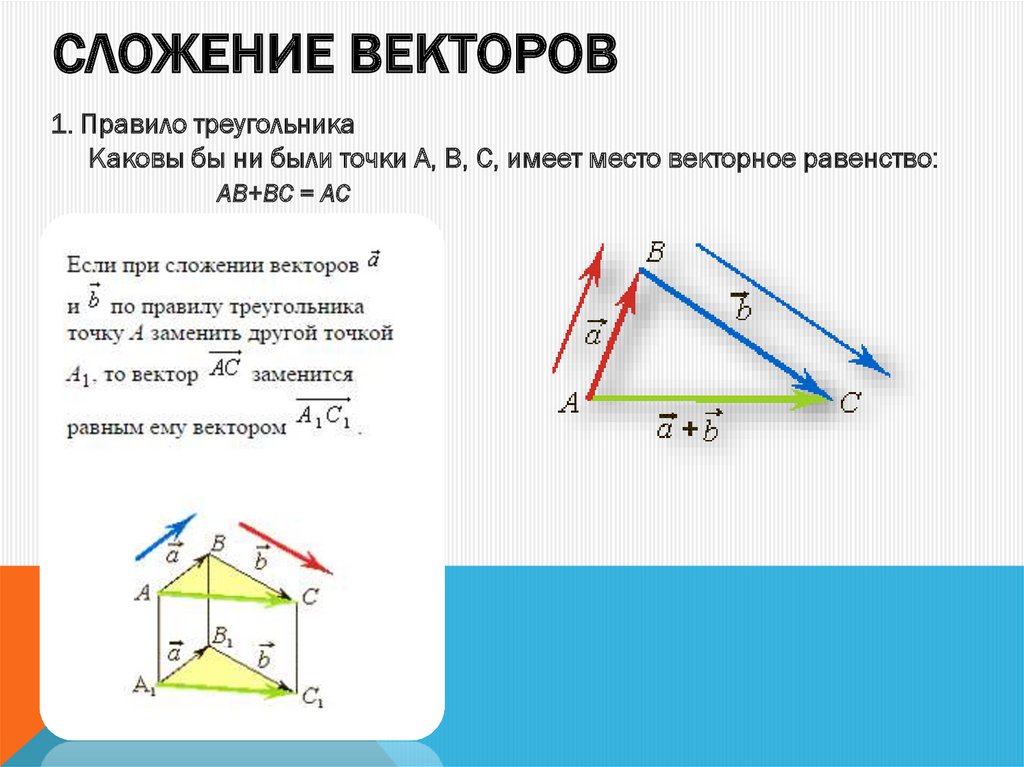

1.  40052
2.  40052
3.  40052
4. 2 40052
5. 2𝐵𝐸

Ответ

Мы начнем с добавления всех векторов в сумму на диаграмму.

Есть два способа определить эту сумму: мы можем сделать это непосредственно с помощью напоминая, что сумма любого количества векторов, проведенных от кончика к хвосту, будет иметь начальная точка первого вектора и конечная точка конечного вектор. На нашей диаграмме это будет вектор 𝐴𝐸 как показано.

Легче думать об этом как о следовании векторам из 𝐴 вплоть до 𝐸. У нас есть 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐸, который является вариантом B.

Чтобы понять, почему это так, нам нужно применить правило треугольника, которое гласит что для любых точек 𝑃, 𝑄, и 𝑅, 𝑃𝑄+𝑄𝑅=𝑃𝑅.

Мы можем применить это к первым двум векторам в сумме, чтобы получить 𝐴𝐵+𝐵𝐶=𝐴𝐶, так 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐶+𝐶𝐷+𝐷𝐸.

Затем мы можем снова применить правило треугольника и увидеть, что 𝐴𝐶+𝐶𝐷=𝐴𝐷, так 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐷+𝐷𝐸.

Наконец, мы применяем правило треугольника еще раз, чтобы получить 𝐴𝐷+𝐷𝐸=𝐴𝐸, и поэтому 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐸.

Следовательно, ответ — вариант Б, 𝐴𝐸.

Давайте закончим, повторив некоторые важные моменты этого объяснитель.

Ключевые точки

• Правило треугольника для векторов говорит нам, что для любых трех точек 𝐴, 𝐵 и 𝐶, 𝐴𝐵+𝐵𝐶=𝐴𝐶.
• Правило треугольника для векторов позволяет нам складывать два вектора графически, рисуя их так, что начальная точка одного вектора является конечной точкой другого.
• Правило параллелограмма для векторов говорит нам, что 𝐴𝐵+𝐴𝐷=𝐴𝐶, где 𝐶 — точка, из которой 𝐴𝐵𝐶𝐷 параллелограмм.
• Правило параллелограмма для векторов позволяет нам складывать векторы графически, рисуя их так, чтобы они имели одну и ту же начальную точку. Тогда их результирующая будет задается диагональю параллелограмма, натянутого на векторы.
• Мы можем вычесть два вектора, используя тот факт, что для любых трех точек 𝑃, 𝑄 и 𝑅, 𝑃𝑅−𝑃𝑄=𝑄𝑅.

Векторов

Вектор – это величина, заданная величиной плюс направление в пространстве

Свойства векторов

Любой вектор однозначно определяется тремя его компонентами x, y, z, которые являются проекциями вектора на координатные оси с единичными векторами (такими, что )

Обозначение вектора с координатами имеет вид

 это

Величина вектора  (или его длина) определяется теоремой Пифагора

|| =

Добавление векторов

Сложение векторов   и  является вектором суммы

 

Суммарный вектор определяется Правилом сложения параллелограмма

Величина вектора суммы определяется законом косинусов

где:

 и  являются величинами векторов  и

 это угол между ними

Компоненты вектора суммы:

х = х ₁ + х ₂

у = у ₁ + у ₂

z = z ₁ + z ₂

Правило сложения параллелограмма является частным случаем общего Правила многоугольника , используемого для сложения нескольких векторов

Вычитание векторов

Вычитание векторов   и   является разностью векторов

 

Разность векторов определяется методом вычитания треугольников

Величина разности векторов

Компоненты разности векторов:

х = х ₁ — х ₂

у = у ₁ — у ₂

z = z ₁ — z ₂

Скалярное произведение

Скалярное (или точечное) произведение векторов и — это скалярная величина, определяемая числом

.