векторы на основе наноматериалов

векторы на основе наноматериалов иначе наноконтейнеры для направленной доставки веществ (англ. nanomaterial-based vectors) — наноразмерные устройства для направленной доставки биологически активных веществ в клетки.

Описание

В биологии и медицине термином «вектор» обозначают переносчик. В генной инженерии плазмидная ДНК или вирусная ДНК и РНК служат векторами для переноса клонированных в них генов в целевые клетки. В фармакологии вектор — это устройство или молекула для направленной доставки лекарственных веществ. Основная задача вектора — обеспечить поступление биологически активных соединений (лекарств, токсинов, белков, олигонуклеотидов, генов и т.д.) в целевые клетки организма, в том числе в требуемый внутриклеточный компартмент (ядро, цитоплазма, органеллы), в очаг патологического поражения, одновременно предотвращая инактивацию и проявление биологической активности этих веществ до накопления в заданной области.

В общем виде в состав вектора входит наноконтейнер, в который упаковывают терапевтические субстанции, и система адресной доставки, расположенная на внешней поверхности наноконтейнера. В ряде случаев (наноконъюгаты, «двуликие» частицы, наносомы, многофункциональные наночастицы в медицине) эту систему адресной доставки (особенно при молекулярном конструировании в биофармакологии) также называют вектором. В качестве наноматериалов для создания векторов используют наночастицы из биосовместимых линейных полимеров (полиэтиленгликоль, полимолочная кислота и др.) и ветвящихся полимеров (дендримеров), липосомы, а также вирусные частицы, лишенные способности к размножению. Изучаются перспективы использования для этих целей фуллеренов, нанотрубок и других небиологических нанообъектов, модифицированных для придания им биосовместимости. Одним из вариантов такой модификации является ПЭГилирование, т. е. покрытие наночастиц оболочкой из полиэтиленгликоля (ПЭГ). Для адресации наноконтейнеров их модифицируют молекулами, узнающими поверхностные рецепторы клеток-мишеней, например, антителами к этим рецепторам, молекулами фолиевой кислоты и др.

Предложены векторные системы доставки лекарств без наноконтейнеров, в которых адресная молекула непосредственно прикрепляется к лекарственному веществу. Так, с помощью генно-инженерных технологий создана гибридная молекула, состоящая из антитела к рецептору ферритина на поверхности клеток и биотин-связывающего белка авидина. Доставляемые вещества химически биотинилируют (модифицируют биотином), и они прочно связываются с авидином. Затем такие комплексы доставляются к клеткам, в частности, к клеткам центральной нервной системы путем активного транспорта через эндотелий капилляров мозга.

В некоторых органах (печень, легкие, селезенка) возможно достичь повышенного накопления наноконтейнеров с лекарствами даже без применения специфической адресации. Это связано с естественной барьерной функцией этих органов. Накопление также происходит в опухолях, которые кровоснабжаются высокопроницаемыми микрососудами, в результате чего даже крупные молекулы и частицы из крови легко переходят в межклеточное пространство. Однако разница в степени накопления терапевтических агентов в опухоли и в здоровой ткани зачастую невелика, поэтому в большинстве случаев требуется разработка высокоспецифичных адресных молекул или других методов наведения, чтобы сделать векторы высокоточными «магическими пулями».

Иллюстрации

Варианты наноконтейнеров для упаковки лекарственных веществ. Оборудование их системой адресной доставки превращает их в векторы.

Автор

• Ширинский Владимир Павлович

Источники

1. Rajesh S., James W., Lillard Jr. Nanoparticle-based targeted drug delivery // Experimental and Molecular Pathology. 2009. V. 86. P. 215–223.
2. Kaparissides C., Alexandridou S., Kotti K., Chaitidou S. Recent Advances in Novel Drug Delivery Systems // J. Nanotechnology Online, 2006. —www.azonano.com/Details.asp?ArticleID=1538

Напишите нам

• А
• Б
• В
• Г
• Д
• Ж
• З
• И
• К
• Л
• М
• Н
• О
• П
• Р
• С
• Т
• У
• Ф
• Х
• Ц
• Ч
• Ш
• Э
• Я

• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Z

Лекция Векторная алгебра.

Векторы.

    Скачать с Depositfiles 

ВЕКТОРНАЯ АЛГЕБРА

Лекция № 4. Тема 1 : Векторы

1.1. Определение вектора

Все величины, с которыми нам приходилось встречаться до настоящего времени в физике, технике были двух видов: скалярные, которые харак-теризуются одним числовым значением и векторные,  характеризуются числовым значением и направлением.

Пример 1. Скалярные величины: масса, объём, температура и т.д. Векторные величины: сила, скорость, ускорение и т. д.

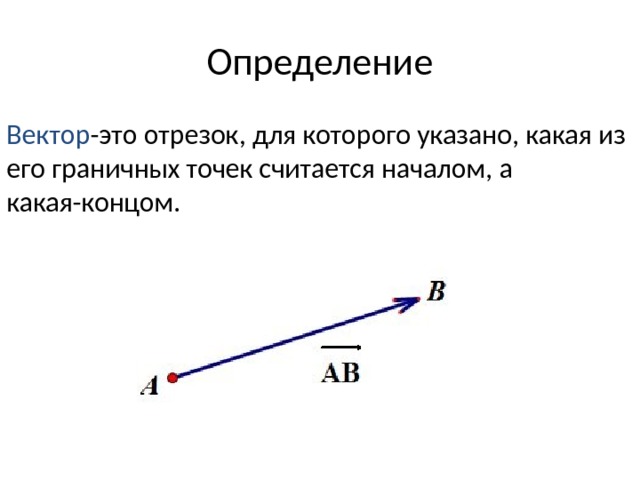
Определение 1. Направленный отрезок называется вектором и обозна-чается .А

В

Определение 2. Расстояние между началом и концом вектора называется его длиной или модулем и обозначается 

Если  или , то векторы называются соответственно единичным и нулевым.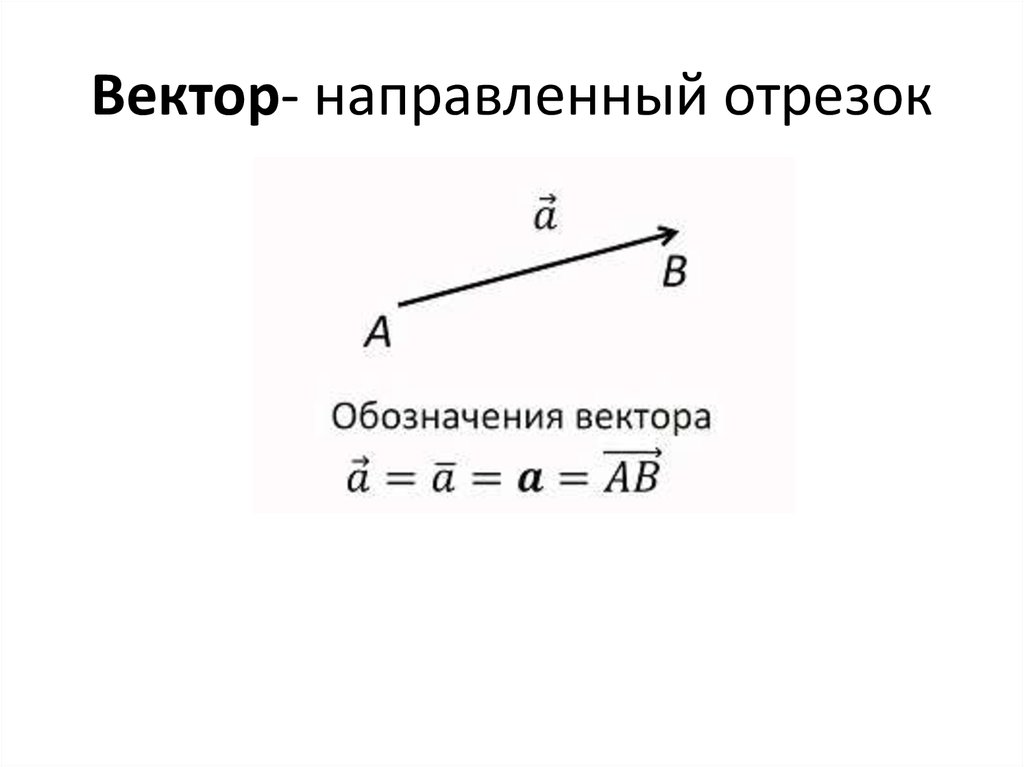

Определение 3. Векторы называются коллинеарными, если существует прямая, которой они параллельны.

Определение 4. Векторы называются компланарными, если существует плоскость, которой они параллельны.

Определение 5. Два вектора называются равными, если они коллине-арные, одинаково направлены и имеют равные модули (равные длины).

Пусть задан некоторый вектор  и ось l.

Определение 6. Проекцией вектора  на ось l называется величина  где   угол между вектором  и осью l.

В

А

l

1.2. Линейные операции над векторами

1. Произведение вектора на число.

Определение 7. Произведением вектора  на число  называется вектор  определяемый следующими условиями: вектор  коллинеарен вектору векторы  и  одинаково направлены, если  и противоположны, если 

Пример 2. Построить вектор  

Из этого определения следует условие коллинеарности двух векторов:

Пусть  ненулевой вектор, тогда для любого коллинеарного ему вектора  существует единственное число  удовлетворяющее равенству 

Действительно,  если векторы одинаково направлены и  если они противоположно направлены.

2. Сложение векторов.

Определение 8. Суммой двух векторов  и  называется вектор  выходящий из их общего начала, который служит диагональю паралле-лограмма, сторонами которого являются векторы  и , и обозначается

 

 или 

Второй способ построения суммы двух векторов легко распространить на любое число слагаемых. В результате получаем, так называемое правило многоугольника:

Чтобы построить сумму векторов, нужно в конце первого вектора построить второй, в конце второго – третий и т.д. Вектор, соединяющий начало первого с концом последнего и представляет собой искомую сумму.

 

  

С помощью рисунков легко убедиться в справедливости следующих свойств:

1.  сложение коммутативно;

2.  ассоциативно.

3. Вычитание векторов.

Определение 9. Вектор, коллинеарный данному вектору , равный ему по модулю и противоположно направленный, называется противоположным вектором и обозначается 

Определение 10. Разностью  векторов  и  называется сумма векторов  и  т.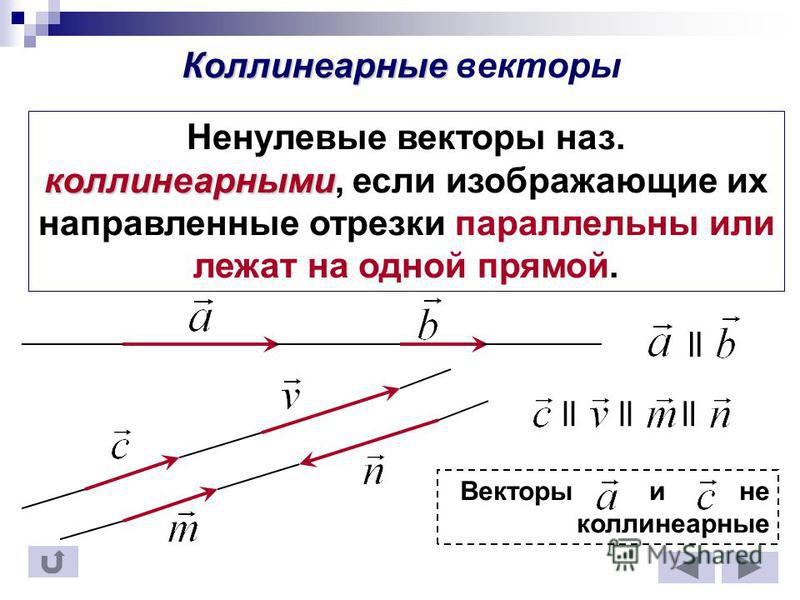 е. 

Построение вектора   

основано на построении суммы 

векторов   

Замечание 1. Из определений 6 и 8 геометрически весьма просто показать следующие свойства:

1. 

2. 

1.3. Декартова система координат

Зададим в пространстве три единичных взаимно перпендикулярных вектора:  Приведём их к общему началу – точке О. Рассмотрим систему координат, направление осей: z

Ох, Оу, Оz, которой заданы этими

векторами  Такая система

координат называется декартовой M

системой координат. Векторы  

называются базисом, а каждый из 

этих векторов – ортом.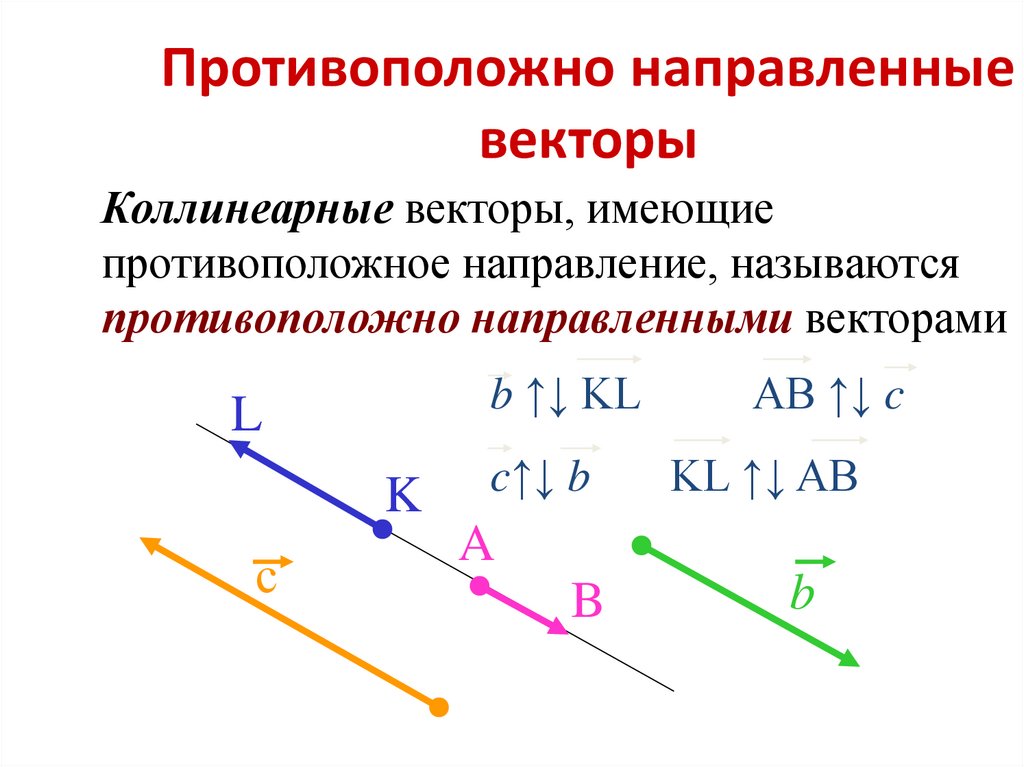    y

Покажем, что если задан базис O B

, то любой вектор  A N

пространства можно единственным x

образом разложить по нему, т.е. представить в виде

 (1)

Приведём вектор  к началу системы координат – точке О. Из конца вектора   точки М опустим перпендикуляр MN на плоскость Оху. Проведём из точки Nпрямые, параллельные осям координат. Построим векторы  Из построения получаем

 (2)

А так как  то выражение (2) примет следующий вид

 (3)

В силу коллинеарности векторов  и   и   и  существуют такие числа , для которых выполняется

 (4)

Тогда формула (3) с учетом (4) принимает вид (1), что и требовалось доказать. Единственность разложения легко доказать от противного.

Сокращенно формула (1) записывается в виде 

Определение 11. Числа  называются координатами вектора  или его компонентами.

Используя соотношение (1), легко доказать следующие теоремы:

Теорема 1. Если  и , то их сумма

Теорема 2. Если  и   любое число, то произведение вектора  на это число 

Следствие. Если векторы  и  коллинеарны, то    и тогда условие коллинеарности векторов имеет вид

  (6)

Определение 12. Радиус-вектором точки М z

называется вектор  М

Определение 13. Координаты радиус–вектора 

точки М называются координатами точки М

и при этом пишут  x O y

Замечание 2.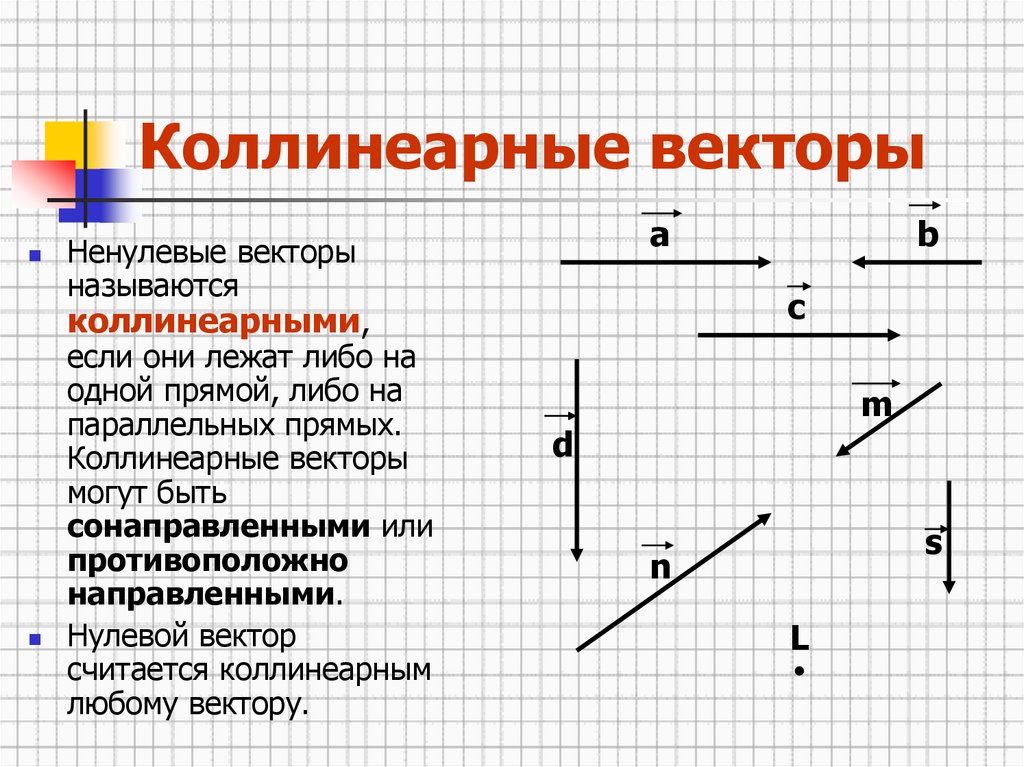  Аналогично определяется система координат на плоскости Оху. Здесь образуют базис векторы  и , а оси  Ох и Оу. Тогда получим

.

Замечание 3. Из доказательства формулы (1) следует, что геометрически координаты вектора – суть его проекции на соответствующие координатные оси.

Замечание 4. Аналогично можно показать, что базис в пространстве образуют любые три некомпланарных вектора:  т.е. любой вектор  можно представить в виде 

Объяснение урока: Параллельные и перпендикулярные векторы в пространстве

В этом объяснении мы научимся распознавать параллельные и перпендикулярные векторы в пространстве.

Вектор в пространстве определяется двумя величинами: величиной и направлением. Особые отношения формируются между двумя или более векторами когда они указывают в одном направлении или в противоположных направлениях. В этом случае говорят, что векторы параллельны.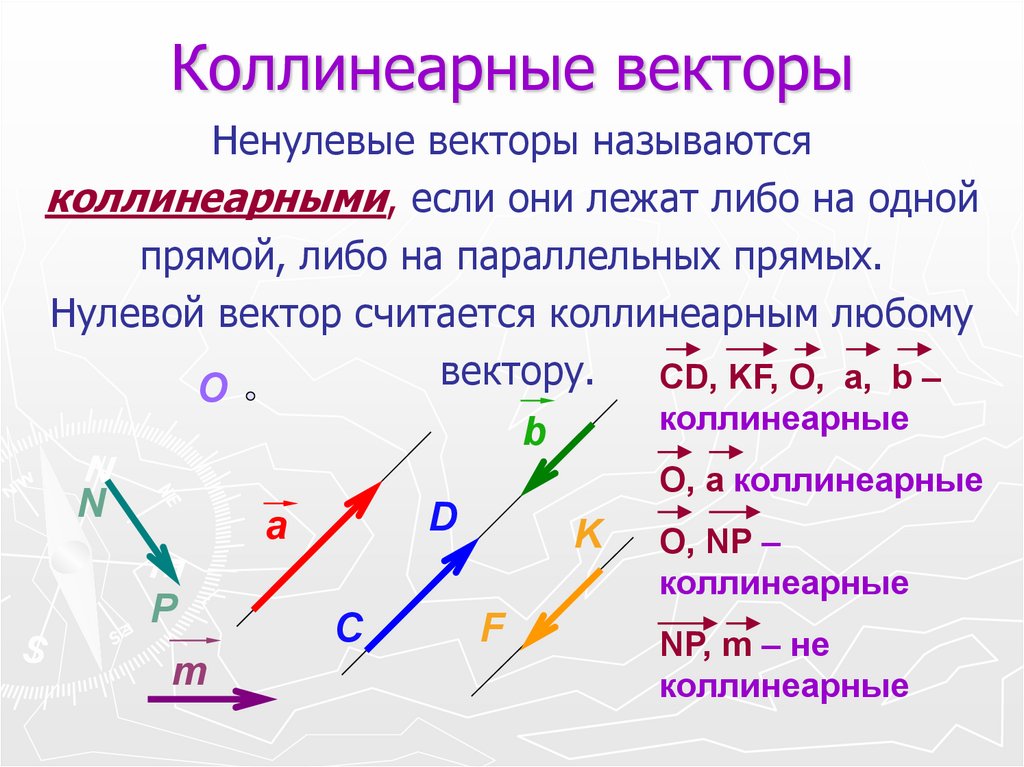 Это может быть представлен математически.

Определение: параллельные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 параллельны тогда и только тогда, когда они скалярны. кратны друг другу: ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевое действительное число.

Другой способ думать об этом состоит в том, что если два вектора параллельны, то отношения каждого из их соответствующих компоненты одинаковые. Итак, если у нас есть два вектора ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, то 𝑎𝑏=𝑎𝑏=𝑎𝑏.

Второе особое отношение, которое может возникнуть между двумя векторами, — это когда направления двух векторов образуют 9угол 0∘. Когда это происходит, мы говорим, что два вектора перпендикулярны друг другу. Чтобы определить, когда два вектора перпендикулярны, мы можем использовать скалярное произведение.

Определение: скалярное произведение

Скалярные произведения двух векторов, ⃑𝐴 и ⃑𝐵, можно определить как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖𝜃, потому что где 𝜃 — угол, образованный между ⃑𝐴 и ⃑𝐵.

В случае, когда векторы ⃑𝐴 и ⃑𝐵 перпендикулярны, 𝜃=90∘. Следовательно, cos𝜃=0, а значит, ⃑𝐴⋅⃑𝐵=0.

Примечание:

Когда два вектора параллельны, угол между ними равен 0∘ или 180∘.

Другой способ определения скалярного произведения двух векторов ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 находится по формуле ⃑𝐴⋅⃑𝐵=𝑎𝑏+𝑎𝑏+𝑎𝑏.

Конечно, если векторы перпендикулярны, то эта сумма произведений соответствующих компонент будет равна нулю: 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.

Определение: перпендикулярные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ⃑𝐴⋅⃑𝐵=0.

Давайте теперь рассмотрим несколько примеров с параллельными и перпендикулярными векторами.

Пример 1. Использование свойств параллельных и перпендикулярных векторов для решения задачи

Верно или неверно: если составляющая вектора в направлении другого вектора равна нулю, то они параллельны.

Ответ

Чтобы наглядно представить, что здесь происходит, начнем с рассмотрения двух векторов, ⃑𝐴 и ⃑𝐵. Это могут быть любые два произвольных вектора. Предположим, что эти векторы начинаются в одной и той же точке. Вот как они могут выглядеть.

Теперь добавим компонент ⃑𝐴 в направлении ⃑𝐵.

Используя эту диаграмму вместе с некоторой правой тригонометрией, мы можем видеть, что величина компонента ⃑𝐴 в направлении ⃑𝐵 можно рассчитать, используя ‖‖⃑𝐴‖‖𝜃cos.

В вопросе указано, что эта величина должна быть равна нулю. С ‖‖⃑𝐴‖‖≠0, cos𝜃 должен быть равен нулю. Решение это для 𝜃 дает нам 𝜃=90.∘

Это говорит нам о том, что когда компонент ⃑𝐴 в направлении ⃑𝐵 равен 0, угол между векторами должен быть прямым. Следовательно, ⃑𝐴 и ⃑𝐵 перпендикулярны друг другу.

Наше решение вопроса — «Ложь»: если составляющая вектора в направлении другого вектора равна нулю, то они не параллельны.

Еще один способ решить эту задачу — изобразить два параллельных вектора, как показано на рисунке.

Поскольку векторы ⃑𝐴 и ⃑𝐵 параллельны, угол между двумя векторами 𝜃=0∘. Следовательно, составляющая ⃑𝐴 в направлении ⃑𝐵 есть ‖‖⃑𝐴‖‖(0)cos∘. С cos(0)=1∘, эта компонента есть просто вектор ⃑𝐴. ⃑𝐴 отличен от нуля; следовательно, ответ на вопрос должен быть «Неверно».

В следующем примере мы найдем недостающие параметры, чтобы два заданных вектора были параллельны.

Пример 2. Поиск пропущенного значения с помощью пары параллельных векторов

Найдите значения 𝑚 и 𝑛 так, чтобы вектор 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘 параллелен вектору 6⃑𝑖+𝑛⃑𝑗−21⃑𝑘.

Ответ

Чтобы решить эту задачу, мы можем использовать тот факт, что когда два вектора параллельны друг другу, они скалярно кратны друг другу. Поэтому, 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘=𝑐6⃑𝑖+𝑛⃑𝑗+21⃑𝑘, где 𝑐 — это просто константа, которую можно найти.

Приравнивая коэффициенты каждой из компонент вектора, мы получаем три уравнения: 2=6𝑐,7=𝑐𝑛,𝑚=−21𝑐.

Мы можем решить первое из этих уравнений, чтобы найти 𝑐. При этом получаем 𝑐=13.

Теперь нам просто нужно подставить это значение в два других уравнения и найти недостающие значения. Чтобы найти 𝑛, мы имеем 7=𝑛3𝑛=21.

Чтобы найти 𝑚, у нас есть 𝑚=−213𝑚=−7.

Теперь мы пришли к нашему решению, которое состоит в том, что значения 𝑚 и 𝑛, которые делают векторы параллельными, равны 𝑚=−7 и 𝑛=21.

Мы можем проверить наше решение, убедившись, что отношения соответствующих компонентов двух векторов равны.

Для двух параллельных векторов должно быть верно, что 26=7𝑛=𝑚−21.

Если мы подставим полученные значения, то получим 26=721=-7-21, которые все упрощаются до 13. Это подтверждает правильность нашего решения.

В следующем примере мы рассмотрим, как мы можем идентифицировать перпендикулярные векторы.

Пример 3. Определение вектора, не перпендикулярного заданной прямой

Какой из следующих векторов не

перпендикулярен прямой, вектор направления которой ⃑𝑟 равен (2,−3,5)?

1. (10,10,2)
2. (-10,-5,1)
3. (2,-2,-2)
4. (1,-2,3)
5. (2,3,1) )

Ответ

Чтобы два вектора были перпендикулярны друг другу, должно быть верно, что их скалярное произведение равно нулю. Чтобы найти решение, нам просто нужно найти, какой из векторов не дает нуля при расставлении точек (2,−3,5).

Начнем с вектора в A. Мы находим, что скалярное произведение дает нам (10,10,2)⋅(2,−3,5)=10×2+10×(−3)+2×5=20−30+10=0.

Следовательно, (10,10,2) перпендикулярно (2,−3,5).

Далее мы можем проверить вектор в B. Получаем (−10,−5,1)⋅(2,−3,5)=(−10)×2+(−5)×(−3)+1×5=−20+15+5=0.

Так как это ноль, ответ также не B.

Расставляя точки над вектором в C с помощью (2,−3,5), мы получаем (2,−2,−2)⋅(2,−3,5)=2×2+(−2)×(−3)+(−2)×5=4+6−10=0.

Таким образом, решение тоже не может быть C.

Далее нам нужно проверить вектор D: (1,−2,3)⋅(2,−3,5)=1×2+(−2)×(−3)+3×5=2+6+15=23.

Поскольку это скалярное произведение не равно нулю, (1,−2,3) и (2,−3,5) не перпендикулярны. Итак, наше решение вопроса состоит в том, что вектор, не перпендикулярный прямой, равен D, (1,−2,3).

Мы можем быстро проверить вектор E, просто чтобы убедиться, что этот вектор перпендикулярен прямой: (2,3,1)⋅(2,−3,5)=2×2+3×(−3)+1×5=4−9+5=0.

Поскольку этот результат равен нулю, это помогает подтвердить наше решение: D.

В следующем примере мы будем определять, являются ли два вектора параллельными, перпендикулярными или ни тем, ни другим.

Пример 4. Определение того, являются ли два вектора параллельными, перпендикулярными или нет

Даны два вектора ⃑𝐵=(64⃑𝑖−56⃑𝑗+8⃑𝑘), определите, являются ли эти два вектора параллельны, перпендикулярны или иным образом.

Ответ

Начнем с того, что вспомним условия, при которых эти векторы параллельны или перпендикулярны. Векторы параллельны, если ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевая действительная константа. Векторы перпендикулярно, если ⃑𝐴⋅⃑𝐵=0. Если ни одно из этих условий не выполняется, то векторы не параллельны и не перпендикулярны друг другу.

Начнем с проверки, параллельны ли они. Если они параллельны, то верно, что (8⃑𝑖−7⃑𝑗+⃑𝑘)=𝑘(64⃑𝑖−56⃑𝑗+8⃑𝑘).

Мы можем проверить, так ли это, попытавшись найти значение 𝑘. Мы можем составить три уравнения, приравнивая компоненты этих векторов. Мы получаем 8 = 64 𝑘, −7 = −56 𝑘, 1 = 8 𝑘.

Решив любое из этих уравнений, мы получим одно и то же значение 𝑘=18. Это говорит нам о том, что наши векторы на самом деле параллельны.

Мы уже нашли решение, но для иллюстрации метода завершим доказательство того, что они не перпендикулярны. Находим скалярное произведение ⃑𝐴 и ⃑𝐵 быть (8⃑𝑖−7⃑𝑗+⃑𝑘)⋅(64⃑𝑖−56⃑𝑗+8⃑𝑘)=8×64+(−7)×(−56)+1×8=512+392+8=912.

Так как это не равно нулю, векторы не перпендикулярны, что не противоречит нашему решению, что векторы параллельны.

Теперь мы знаем, как определить, параллельны два вектора или перпендикулярны. Мы можем использовать это, чтобы выяснить, параллельны или перпендикулярны две прямые линии. В следующем примере мы увидим, как мы можем найти недостающую константу в уравнении прямой линии по другой линии, перпендикулярной ей.

Пример 5. Решение задачи с парой перпендикулярных прямых

Если прямая 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 перпендикулярна 𝑥+5−4=𝑦+810 и 𝑧=8, найдите 𝑚.

Ответ

Итак, нам дали уравнения двух прямых в трехмерном пространстве и сказали, что они перпендикулярны друг другу. Мы можем использовать эту информацию, чтобы найти недостающую константу.

Во-первых, нам нужно найти вектор направления каждой линии. Мы знаем, что строка вида 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐 проходит через точку (𝑥,𝑦,𝑧) и имеет вектор направления (𝑎,𝑏,𝑐).

Используя это, мы можем видеть, что линия 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 имеет вектор направления (−10,𝑚,−8).

Другая строка не совсем такого вида, потому что у нас 𝑧=8. Однако это всего лишь означает, что 𝑧-координата этой прямой постоянна, так как наша прямая существует в плоскости 𝑧=8. Итак, в векторе направления 𝑧-компонента будет быть нулем. Следовательно, вектор направления линии 𝑥+5−14=𝑦+810 при 𝑧=8 равен (−4,10,0).

Теперь, когда у нас есть векторы направления двух прямых, нам нужно взять скалярное произведение этих векторов и установите его равным нулю, так как две линии перпендикулярны друг другу. Это дает нам (−10,𝑚,−8)⋅(−4,10,0)=0.

Все, что нам нужно сделать, это решить это, чтобы найти 𝑚. Мы получаем (-10)×(-4)+𝑚×10+(-8)×0=040+10𝑚=010𝑚=-40𝑚=-4.

Вот мы и пришли к решению: чтобы эти две прямые были перпендикулярны, 𝑚=−4.

Теперь мы видели множество примеров того, как мы можем находить и использовать параллельные и перпендикулярные векторы. Напомним некоторые ключевые моменты эксплейнера.

Ключевые точки

• Когда два вектора параллельны, угол между ними равен 0∘ или 180∘. Когда два вектора перпендикулярны, угол между ними равен 90∘.
• Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 параллельны, если ⃑𝐴=𝑘⃑𝐵. Это эквивалентно тому, что отношения соответствующих компонентов каждого из векторов равны: 𝑎𝑏=𝑎𝑏=𝑎𝑏.
• Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, перпендикулярны, если их скалярное произведение равно нулю, ⃑𝐴⋅⃑𝐵=0, или если 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.
• Мы можем использовать приведенные выше отношения между параллельными и перпендикулярными векторами, чтобы определить, параллельны или перпендикулярны две прямые. 9n\) для любых \(n\) или векторных пространств, таких как полиномиальные пространства. Более формальное определение вместе с некоторыми примерами рассмотрено ниже. n\) и посмотрим, как определить, линейно независимы эти векторы или нет. Давайте перейдем к первому примеру!

  Пример

  Векторы \(\vec{v}_1 = \left[\begin{array}{c} 1\\ 4\\ 0\\\end{array}\right], \vec{v}_2 = \left [\begin{array}{c} 10\\ 2\\ 1\\\end{массив}\right], \vec{v}_3 = \left[\begin{array}{c} -5\\ 0 \\ 6\\\end{массив}\right]\) линейно независимы?

  Решение

  Это вопрос «имеет ли следующее уравнение только тривиальное решение (все нули)?»

  \(c_1\left[\begin{array}{c} 1\\ 4\\ 0\\\end{массив}\right] + c_2\left[\begin{array}{c} 10\\ 2\\ 1\\\end{массив}\right] + c_3\left[\begin{массив}{c} -5\\ 0\\ 6\\\end{массив}\right] = \left[\begin{массив }{c} 0\\ 0 \\ 0 \\ \end{массив}\right]\)

  Каждое векторное уравнение (в реальных пространствах) эквивалентно матричному уравнению и расширенной матрице. Расширенная матрица была бы наиболее полезной здесь. Нам нужно будет сократить ряд с помощью калькулятора.

  \(\left[\begin{array}{ccc|c} 1 & 10 & -5 & 0\\ 4 & 2 & 0 & 0\\ 0 & 1 & 6 & 0\\ \end{массив}\right ] \sim \left[\begin{array}{ccc|c} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{массив}\right ] \)

  Как видно из этой матрицы, решение векторного уравнения (поскольку оно эквивалентно) есть \(c_1 = c_2 = c_3 = 0\), тривиальное решение. Мы знаем, что это единственное решение, потому что в уравнении нет свободных переменных. Поскольку единственным решением векторного уравнения является тривиальное решение, эти векторы линейно независимы.

  Пример

  Векторы \(\vec{v}_1 = \left[\begin{array}{c} 6\\ 2\\ 9\\ 1 \\\end{array}\right], \vec{v}_2 = \left[\begin{array}{c} 12\\ 4\\ 18\\ 2\\\end{массив}\right], \vec{v}_3 = \left[\begin{array}{c } 8\\ 0\\ 0\\ 0\\\end{массив}\right], \vec{v}_4 = \left[\begin{массив}{c} -2\\ 1\\ 1\\ 5\\\end{массив}\right]\) линейно независимы?

  Решение

  Вы можете заметить, что вектор 2 кратен вектору 1. Это означает, что векторы не линейно независимы, а линейно зависимы. Но как это будет выглядеть в матрице? Давайте взглянем.

  \(\left[\begin{array}{cccc|c} 6 & 12 & 8 & -2 & 0\\ 2 & 4 & 0 & 1 & 0\\ 9 & 18 & 0 & 1 & 0 \\ 1 & 2 & 0 & 5 & 0 \\ \end{массив}\right] \sim \left[\begin{array}{cccc|c} 1 & 2 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{массив}\right]\)

  У нас есть столбец (столбец 2), который не является сводным столбцом. Это означает, что у нас есть свободная переменная в векторном уравнении, лежащем в основе этой матрицы. Это означает, что существует бесконечно много решений, т. Е. Нетривиальных решений (решений, в которых не все константы равны нулю). Поэтому эти векторы линейно зависимы.

  Свойства линейно независимых векторов

  Хотя вы всегда можете использовать расширенную матрицу в реальных пространствах, вы также можете использовать некоторые свойства линейно независимых векторов. Мы будем использовать их без доказательств, которые можно найти в большинстве учебников по линейной алгебре.

  • Множество с одним вектором линейно независимо.
  • Набор из двух векторов линейно зависим, если один вектор кратен другому.

    \(\left[\begin{array}{c} 1 \\ 4\\ \end{массив}\right]\) и \(\left[\begin{array}{c} -2 \\ -8\ \\end{array}\right]\) линейно зависимы, так как они кратны.

    \(\left[\begin{array}{c} 9 \\ -1\\ \end{array}\right]\) и \(\left[\begin{array}{c} 18 \\ 6\\ \end{array}\right]\) линейно независимы, так как не являются кратными.

  • Любое множество, содержащее нулевой вектор, является линейно зависимым множеством.
    Это связано с тем, что перед нулевым вектором можно написать любую константу, чтобы получить нетривиальное решение векторного уравнения из определения.

    Векторов:

    \(\left[\begin{array}{c} 5 \\ 0\\ \end{массив}\right]\), \(\left[\begin{array}{c} 2 \\ 6\\ \ конец {массив}\справа]\), \(\слева[\начало{массив}{с} 0 \\ 0\\ \конец{массив}\справа]\)

    линейно зависимы, поскольку набор содержит нулевой вектор.

  • Любой набор, в котором один вектор является линейной комбинацией других, линейно зависим.
    Мы видели это выше. Это верно для набора любого размера.
  • Набор, в котором векторов больше, чем элементов в векторах, линейно зависим.
    Векторы:

    \(\left[\begin{array}{c} 2 \\ 6\\ \end{массив}\right]\), \(\left[\begin{array}{c} 1 \\ 1\\ \ конец {массив}\справа]\), \(\слева[\начало{массив}{с} -1 \\ 5\\ \конец{массив}\справа]\)

    линейно зависимы, потому что есть 3 вектора, но каждый вектор имеет 2 элемента.