История возникновения понятия вектор — Мир геометрии
Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики
Векторные величины — PhysBook
Векторные величины и скаляры
В курсе физике часто встречаются такие величины, для описания которых достаточно знать только числовые значения. Например, масса, время, длина.
Величины, которые характеризуются только числовым значением, называются скалярными или скалярами.
Кроме скалярных величин, используются величины, которые имеют и числовое значение и направление. Например, скорость, ускорение, сила.
Величины, которые характеризуются числовым значением и направлением, называются векторными или векторами.
Обозначаются векторные величины соответствующими буквами со стрелкой наверху или выделяются жирным шрифтом. Например, вектор силы обозначается \(\vec F\) или F. Числовое значение векторной величины называется модулем или длиной вектора. Значение вектора силы обозначают F или \(\left|\vec F \right|\).
Изображение вектора
Векторы изображают направленными отрезками. Началом вектора называют ту точку, откуда начинается направленный отрезок (точка
Два вектора называются равными, если они имеют одинаковую длину и направлены в одну сторону. Такие вектора изображают направленными отрезками, имеющими одинаковые длины и направления. Например, на рис. 2 изображены векторы \(\vec F_1 =\vec F_2\).
Рис. 2.При изображении на одном рисунке двух и более векторов, отрезки строят в заранее выбранном масштабе. Например, на рис. 3 изображены вектора, длины которых \(\upsilon_1\) = 2 м/c, \(\upsilon_2\) = 3 м/c.
Рис. 3.Способ задания вектора
На плоскости вектор можно задавать несколькими способами:
1. Указать координаты начала и конца вектора. Например, вектор \(\Delta\vec r\) на рис. 4 задан координатами начала вектора – (2, 4) (м), конца – (6, 8) (м).
2. Указать модуль вектора (его значение) и угол между направлением вектора и некоторым заранее выбранным направлением на плоскости. Часто за такое направление в положительную сторону оси 0Х. Углы, измеренные от этого направления против часовой стрелки, считаются положительными. На рис. 5 вектор \(\Delta\vec r\) задан двумя числами b и \(\alpha\) , указывающими длину и направление вектора.
Рис. 5.Вектор (геометрия) — это… Что такое Вектор (геометрия)?
Под направленным отрезком 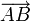
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют нулевым:

- Вектор

 .
.
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка:
 .
.
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Определение. Говорят, что свободные векторы 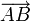 и
и 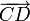
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы 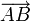 и
и 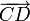
Определение. Говорят, что скользящие векторы 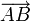 и
и 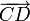 равны, если
равны, если
- точки A,B,C,D располагаются на одной прямой,
- векторы

 равны между собой как свободные векторы.
равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы 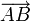 и
и 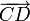 равны, если попарно совпадают точки A и C, B и D.
равны, если попарно совпадают точки A и C, B и D.
Операции над векторами
Сложение векторов
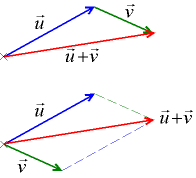
Два вектора u, v
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника. Для сложения двух векторов 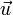 и
и 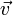 по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Правило параллелограмма
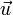 и
и 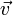 по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы 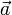 и
и 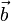 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы 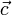 и
и 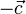 , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы 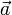 и
и 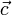 ,
, 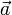 и
и 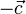 пересекаются. Поэтому определены векторы
пересекаются. Поэтому определены векторы
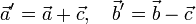
Прямые, на которых расположены векторы 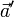 и
и 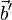 , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы 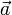 и
и 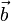 равны по величине и противоположны по направлению, в котором говорят, что векторы
равны по величине и противоположны по направлению, в котором говорят, что векторы 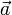 и
и 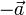 образуют пару (векторов).
образуют пару (векторов).
Таким образом, под суммой векторов 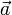 и
и 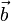 можно понимать сумму векторов
можно понимать сумму векторов 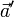 и
и 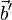 , и эта сумма векторов определена корректно во всех случаях, когда векторы
, и эта сумма векторов определена корректно во всех случаях, когда векторы 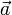 и
и 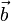 не образуют пару.
не образуют пару.
Произведение вектора на число
Произведением вектора 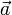 и числа λ называется вектор, обозначаемый
и числа λ называется вектор, обозначаемый 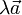 (или
(или 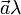 ), модуль которого равен
), модуль которого равен  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора 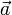 , если
, если 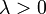 , и противоположно ему, если
, и противоположно ему, если 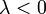 . Если же
. Если же 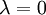 , или вектор
, или вектор 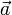 нулевой, тогда и только тогда произведение
нулевой, тогда и только тогда произведение 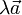 — нулевой вектор.
— нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе,
 .
.
Из определения произведения вектора на число легко вывести следующие свойства:
- если
 , то
, то  . Наоборот, если
. Наоборот, если  , то при некотором λ верно равенство
, то при некотором λ верно равенство  ;
; - всегда
 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Скалярным произведением векторов 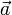 и
и 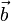 называют число, равное
называют число, равное 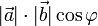 , где
, где  — угол между векторами
— угол между векторами 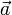 и
и 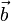 . Обозначения:
. Обозначения: 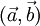 или
или 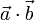 .
.
Если один из векторов является нулевым, то несмотря на то, что угол 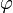 не определён, произведение равно нулю.
не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
 — коммутативность.
— коммутативность. — дистрибутивность.
— дистрибутивность. — линейность по отношению к умножению на число.
— линейность по отношению к умножению на число. — норма вектора.
— норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора 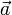 с единичным вектором есть ортогональная проекция вектора
с единичным вектором есть ортогональная проекция вектора 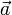 на направление единичного вектора.
на направление единичного вектора.
Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними
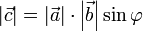
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.
Обозначение: ![\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b](/800/600/https/dikc.academic.ru/pictures/wiki/files/56/8a8df77cfa301a9a6e5c4e01235165ad.png)
Геометрически векторное произведение 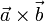 есть ориентированная площадь параллелограмма, построенного на векторах
есть ориентированная площадь параллелограмма, построенного на векторах 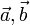 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Сме́шанное произведе́ние 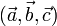 векторов
векторов 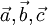 — скалярное произведение вектора
— скалярное произведение вектора 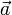 на векторное произведение векторов
на векторное произведение векторов 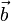 и
и 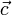 :
:
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение 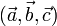 есть (ориентированный) объем параллелепипеда, построенного на векторах
есть (ориентированный) объем параллелепипеда, построенного на векторах 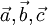 .
.
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора 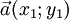 и
и 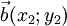 . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
. Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора  и
и 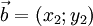 . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где
. Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где 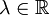
См. также
Ссылки
Wikimedia Foundation. 2010.
Векторное исчисление — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 августа 2016; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 августа 2016; проверки требует 1 правка.Ве́кторное исчисле́ние — раздел математики, в котором изучаются свойства операций над векторами[1]. В связи с разнообразием особенностей векторов, зависящих от пространства, в котором они исследуются, векторное исчисление подразделяется на:
- векторную алгебру;
- векторный анализ;
- функциональный анализ.
Расширением векторного исчисления является тензорное исчисление, изучающее тензоры и тензорные поля. Тензорное исчисление в свою очередь разделяется на тензорную алгебру (входящую в качестве основной части в полилинейную алгебру) и тензорный анализ, изучающий дифференциальные операторы на алгебре тензорных полей.
Тензорное исчисление является составной частью дифференциальной геометрии, используемой, в том числе, в современной теоретической физике[2].
Векторная алгебра[править | править код]
В данном разделе векторного исчисления изучаются свойства линейных операций с векторами: сложение, умножение векторов на число, различные произведения векторов — скалярное, псевдоскалярное, векторное, смешанное, двойное векторное и т. д.[3]. В приложении к аналитической геометрии исследуются геометрические свойства векторов и их совокупности. В частности, коллинеарность, компланарность векторов, свойства векторного базиса. В аналитической и теоретической механике на базе законов векторной алгебры исследуются движение и взаимодействие материальных тел[4]
Расширением векторной алгебры является тензорная алгебра, в которой исследуются алгебраические операции над тензорами[5].
Векторный анализ[править | править код]
Раздел векторного исчисления, в котором исследуются статические, стационарные и динамические векторные и скалярные поля. Векторный анализ оперирует с понятиями поток вектора, циркуляция вектора,[6]. Оперируя данными понятиями, исследуются взаимоотношения определяющих поля скаляров и векторов и доказываются базовые теоремы векторного анализа:
Расширением векторного анализа является тензорный анализ, изучающий дифференциальные операторы, действующие на алгебре D(M){\displaystyle D\left(M\right)}. Рассматриваются и более общие операторы: тензорные плотности, дифференциальные формы со значениями в векторном расслоении[8].
Функциональный анализ[править | править код]
Функциональный анализ является частью современного математического анализа, основной целью которого является изучение функций y=f(x){\displaystyle y=f\left(x\right)}, где по крайней мере одна из переменных x,y{\displaystyle x,\,y} меняется по бесконечному пространству[9].
Методы, основанные на векторном представлении функций, нашли широкое применение в теории линейных интегральных уравнений[10], в теории обработки сигналов[11], в теории обыкновенных дифференциальных уравнений[12], алгебраической геометрии[13] и т. д.
- ↑ Иванов А. Б. Векторное исчисление. Математическая энциклопедия под ред. Виноградова И. М., М., Советская энциклопедия, т. 1, с. 640
- ↑ Онищук А. Л. Тензорное исчисление. Математическая энциклопедия. Под ред. Виноградова И. М., М., Советская энциклопедия, т. 5, с. 330
- ↑ Пытьев Ю. П. Векторная алгебра. Математическая энциклопедия под ред. Виноградова И. М., М., Советская энциклопедия, т. 1, с. 632—636
- ↑ Ольховский И. И. Курс теоретической механики для физиков. М., Наука, 1970
- ↑ Онищук А. Л. Тензорная алгебра. Математическая энциклопедия. Под ред. Виноградова И. М., М., Советская энциклопедия, т. 5, с. 329
- ↑ Иванов А. Б. Векторный анализ. Математическая энциклопедия под ред. Виноградова И. М., М., Советская энциклопедия, т. 1, с. 648
- ↑ движения энергии в телах (Умов)/I
- ↑ Онищук А. Л. Тензорный анализ. Математическая энциклопедия. Под ред. Виноградова И. М., М., Советская энциклопедия, т. 5, с. 333
- ↑ Березанский Ю. М., Левитан Б. М. Функциональный анализ. Математическая энциклопедия. Под ред. Виноградова И. М., М., Советская энциклопедия, т. 5, с. 705—712
- ↑ Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М., Наука, 1968, с. 399
- ↑ Самойло К. А. Радиотехнические цепи и сигналы. М., Радио и связь, 1982, с. 39
- ↑ Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М., Наука, 1970, с. 103
- ↑ Чеботарёв Н. Г. Теория алгебраических функций. М., ОГИЗ, 1948, с. 385


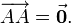
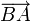
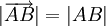 .
.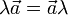 .
.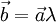 , то
, то 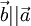 . Наоборот, если
. Наоборот, если 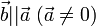 , то при некотором λ верно равенство
, то при некотором λ верно равенство 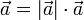 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.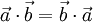 — коммутативность.
— коммутативность.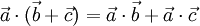 — дистрибутивность.
— дистрибутивность.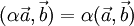 — линейность по отношению к умножению на число.
— линейность по отношению к умножению на число.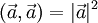 — норма вектора.
— норма вектора.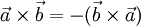
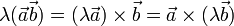
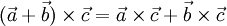
![(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)](/800/600/https/dikc.academic.ru/pictures/wiki/files/50/2def1ecac1759e7c06c5e879e157d6eb.png)