4. О векторном произведении двух векторов
4. О векторном произведении двух векторов
Предпошлём определению векторного произведения двух векторов ряд необходимых в дальнейшем понятий.
Три некомпланарных вектора будем называть упорядоченной тройкой векторов, если указано, какой из них является первым, какой — вторым и какой — третьим.
Записывая упорядоченную тройку векторов, мы будем располагать эти векторы в порядке их следования. Так, запись означает, что первым элементом тройки является вектор , вторым — вектор и третьим — вектор . Таким образом, и — две различные упорядоченные тройки векторов.
В дальнейшем мы будем рассматривать только упорядоченные тройки векторов, поэтому слово «упорядоченная» будем опускать и говорить просто «тройка векторов».
Определение. Тройка некомпланарных векторов называется правой, если выполнено одно из следующих трёх условий.
1. Eсли после приведения всех трёх векторов к общему началу кратчайший поворот от к мы видим из конца вектора совершающимся против часовой стрелки (рис. 264, а).
264, а).
2. Ecли, находясь внутри трёхгранного угла, определяемого приведёнными к общему началу векторами , , , мы видим поворот от к и от него к совершающимся против часовой стрелки (рис. 264, б).
Рис. 264
3. Ecли, будучи приведёнными к общему началу, векторы , и располагаются так, как могут быть расположены большой (), указательный () и средний () пальцы правой руки (рис. 264, в).
Вы можете легко проверить эквивалентность условий один, два и три.
Если кратчайший поворот от к упомянутый в условиях 1 и 2, мы видим из конца вектора совершающимся по часовой стрелке (рис. 265, а, б), то тройка некомпланарных векторов называется левой; также тройка некомпланарных векторов называется левой, если, будучи приведёнными к общему началу, векторы , и располагаются так, как могут быть расположены большой (), указательный () и средний () пальцы левой руки (рис. 265, в). Вы можете легко убедиться в эквивалентности всех трёх определений левой тройки некомпланарных векторов.
Заметим, что для компланарных векторов понятие правой (левой) тройки смысла не имеет.
Если две тройки векторов обе — правые (обе — левые), то говорят, что эти тройки имеют одинаковую ориентацию (тройки одной ориентации). Если же из двух троек векторов одна — правая, а другая — левая, то говорят, что эти тройки имеют противоположную ориентацию (тройки противоположной ориентации). Например, тройки векторов и имеют одинаковую ориентацию, а тройки и — тройки противоположной ориентации (убедитесь в этом с помощью рисунка).
Рис. 265
Из трёх векторов , , можно составить лишь следующие шесть троек: , , , , , . Вы можете убедиться, что если первые три тройки — правые, то остальные три тройки — левые.
Заметим, что тройка векторов , , декартова прямоугольного базиса (ортонормированного репера) трёхмерного векторного пространства является правой, если кратчайший поворот от к наблюдается из конца вектора против часовой стрелки, и является левой, если кратчайший поворот от к наблюдается из конца вектора по часовой стрелке. В нашем учебнике тройка векторов , , предполагается правой.
В нашем учебнике тройка векторов , , предполагается правой.
Теперь введём определение векторного произведения двух векторов.
Определение. Если ненулевые векторы и неколлинеарны, то векторным произведением вектора на вектор называется такой третий вектор , обозначаемый символом × и определяемый следующими тремя условиями: 1) модуль вектора равен произведению модулей векторов и на синус угла ϕ между ними, т. е.
| | = | × | = | |•| |•sin ϕ;(*)
2) вектор перпендикулярен каждому из векторов и ; 3) вектор направлен так, что тройка векторов является правой (рис. 266).
Рис. 266
Рис. 267
Если векторы и коллинеарны, то по определению их векторное произведение полагают равным (нуль-вектору).
Свойства векторного произведения
1. Длина вектора, равного векторному произведению неколлинеарных векторов и , численно равна площади параллелограмма, построенного на приведённых к общему началу векторах и , как на сторонах (рис. 267).
Справедливость этого утверждения основана на том, что площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними, что, в свою очередь, следует непосредственно из условия (*): | | = | × | = | |•| | sin ϕ в определении векторного произведения векторов и .
2. × = –( × ) (свойство антиперестановочности сомножителей).
Рис. 268
Для доказательства этого свойства обозначим: = × , = × . Если || , то = = и свойство доказано. Если векторы и неколлинеарны (рис. 268), то: 1) | | = | |; 2) векторы = × и = × коллинеарны, так как каждый из них перпендикулярен плоскости, определяемой векторами и , приведёнными к общему началу. Тогда либо = , либо = –. Если бы имело место = , то обе тройки векторов и были бы правыми, что невозможно, так как эти тройки противоположной ориентации. Значит, остаётся = –, а это означает: × = – ( × ), что и требовалось доказать. ▼
3. (m•) × = m•( × ) (сочетательное свойство относительно числового (скалярного) множителя).
Для доказательства этого свойства обозначим = (m•) × и = m•( × ) и рассмотрим случаи.
а) Если векторы и коллинеарны, то, вследствие коллинеарности векторов m• и , векторы m• и также коллинеарны. Тогда на основании определения векторного произведения имеем: (m•) × = и m•( × ) = , т. е.
= (m•) × = m•( × ) = .
б) Если m = 0, то m• = и тогда = (m•) × = × = (вектор коллинеарен любому вектору). Обозначим × = , тогда m•( × ) = 0• = . Опять получили:
р = (m•) × = m•( × ) = .
в) Если векторы и неколлинеарны и m ≠ 0, то неколлинеарны и векторы m• и . Обозначим: α = ∠ (; ), β = ∠ (m; ). Тогда
| | = | (m) |•| | sin β = | m |•| |•| | sin β;
| | = | m |•| × | = | m |•| |•| |•sin α.
Учитывая, что α = β при m > 0 (рис. 269, а) и α + β = π при m < 0 (рис. 269, б), приходим к выводу, что sin β = sin α. Это означает, что и при m > 0, и при m < 0 длины векторов и равны.
Осталось доказать, что векторы и коллинеарны и сонаправлены.
Рис. 269
Коллинеарность этих векторов следует из того, что если вектор перпендикулярен плоскости, которой компланарны векторы и (рис. 269, в), то этот вектор перпендикулярен и плоскости, которой компланарны векторы m и , так как m || . Но этой плоскости перпендикулярен и вектор . Значит, || .
И, наконец, докажем, что ⇈ . Если m > 0, то m• ⇈ , значит, ( × ) ⇈ (m•) × . А так как m•( × ) ⇈ ( × ) при m > 0, то m•( × ) ⇈ (m•) × , т. е. ⇈ . Если m < 0, то m• ⇅ , значит, ( × ) ⇅ (m•) × . А так как m•( × ) ⇅ ⇅ ( × ) при m < 0, то m•( × ) ⇈ (m•) × , т. е. ⇈ .
Таким образом, и при m > 0, и при m < 0 имеем | | = | | и ⇈ . Это означает: = , т. е. (m•) × = m•( × ), что и требовалось доказать. ▼
4. ( + ) × = × + × (свойство распределительности векторного произведения относительно сложения векторов).
Преждe чeм доказывать этo свойство векторного произведения векторов, рассмотрим следующий интересный и полезный в дальнейшем геометрический факт.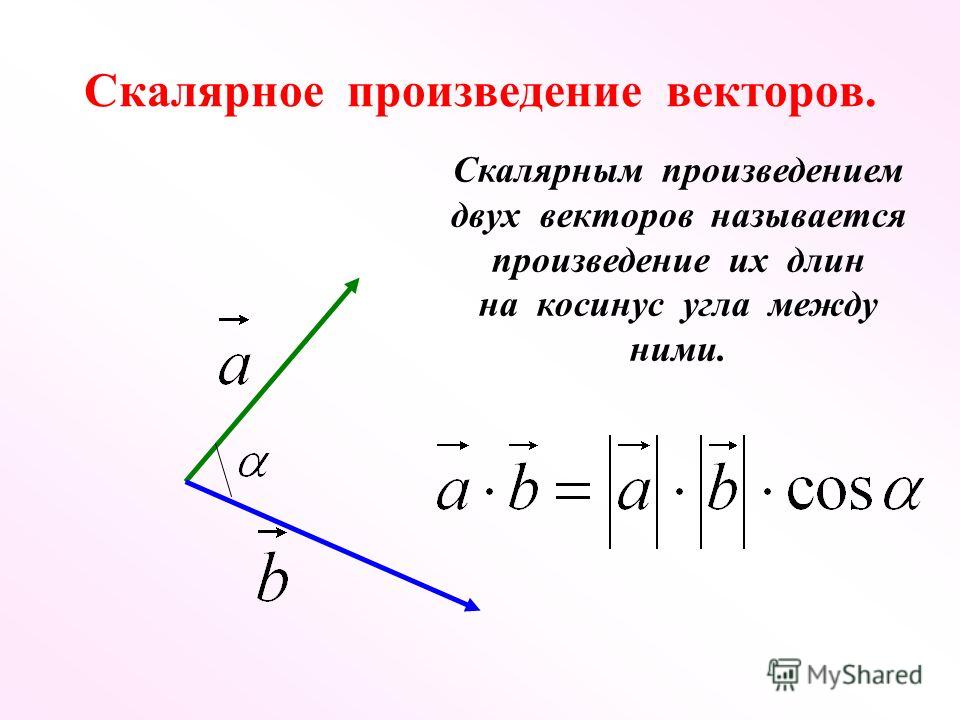
Пусть неколлинеарные векторы и приведены к общему началу O: = , = , ∠ (; ) = ϕ; α — плоскость, проходящая через точку O перпендикулярно вектору (рис. 270).
Рис. 270
Спроектируем ортогонально вектор на плоскость α и полученный вектор повернём в плоскости α вокруг точки О на угол 90° так, чтобы этот поворот наблюдался из конца вектора происходящим по часовой стрелке. Получим вектор , для которого: a) | | = | | = | |•sin ϕ; б) ⟂ , ⟂ ; в) векторы , , образуют правую тройку. Умножив, далее, вектор на число, равное модулю вектора , получим такой вектор , что | | = | |•| | = | |•| |•sin ϕ. Так как, кроме того, ⇈ , то — правая тройка векторов и ⟂ , ⟂ . Это означает, что вектор равен векторному произведению векторов и , т. е. = × .
Докажем теперь свойство ( + ) × = × + × векторного произведения векторов, для чего отложим векторы = , = , = , = = + от точки О и ортогонально спроектируем их на плоскость δ, перпендикулярную вектору . При этом параллелограмм ОАРВ проектируется в такой параллелограмм O1A1P1B1 (рис.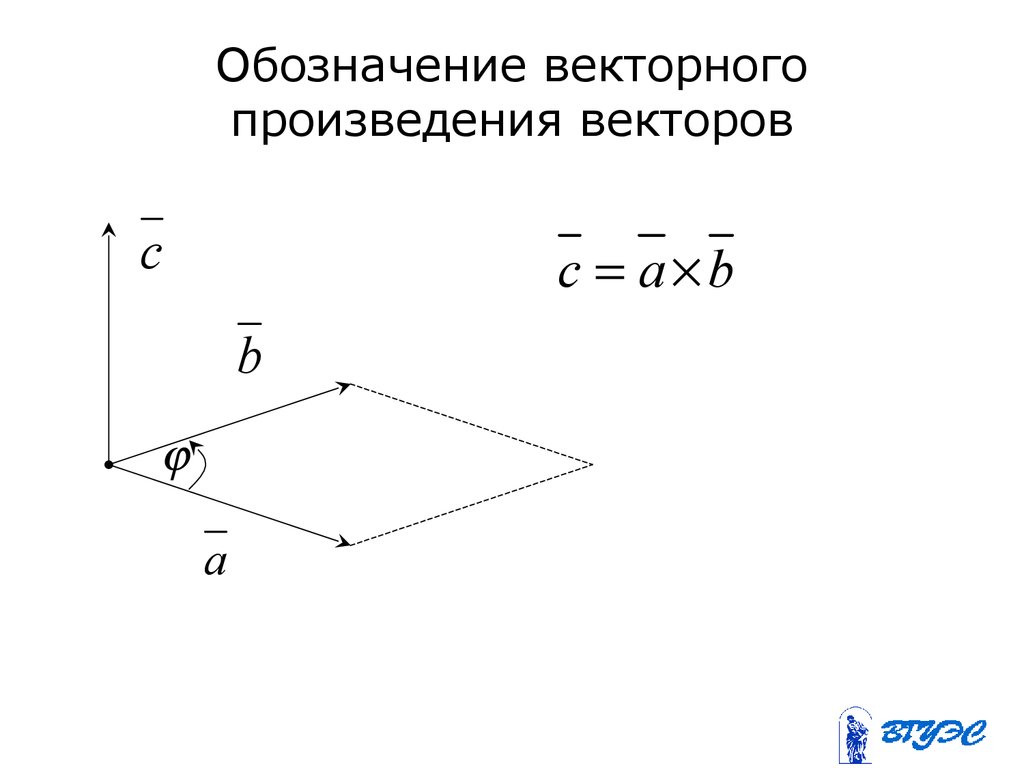 271), что для векторов = , = , = , являющихся ортогональными проекциями соответственно векторов , , , выполняется: + = и | | = | |•sin α, | | = | |•sin β, | | = | |•sin γ, гдe α = ∠ (; ), β = ∠ (; ), γ = ∠ (; ).
271), что для векторов = , = , = , являющихся ортогональными проекциями соответственно векторов , , , выполняется: + = и | | = | |•sin α, | | = | |•sin β, | | = | |•sin γ, гдe α = ∠ (; ), β = ∠ (; ), γ = ∠ (; ).
Рис. 271
Далее рассмотрим такой поворот пространства вокруг прямой O1C на угол 90°, при котором индуцируемый в плоскости δ поворот вокруг точки О наблюдается из точки C совершающимся по часовой стрелке. Этот поворот отображает параллелограмм O1A1P1B1 на параллелограмм O1A2P2B2, а каждый из векторов , , — на перпендикулярный ему и равный по модулю соответственно вектор , , . Умножив каждый из этих векторов на | |, получим соответственно такие векторы = , = , = , что:
1) | | = | |•| | = | |•| | = (| |•sin α)•| | = | |•| |•sin α;
аналогично, | | = | |•| |•sin β; | | = | |•| |•sin γ;
2) ⟂ , ⟂ ; ⟂ , ⟂ ; ⟂ , ⟂ ;
3) тройки векторов , и правые.
Это означает, что = × , = × и = × = ( + ) × . Так как в параллелограмме O1A3P3B3 вектор = + , то получаем ( + ) × = × + × , что и требовалось доказать. ▼
▼
5. Для любого вектора справедливо × = , так как любой вектор коллинеарен сам с собой.
Выражение векторного произведения в декартовых координатах
Векторное произведение × двух векторов и есть вектор, координаты которого нужно уметь находить, если известны координаты векторов сомножителей и .
Предварительно найдём все возможные векторные произведения базисных векторов , , .
Рис. 272
Из определения векторного произведения, учитывая, что векторы , , попарно взаимно перпендикулярны (рис. 272) и являются единичными, имеем:
× = , × = , × = ,(**)
× = –, × = –, × = –.
Теперь найдём координаты векторного произведения × векторов и , заданных в декартовом прямоугольном базисе (; ; ) своими координатами: (x1; y1; z1), (x2; y2; z2) или в виде разложения по базисным векторам , , :
= x1 + y1 + z1, = x2 + y2 + z2.
Принимая во внимание свойства векторного произведения векторов, используя соотношения (**) и учитывая, что тройка базисных векторов является правой, находим:
× = (x1 + y1 + z1) × (x2 + y2 + z2) = (x1x2)•( × ) +
+ (x1y2)•( × ) + (x1z2)•( × ) + (y1x2)•( × ) + (y1y2)•( × ) +
+ (y1z2)•( × ) + (z1x2)•( × ) + (z1y2)•( × ) +
+ (z1z2)•( × ) = (x1x2)• + (x1y2)• + (x1z2)•(–) +
+ (y1x2)•(–) + (y1y2)• + (y1z2)• + (z1x2)• + (z1y2)•(–) + + (z1z2)• = (y1z2 – y2z1)• + (z1x2 – x1z2)• + (x1y2 – x2y1)•.
Таким образом, векторное произведение × = векторов (x1; y1; z1) и (x2; y2; z2) имеет координаты:
× = (y1z2 – y2z1; z1x2 – x1z2; x1y2 – x2y1).
Таблица составленная из четырёх чисел a, b, с и d, называется квадратной матрицей второго порядка. Числа а, b, с и d называются элементами матрицы, при этом числа a и b называются элементами первой строки, числа с и d — элементами второй строки; числа a и c — элементами первого столбца, числа b и d — элементами второго столбца; числа a и d — элементами главной диагонали матрицы.
Определение. Число a•d – b•c называется определителем (или детерминантом) матрицы и обозначается так: .
Из определения видно, что определитель матрицы равен разности произведений чисел a и d главной диагонали и чисел b и c второй диагонали определителя, т. е.
= a•d – b•c.
Например, = 3•(–2) – 1•(– 4) = –2.
Тогда координатами X = y1z2 – y2z1, Y = z1x2 – x1z2, Z = x1y2 – x2y1 векторного произведения × = (X; Y; Z) векторов (x1; y1; z1) и (x2; y2; z2) являются определители второго порядка, составленные из координат векторов — сомножителей. Действительно,
Действительно,
X = y1z2 – y2z1 = ; Y = z1x2 – x1z2 = ;
Z = x1y2 – x2y1 = .
Таким образом,
× =
или в виде разложения по базису имеем:
× = = • + • + •.
ЗАДАЧА. Найдём, например, площадь параллелограмма, построенного на приведённых к общему началу векторах = 2 + 3 – 5 и = – 2 + 4, как на сторонах.
Решение. Так как площадь S параллелограмма, построенного на векторах и , как на сторонах, равна модулю векторного произведения × , то найдём | × |.
Имеем:
× = • + • + • =
= (3•4 – (– 2)•(–5))• + ((–5)•1 – 4•2)• +
+ (2•(–2) – 1•3)• = 2 – 13 – 7,
откуда | × | = = Значит, искомая площадь S параллелограмма равна
В высшей школе вы подробнее познакомитесь с векторным произведением и его приложениями в естественных науках. Кроме того, вам расскажут и о смешанном произведении () = (•)• векторов , и , его свойствах и приложениях.
Самостоятельно решите следующие задачи.
1. Найдите площадь треугольника с вершинами А(1; 1; 1), В(2; 3; 4), С(4; 3; 2). (Ответ: )
(Ответ: )
2. На векторах (4; 6; 2) и (–2; 2; 4) построен треугольник. Найдите его площадь и высоты.
S = 18,75; h2 = h3 = ; h4 =
3. Найдите площадь параллелограмма, построенного на векторах + 3 и 3 + , если | | = | | = 1, ∠ (; ) = 30°. (Ответ: 4.)
4. Дан треугольник АВС площади S. Докажите, что площадь треугольника, сторонами которого являются медианы данного треугольника, равна S.
Сообщество Экспонента
- вопрос
- 22.09.2022
Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
8 Ответов
- вопрос
- 20.
 09.2022
09.2022
Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.
 09.2022
09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.
 08.2022
08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
Нахождение площади и объема с помощью векторов. Векторное произведение векторов
Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
Векторное произведение обладает распределительным свойством , то есть
Выражение векторного произведения через координаты векторов.
Пусть даны два вектора
(как найти координаты вектора по координатам его начала и конца — см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Зачем нужно векторное произведение?
Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.
Также огромное количество применений существует в электричестве и магнетизме.
Он-лайн калькулятор векторного произведения.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов , пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Использование векторного произведения ВЕКТОРОВ
для вычисления площади
некоторых геометрических фигур
Исследовательская работа по математике
Ученика 10 Б класса
МОУ СОШ №73
Перевозникова Михаила
Руководители:
Ассистент каф. математического анализа механико-математического факультета СГУ им. Н.Г. Чернышевского Бердников Глеб Сергеевич
Саратов, 2015
Введение.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трёхмерном Евклидовом пространстве: определение понятия.
1.5. Координаты векторного произведения векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма. Выведение формулы и геометрический смысл векторного произведения векторов.
2.2. Зная только координаты точек, найти площадь треугольника. Доказательство теоремы
2.3. Проверка на примерах правильности формулы.
2.4. Практическое использование векторной алгебры и произведения векторов.
Заключение
Введение
Как известно, многие геометрические задачи имеют два ключевых способа решения – графический и аналитический. Графический метод связан с построением графиков и чертежей, а аналитический предполагает решение задач преимущественно с помощью алгебраических действий.
В связи с широким распространением трехмерных пространственных технологий, изучение свойств некоторых геометрических фигур с использованием векторного произведения представляется актуальным.
В связи с этим была обозначена цель данного проекта – использование векторного произведения векторов для вычисления площади некоторых геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и дать определение векторному произведению векторов в системе координат;
2. Проанализировать наличие связи векторного произведения с площадью треугольника и параллелограмма;
Проанализировать наличие связи векторного произведения с площадью треугольника и параллелограмма;
3. Вывести формулу площади треугольника и параллелограмма в координатах;
4. Проверить на конкретных примерах верность выведенной формулы.
1. Теоретический обзор.
Векторы и вычисления с векторами
Векторомназывается направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка А , концом отрезка – точка В . Сам вектор обозначен через
или . Чтобы найти координаты вектора
, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
= { B x — A x ; B y — A y }
Коллинеарными называются векторы, лежащие на параллельных прямых или на одной прямой. При этом вектор отрезок, характеризующийся длиной и направлением.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
Длина вектора || в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
С векторами можно совершать различные действия.
Например, сложение. Чтобы их сложить, нужно провести сначала второй вектор из конца первого, а потом соединить начало первого с концом второго (рис. 1). Суммой векторов является другой вектор с новыми координатами.
Сумму векторов = {a x ; a y } и = {b x ; b y } можно найти воспользовавшись следующей формулой:
+ = {a x + b x ; a y + b y }
Рис. 1. Действия с векторами
Вычитая векторы, нужно сначала провести их из одной точки, а потом соединить конец второго с концом первого.
Разность векторов = {a x ; a y } и = {b x ; b y } можно найти по формуле:
— = { a x — b x ; a y — b y }
Также, векторы можно умножать на число. Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Произведение вектора = {a x ; a y } и числа k можно найти воспользовавшись следующей формулой:
k · = {k · a x ; k · a y }
А можно ли умножать вектор на вектор? Конечно, и даже двумя вариантами!
Первый вариант – скалярное произведение.
Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов можно использовать угол между данными векторами, показанный на рисунке 3.
Из формулы следует, что скалярное произведение равно произведению длин данных векторов на косинус угла между ними, его результатом является число. Важно, что если векторы перпендикулярны, то их скалярное произведение равно нулю, т.к. косинус прямого угла между ними равен нулю.
В координатной плоскости вектор также имеет координаты.
Вектора, их координаты и скалярное произведение являются одними из самых удобных методов вычисления угла между прямыми (или их отрезками), если введена система координат.
И если координаты
, то их скалярное произведение равно:
В трехмерном пространстве существует 3 оси и, соответственно, у точек и векторов в такой системе будет по 3 координаты, а скалярное произведение векторов вычисляется по формуле:
1.2. Векторное произведение векторов в трехмерном пространстве.
Вторым вариантом вычисления произведения векторов является векторное произведение. Но, чтобы его определить требуется уже не плоскость, а трехмерное пространство, в котором начало и конец вектора имеют по 3 координаты.
В отличие от скалярного произведения векторов в трёхмерном пространстве операция «векторное умножение» над векторами приводит к иному результату. Если в предыдущем случае скалярного умножения двух векторов результатом было число, то в случае векторного умножения векторов результатом будет другой вектор, перпендикулярный обоим вступившим в произведение векторам. Поэтому это произведение векторов называется векторным.
Поэтому это произведение векторов называется векторным.
Очевидно, что при построении результирующего вектора , перпендикулярного двум, вступившим в произведение — и , может быть выбрано два противоположных направления. При этом направление результирующего вектора определяется по правилу правой руки, или правилу буравчика.Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
Рис. 7. Правило правой руки
1.3. Свойства векторного произведения векторов.
Длина результирующего вектора определяется по формуле
.
При этом
векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен
, а его направление определяется по правилу правой руки.
Векторное произведение зависит от порядка сомножителей, именно:
Векторное произведение ненулевых векторов равно 0, если они коллинеарны, тогда синус угла между ними будет равен 0.
Координаты векторов в трехмерном пространстве выражаются следующим образом: . Тогда координаты результирующего вектора находим по формуле
Длина результирующего вектора находится по формуле:
.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма в плоскости. Геометрический смысл векторного произведения векторов.
Пусть нам дан треугольник ABC (рис. 8). Известно, что .
Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника мы находим выражение векторного произведения векторов:
Из выше сказанного можно определить геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки.
Другими словами, длина векторного произведения векторов и равна площади параллелограмма,
построенного на векторах
и
,
со сторонами и и углом между ними, равным .
Рис. 9. Геометрический смысл векторного произведения векторов
В связи с этим, можно привести еще одно определение векторного произведения векторов:
Векторным произведением вектора на вектор называется вектор , длина которого численно равна площади параллелограмма построенного на векторах и , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от к вокруг вектора осуществлялось против часовой стрелки, если смотреть с конца вектора (рис. 10).
Рис. 10. Определение векторного произведения векторов
с использованием параллелограмма
2.2. Вывод формулы для нахождения площади треугольника в координатах.
Итак, нам дан треугольник АВС в плоскости и координаты его вершин. Найдем площадь этого треугольника (рис. 11).
Рис. 11. Пример решения задачи на нахождение площади треугольника по координатам его вершин
Решение.
Для начала, рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и АС.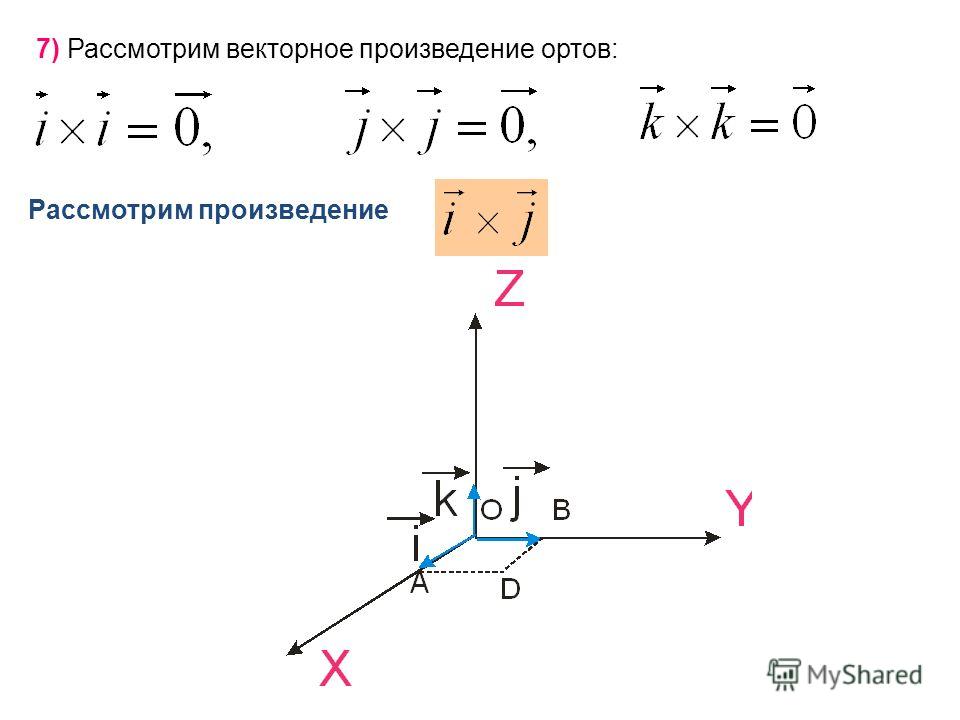
По данной прежде формуле подсчитаем координаты их векторного произведения. Длина этого вектора равна 2 площадям треугольника АВС. Площадь треугольника равна 10.
Более того, если мы рассмотрим треугольник на плоскости, то первые 2 координаты векторного произведения всегда будут равны нулю, поэтому мы можем сформулировать следующую теорему.
Теорема: Пусть дан треугольник АВС и координаты его вершин (рис. 12).
Тогда .
Рис. 12. Доказательство теоремы
Доказательство.
Рассмотрим точки в пространстве и вычислим координаты векторов ВС и ВА. . По приведенной раньше формуле вычислим координаты векторного произведения этих векторов. Обратим внимание, что все члены, содержащие z 1 или z 2, равны 0, т.к. z 1и z 2 = 0. УБРАТЬ!!!
Итак, следовательно,
2.3. Проверка правильности формулы на примерах
Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
a × b=
I(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
I(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5 j — 5 k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
| a × b| =
√ 02 + 52 + 52 =
√ 25 + 25 =
√ 50 =
5√ 2
Ответ: SΔ = 2. 5√2.
5√2.
Заключение
2.4. Приложения векторной алгебры
и скалярного и векторного произведения векторов.
Где же нужны векторы? Векторное пространство и векторы носят не только теоретический характер, но и имеют вполне реальное практическое применение в современном мире.
В механике и физике многие величины имеют не только численное значение, но и направление. Такие величины называются векторными. Вместе с использованием элементарных механических понятий, опираясь на их физический смысл, многие величины рассматриваются как скользящие векторы, а их свойства описываются как аксиомами, как это принято в теоретической механике, так и при помощи математических свойств векторов. Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, момент импульса и сила Лоренца математически записываются с помощью векторов.
В физике важны не только сами вектора, но в большой степени важны и их произведения, которые помогают вычислять некоторые величины. Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Еще один пример: скалярное произведение используется для вычисления работы по приведенной ниже формуле, где F – вектор силы, а s – вектор перемещения.
Одним из примеров использования произведения векторов является момент силы, равный произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое из того, что вычисляется в физике по правилу правой руки является векторным произведением. Найти подтверждения, привести примеры.
Стоит еще заметить, что двухмерным и трехмерным пространством не исчерпываются возможные варианты векторных пространств. Высшая математика рассматривает пространства большей размерности, в которых также определяются аналоги формул для скалярного и векторного произведения. Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
В то же время результатом векторного произведения векторов в трёхмерном Евклидовом пространстве является не число, а результирующий вектор со своими координатами, направлением и длиной.
Направление результирующего вектора определяется по правилу правой руки, что является одним из самых удивительных положений аналитической геометрии.
Векторное произведение векторов может быть использовано в нахождении площади треугольника или параллелограмма по заданным координатам вершин, что было подтверждено выведением формулы, доказательством теоремы и решением практических задач.
Векторы широко используются в физике, где такие показатели как скорость, импульс и сила могут быть представлены в виде векторных величин и вычисляются геометрически.
Список использованных источников
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с.
С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: , 2013. 383 с.
Атанасян Л.С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10-11 классы: учебник для общеобразовательных организаций: базовый и профильный уровни. М.: , 2013. 255 с.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
Математика. Клевер.
Изучение математики онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm
Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.
Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой , если по часовой стрелке – левой .
Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1
Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a → и b → коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a → и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
- его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
- тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.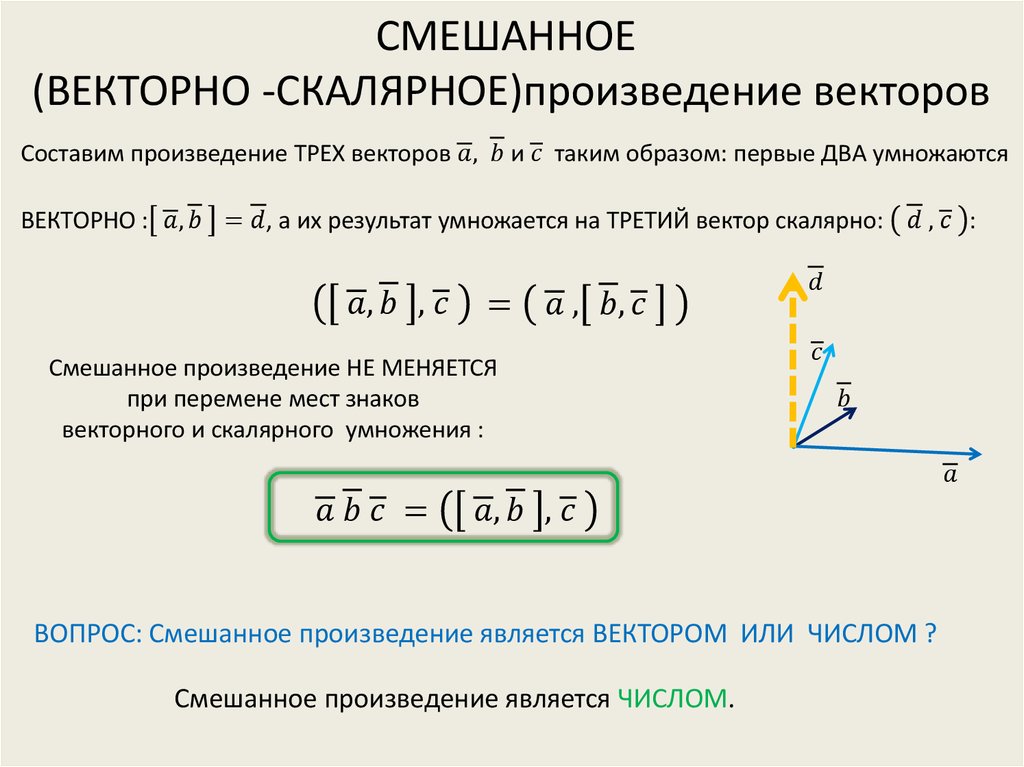
Определение 2
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) называют вектор c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , где i → , j → , k → являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k →
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a → × b → = — b → × a → ;
- дистрибутивность a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- ассоциативность λ · a → × b → = λ · a → × b → или a → × (λ · b →) = λ · a → × b → , где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативности
По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = — i → j → k → b x b y b z a x a y a z = — b → × a → , что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .
Пример 1
Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .
Решение
С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Ответ: 15 2 2 .
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) .
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2
В прямоугольной системе координат заданы два вектора a → = (2 ; 1 ; — 3) , b → = (0 ; — 1 ; 1) . Найдите их векторное произведение.
Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x — a x · b z) · j → + (a x · b y — a y · b x) · k → = = (1 · 1 — (- 3) · (- 1)) · i → + ((- 3) · 0 — 2 · 1) · j → + (2 · (- 1) — 1 · 0) · k → = = — 2 i → — 2 j → — 2 k → .
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k → .
Ответ: a → × b → = — 2 i → — 2 j → — 2 k → .
Пример 3
Найдите длину векторного произведения векторов i → — j → и i → + j → + k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i → — j → × i → + j → + k → в данной прямоугольной системе координат.
Известно, что векторы i → — j → и i → + j → + k → имеют координаты (1 ; — 1 ; 0) и (1 ; 1 ; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → .
Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты (- 1 ; — 1 ; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6 .
Ответ: i → — j → × i → + j → + k → = 6 . .
Пример 4
В прямоугольной декартовой системе координат заданы координаты трех точек A (1 , 0 , 1) , B (0 , 2 , 3) , C (1 , 4 , 2) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.
Решение
Векторы A B → и A C → имеют следующие координаты (- 1 ; 2 ; 2) и (0 ; 4 ; 1) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → и к A C → , то есть, является решением нашей задачи.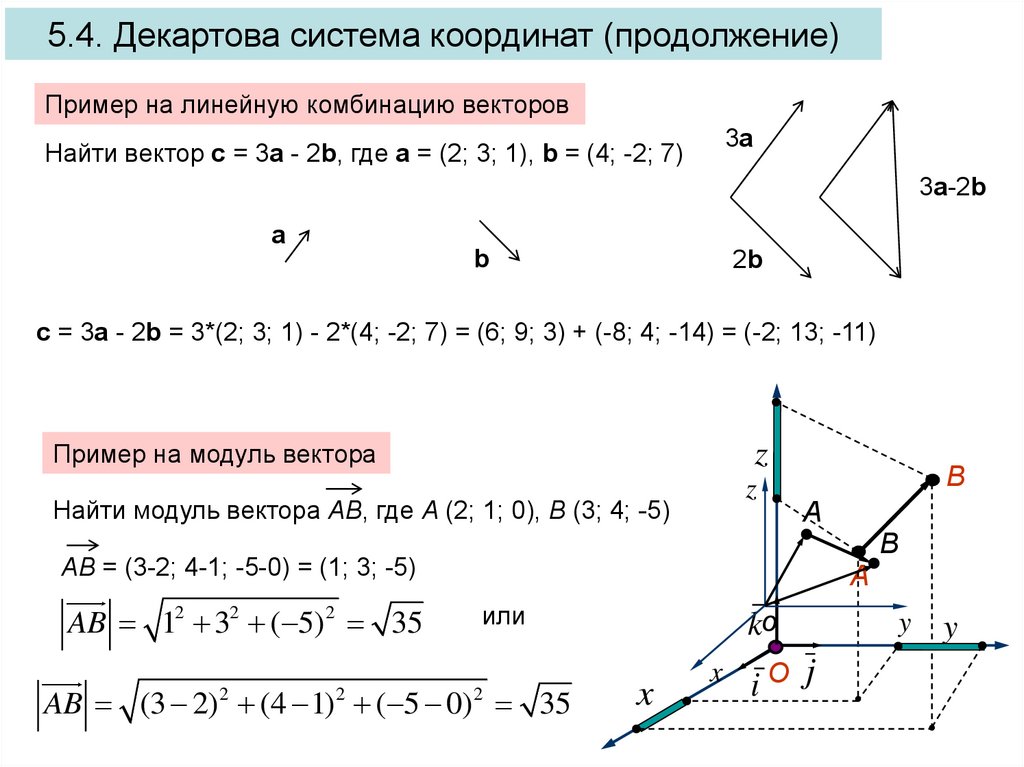 Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .
Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .
Ответ: — 6 i → + j → — 4 k → . — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Пример 5
Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → .
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b →
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b →
Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b → = — 6 · a → × b → — b → × a → . .
.
Из антикоммутативности векторного произведения следует — 6 · a → × b → — b → × a → = — 6 · a → × b → — (- 1) · a → × b → = — 5 · a → × b → . .
Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → — b → × a → — 2 · b → = = — 5 · a → × b → .
По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → — b → × a → — 2 · b → = — 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Ответ: 3 · a → — b → × a → — 2 · b → = 60 .
Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → . j
;
j
;
2) |k |=1, но | i x j | = |i | |J | sin(90°)=1;
3) векторы i , j и k образуют правую тройку (см. рис. 16).
7.2. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).
Векторы а хb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , b x a противоположной ориентации). Стало быть a xb = -(b xa ).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l (а хb ) = (l а ) х b = а х (l b ).
Пусть l >0. Вектор l (а хb ) перпендикулярен векторам а и b . Вектор ( l а )хb также перпендикулярен векторам а и b (векторы а , l а лежат в одной плоскости). Значит, векторы l (а хb ) и ( l а )хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
Поэтому l
(a
хb
)=
l
а
хb
. Аналогично доказывается при
l
Аналогично доказывается при
l
3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а ||b а хb =0 .
В частности, i *i =j *j =k *k =0 .
4. Векторное произведение обладает распределительным свойством:
(a +b ) хс = а хс +b хс .
Примем без доказательства.
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов i , j и k :
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а =а х i +a y j +a z k и b =b x i +b y j +b z k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
Полученную формулу можно записать еще короче:
так как правая часть равенства (7. 1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
7.4. Некоторые приложения векторного произведения
Установление коллинеарности векторов
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а | * |b |sin g , т. е. S пар = |а х b |. И, значит, D S =1/2|а х b |.
Определение момента силы относительно точки
Пусть в точке А приложена сила F =АВ и пусть О — некоторая точка пространства (см. рис. 20).
Из физики известно, что моментом си лы F относительно точки О называется вектор М , который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо
3) образует правую тройку с векторами ОА
и
A
В
.
Стало быть, М =ОА х F .
Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ , где О-некоторая неподвижная точка оси (см. рис. 21).
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Определение:
Векторным произведением вектора a
на вектор b
в пространстве R 3 называется вектор c
, удовлетворяющий следующим требованиям:
длина вектора c равна произведению длин векторов a и b на синус угла φ между ними:
|c|=|a||b|sin φ;
вектор c ортогонален каждому из векторов a и b;
вектор c направлен так, что тройка векторов abc является правой;
в случае пространства R7 требуется ассоциативность тройки векторов a,b,c.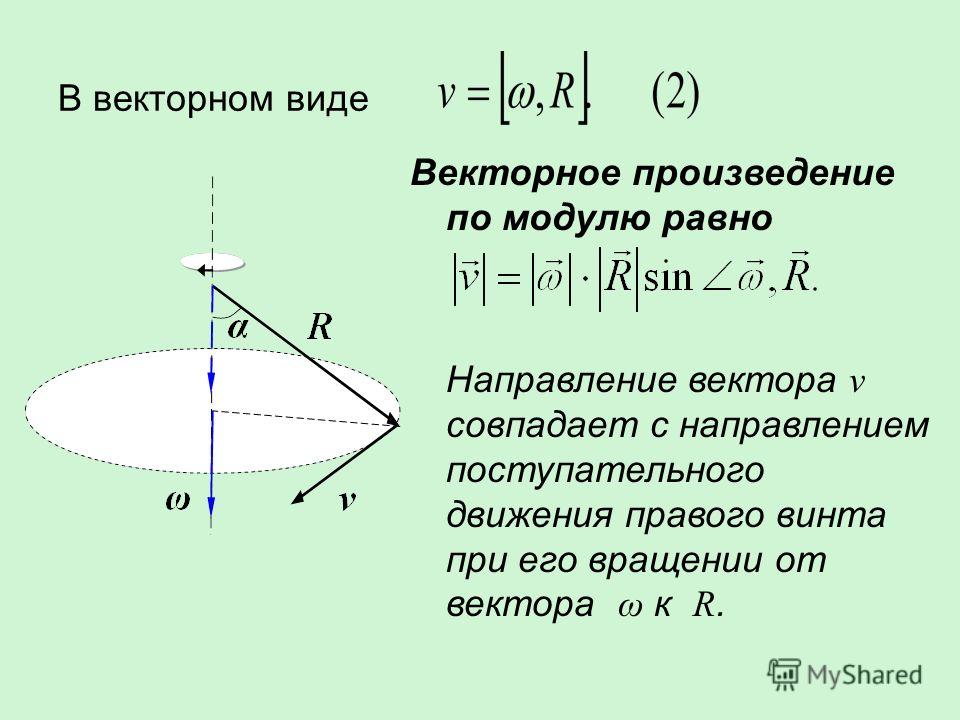
Обозначение:
c===a × b
Рис. 1. Площадь параллелограмма равна модулю векторного произведения
Геометрические свойства векторного произведения :
Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
Модуль векторного произведения равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b (см. рис.1).
Если e — единичный вектор, ортогональный векторам a и b и выбранный так, что тройка a,b,e — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
=S e
Рис.2. Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений
Если c — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, e — единичный вектор, лежащий в плоскости π и ортогональный к c,g — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула:
=Pr e a |c|g
где Pr e a проекция вектора e на a
|c|-модуль вектора с
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c . Такое произведение трех векторов называется смешанным.
Такое произведение трех векторов называется смешанным.
V=|a (b×c)|
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
V=a×b c=a b×c
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Выражение для векторного произведения в декартовых координатах
Если два вектора a и b определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
а система координат правая, то их векторное произведение имеет вид
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Для запоминания этой формулы:
i =∑ε ijk a j b k
где ε ijk — символ Леви-Чивиты.
Векторное произведение векторов. Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Yandex.RTB R-A-339285-1
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Определение 1
Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = (a → × b → , d →) .
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i → , j → , k →
Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Определение 2
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Из этого следует:
a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a → × b → = (a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k →) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z
Таким образом, можно сделать вывод, что:
a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z
Определение 3
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z .
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение.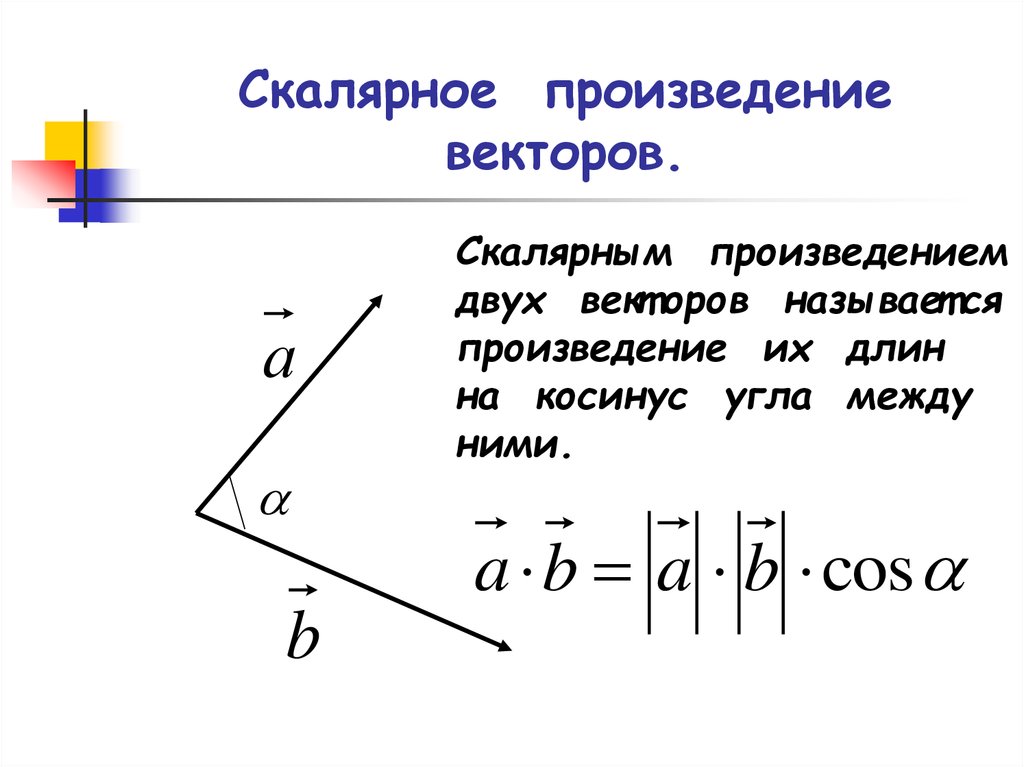 Ниже мы приведем основные свойства.
Ниже мы приведем основные свойства.
- (λ · a →) · b → · d → = a → · (λ · b →) · d → = a → · b → · (λ · d →) = λ · a → · b → · d → λ ∈ R ;
- a → · b → · d → = d → · a → · b → = b → · d → · a → ; a → · d → · b → = b → · a → · d → = d → · b → · a → ;
- (a (1) → + a (2) →) · b → · d → = a (1) → · b → · d → + a (2) → · b → · d → a → · (b (1) → + b (2) →) · d → = a → · b (1) → · d → + a → · b (2) → · d → a → · b → · (d (1) → + d (2) →) = a → · b → · d (2) → + a → · b → · d (2) →
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ([ a → × b → ] , d →) = (0 → , d →) = 0 .
Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Пример 1
Докажите равенство ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) , где λ — некоторое действительное число.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →)
Мы разобрали, что (([ a → × b → ] , b →) = 0 . Из этого следует, что
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →) = = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + 0 = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →)
Согласно первому свойству ([ a ⇀ × b ⇀ ] , λ · a →) = λ · ([ a ⇀ × b ⇀ ] , a →) , а ([ a ⇀ × b ⇀ ] , a →) = 0 . , d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
, d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
Неравенство доказано.
Разбор типовых задач
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z .
Пример 3
В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = (1 , — 2 , 3) , b → (- 2 , 2 , 1) , d → = (3 , — 2 , 5) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → .
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + (- 1) · 1 · 3 + 3 · (- 2) · (- 2) — 3 · 2 · 3 — (- 1) · (- 2) · 5 — 1 · 1 · (- 2) = — 7
Пример 4
Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = (1 , 1 , 0) i → + j → — k → = (1 , 1 , — 1) i → + j → + 2 · k → = (1 , 1 , 2)
Используем формулу, которая использовалась выше
i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 1 1 0 1 1 — 1 1 1 2 = 0 i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
Пример 5
В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора.
Обозначим c → = a → × b → .
Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a → · b → · d → = ([ a → × b → ] , d →) = c → , d → = c → · d → · cos (c → , d → ^) .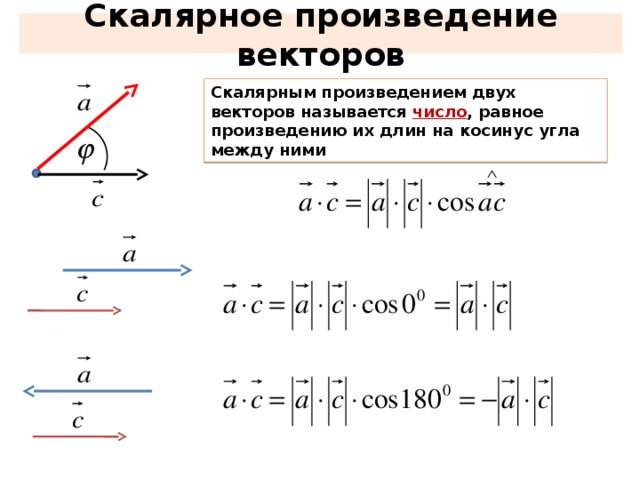 ) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → .
Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → .
Определение 4
Абсолютная величина векторного произведения является объемом параллелепипеда : V п а р а л л е л е п и п и д а = a → · b → · d → .
Данная формула и является геометрическим смыслом.
Определение 5
Объем тетраэдра , который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → .
Для того, чтобы закрепить знания, разберем несколько типичных примеров
Пример 6
Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = (3 , 6 , 3) , A C → = (1 , 3 , — 2) , A A 1 → = (2 , 2 , 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · (- 2) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · (- 2) · 2 = — 18
Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 .
V п а р а л л е л е п и п и д а = 18
Пример 7
В системе координат заданы точки A (0 , 1 , 0) , B (3 , — 1 , 5) , C (1 , 0 , 3) , D (- 2 , 3 , 1) . Следует определить объем тетраэдра, который расположен на этих точках.
Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = (3 — 0 , — 1 — 1 , 5 — 0) = (3 , — 2 , 5) A C → = (1 — 0 , 0 — 1 , 3 — 0) = (1 , — 1 , 3) A D → = (- 2 — 0 , 3 — 1 , 1 — 0) = (- 2 , 2 , 1)
Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · (- 1) · 1 + (- 2) · 3 · (- 2) + 5 · 1 · 2 — 5 · (- 1) · (- 2) — (- 2) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 .
V т э т р а э д р а = 7 6 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение b x c , т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc .
Назначение . Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word . Дополнительно создается шаблон решения в Excel .
a (; ; )b (; ; )
c (; ; )
При вычислении определителя использовать правило треугольников
Признаки компланарности векторов
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.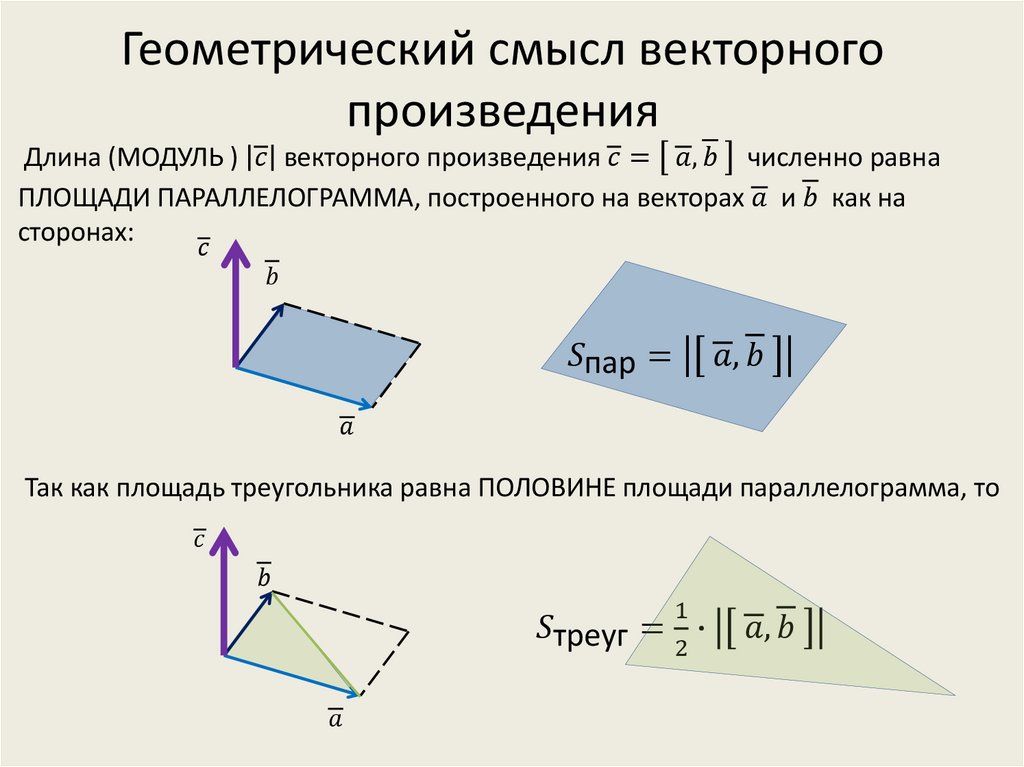
Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая.
Свойства смешанного произведения
- При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
Вытекает из геометрического смысла. - (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
Вытекает из определения смешанного произведения. - (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
- Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0 .
Пример №1 . Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc .
Пример №2 . (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca . Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc .
Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k .
Решение . Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде.
Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c .
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать:
| abc =([ab ],c ) |
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю.
Следствие 1. Имеет место следующее равенство:
Следовательно нам достаточно доказать, что
| ([ab ],c )=([bc ],a ) | (3) |
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Последнее выражение можно записать, используя определители второго порядка:
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
| . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс , где
Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1:
Конечная точка вектора a .
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒ Скалярное произведение векторов — число = произвед длин на косинус между ними. Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось. Свойства: 1.a*b=b*a 2. (C*a)*b=C*(a*b) 3. a(b+c)=a*c+b*c; 4. 5. (a, b) = 0 => 6. ij = jk = kj = 0. Теорема 1: в пространстве R3 в ортонормированном базисе : Следствие из Т1: Для вектора : Механический смысл скалярного произведения: Пусть — сила, которая перемещает тело в направлении вектора S ( на длину ) => 13. векторное произведение векторов. Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой. Векторное произведение вектора a на b — это c, который: 1)с перпендикулярно a и b; 2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку. Замечание: Из определения вытекает след соотношения между ортами ijk: 1. 2. j*k=i; 3. k*i=j; Свойства: 1)векторное произ при перестановке множителей меняет знак. ( ) 2)два ненулевых вектора коллинеарны, когда их векторное произв =0. Пункты: 1)условие коллиниарности: a//b => a*b=0; 2)нахождение S параллелограмма и S треуг. Sпар= sin . Sтр=0,5* 3)определение момента силы. |M|=|F|*|S|. Теорема: ,
Смешанное произведение векторов. Определение. Вычисление. Свойства. Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку. Свойства: 1)смешанное произв не меняется при циклической перестановке его множителей. ( . 2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей 3)смешанное произ ненулевых векторов =0 тога, когда они компланарны. Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов. Приложение. 1)определение взаимных ориентаций векторов в пространстве: если >0 ( <0), то правая (левая) тройка векторов 2)комплонарность векторов: компланарны, когда их произв =0. 3)Геометрический смысл: Vпараллелепипеда= . Vтр=1/6( ). Вычисление: ,
Прямая на плоскости. Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной система координат разные виды ее уравнений. 1. Уравнение прямой с угловым коэффициентом: Пусть: tg =k, , тогда: y = kx + b. Число tg =k называется угловым коэффициентом прямой, а уравнение – уравнением прямой с угловым коэффициентом. ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Перекрестное произведение — определение, Перекрестное произведение для двух векторов, Правило правой руки, Свойства и примеры решения вектор представляет собой длину прямой линии
AB и его направление от A до B . Точка A называется начальной точкой вектора, а B называется -й точкой.0006 конечная точка .Величина или модуль вектора может рассматриваться как положительное число, которое измеряет его длину и обозначается как модуль вектора, иногда записывается как a .
Теперь над этими векторами можно выполнять различные типы операций, такие как сложение, вычитание, умножение, деление и т. д.
Мы увидим, как выполнять векторное произведение векторов, их формулы и их свойства на некоторых примерах. через эту статью.
Что такое кросс-произведение?
Перекрестное произведение может быть указано как произведение двух векторов. Перекрестное произведение представлено знаком умножения (между двумя векторами. Перекрестное произведение также можно рассматривать как двоичный вектор, работающий в трехмерной системе.
Перекрестное произведение представлено знаком умножения (между двумя векторами. Перекрестное произведение также можно рассматривать как двоичный вектор, работающий в трехмерной системе.
Если взять перекрестное произведение двух векторов, то оно всегда будет давать третий вектор, который перпендикулярен взятым векторам.У нас также есть много онлайн-калькуляторов перекрестного произведения , где вы можете найти векторное произведение между двумя векторами за секунды.
Перекрестное произведение иногда используется для определения вектора, перпендикулярного плоской поверхности, пересекающей два вектора. Перекрестное произведение двух векторов, скажем, a, b, равно другому вектору, который находится под прямым углом к обоим векторам, и встречается в трех измерениях.
Выбор редактора: разница между скалярной и векторной величиной (все новые)
Определение
Если A и B взяты как два независимых вектора, то векторное произведение этих двух векторов (AB) будет перпендикулярно обоим векторам, и это будет нормально к плоскости, имеющей оба вектора.
Важно помнить, что результатом является вектор, а НЕ скалярное значение. Вот почему он известен как векторный продукт. Чтобы определение было легко запомнить, мы обычно используем определители для вычисления перекрестных произведений.
Формула
a ⨯ b = |a| |б| sin (θ) n
- | а | и | б | – Длина двух векторов.
- θ – Угол между двумя векторами a и b.
- n – Единичный вектор, перпендикулярный обоим векторам a и b.
Перекрестное произведение двух векторов
Формула перекрестного произведения двух векторов может быть получена следующим методом.
Возьмем два вектора в качестве
A = ai + bj + ck
B= xi + yj + zk
Мы знаем, что i , j и k являются стандартными базисными векторами, которые имеют приведенные ниже равенства.
i j = k и j i = -k
j k = i и K J = -i
K I = J и I K = -J
также,
I × I = J × J = K × K = 0
Теперь сейчас ,
A × B = ( a i + b j + c k) × ( x i + y j + z k) × 90 (
= a) ) + ay( i × j )+ az( i × k ) + bx( j × i ) + by( j × j) + bz( j × k ) + cx( k × i ) + cy( k × j ) + cz( k × k )
Примените векторы, как указано выше, равенства-
A × B = ax(0) + ay( k ) + az( -j ) + bx( -k ) + by(0) + bz( i ) + cx( j ) + cy( -i ) + cz(0) = (bz – cy) i + (cx – az) j + (ay – bx) k
Здесь заметим, что i × j j × i; , таким образом, векторное произведение некоммутативно, и закон ассоциативности не выполняется.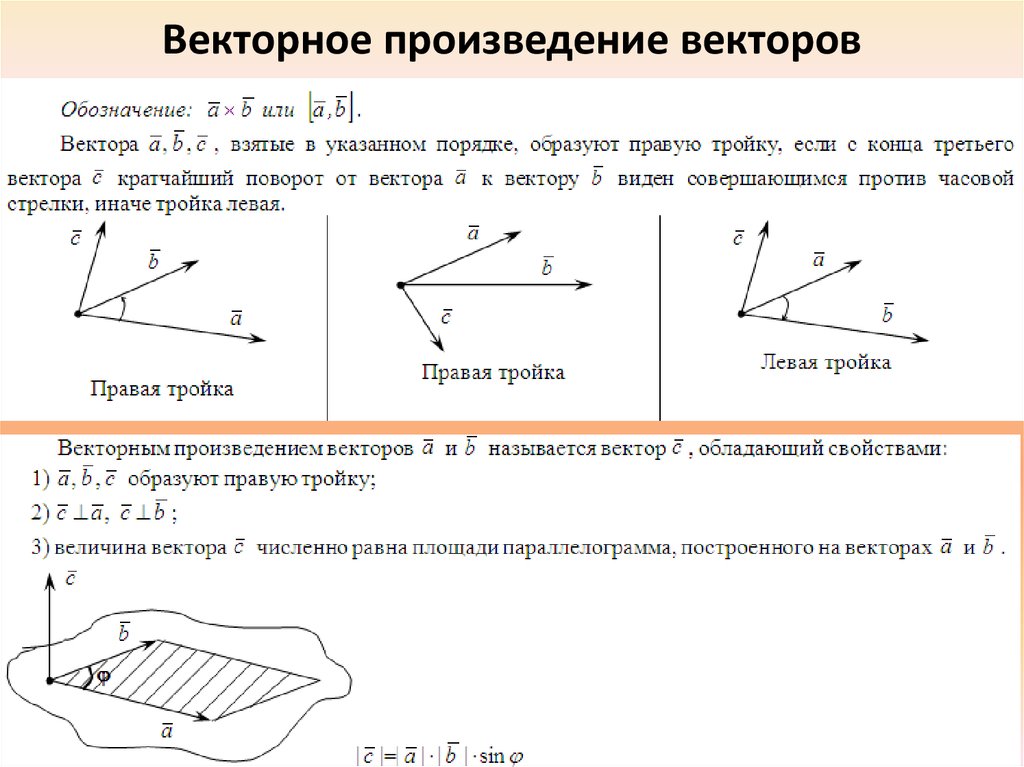 (a × b) × c a × (b × c)
(a × b) × c a × (b × c)
Примеры
Пример: Найдите векторное произведение приведенных ниже двух векторов
= (3, 4, 5) и = (7) , 8, 9)
Решение:
Перекрестное произведение определяется как:
a = 3i + 4j + 5k
b = 7i + 8j + 9k ;
a×b = i – j + k
= ( 36 – 40)i – (27 – 35)j + (24 – 28)k = -4i + 8j -4k
Итак, × = -4i + 8j – 4k
Правило правой руки для перекрестного произведения
Мы можем найти направление единичного вектора, принимая во внимание правило правой руки . Чтобы определить правильное перекрестное произведение, у нас есть правило правой руки.
Чтобы воспользоваться этим правилом, вы поднимаете правую руку вверх, затем поднимаете указательный палец и направляетесь к первому вектору, а теперь указываете средним пальцем в направлении второго вектора.
При этом большой палец правой руки будет показывать направление единичного вектора.
Принимая во внимание правило правой руки, мы можем легко показать и засвидетельствовать, что векторное произведение векторов некоммутативно.
Свойства
Мы обозначаем векторное произведение двух векторов как « a » пересечение « b » (a × b).
Предположим, что a × b = c .
Здесь вектор c демонстрирует два уникальных свойства.
Во-первых, единичный вектор здесь ортогонален как a , так и b . Это также является причиной того, что кросс-произведение работает только в трех измерениях. Поскольку в двух измерениях векторы не всегда перпендикулярны какой-либо паре других векторов.
Во-вторых, длина c показывает меру того, насколько далеко a и b направлены и возвышаются по своим величинам.
Если a, b и c являются векторами, а c является скаляром, то свойства векторного произведения: a) × b = c (a × b) = a × (cb)
Длина векторного произведения a×b, a×b равна площади параллелограмма, определяемой сторонами a и b.
Пример 1: Найдите площадь треугольника с вершинами P(0,1,4), Q(-5, 9,2) и R(7, 2, 8)
Решение:
PQ = (-5, 8, -2) и PR = (7, 1,4)
Итак, PQ × PR = (34, 6, -61)
Площадь параллелограмма = PQ × PR = (34² +6² +(-61)²)= 17(17)
Таким образом, площадь треугольника = 17(17)/2 35
Объем параллелепипеда, вычисленный по векторам a, b и c, дает величину их скалярного тройного произведения.
V = а. (b ×c)
Если тройное скалярное произведение равно 0, то это означает, что векторы лежат в одной плоскости; то есть они компланарны.
Пример 2: Найдите объем параллелепипеда, заданного векторами a, b и c.
a = (6, 3,4), b = (0, 2, 1), c = (5, -1, 2)
Решение:
b×c = (5, 5,-10)
а.(b×c) = (6, 3,-4) . (5, 5, -10) = 85
V= a. (b×c) = 85
(b×c) = 85
Выбор редактора: Скалярный продукт против перекрестного произведения (табличная форма)
Важные моменты:
- Перекрестное произведение двух векторов всегда показывает вектор, который перпендикулярен или ортогонален этим двум векторам.
- Направление двух векторов в векторном произведении может быть задано правилом большого пальца правой руки, а величина векторов показана площадью параллелограмма, образованного исходными векторами.
- Перекрестное произведение двух линейных или параллельных векторов всегда является нулевым вектором, который является скалярной величиной.
Это все для этого поста. Если вам понравилась эта статья, поделитесь ею, если хотите, лайкните, если поделитесь. Вы также можете найти нас на Mix, Twitter, Pinterest и Facebook. Эй, чувак, если ты зашел так далеко, дай нам отзыв в разделе комментариев. Это сделало бы мой день. Вы также можете сделать пожертвование . Ваши пожертвования помогут нам запустить наш веб-сайт и обслуживать вас ЛУЧШЕ. Ваше здоровье!!!
Ваши пожертвования помогут нам запустить наш веб-сайт и обслуживать вас ЛУЧШЕ. Ваше здоровье!!!
Пожертвовать сейчас
Вам также могут понравиться:
- Скалярная величина – определение, типы, свойства, примеры решения
- Векторная величина – определение, типы, свойства, примеры решения
- Скалярное произведение – определение, типы, свойства и Решенные примеры
Распространение любви
Определение, как сделать перекрестное произведение и свойства
В векторной алгебре описываются различные типы векторов, и над этими векторами можно выполнять различные операции, такие как сложение, вычитание, произведение или умножение . Умножение векторов может быть выполнено двумя способами: точечным произведением и перекрестным произведением. Перекрестное произведение векторной алгебры помогает в вычислении ортогональности двух заданных векторов, вычислении крутящего момента и т. д.
В этой статье мы постараемся узнать о перекрестном произведении двух векторов с определением, правилами, решенными примерами и свойствами перекрестного произведения. Перемножение двух векторов — это процесс умножения двух векторов. Перекрестное произведение выражается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, проиллюстрированная в трехмерной системе.
Перемножение двух векторов — это процесс умножения двух векторов. Перекрестное произведение выражается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, проиллюстрированная в трехмерной системе.
Перекрестное произведение — это своего рода умножение векторов, выполняемое между двумя векторами различной природы. Вектор обладает как величиной, так и направлением. Мы можем умножать два или более векторов на перекрестное произведение и скалярное произведение.
В результате перекрестного произведения двух векторов третий вектор перпендикулярен двум главным векторам. Его величина представлена площадью параллелограмма среди них, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также признается векторным произведением, поскольку результирующая векторного произведения двух векторов является векторной величиной.
Узнайте больше о наборах здесь.
Когда два вектора перемножаются друг с другом и конечный продукт данных векторов также является векторной величиной, тогда полученный вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен грани, несущей два заданных вектора.
Векторное произведение или перекрестное произведение двух векторов, скажем, вектора «a» и вектора «b», обозначается как a × b , а его результирующий вектор перпендикулярен векторам а и б . Перекрестное произведение в основном применяется для определения вектора, который перпендикулярен плоской поверхности, натянутой на два вектора. Однако скалярное произведение применяется для определения угла между двумя векторами или длины вектора.
Перекрестное произведение двух векторов, скажем, a × b , эквивалентно другому вектору, расположенному под прямым углом к обоим, и появляется в трехмерном пространстве.
Формула перекрестного произведения между любыми двумя заданными векторами дает площадь между этими векторами. Формула векторного произведения отражает величину результирующего вектора, который представляет собой площадь параллелограмма, натянутого на два вектора.
Если \(\theta\) является углом между заданными двумя векторами a и b, , то формула векторного произведения векторов: Математически выражается как:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\hat{n}\)
Где \(\left|\vec{a}\right|\) и \(\left|\vec{b}\right|\) обозначают величину векторов \(\vec{a}\) и \(\vec{b}\) и \(\theta\) — угол между векторами \(\vec{a}\) и \(\vec{b}\) и \(\hat{n}\ ) — единичный вектор, перпендикулярный обоим векторам \(\vec{a}\) и \(\vec{b}\).
Прочтите эту статью о детерминантах.
- 9{\circ}\) так, чтобы векторное произведение двух векторов было максимальным.

Мы можем предположить это на примере того, что если у нас есть два вектора, простирающиеся в плоскости X-Y, то их векторное произведение даст окончательный результирующий вектор в направлении оси Z, которая перпендикулярна плоскости X-Y. Символ × используется в исходных векторах.
Как найти векторное произведение двух векторов? Рассмотрим два вектора \(\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b}=b_1\hat{i }+b_2\шляпа{j}+b_3\шляпа{k}\). Пусть \(\theta\) — угол, образованный между \(\vec{a}\) и \(\vec{b}\), а \(\hat{n}\) — единичный вектор, перпендикулярный плоскости, содержащей как \(\vec{a}\), так и \(\vec{b}\) . Перекрестное произведение двух векторов можно определить следующим образом:
\(\vec{a}\times\vec{b}=\left(a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\right)\times\left(b_1\hat {i}+b_2\шляпа{j}+b_3\шляпа{k}\право)\)
\(\vec{a}\times\vec{b}=a_1b_1\left(\шляпа{i}\times\ шляпа{i}\правая)+a_1b_2\левая(\шляпа{i}\раз\шляпа{j}\правая)+a_1b_3\левая(\шляпа{i}\раз\шляпа{k}\правая)+a_2b_1\ влево (\ шляпа {j} \ раз \ шляпа {i} \ вправо) \) + \ (a_2b_2 \ влево (\ шляпа {j} \ раз \ шляпа {j} \ вправо) + a_2b_3 \ влево (\ шляпа {j }\times\hat{k}\right)+a_3b_1\left(\hat{k}\times\hat{i}\right)+a_3b_2\left(\hat{k}\times\hat{j}\right )+a_3b_3\влево(\шляпа{к}\раз\шляпа{к}\право)\)
По свойству векторов перекрестного умножения:
\(\hat{i}\times\hat{i}=\hat{j}\times\hat{j}=\hat{k}\times\hat{ k}=0\)
\(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \шляпа{j}\times\шляпа{k}=\шляпа{i},\ \ шляпа {k} \ раз \ шляпа {i} = \ шляпа {j} \)
\ (\ шляпа {j} \ раз \ шляпа {i} = — \ шляпа {k}, \ \ шляпа {k} \times\hat{j}=-\hat{i},\ \hat{i}\times\hat{k}=-\hat{j}\)
Следовательно, уравнение принимает вид:
\(\vec {a}\times\vec{b}=a_1b_2\шляпа{k}-a_1b_3\шляпа{j}-a_2b_1\шляпа{k}+a_2b_3\шляпа{i}+a_3b_1\шляпа{j}-a_3b_2\шляпа{ я}\)
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\hat{i}+\left(a_3b_1-a_1b_3\right)\hat{j}+\left( a_1b_2-a_2b_1\right)\шляпа{k}\)
ИЛИ
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\шляпа{i}-\left (a_1b_3-a_3b_1\справа)\шляпа{j}+\слева(a_1b_2-a_2b_1\справа)\шляпа{k}\)
Ознакомьтесь с этой статьей о матрицах.
Матрица перекрестного произведения
Тот же полученный результат перекрестного произведения может быть сформулирован в матричной форме следующим образом:
\(\vec{a}\times\vec{b}=\left(a_1\hat{i}+ a_2\шляпа{j}+a_3\шляпа{k}\право)\раз\влево(b_1\шляпа{i}+b_2\шляпа{j}+b_3\шляпа{k}\право)\)
Что эквивалентно:
\(\vec{a}\times\vec{b}=a_1b_2\hat{k}-a_1b_3\hat{j}-a_2b_1\hat{k}+a_2b_3\hat{i }+a_3b_1\шляпа{j}-a_3b_2\шляпа{i}\)
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\шляпа{i}+\ влево(a_3b_1-a_1b_3\вправо)\шляпа{j}+\влево(a_1b_2-a_2b_1\вправо)\шляпа{k}\)
ИЛИ
\(\vec{a}\times\vec{b}= \left(a_2b_3-a_3b_2\right)\hat{i}-\left(a_1b_3-a_3b_1\right)\hat{j}+\left(a_1b_2-a_2b_1\right)\hat{k}\)
Матрица представительство:
\(\vec{a}\times\vec{b}=\left[\begin{matrix}\hat{i}&\hat{j}&\hat{k}\\
a_1&a_2&a_3\\
b_1&b_2&b_3\ end{matrix}\right]\)
Также читайте о статистике в этой статье.
Правило правой руки – векторное произведение двух векторов Мы можем определить направление единичного вектора с помощью правила правой руки.
В этом конкретном правиле вытяните правую руку так, чтобы указательный палец правой руки был в направлении первого вектора i,e вектора «A» плюс средний палец был в направлении второго вектора, который является вектором «В». Затем большой палец правой руки показывает направление единичного вектора n.
Это положение большого пальца в направлении векторного произведения двух векторов. Применяя правило правой руки, мы можем просто показать, что векторное произведение векторов не коммутативно. Посмотрите на изображение ниже, чтобы полностью понять этот подход.
Свойства векторного произведенияЧтобы получить векторное произведение двух векторов, мы можем применить свойства. Такие свойства, как антикоммутативность, ассоциативность, дистрибутивность, свойство нулевого вектора, играют жизненно важную роль в получении перекрестного произведения двух векторов. Итак, давайте проверим эти свойства один за другим:
- Длина векторного произведения двух векторов =
- \(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\ right|\sinθ\hat{n}\)
- Векторные произведения некоммутативны.

- Если \(\vec{x}\) и \(\vec{y}\) любые два вектора, то:
- \(\vec{x}\times\vec{y}=-\left( \vec{y}\ \times\vec{x}\right)\)
- Векторное произведение ассоциативно относительно скалярного умножения.
- Если \(\vec{x}\) и \(\vec{y}\) — любые два вектора и λ — скаляр, то;
- \(\lambda\left(\vec{x}\times\vec{y}\right)=\left(\lambda\vec{x}\right)\times\vec{y}=\vec{x }\times\left(\lambda\vec{y}\right)\)
- Векторный продукт — это дистрибутив относительно сложения векторов.
- Если \(\vec{x}\), \(\vec{y}\) и \(\vec{z}\) — любые три вектора, то:
- \(\vec{x}\times \left(\vec{y}+\vec{z}\right)=\left(\vec{x}\times\vec{y}\right)+\left(\vec{x}\times\vec{ z}\right)\)
- Перекрестное произведение нулевого вектора или свойство нулевого вектора: \(\vec{a}\times\vec{b}=0\), если a=0 или b=0.
- \(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \ \шляпа{j}\times\шляпа{k}=\шляпа{i}\ и\ \ \ \hat{k}\times\hat{i}=\hat{j}\ \ \)
- \(\hat{i}\times\hat{i}=\ \hat{j}\times\ шляпа {j} = \ \ шляпа {k} \ раз \ шляпа {k} = 0 \)
- \ (\ шляпа {j} \ раз \ шляпа {i} = — \ шляпа {k}, \ \ шляпа { k}\times\hat{j}=-\hat{i},\ \hat{i}\times\hat{k}=-\hat{j}\)
- \(\text{If} \vec {x}=x_1\шляпа{i}+x_2\шляпа{j}+x_3\шляпа{k} \text{ и }\vec{y}=y_1\шляпа{i}+y_2\шляпа{j}+y_3 \hat{k}\text{ два вектора, тогда:}\)
- \(\vec{x}\times \vec{y}\left[\begin{matrix}\hat{i}&\hat{j}&\hat{k}\\
x_1&x_2&x_3\\
y_1&y_2&y_3\end {matrix}\right] \) - Тройное перекрестное произведение
Перемножение вектора с двумя другими векторами означает тройное перекрестное произведение векторов. Конечным результатом тройного векторного произведения является сам вектор.
Конечным результатом тройного векторного произведения является сам вектор. - \(\left(\vec{a}\times\vec{b}\right)\times\vec{c}=\left(\vec{a}⋅\vec{c}\right)\vec{ b}−\left(\vec{b}⋅\vec{c}\right)\vec{a}\) Здесь a, b и c — векторы.
Прочтите эту статью об отношениях и функциях.
Векторы, представляющие собой комбинацию величины и направления, могут применяться для представления физических величин, обычно в физике векторы используются для обозначения смещения, скорости и ускорения, поскольку это становится полезным для анализа физических величин. (включая размер и направление) в виде векторов. Перекрестное произведение векторов находит применение при определении ортогональности двух заданных векторов, вычислении крутящего момента, площади треугольника, параллелограмма и т. д.
- Если \(\vec{x}\) и \(\vec{y}\) две смежные стороны параллелограмма, то площадь параллелограмма:
- \(=\left|\vec{x }\times\vec{y}\right|\)
- Если \(\vec{x}\) и \(\vec{y}\)диагонали параллелограмма, то площадь параллелограмма:
- \(=\left|\vec{x}\times\vec{y}\right|\)
- Если \(\vec{x}\) и \(\vec{y}\) две смежные стороны треугольника, то площадь треугольника:
- \(=\frac{1}{2}\left|\vec{x}\times\vec{y}\right|\)
- Угол между двумя векторами \(\vec{x}\) и \(\vec{y}\) можно определить с помощью векторного произведения по формуле = \(\sinθ=\frac{\left|\vec {a}\times\vec{b}\right|}{\left|\vec{a}\right|\left|\vec{b}\right|}\).

- Поскольку перекрестное произведение двух векторов ортогонально каждому из векторов.
- Перекрестное произведение перпендикулярных векторов =
- \(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\ шляпа{n}=\left|\vec{a}\right|\left|\vec{b}\right|\sin9{\ circ} \ hat {n} = 0 \)
Другие темы по математике смотрите здесь.
Примеры решения перекрестного произведенияНиже приведены некоторые примеры решения по этой теме:
Пример решения 1: C = 4i + 5j и D = 6i – 4j. Вычислить векторное произведение векторов C и D:
ПОЯСНЕНИЯ:
We C × D = (4i + 5j) × (6i – 4j)
= 24 (i × i ) – 16( i × j ) + 30(j × i) – 20 (j × j)
Мы знаем, что:
\(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \ \шляпа{j}\times\шляпа{k}=\шляпа{i}\ и \\ \шляпа{k}\times\шляпа{i}=\шляпа{j}\)
\(\шляпа{i}\times\шляпа{i}=\ \шляпа{j}\times\шляпа {j}=\ \шляпа{k}\times\шляпа{k}=0\)
\(\шляпа{j}\times\шляпа{i}=-\шляпа{k},\ \шляпа{k }\times\hat{j}=-\hat{i},\ \\hat{i}\times\hat{k}=-\hat{j}\)
Отсюда получаем:
C × D = -16k -30k = -46 k
, поэтому перекрестное произведение C и D представляет собой вектор величины 46 и в отрицательном направлении z.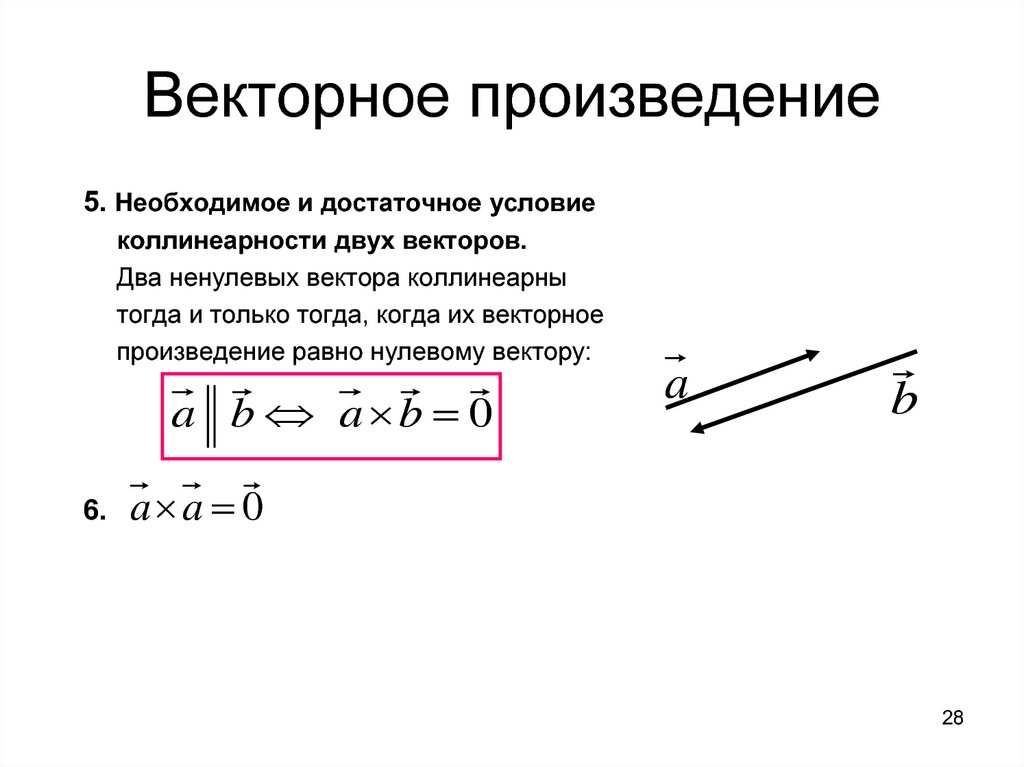
Поскольку C и D находятся в плоскости XY, очевидно, что векторное произведение должно быть перпендикулярно этой плоскости, то есть оно должно быть в направлении z.
Решенный Пример 2: Какова величина результирующего перекрестного произведения двух параллельных векторов \(\vec{a}\) и \(\vec{b}\)?
КОНЦЕПЦИЯ:
Векторное произведение: также известно как перекрестное произведение, величина которого равна произведению величины двух векторов и синуса угла между ними, направление которых перпендикулярно плоскости из двух векторов.
Математически это записывается так:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\ hat{n}\)
Где \(\theta\) — угол между вектором \(\vec{a}\) и \(\vec{b}\). и \(\hat{n}\) — единичный вектор, который перпендикулярен обоим векторам \(\vec{a}\) и \(\vec{b}\).
ОБЪЯСНЕНИЕ:
Математически это записывается так:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b} \right|\sinθ\шляпа{n}\) 9{\ circ} \ шляпа {п} = 0 \).
Мы надеемся, что приведенная выше статья о перекрестном произведении поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о перекрестном произведенииВ.1 Что такое определение перекрестного произведения?
Ответ 1 Когда два вектора перемножаются друг с другом и конечный продукт данных векторов также является векторной величиной, тогда полученный вектор называется перекрестным произведением двух векторов или векторным произведением.
В.2 Как рассчитать перекрестное произведение?
Ans.2 Векторное произведение или перекрестное произведение двух векторов, скажем, вектора «a» и вектора «b», обозначается как a × b, а его результирующий вектор перпендикулярен векторам a и b.
Q.3 Для чего используется перекрестное произведение?
Ответ 3 Перекрестное произведение, используемое для вычисления угла между двумя заданными векторами, для оценки вектора, нормального к плоскости, для вычисления момента силы относительно точки и для определения момента силы о линии.
Q.4 Чему равно векторное произведение двух векторов?
Ответ 4 В результате перекрестного произведения двух векторов третий вектор перпендикулярен двум главным векторам. Его величина представлена площадью параллелограмма среди них, а его направление можно определить по правилу большого пальца правой руки.
В.5 Как работает кросс-произведение?
Ответ 5 Скалярное произведение работает в любом количестве измерений, но перекрестное произведение просто работает в 3D. Скалярное произведение измеряет, насколько два вектора ведут в одном и том же направлении, а векторное произведение измеряет, насколько два вектора указывают в противоположных направлениях.
»
Q.6 Каковы свойства перекрестного произведения?
Ответ 6 Ниже приведены некоторые важные свойства векторных произведений:
- Произведения векторов некоммутативны.
- Векторное произведение ассоциативно относительно скалярного умножения.
- Продукт Vector является дистрибутивным в отношении сложения векторов.
- Перекрестное произведение параллельного вектора = 0.
”
Q.7 В чем разница между скалярным произведением и перекрестным произведением?
Ответ 7 Основное различие между скалярным произведением и перекрестным произведением заключается в том, что скалярное произведение определяется как произведение величины векторов и cos угла между векторами, с другой стороны, перекрестное произведение Произведение представляет собой произведение величины вектора на синус угла.
Q. 8 Каковы типы векторов?
8 Каковы типы векторов?
Ответ 8 Различные типы векторов: нулевой вектор, единичный вектор, вектор положения, ко-начальный вектор, похожие и разные векторы, копланарный вектор, коллинеарный вектор, равный вектор, вектор смещения и отрицательные векторы.
Q.9 В чем разница между вектором и единичным вектором?
Ответ 9 Любая физическая величина, которая имеет как величину, так и направление, называется векторной величиной. Принимая во внимание, что вектор, который имеет величину один, называется единичным вектором.
Q.10 . Что такое точечный продукт?
Ответ 10 Скалярное произведение — это один из способов умножения двух или более заданных векторов. Конечным результатом скалярного произведения векторов является скалярная величина. Следовательно, скалярное произведение также идентифицируется как скалярное произведение. Алгебраически это сумма произведений одинаковых записей двух строк чисел.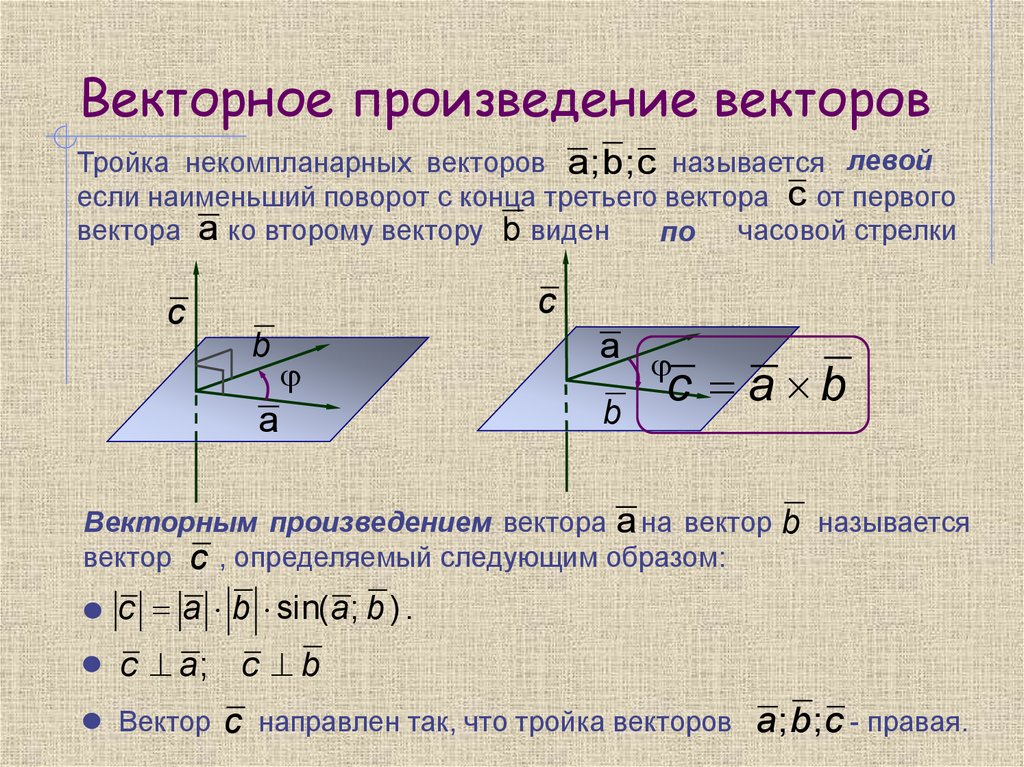
| Формула сечения: Формула внутреннего и внешнего сечения в координатной геометрии с выводом |
| Свойства определителей: Изучите определение, переключение, инвариантность, все нулевые свойства на примерах! |
| Гармоническая прогрессия: значение, формулы, приложения и примеры решений |
| Площадь четырехугольника: изучение формул, расчет площади и др.0797 |
Векторная алгебра: введение в перекрестное произведение
Векторная алгебра: введение в перекрестное произведениечто вы узнаете…
Обзор
Умножение векторов
» Два произведения из-за ортогональности компонентов векторов
→ скалярный продукт определяется для параллельных компонентов p→⋅q→» role=»presentation»>→p⋅→qp→⋅q→=p→⋅a→» role=»presentation»>=→p⋅→a=p→⋅a→
→ перекрестное произведение определяется для компонентов, перпендикулярных p→×q→ ;» role=»презентация»>→p×→qp→×q→=p→×b→» role=»презентация»>=→p×→b=p→×b→
два произведения
Мы узнали, что скалярное произведение вектора определяется как параллельное умножение компонентов. Это определение обеспечивает математическую модель причины и следствия, направленные в одном направлении.
Это определение обеспечивает математическую модель причины и следствия, направленные в одном направлении.
На этой странице шаг за шагом представлен векторный векторный продукт.
Свойство направления причинно-следственных связей: Когда векторная величина x→» role=»presentation»>→xx→ приводит к другой векторной величине y→» role=»presentation»>→yy→ ,
(1) в некоторых сценариях применения направление результата y→» role=»presentation»>→yy→ будет таким же, как направление причины x→ » role=»презентация»>→xx→ или
(2) в некоторых других сценариях применения направление результата y→» role=»presentation»>→yy→ будет перпендикулярно причине x→» роль=»презентация»>→xx→. Это свойство приводит к определению векторного скалярного произведения (в котором взаимодействуют только параллельные компоненты) и векторного векторного произведения (в котором взаимодействуют только перпендикулярные компоненты)
Влияние направления : В математических расчетах векторы обладают следующими свойствами
•
Вектор представлен компонентами вдоль ортогональных направлений.
• При сложении векторов параллельные компоненты складываются.
• Два типа векторного умножения определены для компонента параллельно и перпендикулярно компоненту.
Параллельные компоненты вектора образуют произведение, называемое скалярным произведением векторов. Скалярное произведение векторов имеет значение или практическое применение — причина и следствие параллельны.
Аналогично этому, имеет ли векторное перекрестное произведение какой-либо смысл или практическое применение? ИЛИ это просто абстракция?
Рассмотрим поле с посевами на корню, и нож срезает урожай под углом. Перекрестное произведение (в котором компоненты взаимодействуют перпендикулярно) можно понимать следующим образом:
• Если лезвие проходит под прямым углом к культуре, то оно срезает максимум
• Если лезвие срезает вертикально параллельно культуре, оно не срезать никакую культуру
• Если лезвие срезает под углом θ» role=»presentation»>θθ, то срез культуры пропорционален компоненту, перпендикулярному культуре
И, конечно же, перекрестное произведение также используется в абстрактной форме для вычисления произведений между векторами.
Когда две векторные величины взаимодействуют, образуя произведение, в умножении участвует либо одна из составляющих (1) параллельная, либо (2) перпендикулярная.
В практических сценариях, когда один компонент взаимодействует, другой компонент не взаимодействует и теряется в продукте.
резюме
На абстрактном уровне возможны два продукта. Дан множитель p→» role=»презентация»>→pp→ и множитель q→» роль=»презентация»>→qq→. q→» role=»presentation»>→qq→ разбивается на a→» role=»presentation»>→aa→ и b→» role=»presentation»>→bb→, так что
q→=a→+b→» role=»presentation»>→q=→a+→bq→=a→+b→ и
a→» role=»presentation»>→aa→ параллельно p→» role=»presentation»>→pp→
b→» role=»presentation»>→bb→ находится перпендикулярно p→» role=»presentation»>→pp→
для каждой из этих двух составляющих определены две формы умножения. x22C5;q→=p→⋅a→» role=»presentation»>→p⋅→q=→p⋅→ap→⋅q→=p→⋅a→
• другой компонент, перпендикулярный вектору, называемый векторным векторным произведением. p→×q→=p→×b→» role=»презентация»>→p×→q=→p×→bp→×q→=p→×b→
p→×q→=p→×b→» role=»презентация»>→p×→q=→p×→bp→×q→=p→×b→
Схема
Схема материала для изучения векторной алгебры выглядит следующим образом.
Примечание. Щелкните здесь для подробного ознакомления с векторной алгеброй.
• Знакомство с векторами
→ Знакомство с векторами
→ Представление векторов
• Основные свойства векторов
→ Величина векторов
→ Типы векторов
→ Свойства величины
• Векторы и координатная геометрия
→ Векторы и координатная геометрия
→ Вектор положения точки
→ Направленный косинус
• Роль направления в векторной арифметике
→ Векторная арифметика
→ Понимание направления векторов
• Добавление вектора
→ Надстройка Vector: Первые принципы
→ Добавление вектора: Форма компонента
→ Треугольный закон
→ Закон параллелограмма
• Умножение вектора на скаляр
→ Скалярное умножение
→ Стандартные единичные векторы
→ Вектор как сумма векторов
→ Форма векторного компонента
• Скалярное произведение векторов
→ Введение в векторное умножение
→ Причинно-следственная связь
→ Дополнительный продукт: основные принципы
→ Скалярный продукт: проекционная форма
→ Дополнительный продукт: Форма компонента
→ Скалярный продукт с направлением
• векторное перекрестное произведение
→ Умножение векторов: векторное произведение
→ Перекрестное произведение: основные принципы
→ Перекрестное произведение: площадь параллелограмма
→ Перекрестный продукт: Форма компонента
→ Перекрестное произведение: направление удалено
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах, которые обеспечивают чувствительность к регистру 9Пример 0006 e и пример E не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Неработающее изображениеЕсли на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным размером X , где отсутствует изображение. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера, если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».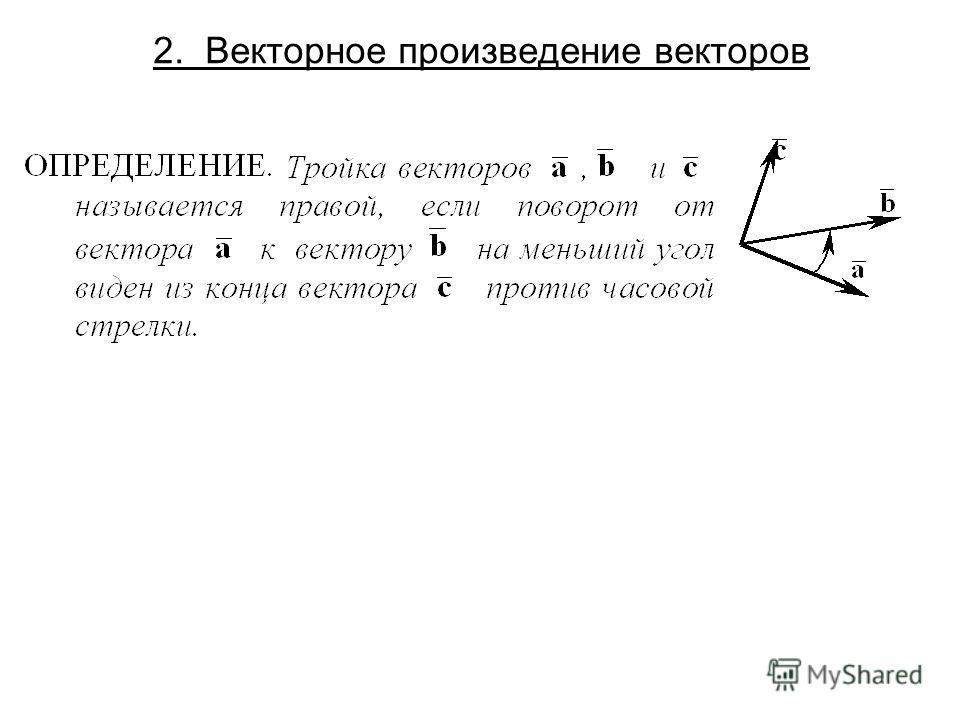
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/ пример. На платформах с учетом регистра символов PNG и png не совпадают.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать при активации новой темы или изменении правил перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .

- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки . 9index.php$ — [L]
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Использовать SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
- Войдите в cPanel.

- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.

- При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает. 93$, то перекрестное произведение $\vec{u}$ и $\vec{v}$ , обозначаемое $\vec{u} \times \vec{v}$, является уникальным вектором, перпендикулярным обоим $\ vec{u}$ и $\vec{v}$ и образует правую систему с $\vec{u}$, $\vec{v}$ и $\vec{u} \times \vec{v}$ соответственно. Перекрестное произведение $\vec{u} \times \vec{v}$ можно рассчитать как $\vec{u} \times \vec{v} = (u_2v_3 — u_3v_2)\vec{i} + (u_3v_1 — u_1v_3 )\vec{j} + (u_1v_2 — u_2v_1) \vec{k}$. В качестве альтернативы $\vec{u} \times \vec{v} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ u_1 & u_2 & u_3\\ v_1 & v_2 & v_3 \end{vmatrix}$ при вычислении путем расширения кофактора по первой строке.

Используя последнее определение перекрестного произведения двух векторов в терминах определителя 3 x 3:
(1)
\begin{align} \begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ u_1 & u_2 & u_3\\ v_1 & v_2 & v_3 \end{vmatrix} = \ begin{vmatrix} u_2 & u_3\\ v_2 & v_3 \end{vmatrix} \vec{i} — \begin{vmatrix} u_1 & u_3\\ v_1 & v_3 \end{vmatrix} \vec{j} + \begin{ vmatrix} u_1 и u_2\\ v_1 и v_2 \end{vmatrix} \vec{k} \end{align} 93$ и $k$ является скаляром, то выполняются следующие свойства перекрестных произведений:
а) $\vec{u} \times \vec{u} = \vec{0}$.
b) $\vec{u} \cdot (\vec{u} \times \vec{v}) = 0$ и $\vec{v} \times (\vec{u} \times \vec{ v}) = \vec{0}$.
в) $\vec{u} \times \vec{v} = — \vec{v} \times \vec{u}$. (Антикоммутативное свойство)
d) $\vec{u} \times (\vec{v} \times \vec{w}) = (\vec{u} \cdot \vec{w}) \vec{ v} — (\vec{u} \cdot \vec{v})\vec{w}$.
e) $\vec{u} \times (\vec{v} + \vec{w}) = \vec{u} \times \vec{v} + \vec{u} \times \vec{ w}$ и $(\vec{u} + \vec{v}) \times \vec{w} = \vec{u} \times \vec{w} + \vec{v} \times \vec{w }$. (Распределительные свойства).
f) $\vec{u} \cdot ( \vec{v} \times \vec{w} ) = (\vec{u} \times \vec{v}) \cdot \vec{w}$ .
g) $(k \vec{u}) \times \vec{v} = \vec{u} \times (k \vec{v}) = k (\vec{u} \times \vec{ в})$.- Доказательство a)
(2)
\begin{align} \vec{u} \times \vec{u} = \begin{vmatrix} u_2 & u_3\\ u_2 & u_3\end{vmatrix} \vec{i} — \begin{vmatrix} u_1 & u_3\\ u_1 & u_3\end{vmatrix} \vec{j} + \begin{vmatrix} u_1 & u_2\\ u_1 & u_2\end{vmatrix} \vec{k} \\ \vec{u} \times \vec{u}= (u_2u_3 — u_2u_3)\vec{i} — (u_1u_3 — u_1u_3)\vec{j} + (u_1u_2 — u_1u_2)\vec{k} \\ \vec{u} \times \vec{ u}= 0\vec{i} + 0\vec{j} + 0\vec{k} \\ \vec{u} \times \vec{u}= \vec{0} \end{align}
- Доказательство c) Рассмотрим следующий геометрический аргумент:
- Обратите внимание, что $\vec{u} \times \vec{v}$ — это вектор, перпендикулярный $\vec{u}$ и $\vec{v}$, образующий правую систему с $\vec {u}$, $\vec{v}$ и $\vec{u} \times \vec{v}$ соответственно.
 Теперь обратите внимание, что $\vec{v} \times \vec{u}$ — это вектор, перпендикулярный $\vec{u}$, и $\vec{v}$ по-прежнему, однако вместо $\vec{v} \times \ vec{u}$ образует правую систему с $\vec{v}$, $\vec{u}$ и $\vec{v} \times \vec{u}$ соответственно. 92 \тета\\\четверка \четверка\| \vec{u} \times \vec{v} \| = \| \vec{и} \| \| \vec{v} \| \sin \theta \quad \blacksquare \end{align}
Теперь обратите внимание, что $\vec{v} \times \vec{u}$ — это вектор, перпендикулярный $\vec{u}$, и $\vec{v}$ по-прежнему, однако вместо $\vec{v} \times \ vec{u}$ образует правую систему с $\vec{v}$, $\vec{u}$ и $\vec{v} \times \vec{u}$ соответственно. 92 \тета\\\четверка \четверка\| \vec{u} \times \vec{v} \| = \| \vec{и} \| \| \vec{v} \| \sin \theta \quad \blacksquare \end{align}Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3.0 License
Численность, математика и статистика — набор академических навыков
Cross Product
Главное меню ContentsToggle 1 Определение 2 Расчет перекрестного произведения 3 Свойства 4 Рабочий пример 5 Рабочая тетрадь 6 Проверьте себя 7 См. также 8 Внешние ресурсы
Определение
Определено перекрестное произведение двух векторов $\boldsymbol{\mathrm{a} }$ и $\boldsymbol{\mathrm{b} }$, разделенных углом $\theta$ радиан. следующим образом:
\[\boldsymbol{\mathrm{a}}\times\boldsymbol{\mathrm{b}}=\lvert\boldsymbol{\mathrm{a}}\rvert\lvert\boldsymbol{\mathrm{b } }\rvert \sin{(\theta)}\;\boldsymbol{\mathrm{\hat{n} } }\]
$\boldsymbol{\mathrm{\hat{n} } }$ — единичный вектор перпендикулярно к $\boldsymbol{\mathrm{a}}$ и $\boldsymbol{\mathrm{b}}$ таким, что $\boldsymbol{\mathrm{a}}$, $\boldsymbol{\mathrm{b}}$ и $\boldsymbol{\mathrm{\hat{n} } }$ образуют правую систему.

Перекрестное произведение дает вектор, перпендикулярный как $\boldsymbol{\mathrm{a}}$, так и $\boldsymbol{\mathrm{b}}$
|250px
Вычисление векторного произведения
Представление векторного произведения в виде определителя матрицы позволяет нам явно вычислить каждый компонент:
\begin{align} \boldsymbol{\mathrm{a} }\times\boldsymbol{\mathrm {b} } &= \begin{vmatrix} \boldsymbol{\mathrm{e}}_1 & \boldsymbol{\mathrm{e}}_2 & \boldsymbol{\mathrm{e}}_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \\ &=(a_2b_3-a_3b_2)\boldsymbol{\mathrm{e}}_1 + (a_3b_1-a_1b_3)\boldsymbol{\mathrm{e}}_2 + (a_1b_2 -a_2b_2)\boldsymbol{\mathrm{e} }_3 \end{align}
Напомним, что $\boldsymbol{\mathrm{e} }_1$, $\boldsymbol{\mathrm{e} }_2$ и $\boldsymbol{\mathrm{e} }_3$ образуют единичные базисные векторы.
Свойства
Перекрестное произведение антикоммутативно:
- $\boldsymbol{\mathrm{b}}\times\boldsymbol{\mathrm{a}}=-\boldsymbol{\mathrm{a}}\times\boldsymbol {\ mathrm{b}}.
 $
$
Перекрестное произведение является дистрибутивным над сложением:
- $\boldsymbol{\mathrm{a}}\times(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}})=\boldsymbol{ \mathrm{a}}\times\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{a}}\times\boldsymbol{\mathrm{c}},$
- $(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}})\times\boldsymbol{\mathrm{a}}=\boldsymbol{\mathrm{b}}\times\boldsymbol {\ mathrm{a}} =\boldsymbol{\mathrm{c}}\times\boldsymbol{\mathrm{a}}.$
Поскольку угол между параллельными векторами равен $0$ и $\sin{0}=0$, векторное произведение вектора на себя равно $0$:
- $\boldsymbol{\mathrm{a}}\times \boldsymbol{\mathrm{a}} = \boldsymbol{0}.$
Согласно тому же аргументу, если $\boldsymbol{\mathrm{a}}$ и $\boldsymbol{\mathrm{b}}$ параллельны, то их векторное произведение равно $0$:
- $\boldsymbol{\mathrm{a}}\times\boldsymbol{\mathrm{b}}=\boldsymbol{\mathrm{b}}\times\boldsymbol{\mathrm{a}}=\boldsymbol{0 }.
 $
$
Рабочий пример
Пример 1
Данные векторы $\boldsymbol{\mathrm{a} }=(4,\,7,\,-3)$ и $\boldsymbol{\mathrm{b} }=(5 ,-8,11)$, вычислить $\boldsymbol{\mathrm{a}}\times\boldsymbol{\mathrm{b}}$.
Решение
Напомним, что векторное произведение можно вычислить путем оценки определителя.
\begin{align} \boldsymbol{\mathrm{a}}\times\boldsymbol{\mathrm{b}} &= \begin{vmatrix} \boldsymbol{\mathrm{e}}_1 & \boldsymbol{\mathrm {e} }_2 & \boldsymbol{\mathrm{e} }_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \\ &=(a_2b_3-a_3b_2)\boldsymbol{\mathrm{ e} }_1+(a_3b_1-a_1b_3)\boldsymbol{\mathrm{e}}_2+(a_1b_2-a_2b_1). \end{align}
Для заданных векторов векторное произведение равно
\begin{align} \boldsymbol{\mathrm{a} }\times\boldsymbol{\mathrm{b} } &= \begin{vmatrix} \ boldsymbol{\mathrm{e}}_1 & \boldsymbol{\mathrm{e}}_2 & \boldsymbol{\mathrm{e}}_3 \\ 4 & 7 & -3 \\ 5 & -8 & 11 \end{ vmatrix} \\ &=(7\cdot11-(-3)\cdot(-8))\boldsymbol{\mathrm{e}}_1+((-3)\cdot5-4\cdot11)\boldsymbol{\mathrm{ e} }_2+(4\cdot(-8)-7\cdot5)\boldsymbol{\mathrm{e}}_3 \\ &=(77-24)\boldsymbol{\mathrm{e}}_1+(-15- 44)\boldsymbol{\mathrm{e}}_2+(-32-35)\boldsymbol{\mathrm{e}}_3 \\ &=53\boldsymbol{\mathrm{e}}_1-59\boldsymbol{\mathrm{e}}_2-67\boldsymbol{\mathrm{e}}_3 \end{align}
Следовательно,
\[\boldsymbol{\mathrm{a}}\times\boldsymbol{\ mathrm{b}}= 53\boldsymbol{\mathrm{e}}_1-59\boldsymbol{\mathrm{e}}_2-67\boldsymbol{\mathrm{e}}_3.

- $\boldsymbol{\mathrm{b}}\times\boldsymbol{\mathrm{a}}=-\boldsymbol{\mathrm{a}}\times\boldsymbol {\ mathrm{b}}.
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в . htaccess, чтобы эти скрипты могли работать.
htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что нужно изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccessСамый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер

 09.2022
09.2022 09.2022
09.2022 08.2022
08.2022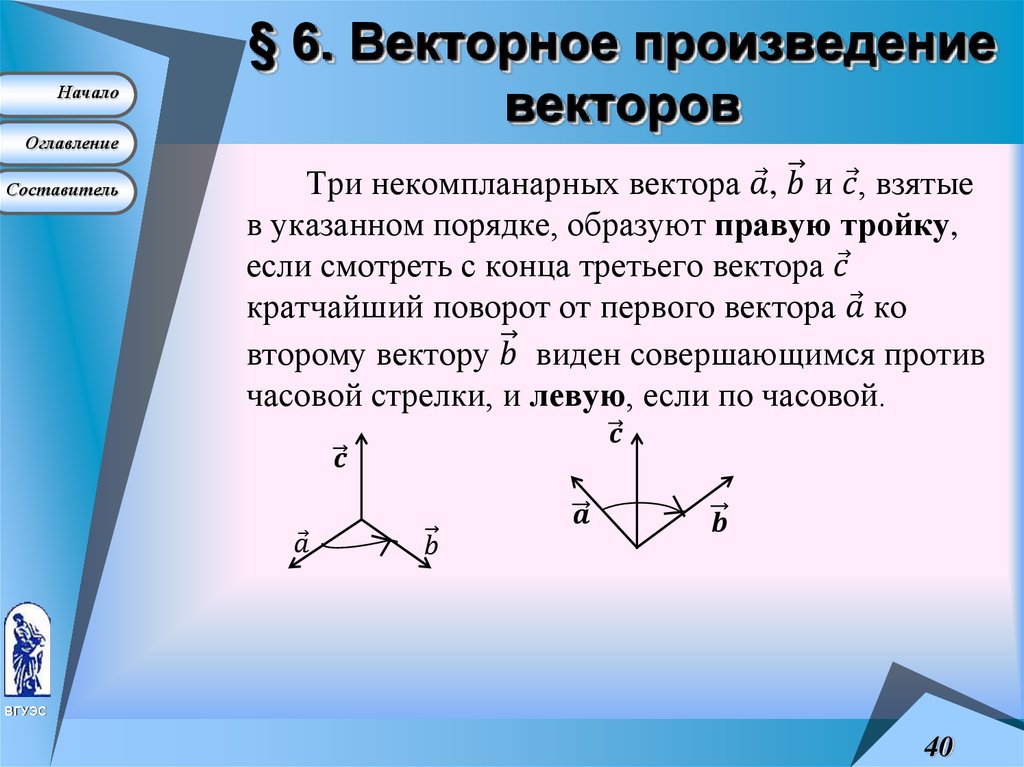


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Определение. Вычисление. Свойства.
Определение. Вычисление. Свойства. i*j=k;
i*j=k;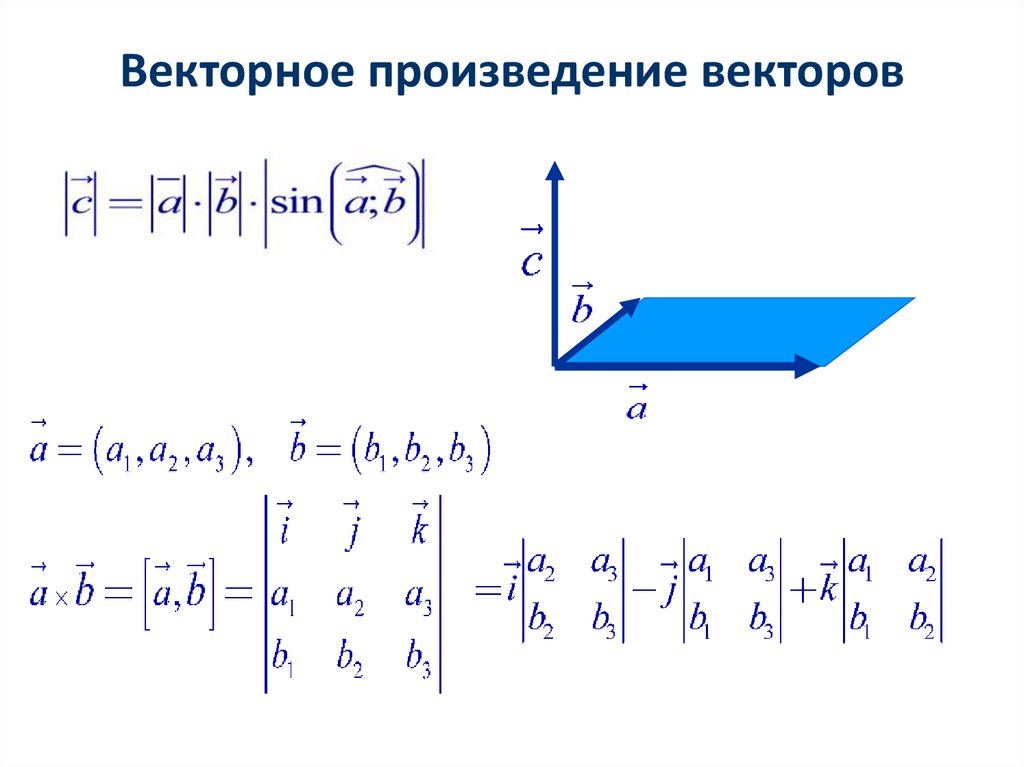

 Обратная связь — 161.97.168.212 (0.008 с.)
Обратная связь — 161.97.168.212 (0.008 с.)
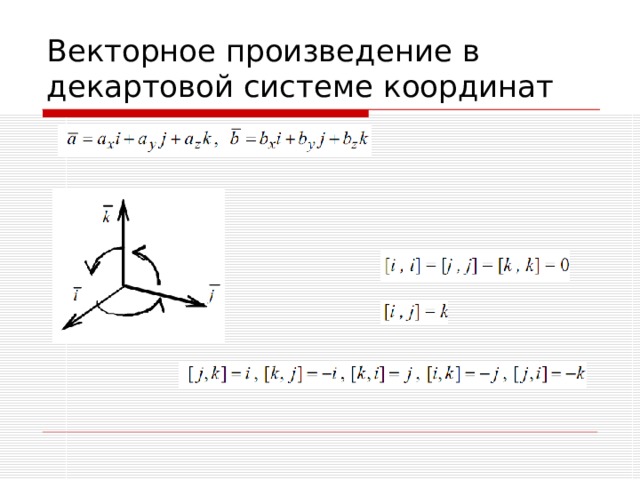 Конечным результатом тройного векторного произведения является сам вектор.
Конечным результатом тройного векторного произведения является сам вектор.
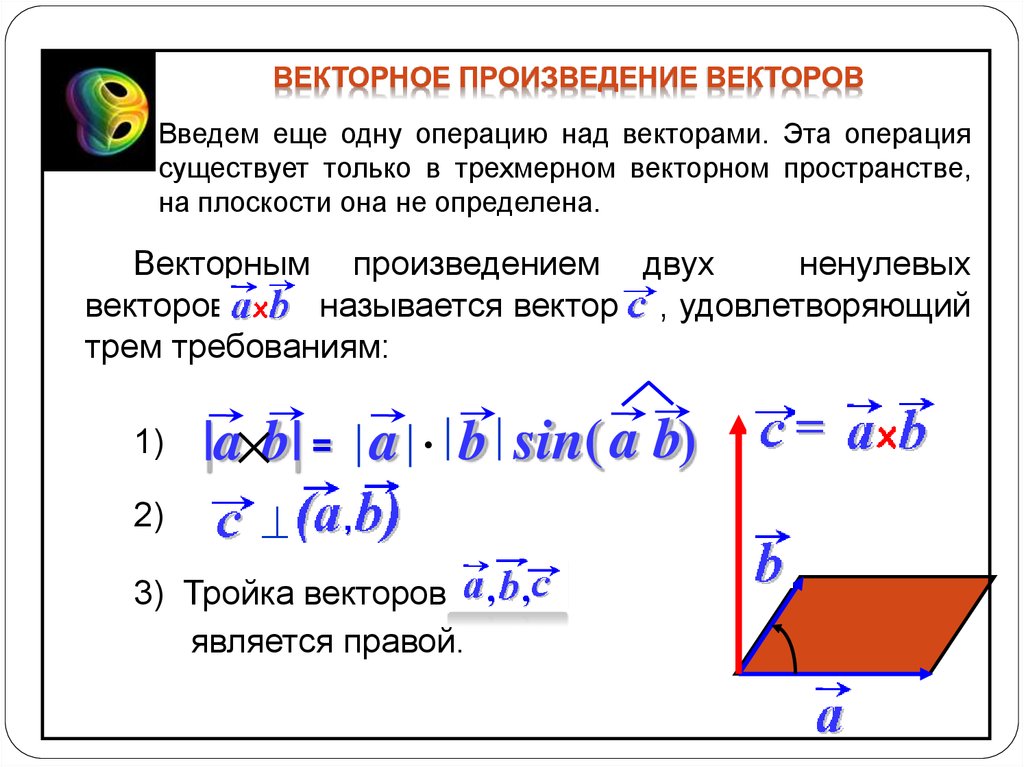



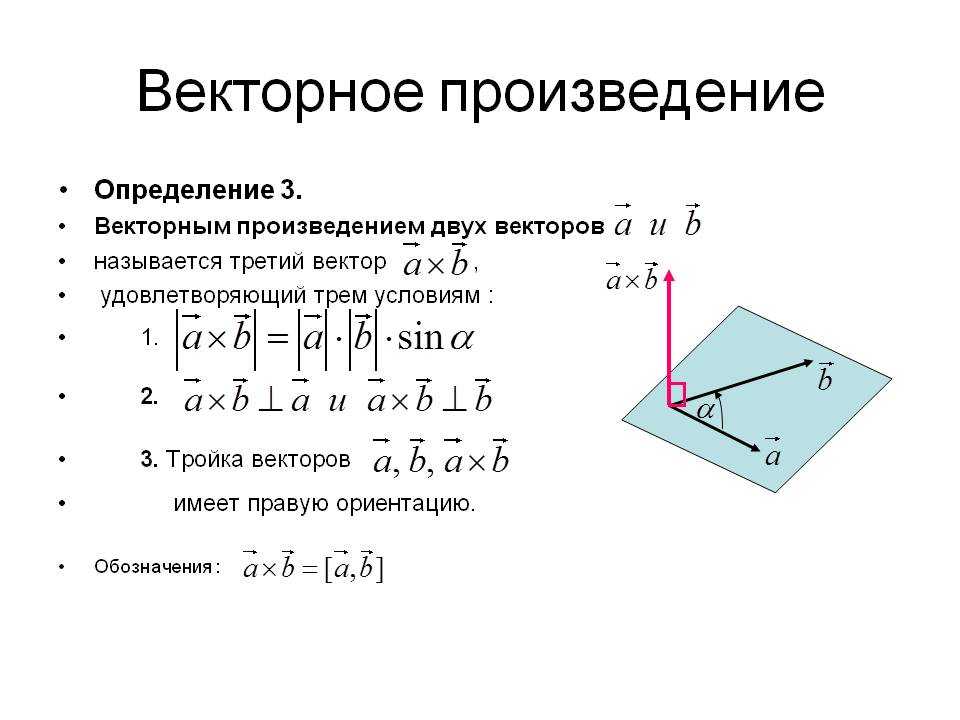
 Теперь обратите внимание, что $\vec{v} \times \vec{u}$ — это вектор, перпендикулярный $\vec{u}$, и $\vec{v}$ по-прежнему, однако вместо $\vec{v} \times \ vec{u}$ образует правую систему с $\vec{v}$, $\vec{u}$ и $\vec{v} \times \vec{u}$ соответственно. 92 \тета\\\четверка \четверка\| \vec{u} \times \vec{v} \| = \| \vec{и} \| \| \vec{v} \| \sin \theta \quad \blacksquare \end{align}
Теперь обратите внимание, что $\vec{v} \times \vec{u}$ — это вектор, перпендикулярный $\vec{u}$, и $\vec{v}$ по-прежнему, однако вместо $\vec{v} \times \ vec{u}$ образует правую систему с $\vec{v}$, $\vec{u}$ и $\vec{v} \times \vec{u}$ соответственно. 92 \тета\\\четверка \четверка\| \vec{u} \times \vec{v} \| = \| \vec{и} \| \| \vec{v} \| \sin \theta \quad \blacksquare \end{align}
 $
$ $
$