Координатная форма векторного произведения.
ТЕОРЕМА
22.1. Пусть
в пространстве выбран ортонормированный
базис 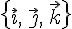 ,
в котором
,
в котором 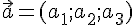 и
и 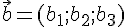 .
Тогда
.
Тогда
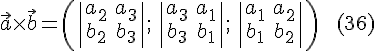
Доказательство. Рассмотрим
ортонормированный базис 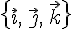 ,
определяющий ориентацию пространства
,
определяющий ориентацию пространства  и
вычислим векторные произведения базисных
векторов. Результаты занесем в таблицу
и
вычислим векторные произведения базисных
векторов. Результаты занесем в таблицу
По определению координат вектора в базисе имеем
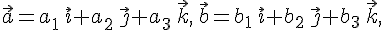
поэтому

Используя доказанные свойства векторного произведения, получаем
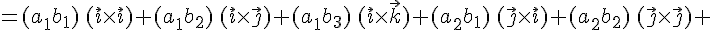
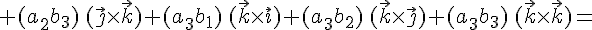
Используя результаты векторного произведения базисных векторов из таблицы, получим
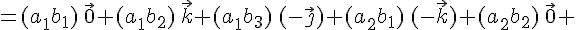
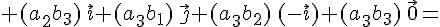
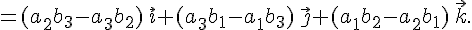
Нетрудно
видеть, что это подробная запись  .
Теорема доказана.
.
Теорема доказана.
Приложения векторного произведения.
Вычисление площадей.
Задача
22.1. Пусть
треугольник 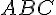 задан
координатами своих вершин
задан
координатами своих вершин 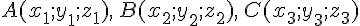 в
декартовой системе координат. Найти
площадь треугольника
в
декартовой системе координат. Найти
площадь треугольника 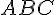
Решение. Из свойства 4. векторного произведения векторов получаем, что

Далее
по формуле  находим
находим

Наконец,
используя формулы 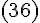 и
и 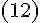
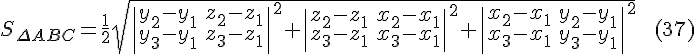
Если  ,
то есть
,
то есть 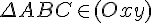 ,
то формула
,
то формула 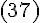 приобретает
вид:
приобретает
вид:
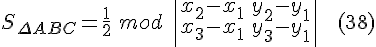
23 Двойное векторное произведение.
Определение
23.1. Вектор 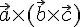
Отметим,
что векторы и 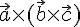 компланарны.
В самом деле это так, если
векторы
компланарны.
В самом деле это так, если
векторы  и
и 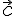 коллинеарны.
Если же векторы
коллинеарны.
Если же векторы 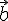 и
и 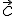 не
коллинеарны, то вектор
не
коллинеарны, то вектор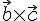
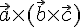 ,
перпендикулярный вектору
,
перпендикулярный вектору 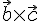 ,
будет компланарен с векторами
,
будет компланарен с векторами 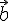 и
и 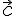 .
Значит, если векторы
.
Значит, если векторы 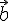 и
и 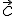 неколлинеарны,
то вектор
неколлинеарны,
то вектор 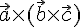
 и
и 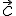 .
.Приводимая
ниже формула и дает разложение этого
вектора по векторам 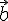 и
и 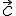 :
:
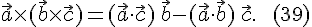
Для
доказательства этой формулы введем
ортонормированный базис, взяв первый
единичный вектор 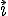
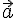 и
расположив второй единичный вектор
и
расположив второй единичный вектор 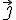 этого
базиса перпендикулярно
этого
базиса перпендикулярно 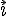 и
так, чтобы векторы
и
так, чтобы векторы 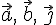 были
компланарны.
Тогда
были
компланарны.
Тогда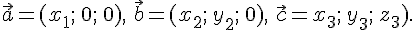
По
формуле 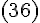 последовательно
находим
последовательно
находим
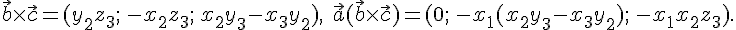
С
другой стороны, по формуле 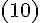 имеем
имеем
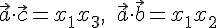
поэтому
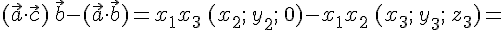

Нетрудно
проверить, что и в случае коллинеарности
векторов 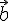 и
и 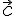 формула
формула 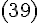 дает
верный результат.
дает
верный результат.
Отметим еще формулу
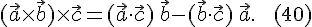
Действительно,
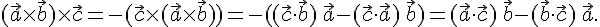
24 Смешанное произведение векторов.
Определение
24.1. Смешанным
произведением векторов 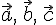
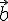 на
вектор
на
вектор 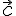 .
.Обозначается
смешанное произведение
векторов 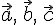 через
через  .
Используя
данное обозначение, определение
смешанного произведения кратко можно
записать так:
.
Используя
данное обозначение, определение
смешанного произведения кратко можно
записать так:
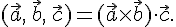
Докажем
теперь теорему, раскрывающую геометрический
смысл смешанного произведения трех
векторов в пространстве  ,
ориентированном правой тройкой.
,
ориентированном правой тройкой.
ТЕОРЕМА
24.1. Смешанное
произведение некомпланарных
векторов 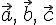 численно
равно объему параллелепипеда, построенного
на этих векторах, как на ребрах, и взятого
со знаком «
численно
равно объему параллелепипеда, построенного
на этих векторах, как на ребрах, и взятого
со знаком «
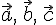 —
правая, и со знаком «
—
правая, и со знаком « «,
если тройка
«,
если тройка 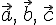 —
левая. Смешанное
произведение компланарных векторов
равно нулю.
—
левая. Смешанное
произведение компланарных векторов
равно нулю.Доказательство. По определению смешанного произведения векторов имеем
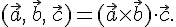
Далее по определению скалярного произведения получаем, что
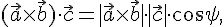
где 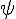 —
угол между векторами
—
угол между векторами 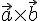 и
и 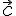 .
Используя формулу
.
Используя формулу 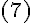 ,
получаем
,
получаем 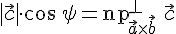 ,
а по свойству 5. векторного произведения
имеем
,
а по свойству 5. векторного произведения
имеем 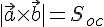 .
Поэтому
.
Поэтому
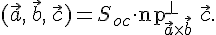
Заметим,
что 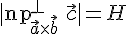 ,
где
,
где  —
высота параллелепипеда. Так как
—
высота параллелепипеда. Так как 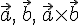 —
правая, то:
—
правая, то:
1. если 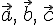 —
правая, то
—
правая, то 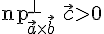 (см.
рис. 1) и
(см.
рис. 1) и

2. если 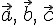 —
левая, то
—
левая, то  (см.
рис. 2) и
(см.
рис. 2) и
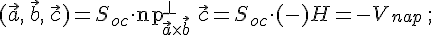
3. если 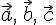 —
компланарны, то, очевидно,
—
компланарны, то, очевидно, 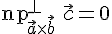 и
и
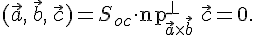
Свойства смешанного произведения.
1. При перестановке двух сомножителей смешанное произведение меняет знак. Циклическая перестановка не меняет знак смешанного произведения.
Доказательство. Действительно,
из доказанной теоремы следует, что при
любом порядке сомножителей смешанные
произведения равны по абсолютной
величине. С другой стороны, из определения
ориентации пространства следует, что
тройки векторов 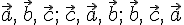 определяют
одну
ориентацию пространства, а тройки
векторов
определяют
одну
ориентацию пространства, а тройки
векторов 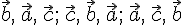 другую.
Поэтому имеем равенства
другую.
Поэтому имеем равенства
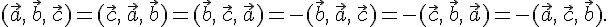
2. Скалярный множитель при любом аргументе можно выносить за знак смешанного произведения, т.е.
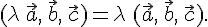
3. Смешанное произведение линейно относительно каждого аргумента, т.е.

Доказательство свойств 2. и 3. следует из аналогичных свойств векторного и скалярного произведений.
4. 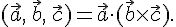
Доказательство. В самом деле, по доказанному свойству 1.
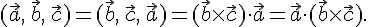
5. Для того чтобы смешанное произведение трех векторов равнялось нулю необходимо и достаточно, чтобы эти векторы были компланарны.
Доказательство. Нам нужно доказать только необходимость, поскольку достаточность доказана в теореме 24.1.
Пусть 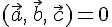 ,
тогда по определению получаем
,
тогда по определению получаем
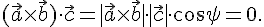
Но это возможно только в случаях:
(a) 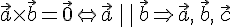 —
компланарны;
—
компланарны;
(b) 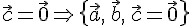 —
линейно зависимы, а значит, компланарны;
—
линейно зависимы, а значит, компланарны;
(c) 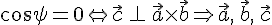 —
компланарны.
—
компланарны.
Координатная форма смешанного произведения.
ТЕОРЕМА
24.2. Пусть
в пространстве выбран ортонормированный
базис 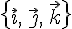 ,
в котором
,
в котором 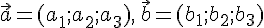 и
и 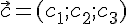 . Тогда
. Тогда
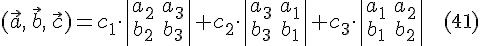
или 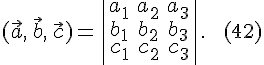
Доказательство. По определению смешанного произведения векторов имеем
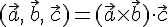
По
формуле 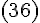 получаем
получаем
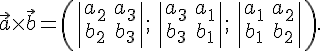
Используя
формулу 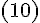 ,
приходим к формуле
,
приходим к формуле 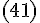 .
Легко видеть, что правая часть
формулы
.
Легко видеть, что правая часть
формулы 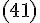 есть
разложение определителя третьего
порядка, стоящего в правой части
формулы
есть
разложение определителя третьего
порядка, стоящего в правой части
формулы 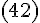 по
элементам третьей строки. Теорема
доказана.
по
элементам третьей строки. Теорема
доказана.
Замечание
24.1. Если
векторы 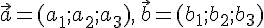 и
и 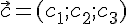 заданы
относительно произвольного аффинного
базиса
заданы
относительно произвольного аффинного
базиса 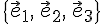 ,
то формула
,
то формула 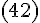 приобретает
вид:
приобретает
вид:
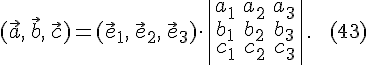
Следствие
24.1. Для
того чтобы векторы 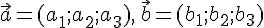 и
и 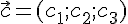 ,
заданные относительно произвольного
аффинного базиса
,
заданные относительно произвольного
аффинного базиса 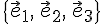 были
компланарны необходимо и достаточно,
чтобы
были
компланарны необходимо и достаточно,
чтобы
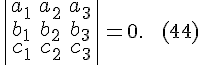
Приложения смешанного произведения.
Решим следующую задачу
Задача
24.1. Пусть
три ребра тетраэдра (произвольная
треугольная пирамида), выходящие из
одной вершины совпадают с векторами 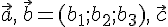 .
Найти объем этого тетраэдра.
.
Найти объем этого тетраэдра.
Решение. Из школьного курса геометрии известно, что объемы параллелепипеда и пирамиды вычисляются по формулам
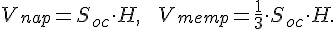
Поскольку основанием параллелепипеда является параллелограмм, а oснованием тетраэдра является треугольник, то площадь основания параллелепипеда в два раза больше площади основания тетраэдра. Поэтому получаем равенство

Из
теоремы 24.1. следует, что 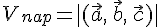 ,
поэтому получаем, что
,
поэтому получаем, что
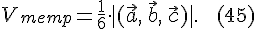
Векторное произведение базисных ортов
А векторное произведение различных базисных ортов должно быть ортогонально им и иметь единичную длину. ( как площадь квадрата , сторона которого равна длине базисного орта т.е. единице), т.е. такое векторное произведение – это «плюс» или «минус»- третий базисный орт. По правилу правой руки определяем, что
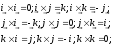
26 вопрос
Вычисление векторного произведения через
координаты сомножителей
Вектор 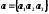 ,а
вектор
,а
вектор 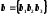
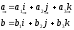
Тогда из (25.14) и свойств 2) и 3) векторного произведения следует:
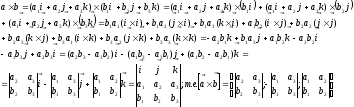
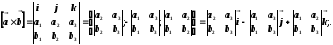 (26.1)
(26.1)
27 вопрос
Смешанное произведение векторов и его свойство
Определение смешанного произведения
Определение.
Смешанным произведением векторов называется
величина
называется
величина 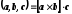 (вектор
(вектор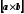 —векторное
произведение скалярно умножается на
третий вектор
—векторное
произведение скалярно умножается на
третий вектор 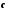
Геометрический смысл смешанного произведения
Если 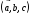 >
0, значит векторы
>
0, значит векторы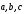 образуют правую систему (т.е. имеют такую же ориентацию, как
соответственно большой, указательный,
и пальцы правой руки и её ладони)
образуют правую систему (т.е. имеют такую же ориентацию, как
соответственно большой, указательный,
и пальцы правой руки и её ладони)
Если 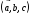 <
0, значит векторы
<
0, значит векторы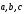 образуют левую систему (аналогично для пальцев и ладони левой
руки).
образуют левую систему (аналогично для пальцев и ладони левой
руки).

Рис. 27.1
Абсолютная величина
смешанного произведения 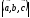 -это
объём паралелепипида
-это
объём паралелепипида 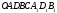 стороны
которого составляют вектора
стороны
которого составляют вектора 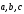
В самом деле по определению ( см. 23.6)
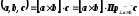 (27.1)
(27.1)
Однако первый
множитель в правой части равенства
(27.1) это площадь параллелограмма OADB
(см условие 2)определения векторного
произведения (§25.1,
25.1)т.е. площадь основания
паралелелипипеда 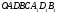 .
Проекция третьей стороны паралелепипеда
на перпендикуляр
.
Проекция третьей стороны паралелепипеда
на перпендикуляр 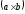 опускаемый на основаниеOADB
(см. условие 1) (определение векторного
произведения в начале параграфа 25) –
это опущенная на OADB
высота данного паралелепипеда. Поэтому
их произведение-это объём паралелепипеда
опускаемый на основаниеOADB
(см. условие 1) (определение векторного
произведения в начале параграфа 25) –
это опущенная на OADB
высота данного паралелепипеда. Поэтому
их произведение-это объём паралелепипеда
Свойства смешанного произведения
1.  -перестановка
сомножителей меняет знак.
-перестановка
сомножителей меняет знак.
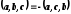
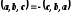
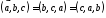 —
циклическая замена не меняет знак.
—
циклическая замена не меняет знак.
2. 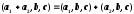
3. 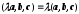
Эти свойства доказаны в конце §28
Необходимое и достаточное условие компланарности трех векторов
Теорема 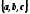 — компланарная
тогда и только тогда когда
— компланарная
тогда и только тогда когда 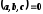
Доказательство:
Если 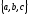 компланарные , то паралелепипед
компланарные , то паралелепипед 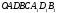 имеет нулевой объем (см. Рис 27.1)т.е.
получим , что
имеет нулевой объем (см. Рис 27.1)т.е.
получим , что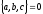 ,
Справедливо рассуждение и в обратную
сторону, что читателю предлагается
провести самостоятельно.
,
Справедливо рассуждение и в обратную
сторону, что читателю предлагается
провести самостоятельно.
28 Вопрос Смешанное произведение векторов в координатной форме
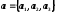

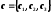
(см. (24.9)и (26.1))
Рассмотрим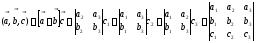
Последнее равенство
получается разложением определителя  по его третей строке.
по его третей строке.
Значит: 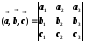 (28.1)
(28.1)
Следствие: Определитель третьего порядка равен нулю, тогда и только тогда, когда его строки линейно зависимы.
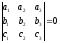

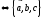 -коллинеарные
и линейно зависимые.
-коллинеарные
и линейно зависимые.
Свойства же 1),2),3) смешанного произведения (см. §27 п. 27.3) теперь легко следует из свойств 2),4) и 7) определителя третьего порядка( см. §1, п. 1.3)
36 Вопрос
А)
Уравнение плоскости по точке и нормали
Определение
36.1. Плоскостью будем называть геометрическое место
точек, такое что, при некотором ненулевом
векторе 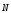 для всех точек
для всех точек и
и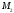 из данного множества вектор
из данного множества вектор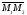 ортогонален заданному вектору.
ортогонален заданному вектору.
Определение
36.2. Вектор 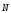 ,
заданный в определении 36.1, называетсянормалью (или нормальным вектором)
к заданной плоскости.
,
заданный в определении 36.1, называетсянормалью (или нормальным вектором)
к заданной плоскости.
(Определение 36.1
геометрически означает, что если прямая
линия, имеющая направляющий вектор ,
перпендикулярный плоскости  ,
то она ортогональна любой прямой ,
лежащей в этой плоскости.)
,
то она ортогональна любой прямой ,
лежащей в этой плоскости.)
Получим общее уравнение плоскости.
Пусть нормаль  .
Так как
.
Так как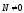 ,
то
,
то
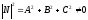 (36.1)
(36.1)
Положим, 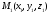 —
некоторая точка плоскости. Тогда для
любой точки
—
некоторая точка плоскости. Тогда для
любой точки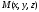 из плоскости
из плоскости вектор
вектор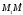 ,
по определению 36.1, ортогонален вектору
,
по определению 36.1, ортогонален вектору ,
т.е. их скалярное произведение
,
т.е. их скалярное произведение
 (36.2)
(36.2)
Выписывая равенство
(36.2) покоординатно (из §21 вектор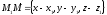 ,
из равенства (24.9) имеем:
,
из равенства (24.9) имеем:
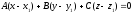 (36.3)
(36.3)
Раскрывая скобки
в равенстве (36.3) и обозначив за 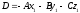 ,
,
получим:
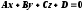 (36.4)
(36.4)
С условием 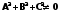 (36.1)
(36.1)
Мы показали, что координаты всех точек любой плоскости удовлетворяют некоторому линейному уравнению (36.4) с условием (36.1)
Покажем обратное,
т.е. если координаты всех точек некоторого
множества  удовлетворяют линейном уравнению
(36.4) с условием (36.1) то это множество
является плоскостью.
удовлетворяют линейном уравнению
(36.4) с условием (36.1) то это множество
является плоскостью.
Отметим, что данное
множество π≠Ø, ибо если 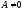 (см.(36.1)) то точка с координатами
(см.(36.1)) то точка с координатами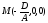 удовлетворяет уравнению (36.4)
удовлетворяет уравнению (36.4)
Тогда пусть 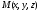 и
и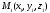 —
произвольные точки множества
—
произвольные точки множества ,
т.е. их координаты удовлетворяют (36.4)
и следующему уравнению (для точки
,
т.е. их координаты удовлетворяют (36.4)
и следующему уравнению (для точки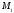 )
)
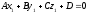 (36.5)
(36.5)
Вычитая из уравнения
(36.4) равенство (36.5), получим формулу
(36.3), что означает, что вектора 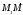 и
и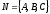 ( из условия (36.1)), следует,что вектор
( из условия (36.1)), следует,что вектор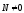 )
удовлетворяет равенству (36.2), т.е они
ортогональны. Поэтому выполняются все
условия определения 36.1, т.е. множество
)
удовлетворяет равенству (36.2), т.е они
ортогональны. Поэтому выполняются все
условия определения 36.1, т.е. множество ,
координаты всех точек которого
удовлетворяют некоторому линейному
уравнению (36.4) с условием (36.1), является
плоскостью.
,
координаты всех точек которого
удовлетворяют некоторому линейному
уравнению (36.4) с условием (36.1), является
плоскостью.
Определение 36.4. Поэтому уравнение (36.4) с условием (36.1) называется общим уравнением плоскости.
Б)
14Векторное произведение векторов в координатной форме
Векторное произведение 2х векторов.
левая —— правая
Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки — левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям:
1. |c|=|a|*|b|*sin.
2. ca и cb.
3. тройка а,в,с-правая.
Векторное произведение.
Векторным произведением вектора а на вектор в называется вектор с, который определяется следующим образом:
1) модуль с численно равен площади параллелограмма, построенного на перемножаемых векторах как на сторонах с=ав Sin.
2) вектор с перпендикулярен обоим перемножаемым векторам;
3) направление вектора с таково, что если смотреть из его конца вдоль вектора а к вектору в, осуществляется против часовой стрелки. Геометрич. смысл векторного произведения –модуль векторн.пр-я равен площади параллелограмма, построенного на перемножаемых векторах. Если векторы заданы в координатной форме, то их векторн. Произведение находится по формуле: а в = i j k
ax ay az
bx by bz.
Свойства векторного произведения.
1. При перестановке сомножителей векторное произведение меняет свой знак на противоположный, сохраняя при этом свой модуль: а в =в) а.
2)Векторн.пр-е обладает сочетательным св-вом относительно числового (скалярного) множителя: ававав.
3)Векторн.пр-е обладает распределительным св-ом.
4) Если векторн.пр-е 2-х векторов равно 0-вектору, то либо равен 0 один из перемножаемых векторов, любо синус угла между ними, т.е. векторы коллиниарны (параллельны). Для того, чтобы 2 ненулевых вектора были коллиниарны необходимо и достаточно, чтобы их векторное пр-е было равно нуль-вектору.
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов i,j иk:
 если
направление кратчайшего пути от первого
вектора к второму совпадает с направлением
стрелки, то произведение равно третьему
вектору, если не совпадает — третий
вектор берется со знаком «минус».
если
направление кратчайшего пути от первого
вектора к второму совпадает с направлением
стрелки, то произведение равно третьему
вектору, если не совпадает — третий
вектор берется со знаком «минус».
Пусть
заданы два вектора а=ахi +ayj +azk и b =bxi +byj
+bzk . Найдем векторное произведение этих
векторов, перемножая их как многочлены
(согласно свойств векторного произведения):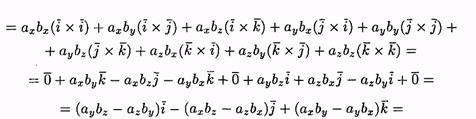
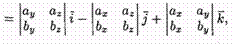
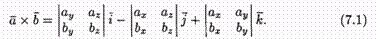 Полученную формулу можно записать еще
короче:
Полученную формулу можно записать еще
короче: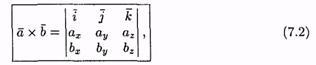 так как правая часть равенства (7.1)
соответствует разложению определителя
третьего порядка по элементам первой
строки.Равенство (7.2) легко запоминается.
так как правая часть равенства (7.1)
соответствует разложению определителя
третьего порядка по элементам первой
строки.Равенство (7.2) легко запоминается.
7.4. Некоторые приложения векторного произведения
Установление
коллинеарности векторов. 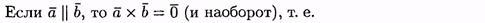
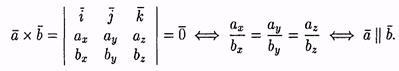 Нахождение площади параллелограмма и
треугольника
Нахождение площади параллелограмма и
треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sing , т. е. S пар = |а х b |. И, значит, DS =1/2|а х b |.
Определение момента силы относительно точки
Пусть в точке
А приложена сила F =АВ и пусть О — некоторая
точка пространства 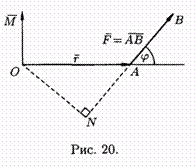 Из физики известно, что моментом си лы
F относительно точки О называется вектор
М, который проходит через точку О и:
Из физики известно, что моментом си лы
F относительно точки О называется вектор
М, который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно
равен произведению силы на плечо 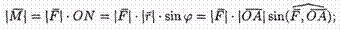 3) образует правую тройку с векторами
ОА и A В.
3) образует правую тройку с векторами
ОА и A В.
Стало быть, М=ОА х F . Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ, где О—некоторая неподвижная точка оси (см. рис. 21).
Угол между векторами
Из
определения скалярного произведения
двух векторов следует, что
Если векторы 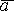 и
и  заданы
координатами
заданы
координатами 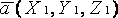 и
и 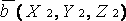 ,
то формула (1.6.3.1) запишется в виде:
,
то формула (1.6.3.1) запишется в виде: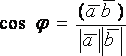
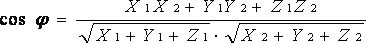
Площадь параллелограмма,построенных на векторах
Задачи на измерение длин отрезков, расстояний между точками, площадей поверхностей и объемов тел относятся к важному классу проблем, которые принято называть метрическими. В предыдущем разделе мы познакомились с тем, как использовать векторную алгебру для вычисления длин отрезков и расстояний между точками. Теперь мы собираемся найти способы вычисления площадей и объемов. Векторная алгебра позволяет ставить и решать подобные задачи только для достаточно простых случаев. Для вычисления площадей произвольных поверхностей и объемов произвольных тел требуются методы анализа. Но методы анализа в свою очередь существенным образом опираются на те результаты, которые дает векторная алгебра.
Для решения поставленной задачи, мы избрали достаточно долгий и непростой путь, подсказанный Гильбертом Стренгом [19], связанный с многочисленными геометрическими преобразованиями и кропотливыми алгебраическими вычислениями. Мы избрали этот путь несмотря на то, что существуют другие подходы, которые быстрее приводят к цели потому, что он показался нам прямым и естественным. Прямой путь в науке не всегда оказывается самым простым. Люди искушенные знают об этом и предпочитают пути окольные, но если не попытаться пройти прямиком, то можно так и остаться в неведении относительно некоторых тонкостей теории.
На избранном нами пути естественным образом появляются такие понятия как ориентация пространства, определитель, векторное и смешанное произведения. Особенно наглядно, как под микроскопом, проявляется геометрический смысл определителя и его свойств. Традиционно понятие определителя вводится в теории систем линейных уравнений, но именно для решения таких систем определитель почти бесполезен. Геометрический же смысл определителя существенен для векторной и тензорной алгебры.
А теперь запасемся терпением и начнем с самых простых и понятных случаев.
1. Векторы ориентированы вдоль координатных осей декартовой системы координат.
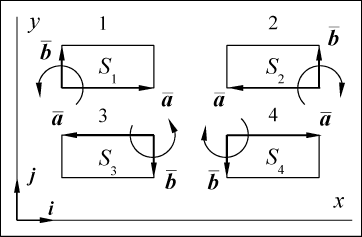 Пусть
вектор a
направлен по оси x, а вектор b
вдоль оси y. На рис. 21 показаны четыре
различных варианта расположения векторов
по отношению к осям координат.
Пусть
вектор a
направлен по оси x, а вектор b
вдоль оси y. На рис. 21 показаны четыре
различных варианта расположения векторов
по отношению к осям координат.
Векторы
a
и b
в координатной форме: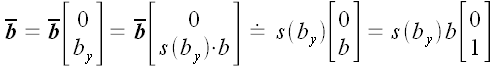 Где a и b означают модуль соответствующего
вектора, а – знак координаты вектора.
Где a и b означают модуль соответствующего
вектора, а – знак координаты вектора.
Поскольку векторы ортогональны, то параллелограммы, построенные на них, являются прямоугольниками. Их площади равны просто произведению их сторон. Выразим эти произведения через координаты векторов для всех четырех случаев.

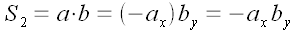
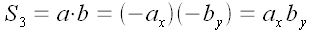
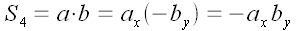
Все четыре
формулы для вычисления площади одинаковы
за исключением знака. Можно было бы
просто закрыть на это глаза и записать, 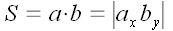 что во всех случаях. Однако более
продуктивной оказывается другая
возможность: придать знаку какой-то
смысл. Посмотрим внимательно на рис.
21. В тех случаях, когда
что во всех случаях. Однако более
продуктивной оказывается другая
возможность: придать знаку какой-то
смысл. Посмотрим внимательно на рис.
21. В тех случаях, когда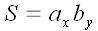 , поворот вектора к вектору осуществляется
по часовой стрелке. В тех же случаях,
когда мы вынуждены использовать в
формуле знак минус, поворот вектора к
вектору осуществляется против часовой
стрелки. Это наблюдение позволяет
связать знак в выражениях для площади
с ориентацией плоскости.
, поворот вектора к вектору осуществляется
по часовой стрелке. В тех же случаях,
когда мы вынуждены использовать в
формуле знак минус, поворот вектора к
вектору осуществляется против часовой
стрелки. Это наблюдение позволяет
связать знак в выражениях для площади
с ориентацией плоскости.
Площадь
прямоугольника, построенного на векторах
aиb, со
знаком плюс или минус будем считать
ориентированной площадью, при этом знак
будем связывать с ориентацией, задаваемой
векторами. Для ориентированной площади
мы можем записать единую формулу для
всех рассмотренных четырех случаев: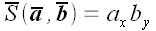 . Знак «векторной» черты над буквой
S вводится для того, чтобы отличить
обычную площадь, которая всегда
положительна, от ориентированной.
. Знак «векторной» черты над буквой
S вводится для того, чтобы отличить
обычную площадь, которая всегда
положительна, от ориентированной.
При этом,
очевидно, что те же самые векторы, взятые
в другом порядке, определяют противоположную
ориентацию, поэтому, 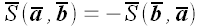 . Просто площадь будем по-прежнему
обозначать буквой S и, следовательно,
.
. Просто площадь будем по-прежнему
обозначать буквой S и, следовательно,
.
Теперь, когда
казалось бы ценой расширения понятия
площади, мы получили общее выражение,
внимательный читатель скажет, что мы
рассмотрели не все возможности.
Действительно, кроме четырех вариантов
расположения векторов, представленных
на рис. 21, имеются еще четыре (рис. 22) 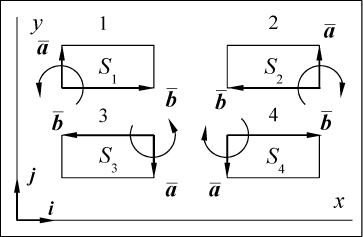 Запишем снова векторы и в координатной
форме:
Запишем снова векторы и в координатной
форме: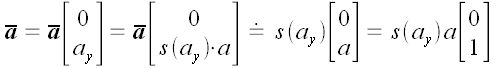
 Выразим площади через координаты
векторов.
Выразим площади через координаты
векторов.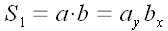
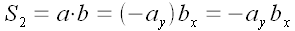
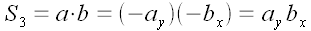 4.
4. 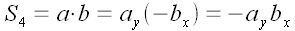 .
Знаки
в новых выражениях не поменялись, но, к
сожалению, поменялась ориентация по
отношению к предыдущим четырем случаям.
Поэтому для ориентированной площади
мы вынуждены записать:
.
Знаки
в новых выражениях не поменялись, но, к
сожалению, поменялась ориентация по
отношению к предыдущим четырем случаям.
Поэтому для ориентированной площади
мы вынуждены записать: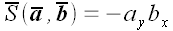 . Хотя надежда на гениальную простоту
и не оправдалась, но, тем не менее, мы
все-таки можем записать общее выражение
для всех четырех случаев.
. Хотя надежда на гениальную простоту
и не оправдалась, но, тем не менее, мы
все-таки можем записать общее выражение
для всех четырех случаев.
 То
есть, ориентированная площадь
прямоугольника, построенного на векторах,
как на сторонах, равна определителю,
составленному из координат векторов,
как из столбцов.
То
есть, ориентированная площадь
прямоугольника, построенного на векторах,
как на сторонах, равна определителю,
составленному из координат векторов,
как из столбцов.
Мы
полагаем, что с теорией определителей
читатель знаком, поэтому, мы не
останавливаемся подробно на этом
понятии. Тем не менее, мы даем соответствующие
определения, для того чтобы изменить
акценты и показать, что к этому понятию
можно прийти из чисто геометрических
соображений.Итак,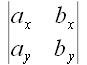 ,
,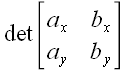 ,
,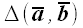 , – различные формы обозначения для
одного и того же понятия – определителя,
составленного из координат векторов,
как из столбцов. Равенство
, – различные формы обозначения для
одного и того же понятия – определителя,
составленного из координат векторов,
как из столбцов. Равенство 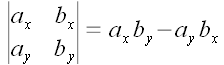 может быть принято за его определение
для двухмерного случая.
может быть принято за его определение
для двухмерного случая.
Теперь мы можем считать, что для всех частных случаев расположения векторов относительно декартовой системы координат у нас есть общее выражение для ориентированной площади.
2.
Вектор b
не параллелен оси x; вектор a/
является произвольным вектором.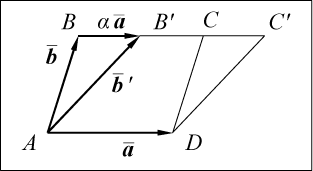
Для того чтобы свести этот случай к уже известным, рассмотрим некоторые геометрические преобразования параллелограмма, построенного на векторах и (рис. .смешанные произведения векторов и его свойства
4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме
Скалярным
произведением двух ненулевых векторов называется
число, равное произведению длин этих
векторов на косинус угла между ними 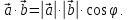
Формулу для скалярного произведения векторов можно записать в виде
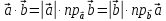 .
.
Скалярное произведение двух векторов равно модулю одного из них, помноженному на алгебраическую проекцию другого вектора на направление первого.
Скалярное
умножение нельзя распространить на
случай трех сомножителей. Действительно,
скалярное произведение двух векторов  и
и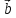 есть число и если это число умножить на
вектор
есть число и если это число умножить на
вектор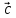 ,
то в произведении получим вектор
,
то в произведении получим вектор
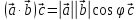
коллинеарный
с вектором 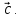
Свойства скалярного произведения векторов:
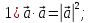
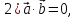 если
если 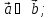

 ;
;
Если
рассматривать векторы 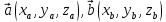 в
декартовой системе координат, то
скалярное произведение двух векторов
равно сумме произведений соответствующих
координат этих векторов
в
декартовой системе координат, то
скалярное произведение двух векторов
равно сумме произведений соответствующих
координат этих векторов
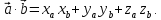
Используя полученное равенство, можно записать формулу для вычисления угла между векторами
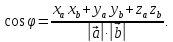
Рассмотрим
пример. Найти 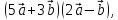 если
если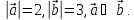
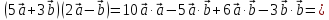
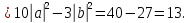
Так
как 
Рассмотрим
пример. Найти
угол между векторами 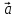 и
и если
если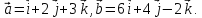
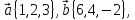
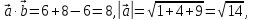
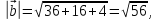
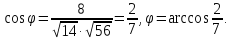
Рассмотрим пример. Найти скалярное произведение
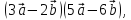 если
если 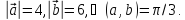
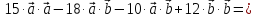
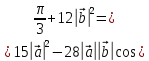

4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме
Векторное
произведение векторов 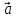 и
и 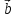 называется вектор
называется вектор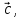 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям:
модуль вектора
 равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах и
и
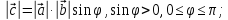
направление вектора
 перпендикулярно плоскости параллелограмма
построенного на векторах
перпендикулярно плоскости параллелограмма
построенного на векторах и
и ;
;векторы
 ,
, и
и после приведения к общему началу
ориентированы по отношению друг к другу
соответственно как орты
после приведения к общему началу
ориентированы по отношению друг к другу
соответственно как орты
Свойства векторного произведения векторов.
Векторное произведение не обладает переместительным свойством

Коллинеарность ненулевых векторов
 если
если
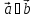 или
или 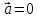 или
или 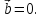
Сочетательное свойство

Распределительное свойство
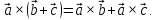
Если
заданы векторы 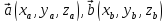 в
декартовой системе координат, то их
векторное произведение находят следующим
образом
в
декартовой системе координат, то их
векторное произведение находят следующим
образом
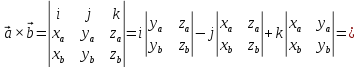
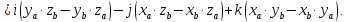
Рассмотрим
пример. Найти
векторное произведение двух векторов 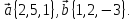
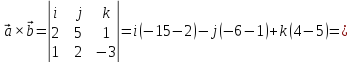
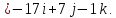
4.6. Применение векторного произведения векторов к решению задач
Площадь
параллелограмма построенного на векторах 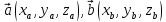 вычисляется по формуле
вычисляется по формуле
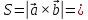
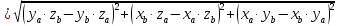
Площадь
треугольника построенного на векторах  вычисляется по формуле
вычисляется по формуле
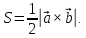
Рассмотрим
пример. Вычислить
площадь треугольника с вершинами в
точках 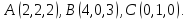
Найдем
координаты векторов 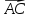 и
и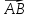 ,
на которых построен треугольник
,
на которых построен треугольник
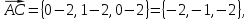
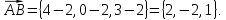
Векторное
произведение векторов  и
и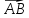
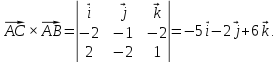
Вычислим
площадь треугольника 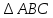
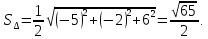
4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме
Смешанное произведение векторов.
Смешанным
произведением векторов 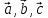 называется скалярное произведение
вектора
называется скалярное произведение
вектора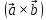 на вектор
на вектор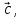 т.е.
т.е.

Обращение
в нуль смешанного произведения векторов 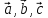 есть признак компланарности векторов
есть признак компланарности векторов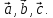
Смешанное
произведение трех векторов 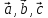 по модулю равно объему параллепипеда,
построенного на этих векторах.
по модулю равно объему параллепипеда,
построенного на этих векторах.
Свойства смешанного произведения трех векторов.
1. При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный
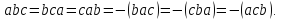
2.
Свойство распределительности 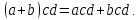
3.
Свойство сочетательности относительно
скалярного множителя 
4.
Смешанное произведение, имеющее хотя
бы два равных сомножителя, равно нулю 
Пусть векторы заданы их разложениями по ортам
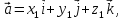
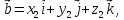
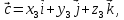
тогда смешанное произведение векторов



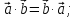
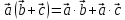 ;
;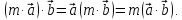
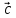 равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах и
и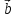
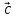 перпендикулярно плоскости параллелограмма
построенного на векторах
перпендикулярно плоскости параллелограмма
построенного на векторах и
и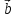 ;
; ,
, и
и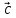 после приведения к общему началу
ориентированы по отношению друг к другу
соответственно как орты
после приведения к общему началу
ориентированы по отношению друг к другу
соответственно как орты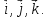
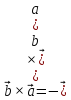
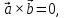 если
если