Смешанное произведение векторов.
Смешанное произведение векторов.Навигация по странице:
- Определение смешанного произведения векторов
- Формула вычисления смешанного произведения векторов
- Свойства смешанного произведения векторов
- Примеры задач на вычисления смешанного произведения векторов
Онлайн калькулятор. Смешанное произведение векторов.
Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.
Формулы вычисления смешанного произведения векторов
Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Смешанное произведение векторов a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Свойства смешанного произведения векторов
Геометрический смысл смешанного произведения.

Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:
Vпарал = |a · [b × c]|
Геометрический смысл смешанного произведения.
Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:
Vпир = 1 |a · [b × c]| 6 Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
a · [b × c] = b · (a · c) — c · (a · b)
a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]
a · [b × c] + b · [c × a] + c · [a × b] = 0 —
Примеры задач на вычисления смешанного произведения векторов
Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.
Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.
Решение:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Пример 2.
Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.
Решение: Найдем смешанное произведение этих векторов:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | -1 | 1 | ||
| 2 | 0 | -1 |
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 — 3·(-1)·2 — 2·1·(-1) — 1·1·0 =
= 1 + 4 + 0 + 6 + 2 — 0 = 13
Найдем объем пирамиды воспользовавшись свойствами:
| Vпир = | 1 | |a · [b × c]| = | 13 | = 2 | 1 |
| 6 | 6 | 6 |
Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора.
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Смешанное произведение векторов
Содержание:
- Геометрический смысл смешанного произведения
- Свойства смешанного произведения:
Определение
Смешанным произведением трех векторов $\overline{a}$, $\overline{b}$, $\overline{c}$ называется число, равное скалярному произведению вектора $\overline{a} \times \overline{b}$ на вектор $\overline{c}$: $(\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c})$
Геометрический смысл смешанного произведения
Геометрический смысл смешанного произведения: если
тройка векторов $\{\overline{a}, \overline{b}, \overline{c}\}$ правая,
то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: $(\overline{a}, \overline{b}, \overline{c})=V$.
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах $\overline{a}$, $\overline{b}$ и $\overline{c}$ равен модулю смешанного произведения этих векторов:
$$V_{\text {парал }}=|(\bar{a}, \bar{b}, \bar{c})|$$
Объем пирамиды, построенной на этой тройке векторов равен
$$V_{\text {пир }}=\frac{1}{6}|(\bar{a}, \bar{b}, \bar{c})|$$
Свойства смешанного произведения:
1 $(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])$
2 $(\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b})$
3 Три вектора компланарны тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})=0$
4 Тройка векторов является правой тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})>0$.
5 $(\lambda \overline{a}, \overline{b}, \overline{c})=(\overline{a}, \lambda \overline{b}, \overline{c})=(\overline{a}, \overline{b}, \lambda \overline{c})=\lambda(\overline{a}, \overline{b}, \overline{c})$
6 $\left(\overline{a}_{1}+\overline{a}_{2}, \overline{b}, \overline{c}\right)=\left(\overline{a}_{1}, \overline{b}, \overline{c}\right)+\left(\overline{a}_{2}, \overline{b}, \overline{c}\right)$
7 $\left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right)$
8 $\left(\overline{a}, \overline{b}, \overline{c}_{1}+\overline{c}_{2}\right)=\left(\overline{a}, \overline{b}, \overline{c}_{1}\right)+\left(\overline{a}, \overline{b}, \overline{c}_{2}\right)$
9 $([\overline{a}, \overline{b}], \overline{c})=\overline{b}(\overline{a}, \overline{c})-\overline{a}(\overline{b}, \overline{c}) ;(\overline{a},[\overline{b}, \overline{c}])=\overline{b}(\overline{a}, \overline{c})-\overline{c}(\overline{a}, \overline{b})$
10 Тождество Якоби: $(\overline{a},[\overline{b}, \overline{c}])+(\overline{b},[\overline{c}, \overline{a}])+(\overline{c},[\overline{a}, \overline{b}])=0$
Если векторы $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ и $\overline{c}=\left(c_{1}, c_{2}, c_{3}\right)$ заданы своими координатами, то их смешанное произведение вычисляется по формуле
$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}} \\ {c_{1}} & {c_{2}} & {c_{3}}\end{array}\right|$
Пример
Задание.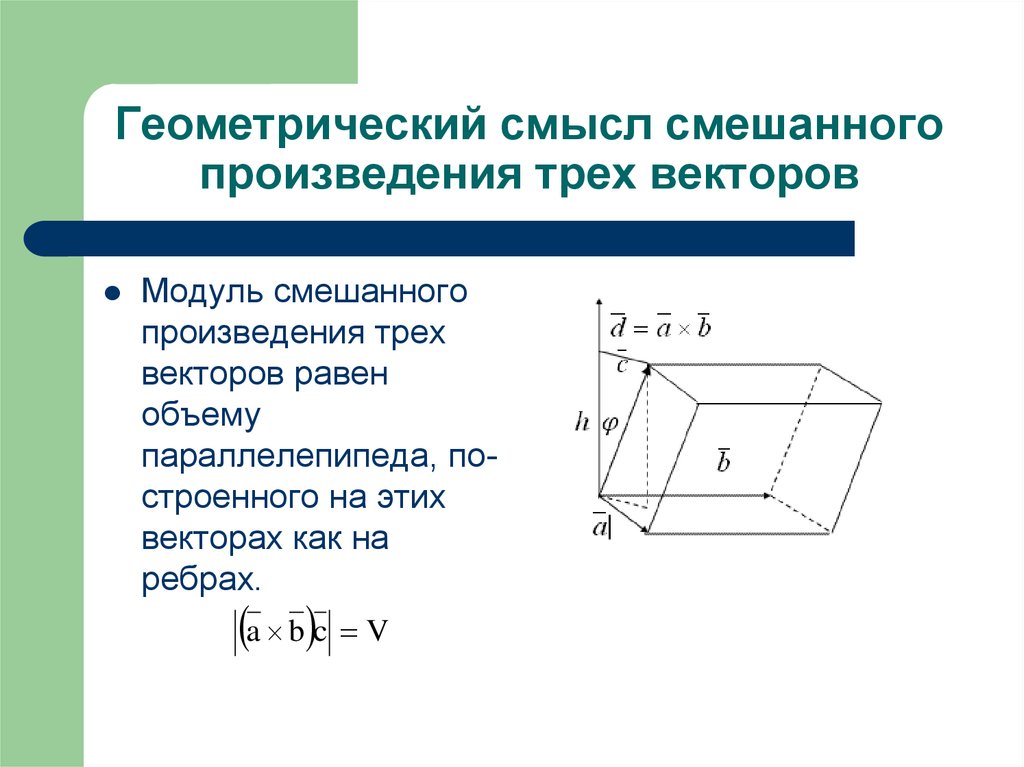
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов $\overline{a}$, $\overline{b}$ и $\overline{c}$:
$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$
$-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$
$$V_{\text {пир }}=\frac{1}{6}|(\bar{a}, \bar{b}, \bar{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}(\text { куб. ед. })$$
Читать дальше: свойства векторов.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Скалярное тройное произведение – формула, геометрическая интерпретация, примеры, свойства скалярное тройное произведение есть a · (b × c).
 Он также широко известен как тройное скалярное произведение, коробочное произведение и смешанное произведение. Скалярное тройное произведение дает объем параллелепипеда, где три вектора представляют собой смежные стороны параллелепипеда.
Он также широко известен как тройное скалярное произведение, коробочное произведение и смешанное произведение. Скалярное тройное произведение дает объем параллелепипеда, где три вектора представляют собой смежные стороны параллелепипеда.В этой статье мы рассмотрим концепцию скалярного тройного произведения, его формулу, доказательство и свойства. Мы также изучим геометрическую интерпретацию скалярного тройного произведения и решим несколько примеров, основанных на этой концепции, чтобы понять ее применение.
| 1. | Что такое скалярное тройное произведение? |
| 2. | Скалярная формула тройного произведения |
| 3. | Геометрическая интерпретация скалярного тройного произведения |
| 4. | Свойства скалярного тройного произведения |
| 5. | Часто задаваемые вопросы о скалярном тройном продукте |
Что такое скалярное тройное произведение?
Скалярное тройное произведение трех векторов a, b, c — это скалярное произведение вектора a на векторное произведение векторов b и c, т. е. a · (b × c). Символически это также записывается как [a b c] = [a, b, c] = a · (b × c). Скалярное тройное произведение [a b c] дает объем параллелепипеда со смежными сторонами a, b и c. Если нам даны три вектора a, b, c, то их скалярное тройное произведение [a b c] равно:
е. a · (b × c). Символически это также записывается как [a b c] = [a, b, c] = a · (b × c). Скалярное тройное произведение [a b c] дает объем параллелепипеда со смежными сторонами a, b и c. Если нам даны три вектора a, b, c, то их скалярное тройное произведение [a b c] равно:
- а · (б × в)
- а · (в × б)
- б · (а × в)
- б · (в × а)
- в · (б × а)
- с · (а × б)
Теперь, прежде чем перейти к формуле скалярного тройного произведения, нужно отметить, что:
- [a, b, c] = a · (b × c) = b · (c × a) = c · (а × б)
- а · (б × с) = — а · (с × б)
- б · (с × а) = — б · (а × с)
- с · (а × б) = — с · (б × а)
- а · (б × с) = (а × б) · с
Скалярная формула тройного произведения
Если даны три вектора a = a 1 i + a 2 j + a 3 k, b = b 1 i + b 2 j + b 3 k, c = c 1 i + c 2 j + c 3 k, то их скалярное тройное произведение равно определителю компонент трех векторов. Формула скалярного тройного произведения векторов a, b, c имеет вид,
Формула скалярного тройного произведения векторов a, b, c имеет вид,
Доказательство скалярного тройного произведения
Теперь докажем формулу скалярного тройного произведения трех векторов a, b, c. Используя определение перекрестного произведения и скалярного произведения, мы имеем
a · (b × c) = \(\overrightarrow{a} \cdot \left|\begin{array}{lll}\hat{i} & \ шляпа{j} & \шляпа{k} \\b_{1} & b_{2} & b_{3} \\c_{1} & c_{2} & c_{3}\end{массив}\right| \)
= \([(b_2c_3 — c_2b_3)\шляпа{i} — (b_1c_3-c_1b_3)\шляпа{j} + (b_1c_2-c_1b_2)\шляпа{k}] \cdot (a_1\шляпа{i} + a_2\шляпа{j} + a_3\шляпа{k})\)
= (b 2 c 3 — c 2 b 3 )a 1 + (c 1 b 3 — b 1 c 3 )a 2 + (b 1 c 2 — c 1 b 2 )a 3
= \( \left|\begin{array}{lll}a_1 & a_2& a_3 \\b_{1} & b_{2} & b_{3} \\c_{1} & c_{2} & c_{3}\end{array}\right|\)
Таким образом, мы доказали формулу скалярного тройного произведения три вектора a, b, c.
Геометрическая интерпретация скалярного тройного произведения
Теперь мы знаем, что для любых трех векторов a, b, c скалярное тройное произведение равно a · (b × c), которое равно определителю компонентов трех векторов. Давайте теперь поймем геометрическую интерпретацию скалярного тройного произведения. Абсолютное значение скалярного тройного произведения a · (b × c) дает объем параллелепипеда, где a, b, c образуют смежные стороны параллелепипеда. Перекрестное произведение (b × c) дает площадь параллелограмма, образованного векторами b и c. Используя перекрестное произведение определения, b × c перпендикулярно плоскости, содержащей векторы b и c.
Свойства скалярного тройного произведения
Мы рассмотрели концепцию скалярного тройного произведения вместе с его геометрической интерпретацией и формулой. Давайте теперь пройдемся по некоторым его важным свойствам для лучшего понимания концепции:
- Скалярное тройное произведение трех векторов равно нулю, если любые два из них параллельны, т.
 е. [a a b] = 0
е. [a a b] = 0 - [(а + b) c d] = [а c d] + [b c d]
LHS = [(a + b) c d]
= (а + б) · (с × г)
= а · (с × d) + б · (с × d)
= [a c d] + [b c d]
= RHS - [λa b c] = λ [ab c], где λ — действительное число.
- Скалярное тройное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.
- Так как скалярное произведение коммутативно, то имеем
- а · (б × с) = (б × с) · а
- б · (с × а) = (с × а) · б
- с · (а × b) = (а × b) · с
Важные примечания о скалярном тройном произведении
- [a, b, c] = [b, c, a] = [c, a, b]
- [a (b+c) d] = [a b d] + [a c d], [a b (c + d)] = [a b c] + [a b d]
- [λa b c] = [a λb c] = [a b λc] = λ [a b c], где λ — действительное число.
- Скалярное тройное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.
Связанные темы по скалярному тройному произведению
- Произведение векторов
- Калькулятор скалярного произведения
Часто задаваемые вопросы о скалярном тройном продукте
Что такое скалярное тройное произведение в теории векторов?
Скалярное тройное произведение — это скалярное произведение вектора на векторное произведение двух других векторов, т.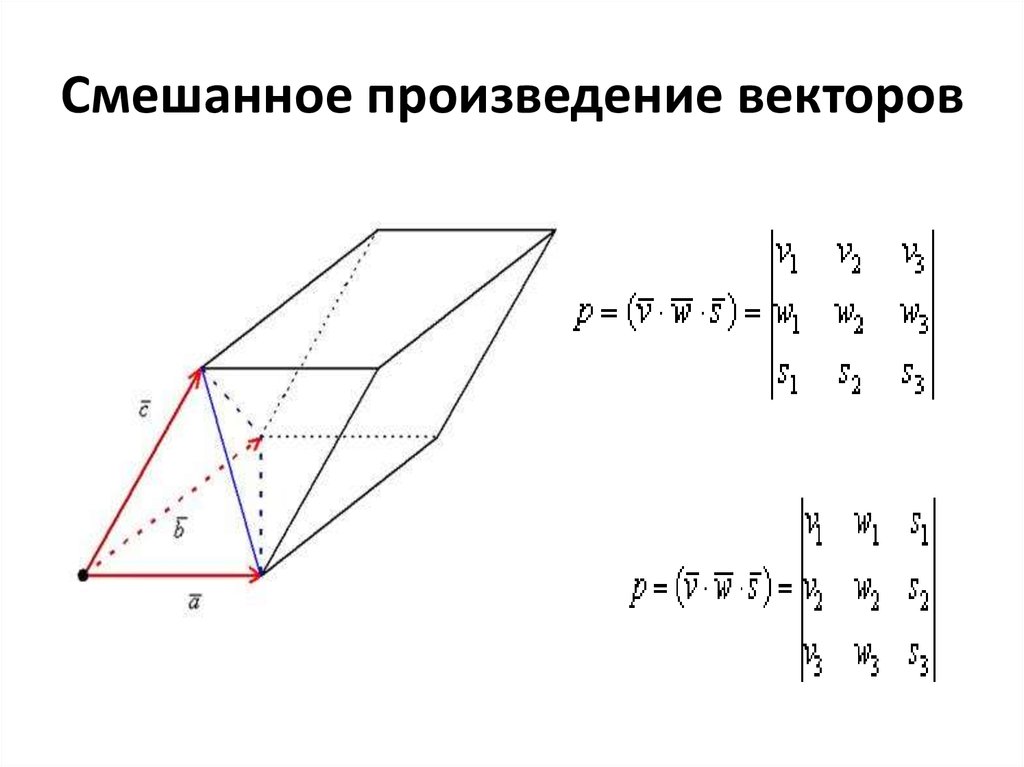 е. если a, b, c — три вектора, то их скалярное тройное произведение равно a · (b × c).
е. если a, b, c — три вектора, то их скалярное тройное произведение равно a · (b × c).
Что такое скалярная формула тройного произведения?
Формула скалярного тройного произведения векторов а = а 1 i + a 2 j + a 3 k, b = b 1 i + b 2 j + b 3 k, c = c 1 i + 1 c 9009 j + c 3 k определяется выражением \( \left|\begin{array}{lll}a_1 & a_2& a_3 \\b_{1} & b_{2} & b_{3} \\c_{1} & c_{2} & c_{3}\end{array}\right|\)
Почему скалярное тройное произведение трех копланарных векторов равно нулю?
Предположим, что a, b, c — три ненулевых вектора. Тогда [a, b, c] = 0 ⇔ (a × b) · c = 0 ⇔ c перпендикулярно a × b ⇔ c лежит в плоскости, параллельной как a, так и b ⇔ a, b, c компланарны.
Когда скалярное тройное произведение равно нулю?
Скалярное тройное произведение трех векторов равно нулю, если любые два из них равны параллельным векторам.
Какова геометрическая интерпретация скалярного тройного произведения трех векторов?
Геометрическая интерпретация скалярного тройного произведения трех векторов заключается в том, что оно дает объем параллелепипеда, а три вектора представляют соприкасающиеся ребра параллелепипеда. Если скалярное тройное произведение равно нулю, то объем будет равен нулю и означает, что все ребра лежат в одной плоскости, а значит, векторы компланарны.
Если скалярное тройное произведение равно нулю, то объем будет равен нулю и означает, что все ребра лежат в одной плоскости, а значит, векторы компланарны.
Почему скалярное тройное произведение называется коробочным произведением?
Скалярное тройное произведение трех векторов a, b, c записывается в рамке как [a, b, c]. Кроме того, абсолютное значение скалярного тройного произведения дает объем коробки (параллелепипеда).
Урок Видео: Скалярное тройное произведение
Расшифровка видео
В этом видео мы научимся вычислить скалярное тройное произведение и применить его в геометрических приложениях.
Скалярное тройное произведение,
иногда также называемый смешанным произведением или коробочным произведением, является скалярным или точечным
произведение одного вектора на произведение двух других векторов. Вы уже должны быть знакомы с
скаляр и векторное произведение векторов. Скалярное тройное произведение трех
векторов 𝐀, 𝐁 и 𝐂 определяется как скалярное произведение или скалярное произведение вектора
𝐀 с векторным произведением векторов 𝐁 и 𝐂.
Если мы разберем это, то узнаем, что результатом перекрестного произведения двух векторов 𝐁 и 𝐂 является другой вектор. Назовем это 𝐃. Если мы затем возьмем скалярное произведение вектора 𝐀 с вектором 𝐃, мы знаем, что скалярное или скалярное произведение приводит к скаляр. Назовем это 𝜆. Таким образом, скалярное тройное произведение находится в фактически скаляр, отсюда и название скалярного тройного произведения. Стоит отметить, что мы не на самом деле нужны круглые скобки, так как если бы мы попытались взять скалярное произведение, это скаляр произведения 𝐀 с 𝐁 во-первых, это даст нам скаляр. Тогда у нас был бы скаляр, скрещенный с вектором, чего мы не можем сделать, так как невозможно скрестить скаляр с вектором. вектор.
Таким образом, скалярное тройное произведение равно
скалярное произведение вектора 𝐀 на векторное произведение векторов 𝐁 и 𝐂. Теперь давайте посмотрим, что такое скаляр
Тройное произведение выглядит как составная часть. Если 𝐢, 𝐣 и 𝐤 единицы
векторов в 𝑥-, 𝑦- и 𝑧-направлениях, то наши три вектора записываются в
Форма компонента, как показано. И если мы напишем векторное произведение
векторов 𝐁 и 𝐂 в компонентной форме имеем 𝐁 крест 𝐂 есть 𝐁 𝑦 𝐂 𝑧 минус 𝐁
𝑧 𝐂 𝑦 раз 𝐢 минус 𝐁 𝑥 𝐂 𝑧 минус 𝐁 𝑧 𝐂 𝑥 раз 𝐣 плюс 𝐁 𝑥 𝐂 𝑦
минус 𝐁 𝑦 𝐂 𝑥 раз 𝐤. И теперь, если мы возьмем скаляр
произведение вектора 𝐀 на это, то есть умножаем коэффициенты каждого из
единичные векторы вместе, так что, например, наш первый член равен 𝐀 𝑥 раз 𝐁 𝑦 𝐂
𝑧 минус 𝐁 𝑧 𝐂 𝑦.
Теперь давайте посмотрим, что такое скаляр
Тройное произведение выглядит как составная часть. Если 𝐢, 𝐣 и 𝐤 единицы
векторов в 𝑥-, 𝑦- и 𝑧-направлениях, то наши три вектора записываются в
Форма компонента, как показано. И если мы напишем векторное произведение
векторов 𝐁 и 𝐂 в компонентной форме имеем 𝐁 крест 𝐂 есть 𝐁 𝑦 𝐂 𝑧 минус 𝐁
𝑧 𝐂 𝑦 раз 𝐢 минус 𝐁 𝑥 𝐂 𝑧 минус 𝐁 𝑧 𝐂 𝑥 раз 𝐣 плюс 𝐁 𝑥 𝐂 𝑦
минус 𝐁 𝑦 𝐂 𝑥 раз 𝐤. И теперь, если мы возьмем скаляр
произведение вектора 𝐀 на это, то есть умножаем коэффициенты каждого из
единичные векторы вместе, так что, например, наш первый член равен 𝐀 𝑥 раз 𝐁 𝑦 𝐂
𝑧 минус 𝐁 𝑧 𝐂 𝑦.
Но что это нам напоминает
из? Хорошо, помните, что определитель
матрицы два на два с элементами 𝑎, 𝑏, 𝑐, 𝑑 равно 𝑎𝑑 минус 𝑏𝑐. Так, например, в нашем первом семестре
𝐁 𝑦 𝐂 𝑧 минус 𝐁 𝑧 𝐂 𝑦 на самом деле является определителем матрицы два на два
с элементами 𝐁 𝑦, 𝐁 𝑧, 𝐂 𝑦, 𝐂 𝑧. Итак, наш первый член скаляра
тройное произведение в 𝐀 𝑥 раз больше определителя матрицы с элементами 𝐁 𝑦, 𝐁
𝑧, 𝐂 𝑦, 𝐂 𝑧 и аналогично для наших вторых двух членов.
Итак, наш первый член скаляра
тройное произведение в 𝐀 𝑥 раз больше определителя матрицы с элементами 𝐁 𝑦, 𝐁
𝑧, 𝐂 𝑦, 𝐂 𝑧 и аналогично для наших вторых двух членов.
Теперь это должно выглядеть знакомо потому что это определитель матрицы три на три, состоящей из компоненты векторов 𝐀, 𝐁 и 𝐂. Так что на самом деле скалярная тройка Произведение трех векторов 𝐀, 𝐁 и 𝐂 есть просто определитель матрица три на три, состоящая из компонентов трех векторов. И, конечно же, определитель матрица является скаляром. Давайте теперь посмотрим, как мы можем применить это в примере.
Данные векторы 𝐀, 𝐁 и 𝐂, где 𝐀 имеет компоненты один, пять, минус пять; 𝐁 имеет компоненты два, четыре, три; а также 𝐂 имеет компоненты ноль, пять, минус четыре, найдите скалярное тройное произведение 𝐀, 𝐁 и 𝐂.
Нас просят вычислить скаляр
тройное произведение векторов 𝐀, 𝐁 и 𝐂. И мы знаем, что это эквивалентно
к вычислению определителя матрицы, состоящей из компонент
три вектора, как показано. Итак, с нашими векторами 𝐀, 𝐁 и 𝐂,
мы хотим найти определитель матрицы, первая строка которой состоит из
компоненты вектора 𝐀, вторая строка которого содержит компоненты вектора 𝐁, а
третья строка содержит компоненты вектора 𝐂.
И мы знаем, что это эквивалентно
к вычислению определителя матрицы, состоящей из компонент
три вектора, как показано. Итак, с нашими векторами 𝐀, 𝐁 и 𝐂,
мы хотим найти определитель матрицы, первая строка которой состоит из
компоненты вектора 𝐀, вторая строка которого содержит компоненты вектора 𝐁, а
третья строка содержит компоненты вектора 𝐂.
И не забудьте рассчитать
Определитель матрицы три на три, используя первую строку в качестве опорной, мы берем
первый верхний левый элемент 𝐀 𝑥 и умножить его на определитель два на два
матрица в правом нижнем углу. Затем мы берем отрицательное значение
второй элемент в верхней строке и умножьте его на указанный определитель. И, наконец, мы добавляем третий
элемент в верхней строке, умножьте его на определитель, образованный четырьмя элементами
в Нижнем левом углу.
В нашем случае это означает один раз матрица два на два с элементами четыре, три, пять, минус четыре минус пятикратный определитель матрицы с элементами два, три, нуль и минус четыре плюс минус пять, умноженный на определитель матрицы два на два с элементами два, четыре, ноль, пять. А теперь вспомнив, что определитель матрицы два на два с элементами 𝑎, 𝑏, 𝑐, 𝑑 равен 𝑎𝑑 минус 𝑏𝑐, у нас есть один раз четыре раза минус четыре минус три раза пять минус пять раз два раза минус четыре минус три раза ноль минус пять снова раз два раза пять минус четыре раза ноль.
Однократное минус 16 минус
15 минус пять раз минус восемь минус ноль минус пять раз 10 минус ноль. Оценка этого дает нам отрицательное
31 плюс 40 минус 50, что отрицательное 41. Скалярное тройное произведение
поэтому векторы 𝐀, 𝐁 и 𝐂 отрицательны 41.
Мы видели, что скалярная тройка произведение трех векторов эквивалентно определителю три на три матрица, состоящая из их компонентов. И получается, что если мы переключим два вектора вокруг, это меняет знак нашего результата.
И это, конечно, то, что мы можно было бы ожидать, поскольку если мы поменяем местами две строки в нашем определителе, это изменит знак. Если бы мы затем выполнили дальнейшая перестановка, например, чтобы поменять местами 𝐀 с 𝐂 или 𝐁 с 𝐂, знак снова меняется. И это говорит нам о том, что скаляр тройное произведение 𝐀 точка 𝐁 крест 𝐂 такое же, как 𝐁 точка 𝐂 крест 𝐀. А это то же самое, что 𝐂 точка 𝐀 крест 𝐁. И это говорит нам о том, что когда циклический порядок трех векторов остается неизменным, их скалярная тройка произведения равны.
Рассмотрим это свойство
скалярное тройное произведение в примере.
Найдите сумму скалярной тройки продукт 𝐢 точка 𝐣 крест 𝐤 плюс 𝐣 точка 𝐤 крест 𝐢 плюс 𝐤 точка 𝐢 крест 𝐣.
Нам дана сумма трех скалярных тройные произведения тех же трех единичных векторов 𝐢, 𝐣 и 𝐤, где это единичные векторы в 𝑥-, 𝑦- и 𝑧-направлениях. Эти три скалярных тройных произведения находятся в разном порядке. Первый является скалярным произведением 𝐢 с 𝐣 крестом 𝐤. Второй является скалярным произведением 𝐣 с 𝐤 крестом 𝐢. И третье — скалярное произведение из 𝐤 с 𝐢 крестом 𝐣. Однако мы знаем, что, поскольку эти три скалярных тройных произведения имеют одни и те же три вектора, абсолютные значения скалярных тройных произведений будет одинаковым.
Мы также знаем, что только если три
векторы находятся в одном и том же циклическом порядке, будут ли они иметь одинаковый знак. В нашем случае циклический порядок
первый тройной продукт — это от 𝐢 до 𝐣 до 𝐤. А теперь, если мы посмотрим на второй
тройной продукт, у нас есть от 𝐣 до 𝐤 до 𝐢, которые находятся в том же направлении цикла. И идет третье тройное произведение
от 𝐤 к 𝐢 к 𝐣, который снова находится в том же циклическом направлении.
А теперь, если мы посмотрим на второй
тройной продукт, у нас есть от 𝐣 до 𝐤 до 𝐢, которые находятся в том же направлении цикла. И идет третье тройное произведение
от 𝐤 к 𝐢 к 𝐣, который снова находится в том же циклическом направлении.
И поскольку все это в
положительном направлении, если мы находим одно из скалярных тройных произведений, мы просто умножаем
наш результат на три, так как все они имеют одинаковую величину. Теперь, используя нашу циклическую диаграмму на
правильно, из циклических свойств это говорит нам, что 𝐣 крест 𝐤 равен 𝐢 и
аналогично 𝐤 крест 𝐢 равен 𝐣 и что 𝐢 крест 𝐣 равен 𝐤. Это говорит нам о том, что скаляр
произведение 𝐢 на перекрестное произведение 𝐣 и 𝐤 является просто скалярным произведением 𝐢
с собой. И мы знаем, что это просто
модуль или величина 𝐢 в квадрате. А так как 𝐢 — единичный вектор,
это равно единице.
И вспомним, что все наши скаляры тройные произведения имеют одинаковую величину. А так как все три в одном направлении, они все равны. Таким образом, мы можем сказать, что сумма наших три скалярных тройных произведения в три раза больше одного из скалярных тройных произведений. А так как мы обнаружили, что скаляр тройное произведение 𝐢 с 𝐣 крестом 𝐤 равно единице, у нас есть три умножения на единицу, что равно трем. Сумма наших трех скалярных троек произведение, следовательно, равно трем.
Стоит отметить, что мы могли также использовали детерминантный метод, чтобы решить это. Мы снова воспользуемся тем, что их все величины равны единице и находятся в одном и том же циклическом направление. Итак, найдя один из наших определителей, умножьте это на три. И снова наш ответ — три.
Теперь рассмотрим другое свойство
скалярного тройного произведения, связанного с компланарными векторами. Напомним, что перекрестное произведение
вектор 𝐁 с другим вектором 𝐂 — это другой вектор, перпендикулярный плоскости
определяется двумя векторами 𝐁 и 𝐂. Теперь, если вектор 𝐀 находится в том же
плоскость как 𝐁 и 𝐂, то 𝐀 также должна быть перпендикулярна 𝐁 пересечению 𝐂. Теперь, если мы подумаем о скаляре
произведение двух векторов, если векторы перпендикулярны, то их скалярное произведение
равен нулю, так как угол между ними равен 90 градусов и косинус 90
градусов равен нулю.
Напомним, что перекрестное произведение
вектор 𝐁 с другим вектором 𝐂 — это другой вектор, перпендикулярный плоскости
определяется двумя векторами 𝐁 и 𝐂. Теперь, если вектор 𝐀 находится в том же
плоскость как 𝐁 и 𝐂, то 𝐀 также должна быть перпендикулярна 𝐁 пересечению 𝐂. Теперь, если мы подумаем о скаляре
произведение двух векторов, если векторы перпендикулярны, то их скалярное произведение
равен нулю, так как угол между ними равен 90 градусов и косинус 90
градусов равен нулю.
Теперь, если мы вернемся к нашему скаляру
тройное произведение, если наши векторы 𝐀, 𝐁 и 𝐂 лежат в одной плоскости, то 𝐀
перпендикулярно 𝐁 пересекают 𝐂 и их скалярное тройное произведение равно нулю. Верно и обратное. Если скалярное тройное произведение
равны нулю, то векторы 𝐀, 𝐁 и 𝐂 должны быть компланарны. Давайте использовать это свойство в нашем следующем
пример.
Найдите значение 𝑘, для которого четыре точки один, семь, минус два; три, пять, шесть; отрицательный один, шесть, отрицательный четыре; и минус четыре, минус три, 𝑘 все лежат в одной плоскости.
Нам дали четыре очка, которые нам говорят, что они компланарны; то есть все они лежат в одной плоскости. И нас просят найти значение неизвестной константы 𝑘. Для этого мы будем использовать скалярное тройное произведение, поскольку мы знаем, что если скалярное тройное произведение трех vectors равен нулю, то эти три вектора должны быть компланарны. Однако прежде чем мы это сделаем, нам нужно чтобы проверить, что наши три известные точки неколлинеарны. Мы делаем это, потому что нам нужно быть уверены, что мы не просто берем скалярное произведение с нулевым вектором в нашем скалярное тройное произведение.
Обозначим наши точки 𝐀, 𝐁, 𝐂,
и 𝐃. И мы можем взять любые два из
векторы, образованные точками 𝐀, 𝐁 и 𝐂. Давайте выберем 𝐁𝐀 и 𝐁𝐂. Мы знаем, что 𝐁𝐀 равно 𝐎𝐀
минус 𝐎𝐁. И вычитание подобных за подобным
компоненты, у нас есть минус два, два, минус восемь. Точно так же 𝐁𝐂 равно 𝐎𝐂 минус
𝐎𝐁. А это равно минус четырем,
один, отрицательное 10. Мы знаем, что векторное произведение
𝐁𝐀 с 𝐁𝐂 задается показанным определителем, где 𝐢, 𝐣 и 𝐤 — единица
векторы в 𝑥-, 𝑦- и 𝑧-направлениях, так что наш определитель равен 𝐢 умноженному на два
минус 10 минус минус восемь раз один, что в 𝐢 раз больше определителя
матрицы два на два в нижнем углу минус 𝐣 умноженный на определитель
матрица с элементами минус два, минус восемь, минус четыре и минус 10
плюс 𝐤 умноженный на определитель матрицы с отрицательными элементами два, два,
минус четыре и один.
И мы можем взять любые два из
векторы, образованные точками 𝐀, 𝐁 и 𝐂. Давайте выберем 𝐁𝐀 и 𝐁𝐂. Мы знаем, что 𝐁𝐀 равно 𝐎𝐀
минус 𝐎𝐁. И вычитание подобных за подобным
компоненты, у нас есть минус два, два, минус восемь. Точно так же 𝐁𝐂 равно 𝐎𝐂 минус
𝐎𝐁. А это равно минус четырем,
один, отрицательное 10. Мы знаем, что векторное произведение
𝐁𝐀 с 𝐁𝐂 задается показанным определителем, где 𝐢, 𝐣 и 𝐤 — единица
векторы в 𝑥-, 𝑦- и 𝑧-направлениях, так что наш определитель равен 𝐢 умноженному на два
минус 10 минус минус восемь раз один, что в 𝐢 раз больше определителя
матрицы два на два в нижнем углу минус 𝐣 умноженный на определитель
матрица с элементами минус два, минус восемь, минус четыре и минус 10
плюс 𝐤 умноженный на определитель матрицы с отрицательными элементами два, два,
минус четыре и один.
Освободив место, это оценивается как
минус 12, 12, шесть, что не равно нулевому вектору. Итак, мы знаем, что наши три точки
не коллинеарны. И мы можем перейти к использованию
скалярное тройное произведение, чтобы найти значение 𝑘. Нам говорят, что все четыре точки 𝐀,
𝐁, 𝐂 и 𝐃 компланарны. И мы знаем, что скалярная тройка
произведение трех компланарных векторов равно нулю. У нас уже есть часть нашего скаляра
тройное произведение. Это с перекрестным произведением
𝐁𝐀 и 𝐁𝐂. Теперь, если все четыре точки лежат в
плоскости, то вектор 𝐀𝐃 также должен лежать в плоскости. Вектор 𝐀𝐃 задается 𝐎𝐃
минус 𝐎𝐀. И это минус пять, минус
10, 𝑘 плюс два.
Итак, мы знаем, что наши три точки
не коллинеарны. И мы можем перейти к использованию
скалярное тройное произведение, чтобы найти значение 𝑘. Нам говорят, что все четыре точки 𝐀,
𝐁, 𝐂 и 𝐃 компланарны. И мы знаем, что скалярная тройка
произведение трех компланарных векторов равно нулю. У нас уже есть часть нашего скаляра
тройное произведение. Это с перекрестным произведением
𝐁𝐀 и 𝐁𝐂. Теперь, если все четыре точки лежат в
плоскости, то вектор 𝐀𝐃 также должен лежать в плоскости. Вектор 𝐀𝐃 задается 𝐎𝐃
минус 𝐎𝐀. И это минус пять, минус
10, 𝑘 плюс два.
Итак, взяв скалярное тройное произведение
𝐀𝐃 с 𝐁𝐀 и 𝐁𝐂, мы просто имеем скалярное произведение двух векторов
показано. Это оценивается как минус пять
умножить на минус 12 плюс минус 10 раз на 12 плюс 𝑘 плюс два раза шесть. Это 60 минус 120 плюс шесть 𝑘
плюс 12, что упрощается до шести 𝑘 минус 48. Если векторы компланарны, это
должен быть равен нулю. Прибавляя 48 к обеим сторонам, получаем
нас шесть 𝑘 равно 48. И разделив обе части на шесть,
это дает нам 𝑘 равно восьми. Следовательно, значение 𝑘, для которого
все четыре заданные точки лежат в одной плоскости, если 𝑘 равно восьми.
Если векторы компланарны, это
должен быть равен нулю. Прибавляя 48 к обеим сторонам, получаем
нас шесть 𝑘 равно 48. И разделив обе части на шесть,
это дает нам 𝑘 равно восьми. Следовательно, значение 𝑘, для которого
все четыре заданные точки лежат в одной плоскости, если 𝑘 равно восьми.
Последнее свойство скаляра
Тройной продукт, который мы собираемся рассмотреть, возникает из того, что он означает.
геометрически. Помните, что перекрестное произведение 𝐁
крест 𝐂 — вектор, перпендикулярный плоскости, определяемой векторами 𝐁 и
𝐂. Величина этого перекрестного произведения
площадь параллелограмма, натянутого на векторы 𝐁 и 𝐂. Теперь, если мы добавим еще один вектор 𝐀 и
рассмотрим параллелепипед, натянутый в трех измерениях векторами 𝐀, 𝐁 и
𝐂, мы знаем, что его объем — это площадь параллелограмма, натянутого на векторы
𝐁 и 𝐂, умноженные на высоту перпендикуляра ℎ. Мы также знаем, что эта высота ℎ равна
равно величине вектора 𝐀, умноженной на косинус 𝜃, который является острым
угол между 𝐀 и ℎ.
Мы также знаем, что эта высота ℎ равна
равно величине вектора 𝐀, умноженной на косинус 𝜃, который является острым
угол между 𝐀 и ℎ.
Итак, у нас есть объем
параллелепипед — это величина перекрестного произведения 𝐁 и 𝐂, умноженного на
величина вектора 𝐀 умножается на косинус 𝜃. И по определению это
величина скалярного тройного произведения 𝐀 на 𝐁 крест 𝐂. Стоит отметить, что если
ориентация 𝐁 креста 𝐂 изменилась на вниз, затем угол между 𝐀 и 𝐁 крестом
𝐂 будет 𝜃 простым числом, что равно 180 минус 𝜃. А так как cos 180 минус 𝜃 равно
отрицательное значение cos 𝜃, мы имеем абсолютное значение cos 𝜃 простое число является абсолютным значением
потому что 𝜃. Итак, взяв величину
скалярное тройное произведение, мы имеем объем параллелепипеда, каким бы
ориентация креста 𝐁 𝐂. Давайте теперь посмотрим на пример
нахождение объема параллелепипеда с помощью скалярного тройного произведения.
Найти объем параллелепипед с прилегающими сторонами 𝐮 равен единице, единице, трем; 𝐯 это вектор два, один, четыре; а 𝐰 — вектор пять, один, минус два.
Параллелепипед, как он определен, закручивается векторами 𝐮, 𝐯 и 𝐰. И мы знаем, что найти объем такого параллелепипеда мы можем использовать скалярное тройное произведение. То есть объем параллелепипед со смежными сторонами 𝐮, 𝐯 и 𝐰 — величина скаляра тройное произведение. Мы также знаем, что скалярная тройка произведение есть определитель матрицы, строки которой являются элементами векторов 𝐮, 𝐯 и 𝐰. Так что на самом деле объем величина этого.
В нашем случае это
величина определителя матрицы, элементы которой равны единице, единице, трем; два,
один, четыре; и пять, один, минус два. Вот где ряды наши
векторы 𝐮, 𝐯 и 𝐰. Это один раз определитель
матрицы два на два с элементами один, четыре, один, минус два минус один раз
матрица два на два с элементами два, четыре, пять и минус два плюс три
умножить на определитель матрицы два на два с элементами два, один, пять и
один.
И, используя тот факт, что определитель матрицы два на два с элементами 𝑎, 𝑏, 𝑐, 𝑑 равен 𝑎𝑑 минус 𝑏𝑐, это оценивается величиной минус шесть плюс 24 минус девять, что составляет девять. Объем параллелепипеда с прилегающими сторонами 𝐮, 𝐯 и 𝐰, следовательно, составляет девять кубических единиц.
Давайте завершим это видео, отметив
некоторые из ключевых моментов, которые мы рассмотрели. Мы знаем, что скалярная тройка
произведение трех векторов 𝐀, 𝐁 и 𝐂 является скаляром. Скалярное тройное произведение равно
эквивалентно определителю матрицы три на три, строки которой являются
компонента векторов 𝐀, 𝐁 и 𝐂. Скалярные тройные произведения равны, если
циклический порядок неизменен. Если векторы 𝐀, 𝐁 и 𝐂
компланарны, то их скалярное тройное произведение равно нулю. И, наконец, объем
параллелепипед, натянутый на векторы 𝐀, 𝐁 и 𝐂, задается величиной
их скалярное тройное произведение.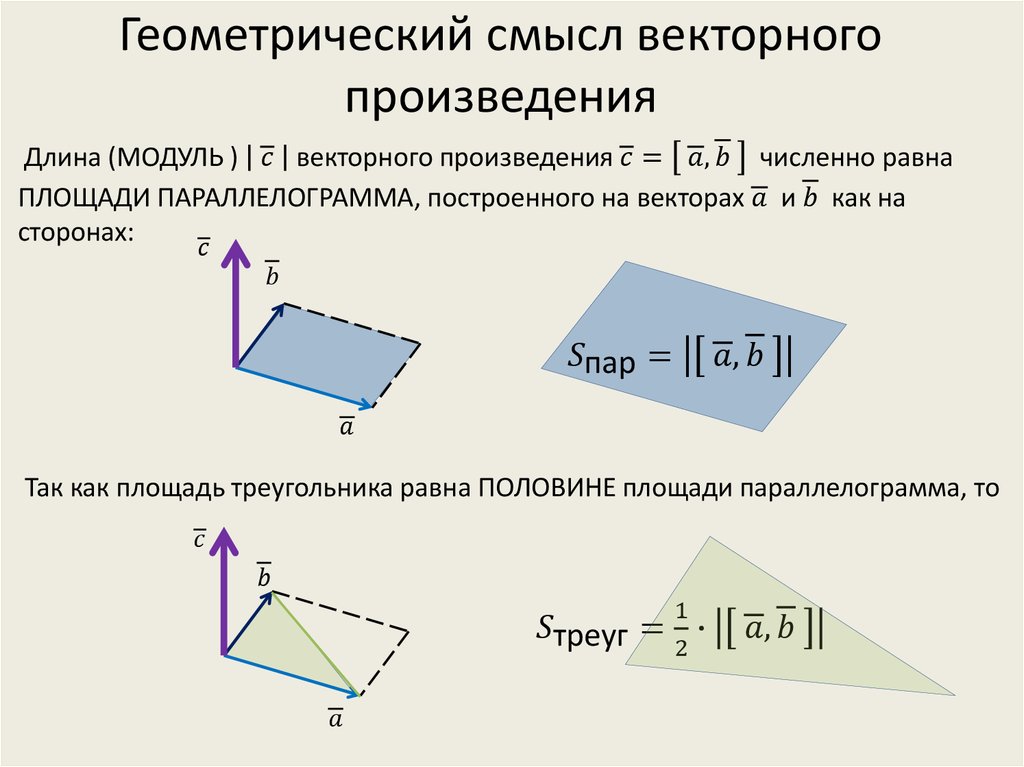



 е. [a a b] = 0
е. [a a b] = 0