Что такое векторная сумма сил?

Творчество › К чему › Чему равна равнодействующая двух сил приложенных к телу в точке а

Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.

1. Что такое векторная сумма?
2. Как определить векторную сумму сил?
3. Что такое сумма сил?
4. Чему равна сумма векторов?
5. Что такое векторная величина примеры?
6. Что такое векторная графика простыми словами?
7. Что такое вектор силы?
8. Какой вектор представляет собой сила?
9. Сколько способов сложения векторов?
10. Как называется сумма сил?
11. Когда сумма всех сил равна нулю?
12. Какие виды сил вы знаете?
13. Как обозначается сумма векторов?
14. Как найти сумму 4 векторов?
15. Когда вектор равен нулю?
16. Что лучше растровая или векторная?
17. Как вычитать векторы?
18. Как начертить сумму векторов?
19. Как сложить силы?
20. Как найти вектор равный сумме векторов?
21. Когда сумма трех векторов равна нулю?
22. Как найти сумму векторов в ромбе?
23. Что такое векторная величина в геометрии?

Что такое векторная сумма?

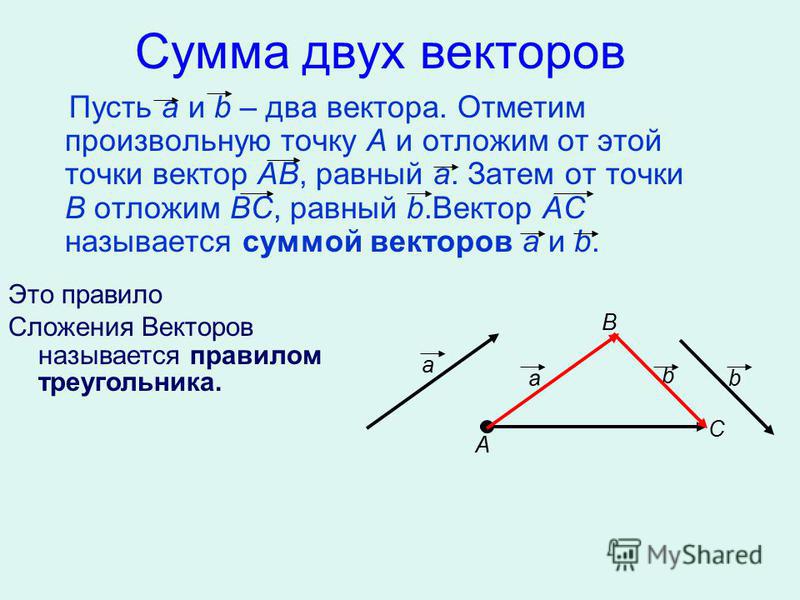
От конца вектора a → откладываем вектор, равный b →. Соединяем начало первого вектора и конец второго. Получившийся вектор, начало которого совпадает с началом вектора a →, а конец — с концом вектора b →, называется суммой этих векторов.

Как определить векторную сумму сил?

Векторная сумма всех сил, одновременно действующих на тело, называется равнодействующей силой и определяется правилом векторного сложения сил: R → = F → 1 + F → 2 + F → 3 + ⋯ + F → n = ∑ i = 1 n F → i.

Что такое сумма сил?

Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил: ∑ F → = m a →.

Чему равна сумма векторов?

Координаты суммы векторов равны суммам соответствующих координат слагаемых; например, на плоскости: (x; y) + (x1; y1) = (x +x1; y + y1).

Что такое векторная величина примеры?

Векторной называется величина, которая кроме числового значения имеет направление. Векторная величина это направленный отрезок, который имеет длину и направление. К векторным величинам относятся: скорость движения V, перемещение S, ускорение a, сила F, импульс p, момент силы M.

Что такое векторная графика простыми словами?

Векторная графика — это изображения, сформированные множеством точек, объединенных математическими соотношениями. Каждый объект — это визуализация математической функции. Векторное изображение имеет преимущество перед растровым по качеству: при любом увеличении оно сохраняет идеальную четкость.

Что такое вектор силы?

Вектор силы — образное представление, видение того, какие линии сил организуют тело человека. Вектор силы — это то, что создает впечателение о человеке. Вектор силы — это способ самоорганизации своего тела и своего статуса, способ самовнушение телом.

Какой вектор представляет собой сила?

Сила является векторной величиной. Она характеризуется модулем, направлением и точкой приложения. Также используют понятие линия действия силы, означающее проходящую через точку приложения силы прямую, вдоль которой направлена сила.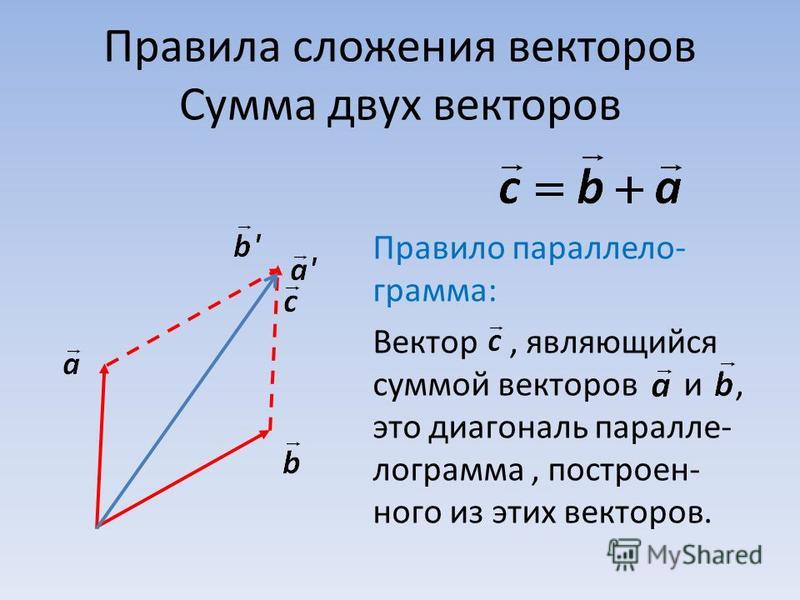

Сколько способов сложения векторов?

Существует три способа сложить вектора: 1. Правило треугольника. Необходимо расположить вектора так, чтобы начало одного вектора совпало с концом второго.

Как называется сумма сил?

Если на тело одновременно действует несколько сил, тогда состояние тела или его движение определяет результирующая сила — сумма всех сил.

Когда сумма всех сил равна нулю?

Когда сумма всех сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое. Такое движение при отсутствии влияния каких либо сил называется инерцией.

Какие виды сил вы знаете?

11 различных типов сил:

• Гравитационная сила G — универсальная гравитационная постоянная, которая варьируется в зависимости от различных астрономических тел.
• Электромагнитная сила Тип: Бесконтактная сила
• Сильная ядерная сила
• Слабая ядерная сила
• Прикладная сила
• Сила трения
• Нормальная сила
• Сила натяжения

Как обозначается сумма векторов?

Сумма векторов ⃗ и ⃗ обозначается так: ⃗ ⃗.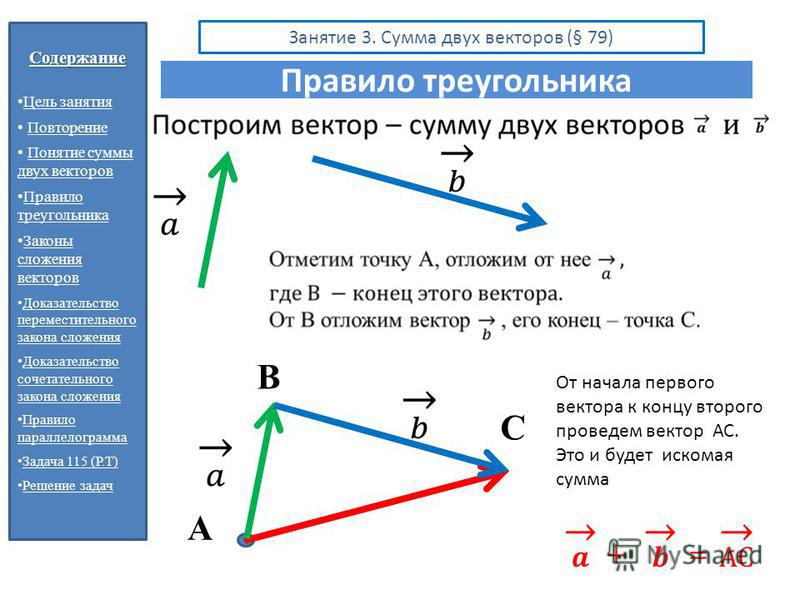 Правило треугольника можно сформулировать также следующим образом: если A, B и C — произвольные точки, то ⃗ ⃗ ⃗. Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.

Как найти сумму 4 векторов?

Сумму нескольких векторов получаем так: складываем первый и второй вектор, затем к их сумме прибавляем третий вектор и т. д. Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.

Когда вектор равен нулю?

Нулевой вектор принято считать сонаправленным любому вектору. Можно считать, что нулевой вектор одновременно коллинеарен и ортогонален любому вектору пространства (легко выводится из определения). Все координаты нулевого вектора в любой аффинной системе координат равны нулю.

Что лучше растровая или векторная?

Преимущество растровой графики — в цветовых возможностях. Она позволяет хорошо передавать градиенты и цветовые переходы на сложных иллюстрациях.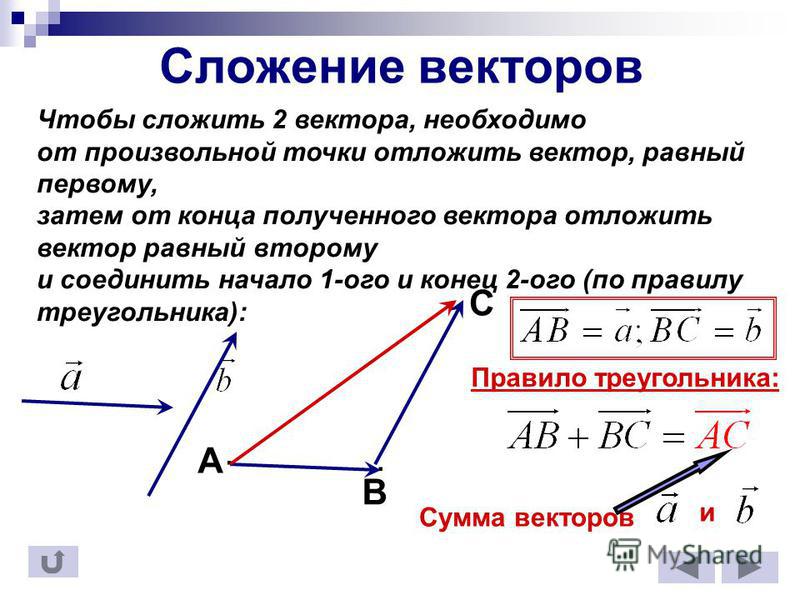 Но при увеличении изображения его качество будет ухудшаться. Преимущество векторной графики — в бесконечном размере.

Как вычитать векторы?

Существует отдельное правило для их вычитания:

• Отложим один вектор от начала другого.
• Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.

Как начертить сумму векторов?

Правило треугольника

Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго — это и будет сумма двух векторов.

Как сложить силы?

Если силы параллельны и сонаправлены, то их модули складываются. Для вычислений используют формулу: F рез = F 1 + F 2.

Как найти вектор равный сумме векторов?

Чтобы найти вектор с = (х; у), равный сумме векторов a и b, необходимо сложить соответствующие координаты векторов a и b.

Когда сумма трех векторов равна нулю?

Заметим, что если сумма трёх единичных векторов равна нулю, то сумма каждых двух из них равна третьему с обратным знаком, то есть её модуль равен 1. Три таких единичных вектора можно расположить по разному.

Как найти сумму векторов в ромбе?

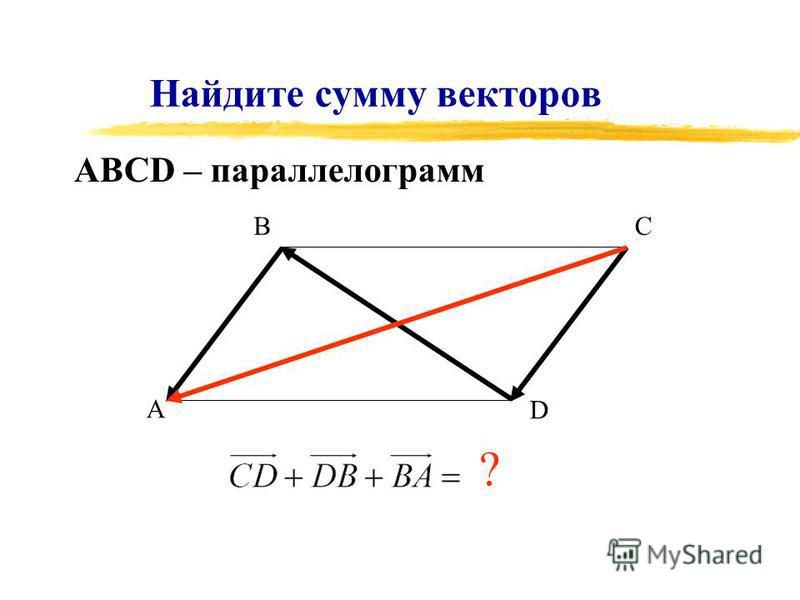
У ромба все стороны равны, а противоположные стороны параллельны, тогда сумма векторов АВ + АД = АВ + ВС.

Что такое векторная величина в геометрии?

Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление.

Раздел 2. Векторная алгебра на плоскости и в пространстве

2.1 Понятие о векторах и скалярах

Векторной величиной или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной или скаляром называется всякая величина, направлением не обладающая. Например, сила, действующая на материальную точку, есть вектор, так как она обладает направлением.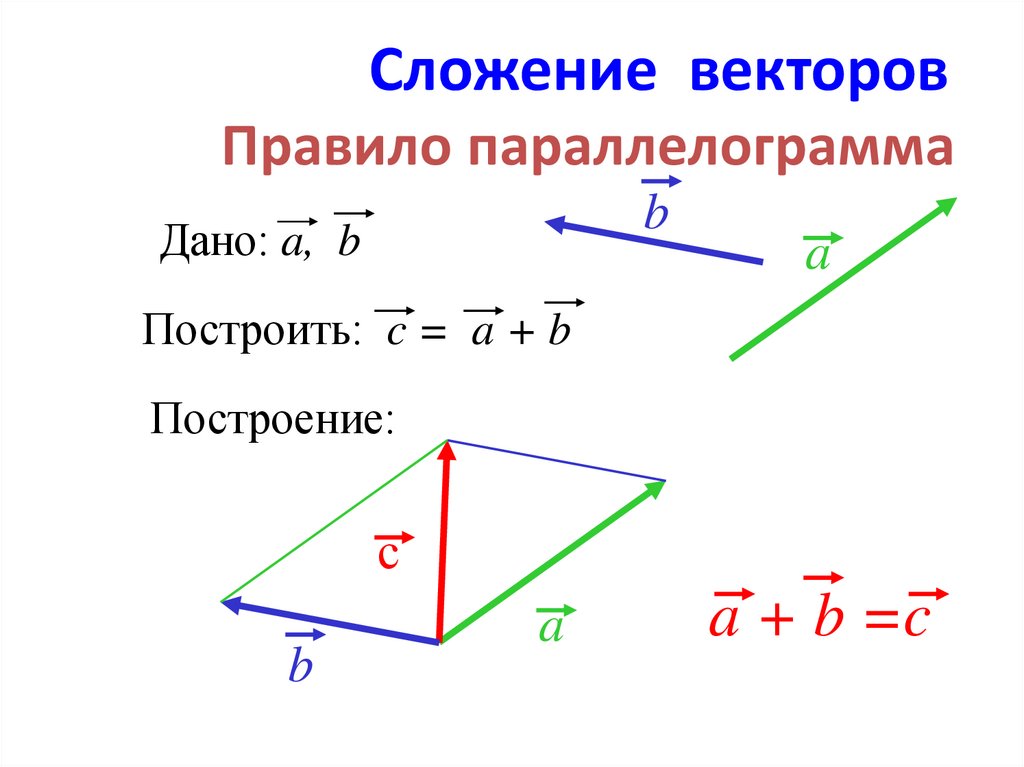

Скорость также является вектором. Температура тела – это скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность – также скалярные величины.

Если отвлечься от направления векторной величины, то ее, как и скалярную величину, можно измерить, выбрав соответствующую масштабную единицу. Но число, полученное в результате измерения, характеризует скалярную величину полностью, а векторную – лишь частично.

Векторную величину полностью можно охарактеризовать направленным отрезком, предварительно задав линейный масштаб.

2.2 Вектор в геометрии

Вектором называется направленный отрезок. Вектор с началом в точке

А и концом в точке В обозначается символом (или одной буквой,,, …). Длина отрезкаАВ называется длиной, или модулем вектора и обозначается,.

Векторы иназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых; записывают . Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) или противоположное.

Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается или просто 0. По определению нулевой вектор не имеет направления и коллинеарен любому вектору.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через .

Единичный вектор, направление которого совпадает с направлением вектора , называетсяортом вектора и обозначается. Два ненулевых вектора называютсяпротивоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору , обозначается; векторпротивоположен вектору().

Два коллинеарных вектора иназываются

равными (), если они сонаправлены и имеют равные длины.

Замечание. Нельзя смешивать понятия «равенство отрезков» и «равенство векторов». Говоря: «отрезки равны», мы утверждаем, что их можно совместить наложением. Но для этого один из них может быть придется подвергнуть повороту. Два вектора будут равны лишь в том случае, когда их можно совместить, не применяя поворот.

Совместим параллельным переносом начала неколлинеарных векторов и. Начало и концы векторов образуют вершины треугольника.Углом между векторами иназывается угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°.

2.3 Векторная алгебра

Над векторами производят действия, называемые сложением, вычитанием и умножением векторов. Эти действия имеют много общих свойств с одноименными алгебраическими действиями. Поэтому учение о действиях над векторами называется векторной алгеброй.

Суммой двух векторов иназывается вектор, соединяющий начало векторас концом вектора, отложенного от конца вектора.

Обозначение: .

Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рис. 1 и 2 соответственно.

При сложении векторов имеют место неравенства:

1) ,

2) ,

выражающие, что сторона треугольника меньше суммы и больше разности двух других сторон (неравенство треугольника). В первой формуле равенство имеет место только для сонаправленных векторов, во второй – только для противоположно направленных векторов.

Сумма противоположных векторов равна нуль-вектору: .

Суммой векторов называется вектор, получающийся после ряда последовательных сложений: к векторуприбавляется вектор, к полученному вектору прибавляется вектори так далее.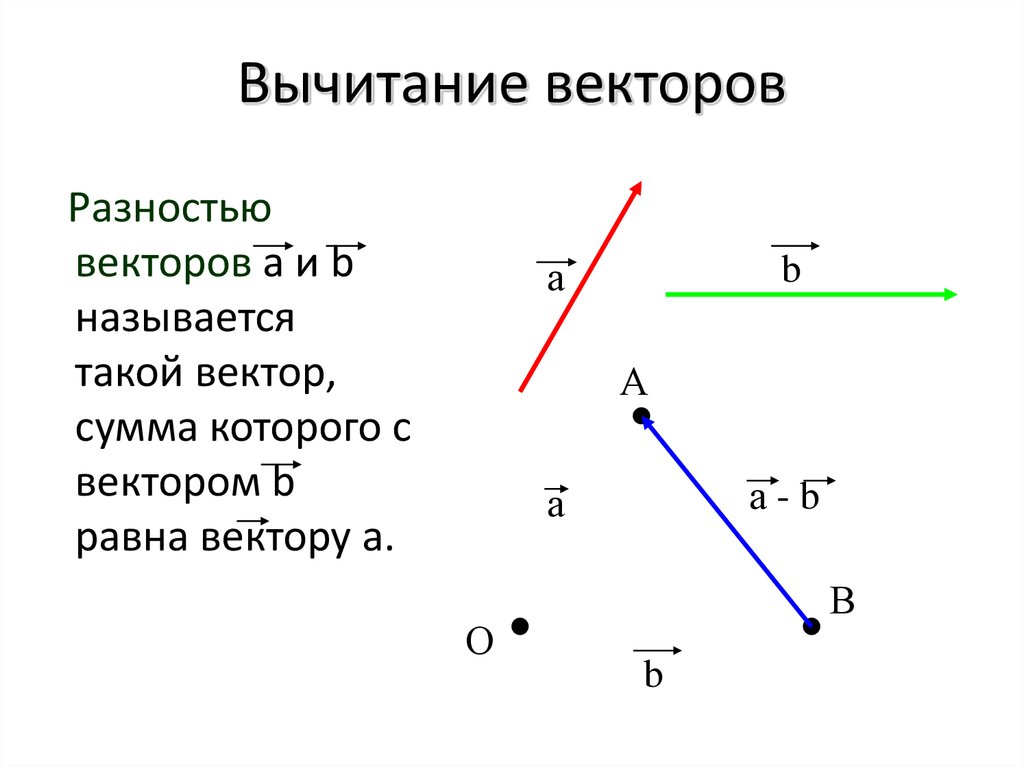

Из определения вытекает следующее построение (правило многоугольника или правило цепи).

Из произвольного начала О откладываем вектор , из точкиА₁, как из начала, откладываем вектор , из точкиА₂ строим вектор и так далее. Векторесть сумма векторов.

Сложение векторов подчиняется коммутативному и ассоциативному свойствам:

1) ,

2) .

Коммутативность и ассоциативность сложения векторов позволяет нам находить сумму векторов в любом удобном порядке.

Правило параллелепипеда. Если три вектора ,ипосле приведения к общему началуне лежат в одной плоскости, то сумму можно найти следующим построением. Из общего началаО строим векторы ,,. На отрезкахОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали равен сумме векторов,и, так как,,и.

Под разностью векторов ипонимается вектортакой, что. Обозначение:. Справедливо равенство.

Произведением вектора на числоназывается вектор, который имеет длину, его направление еслии противоположное направление, если.

Обозначение: .

Отметим, что , т. е. каждый вектор равен произведению его модуля на орт.

Два ненулевых вектора иколлинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т. е., λ – число (признак коллинеарности векторов).

Три ненулевых вектора ,,компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например,(λ

1, λ₂ – числа не равные нулю одновременно) (признак компланарности векторов).

Умножение вектора на число подчиняется тем же законам, что и умножение чисел:

1. (дистрибутивный закон по отношению к числовому множителю).

2. (дистрибутивный закон по отношению к векторному множителю).

3. (ассоциативный закон).

Пример 1: В треугольнике ABC дано: ,, точкаМ – середина стороны

ВС. Выразить вектор через векторыи .

Решение:

Через точкуМ проведем прямые, параллельные сторонам АВ и АС. Получим параллелограмм АВ₁МС₁ (рис. 3), в котором AM является диагональю. Следовательно, . Но,(B₁M и C₁M – средние линии, поэтому AB₁ = B₁B, AC₁ = С₁С). Получаем , т.е..

Пример 2: Какому условию должны удовлетворять ненулевые векторы и, чтобы имело место соотношение?

Решение:

Построим на векторахи, отложенных от точкиО, параллелограмм OADB (рис. 4). Тогда ,. Равенствоозначает, что длины диагоналей параллелограмма равны, т.е.. Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторыиперпендикулярны.

Добавление векторов (базовый) — Frega Physics

Физика‎ > ‎Концепции и задачи‎ > ‎ Добавление векторов (основное) Вектор обозначается стрелкой, указывающей величину и направление. Векторы традиционно измеряются в следующих единицах (но не ограничиваются ими): м , мили, км, мили в час, м/с , км/ч, м/с 2 и северной широты  Когда более одного вектора объединены вместе, это называется добавление векторов или разрешение вектора . Результирующий вектор от сложения векторов называется результирующим . 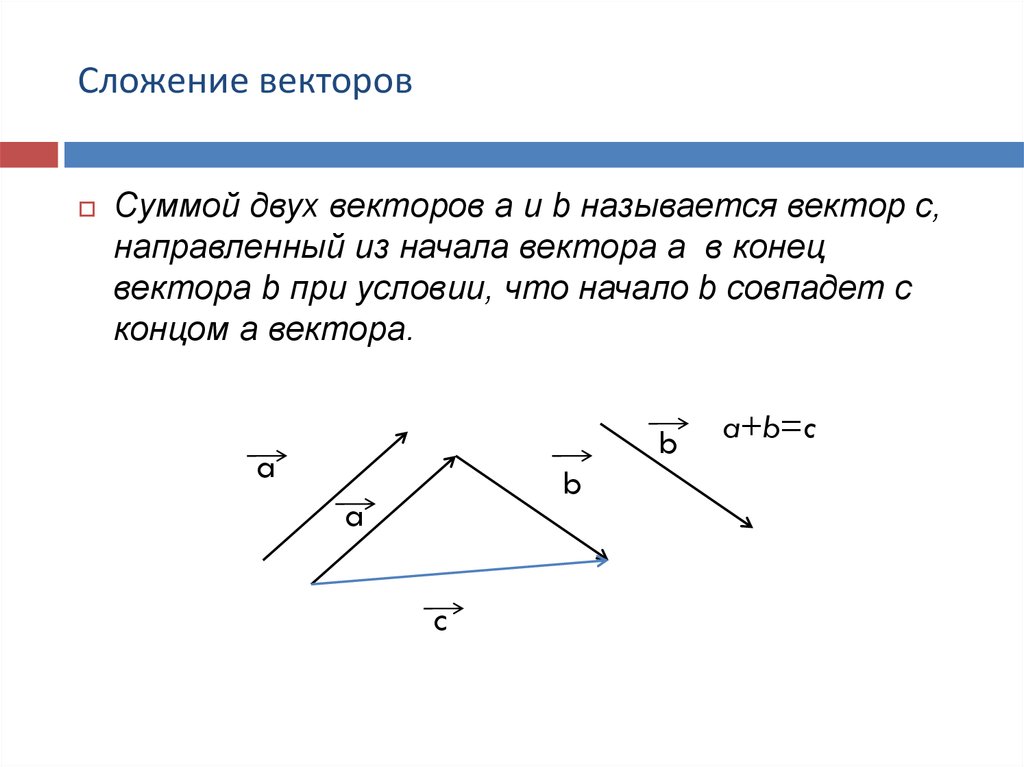Когда векторы складываются, результатом является не просто сумма величин векторов; необходимо учитывать и направление. 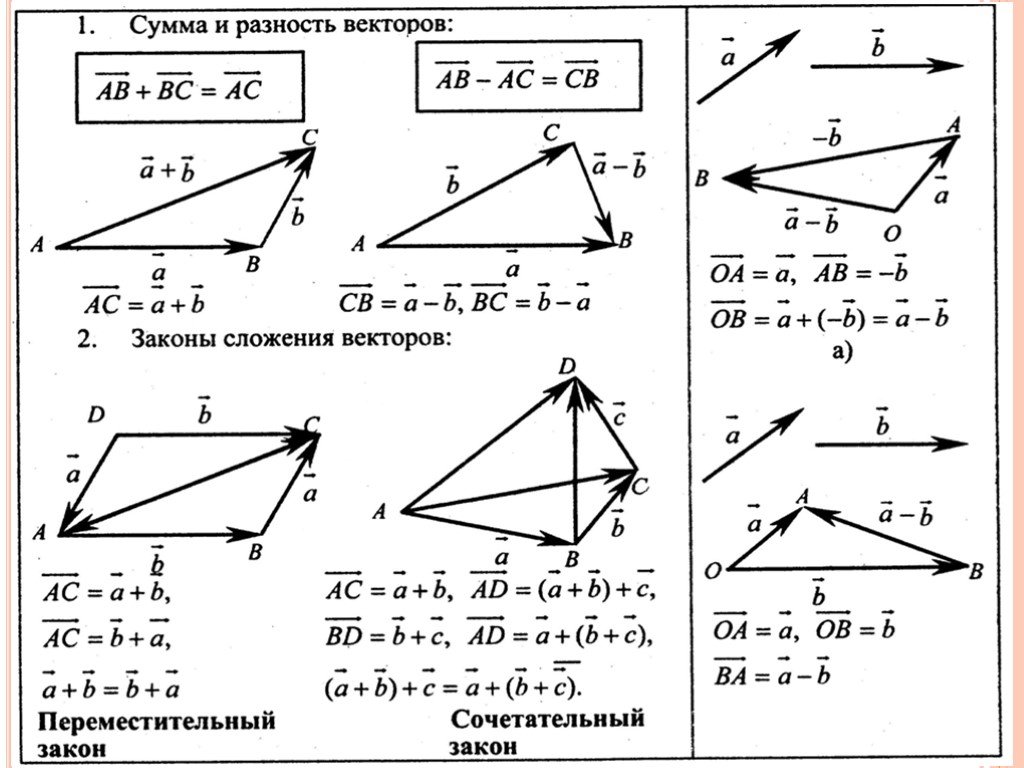Чтобы добавить векторы, направления должны быть установлены единообразно, чтобы избежать путаницы. В качестве основы используется декартова плоскость (она же координатная плоскость, оси x и y, график). Это описано ниже:    X Axis Y Axis  Positive  East North  Negative West  South Если направления не указаны, то используются положительные и отрицательные направления на декартовой плоскости, как описано ниже:   X axis  Y axis  Positive To the right Up  Negative  To the left Вниз Первый вектор всегда должен начинаться в начале координат любого графа (если не указано иное). Это упрощает расчеты. Всякий раз, когда вы рисуете свои векторы, вы хотите рисовать их» от кончика до хвоста », что означает, что кончик стрелки первого вектора указывает, где должен начинаться хвост стрелки для второго вектора.  Это точно так же, как если бы вы действительно двигались. Если вам говорят пройти 5 футов на запад и затем 5 футов к югу, вы не поворачиваете назад после того, как идете на запад, чтобы вернуться к началу (исходной точке), а затем идете на юг.  Вы идете на запад, а затем на юг.  То же самое касается любого другого вектора.  Направление результирующий вектор всегда берется из начала координат. Направление включает в себя как географическое направление (СВ, ЮЗ), так и угол, если только это не чистое направление (С, В, Ю и З). подразумевается угол 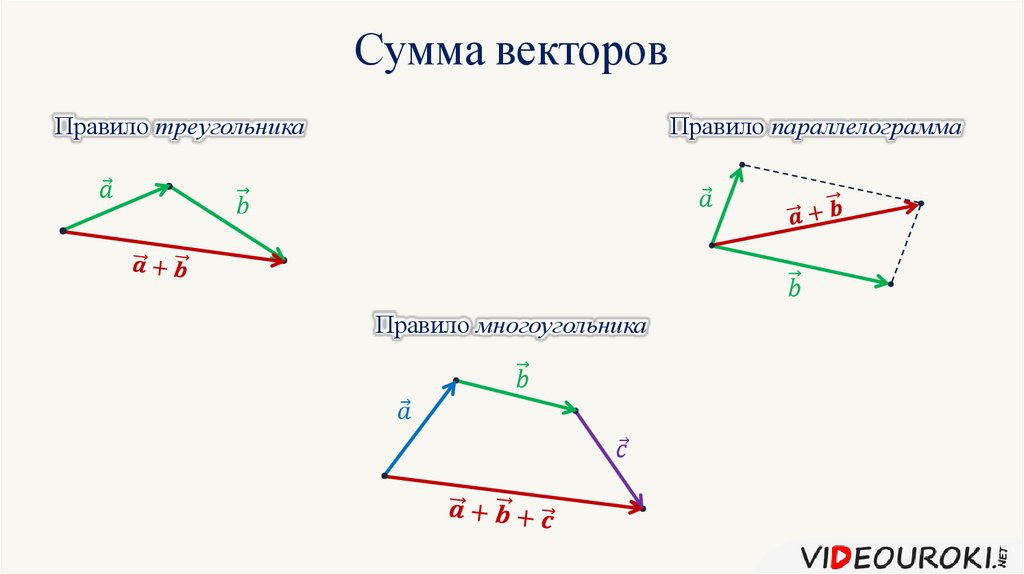Добавление векторов в одно измерение Это наиболее упрощенная версия разрешения векторов. Если векторы расположены в одной плоскости, только вдоль оси X или только только вдоль оси Y, вам нужно только сложить их вместе. Не забудьте сделать W и S отрицательными. В окончательном ответе, если результат отрицательный, он используется только для направления. В качестве величины принять абсолютное значение равнодействующей. Включение негатива с направлением повторяется. 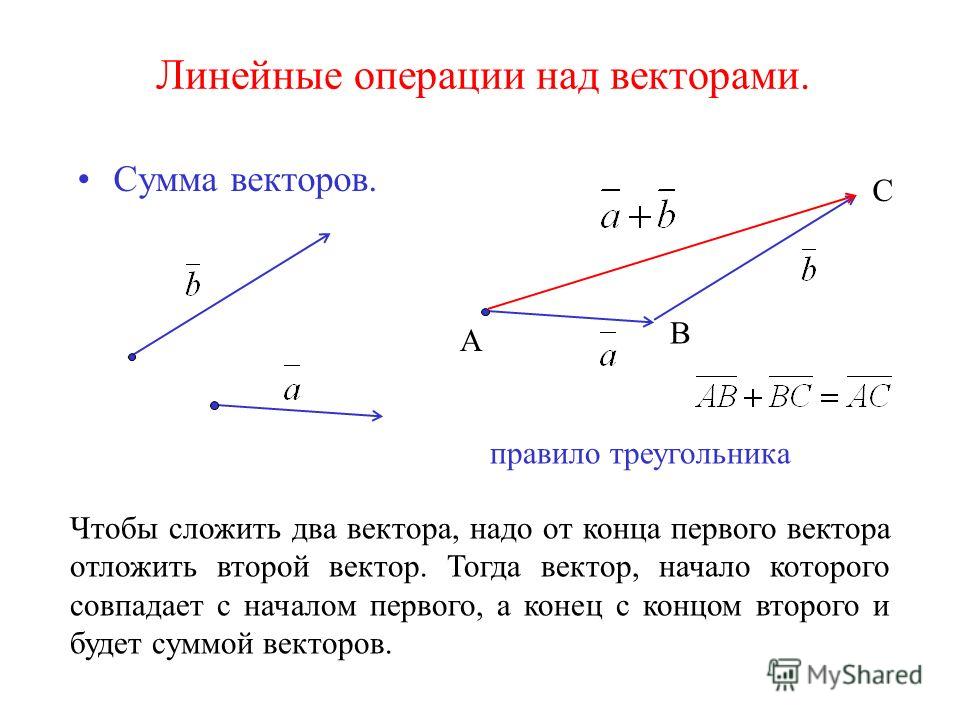Ex: Найдите результирующий вектор для каждого из следующих: 10 м и 8 м W (-10) + (-8) = -18 м 18 М. W 23 м/с n и 18 м/с с. 208) + 180 = -28 миль          28 миль З Добавление векторов в двух измерениях Это немного сложнее, чем разрешение одномерного вектора, потому что теперь вы имеете дело с осями X и Y одновременно, то есть мы больше не можем просто складывать или вычитать. Приходится пользоваться некоторой тригонометрией и теоремой Пифагора. Нарисуйте векторы на декартовой плоскости. Не забудьте начать с исходной точки и рисовать их от кончика к хвосту. В результате получается прямая линия от начала координат до вершины последнего вектора. Поскольку две стороны перпендикулярны друг другу, они образуют прямой угол, а это означает, что с равнодействующей у вас будет прямоугольный треугольник. 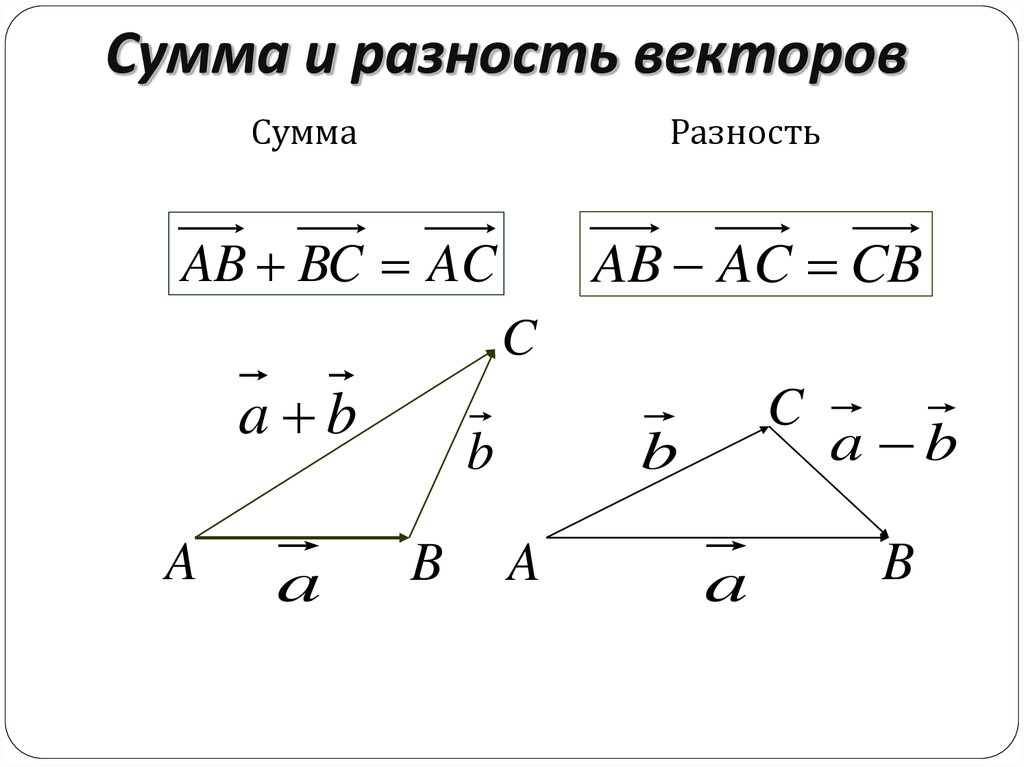Чтобы найти величину равнодействующей, используйте теорему Пифагора. Возьмите абсолютное значение величин векторов. Положительное и отрицательное служат только функции направления. Ненужные отрицания просто увеличивают вероятность ошибки при вводе калькулятором. R = √(x 2 + y 2 ) Чтобы вычислить угол, нужно использовать тригонометрию. Помните, что вы ищете угол от начала координат. tan -1 (opp/adj) = θ (угол) Направление будет зависеть от того, как вы нарисовали свои векторы. Вы можете пройти 5 футов на юг, а затем 5 футов на запад, или вы можете пройти 5 футов на запад, а затем 5 футов на юг, и вы окажетесь в том же положении. Разница заключается в названии угла и направления, которое вы взяли. Если вы хотите W, а затем S, ваше направление будет S o W. Если вы пойдете S, а затем W, ваше направление будет W o S. Легкий способ выяснить направление угла — посмотреть на какой оси касается угол. Какой бы стороны ни касался угол, это ваше второе направление. Итак, если угол касается южной стороны, то это будет W o южной широты. Если угол касается западной стороны, это будет ю.ш. o западной долготы. Полный ответ должен включать как величину, так и направление. Вот общепринятый формат записи результирующего вектора: # единица @ угол ˚ направление Пример: Найдите результирующий вектор для каждого из следующих:             3 мили в. (x 2 + y 2 )             R = √(3 2 + 4 2 ) = 5 миль θ = TAN -1 (OPP/ADJ) θ = TAN -1 (4/3) = 53К N O E или θ = Tan -1 (3/4) = 37 ° E O N 5 миль @ 53 n O E или 5 миль @ 37 ° E O N

Добавление вектора

Математика и наука были изобретены людьми для описания и понимать окружающий мир. Заметим, что существуют некоторые величины и процессы в наш мир, которые зависят от направления , в котором они происходят, и есть некоторые величины, которые не зависят по направлению. Математики и ученые называют количество который зависит от направления векторной величины . Количество который не зависит от направления, называется скалярная величина . А векторное количество имеет две характеристики: величина и направление . Когда сравнение две векторные величины одного и того же типа, вы должны сравнить обе величина и направление. На этом слайде мы описываем метод сложения двух векторов. Сложение векторов — это один из аспектов большой векторной алгебры, которую мы изучаем. , а не будут представлены на этом сайте. Добавление вектора представлено здесь, потому что это встречается довольно часто при изучении движения и потому что он демонстрирует некоторые фундаментальные различия между векторы и скаляры. Векторы обычно обозначаются на рисунках стрелкой. Длина стрелки указывает величину и кончик стрелки указывает направление. Вектор помечены буквой в алфавитном порядке буква с линией сверху, чтобы отличить ее от скаляра. Величину вектора будем обозначать символом |a| . Направление будет измеряться углом фи относительно координаты ось х . Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе векторы! Они имеют величину и направление. Сначала ты столкнуться с осями координат, когда вы учитесь строить графики. Так что у тебя есть использовал векторы в течение некоторого времени, даже не подозревая об этом! Если мы построим пунктирную линию от кончика вектора a идущий параллельно оси х, он пересекает ось у в том месте, где мы этикетка и . Точно так же линия от кончика вектора параллельно оси у пересекает ось х на топор . Величины x и ay называются компоненты вектора, и оба являются скалярными квантитами. Чтобы добавить два вектора, a и b , мы сначала разбиваем каждый вектор на его компоненты, x и a , и bx и по , как показано на рисунке. Из правил, регулирующих равенство векторов, синий вектор b равен черному вектору b потому что он имеет одинаковую равную длину и одинаковое направление. Теперь, поскольку компоненты вектор и вектор b являются скалярами, мы можем добавить x-компонент для генерации x-компонент нового вектора c : сх = топор + Ьх Точно так же мы можем добавить y-компонентов : су = ау + по Новые компоненты cx и cy полностью определяют новый вектор c , указав как величину, так и направление. Внимательно взглянув на диаграмму, мы видим, что сложение двух векторов дает новый вектор, равный , а не в направлении любого из исходные векторы, величина которых равна , а не , равной сумме величин исходных векторов. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника