Теория и задачи механики сплошных сред
Теория и задачи механики сплошных сред
ОглавлениеПредисловие редактора переводаГлава 1.  Математические основы Математические основы1.1. Тензоры и механика сплошной среды 1.2. Тензоры. Декартовы тензоры. Ранг тензора 1.3. Векторы и скаляры 1.4. Векторное сложение. Умножение вектора на скаляр 1.5. Скалярное и векторное произведения векторов 1.6. Диады и диадики 1.7. Системы координат. Базисные векторы. Триэдр единичных векторов 1.8. Линейные векторные функции. Диадики как линейные векторные операторы 1.9. Индексные обозначения. Интервал изменения индексов и соглашение о суммировании 1.10. Соглашение о суммировании в символических обозначениях 1.11. Преобразование координат. Общее понятие тензора 1.12. Метрический тензор. Декартовы тензоры 1.14. Сложение декартовых тензоров. Умножение на скаляр 1.15. Умножение тензоров 1.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор 1.17. Матрицы Матричные представления декартовых тензоров 1.  18. Симметрия диадиков, матриц и тензоров 18. Симметрия диадиков, матриц и тензоров1.19. Главные значения и главные направления симметричных тензоров второго ранга 1.20. Степени тензоров второго ранга. Соотношение Гамильтона — Кэли 1.21. Тензорные поля. Дифференцирование тензоров 1.23. Теорема Гаусса — Остроградского Глава 2. Анализ напряженного состояния 2.1. Понятие сплошной среды 2.2. Однородность. Изотропия. Массовая плотность 2.3. Массовые силы. Поверхностные силы 2.4. Принцип напряжения Коши. Вектор напряжения 2.5. Напряженное состояние в точке. Тензор напряжений 2.6. Связь между тензором напряжений и вектором напряжения 2.7. Равновесие сил и моментов. Симметрия тензора напряжений 2.8. Законы преобразования напряжений 2.9. Поверхности напряжений Коши 2.10. Главные напряжения. Инварианты тензора напряжений. Эллипсоид напряжений 2.11. Максимальное и минимальное касательное напряжение 2.  13. Плоское напряженное состояние 13. Плоское напряженное состояние2.14. Девиатор и шаровой тензор напряжений Глава 3. Деформации 3.2. Конфигурация сплошной среды. Деформация и течение 3.3. Радиус-вектор. Вектор перемещения 3.4. Лагранжево и эйлерово описания движения 3.5. Градиенты деформации. Градиенты перемещения 3.6. Тензоры деформаций. Тензоры конечных деформаций 3.7. Теория малых деформаций. Тензоры бесконечно малых деформаций 3.8. Относительное перемещение. Тензор линейного поворота. Вектор поворота 3.10. Коэффициент длины. Интерпретация конечных деформаций 3.11. Тензоры коэффициентов длины. Тензор поворота 3.12. Свойства преобразований тензоров деформаций 3.13. Главные деформации. Инварианты деформации. Кубическое расширение 3.14. Шаровой тензор и девиатор деформаций 3.15. Плоская деформация. Круги Мора для деформации 3.16. Уравнения совместности для линейных деформаций Глава 4. Движение и течение 4.  1. Движение. Течение. Материальная производная 1. Движение. Течение. Материальная производная4.2. Скорость. Ускорение. Мгновенное поле скоростей 4.4. Скорость деформации. Завихренность. Приращения деформации 4.5. Физическая интерпретация тензоров скоростей деформации и завихренности 4.6. Материальные производные по времени от элемента объема, элемента поверхности и линейного элемента 4.7. Материальные производные по времени от интеграла по объему, интеграла по поверхности и линейного интеграла Глава 5. Основные законы механики сплошной среды 5.1. Сохранение массы. Уравнение неразрывности 5.2. Теорема об изменении количества движения. Уравнения движения. Уравнения равновесия 5.3. Теорема об изменении момента количества движения 5.4. Сохранение энергии. Первый закон термодинамики. Уравнение энергии 5.6. Неравенство Клаузиуса — Дюгема. Диссипативная функция 5.7. Определяющие уравнения.  Термомеханический и механический континуумы Термомеханический и механический континуумыГлава 6. Линейная теория упругости 6.1. Обобщенный закон Гука. Функция энергии деформации 6.2. Изотропные и анизотропные среды. Симметрия упругих свойств 6.3. Изотропные среды. Упругие постоянные 6.4. Постановка статических и динамических задач теории упругости 6.5. Теорема о суперпозиции. Единственность решений. Принцип Сен-Венана 6.6. Плоские задачи теории упругости. Плоское напряженное состояние и плоская деформация 6.8. Двумерные статические задачи теории упругости в полярных координатах 6.9. Гикерупругость. Гипоупругость 6.10. Линейная термоупругость Глава 7. Жидкости 7.1. Давление жидкости. Тензор вязких напряжений. Баротропное течение 7.2. Определяющие уравнения. Стоксовы жидкости. Ньютоновы жидкости 7.3. Основные уравнения ньютоновой жидкости. Уравнения Навье — Стокса — Дюгема 7.4. Установившееся течение. Гидростатика. Безвихревое течение 7.  5. Идеальная жидкость. Уравнение Бернулли. Циркуляция 5. Идеальная жидкость. Уравнение Бернулли. ЦиркуляцияГлава 8. Теория пластичности 8.2. Идеализированные диаграммы пластического поведения 8.3. Условия пластичности. Критерии Треска и Мизеса 8.4. Пространство напряжений. П-плоскость. Поверхность текучести 8.5. Поведение материала за пределом текучести. Изотропное и кинематическое упрочнение 8.6. Соотношения между напряжениями и деформациями в пластическом состоянии. Теория пластического потенциала 8.7. Эквивалентное напряжение. Эквивалентное приращение пластической деформации 8.8. Работа на пластических деформациях. Гипотезы упрочнения 8.9. Деформационная теория пластичности 8.10. Задачи упругопластичности Глава 9. Линейная вязкоупругость 9.1. Вязкоупругое поведение материала 9.2. Простейшие механические модели вязкоупругого поведения 9.3.  Обобщенные модели. Линейное дифференциальное операторное уравнение Обобщенные модели. Линейное дифференциальное операторное уравнение9.4. Ползучесть и релаксация 9.5. Функция ползучести. Функция релаксации. Интегралы наследственности 9.6. Комплексные модули и податливости 9.7. Трехмерная теория 9.8. Анализ вязкоупругого напряженного состояния. Принцип соответствия |
«Скалярное, векторное и смешанное произведения векторов»
Выберите предмет
Авиационная и ракетно-космическая техника
Автоматизация технологических процессов
Автоматика и управление
Агрохимия и агропочвоведение
Актерское мастерство
Анализ хозяйственной деятельности
Английский язык
Антикризисное управление
Археология
Архитектура и строительство
Астрономия
Базы данных
Банковское дело
Безопасность жизнедеятельности
Библиотечно-информационная деятельность
Бизнес-планирование
Биология
Биотехнология
Бухгалтерский учет и аудит
Ветеринария
Внешнеэкономическая деятельность
Водные биоресурсы и аквакультура
Воспроизводство и переработка лесных ресурсов
Высшая математика
География
Геодезия
Геология
Геометрия
Гидравлика
Гидрометеорология
Гостиничное дело
Государственное и муниципальное управление
Деловой этикет
Деньги
Детали машин
Дизайн
Документоведение и архивоведение
Естествознание
Железнодорожный транспорт
Журналистика
Землеустройство и кадастр
Издательское дело
Инвестиции
Инженерные сети и оборудование
Инновационный менеджмент
Информатика
Информационная безопасность
Информационные технологии
Искусство
История
Картография и геоинформатика
Китайский язык
Конфликтология
Краеведение
Кредит
Криминалистика
Кулинария
Культурология
Литература
Логика
Логистика
Маркетинг
Материаловедение
Машиностроение
Медицина
Международные отношения
Международные рынки
Менеджмент
Менеджмент организации
Металлургия
Метрология
Механика
Микро-, макроэкономика
Микропроцессорная техника
Морская техника
Музыка
Налоги
Наноинженерия
Начертательная геометрия
Немецкий язык
Нефтегазовое дело
Организационное развитие
Парикмахерское искусство
Педагогика
Пожарная безопасность
Полиграфия
Политология
Почвоведение
Право и юриспруденция
Приборостроение и оптотехника
Природообустройство и водопользование
Программирование
Производственный маркетинг и менеджмент
Промышленный маркетинг и менеджмент
Процессы и аппараты
Психология
Работа на компьютере
Радиофизика
Режиссура
Реклама и PR
Религия
Русский язык
Рынок ценных бумаг
Садоводство
Сварка и сварочное производство
Связи с общественностью
Сельское и рыбное хозяйство
Сервис
Сопротивление материалов
Социальная работа
Социология
Стандартизация
Статистика
Страноведение
Стратегический менеджмент
Страхование
Таможенное дело
Театроведение
Текстильная промышленность
Телевидение
Теоретическая механика
Теория вероятностей
Теория игр
Теория машин и механизмов
Теория управления
Теплоэнергетика и теплотехника
Технологические машины и оборудование
Технология продовольственных продуктов и товаров
Товароведение
Торговое дело
Транспортные средства
Туризм
Управление качеством
Управление персоналом
Управление проектами
Фармация
Физика
Физическая культура
Философия
Финансовый менеджмент
Финансы
Французский язык
Химия
Хирургия
Холодильная техника
Ценообразование и оценка бизнеса
Чертежи
Черчение
Экология
Эконометрика
Экономика
Экономика предприятия
Экономика труда
Экономическая теория
Экономический анализ
Электроника, электротехника, радиотехника
Энергетическое машиностроение
Этика
Ядерная энергетика и теплофизика
Ядерные физика и технологии
Языки (переводы)
Языкознание и филология
EVIEWS
SPSS
STATA
Другое
Скалярное тройное произведение
Скалярное тройное произведение , как следует из названия, представляет собой способ умножения трех векторов, который дает в результате скалярное значение . Он фактически объединяет операции скалярного произведения и перекрестного произведения для получения скалярного значения с использованием трех векторов, которые в целях этого обсуждения мы будем называть векторами a , b и c . Скалярное тройное произведение векторов a , b и c записывается как ( a b c ) и определяется как:
Он фактически объединяет операции скалярного произведения и перекрестного произведения для получения скалярного значения с использованием трех векторов, которые в целях этого обсуждения мы будем называть векторами a , b и c . Скалярное тройное произведение векторов a , b и c записывается как ( a b c ) и определяется как:
( a b c ) = a · ( b × c )
Иногда вы можете видеть, что круглые скобки опущены, поскольку оператор векторного произведения имеет приоритет над оператором скалярного произведения. Скалярное тройное произведение векторов a , b и c 9Таким образом, 0004 является скалярным произведением вектора на и вектора, заданного перекрестным произведением векторов b и c . Прежде чем мы продолжим, может быть полезно рассмотреть, что скалярное тройное произведение трех векторов не равно (и почему). Рассмотрим следующие схемы, включающие три вектора и операторы скалярного или векторного произведения:
Рассмотрим следующие схемы, включающие три вектора и операторы скалярного или векторного произведения:
( а · б ) · c
( a · b ) × c
( a × b )3 ×
Первая схема не будет работать, потому что скалярное произведение векторов a и b будет скалярным значением, и мы не сможем впоследствии найти скалярное произведение скалярного значения и вектора. Второе расположение также не является стартовым, потому что снова скалярное произведение векторов a и b будут скалярным значением, и мы не можем найти перекрестное произведение скалярного значения и вектора. Третье расположение вполне осуществимо, так как векторное произведение векторов на и b на будет вектором, и мы можем найти векторное произведение двух векторов. Это последнее расположение, однако, отличается от того, что мы рассматриваем на этой странице, и на самом деле производит нечто, называемое векторным тройным произведением (другой вектор, а не скалярное значение).
Это последнее расположение, однако, отличается от того, что мы рассматриваем на этой странице, и на самом деле производит нечто, называемое векторным тройным произведением (другой вектор, а не скалярное значение).
Скалярное тройное произведение часто используется в геометрии для нахождения объема параллелепипеда , который представляет собой трехмерную фигуру с шестью гранями, каждая из которых является параллелограммом . Три вектора можно рассматривать как три соседних ребра параллелепипеда, исходящие из общей вершины. Значение скалярного тройного произведения, если оно не равно нулю, будет положительным значением, если векторы a , b и c определены с использованием правая система координат , иначе будет отрицательно. Очевидно, что при использовании для нахождения объема параллелепипеда необходимо использовать абсолютное (беззнаковое) значение независимо от направления системы координат.
Скалярное тройное произведение также является проверкой того, являются ли три вектора линейно независимыми . Если векторы , а не линейно независимы, значение скалярного тройного произведения будет равно ноль . Линейная зависимость означает, что для данного набора векторов по крайней мере один из векторов может быть продублирован некоторой комбинацией одного или нескольких других векторов в наборе (или их кратных). Это означает, что для того, чтобы наши три вектора были линейно независимыми, не более двух векторов могут лежать в одной плоскости, а векторы, из которых составляют , лежат в одной плоскости, должны указывать в разных направлениях. (т.е. они должны быть непараллельными).
Давайте подумаем об этом по-другому. Мы сказали, что скалярное тройное произведение дает нам объема параллелепипеда. Если скалярное тройное произведение имеет значение ноль , параллелепипеда нет, так как трехмерный объект не может иметь объем, равный нулю.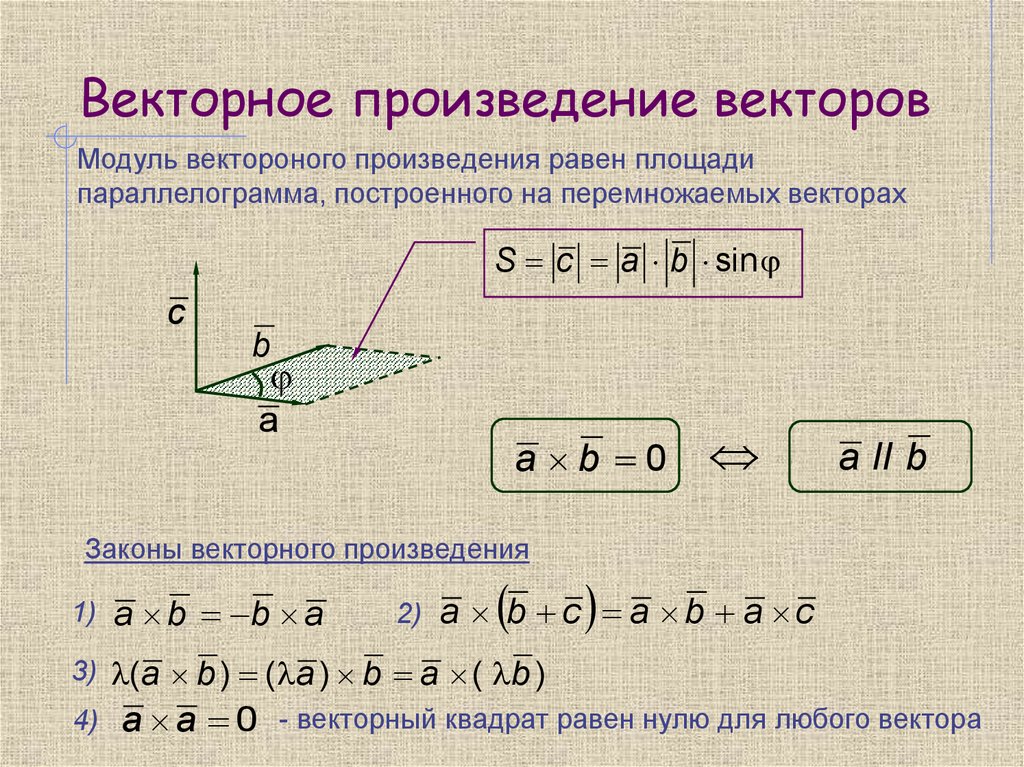 Рассмотрим иллюстрацию ниже, на которой изображен параллелепипед. Три смежных ребра параллелепипеда образованы векторами a = (1, 1, 1), b = (4, 2, 0) и с = (0, 2, -1). Оси x , y и z включены, чтобы показать ориентацию используемой системы координат (в данном случае правосторонней).
Рассмотрим иллюстрацию ниже, на которой изображен параллелепипед. Три смежных ребра параллелепипеда образованы векторами a = (1, 1, 1), b = (4, 2, 0) и с = (0, 2, -1). Оси x , y и z включены, чтобы показать ориентацию используемой системы координат (в данном случае правосторонней).
Векторы a , b и c образуют три смежных ребра параллелепипеда
Чтобы найти скалярное тройное произведение векторов a , b и c , нам сначала нужно найти векторное произведение векторов b и c . Если вы читали страницу, озаглавленную «Перекрестное произведение двух векторов», вы знаете, что мы можем найти компоненты x , y и z вектора перекрестного произведения (которое для удобства мы будем называть вектором ). d ) с использованием компонентов x , y и z векторов b и c следующим образом:
d x = b y c z — b z c y = (2)(-1) — (0)(2) = -2
d y = b z c x — b x c z = (0) (0)-(4) (-1) = 4
D Z = B x C Y — B Y — B Y — Y — Y — B Y — Y — y c x = (4)(2) — (2)(0) = 8
Теперь нам нужно найти скалярное произведение векторов a и d . Если вы читали страницу, озаглавленную «Скалярное произведение двух векторов», вы знаете, что найти скалярное произведение несложно, если вы знаете x , y и z компоненты двух векторов, и находится следующим образом:
Если вы читали страницу, озаглавленную «Скалярное произведение двух векторов», вы знаете, что найти скалярное произведение несложно, если вы знаете x , y и z компоненты двух векторов, и находится следующим образом:
a · d = a x d x + a y d y + a z 10
Мы также можем получить скалярное тройное произведение несколько более прямым способом, используя матричную арифметику. Скалярное произведение будет определителем матрицы три на три , каждая строка которой будет состоять из компонентов x , y и z одного из векторов. Первая строка будет координатами x , y и z вектора a , вторая строка будет x , y и z координаты вектора b , а третья строка будет координатами x , y и z вектора c . Матрица для векторов a , b и c показана ниже.
Матрица для векторов a , b и c показана ниже.
| a x | a y | a z | ||
| b x | b y | b z | ||
| c x | c y | в г |
Вектор векторного произведения получается путем нахождения определителя этой матрицы. Если вы не знакомы с матрицами, возможно, вы захотите просмотреть страницу о матрицах в Раздел Алгебра , чтобы увидеть, как находится определитель матрицы три на три. Ниже приведен фактический расчет для нахождения определителя вышеуказанной матрицы (т. е. скалярного тройного произведения векторов a , b и c ). Обратите внимание, что определитель матрицы записывается в том же формате, что и исходная матрица, но вместо скобок столбцы заключены в вертикальные черточки.
е. скалярного тройного произведения векторов a , b и c ). Обратите внимание, что определитель матрицы записывается в том же формате, что и исходная матрица, но вместо скобок столбцы заключены в вертикальные черточки.
| ( а б в ) = a · ( b × c ) = | a x | a y | a z | = a x | b y | b z | — a y | b x | b z | + a z | b x | b y | |||||||||
| b x | b y | b z | c y | c z | c x | c z | c x | c z | |||||||||||||
| c x | c y | c z | |||||||||||||||||||
Подставляя фактические значения, получаем:
| ( a b c ) = a · ( b × c ) = | 1 | 1 | 1 | = | 2 | 0 | — | 4 | 0 | + | 4 | 2 | ||||||||
| 4 | 2 | 0 | 2 | -1 | 0 | -1 | 0 | 2 | ||||||||||||
| 0 | 2 | — 1 | ||||||||||||||||||
Тогда расчет становится:
( a b c ) = a · ( b × c ) = ((2)(-1) — (2)(0)) — ((4)(-1) — (0 )(0)) + ((4)(2) — (0)(2))
( a b c ) = a · ( b × c ) = -2 + 4 + 8 = 10
Это дает нам тот же результат, что и раньше, как и должно быть. Прежде чем мы покинем скалярное тройное произведение, стоит отметить пару вещей о нем. Во-первых, тот же результат можно получить, используя другой порядок векторов, при условии, что циклический порядок, в котором они появляются, остается постоянным. Это дает нам следующие эквивалентности:
Прежде чем мы покинем скалярное тройное произведение, стоит отметить пару вещей о нем. Во-первых, тот же результат можно получить, используя другой порядок векторов, при условии, что циклический порядок, в котором они появляются, остается постоянным. Это дает нам следующие эквивалентности:
( A B C ) = ( B C A ) = ( C A B ) = A · ( B × C ) = B · ( C × A ) = = ( C × A ) = ( C × ) = · ( C × ) = · ( C ) = ) = ( C ) = ) = ( C ) = ) = ( C ) = · ( C ). с · ( а × б )
Во-вторых, замена двух векторов в перекрестном произведении части выражения скалярного тройного произведения инвертирует значение скалярного тройного произведения (0003 абсолютное значение остается прежним, но меняется знак ). Это дает нам следующее:
Это дает нам следующее:
( a b c ) = ( b c a ) = ( c a b ) = — ( a c b ) = — ( b a c ) = — ( b a c ) = — ( c0 b a )
Это означает:
а · ( б × в ) = — а · ( c × b )
b · ( c × a ) = — b · ( a × c )
c · ( a × b ) = — c · ( b × a )
По сути, любая нециклическая перестановка приводит к изменению знака результата.
математика — Скалярное тройное произведение и определяемое
спросил
Изменено 13 лет, 10 месяцев назад
Просмотрено 2к раз
Я заметил кое-что, когда сегодня пытался решить проблему. Скалярное тройное произведение такое же, как определитель или матрица три на три с тремя векторами в качестве строк:
Скалярное тройное произведение такое же, как определитель или матрица три на три с тремя векторами в качестве строк:
A = [ A , B , C ]
DET (A) = ( A X B ) * C
I столкнулся с этим в RALTER DIMER 44, 4, ,
I столкнулся с этим. и я действительно не могу понять, почему это так, и если это даже полезно. Кажется, это как-то связано с кратким методом вычисления перекрестного произведения с использованием детерминанта, в котором вы записываете единичные векторы вдоль верхней части матрицы, но я всегда думал, что это скорее мнемоника, а не на самом деле здравая математика.
Есть ли здесь настоящие отношения или это просто какое-то счастливое стечение обстоятельств?
С точностью до знака определитель матрицы размера n на n представляет собой объем параллелепипеда, натянутого на его n n-мерных векторов строк (или столбцов) (или объем единичного куба
линейно преобразуется этой матрицей). Произведение (axb).c в трех измерениях делает то же самое; axb задает вектор, перпендикулярный a и b и имеющий длину, равную площади параллелограмма, натянутого на a и b; (axb).c дает высоту c над этим параллелограммом, умноженную на его площадь. Так что нет, это не случайно.
Произведение (axb).c в трех измерениях делает то же самое; axb задает вектор, перпендикулярный a и b и имеющий длину, равную площади параллелограмма, натянутого на a и b; (axb).c дает высоту c над этим параллелограммом, умноженную на его площадь. Так что нет, это не случайно.
Совершенно не случайно; это довольно стандартный результат. Обратите внимание, что векторные произведения a X b часто сами записываются в детерминантной форме, где верхняя строка представляет собой единичные векторы i j k , следующая строка представляет собой a1 a2 a3, а нижняя строка представляет собой b1 b2 b3.
|i j k| |а1 а2 а3| |б1 б2 б3|
Теперь, взяв скалярное произведение этого с другим вектором c, вы получите то же самое, как если бы вы только что написали c в верхней строке.
|i j k| |с1 с2 с3| |с1 с2 с3| |а1 а2 а3| |а1 а2 а3| . (c1,c2,c3) = |a1 a2 a3| = -|а1 а2 а3| = |b1 b2 b3| |б1 б2 б3| |б1 б2 б3| |б1 б2 б3| |с1 с2 с3|
Редактировать: Также на странице википедии для скалярного тройного произведения говорится, что это эквивалентно определителю матрицы с использованием векторов в виде строк или столбцов.

