Сложение сил – правило для системы
4.7
Средняя оценка: 4.7
Всего получено оценок: 114.
4.7
Средняя оценка: 4.7
Всего получено оценок: 114.
Если на тело действует несколько сил, то для определения результата их действия необходимо учитывать их все. Это возможно с помощью правил сложения сил. Познакомимся с этими правилами поближе.
Равнодействующая сила
Ситуации, когда на тело действует только одна сила, в Природе сравнительно редки. Практически всегда на любое тело действует сила тяжести, а кроме того, присутствуют силы трения.
Поэтому встает задача определения результата совместного действия всех сил, действующих на тело. Сколько бы таких сил не было – тело либо останется в покое, либо начнет совершать движение. Причем, это всегда будет происходить так, как будто на тело действует только одна сила. Сколько бы сил не действовало на тело, всегда можно подобрать одну такую силу, результат действия которой будет равен действую всех сил, приложенных к телу.
Сила, которая производит то же действие, как и несколько других сил, называется равнодействующей.
Рис. 1. Равнодействующая сила.Равнодействующая сила используется при решении задач. Заменив силы, действующие на тело, равнодействующей, дальше для определения результата считают, что на тело действует только она.
Правила сложения сил
Действие по нахождению равнодействующей нескольких сил называется сложением сил. Для сложения сил существует переместительный и сочетательный законы. Поэтому, если на тело действует более двух сил, сперва складывают две из них, потом к результату прибавляют третью, потом четвертую – и так до последней силы.
Само сложение пары сил отличается от простого арифметического сложения.
В первую очередь, надо убедиться, что силы приложены к одной точке. Силы, приложенные к разным точкам складывать нельзя.
Во-вторых, необходимо учесть, что сила – величина векторная, а значит, для сложения двух сил необходимо пользоваться не обычным арифметическим сложением, а сложением по векторным правилам.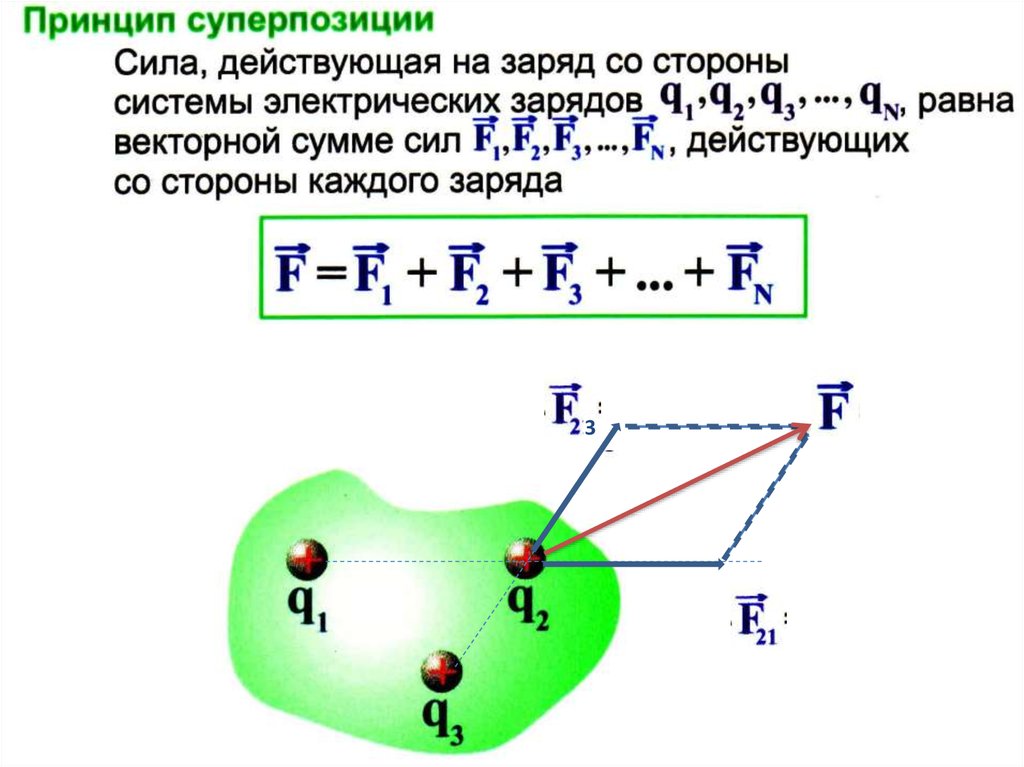 Для сложения сил необходимо найти их проекции на оси системы координат, сложить эти проекции, а потом по проекциям найти результирующую силу.
Для сложения сил необходимо найти их проекции на оси системы координат, сложить эти проекции, а потом по проекциям найти результирующую силу.
В простейшем случае, когда координатная ось одна – модули проекций равны модулям самих сил, и их знак совпадает с их направлением. В результате, равнодействующая сил, направленных в одну сторону, направлена в ту же сторону, а ее модуль равен сумме модулей сил. Если силы направлены в разные стороны, равнодействующая их будет направлена в сторону большей по модулю силы, а ее модуль будет равен разности модулей большей и меньшей силы.
Если координатных осей две или три – необходимо определять проекции на все оси, складывать или вычитать их, в зависимости от направления, а затем, по полученным суммам определять модуль и направление равнодействующей.
Для двух координатных осей при сложении сил нередко удобно использовать правила параллелограмма или треугольника – это приводит к нахождению равнодействующей быстрее.
Что мы узнали?
Сила, производящая такой же результат, как несколько других, называется равнодействующей. Для ее нахождения необходимо убедиться, что исходные силы приложены к одной точке, а потом сложить их по правилам сложения векторов.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Всего получено оценок: 114.
А какая ваша оценка?
Формула равнодействующей силы, F
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Формулы по физике Формула равнодействующей силы
В соответствии с первым законом Ньютона в инерциальных системах отсчета тело может изменять свою скорость только, если на него действуют другие тела.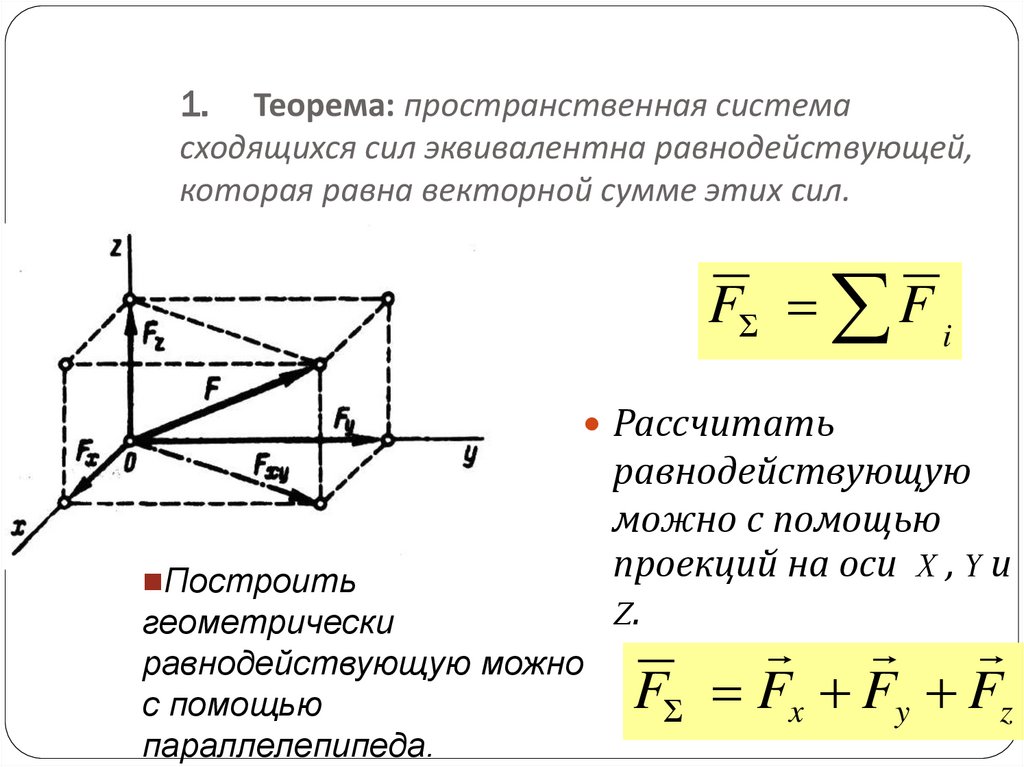
Основной закон, при помощи которого определяют направление и величину равнодействующей силы – это второй закон Ньютона:
где m – масса тела, на которое действует сила ; – ускорение, которое сила сообщает рассматриваемому телу. Сущность второго закона Ньютона состоит в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Необходимо помнить, что второй закон Ньютона работает для инерциальных систем отсчета.
В том случае, если на тело действует несколько сил, то их совместное действие характеризуют при помощи равнодействующей силы. Допустим, что на тело действует одновременно несколько сил, при этом тело перемещается с ускорением, равным векторной сумме ускорений, которые появились бы при воздействии каждой из сил в отдельности. Силы, действующие на тело, и приложенные к одной его точке необходимо складывать по правилу сложения векторов. Векторная сумма всех сил, действующих на тело в один момент времени, называется равнодействующей силой ():
Допустим, что на тело действует одновременно несколько сил, при этом тело перемещается с ускорением, равным векторной сумме ускорений, которые появились бы при воздействии каждой из сил в отдельности. Силы, действующие на тело, и приложенные к одной его точке необходимо складывать по правилу сложения векторов. Векторная сумма всех сил, действующих на тело в один момент времени, называется равнодействующей силой ():
Выражение (2) можно считать формулой для вычисления равнодействующей силы. Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты.
При действии на тело нескольких сил, второй закон Ньютона записывают как:
Равнодействующая всех сил, действующих на тело, может быть равна нулю, в том случае, если происходит взаимная компенсация сил, приложенных к телу. В таком случае тело движется с постоянной скоростью или находится в покое.
При изображении сил, действующих на тело, на чертеже, в случае равноускоренного перемещения тела, равнодействующую силу, направленную по ускорению следует изображать длиннее, чем противоположно ей направленную силу (сумму сил).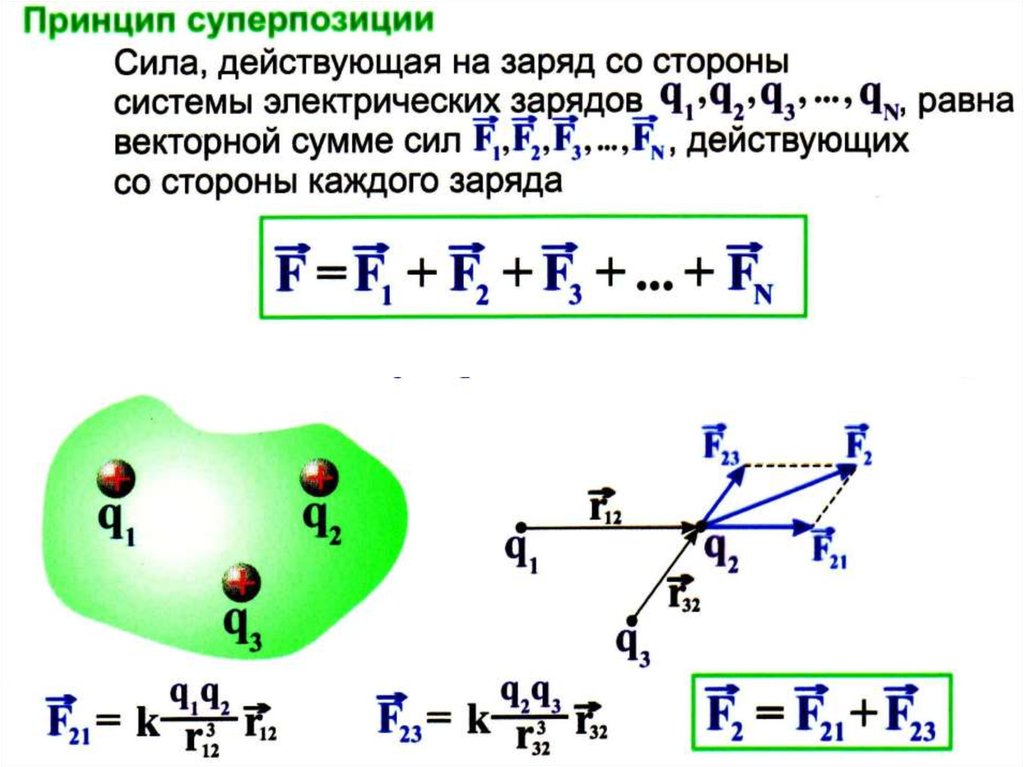 В случае равномерного движения (или покоя) дина векторов сил, направленных в противоположные стороны одинакова.
В случае равномерного движения (или покоя) дина векторов сил, направленных в противоположные стороны одинакова.
Для нахождения равнодействующей силы, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.
| Понравился сайт? Расскажи друзьям! | |||
Очень простая концепция при работе с силы это идея равновесия или равновесия . В общем случае на объект может действовать несколько сил. в то же время. Сила — это векторное количество что значит что он имеет как величину, так и направление, связанное с это. Две силы с одинаковой величиной, но разными направлениями не равные силы. Векторная сумма всех сил, действующих на тело, единая сила, называемая  Если результирующая сила равна нулю,
говорят, что объект находится в равновесии .
Поскольку на объект, находящийся в равновесии, не действует результирующая сила,
затем из Ньютона
первый закон
движения, объект продолжает
двигаться
с постоянной скоростью. Если результирующая сила равна нулю,
говорят, что объект находится в равновесии .
Поскольку на объект, находящийся в равновесии, не действует результирующая сила,
затем из Ньютона
первый закон
движения, объект продолжает
двигаться
с постоянной скоростью.На другой странице мы показываем простейший пример равновесия с Две силы, действующие на объект. На этой странице мы рассмотрим случай планер, на который в полете действуют три силы. А на другой странице мы рассматриваем случай летательный аппарат в крейсерская, где на самолет действуют четыре силы. В примере 1 мы показываем компьютерный рисунок
планер при снижении. На планер действуют три силы;
лифт (L),
перетащить (D),
и
вес (Вт).
Вес всегда направлен к центру земли, подъемной
направлен перпендикулярно траектории полета, а лобовое сопротивление – вдоль траектории полета
путь. Траектория полета наклонена к горизонтали на
угол и .
Когда самолет находится в равновесии, векторная сумма этих трех сил
равен нулю. W — L * cos(a) — D * sin(a) = V = 0 D * cos(a) — L * sin(a) = H = 0 Самолет имеет постоянную скорость вперед и вниз по траектория полета. Обратите внимание, что подъемная сила, сопротивление и вес продолжают действовать на самолет. В состоянии равновесия действие некоторых сил равно уравновешивается или компенсируется другими силами. В примере 2
спойлер
размещается на верхней части крыла планера, уменьшая подъемную силу и увеличивая сопротивление.
Вес остается прежним.
Планера больше нет
равновесие. Уравнения для сил остались прежними, но теперь
чистые горизонтальные и вертикальные силы; V и H не равны нулю. Навигация..
|
векторов — Где я запутался в добавлении силы?
Не бойся! Вы не одиноки в своем замешательстве. Хотя в наши дни принято учить, что силы являются векторами и следуют векторному сложению (как прекрасно это представляют другие ответы), исторически вы сталкивались с затруднительным положением, которое лежало в центре спора на протяжении большей части 19века, с участием таких персонажей, как Ньютон, Лагранж, Хевисайд, Пуассон, Максвелл, Бернулли, Де Морган, Янг, Эрншоу, и это лишь некоторые из тех, кого вы можете узнать.
Полный отчет обо всех разговорах, которые произошли, и полный анализ веса представленных аргументов см. в A Tale of Two Vectors Марка Ланге (2009) [doi][pdf], который послужило мне введением в полемику и ссылкой для подготовки того, что следует.
Как вы намекаете в своем ответе, это заставляет следует добавить в качестве векторов, является полностью интуитивным, и поэтому неизвестно, кто первым придумал эту идею. Во все времена все сходились во мнении, каким должен быть ответ при сложении двух сил (что можно легко проверить в повседневной жизни), но спор заключался именно в том, почему должно принимать именно такую форму. Есть намеки на то, что оно появилось в утерянном труде Аристотеля (384–322 гг. до н. э.) и определенно фигурировало в «Механике» Герона (I в. н. э.) [цитировать]
Ньютон и динамика
Но именно в Principia (1687) Ньютона [wikisource] мы видим первое доказательство , прямо вверху в Следствии I:
Следствие I: Тело под действием двух соединенных сил будет описывать диагональ параллелограмма за то же время, что и стороны, под действием этих сил порознь.
Если тело за данное время силой $M$, раздвинутой в месте $A$, должно быть равномерным движением перенесено из $A$ в $B$; и под действием силы $N$, раздвинутой в том же месте, должен быть перенесен из $A$ в $C$; завершите параллелограмм $ABCD$, и обе силы, действующие вместе, одновременно перенесут его по диагонали из $A$ в $D$.
Поскольку сила $N$ действует в направлении линии $AC$, параллельной $BD$, эта сила (согласно второму закону) нисколько не изменит скорость, создаваемую другой силой $M$, под действием которой тело переносится к прямой $BD$. Таким образом, тело прибудет на линию $BD$ за одно и то же время, независимо от того, будет приложена сила $N$ или нет; и поэтому по истечении этого времени он будет найден где-то в строке $BD$. По тому же аргументу по истечении того же времени он будет найден где-то в строке $CD$. Следовательно, он будет находиться в точке $D$, где пересекаются обе прямые. Но он будет двигаться по прямой линии от $A$ до $D$ по закону I 9.0016
Итак, здесь Ньютон доказывает, что сложение сил должно принимать форму сложения векторов (векторы не будут изобретены еще добрых 150 лет), и приводит в качестве доказательства динамическое доказательство, основанное на идеях динамики. Он использует движение, которое должно быть создано силами, воздействующими на некоторую гипотетическую массу $m$, в соответствии со своим законом движения $\vec F = m \vec a$, чтобы доказать, как должны складываться силы, если мы знаем, как складываются траектории.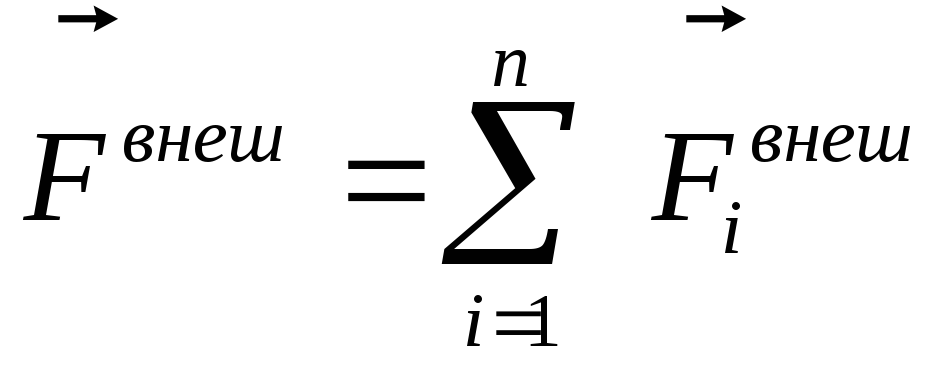
Это породило бы разногласия между теми, кто в в динамическом лагере и в статическом лагере .
Я думаю, что Бернулли † дал самое убедительное проклятие динамическому доказательству, в котором он указал, что даже если бы мы жили во Вселенной, где не соблюдался бы закон Ньютона, а вместо этого выполнялся какой-то другой закон $\vec F = m \vec v$, скажем, силы все равно будут складываться по закону параллелограмма, поэтому конечная причина, по которой силы складываются таким образом, должна быть независима от самой динамики.
†: Здесь Даниил Бернулли, один из многих известных Бернулли, ответственный за принцип Бернулли
Дючайла и статика
В качестве альтернативы динамическому объяснению Ньютона статическое доказательство, которое обычно приводится, в конечном итоге восходит к Шарлю Доминику Мари Бланке Дючайла (имя, если я когда-либо видел его) в 1804 году. В котором его доказательство происходит по индукции, с индуктивным шагом:
Если силы $P$ и $Q$, действующие вместе в одной точке, приводят к возникновению силы, направленной по диагонали параллелограмма, представляющего две силы, а также силы $P$ и $R$, действующие вместе в одной точке , где $R$ действует в направлении $Q$, то аналогично для $P$ вместе с равнодействующей $Q$ и $R$.
И доказательство индуктивного шага:
Пусть $P$ представлен отрезком $AB$. Предположим, что равнодействующая $Q$ и $R$ направлена в их общее направление и равна по величине сумме их величин; пусть он будет представлен отрезком $AE$, а $Q$ представлен отрезком $AC$, так что отрезок $CE$ является правильной длиной и направлением для представления $R$, за исключением того, что $R$ на самом деле применяется к $A$, а не чем в $C$. Тем не менее, когда сила действует на тело, результат один и тот же в любой точке, жестко связанной с телом, к которой она приложена, при условии, что линия, проходящая через эту точку и фактическую точку приложения силы, проходит вдоль направления силы. . Таким образом, хотя $R$ применяется в $A$, его эффект будет таким же, если он применяется в $C$, поскольку $AC$ направлен в направлении действия сил. Продолжая рассматривать параллелограммы на рисунке как твердое тело, мы можем перемещать точки приложения трех сил в другие точки вдоль линий действия сил, не изменяя их равнодействующую.
Мы не можем переместить точку приложения $P$ прямо в $C$, так как $AC$ не лежит вдоль направления $P$. Но по условию равнодействующая $P$ и $Q$ действует по диагонали $AD$, поэтому результант можно применить в $D$. Затем его можно разложить на $P$ и $Q$, которые теперь действуют в $D$. Направление $Q$ лежит вдоль $DG$, поэтому $Q$ можно перевести в $G$. Направление $P$ лежит вдоль $CD$, поэтому $P$ можно перевести в $C$, где он встречается с $R$. По условию их равнодействующая действует по диагонали $CG$, поэтому ее можно перенести на $G$, где она пересекается с $Q$. Согласно обратному принципу передачи силы, $AG$ должна лежать вдоль линии действия силы, возникающей из $P$, составленной из равнодействующей $Q$ и $R$…
Цитата и рисунок воспроизведены из статьи Ланге
Отсюда продолжается доказательство, чтобы установить, что вы также можете продемонстрировать, что оно получает правильные направления и величины, полное воспроизведение см. в статье Ланге.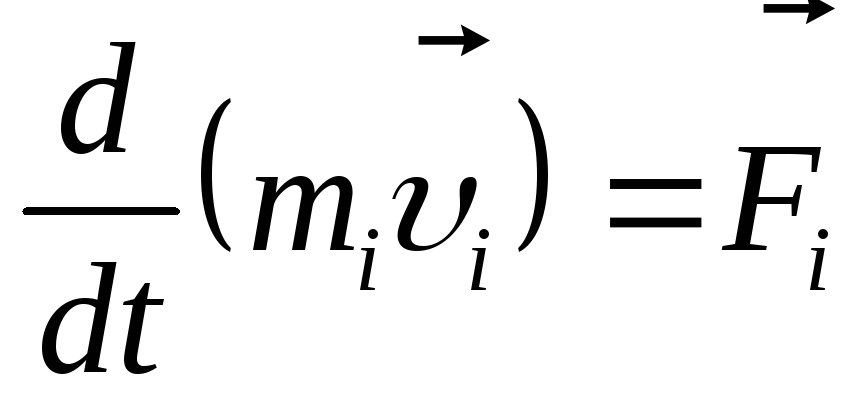
Это доказательство немного трудно читать, и отзывы были неоднозначными, некоторые думали, что это лучшее, что есть после нарезанного хлеба, «очень просто и красиво», например, Митчелл, Янг, Имрей, Эрншоу и Пратт, другие, не так много:
вынужденное и неестественное… пустая трата времени
Безант 1883, Замок 1888
доказательство нашей молодости… теперь признан громоздким и устаревшим и оставлен только как проверка логической силы
А.Г.Г. 1890
трата мозгов… продуманная и кропотливая, но ошеломляющая
Хевисайд 1893
конечно убедительно… но… по существу искусственно… хитрость вместо честного аргумента
Гудвин
Пуассон и симметрия
Но не все потеряно. Пуассон предложил альтернативное доказательство статического случая в 1811 году, которое основано на аргументах симметрии, соображениях размерности и ограничении уникальности.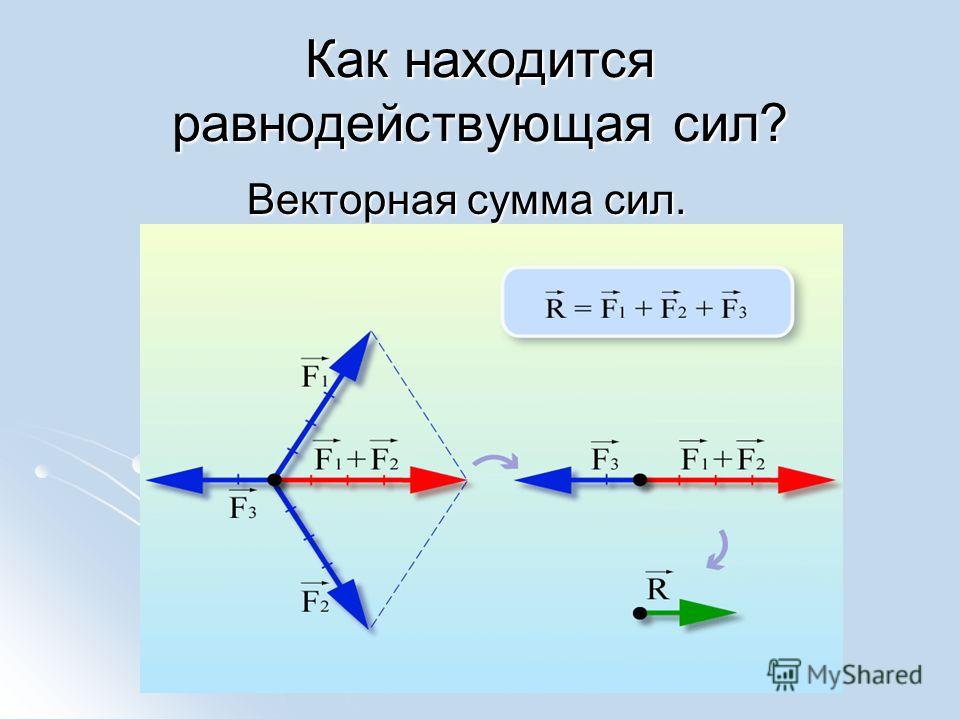 Мне очень нравится эта версия. Вы начинаете с предположения, что у вас есть две силы одинаковой величины $P$, но разных направлений, разделенных углом $2\theta$ (красные силы на диаграмме). Применяя вращательную инвариантность и симметрию, результирующая $R$ (черная) должна делить их пополам в направлении, а ее величина должна быть размерно-согласованной формулой величины $P$ и угла $\theta$ отдельно или иметь вид :
$$ R = Pg(\theta) $$
с некоторой неизвестной функцией $g(\theta)$. Затем, чтобы выяснить функцию, Пуассон рассматривает две новые задачи:
Мне очень нравится эта версия. Вы начинаете с предположения, что у вас есть две силы одинаковой величины $P$, но разных направлений, разделенных углом $2\theta$ (красные силы на диаграмме). Применяя вращательную инвариантность и симметрию, результирующая $R$ (черная) должна делить их пополам в направлении, а ее величина должна быть размерно-согласованной формулой величины $P$ и угла $\theta$ отдельно или иметь вид :
$$ R = Pg(\theta) $$
с некоторой неизвестной функцией $g(\theta)$. Затем, чтобы выяснить функцию, Пуассон рассматривает две новые задачи:
Вверху и внизу мы создали две новые копии одной и той же задачи, теперь добавляя пары сил $Q$ (синие) для создания $P$, и видим, что
$$ P = Q g(\phi) \подразумевается R = Q g(\theta) g(\phi) $$
Тем временем две внутренние силы $Q$ (чуть более темные синие) и две внешние силы $Q$ (чуть светлее синие) создают один и тот же сценарий, все четыре из них добавляют к результирующей $R$, а каждая пара — часть, и поскольку мы предполагаем, что силы в одном и том же направлении просто складываются по величине, мы также имеем
$$ R = Q g(\theta + \phi) + Q g(\theta — \phi) $$
вместе:
$$ g(\theta) g(\phi) = g(\theta+\phi) + g(\theta-\phi) $$
единственным решением этого функционального уравнения являются решения вида:
$$ g(\theta) = 2 \cos (\alpha \theta) $$
с неизвестным $\alpha$, но мы можем зафиксировать $\alpha = 1$, потребовав, чтобы равные силы в противоположных направлениях сокращались. Итак, наконец, мы восстанавливаем формулу сложения сил для сил равной величины:
$$ R = 2 P \cos\theta $$
отлит в полярной форме. Отсюда легко обобщить результаты сложения полных векторов, разложив силы на различные части.
Итак, наконец, мы восстанавливаем формулу сложения сил для сил равной величины:
$$ R = 2 P \cos\theta $$
отлит в полярной форме. Отсюда легко обобщить результаты сложения полных векторов, разложив силы на различные части.
Мне очень нравится это доказательство, так как оно основано только на симметрии и соображениях размерности и совершенно свободно от каких-либо обсуждений динамики. Но некоторые приравнивают это к дефициту:
Многие были озадачены, обнаружив, что вещь, которая по самому своему определению имеет тенденцию производить движение, рассматривается… в соответствии с договором о том, что любое введение идеи движения было бы неуместным. Статические доказательства… кажется, сплошь геометрия и никакой физики
Август Де Морган (1859)
Но другие находят его довольно элегантным:
Доказательство «параллелограмма сил», данное Пуассоном, применимо к композиции любых величин, такое, что переворачивание их встык равносильно изменению их знака на противоположное
Максвелл в 1873 году
К философскому
В настоящее время люди продолжают спорить о происхождении закона сложения сил, но в основном в философских журналах.


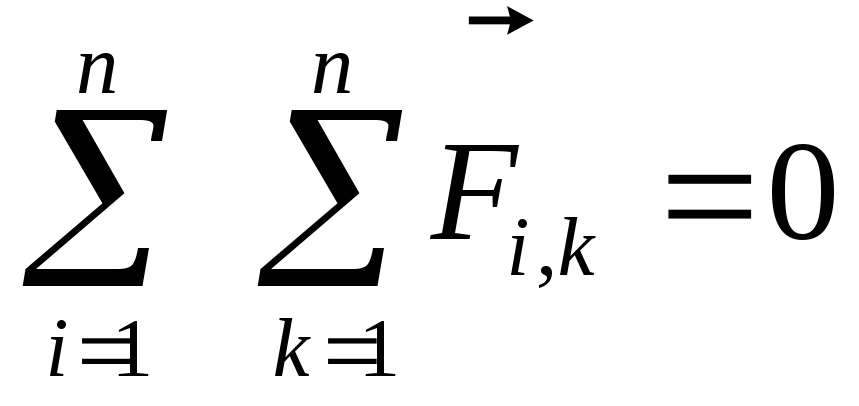 Поскольку это векторная сумма, есть два
компонент
уравнения, одно вертикальное и одно горизонтальное, которые
показано под графиком.
Поскольку это векторная сумма, есть два
компонент
уравнения, одно вертикальное и одно горизонтальное, которые
показано под графиком.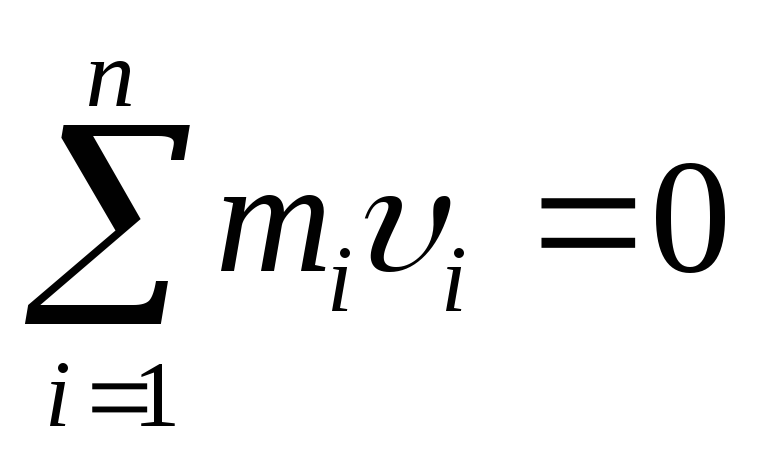 Согласно Ньютону
второй закон
движения, самолет начнет разгоняться вниз и вправо. В примере 2
силы не уравновешены, и самолет не находится в равновесии.
Согласно Ньютону
второй закон
движения, самолет начнет разгоняться вниз и вправо. В примере 2
силы не уравновешены, и самолет не находится в равновесии.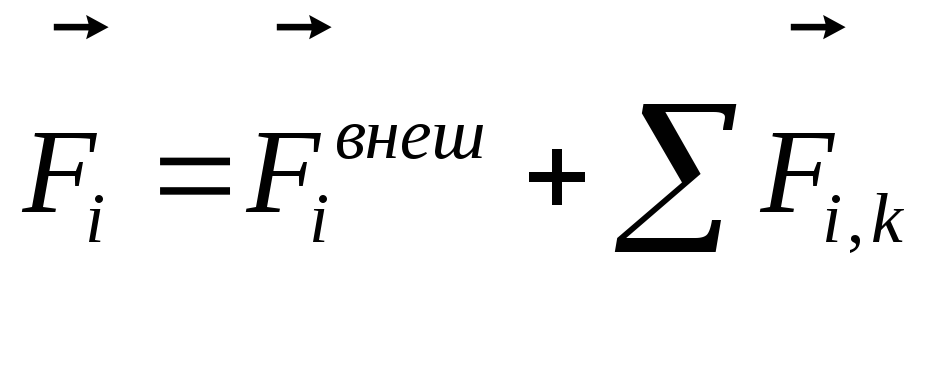 Поскольку сила $N$ действует в направлении линии $AC$, параллельной $BD$, эта сила (согласно второму закону) нисколько не изменит скорость, создаваемую другой силой $M$, под действием которой тело переносится к прямой $BD$. Таким образом, тело прибудет на линию $BD$ за одно и то же время, независимо от того, будет приложена сила $N$ или нет; и поэтому по истечении этого времени он будет найден где-то в строке $BD$. По тому же аргументу по истечении того же времени он будет найден где-то в строке $CD$. Следовательно, он будет находиться в точке $D$, где пересекаются обе прямые. Но он будет двигаться по прямой линии от $A$ до $D$ по закону I 9.0016
Поскольку сила $N$ действует в направлении линии $AC$, параллельной $BD$, эта сила (согласно второму закону) нисколько не изменит скорость, создаваемую другой силой $M$, под действием которой тело переносится к прямой $BD$. Таким образом, тело прибудет на линию $BD$ за одно и то же время, независимо от того, будет приложена сила $N$ или нет; и поэтому по истечении этого времени он будет найден где-то в строке $BD$. По тому же аргументу по истечении того же времени он будет найден где-то в строке $CD$. Следовательно, он будет находиться в точке $D$, где пересекаются обе прямые. Но он будет двигаться по прямой линии от $A$ до $D$ по закону I 9.0016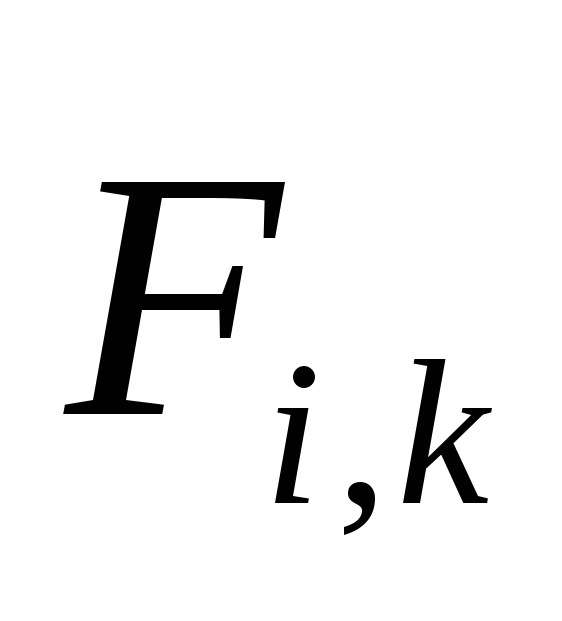
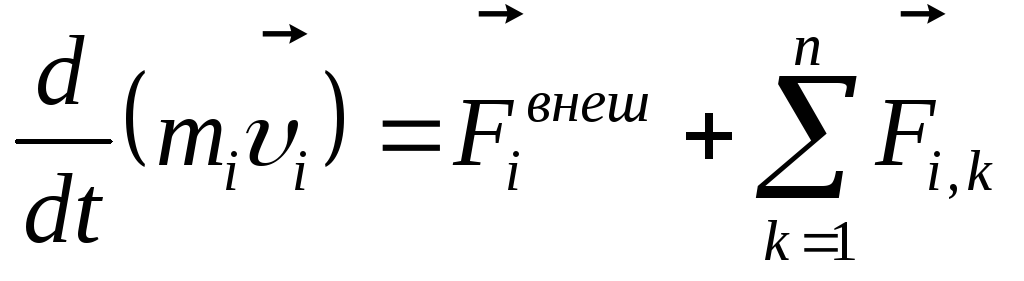 Мы не можем переместить точку приложения $P$ прямо в $C$, так как $AC$ не лежит вдоль направления $P$. Но по условию равнодействующая $P$ и $Q$ действует по диагонали $AD$, поэтому результант можно применить в $D$. Затем его можно разложить на $P$ и $Q$, которые теперь действуют в $D$. Направление $Q$ лежит вдоль $DG$, поэтому $Q$ можно перевести в $G$. Направление $P$ лежит вдоль $CD$, поэтому $P$ можно перевести в $C$, где он встречается с $R$. По условию их равнодействующая действует по диагонали $CG$, поэтому ее можно перенести на $G$, где она пересекается с $Q$. Согласно обратному принципу передачи силы, $AG$ должна лежать вдоль линии действия силы, возникающей из $P$, составленной из равнодействующей $Q$ и $R$…
Мы не можем переместить точку приложения $P$ прямо в $C$, так как $AC$ не лежит вдоль направления $P$. Но по условию равнодействующая $P$ и $Q$ действует по диагонали $AD$, поэтому результант можно применить в $D$. Затем его можно разложить на $P$ и $Q$, которые теперь действуют в $D$. Направление $Q$ лежит вдоль $DG$, поэтому $Q$ можно перевести в $G$. Направление $P$ лежит вдоль $CD$, поэтому $P$ можно перевести в $C$, где он встречается с $R$. По условию их равнодействующая действует по диагонали $CG$, поэтому ее можно перенести на $G$, где она пересекается с $Q$. Согласно обратному принципу передачи силы, $AG$ должна лежать вдоль линии действия силы, возникающей из $P$, составленной из равнодействующей $Q$ и $R$…