Резонанс в электрической 📙 цепи

1. Резонанс в электрической цепи
2. Резонанс токов через реактивные элементы
3. Резонанс напряжений
4. Явление резонанса на практике

Разберемся сначала с важными понятиями.

Резонанс — это такое явление, в процессе которого в системе увеличивается частота своих колебаний под воздействием внешнего возбудителя.

Колебания внешнего воздействия могут усиливать даже незначительные колебания системы. Наибольший резонанс достигается при совпадении частоты колебаний внешнего воздействия с колебаниями системы.

Одним из примеров явления резонанса, есть расшатывание моста ротой солдат. Это происходит, когда частота шагов солдат, которая являются внешним воздействием, совпадает с частотой колебаний моста. Если возникнет такой резонанс, это может разрушить мост. Именно поэтому солдаты не переходят мосты стройным шагом, а идут в вольном режиме.

Часто встречаемым явлением в физике есть электрический резонанс.

Без него невозможно было бы провести телетрансляцию, многие медицинские обследования и прочие важные процессы.

Востребованными резонансами в электрической цепи есть:

• резонанс напряжений;
• резонанс токов.

Резонанс в электрической цепи – это резкое возрастание амплитуды внутренних колебаний системы за счет совпадения частоты внутренних колебаний с частотой внешнего воздействия.

Схема \(RLC\) – это электрическая цепь с последовательными, параллельными или комбинированными соединениями компонентов (резисторами, индукционными катушками и конденсаторами). \(RLC\) – это сочетание сопротивления, индуктивности и емкости.

Векторная диаграмма в случае последовательного соединения \(RLC\)-цепи бывает емкостной, активной или индуктивной.

В индуктивной векторной диаграмме резонанс напряжений появляется лишь при нулевом сдвиге фаз и совпадении сопротивлений индукции и емкости.

Резонанс токов возникает при параллельном соединении реактивных сопротивлений с одинаковыми характеристиками в цепях с переменным током. Во время резонанса токов реактивная индуктивная проводимость приравнивается к реактивной емкостной проводимости, то есть \(BL=BC.\)

Колебания контура с определенной частотой совпадают с частотой колебаний источника.

Простейшим примером цепи, в которой может произойти резонанс токов, есть параллельное соединение катушки с конденсатором.

Поскольку реактивные сопротивления совпадают по модулю, то амплитуды токов конденсатора и катушки также будут совпадать и могут достичь наибольшего значения амплитуды. Согласно первому закону Кирхгофа \(IR\) равняется току источника. Иначе говоря, ток проходит лишь через резистор. Если рассмотреть параллельный контур \(LC,\) то при частоте резонанса его сопротивление будет огромным. В условиях режима гармонии при частоте резонанса в контуре будет расход тока лишь для восполнения потерь на активном сопротивлении.

Значит, в последовательной цепи \(RLC\) импеданс наименьший при частоте резонанса и равняется активному сопротивлению контура, при этом в параллельной цепи \(RLC\) импеданс наибольший при частоте резонанса и равняется сопротивлению утечки, что фактически есть активным сопротивлением контура. Это значит, что для обеспечения резонанса силы тока или напряжения в цепи необходима ее проверка с целью определения суммарного сопротивления и проводимости. Кроме того, ее мнимая часть должна равняться нулю.

Резонанс напряжений имеет место в цепи переменного тока в случае последовательного соединения активного \(R\), емкостного \(C\) и индуктивного \(L\) компонентов. Резонанс напряжений состоит в совпадении внутренних колебаний источника и внешних колебаний контура. Резонанс напряжений применяется с пользой, но бывает и опасен. Например, данное явление применяют в радиотехнике, а опасность его состоит в том, что при резких скачках напряжения может произойти поломка оборудования и даже его возгорание.

Резонанс напряжения достигают несколькими путями:

• подбирая индуктивность катушки;
• подбирая емкость конденсатора;
• подбирая угловую частоту \(ω_0\).

Эти величины подбирают с помощью таких формул:

\(L_0 = {1 \over ω^2 C}\)

\(C_0 = {1 \over ω^2 L}\)

Частота \(ω_0\) – это резонансная величина.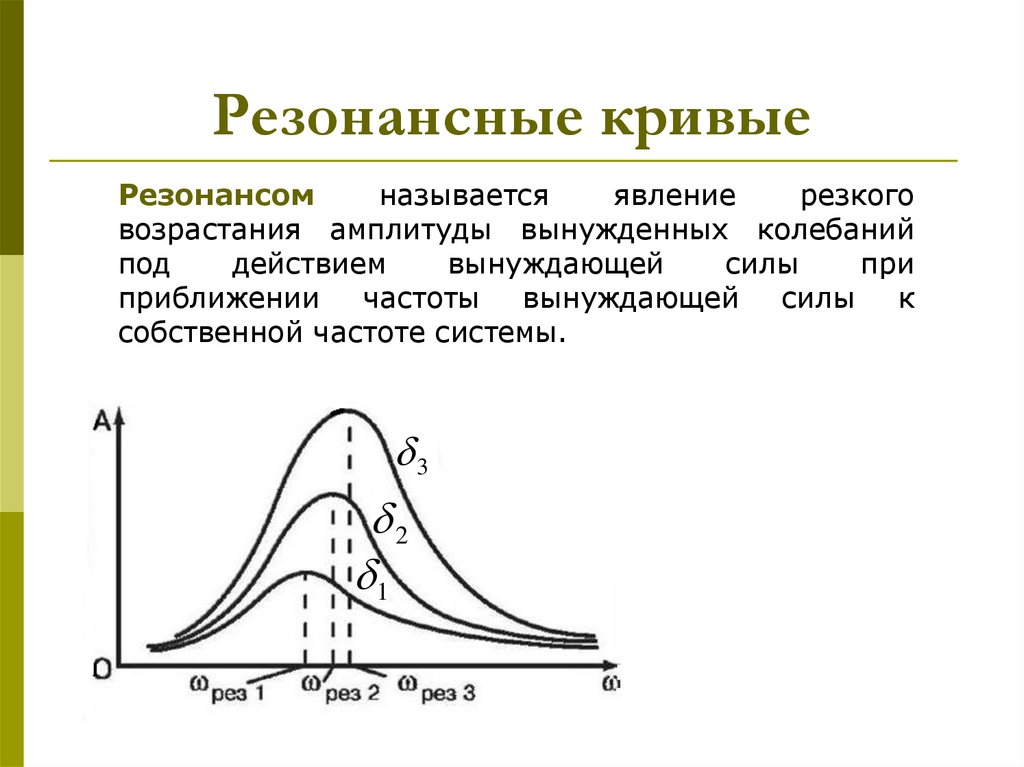 При постоянных напряжении и активном сопротивлении в цепи сила тока в процессе резонанса напряжения наибольшая и равняется отношению напряжения к активному сопротивлению. То есть, сила тока полностью не зависима от реактивного сопротивления. Если реактивные сопротивления индукции и емкости одинаковы и по своей величине превышают активное сопротивление, тогда на зажимах катушки и конденсатора будет напряжение, сильно превышающее напряжение на зажимах контура.

Кратность превышения напряжения на зажимах катушки и конденсатора в соотношении с напряжением контура рассчитывается так:

\(Q = {U_{C0} \over U}\)

Величина \(Q\) является добротностью контура и описывает его резонансные характеристики.

Величина, обратная добротности контура, – это затухание контура \( {1 \over Q}\).

Электрический резонансный трансформатор, который был разработан Николой Теслой в конце XIX века, является ярким примером практического применения резонанса в электрических цепях. Тесла проводил массу экспериментов при разных конфигурациях резонансных цепей.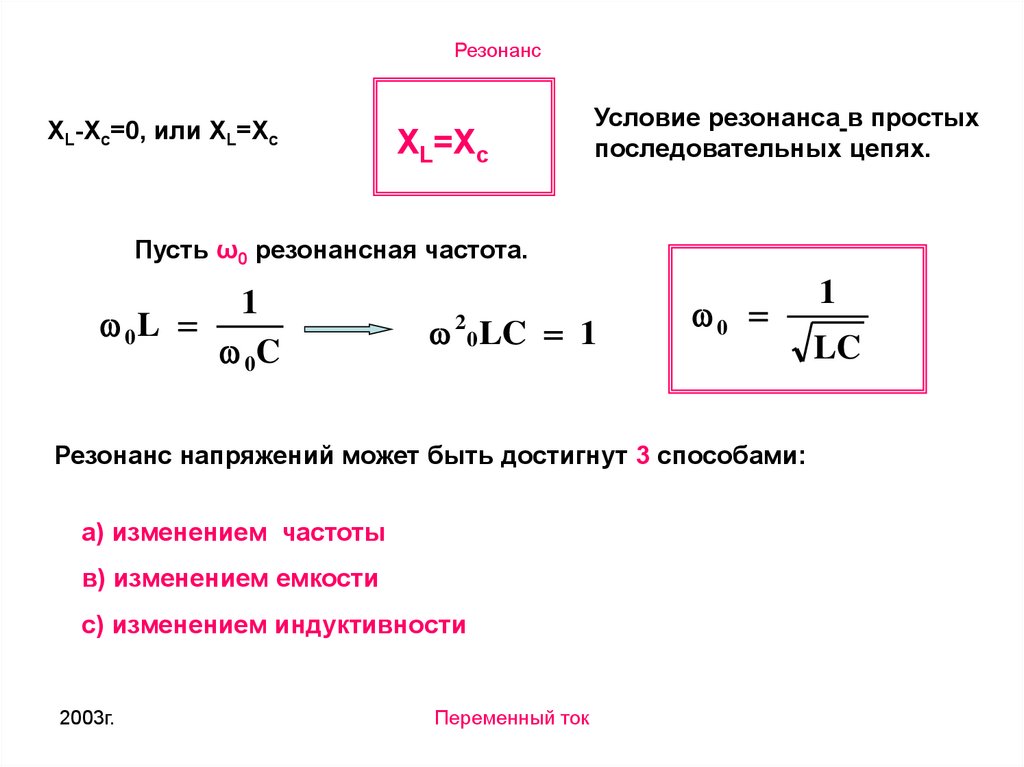

На сегодняшний день словосочетанием «катушка Теслы» называют высоковольтные резонансные трансформаторы. Такие приспособления применяют для генерации высокого напряжения и частоты переменного тока. Если простые трансформаторы используют для передачи энергии с первичной на вторичную катушку, то резонансные — для хранения электрической энергии во временном режиме.

При помощи данного приспособления, посредством управления воздушным сердечником резонансно настроенного трансформатора, при незначительной силе тока получают высокие напряжения. При этом у каждой катушки есть собственная емкость и она работает как резонансный контур. Для создания еще большего напряжения достигают резонанса двух контуров.

Резонанс токов: применение, принцип резонса тока, расчет контура

Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет.

Что такое резонанс?

Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.

Соединение двух ветвей при резонансе

Признаки резонанса:

1. Составляющие реактивных ветвей тока равны между собой IPC = IPL, противофаза образовывается только при равенстве чистой активной энергии на входе;
2. Ток в отдельных ветках, превышает весь ток определенной цепи, при этом ветви совпадают по фазе.

Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:

1. Последовательный;
2. Параллельный.

Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.

Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость.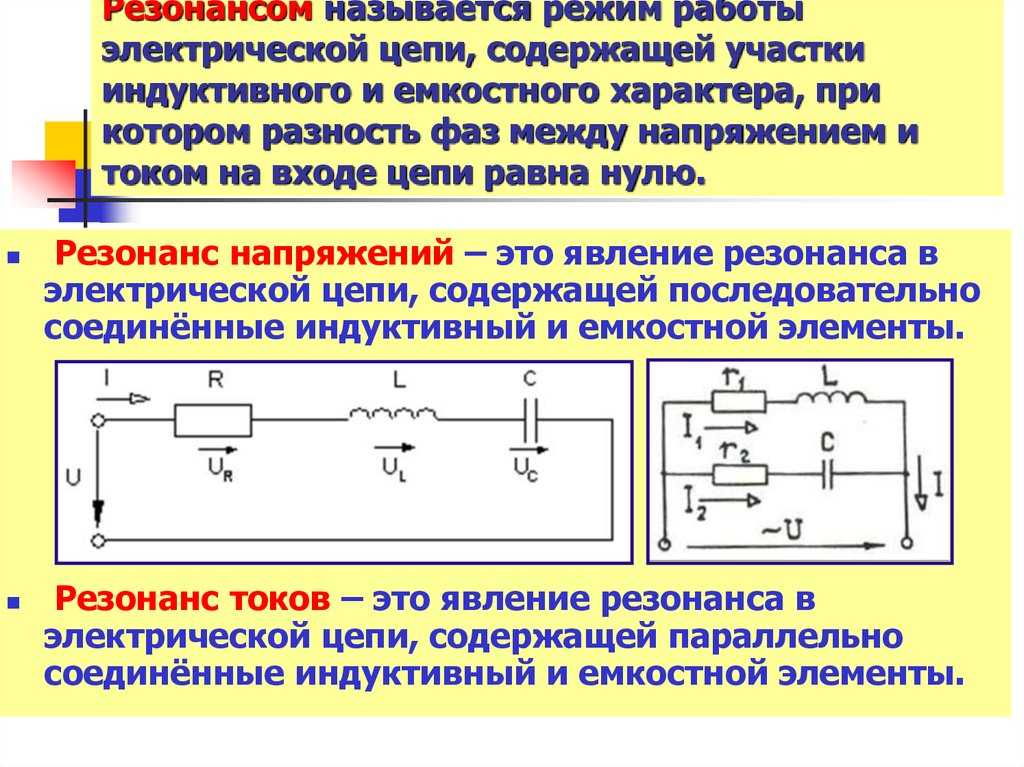 Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.

Применение

Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.

Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.

Принцип резонанса токов

Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:

Схема для питания конденсатора

Переключатель будет отвечать за направление колебаний.

Схема: переключатель резонансной схемы

Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.

Схема: ток в резонансной схеме равен нулю

Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.

Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.

Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.

В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.

Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.

Расчет резонансного контура

Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела.

Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом:

R _ср= I²_конт * R = (V²_конт / Z²) * R.

При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1

Сама же формула резонанса имеет следующий вид:

ω₀ = 1 / √L*C

Нулевой импеданс в резонансе определяется при помощи такой формулы:

F_рез = 1 / 2π √L*C

Резонансная частота колебаний может быть аппроксимирована следующим образом:

F = 1/2 р (LC) 0.5

Где: F = частота

L = индуктивность

C = емкость

Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям:

R = 2 (L / C) 0.5

Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов.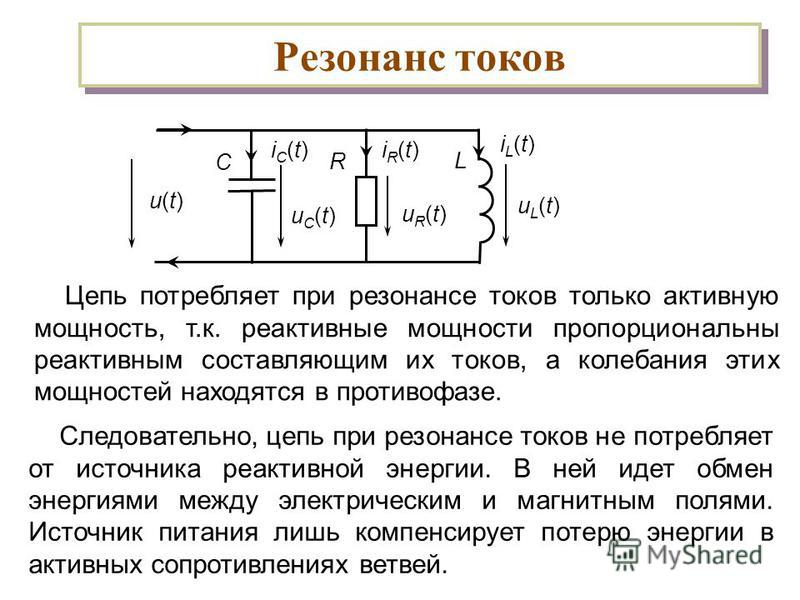 При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока.

Что такое резонансная электрическая цепь? Каковы его виды? Найдите выражение для резонансной частоты последовательного LCR-контура.

Последняя обновленная дата: 09 -й марта 2023 г.

•

Общее представление: 277,5K

•

Просмотры сегодня: 3,59K

Ответ

Проверено

три элемента: катушка индуктивности, конденсатор и резистор. Эти три элемента могут быть соединены последовательно или параллельно. Найдем уравнение тока через цепь LCR и выражение для резонансной частоты, используя явление максимального тока, протекающего через цепь на резонансной частоте. 9{2}}}$

Полный пошаговый ответ:
Электрический резонанс возникает в электрической цепи на определенной резонансной частоте, когда импедансы или проводимости элементов цепи компенсируют друг друга. Резонанс — это явление в электрической цепи, когда выходная мощность электрической цепи максимальна на одной конкретной частоте. Эта конкретная частота известна как резонансная частота. На резонансной частоте емкостное сопротивление и индуктивное сопротивление равны.
В переменном токе, если фаза приложенной разности потенциалов и тока, протекающего в цепи, совпадают, то цепь называется резонансной. Явление, демонстрируемое этими цепями, называется резонансом.

Типы контуров LCR:
Последовательный резонансный контур: три элемента контура; Резистор, катушка индуктивности и конденсатор соединены последовательно в цепи.
Параллельный резонансный контур: три элемента контура; Резистор, индуктивность и конденсатор соединены в цепь параллельно. 9{2}}}$
Где
$R$ — сопротивление
${{X}_{L}}$ — индуктивное сопротивление
${{X}_{C}}$ — емкостное сопротивление
Если $V$ — разность потенциалов, $I$ — ток, $\phi $ — разность фаз, тогда
$\tan \phi =\dfrac{{{X}_{L}}-{{X} _{C}}}{R}$
Ввод,
$\begin{align}
  & {{X}_{L}}=\omega L \\
 & {{X}_{C}}=\ dfrac{1}{\omega C} \\
\end{align}$
$\tan \phi =\dfrac{\omega L-\dfrac{1}{\omega C}}{R}$
Или, 9{2}}=\dfrac{1}{LC} \\
 & \omega =\dfrac{1}{\sqrt{LC}} \\
\end{align}$
Мы знаем,
$\omega = 2\pi f$
Следовательно,
$f=\dfrac{1}{2\pi \sqrt{LC}}$
Это выражение для резонансной частоты для последовательных цепей LCR.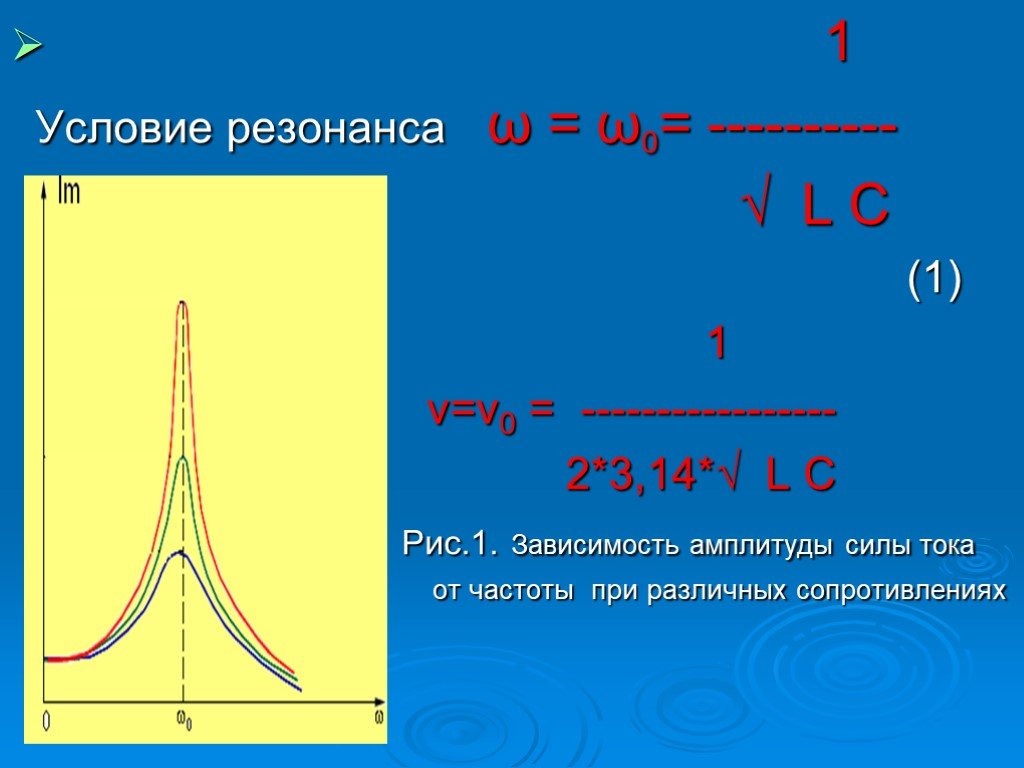

Примечание. Цепь LCR серии означает, что три элемента: резистор, катушка индуктивности и конденсатор соединены в цепь встык. Следует помнить, что сопротивление в электрической цепи не влияет на ее резонансную частоту. Резистор уменьшает задержку, создаваемую конденсатором, с 9 долларов.0$ градусов и уменьшает опережение, производимое индуктором, с $90$ градусов. С обеих сторон эффекты почти равны. Это приводит к нейтрализации, и в конечном итоге общий эффект становится таким же, как и при чистом резонансе резервуара LC.

Что такое резонансная частота?

То, что вы видели в мультфильмах, не обязательно является плодом буйного воображения писателей — некоторые сцены на самом деле уходят корнями в науку. В детстве я думал, что сцена ужасного певца, берущего высокую ноту и разбивающего осколок стекла, была забавной, только чтобы узнать, что это явление возможно в реальной жизни из-за того, что называется резонансной частотой.

Что такое резонансная частота и на что она влияет? В то время как паршивые навыки пения вряд ли разобьют стекло, воспроизведение звука, равного резонансной частоте стекла, будет. По крайней мере, это то, что я помню со школьного урока физики. Со временем я также обнаружил, что резонансная частота связана не только с разбиванием стекла, но и с важным принципом работы некоторых электронных устройств.

Что такое резонансная частота?

Резонансная частота – это собственная частота, при которой среда вибрирует с максимальной амплитудой

Почему стекло может разбиться под воздействием звука? Звук – это акустическая волна, которая заставляет молекулы колебаться. При проецировании от источника вибрация проходит через воздух на физическую структуру стекла. Если акустическая частота звука соответствует собственной частоте стекла, последнее начинает вибрировать с большей амплитудой, потенциально разрушая свою структуру.

Другими словами, стекло может разбиться, когда оно вибрирует на своей резонансной частоте. Резонансную частоту также можно определить как собственную частоту объекта, при котором он имеет тенденцию вибрировать с более высокой амплитудой. Например, вы могли бы почувствовать, как «трясется» мост, если бы общая сила колебаний от транспортных средств заставляла его вибрировать на своей частоте.

Термин «резонансная частота» также часто встречается в электронной технике, хотя он менее драматичен, чем осколки стекла или сильно трясущийся мост.

Резонансная частота в электронных схемах

Резонансная частота в электронных схемах выражается, когда схема демонстрирует максимальную колебательную характеристику на определенной частоте. Это наблюдается для цепи, состоящей из катушки индуктивности и конденсатора.

Чтобы лучше понять, что такое резонансная частота и какую роль она играет в электронике, давайте рассмотрим последовательную RLC-цепь, которая питается от источника переменного тока. Известно, что величина емкостного и индуктивного сопротивления изменяется соответственно частоте. Емкостное реактивное сопротивление определяется уравнением X

c = 1/(2ℼfC), а индуктивное сопротивление определяется уравнением X _L = 2ℼfL.

Зависимость индуктивного и емкостного сопротивления от частот

На графике уменьшение емкостного сопротивления будет пересекаться с увеличением индуктивного сопротивления на определенной частоте. Частота, на которой оба параметра перекрываются, известна как резонансная частота цепи RLC. Следовательно, резонансную частоту можно получить, выразив равное значение как емкостного, так и индуктивного сопротивления следующим образом:

1. Х _Л = Х _С
2. 2ℼfL = 1/(2ℼfC)
3. f _r = 1/(2ℼ √LC)

В последовательной RLC-цепи импеданс минимален, когда он работает на резонансной частоте. Полное сопротивление цепи выражается следующим уравнением:

Z = R + X _L — X _C

В резонансе X _L равно X _C

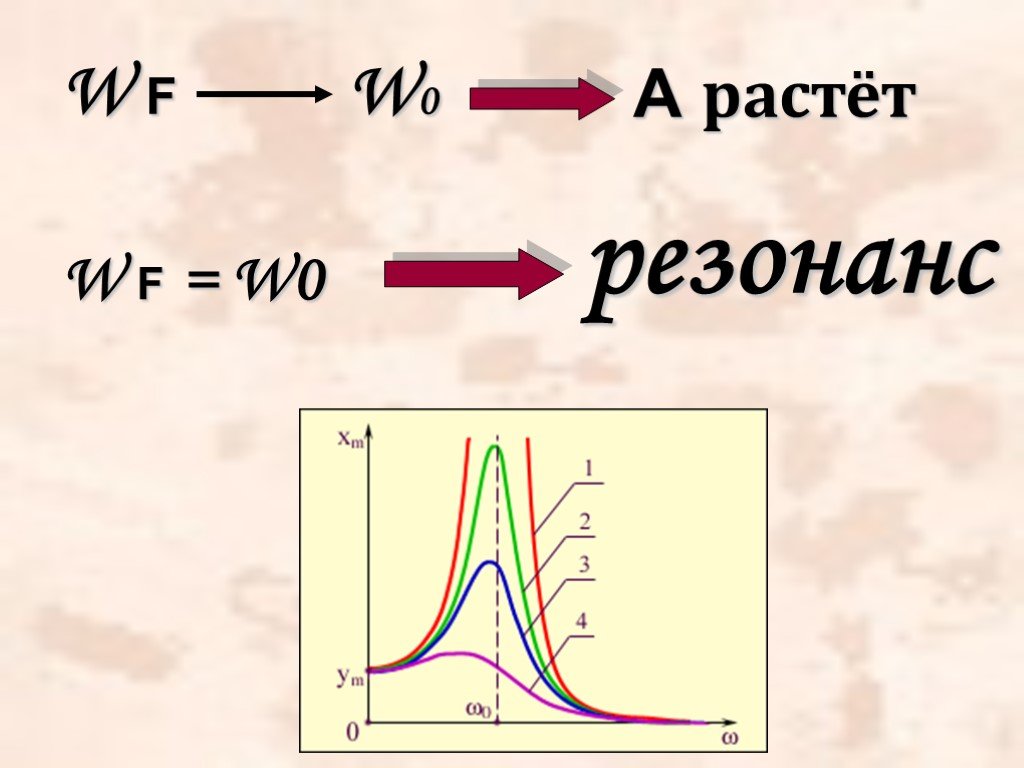, что означает, что они компенсируют друг друга. Это оставляет импеданс цепи чисто резистивным. В результате ток, протекающий через последовательную цепь RLC, достигает своего пика, когда он работает на своей резонансной частоте.

В параллельной RLC-цепи формула расчета резонансной частоты остается прежней. Однако вы обнаружите, что ток подавлен до минимума, так как полное сопротивление цепи максимально. Это происходит, когда LC цепи выглядит как разомкнутая цепь при параллельном соединении.

Применение резонансных цепей

Радиочастотные приемники пропускают сигналы, которые колеблются на резонансной частоте цепи

Концепция возбуждения цепи на ее резонансной частоте используется в различных приложениях. В генераторе в качестве колебательного контура используется параллельный LC, который приводится в движение на своей резонансной частоте. Результатом является непрерывная серия устойчивых, колеблющихся тактовых импульсов, которые управляют такими компонентами, как микроконтроллеры и коммуникационные ИС.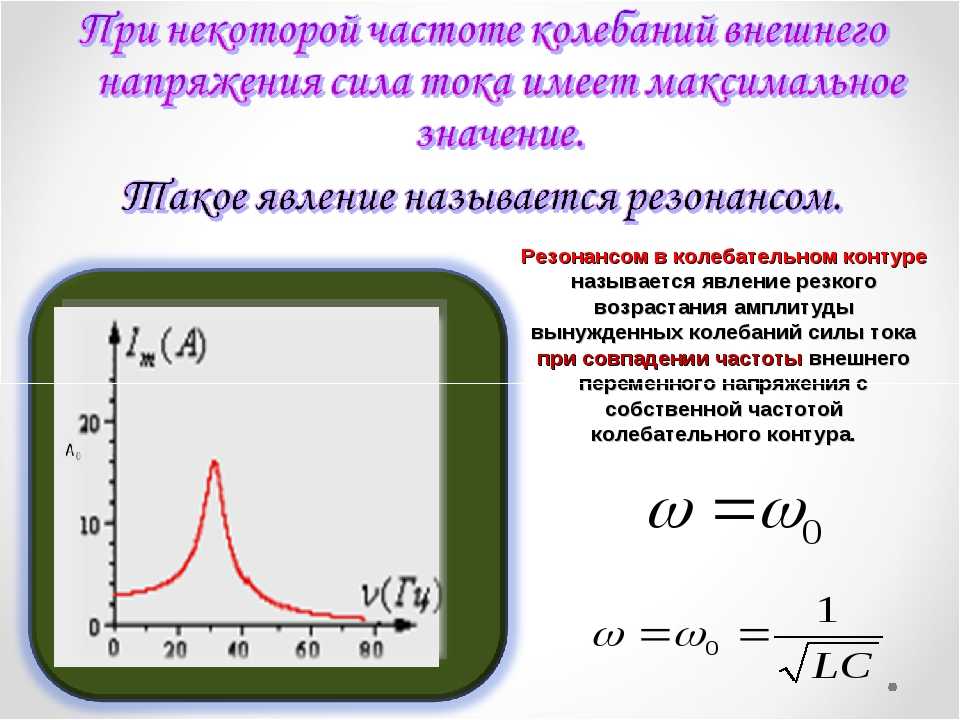

Резонансные контуры также используются в радиочастотных приложениях. Они становятся основой тюнера, усиливая сигналы, соответствующие его резонансной частоте, и подавляя те, которые выходят за пределы его полосы пропускания.

При проектировании резонансных цепей полезно работать с современным программным обеспечением для проектирования печатных плат. Allegro имеет все инструменты компоновки и моделирования, необходимые для обеспечения того, чтобы схема работала соответствующим образом на желаемой резонансной частоте. Вы также можете использовать InspectAR для точной оценки и улучшения печатных плат с помощью дополненной реальности и интуитивно понятного взаимодействия. Проверка, отладка, доработка и сборка печатных плат никогда не были быстрее и проще.

Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Чтобы посмотреть видео по связанным темам или узнать, что нового в нашем наборе инструментов для проектирования и анализа, подпишитесь на наш канал YouTube.