Лекция на тему: «Векторы».
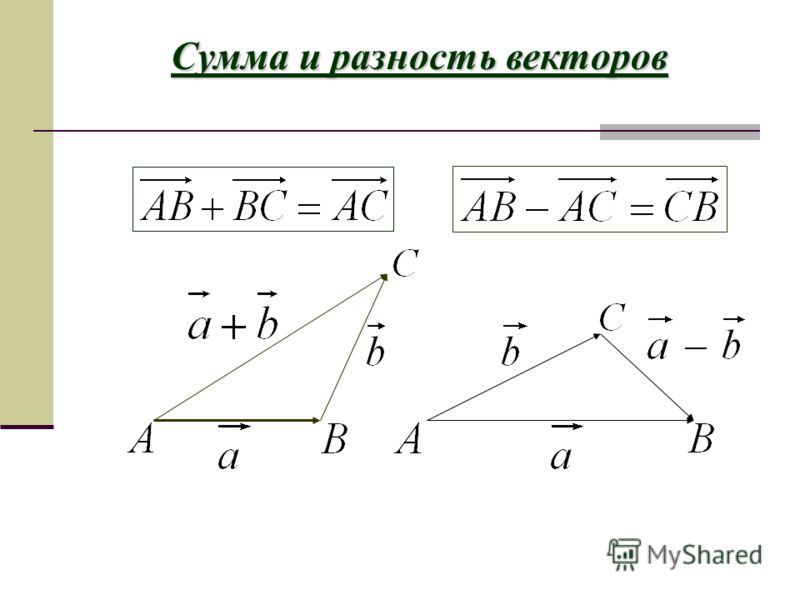
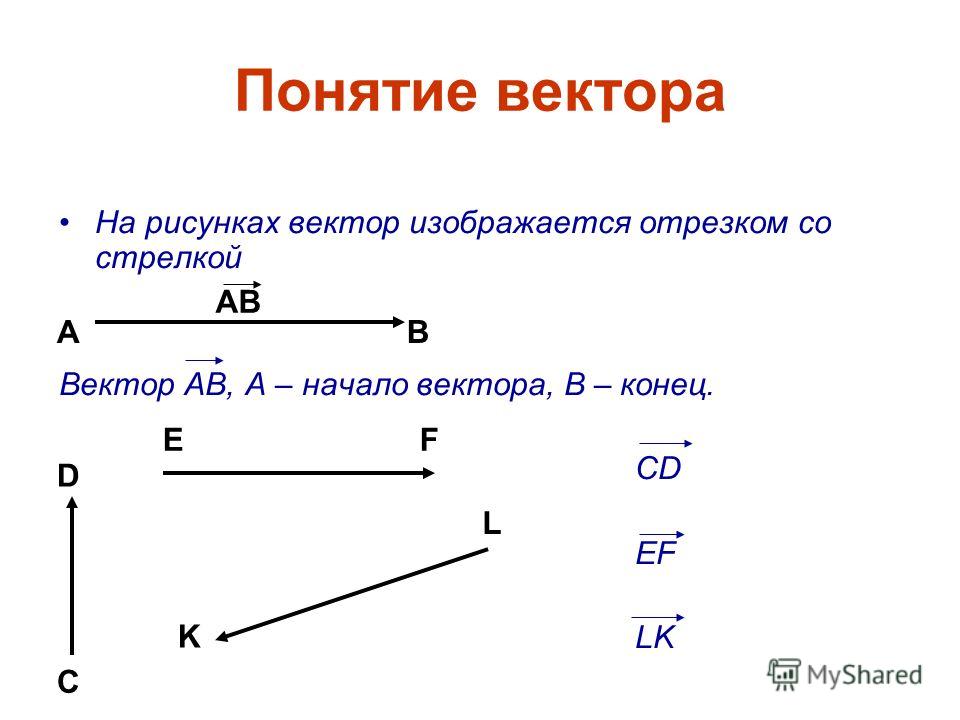
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
Длина вектора
Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные
одной прямой или лежащие на одной прямой называют коллинеарными
векторами (рис. 2).
Вектора, параллельные
одной прямой или лежащие на одной прямой называют коллинеарными
векторами (рис. 2).
рис. 2 | |||||||||
Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b Условия коллинеарности векторов 2. Два вектора коллинеарны N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю. Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных
(пространственных) задач. Ответ: вектора a и b коллинеарны при n = 6 и m = 4. Сонаправленные вектора
Противоположно направленные вектора Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4). Компланарные вектора Определение.
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные. Условия компланарности векторов
Равные вектора Определение.
|
Условие равенства векторов. Вектора равны, если их координаты равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторовПример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.
Решение:
a = b — так как их координаты равны,
a ≠ c —
так как их координаты не равны,
b ≠ c —
так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = {1; 8;}
и b = {1; 2n}
равны.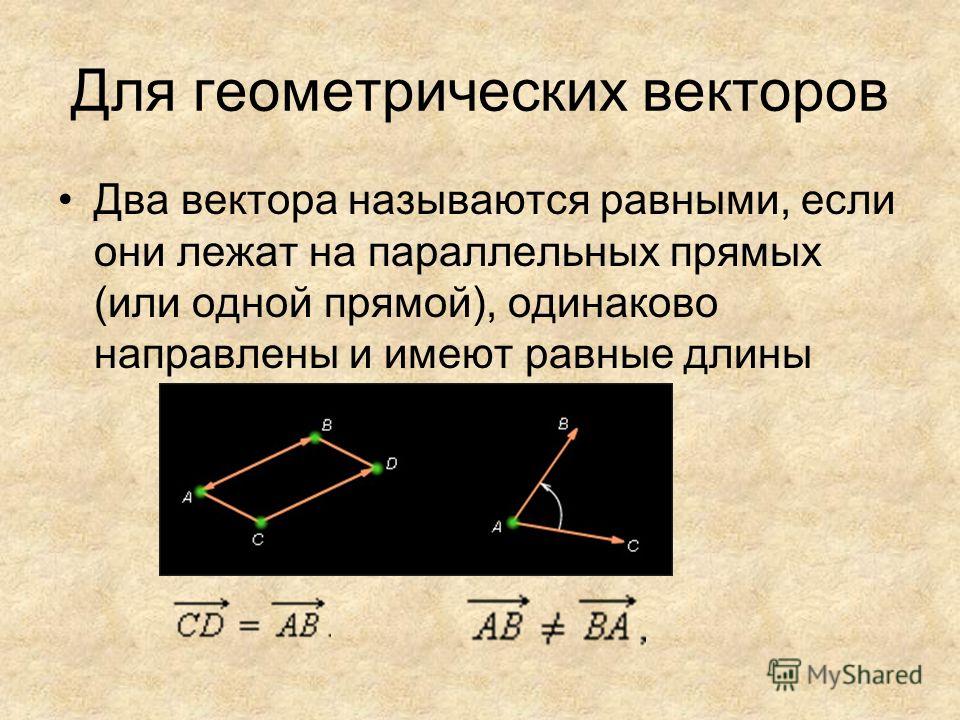
Решение:
Проверим равенство компонентов векторов
ax = bx =
1
ay = by =>
8 = 2n => n =
8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторовПример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.
Решение:
a = c — так как их координаты равны,
a ≠ b —
так как их координаты не равны,
b ≠ c —
так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx =
1
ay = by =
2
az = bz =>
4 = 2n => n =
4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Единичный вектор
Определение. Единичным вектором или

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Ортогональность векторов
Определение.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
рис. 1 |
Условие ортогональности векторов.Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
a · b = 0
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задачВ случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В
случае n-мерного пространства
вектор AB заданный координатами точек A(A1 ; A2 ; .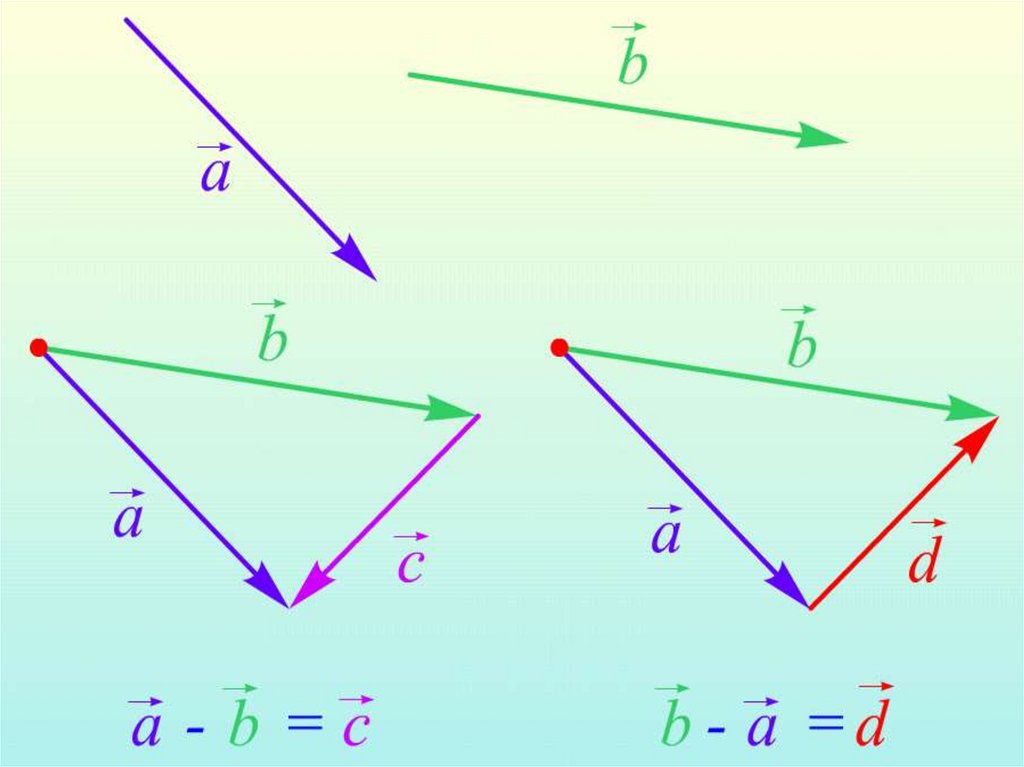
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры для плоских задачПример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).
Решение:
ABx = Bx —
Ax => Bx = ABx +
Ax => B
ABy = By —
Ay => By = ABy +
Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx —
Ax => Ax = Bx —
ABx => Ax = 3 — 5 = -2
ABy = By —
Ay => Ay = By —
ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).
Решение:
ABx = Bx —
Ax => Bx = ABx +
Ax => Bx = 5 + 3 = 8
ABy = By —
Ay => By = ABy +
Ay => By = 1 + (-4) = -3
ABz = Bz —
Az => Bz = ABz +
Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).
Решение:
ABx = Bx —
Ax => Ax = Bx —
ABx => Ax = 3 — 5 = -2
ABy = By —
Ay => Ay = By —
ABy => Ay = -4 — 1 = -5
ABz = Bz —
Az => Az = Bz —
ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).
Решение:
AB1 =
B1 — A1 => B1 =
AB1 + A1 => B1 =
5 + 3 = 8
AB2 = B2 — A2 => B2 =
AB2 + A2 => B2 =
1 + (-4) = -3
AB3 = B3 — A3 => B3 =
AB3 + A3 => B3 =
2 + 3 = 5
AB4 = B4 — A4 => B4 =
AB4 + A4 => B4 =
1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).
Решение:
AB1 =
B1 — A1 => A1 =
B1 — AB1 => A1 =
3 — 5 = -2
AB2 = B2 — A2 => A2 =
B2 — AB2 => A2 =
-4 — 1 = -5
AB3 = B3 — A3 => A3 =
B3 — AB3 => A3 =
1 — 4 = -3
AB4 = B4 — A4 => A4 =
B4 — AB4 => A4 =
8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Определение длины вектора
Определение.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две
вертикальные линии слева и справа |AB|.
Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Формулы длины вектора
Формула длины вектора для плоских задачВ случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2
Формула длины вектора для пространственных задачВ случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2 + az2
Примеры вычисления длины вектора для плоских задачиПример 1. Найти длину вектора a = {2; 4}.
Решение: |a| = √22 + 42 = √4 + 16 = √20 = 2√5.
Пример 2. Найти длину вектора a = {3; -4}.
Решение: |a| = √32 + (-4)2 = √9 + 16 = √25 = 5.
Примеры вычисления длины вектора для пространственных задачиПример 3. Найти длину вектора a = {2; 4; 4}.
Решение: |a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Пример 4. Найти длину вектора a = {-1; 0; -3}.
Решение: |a| = √(-1)2 + 02 + (-3)2 = √1 + 0 + 9 = √10.
Примеры вычисления длины вектора для пространств с размерностью большей 3Пример 5. Найти длину вектора a = {1; -3; 3; -1}.
Решение: |a| = √12 + (-3)2 + 32 + (-1)2 = √1 + 9 + 9 + 1 = √20 = 2√5
Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.
Решение: |a| = √22 +
42 + 42 + 62 + 22 =
√4 + 16
+ 16 + 36 + 4 = √76 = 2√19.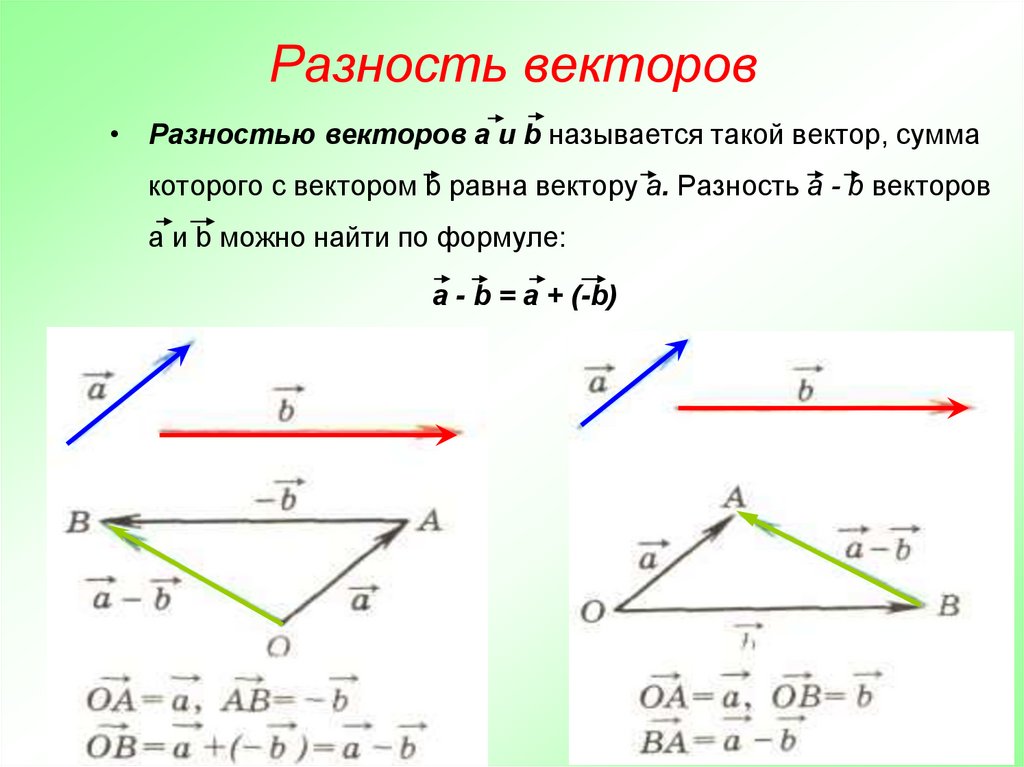
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задачВ случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задачВ случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторовВ
случае n-мерного пространства скалярное произведение
векторов a = {a1 ; a2 ; .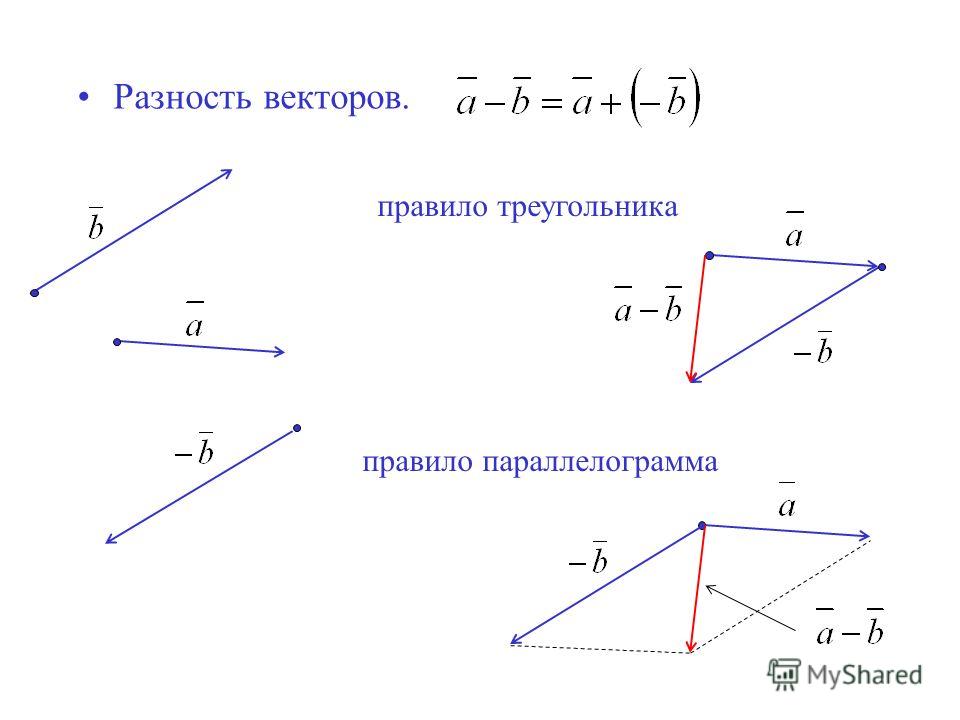 .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей
формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей
формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Определение. Проекцией
вектора AB на ось l называется
число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются
проекциями точек A и B на ось l. (рис. 1).
(рис. 1).
рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Пр ba = | a · b |
|b| |
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
Пр ba = | a · b | = | 11 | =
2. |
|b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачиПример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
Пр ba = | a · b | = | 12 | = 2 |
|b| | 6 |
Ответ: Пр ba =
2.
Конспект по теме: «Понятие вектора в пространстве»
Тема урока: «Понятие вектора в пространстве»
Тип урока: Изучение нового материала
Цели урока:
Образовательные: ввести определение вектора в пространстве и связанные с ним понятия; дать определение равенства векторов; отработать навыки нахождения равных, сонаправленных, противоположно направленных векторов; научить решать задачи по данной теме.
Развивающие: развивать стремление к достижению поставленной цели; совершенствовать пространственное воображение и мышление учащихся; развивать навыки диалоговой культуры.
Воспитательные: воспитать математическую культуру, грамотность; формировать активность, внимательность, наблюдательность; воспитание интереса к предмету и потребности в приобретении знаний.
Методы: беседа, лекция
Оборудование: учебники, тетради, меловая доска
Ход урока
I.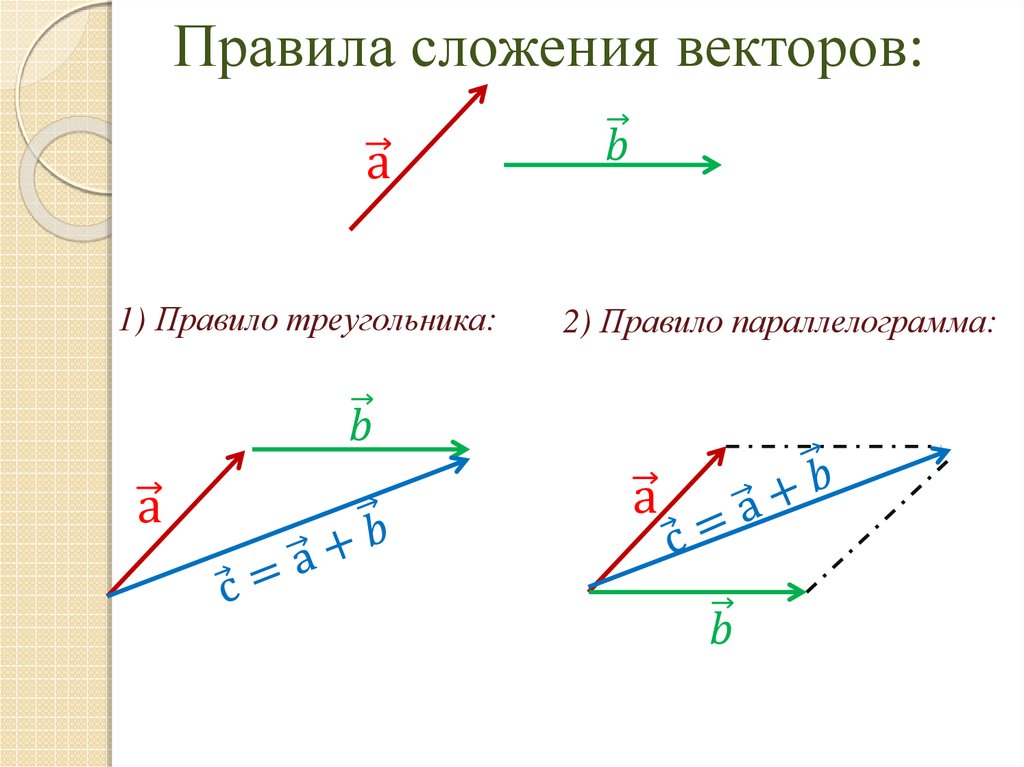 Организационный момент
Организационный момент
Геометрия — увлекательная наука, где есть важные и интересные темы.
Итак, запишите в тетрадях тему урока «Понятие вектора. Равенство векторов»
Сегодня на уроке мы познакомимся
— с понятием вектора в пространстве, с равными векторами в пространстве
— будем отрабатывать навыки нахождения равных, сонаправленных, противоположно направленных векторов
— узнаем, какую роль играют векторы в различных областях науки.
II. Актуализация опорных знаний.
1. Анализ контрольной работы. Подвести итоги контрольной работы. Анализ наиболее часто встречающихся ошибок.
2. Подготовка к восприятию нового материала.
Понятие вектора является одним из наиболее основных в математике, объединяющим такие ее разделы, как геометрия, алгебра, математический анализ. Оно имеет большое прикладное значение, так как многие физические величины (сила, скорость, и другие) характеризуются не только величиной, но и направлением, то есть являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин (векторы напряженности электрического поля, вектор магнитной индукции).
При изучении электрических и магнитных явлений появляются новые примеры векторных величин (векторы напряженности электрического поля, вектор магнитной индукции).
Ⅲ. Изучение нового материала
Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
Определение. Длиной ненулевого вектора считается длина отрезка АВ.
– длина вектора
— длина вектора
= 0
Определение. Коллинеарные векторы – это ненулевые векторы, которые лежат на одной прямой или на параллельных прямых.
Коллинеарные векторы делятся на сонаправленные и противоположно направленные.
Учащиеся называют по чертежу векторы, сонаправленные с вектором и противоположно направленные с вектором
Нулевой вектор считается сонаправленным с любым вектором.
Определение. Векторы называются равными, если они сонаправлены и их длины равны.
IV. Закрепление изученного материала.
Решение задачи № 320.
Найдите длину векторов: .
см, см, см, см, см, см
Вспомнить свойства граней и диагоналей параллелепипеда. По рисунку учащиеся называют все пары:
Найдите длины векторов
см
см
Назовите все векторы, противоположные вектору .
Ответ:
Назовите все векторы, противоположные вектору .
Ответ:
Назовите все векторы, равные вектору
Ответ:
V. Самостоятельная работа (обучающая)
№ 321
VI. Проверка результатов работы.
VII. Итог урока.
VIII. Домашнее задание.
Домашнее задание:
П. 38-39. № 323
векторных шаблонов сайтов | ThemeForest
Цена указана в долларах США без учета налогов
Нет продаж 56
Низкий 62
Середина 702
Высокий 323
Лучшие продавцы 8
Показать все 1 151
1 звезда и выше 119
2 звезды и выше 119
3 звезды и выше 116
4 звезды и выше 109
Любая дата 1 151
В прошлом году 134
В прошлом месяце 10
На прошлой неделе 1
Все версии программного обеспечения 1151
переключатель#переключатель» >❯ Вордпресс 9
WordPress 6. 0.x
3
Вордпресс 5.9.Икс
3
WordPress 5.8.x
8
WordPress 5.7.x
7
WordPress 5.6.x
7
WordPress 5.5.x
7
WordPress 5.4.x
4
WordPress 5.3.x
3
WordPress 5.2.x
3
WordPress 5.1.x
3
WordPress 5.0.x
4
Вордпресс 4.9.Икс
3
0.x
3
Вордпресс 5.9.Икс
3
WordPress 5.8.x
8
WordPress 5.7.x
7
WordPress 5.6.x
7
WordPress 5.5.x
7
WordPress 5.4.x
4
WordPress 5.3.x
3
WordPress 5.2.x
3
WordPress 5.1.x
3
WordPress 5.0.x
4
Вордпресс 4.9.Икс
3
переключатель#переключатель» >❯ Adobe 390
Adobe Фотошоп СС 79 Adobe XD CC 154 Adobe CS2 3 Adobe CS5.5 5 Adobe CS4 16 Adobe CS5 26 Adobe CS3 35 Adobe CS6 39Adobe CS 50 Adobe Photoshop 79 AdobeXD 154
переключатель#переключатель» >❯ Муза 1
Муза CC 2018.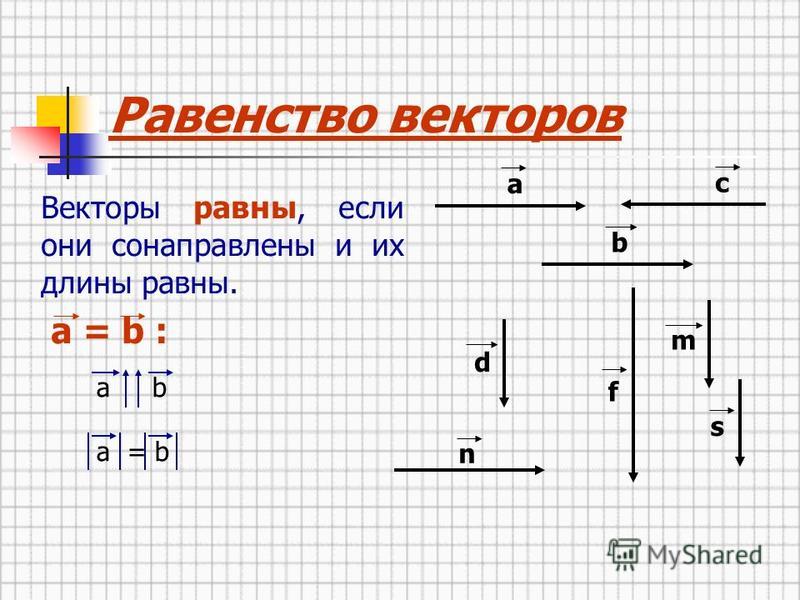 0.x
1
Муза CC
1
0.x
1
Муза CC
1
Эскиз 307
переключатель#переключатель» >❯ Друпал 1
Друпал 8.5.x 1 Друпал 8.4.x 1 Друпал 8.3.x 1 Друпал 8.2.x 1 Друпал 8.1.x 1 Друпал 8.0.x 1
Фигма 277
переключатель#переключатель» >❯ Джекилл 1
Джекилл 4.2.x
1
Джекил 4.1.x
1
Джекилл 4.0.x
1
Джекилл 3.9.Икс
1
Джекилл 3.8.x
1
Джекилл 3.7.x
1
Джекилл 3. 6.x
1
Джекилл (Другое)
1
6.x
1
Джекилл (Другое)
1
переключатель#переключатель» >❯ phpBB 1
phpBB 3.3.x 1 phpBB 3.2.x 1 phpBB 3.1.x 1 phpBB 3.0.x 1
Начальная загрузка 90
WPML 7
WooCommerce 7
Конструктор страниц WPBakery 5
AngularJS 4
Фейсбук 2
Фундамент 2
Элементор 1
РеактJS 1
визуальный композитор 1
1151 Предметы
- Термин: «вектор»
Очистить все
Добавить в корзину
Bulkit — Целевые страницы Saas
- 160+ современных и чистых демонстрационных страниц
- 10 готовых цветовых схем, более 2000 векторных файлов
- 47 страниц набора пользовательского интерфейса
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Venga — музыкальный пользовательский интерфейс
- Всего +140 экранов iPhone X
- +70 темных и +70 светлых экранов версии
- Настраиваемые слои, шрифты и цвета
Добавить в корзину
Добавить в корзину
Добавить в корзину
Добавить в корзину
Мобильный набор пользовательского интерфейса Mocha
- 125 экранов iOS.




 Вектора, параллельные
одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Вектора, параллельные
одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).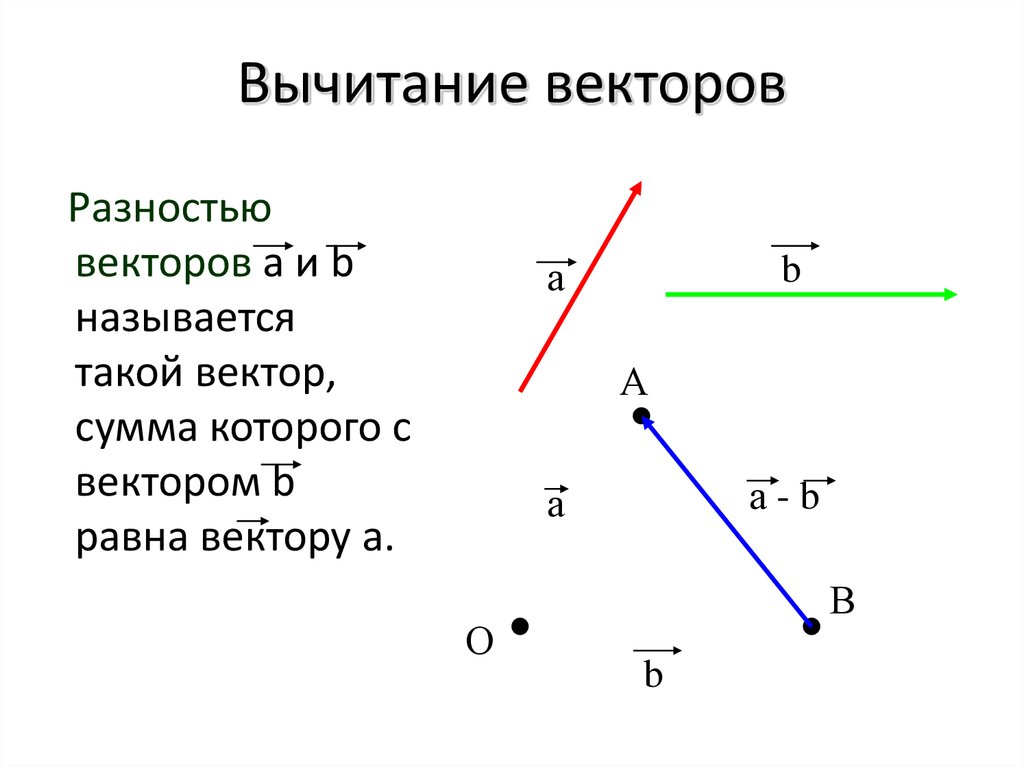 Вектора a и b называются
равными, если они лежат на одной или параллельных прямых, их направления
совпадают, а длины равны (рис. 6).
Вектора a и b называются
равными, если они лежат на одной или параллельных прямых, их направления
совпадают, а длины равны (рис. 6).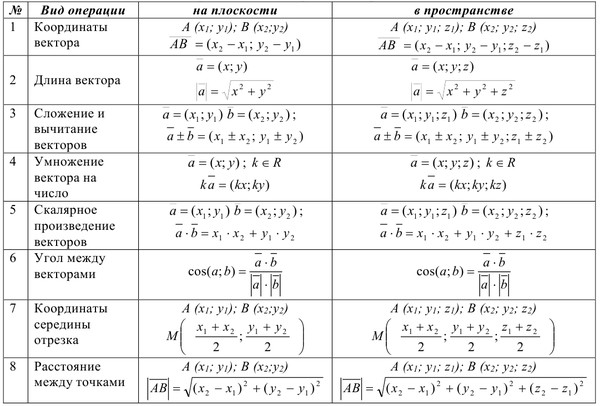 2
2