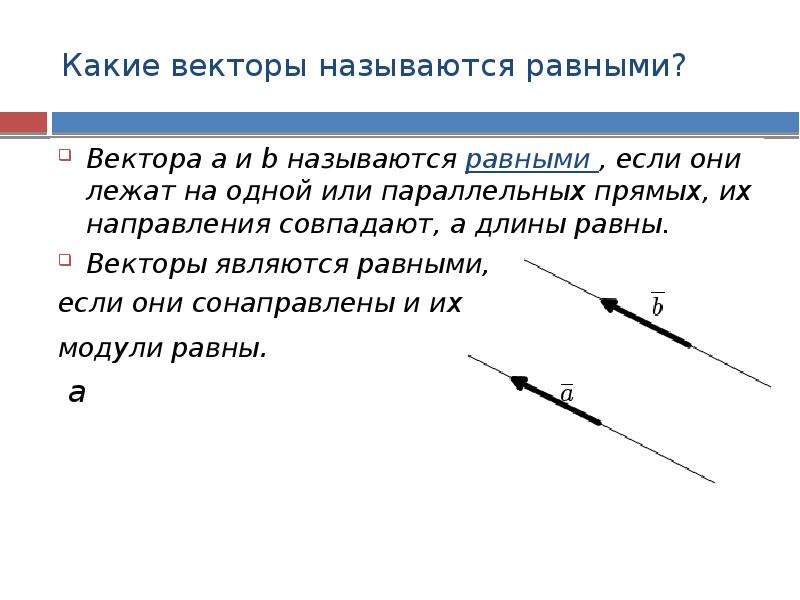
Какие векторы называют равными, а какие
Рассмотрим векторы, имеющие равные длины. Если такие векторы сонаправлены, их называют равными.
У равных векторов совпадает и длина и направление.
Векторы, направленные в противоположные стороны, даже, если у них будут равные длины, равными назвать не получится.
Если совпадает только одна характеристика — длина, то векторы называют равными по модулю.
Равные векторы
Если два вектора равны (т. е. одинаковые), то у них одинаковые:
- длина,
- направление,
- координаты.
Рассмотрим рисунок 1. На рисунке представлены векторы, обозначенные красным и зеленым цветом. Видно, что векторы имеют равные координаты — проекции на оси. Длины проекций для этих векторов: на ось Ox = 2, на ось Oy = 3. Если векторы имеют равные соответственные проекции (координаты), то эти векторы равны.
Рис. 1. Векторы, обозначенные красным и зеленым цветом, имеют равные координаты — проекции на оси
Примечание:
Когда векторы равны, вместо одного из них мы можем использовать второй вектор.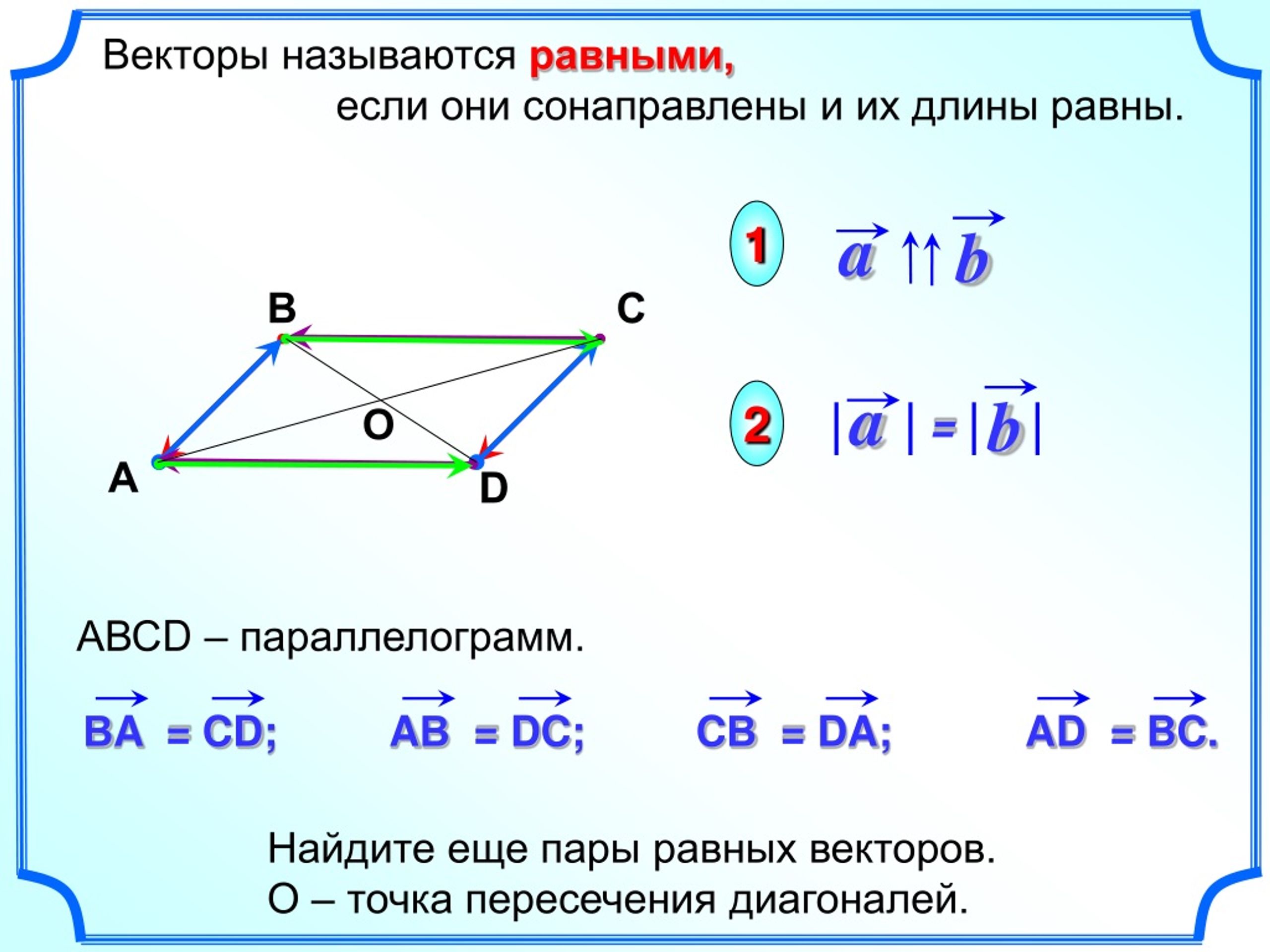 Если нам будет удобнее работать со вторым вектором.
Если нам будет удобнее работать со вторым вектором.
Противоположно направленные векторы
Вектор можно развернуть в противоположную сторону. С точки зрения математики, для этого достаточно перед вектором дописать знак минус.
Пример 1:
Векторы \( \vec{F} \) и \( -\vec{F} \) развернуты в противоположные стороны.
Когда векторы обозначают двумя буквами, то:
Векторы \( \overrightarrow{AB} \) и \( \left( -\overrightarrow{AB}\right) \) направлены в противоположные стороны.
Вектор \( \left(-\overrightarrow{AB} \right) \) — это вектор \( \overrightarrow{BA} \).
На языке математики это записывают так: \( \left(-\overrightarrow{AB}\right) = \overrightarrow{BA} \).
Для вектора \( \overrightarrow{AB} \): точка A — начальная, B — конечная.
А для вектора \(\overrightarrow{BA} \) наоборот: точка B — начальная, A — конечная.
Когда даны координаты вектора, то, чтобы его развернуть в противоположную сторону, нужно изменить знак каждой его координаты на противоположный.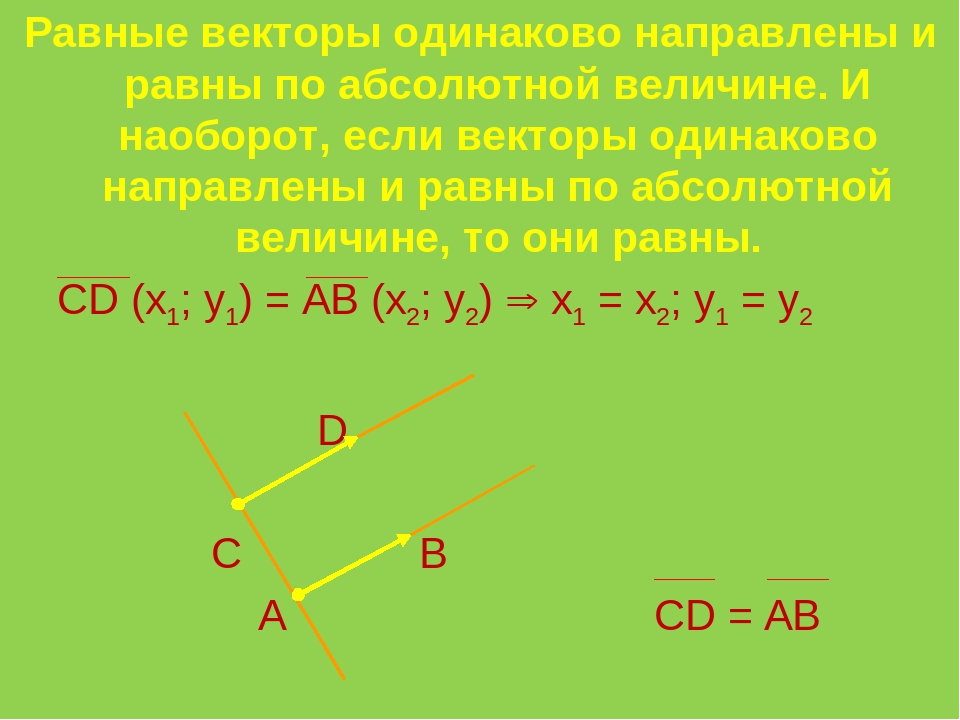
Пример 2:
Векторы \( \vec{a} = \left\{ -2; 7; -5 \right\} \) и \( \vec{b} = \left\{ 2; -7; 5 \right\} \) направлены в противоположные стороны.
Рис. 2. Векторы, на рисунках а) и б), имеют равную длину, а направлены противоположно
Примечание:
Если равны только длины векторов, а направлены они в противоположные стороны, знак равенства между ними записать не получится. Такие векторы не равны!
\( \vec{a} = \left\{ -2; 7; -5 \right\} \)
\( \vec{b} = \left\{ 2; -7; 5 \right\} \)
\( |\vec{a} | = | \vec{b} | \) – равны только длины векторов;
\( \vec{a} \ne \vec{b} \) – векторы не равны, так как их направления различаются;
Физика, равные по модулю противоположно направленне векторы
В физике, в третьем законе Ньютона, идет речь о равных по модулю и противоположно направленных векторах.
Вспомним третий закон Ньютона: \( \vec{F_{12}} = -\vec{ F_{21}} \) – длины векторов равны, а направления противоположны.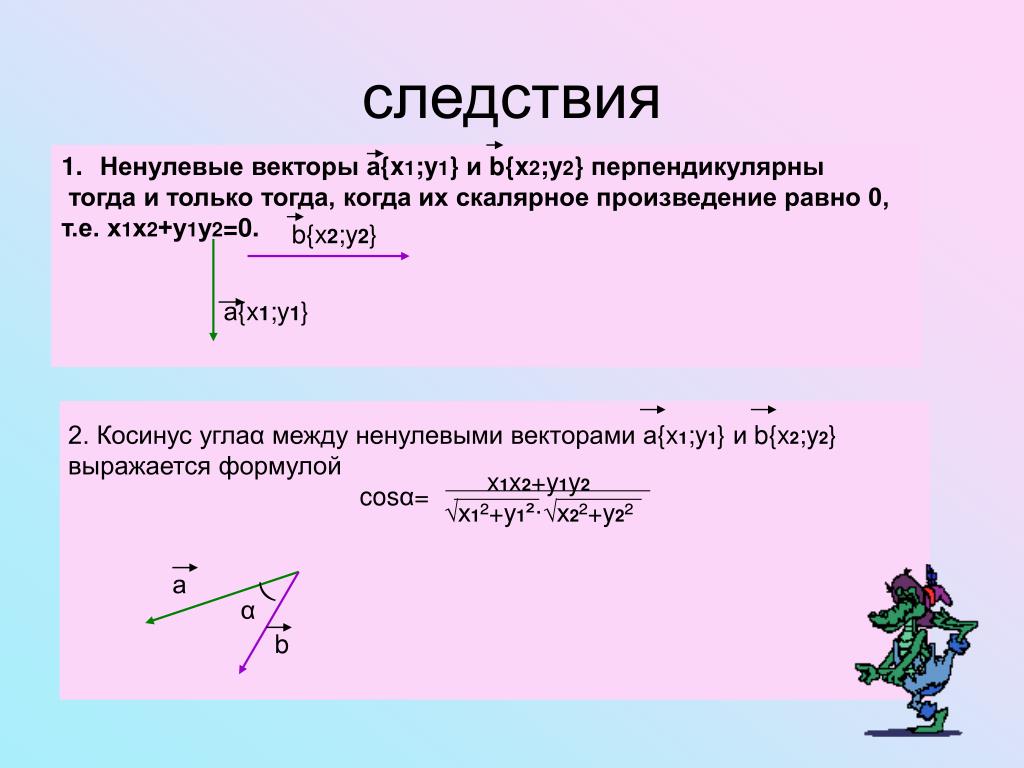
Чтобы приравнять такие векторы, необходимо перед одним из них записать знак минус:
\( \vec{F_{12}} = -\vec{ F_{21}} \) или \( -\vec{F_{12}} = \vec{ F_{21}} \)
Скалярное произведение векторов. Формулы и определение
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Приходите тренироваться в детскую школу Skysmart. Ученики решают захватывающие задачки вместе с красочными героями на интерактивной платформе, чертят вместе с учителем на онлайн-доске и не боятся школьных контрольных.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься в удовольствие уже завтра!
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно.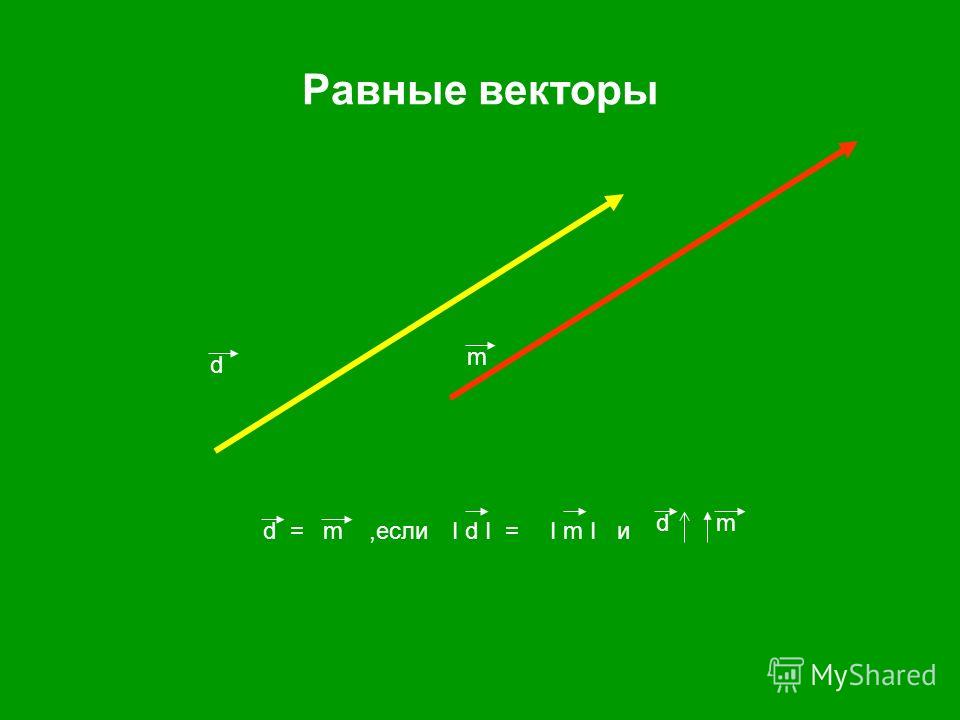 Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Значок угла ∠ можно опустить и писать просто: (→a;→b).
Пусть даны два вектора →a, →b.
Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
→a * →b = →|a| * →|b| * cosα
- Алгебраическая интерпретация.

Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0 так как , то есть cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
- Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
- Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
Так как:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
откуда
- Вспомнив формулу вычисления длины вектора по координатам, получаем
- Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.
- Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.

Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + … + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
- Скалярное произведение вектора самого на себя всегда больше или равно нулю.
 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору.→а * →а > 0
→0 * →0 = 0
- Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
- Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
- Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
- Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
- Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 <=> a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
и,
откуда следует:
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Как решаем:
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Ответ: →a * →b = 5√3.
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: (→a,→b) = 411.
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.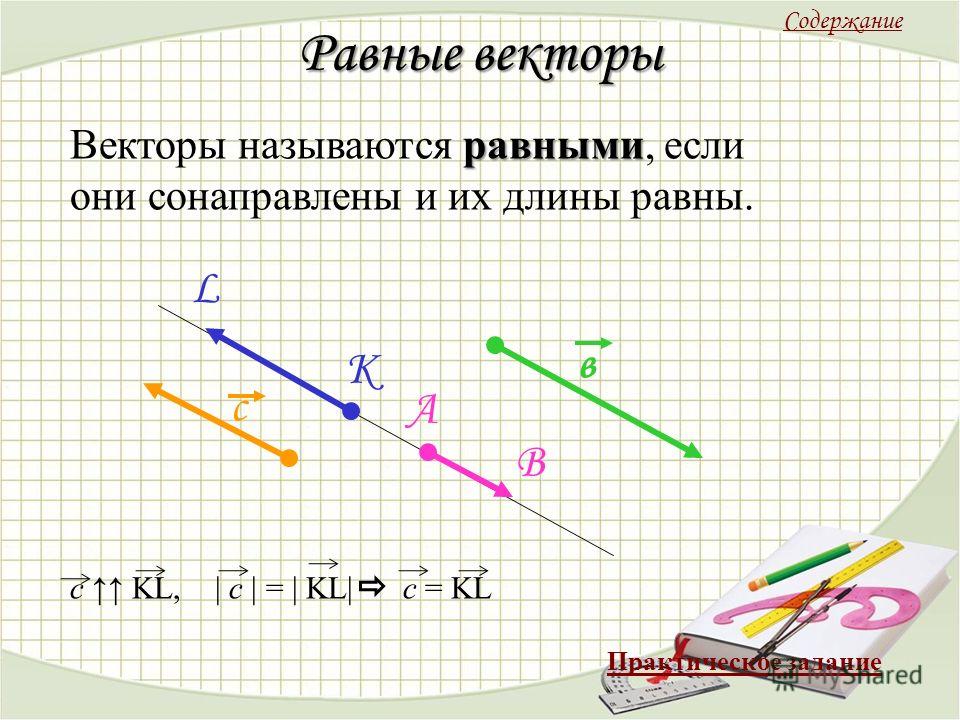
Как решаем:
- Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
- Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
- Найдем координаты векторов →AB1 и →BC1:
- Найдем длины векторов →AB1 и →BC1:
- Найдем скалярное произведение векторов →AB1 и →BC1:
- Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Чтобы знания превратились в практический навык — запишите ребенка на бесплатный вводный урок математики в Skysmart. На занятии покажем, как все устроено, решим пару задачек и дадим рекомендации по программе обучения для вашего ребенка.
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Понятие вектора
Рассмотрим две произвольные точки. Если соединить эти точки стрелкой (рис.1),
Рис.1
то мы получим вектор.
Точку, из которой стрелка выходит, называют началом вектора. Точку, в которую стрелка входит, называют концом вектора.
Чтобы отличить вектор от отрезка с концами в тех же точках, используют обозначение (рис.2) или (рис.3).
| Рис.2 | Рис.3 |
| Рис.2 |
| Рис.3 |
Иногда для вектора используют обозначения (рис.4) или (рис.5).
| Рис.4 | Рис.5 |
| Рис.4 |
| Рис.5 |
Если две точки (начало и конец вектора) совпадают, то говорят, что эти точки задают нулевой вектор.
Координаты вектора
Рассмотрим произвольный вектор и предположим, что в пространстве задана декартова прямоугольная система координат Oxyz (рис. 6).
6).
Рис.6
Если в системе координат Oxyz точки A и B имеют координаты
| A = (a1; a2; a3) и B = (b1; b2; b3) , | (1) |
то координатами вектора называют набор чисел
| (2) |
Этот определение часто формулируют так: «Для того, чтобы найти координаты вектора, нужно из координат конца вектора вычесть координаты начала вектора».
Замечание. В случае, когда рассматриваются векторы, лежащие на некоторой координатной плоскости, в формулах (1) и (2) не будет третьих координат. Если же рассматриваются векторы, лежащие на некоторой координатной прямой, то в формулах (1) и (2) останутся только первые координаты.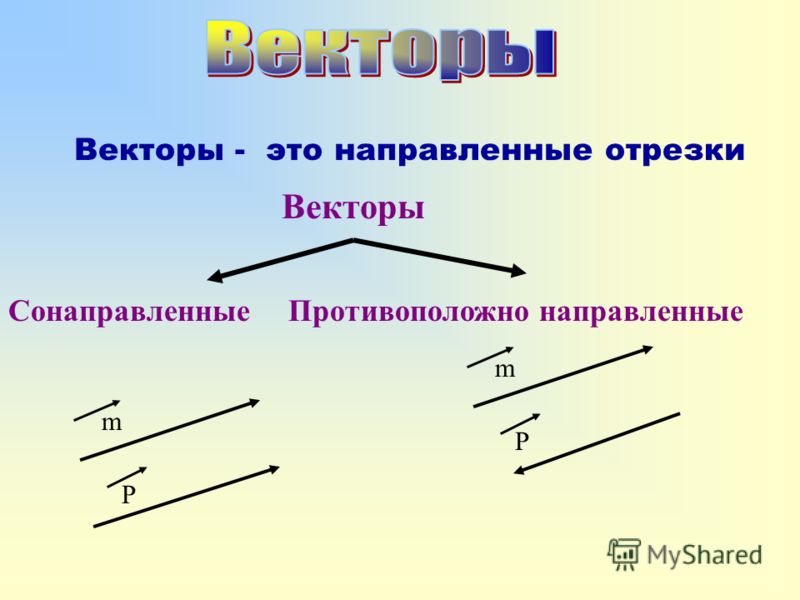
Длина вектора
Длиной (модулем) произвольного вектора называют длину отрезка AB
Длина вектора , координаты которого имеют вид
вычисляется по формуле
| (3) |
Этот факт часто формулируют так: «Длина вектора равна корню квадратному из суммы квадратов его координат».
Замечание. В случае, когда рассматриваются векторы, лежащие на координатной плоскости, формула (3) принимает вид
| (4) |
и совпадает с формулой, позволяющей найти расстояние между двумя точками координатной плоскости.
В случае, когда рассматриваются векторы, лежащие на координатной прямой, формулы (3) и (4) принимают вид
.
Равенство векторов
Векторы называют коллинеарными векторами, если они лежат на одной прямой или на параллельных прямых.
Два вектора
и
являются коллинеарными векторами тогда и только тогда, когда их координаты пропорциональны.
Другими словами, векторы являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства
a1 = tb1, a2 = tb2, a3 = tb3.
Два вектора называют сонаправленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 7.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в одну сторону (концы векторов будут лежать на одном луче).
Рис.7
Два вектора называют противоположно направленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 8.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в разные стороны (концы векторов будут лежать по разные стороны от их общего начала).
Рис.8
Определение. Два вектора равны, если, во-первых, они сонаправленные, а, во-вторых, имеют одинаковую длину.
Другими словами, если совместить начала этих векторов, то их концы совпадут.
Замечание. Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.
Умножение вектора на число
В результате умножения любого вектора на любое действительное число k получается такой вектор , который удовлетворяет следующим условиям:
- При k > 0 вектор сонаправлен с вектором ;
- При k < 0 вектор противоположно направлен с вектором ;
- Длина вектора равна длине вектора , умноженной на число |k|.

Если вектор имеет координаты
то вектор имеет координаты
Другими словами, если вектор умножается на число, то и все его координаты умножаются на это число.
Сложение и вычитание векторов
Для того, чтобы найти сумму двух произвольных векторов и нужно совместить начало вектора с концом вектора . Тогда началом вектора будет начало вектора , а концом вектора будет конец вектора (рис.9).
Рис.9
При этом, если
и
то
Этот факт часто формулируют так: «При сложении векторов их координаты складываются».
Для того, чтобы найти разность двух произвольных векторов и нужно воспользоваться формулой
Операция вычитания двух векторов наглядно изображена на рисунке 10.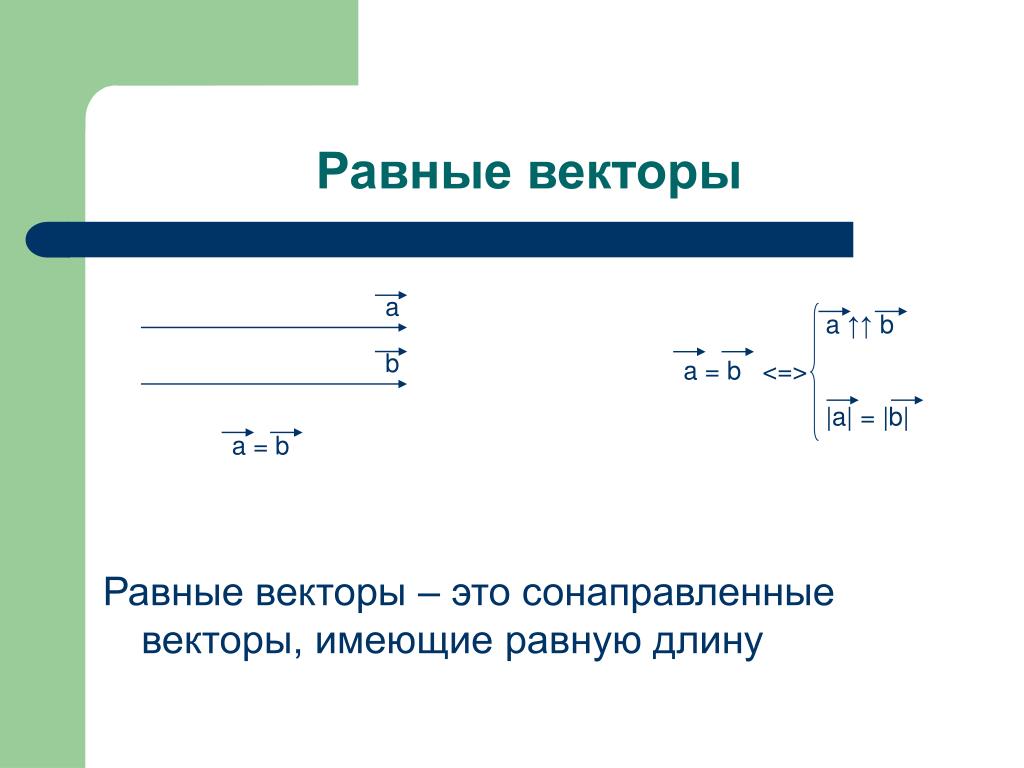
Рис.10
При этом, если
и
то
Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора , нужно из координат вектора вычесть координаты вектора ».
Скалярное произведение векторов
Определение. Скалярным произведением векторов и , которое обозначается называют число, равное произведению длин векторов и , умноженному на косинус угла между этими векторами (рис.11).
Рис.11
Таким образом,
| (5) |
Из формулы (5) вытекает соотношение
которое можно сформулировать так: «Модуль вектора равен корню квадратному из скалярного произведения вектора на себя».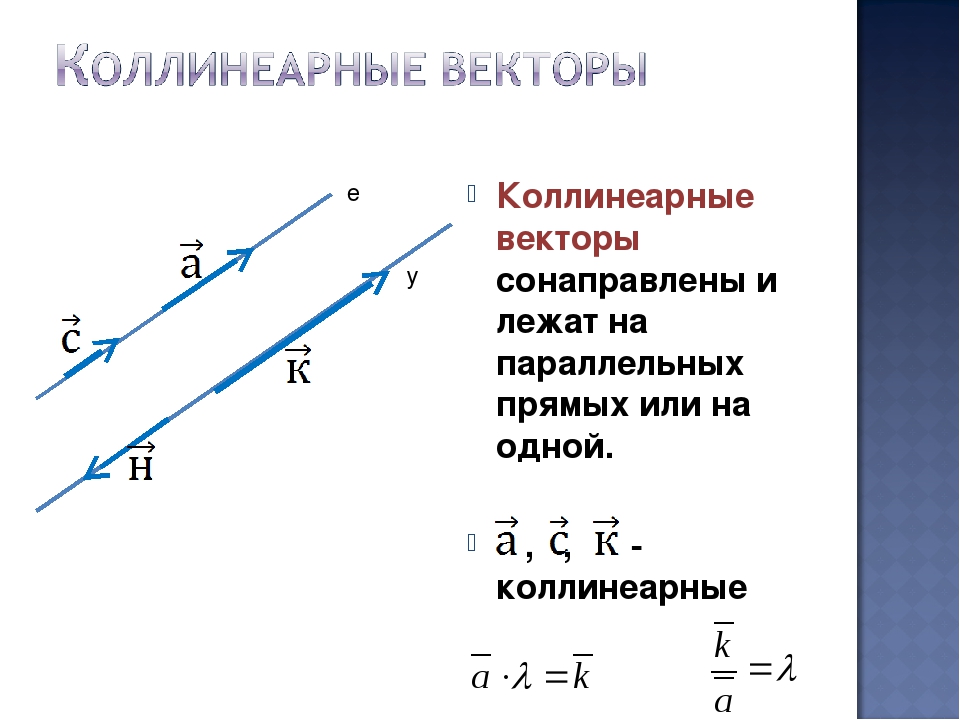
Следствие 1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Утверждение. Если в декартовой прямоугольной системе координат векторы имеют координаты
| и | (6) |
то их скалярное произведение выражается формулой:
| (7) |
Другими словами, в декартовой прямоугольной системе координат скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Замечание. Зная координаты векторов (6), из формул (3), (5) и (7) можно найти косинус угла между векторами и
Примеры решения задач
Пример 1. При каких значениях параметра p векторы и перпендикулярны?
Решение. Воспользовавшись формулой (7), получим
Воспользовавшись формулой (7), получим
Ответ: 4.
Пример 2. При каких значениях параметров α и β векторы (α; – 2; 5) и (1; β; – 4) коллинеарны?
Решение. Векторы, в силу изложенного выше, являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства:
Ответ: .
Пример 3. Длины векторов и равны 2 и 1 , соответственно, а угол между ними равен 60° . Найти длину вектора .
Решение. Рассмотрим рисунок 12.
Рис.12
Воспользовавшись теоремой косинусов, получим
Ответ: .
Пример 4. Длины векторов и равны 3 и 1, соответственно, а угол между ними равен 60°. Найти длину вектора .
Решение.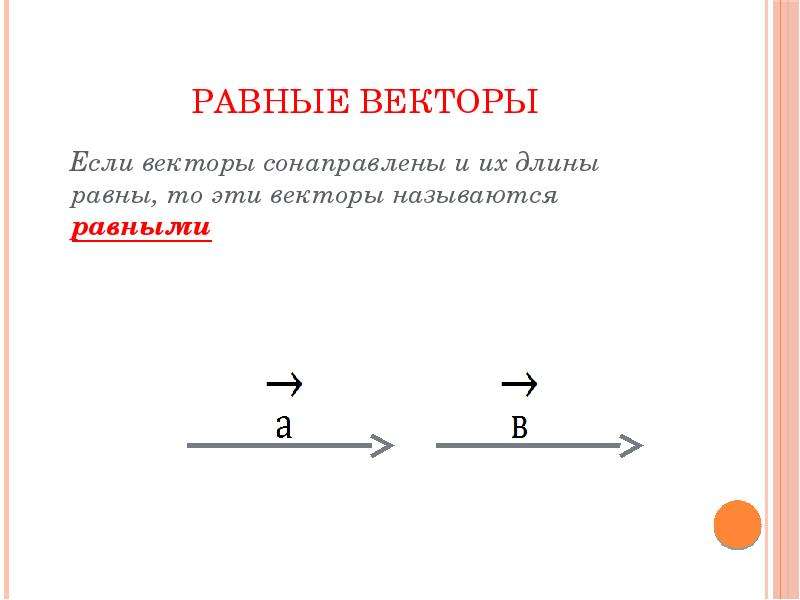 Рассмотрим рисунок 13.
Рассмотрим рисунок 13.
Рис.13
Воспользовавшись теоремой косинусов, получим
Ответ: .
Пример 5. Найти угол между векторами (3; 6; 2) и (4; 7; 4) .
Решение. Воспользовавшись формулой (8), получим
Ответ: .
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ • Большая российская энциклопедия
ВЕ́КТОРНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются векторы евклидова пространства и операции над ними.
Возникновение В. и. связано с потребностями механики и физики. Основы В. и. были заложены исследованиями У. Гамильтона и Г. Грассмана (1844–1850). Их идеи были использованы Дж. К. Максвеллом в его работах по электричеству и магнетизму.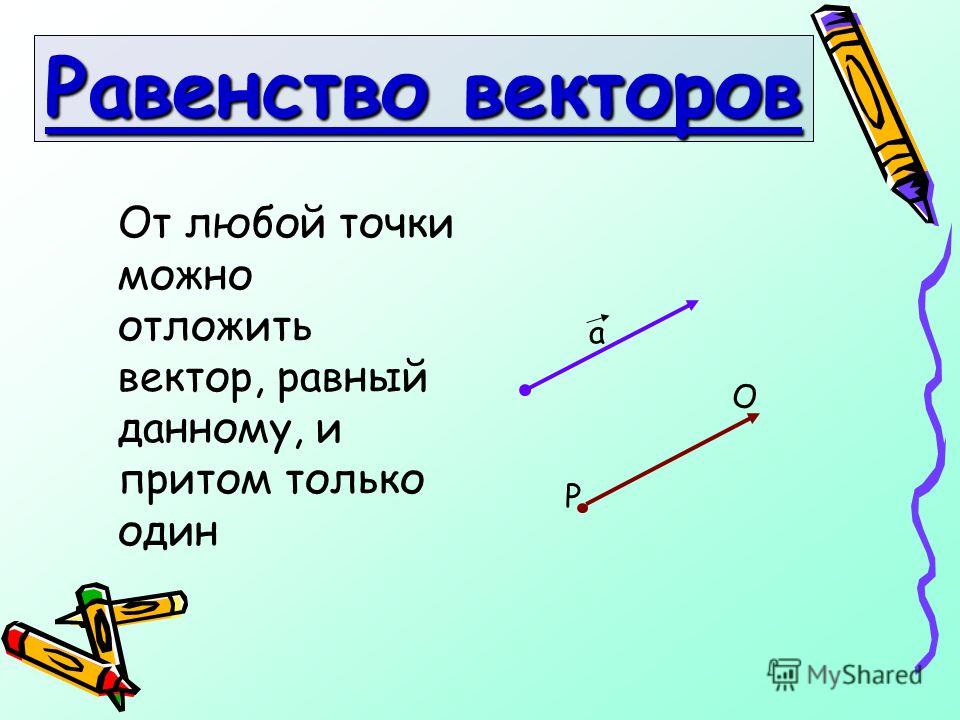 Совр. вид В. и. придал Дж. Гиббс. Значительный вклад в развитие В. и. внёс М. В. Остроградский.
Совр. вид В. и. придал Дж. Гиббс. Значительный вклад в развитие В. и. внёс М. В. Остроградский.
Векторная алгебра
Вектором называется направленный отрезок прямой, у которого один конец (точка $A$) считается началом, другой (точка $B$) – концом вектора. Обычно векторы обозначаются $AB, \overline{AB}, \overrightarrow{AB}, \boldsymbol a, \bar a, \vec a$, или просто $a$. Вектор, начало и конец которого совпадают, называется нулевым и обычно обозначается $\boldsymbol 0$ или 0. Характеристиками вектора являются его модуль (длина), который равен длине отрезка $AB$ (обозначается $|AB|$), и направление от $A$ к $B$. Нулевому вектору приписывают любое направление. Все нулевые векторы считаются равными. Вектор единичной длины называется единичным вектором или ортом. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых, и компланарными, если они лежат на одной плоскости. Вектор называется свободным, если его начальная точка может быть выбрана произвольно. Обычно два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаково направлены.
Вектор называется свободным, если его начальная точка может быть выбрана произвольно. Обычно два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаково направлены.
Кроме свободных векторов в механике и физике часто рассматриваются векторы, которые характеризуются модулем, направлением и положением начальной точки (точкой приложения). Такие векторы называются связанными. Связанные векторы считаются равными, если они имеют не только равные модули и одинаковые направления, но и общую точку приложения. Множество равных между собой векторов, расположенных на одной прямой, называется скользящим вектором. Задание скользящего или связанного вектора может быть заменено заданием двух свободных векторов. В В. и. рассматриваются только свободные векторы.
В векторной алгебре рассматриваются линейные операции над векторами, т.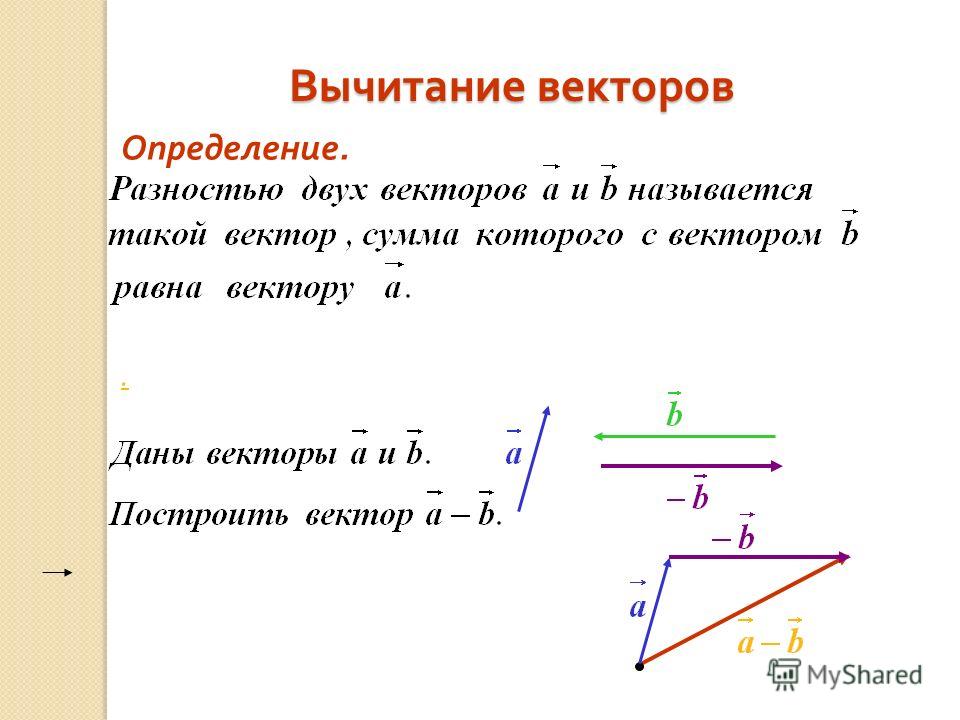 е. сложение векторов и умножение вектора на действительное число.
е. сложение векторов и умножение вектора на действительное число.
Рис. 1.
Рис. 2.
Рис. 3.
Суммой $a+b$ векторов $a$ и $b$ называется вектор, идущий из начала вектора $a$ в конец вектора $b$ при условии, что начало вектора $b$ приложено к концу вектора $a$ (рис. 1), этот вектор равен также диагонали параллелограмма, построенного на векторах $a$ и $b$ (рис. 2). Построение суммы нескольких векторов показано на рис. 3.
Произведением $\alpha a$ вектора $a$ и числа $\alpha$ называется вектор, коллинеарный вектору $a$, имеющий длину $|\alpha|\cdot |a|$ и направление, совпадающее с направлением $a$ при $\alpha > 0$ и противоположное при $\alpha < 0$. Если $\alpha =0$ или/и $a=0$, то $\alpha a = 0$.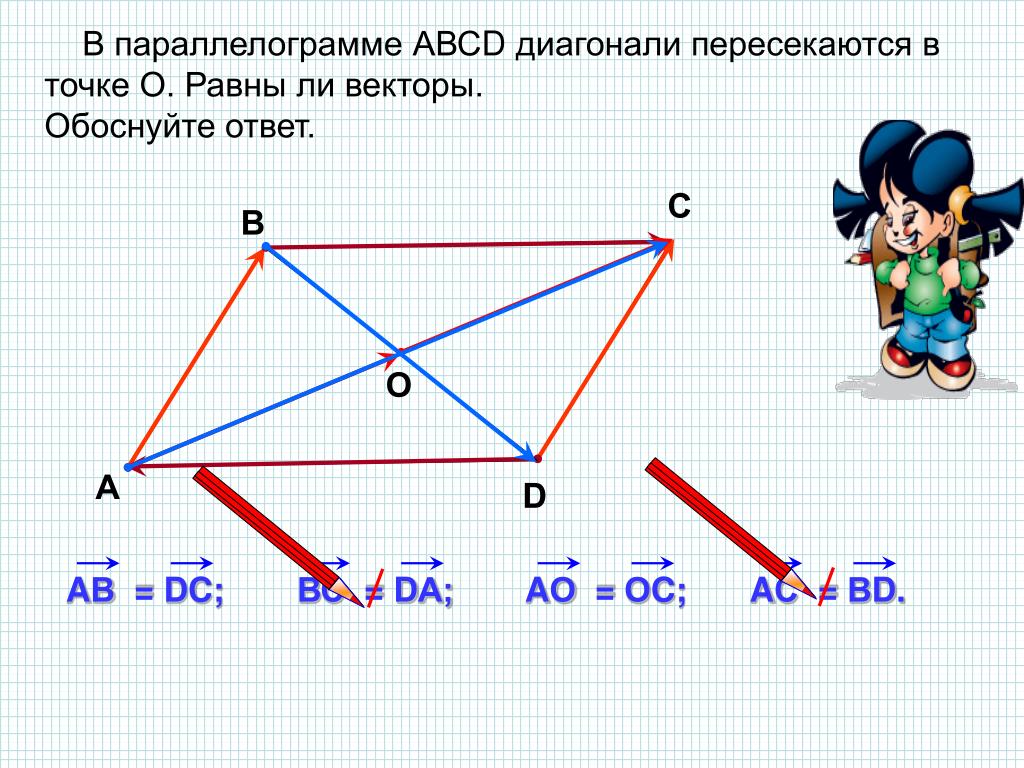
Вектор $-1\cdot a$ называется противоположным вектору $a$ и обозначается $-a$.
Операции сложения векторов и умножения вектора на число обладают свойствами $a+b = b+a, (a+b)+c = a+(b+c), a+0 = a, a+(-a) = 0, 1\cdot a=a, \alpha(\beta a) = (\alpha\beta)a, \alpha(a+b) = \alpha a +\alpha b, (\alpha +\beta)a = \alpha a +\beta a$, где $a,b,c$ – векторы, а $\alpha$ и $\beta$ – действительные числа. Разностью $a-b$ векторов $a$ и $b$ называется вектор $x$ такой, что $x+b = a, x = a+(-b)$. Множество всех векторов евклидова пространства с введёнными в нём операциями сложения и умножения на число образует векторное пространство.
В векторной алгебре часто используются понятия линейной зависимости и линейной независимости векторов. Векторы $a_1, \ldots , a_n$ называются линейно зависимыми, если существуют числа $\alpha_1, \ldots , \alpha_n$, из которых хотя бы одно отлично от нуля, такие, что линейная комбинация $\alpha_1 a_1 + \ldots + \alpha_n a_n = 0$, т.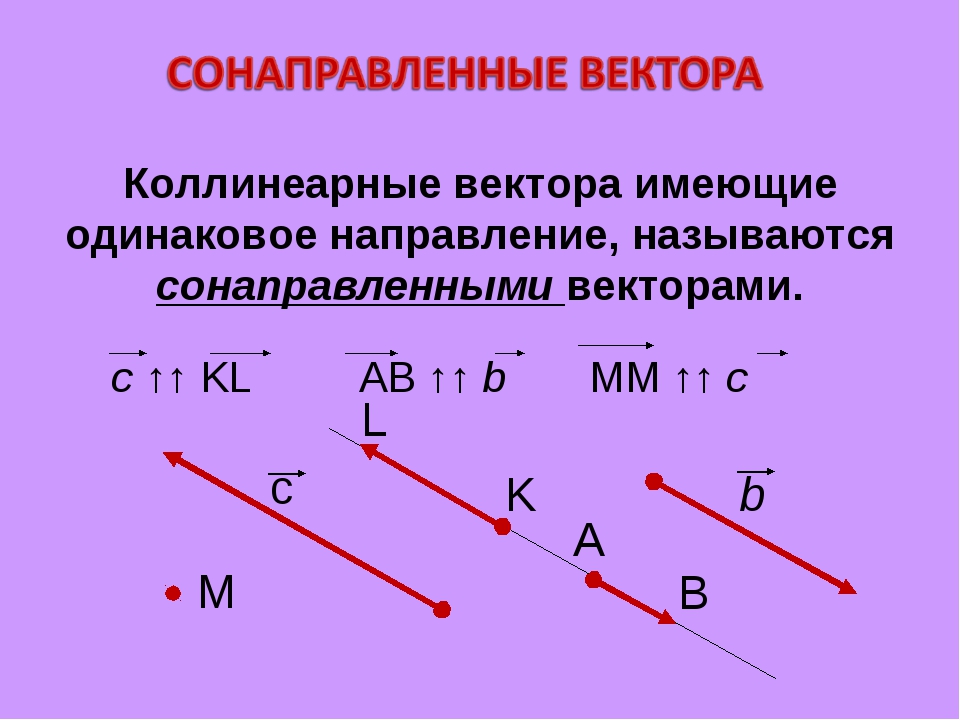 е. сумма векторов в левой части этого равенства равна нулевому вектору. В противном случае векторы $a_1, \ldots, a_n$ называются линейно независимыми.
е. сумма векторов в левой части этого равенства равна нулевому вектору. В противном случае векторы $a_1, \ldots, a_n$ называются линейно независимыми.
Рис. 4.
В механике и физике обычно используются двумерные и трёхмерные векторные пространства. В трёхмерном пространстве существуют тройки линейно независимых векторов, любые четыре вектора линейно зависимы; в двумерном пространстве, т. е. на плоскости, существуют пары линейно независимых векторов, любые три вектора линейно зависимы. Линейно независимые векторы $e_1, e_2, e_3$ трёхмерного евклидова пространства образуют базис, т. е. любой вектор $a$ может быть единственным образом представлен в виде $a = a_1e_1 + a_2e_2 + a_3e_3$, где $a_1, a_2, a_3$ – числа, называемые координатами (компонентами) вектора $a$ в данном базисе.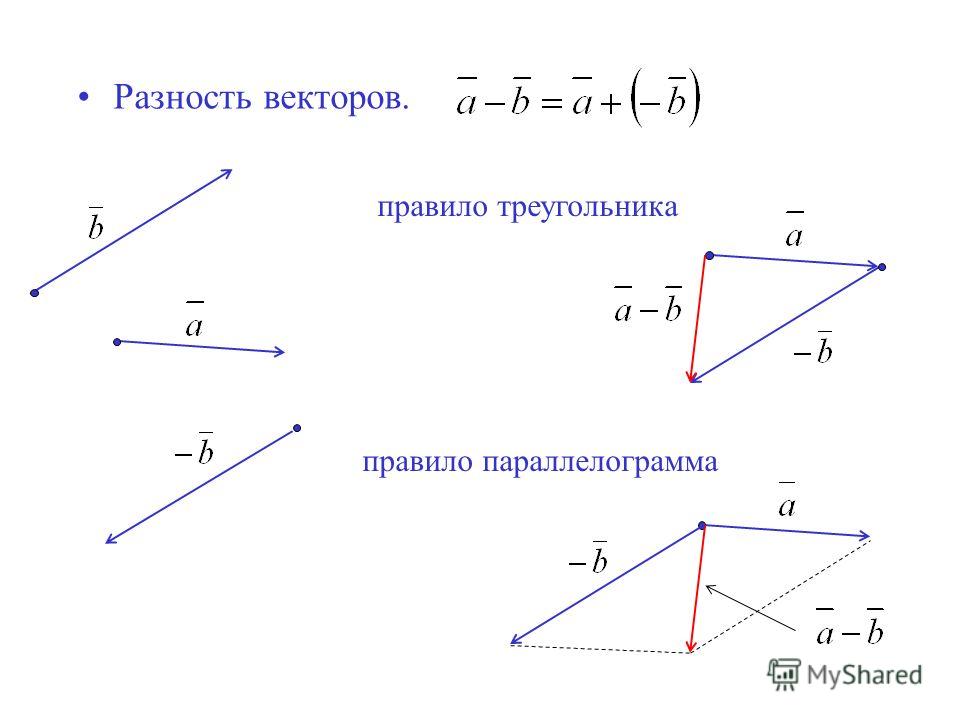 Вектор $a$ c координатами $a_1, a_2, a_3$ часто записывают в виде $a=(a_1,a_2, a_3)$. Три взаимно ортогональных (перпендикулярных) вектора, длины которых равны единице и которые обычно обозначают $i, j, k,$ образуют т. н. ортонормированный базис. Если начала этих векторов поместить в некоторую точку $O$, то получится декартова прямоугольная система координат в трёхмерном пространстве (рис. 4). Указанным выше линейным операциям над векторами соответствуют аналогичные операции над их координатами: если векторы $a$ и $b$ имеют координаты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$, то сумма $a+b$ этих векторов имеет координаты $(a_1 + b_1, a_2 + b_2, a_3 + b_3)$, а вектор $\alpha a$ имеет координаты $(\alpha a_1,\alpha a_2, \alpha a_3)$.
Вектор $a$ c координатами $a_1, a_2, a_3$ часто записывают в виде $a=(a_1,a_2, a_3)$. Три взаимно ортогональных (перпендикулярных) вектора, длины которых равны единице и которые обычно обозначают $i, j, k,$ образуют т. н. ортонормированный базис. Если начала этих векторов поместить в некоторую точку $O$, то получится декартова прямоугольная система координат в трёхмерном пространстве (рис. 4). Указанным выше линейным операциям над векторами соответствуют аналогичные операции над их координатами: если векторы $a$ и $b$ имеют координаты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$, то сумма $a+b$ этих векторов имеет координаты $(a_1 + b_1, a_2 + b_2, a_3 + b_3)$, а вектор $\alpha a$ имеет координаты $(\alpha a_1,\alpha a_2, \alpha a_3)$.
Развитие и применение векторной алгебры тесно связаны с разл. векторными произведениями: скалярным, векторным и смешанным. 2}}$$
2}}$$
Рис. 5.
При определении векторного произведения используется понятие левой и правой упорядоченных троек векторов. Упорядоченная тройка векторов $a, b, c$ ($a$ — первый, $b$ — второй, $c$ — третий векторы), приведённых к общему началу и не лежащих в одной плоскости, называется правой (левой), если они располагаются так, как располагаются соответственно большой, указательный и средний пальцы правой (левой) руки. На рис. 5 изображены слева – правая, а справа – левая тройки векторов.
Векторным произведением векторов $a$ и $b$ называется вектор, обозначаемый $[a ,b]$, такой, что длина вектора $[a, b]$ равна произведению длин векторов $a$ и $b$ на синус угла $\varphi$ между ними, и если $a$ и $b$ неколлинеарны, то вектор $[a, b]$ перпендикулярен векторам $a$ и $b$ и направлен так, что тройка векторов $a, b, [a, b]$ является правой. В случае, если $a$ и $b$ коллинеарны, то $[a, b] = 0$. Векторное произведение обладает следующими свойствами:
В случае, если $a$ и $b$ коллинеарны, то $[a, b] = 0$. Векторное произведение обладает следующими свойствами:
$$[a ,b] = — [b, a], \quad [(\alpha a), b] = \alpha [a, b],$$ $$[c, (a + b)] = [c, a] + [c, b],$$ $$[a, [b, c]] = b(a, c) — c(a, b),$$ $$([a, b], [c, d]) = (a, c)(b, d) — (a, d)(b, c),$$
где $a, b, c, d$ — векторы, $\alpha$ — число.
Если в ортонормированном базисе $i, j, k$, образующем правую тройку, векторы $a$ и $b$ имеют соответственно координаты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$, то
$$[a,b] = (a_2b_3 — a_3b_2, a_3b_1 — a_1b_3, a_1b_2 — a_2b_1),$$
или
$$[a, b] = \begin {vmatrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$$
Понятие векторного произведения применяется в разл. задачах механики и физики. Напр., момент силы $F$, приложенной к точке $M$, относительно точки $O$ равен векторному произведению $[\overline{OM}, F]$.
Смешанным произведением векторов $a, b$ и $c$ называется число, обозначаемое $abc$, равное скалярному произведению $([a, b], c)$ вектора $[a, b]$ на вектор $c$. Смешанное произведение векторов $a, b$ и $c$, не параллельных одной плоскости, равно объёму параллелепипеда, построенного на приведённых к общему началу векторах $a, b$ и $c$, взятому со знаком плюс, если тройка $a, b, c$ правая, и со знаком минус, если тройка левая. Если векторы $a, b$ и $c$ параллельны одной плоскости, то $abc = 0$. Справедливы также равенства $abc = bca = cab$. Если координаты векторов $a, b$ и $c$ в ортонормированном базисе $i, j, k$, образующем правую тройку, суть $(a_1, a_2, a_3), (b_1, b_2, b_3)$ и $(c_1, c_2, c_3)$, то
$$abc = \begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end {vmatrix}$$
Вектор-функции скалярных аргументов
Рис. 6.
6.
В механике, физике, дифференциальной геометрии широко используется понятие вектор-функции одного или нескольких скалярных аргументов. Если каждому значению переменной $t$ из некоторого множества $\{t\}$ ставится в соответствие определённый вектор $r$, то говорят, что на множестве $\{t\}$ задана вектор-функция (векторная функция) $r = r(t)$. Т. к. вектор $r$ определяется координатами $(x, y, z)$ в базисе $i, j, k$, то задание вектор-функции $r = r(t)$ эквивалентно заданию трёх скалярных функций $x = x(t), y = y(t), z=z(t)$.
Понятие вектор-функции становится наглядным, если обратиться к годографу этой функции, т. е. множеству концов всех векторов $r(t)$, приложенных к началу координат $O$ (рис. 6). Если при этом рассматривать аргумент $t$ как время, то вектор-функция $r(t)$ представляет собой закон движения точки $M$, движущейся по кривой $L$ – годографу функции $r(t)$. {\prime}].$$
{\prime}].$$
В дифференциальной геометрии вектор-функции одного аргумента используются для задания кривых. Для задания поверхностей пользуются вектор-функциями двух аргументов.
Векторный анализ
В механике, физике и геометрии широко используются понятия скалярных и векторных полей. Темп-ра неравномерно нагретой пластины и плотность неоднородного тела представляют собой физич. примеры соответственно плоского и пространственного скалярных полей. Примерами векторного поля являются множество всех векторов скоростей частиц установившегося потока жидкости, поле силы тяжести и напряжённость электрич. поля.
Для математич. задания скалярных и векторных полей используются соответственно скалярные и векторные функции. Плотность тела представляет собой скалярную функцию точки, а поле скоростей частиц установившегося потока жидкости – векторную функцию точки. Для геометрич. характеристики скалярного поля используются понятия линий и поверхностей уровня. Линией уровня плоского скалярного поля называется линия, на которой функция, задающая поле, имеет постоянное значение. Аналогично определяется поверхность уровня пространственного скалярного поля. Примерами линий уровня могут служить изотермы – линии уровня скалярного поля температур неравномерно нагретой пластины.
Для геометрич. характеристики скалярного поля используются понятия линий и поверхностей уровня. Линией уровня плоского скалярного поля называется линия, на которой функция, задающая поле, имеет постоянное значение. Аналогично определяется поверхность уровня пространственного скалярного поля. Примерами линий уровня могут служить изотермы – линии уровня скалярного поля температур неравномерно нагретой пластины.
Пусть $M$ – произвольная точка на линии (поверхности) уровня скалярного поля. При движении точки $M$ по линии (поверхности) уровня функция $f$, задающая поле, не меняется, а макс. изменение функции $f$ происходит при смещении по нормали к этой линии (поверхности) в точке $M$. Это изменение характеризуется с помощью т. н. градиента скалярного поля. Градиент представляет собой вектор, направленный по нормали к линии (поверхности) уровня в точке $M$ в сторону возрастания $f$ в этой точке. Величина градиента равна производной функции $f$ в указанном направлении. Градиент обозначается символом $grad \:f$. В базисе $i, j, k$ градиент $grad \:f$ имеет координаты $(\partial f/{\partial x}, \partial f/{\partial y}, \partial f/{\partial z})$ (для плоского поля $(\partial f/{\partial x}, \partial f/{\partial y})$). Градиент скалярного поля представляет собой векторное поле.
Величина градиента равна производной функции $f$ в указанном направлении. Градиент обозначается символом $grad \:f$. В базисе $i, j, k$ градиент $grad \:f$ имеет координаты $(\partial f/{\partial x}, \partial f/{\partial y}, \partial f/{\partial z})$ (для плоского поля $(\partial f/{\partial x}, \partial f/{\partial y})$). Градиент скалярного поля представляет собой векторное поле.
Рис. 8.
Рис. 7.
Для векторных полей вводятся понятия векторной линии, векторной трубки, циркуляции, дивергенции и вихря (ротора). Пусть в некоторой области $\Omega$ задано векторное поле с помощью векторной функции $a= a(M)$ переменной точки $M$ из $\Omega$. Линия $L$ в области $\Omega$ называется векторной линией, если вектор касательной в каждой её точке $M$ направлен по вектору $a(M)$ (рис. 7). Если поле $a$ – поле скоростей частиц стационарного потока жидкости, то векторные линии этого поля – траектории частиц жидкости. Часть пространства в $\Omega$, состоящая из векторных линий, называется векторной трубкой (рис. 8). В случае векторного поля скоростей частиц стационарного потока жидкости векторная трубка есть часть пространства, которую «заметает» при своём перемещении некоторый объём жидкости.
7). Если поле $a$ – поле скоростей частиц стационарного потока жидкости, то векторные линии этого поля – траектории частиц жидкости. Часть пространства в $\Omega$, состоящая из векторных линий, называется векторной трубкой (рис. 8). В случае векторного поля скоростей частиц стационарного потока жидкости векторная трубка есть часть пространства, которую «заметает» при своём перемещении некоторый объём жидкости.
Пусть $AB$ – некоторая гладкая линия в $\Omega, l$ – длина дуги, отсчитываемая от точки $A$ до переменной точки $M$ этой линии, $t$ – единичный вектор касательной к $AB$ в $M$. Циркуляцией поля $a$ вдоль кривой $AB$ называется величина
$$\int _{AB} (a, t) dl.$$
Если $a$ – силовое поле, то циркуляция $a$ вдоль $AB$ представляет собой работу этого поля вдоль пути $AB$.
Дивергенцией векторного поля $a$, имеющего в базисе $i, j, k$ координаты $P, Q, R$, называется сумма
$$\partial P/{\partial x} + \partial Q/{\partial y} + \partial R/{\partial z},$$
которая обозначается $\mathrm{div}\:a$. Напр., дивергенция гравитационного поля, создаваемого некоторым распределением масс, равна объёмной плотности $\rho (x, y, z)$ этого поля, умноженной на $4\pi$.
Напр., дивергенция гравитационного поля, создаваемого некоторым распределением масс, равна объёмной плотности $\rho (x, y, z)$ этого поля, умноженной на $4\pi$.
Вихрь (ротор) векторного поля $a$ представляет собой векторную характеристику вращательной составляющей этого поля, вихрь поля $a$, обозначаемый $\mathrm{rot} \:a$, равен
$$\left ( \frac {\partial R}{\partial y} — \frac {\partial Q}{\partial z}, \frac {\partial P}{\partial z} — \frac {\partial R}{\partial x}, \frac {\partial Q}{\partial x} — \frac {\partial P}{\partial y} \right).$$
Нахождение градиента скалярного поля, дивергенции и вихря векторного поля обычно называют осн. дифференциальными операциями векторного анализа. Справедливы следующие формулы, связывающие эти операции:
$$\mathrm {grad} (fh) = f\: \mathrm {grad}\:h + h\:\mathrm {grad}\: f, $$ $$ \mathrm {div} (fa) = (a, \mathrm {grad}\: f) + f\: \mathrm {div}\: a,$$ $$\mathrm {rot} (fa) = f\: \mathrm {rot}\: a + [\mathrm {grad}\: f, a],$$ $$\mathrm {div} [a, b] = (b, \mathrm {rot}\: a) — (a, \mathrm {rot}\: b),$$
где $f$ и $h$ – скалярные, а $a$ и $b$ – векторные поля.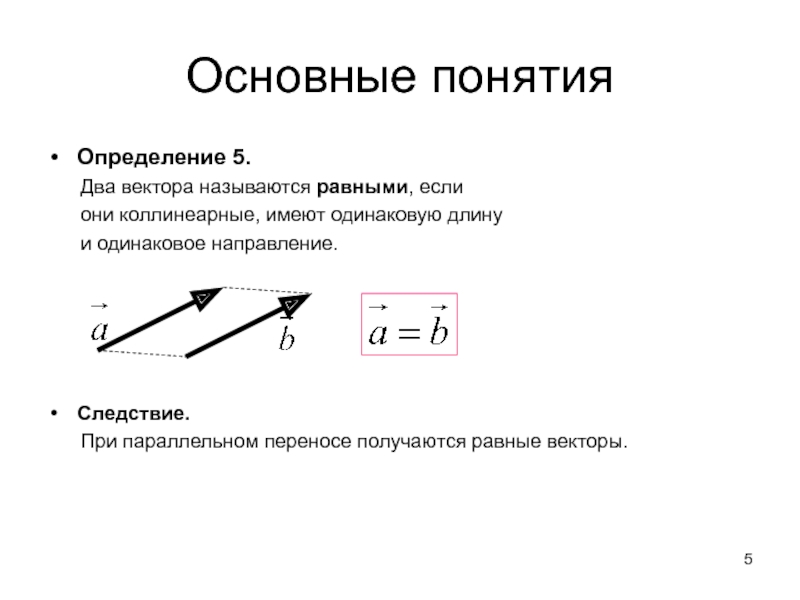 Векторное поле $a$ называется потенциальным полем, если это поле представляет собой градиент некоторого скалярного поля $f$. При этом поле $f$ называется потенциалом векторного поля $a$. Для того чтобы поле $a$, координаты которого $P, Q, R$ имеют непрерывные частные производные, было потенциальным, необходимо и достаточно, чтобы в каждой точке области $\Omega$ вихрь этого поля был равен нулю. Если в односвязной области $\Omega$ задано потенциальное поле $a$, то потенциал $f$ этого поля может быть найден по формуле
Векторное поле $a$ называется потенциальным полем, если это поле представляет собой градиент некоторого скалярного поля $f$. При этом поле $f$ называется потенциалом векторного поля $a$. Для того чтобы поле $a$, координаты которого $P, Q, R$ имеют непрерывные частные производные, было потенциальным, необходимо и достаточно, чтобы в каждой точке области $\Omega$ вихрь этого поля был равен нулю. Если в односвязной области $\Omega$ задано потенциальное поле $a$, то потенциал $f$ этого поля может быть найден по формуле
$$f(M) = \int_{AM} (a, t) dl,$$
в которой $AM$ – любая гладкая кривая, соединяющая фиксированную точку $A$ из $\Omega$ с точкой $M, t$ – единичный вектор касательной к кривой $AM$ и $l$ – длина дуги $AM$, отсчитываемая от точки $A$.
Векторное поле $a$ называется соленоидальным, или трубчатым, если это поле представляет собой вихрь некоторого поля $b$.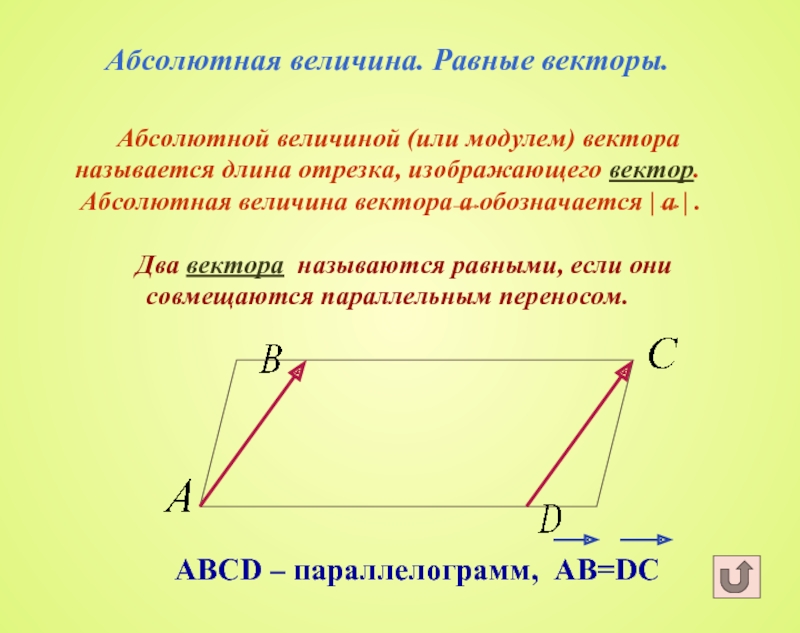 При этом поле $b$ называется векторным потенциалом поля $a$. Для того чтобы поле $a$ было соленоидальным, необходимо и достаточно, чтобы в каждой точке области $\Omega$ дивергенция этого поля была равна нулю. Векторное поле $a$, для которого $\mathrm {div} \:a = 0, \mathrm {rot} \: a = 0$, называется гармоническим.
При этом поле $b$ называется векторным потенциалом поля $a$. Для того чтобы поле $a$ было соленоидальным, необходимо и достаточно, чтобы в каждой точке области $\Omega$ дивергенция этого поля была равна нулю. Векторное поле $a$, для которого $\mathrm {div} \:a = 0, \mathrm {rot} \: a = 0$, называется гармоническим.
В векторном анализе важную роль играют интегральные соотношения: Остроградского формула, именуемая также основной формулой векторного анализа, и Стокса формула.
Координаты и векторы. Исчерпывающий гид (ЕГЭ — 2021)
Нам нужно найти угол между прямыми \( \displaystyle SB\) и \( \displaystyle CD\).
Таким образом, наша задача сводится к поиску координат точек: \( \displaystyle S,B,C,D\).
Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины \( \displaystyle S\) найдем через координату точки \( \displaystyle O\).
Работы навалом, но надо к ней приступать!
a) Координата \( \displaystyle D\): ясно, что ее аппликата и ордината равны нулю. \circ \)
\circ \)
Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.
3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.
Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.
Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:
Базис (Лекция №17)
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
- При умножении вектора на число все его координаты
умножаются на это число, т.е. если .
Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь
.
При сложении векторов их соответствующие координаты складываются, т.
 е. если .
е. если .Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если , то.
Доказательство:
- Пусть вектор коллинеарен , тогда найдется λ такое, что . Значит, и . Поскольку разложение вектора по элементам базиса единственно, то .
- Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно,
, т.е. . Теорема доказана.
Пример.
- Даны векторы . Найти вектор .
.
- Найти координаты вектора в базисе, образованном
векторами , , .
Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:
Итак, .
Рассмотрим две произвольные точки и . Найдем координаты вектора .

Очевидно, что . Но по определению координат вектора и . Следовательно,
Таким образом, чтобы найти координаты вектора , нужно из координат его конца вычесть соответствующие координаты начала.
Примеры.
- Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор .
- Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1). Найти .
- Известно, что. Найти координаты точки D, если
А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).
Пусть тогда
. С другой стороны . Следовательно, должно выполняться равенство (x+3; y+5; z-4)=(5;10;-8). Отсюда
x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).
- Даны векторы . Найти вектор .
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Мы рассмотрели умножение вектора на число. Однако во многих задачах механики и
физики встречается операция умножения вектора на вектор. Но при этом результат
может быть как числом, так и вектором. Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Однако во многих задачах механики и
физики встречается операция умножения вектора на вектор. Но при этом результат
может быть как числом, так и вектором. Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Пусть даны два вектора и , угол между, которыми равен .
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается . Итак, .
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
- Скалярное произведение двух
векторов подчиняется коммутативному закону, т.е. для любых векторов и .
Очевидно, из определения скалярного произведения:
.
- Для любого числа λ и любых векторов имеем:
.
Доказательство.
 Ограничимся случаем, когда λ > 0. В этом случае
угол между векторами и совпадает с
углом между векторами и , .
Ограничимся случаем, когда λ > 0. В этом случае
угол между векторами и совпадает с
углом между векторами и , .Поэтому . Откуда
Аналогично доказывается и равенство .
Случай λ <0 рассмотреть самостоятельно.
- Для любых векторов выполняется
равенство .
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
- Для любого вектора выполняется
соотношение.
Действительно, так как , то .
Из этого свойства в частности следует .
- Скалярное произведение двух
векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан вектор . Известно, что
Найти .
Имеем, т.е. .
Найдем:
Следовательно, .
Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора и .
Рассмотрим сначала все возможные скалярные произведения векторов друг на друга.
Поэтому
Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .
Это соотношение позволяет вычислить длину вектора через его координаты:
.
Далее из определения скалярного произведения находим
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
.
Условие ортогональности двух векторов:
или .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
- Пусть А(-1; 1; 0), B(3; 1; -2), . Найти:
- ;
- и ;
- .
- .
- .
- .
- Найти в , если известны координаты его вершин A(1; 5; 6),
B(5; 3; 10), C(2; 1; 14).
- При каком значении m векторы и перпендикулярны?
Условие ортогональности двух векторов .
. Следовательно, m = 15.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Введем сначала понятие ориентации тройки векторов.
Пусть даны три некомпланарных вектора с общим началом, перечисленных в определенном порядке: первый – , второй – , третий – .
Тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора , то кратчайший поворот от к осуществляется по часовой стрелке.
Векторным произведением векторов и называется новый вектор , удовлетворяющий условиям:
- Длина вектора равна площади параллелограмма, построенного на векторах и .
- Вектор перпендикулярен плоскости этого параллелограмма.
- Он направлен так, что векторы и образуют правую тройку векторов.
Векторное произведение векторов и обозначается символом . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
Векторное произведение обладает следующими свойствами:
- Из определения следует, что
длина векторного произведения численно равна площади параллелограмма,
построенного на векторах, и, следовательно, находится по формуле:
.
Таким образом, и .
- При перестановке
сомножителей векторное произведение меняет свой знак .
Действительно из определения векторного произведения следует, что векторы и имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы и являются противоположными векторами и поэтому .
- Скалярный множитель можно
выносить за знак векторного произведения, т.е. для
любого числа λ и любых векторов
.
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае . Тогда по определению векторного произведения
Вектор перпендикулярен векторам и . Вектор также векторам и , т.к. векторы и , и лежат в одной плоскости. Следовательно, векторы и коллинеарны. Очевидно, что направления их также совпадают. Т. к. , и следовательно, , то .
Поэтому .
Аналогично проводится доказательство для случая λ < 0.
- Для любых векторов имеет место
равенство
.
Примем без доказательства.
- Векторное произведение двух
векторов равно нулевому вектору тогда и только тогда, когда один из
сомножителей равен нулю или векторы коллинеарны.
Действительно, если векторы коллинеарны, то , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В частности .
Примеры.
- Раскрыть скобки
.
- Найти площадь треугольника,
построенного на векторах и , если известно, что и .
.
Найдем .
.
Можно показать, что если и , то координаты векторного произведения векторов и находятся по формуле:
.
Примеры.
- Найти векторное произведение векторов и .
.
- Найти площадь , если A(2; 3; 1), B(-1; -2; 0), C(-3; 0; 1).
- Даны векторы . Найти параметры n, p, q если известно, что векторы и коллинеарны, а
векторы и ортогональны.
Так как векторы и коллинеарны, то . Векторы и ортогональны, поэтому . Итак, получили систему уравнений
Векторы | ЕГЭ по математике (профильной)
Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.
Вектор с началом в точке A и концом в точке B обозначают ${(АВ)}↖{→}$ или строчной (маленькой) буквой, например ${а}↖{→}$
Любая точка плоскости является вектором. В этом случае вектор называется нулевым.
Модуль (длину) вектора обозначают $|АВ|↖{→}$.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.
Векторы называются равными, если они сонаправлены и их длины равны.
Сумма векторов — это вектор, который можно получить двумя способами.
- Правило треугольника (А)
- Правило параллелограмма (Б)
Для любых векторов $a↖{→}, b↖{→}, c↖{→}$ справедливы равенства:
- $a↖{→}+b↖{→}=b↖{→}+a↖{→}$(переместительный закон)
- $(a↖{→}+b↖{→})+c↖{→}=a↖{→}+(b↖{→}+c↖{→})$ (сочетательный закон)
Разность векторов тоже можно получить двумя способами:
Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.
Для любых $a↖{→}$ и $b↖{→}$ справедливо равенство $a↖{→}-b↖{→}=a↖{→}+({-b}↖{→})$
Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖{→}⋅b↖{→}=|a↖{→}|·|b↖{→}|·cosα$
Ненулевые векторы $a↖{→}$ и $b↖{→}$ перпендикулярны, если их произведение равно нулю.2}}$
Найдите угол между векторами $a↖{→}$ и $b↖{→}$
Решение:
- Сначала нужно найти координаты векторов $a↖{→}$ {2-0;6-0} $b↖{→}${8-0;4-0}
- Найдем скалярное произведение векторов $a↖{→}·b↖{→} = 2·8+6·4=16+24=40$
- Найдем длины каждого вектора $|a↖{→}|= √{4+36}=√{40}; |b↖{→}|=√{64+16}=√{80}$
- Найдем косинус угла между векторами $cosα={40}/{√{40}·√{80}}={40}/{√{40·40·2}}={1}/{√2}={√2}/{2}$
- Найдем угол $α=arccos{√2}/{2}=45$
Ответ: 45
Сравнение двух векторов
Математика и естественные науки были изобретены людьми для описания и понять мир вокруг нас. Мы наблюдаем, что есть некоторые количества и процессы в наш мир, который зависит от направления , в котором они происходят, и есть некоторые количества, которые не зависят по направлению. Математики и ученые называют количество которое зависит от направления , вектор, величина . Количество которая не зависит от направления, называется скалярной величиной .А векторная величина имеет две характеристики: звездной величины и направление . При сравнении две векторные величины одного типа, необходимо сравнить обе величина и направление.
На этом слайде мы показываем три примера, в которых два вектора по сравнению. На рисунках векторы обычно обозначаются стрелкой. Длина стрелки указывает величину и кончик стрелки указывает направление.Вектор помечены алфавитным букву с чертой сверху, чтобы отличить ее от скаляра. Наши шрифты для веб-печати не позволяют использовать эту нотацию, поэтому мы будем использовать жирная буква для вектора. Мы будем сравнивать два вектора: и . и b . Это могут быть силы, скорости или ускорения; это не имеет значения.
Пример №1: У нас есть два вектора с одинаковым направлением, но величины (или длины векторов) разные.Вектор а не равно вектору b в этом примере. Этот пример кажется довольно просто, потому что то же правило применяется для скаляров; если величина разная, количества не равны. Объект вес 50 фунтов не равен объекту весом 25 фунтов.
Пример №2: Этот пример немного сложнее. В этом случае у нас есть два вектора с одинаковой величины, но направления разные. Вектор а не равно вектору b в этом примере.Если бы вектор был скорости, это говорит нам о том, что автомобиль, движущийся на 45 миль в час на северо-восток окажется в другом месте, чем другая машина, также едущая со скоростью 45 миль в час прямо на восток. За час они оба пройдут 45 миль, но локации будет иначе. Через два часа они будут еще дальше друг от друга.
Пример № 3: В этом примере у нас есть два вектора одинаковой длины и равное направление. Вектор равен вектору b . Чтобы два вектора были равны, они должны иметь как величину, так и направления равны.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
эквивалентных векторов | векторов, величины, направления
Эквивалентных векторов: Когда два вектора имеют одинаковую величину и направление, такие векторы называются векторами. {2 } $a = $ \ pm $ 3
Практика на эквивалентных векторах
1) Учитывая, что двумя конечными точками двух векторов являются A (-1, 3), B (2, 4) и C (1, -2), D (4, -1).Докажите, что $ \ left \ | \ vec {AB} \ right \ | $ и $ \ left \ | \ vec {CD} \ right \ | $ — векторы равны?2) Учитывая, что две конечные точки двух векторов — это P (-1, 4), Q (5, 2) и R (1, -2), S (4, -5). Проверяем, совпадают ли два вектора $ \ left \ | \ vec {PQ} \ right \ | $ и $ \ left \ | \ vec {RS} \ right \ | $ равны векторам? 11 класс по математике
Дом
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
линейная алгебра — Как лучше всего узнать, равны ли векторы?
линейная алгебра — как лучше всего узнать, равны ли векторы? — Обмен математическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 13к раз
$ \ begingroup $Может быть, это глупый вопрос, но когда я начал думать об этом, я начал чувствовать себя неуверенно.Вопрос в том, как лучше всего узнать, равны ли векторы или, точнее, собственные векторы? Я хочу сравнить два разных метода, которые генерируют собственные значения и собственные векторы, и я хочу показать, что полученные мной собственные векторы более или менее равны. Я знаю, что могу сравнить норму векторов и посмотреть, равны ли они друг другу, но действительно ли это говорит о том, что равны? У них тоже есть направление! Мои собственные векторы содержат много элементов, поэтому я не могу поставить их рядом друг с другом и сказать: «Смотри! Они равны!».Как лучше всего определить, равны ли два собственных вектора?
Создан 11 мая 2015, 18:49.
Джамилла14311 золотой знак11 серебряный знак44 бронзовых знака
$ \ endgroup $ 3 $ \ begingroup $Вы можете вычислить скалярное произведение двух векторов, и если они параллельны (в одном направлении), их скалярное произведение будет равно произведению их индивидуальных норм.Затем вы можете проверить нормы и посмотреть, равны ли и (одинаковые величины).
Создан 11 мая 2015, в 19:04.
животное2,85611 золотых знаков88 серебряных знаков1212 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Два вектора равны тогда и только тогда, когда все его компоненты равны.
Итак, (1,2,3) равно (1,2,3). Но (1,2,3) не
равно (1, 40, 3), поскольку 2-е компоненты различны.
Создан 11 мая ’15 в 18: 512015-05-11 18:51
peter.petrovpeter.petrov10.5k11 золотых знаков1515 серебряных знаков2727 бронзовых знаков
$ \ endgroup $ 4 $ \ begingroup $Один из способов сделать это — взять покомпонентную разницу между векторами и затем проверить, равен ли результирующий вектор вектору $ 0 $.
Этот метод позволяет легче «увидеть» одинаковые векторы. Например, гораздо проще подтвердить $$ (0,0,123) \ ne \ vec {0} $$ вместо $$ (18921049890,128433,352983620) \ ne (18921049890,128433,340593290) $$
Создан 11 мая 2015, 16: 002015-05-11 19:00
Питер ВулфиттПитер Вулфитт20.4k66 золотых знаков4848 серебряных знаков8484 бронзовых знака
$ \ endgroup $ 2 $ \ begingroup $Норма мало что вам скажет, потому что, если $ v $ является собственным вектором, то он является любым, кратным $ v $.
Что вы можете сделать, так это сначала нормализовать все ваши векторы до одинаковой длины. Затем вы можете проверить норму разности двух векторов. Поскольку два вектора равны тогда и только тогда, когда их разность равна $ 0 $, а норма вектора равна $ 0 $ тогда и только тогда, когда вектор равен $ 0 $.
Если у вас есть вырожденные собственные значения, то соответствующие собственные векторы будут охватывать линейное подпространство. Затем вам нужно проверить, совпадают ли подпространства, охватываемые собственными векторами, найденными двумя разными методами.
Создан 11 мая 2015, 18:56.
Андреа Андреа2,1551111 серебряных знаков2626 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Подобно ответу Питера выше, мы должны проверить, что каждый компонент равен своему эквиваленту в другом векторе.Если ваши векторы являются алгебраическими, а не числовыми, тогда, если одно изменение переменных, повторная параметризация или другое преобразование приведет к переходу всех элементов из одного вектора в другой, тогда они могут рассматриваться как равные или связанные при данном преобразовании.
Создан 11 мая 2015, 16: 002015-05-11 19:00
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. + \,: \, \ mathbf {u} = \ lambda \ mathbf {v} \ iff \ hat {\ mathbf {u}} = \ hat {\ mathbf {v}}, \ text {where} \ mathbf {u}, \ mathbf {v} \ ne \ textbf {0} $$
$ «\ implies» $ Пусть $ \ mathbf {u} = \ | \ mathbf {u} \ | \ hat {\ mathbf {u}} $ и $ \ mathbf {v} = \ | \ mathbf {v} \ | \ hat {\ mathbf {v}} $.+ \,: \, \ | \ mathbf {u} \ | \ hat {\ mathbf {u}} = \ lambda \ | \ mathbf {v} \ | \ hat {\ mathbf {v}} \ iff \ hat {\ mathbf {u}} = \ dfrac {\ lambda \ | \ mathbf {v} \ |} {\ | \ mathbf {u} \ |} \ hat { \ mathbf {v}} $$ Определите $ \ lambda ‘= \ dfrac {\ lambda \ | \ mathbf {v} \ |} {\ | \ mathbf {u} \ |} $. Таким образом, $ \ hat {\ mathbf {u}} = \ lambda ‘\ hat {\ mathbf {v}} $, поэтому векторы $ \ hat {\ mathbf {u}}, \ hat {\ mathbf {v} } $ либо параллельны, либо антипараллельны, в зависимости от знака $ \ lambda ‘$, который мы проанализируем: $ \ text {sgn} (\ lambda’) = \ text {sgn} \ left (\ dfrac {\ lambda \ | \ mathbf {v} \ |} {\ | \ mathbf {u} \ |} \ right) = \ text {sgn} \ left (\ dfrac {\ | \ mathbf {v} \ |} {\ | \ mathbf {u} \ |} \ right), \: \ lambda> 0 $.Теперь, я думаю, это просто вопрос соглашения: если кто-то решит работать с тем фактом, что модуль вектора всегда положителен и что ориентация единичного вектора совпадает с ориентацией самого вектора (который, я думаю, является наиболее широко используемое соглашение), то утверждение действительно верно (потому что это означает, что $ \ hat {\ mathbf {u}} $ и $ \ hat {\ mathbf {v}} $ параллельны — и поскольку они являются единичными векторами , их величина составляет $ 1 $, поэтому они фактически совпадают).
$ «\: \ Longleftarrow \:» $ Опять же, пусть $ \ mathbf {u} = \ | \ mathbf {u} \ | \ hat {\ mathbf {u}} $ и $ \ mathbf {v} = \ | \ mathbf {v} \ | \ hat {\ mathbf {v}} $.Тогда утверждение $ \ hat {\ mathbf {u}} = \ hat {\ mathbf {v}} $ эквивалентно $$ \ dfrac {\ mathbf {u}} {\ | \ mathbf {u} \ |} = \ dfrac {\ mathbf {v}} {\ | \ mathbf {v} \ |} \ iff \ mathbf {u} = \ dfrac {\ | \ mathbf {u} \ |} {\ | \ mathbf {v} \ |} \ mathbf {v} = \ lambda \ mathbf {v}, \ text {where} \ lambda = \ dfrac { \ | \ mathbf {u} \ |} {\ | \ mathbf {v} \ |} $$ Если использовать вышеупомянутое соглашение, тогда $ \ lambda> 0 $, значит, мы завершили доказательство.
Свойства векторов | Векторы и скаляры
Векторы — это математические объекты, и теперь мы изучим некоторые из их математических свойств.
Если два вектора имеют одинаковую величину (размер) и в одном направлении, то мы называем их равными друг другу. Например, если у нас есть две силы, \ (\ vec {F_ {1}} = \ text {20} \ text {N} \) в восходящем направлении и \ (\ vec {F_ {2}} = \ text {20} \ text {N} \) в направлении вверх , тогда мы можем сказать, что \ (\ vec {F_ {1}} = \ vec {F_ {2}} \).
Так же, как скаляры, которые могут иметь положительные или отрицательные значения, векторы также могут быть положительными или отрицательными. Отрицательный вектор — это вектор, который указывает в направлении , противоположном , относительно опорного положительного направления .Например, если в конкретной ситуации мы определяем направление вверх как опорное положительное направление, тогда сила \ (\ vec {F_ {1}} = \ text {30} \ text {N} \) вниз будет быть отрицательным вектором и также может быть записано как \ (\ vec {F_ {1}} = — \ text {30} \ text {N} \). В этом случае отрицательный знак (\ (- \)) указывает, что направление \ (\ vec {F_ {1}} \) противоположно направлению опорного положительного направления.
Как и скаляры, векторы также можно складывать и вычитать.Мы исследуем, как это сделать дальше.
Сложение и вычитание векторов (ESAGO)
Сложение векторов
При добавлении векторов нам нужно учесть и их величины, и направления.
Например, представьте себе следующее. Вы с другом пытаетесь переместить тяжелую коробку. Вы стоите позади него и с силой толкаете вперед \ (\ vec {{F} _ {1}} \), а ваш друг стоит впереди и тянет его к себе с силой \ (\ vec {{F} _ {2 }} \).Две силы действуют в направлении в одном и том же направлении (т. Е. Вперед), поэтому общая сила, действующая на коробку, составляет:
Понять концепцию сложения векторов очень легко через действие, использующее вектор смещения .
Смещение — это вектор, который описывает изменение положения объекта. Это вектор, который указывает от начального положения к конечному положению.
Добавление векторов
Материалы
малярная лента
Метод
Приклейте полоску малярной ленты горизонтально через пол.Это будет вашей отправной точкой.
Задача 1 :
Сделайте \ (\ text {2} \) шагов в прямом направлении. Используйте кусок малярной ленты, чтобы отметить конечную точку и обозначить ее A . Затем сделайте еще \ (\ text {3} \) шаг в прямом направлении. Используйте малярную ленту, чтобы отметить конечное положение как B . Убедитесь, что вы стараетесь, чтобы ваши шаги были одинаковой длины!
Задача 2 :
Вернитесь на исходную линию. Теперь сделайте \ (\ text {3} \) шагов вперед.Используйте кусок малярной ленты, чтобы отметить конечную точку и обозначить ее B . Затем сделайте еще \ (\ text {2} \) шаг вперед и используйте новый кусок малярной ленты, чтобы отметить ваше конечное положение как A .
Обсуждение
Что вы заметили?
В задаче 1 первые \ (\ text {2} \) шаги вперед представляют вектор смещения, а вторые шаги \ (\ text {3} \) вперед также образуют вектор смещения. Если бы мы не остановились после первых \ (\ text {2} \) шагов, мы бы сделали \ (\ text {5} \) шагов в прямом направлении в целом.Следовательно, если мы добавим векторы смещения для шагов \ (\ text {2} \) и \ (\ text {3} \) шагов, мы должны получить в общей сложности \ (\ text {5} \) шагов в прямом направлении. направление.
Неважно, делаете ли вы \ (\ text {3} \) шаг вперед, а затем \ (\ text {2} \) шаг вперед, или два шага, за которыми следует еще один \ (\ text {3} \) шаг вперед . Ваша финальная позиция такая же! Порядок добавления значения не имеет!
Мы можем представить сложение векторов графически, основываясь на вышеизложенном действии.Нарисуйте вектор для первых двух шагов вперед, а затем вектор для следующих трех шагов вперед.
Мы добавляем второй вектор в конец первого вектора, так как это то место, где мы сейчас находимся после того, как первый вектор сработал. Тогда вектор от хвоста первого вектора (начальная точка) до головы второго вектора (конечная точка) является суммой векторов.
Как вы можете убедиться, порядок, в котором вы добавляете векторы, не имеет значения. В приведенном выше примере, если вы решили сначала сделать \ (\ text {3} \) шаг вперед, а затем еще один \ (\ text {2} \) шаг вперед, конечный результат все равно будет \ (\ text {5} \) шагает вперед.
Вычитание векторов
Вернемся к проблеме с тяжелым ящиком, который вы и ваш друг пытаетесь переместить. Если вы сначала не связались должным образом, вы оба можете подумать, что вам следует двигаться в своем собственном направлении! Представьте, что вы стоите за ящиком и тянете его к себе с силой \ (\ vec {{F} _ {1}} \), а ваш друг стоит перед ящиком и с силой тянет его к себе \ (\ vec {{F} _ {2}} \). В этом случае две силы действуют в противоположных направлениях .Если мы определим направление, в котором ваш друг тянет, как положительное , тогда сила, которую вы прикладываете, должна быть отрицательной , поскольку она направлена в противоположном направлении. Мы можем записать общую силу, прилагаемую к коробке, как сумму отдельных сил:
На самом деле вы вычли два вектора! Это то же самое, что и сложение двух векторов, имеющих противоположные направления.
Как и раньше, мы можем хорошо проиллюстрировать векторное вычитание, используя векторы смещения.Если вы сделаете \ (\ text {5} \) шагов вперед, а затем вычтите \ (\ text {3} \) шагов вперед, у вас останется только два шага вперед:
Что вы физически сделали, чтобы вычесть \ (\ text {3} \) шагов? Изначально вы сделали \ (\ text {5} \) шагов вперед, но затем вы сделали \ (\ text {3} \) шаги назад , чтобы вернуться назад, сделав только \ (\ text {2} \) шаги вперед. Это обратное смещение представлено стрелкой, указывающей влево (назад) длиной \ (\ text {3} \). Чистый результат сложения этих двух векторов — \ (\ text {2} \) шагов вперед:
Таким образом, вычитание одного вектора из другого аналогично добавлению вектора в противоположном направлении (т.е. вычитание \ (\ text {3} \) шагов вперед аналогично добавлению \ (\ text {3} \) шагов назад).
Вычитание одного вектора из другого аналогично добавлению вектора в противоположном направлении.
Результирующий вектор
Окончательная величина, полученная при сложении или вычитании векторов, называется результирующим вектором . Другими словами, отдельные векторы могут быть заменены результирующими — общий эффект тот же.
- Результирующий вектор
Результирующий вектор — это единственный вектор, действие которого такое же, как у отдельных векторов, действующих вместе.
Мы можем проиллюстрировать концепцию результирующего вектора, рассмотрев две наши ситуации при использовании сил для перемещения тяжелого ящика. В первом случае (слева) вы и ваш друг прикладываете силы в одном направлении. Результирующая сила будет суммой двух ваших сил, приложенных в этом направлении. Во втором случае (справа) силы действуют в противоположных направлениях. Результирующий вектор снова будет суммой двух приложенных вами сил, однако после выбора положительного направления одна сила будет положительной, а другая отрицательной, и знак результирующей силы будет зависеть только от того, какое направление вы выбрали как положительное.Для наглядности посмотрите схемы ниже.
Силы действуют в том же направлении
(положительное направление вправо)
Силы действуют в противоположных направлениях
(положительное направление вправо)
Существует специальное имя для вектора, который имеет ту же величину, что и результирующий вектор, но направление противоположно направлению : равновесный . Если вы сложите результирующий вектор и равновесные векторы вместе, ответ всегда будет равен нулю, потому что равновесие отменяет результирующий.
- Уравновешивающий
Равновесие — это вектор, который имеет ту же величину , , но направление противоположно результирующему вектору.
Если вы обратитесь к изображениям тяжелого ящика ранее, уравновешивающие силы для двух ситуаций будут выглядеть так:
Векторов
Если наша цель — описать и понять движение, тогда просто движение вверх и вниз по линии не хватит.Движение в реальном мире происходит в трех измерениях. Мы Нужен способ описания движения сложный, как у пчелы или игрушечного вертолета. Мы делаем это с помощью векторов.Вначале я хочу, чтобы вы подумали о векторах как о геометрических объектах. Модель для все векторы — смещения. Что-то начинается в одном месте и заканчивается в другом. Один можно протянуть эластичный шнур между двумя точками в пространстве и отметить, на каком конце пункт назначения маленькой бумажной стрелкой.Как видите, у этого есть два аспекта. смещение, которое мы называем вектором. Во-первых, у него есть длина или величина. во-вторых у него есть направление: что-то связано с его углом. Первый пункт нашей повестки дня описание векторов состоит в том, чтобы выяснить, когда два вектора равны.
Давайте совершим еще одно небольшое путешествие такой же длины, как и первое, но взлетим в другом. направление. Если вы натянете шнур между начальной и конечной точками, вы можете визуализируйте два вектора.Они равны? Совершите еще одну поездку в том же направлении, что и первый, а теперь идем дальше. Это еще один вектор. Равно ли оно первому?
Когда векторы равны?
В обоих случаях, когда векторы имеют либо разные направления, либо разную длину, они не равны. Точно так же, если и направление, и длина различны, они не равны. Два вектора равны только тогда, когда оба направления и длины одинаковы. Два вектора могут быть равными, но в разных местах.Векторы, представленные параллельными линиями, которые имеют одинаковые длина и направление равны.Как складывать векторы
Когда что-то совершает одно смещение, затем другое, общее смещение равно сумма двух отдельных. Пусть a представляет первую поездку, а b — вторую поездку. В общее количество поездок определяется путем выстраивания векторов, представляющих поездки от кончика к хвосту. Положите хвост второй поверх хвоста первого.За полное смещение принимается вектор от хвоста первого до кончика второго. Этот способ добавления векторов возникает естественно, когда мы говорим о смещениях. Иногда другой вектор величины, такие как силы, должны быть добавлены. Тогда часто бывает необходимо переместить один вектор так, чтобы его хвост совпадал с хвостом другого, потому что диаграммы сил обычно показывают силы со всеми своими хвостами вместе на объекте, к которому приложена сила. Когда вектор не забудьте сохранить его длину и направление одинаковыми.Коммутативность сложения
Сумма векторов может быть записана как c = a + b . Это означает, что хвост b находится на кончик a и хвост c находится на хвосте a , а кончик c находится на кончике b . Это также можно добавить a к b . Результат такой же, как при добавлении b к a ? Если смещение — это наш вектор модели, то результат будет одним и тем же независимо от того, какое путешествие будет выполнено первым.Итак, мы потребует, чтобы векторы давали одинаковую сумму независимо от того, что добавляется первым. a + b = b + a . Это свойство называется коммутативностью.Не все количества, которым можно назначить размер и направление, обладают этим свойством, и таким образом, эти некоммутативные величины не могут быть векторами. (Это клуб с высокие стандарты!) Например вращения вокруг оси имеют размер, угол поворота, и направление, направление оси вращения.Попробуйте сначала повернуть книгу на 90 ° вокруг вертикальная ось, а затем 90 ° вокруг горизонтальной оси влево-вправо. Обратный порядок эти два поворота, и вы получите книгу в другом положении. В случае вращения, a + b не равно b + a .
На бумаге легко нарисовать векторы, чтобы визуализировать процесс сложения векторов.
Также следует попытаться представить векторы в трех измерениях. Все, что мы говорим о
двумерные векторы, могут быть расширены до трех измерений без особых усилий
трудность.Представьте себе вертолет, выходящий из подвески. Он подруливает 100 м N, затем меняет
направление, такси 200 м E, затем поднимается на 300 м. Общее смещение
Вертолет получается путем сложения всех трех векторов кончик к хвосту, как мы это делаем в двух измерениях.
Отрицательный вектор и вычитание
Всегда бывает, что человек, который сначала отправляется по делу, затем на полпути к цели. пункт назначения передумал и вернулся домой. Два смещения, наружу и назад сложить до нуля.Второе смещение можно записать как отрицательное значение во-первых — он такой же величины, но противоположного направления. Первый этап маршрута — — , второй — и . Следовательно, a + (- a ) = 0. После определения отрицательного значения вектора происходит процесс вычитания.
естественно. Чтобы вычесть b из a , просто найдите отрицательное значение b , затем добавьте это к a .
Другой способ найти a b — соединить хвосты a и b вместе и нарисовать вектор
от наконечника b до наконечника a .Этот метод означает поиск вектора, который вы добавляете к b , чтобы получить a. (Это a = b + ( a — b ))
Попробуйте оба метода вычитания, и вы увидите, что они дают вектор с тем же
величина и направление. (Хотя после постройки они будут в разных местах,
но это не имеет значения.) Вы можете выбрать любой метод вычитания, который вам кажется
чтобы иметь больше смысла для вас.
Умножение на скаляр
Иногда векторы умножаются или делятся на коэффициент масштабирования.Например, если один растягивает эластичный шнур, представляющий вектор, вдвое больше его длины, сохраняя его направление то же самое, то исходный вектор умножается на два. Точно так же, если позволить ему уменьшить до половину своей длины он делится на два или умножается на половину. как вам нравится. Обычные числа называются скалярами, чтобы отличать их от векторов. Ты был используя скаляры, так как вы научились считать.
Существуют также операции с двумя векторами, называемые умножением векторов.Эти мы постараюсь избежать в этом курсе, но вам может потребоваться изучить их, если вы пойдете дальше курсы физики или математики.
Величины, такие как смещение, скорость, ускорение и сила, являются векторами. Масса и время являются скалярами, такими как температура, влажность и энергия.
Векторы скорости и ускорения
Смещение — это наш вектор-прототип. Скорость определяется смещением на разделив его на промежуток времени. Результатом деления вектора на скаляр является вектор.Точно так же деление вектора, представляющего разность скоростей, на временной интервал дает вектор — ускорение. Масса, скаляр, умножающее ускорение, вектор, дает силу, другая векторная величина.Чтобы увидеть, как скорости могут складываться как векторы, я использую игрушечный трактор. Он сидит на длинном куске мясная бумага, покрывающая стол. Допустим, длина стола ориентирована с востока на запад. Ширина стола около 1 м. Если я поставлю его поперек стола на север, он закроет 1 м дистанции за 10 секунд.Это скорость 0,1 м / с на север. Во второй раз я позволил трактор пересекает стол, я тяну бумагу мясника со скоростью около 0,05 м / с, восток, половина скорость трактора и перпендикулярно его курсу. На этот раз трактор пересекает бумага прямо, но, относительно стола, пересекает под углом. Скорость трактора относительно таблицы уже не 0,1 м / с, а векторная сумма 0,1 м / с, север и 0,5 м / с, вост. В сумме, как показано на диаграмме, получается 0.{-1} \ left (\ frac {v _ {\ rm trac}} {v _ {\ rm paper}} \ right) $$
Навигация
Следующая проблема — узнать, как достичь желаемого направления, когда крест дует ветер. Например, мы хотим лететь на самолете прямо на север, но дует поперечный ветер с востока на запад. В каком направлении должен лететь самолет так что в конечном итоге он едет на север? Допустим, дует боковой ветер со скоростью 40 км / ч и что самолет движется со скоростью 100 км / ч по воздуху.Задайте задачу графически как следующим образом:- Проведите прямую линию с севера на юг вдоль желаемого направления.
- Нарисуйте вектор в масштабе, представляющий скорость ветра: 40 км / ч в западном направлении кончиком.
на линии север-юг.
- Скорость самолета составляет 100 км / ч, но мы не знаем, в каком направлении. Поместите вектор
кончиком на хвосте вектора скорости ветра и найдите такой угол, чтобы хвост
Вектор скорости самолета находится на линии север-юг.{-1} \ left (\ frac {v _ {\ rm wind}} {v _ {\ rm airplane}} \ right) $$
В этом случае курс, позволяющий самолету идти строго на север, составляет 23,6 ° к востоку от севера.
а скорость самолета относительно земли — 92 км / ч.
Разгон
Ускорение также является вектором, потому что это разница двух скоростей (вектор). делится на временной интервал (скаляр). Результат — вектор. Закон Ньютона гласит, что сила — это масса, умноженная на ускорение. Масса — скаляр, ускорение — вектор; следовательно, сила тоже вектор.Что удивительно в векторах ускорения и силы, так это то, что они не обязательно указать в направлении движения. Мы узнаем это, когда поговорим о криволинейных движение, и в частности движение по кругу.
Узнайте об эквивалентных векторах | Chegg.com
Когда даны два вектора, можно легко определить их направление, посмотрев на них. Но точную величину угадать не удастся. Итак, необходимо математически найти величину данных векторов.Величину вектора можно найти с помощью формулы расстояния. Если A (x1, y1) A \ left ({{x} _ {1}}, \ text {} \! \! ~ \! \! \ Text {} y {{} _ {1} } \ right) A (x1, y1) и B (x2, y2) B \ left ({{x} _ {2}}, \ text {} \! \! ~ \! \! \ text {} y {{} _ {2}} \ right) B (x2, y2), начальная и конечная точки вектора AB → \ overrightarrow {AB} AB, затем величина AB → \ overrightarrow {AB} AB задается следующим образом:
∥AB → ∥ = (x2 − x1) 2+ (y2 − y1) 2 \ left \ | \ overrightarrow {\ text {AB}} \ right \ | = \ sqrt {{{\ left ({{x} _ {2}} — {{x} _ {1}} \ right)} ^ {2}} + {{\ left ({{y} _ {2}} — {{y} _ {1}} \ right)} ^ {2}}} ∥∥∥∥ AB∥∥∥∥ = (x2 −x1) 2+ (y2 −y1) 2
Рассмотрим пример.




 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору.
 е. если .
е. если .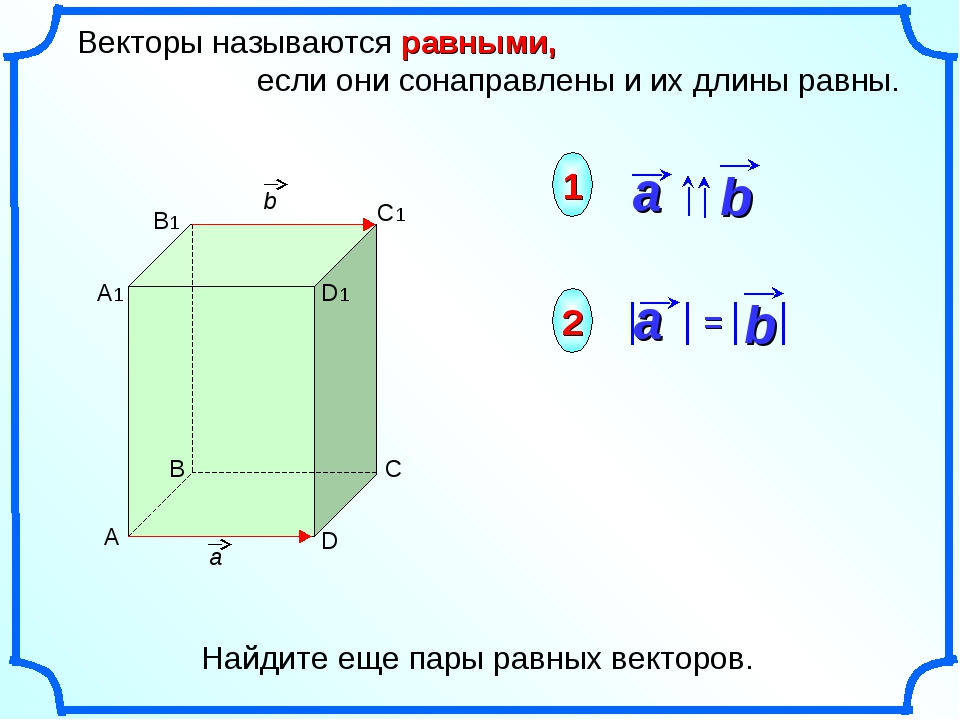
 Ограничимся случаем, когда λ > 0. В этом случае
угол между векторами и совпадает с
углом между векторами и , .
Ограничимся случаем, когда λ > 0. В этом случае
угол между векторами и совпадает с
углом между векторами и , .