 Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лекция 1. Системы счисления 1. История возникновения систем счисления. 2. Позиционные и непозиционные системы счисления. 3. Десятичная система счисления, запись чисел в ней. 4. Разряды
Человеку постоянно приходится иметь дело с числами, поэтому нужно уметь правильно называть и записывать любое число, производить действия над числами. Как правило, все с этим успешно справляются. Помогает здесь способ записи чисел, который в настоящее время используется повсеместно и носит название десятичной системы счисления. Изучение этой системы начинается в начальных классах, и , конечно, учителю нужны определенные знания в этой области. Он должен знать различные способы записи чисел, алгоритмы арифметических действий и их обоснование. Материал данной лекции дает тот минимум, без которого невозможно разобраться с различными методическими подходами к обучению младших школьников способам записи чисел и выполнению над ними действий. История возникновения систем счисления. Понятие числа возникло в глубокой древности. Тогда же появилась необходимость в названии и записи чисел. Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления. Простейшая система записи натуральных чисел требует лишь одной цифры, например «палочки» (или зарубки на дереве, как у первобытного человека, или узелка на веревке, как у индейцев Америки), которая изображает единицу. Повторяя этот знак, можно записать любое число: каждое число n записывается просто n «палочками». В такой системе счисления удобно выполнять арифметические действия. Но подобный способ записи очень не экономичен и для больших чисел неизбежно приводит к ошибкам в счете. Поэтому со временем возникли иные, более экономичные и удобные способы записи чисел. Рассмотрим некоторые из них. В Древней Греции была распространена так называемая аттическая нумерация. Числа 1, 2, 3, 4 обозначались черточками:
Число 5 записывалось знаком Г (древнее начертание буквы «пи», с которой начинается слово «пенте» — пять). Числа 6, 7, 8, 9 обозначались так:
Число 10 обозначалось Δ (начальной буквой слова «дека» — десять). Числа 100, 1000 и 10 000 обозначались Н, Х, М – начальными буквами соответствующих слов.
Другие числа записывались различными комбинациями этих знаков. В третьем веке до нашей эры аттическая нумерация была вытеснена так называемой
Числа 10, 20, 30, 40, 50, 60, 70, 80, 90 – следующими девятью буквами: κ (каппа), λ (ламбда), μ (мю), ν (ню), ξ (кси), ο (омикрон), π (пи), с (копа).
Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 – последними девятью буквами греческого алфавита. Алфавитную нумерацию, подобную древнегреческой, имели в древности евреи, арабы и многие другие народы Ближнего Востока. У какого народа она возникла впервые неизвестно. В Древнем Риме в качестве «ключевых» использовались числа 1, 5, 10, 50, 100, 500 и 1000. Они обозначались соответственно буквами I, V, X, L, C, D и М. Все целые числа (до 5000) записывались с помощью повторения выше приведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей: VI = 6, т.е. 5 + 1; IV = 4, т.е. 5 – 1; Например: XXVIII = 28, XXXIX = 39, CCCXCVII = 397, MDCCCXVIII = 1818. Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Однако римская нумерация сохранилась до настоящего времени. Ее используют для обозначения юбилейных дат, наименования конференций, глав в книгах и т.д. На Руси в старину цифры обозначались буквами. Для указания того, что знак является не буквой, а цифрой, сверху над ними ставился специальный знак, называемый «титло». Первые девять цифр записывались так:
Десятки обозначались так:
Сотни обозначались так:
Тысячи обозначались теми же буквами с «титлами», что и первые девять цифр, но у них слева ставился знак «≠»: ≠А = 1000, ≠В = 2000, ≠Е = 5000.
  Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками: Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками:
= 10 000, = 20 000, = 80 000.
Отсюда произошло выражение «Тьма народу», т.е. очень много народу. Сотни тысяч назывались «легионами», их обозначали, обводя знаки единиц кружками из точек:
= 100 000, = 200 000, = 800 000. Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых:
= 1 000 000, = 2 000 000.
Десятки миллионов назывались «воронами» или «вранами» и их обозначали, обводя знаки единиц кружками из крестиков или ставя по обе стороны букву К: Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение – над буквой и под буквой ставились квадратные скобки:
Иероглифы жителей Древнего Вавилона составлялись из узких вертикальных и горизонтальных клинышков, эти два значка использовались и для записи чисел. Один вертикальный клинышек обозначал единицу, горизонтальный – десяток. В Древнем Вавилоне считали группами по 60 единиц. Например, число 185 представлялось как 3 раза по 60 и еще 5. Записывалось такое число с помощью всего двух знаков, один из которых обозначал, сколько раз взято по 60, а другой — сколько взято единиц. О том, когда и как возникла у вавилонян шестидесятеричная система, существует много гипотез, но ни одна пока не доказана. Одна из гипотез, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывают с числом 60. Шестидесятеричная система, в некоторой степени, сохранилась до наших дней, например, в делении часа на 60 минут, а минуты — на 60 секунд и в аналогичной системе измерение углов: 1 градус равен 60 минутам, 1 минута – 60 секундам. Двоичной системой счисления пользовались при счете некоторые первобытные племена, она была известна еще древнекитайским математикам, но по настоящему развил и построил двоичную систему великий немецкий математик Лейбниц, видевший в ней олицетворение глубокой метафизической истины. Двоичной системой счисления пользуются некоторые (местные) культуры в Африке, Австралии и Южной Америке. Для изображения чисел в двоичной системе счисления требуется лишь две цифры: 0 и 1. По этой причине двоичную запись числа легко представить, пользуясь физическими элементами, которые имеют два различных устойчивых состояния. Именно это и послужило одной из важных причин широкого использования двоичной системы в современных электронных вычислительных машинах. Самой экономичной из всех систем счисления является троичная. Двоичная и равносильная ей, в смысле экономичности, четверичная системы, несколько уступают в этом отношении троичной, но превосходят все основные возможные системы. Если для записи чисел от 1 до 10 в десятичной системе требуется 90 различных состояний, а в двоичной – 60, то в троичной системе достаточно 57 состояний. Наиболее привычная ситуация, в которой проявляется необходимость троичного анализа, — это, пожалуй, взвешивание на чашечных весах. Здесь могут возникнуть три разных случая: либо одна из чашек перевесит другую, либо наоборот, либо же чашки уравновесят друг друга. Четверичной системой счисления пользуются, главным образом, индейские племена Южной Америки и индейцы юкки в Калифорнии, считающих на промежутках между пальцами. Пятеричная система счислениябыла распространена гораздо шире, чем все остальные. Индейцы племени таманакос в Южной Америке употребляют для обозначения числа 5 то же слово, что и для обозначения «всей руки». Слово «шесть» по-таманакски означает «один палец на другой руке», семь – «два пальца на другой руке» и т.д. для восьми и девяти. Десять называется «двумя руками». Желая назвать число от 11 до 14, таманакос протягивают вперед обе руки и считают: «один на ноге, два на ноге» и т.д. до тех пор, пока не доходят до 15 – «всей ноги». Затем следует «один на другой ноге» (число 16) и т.д. до 19. Число 20 по-таманакски означает «один индеец», 21 – «один на руке другого индейца». «Два индейца» означают 40, «три индейца» — 60. У жителей древней Явы и у ацтеков продолжительность недели составляла 5 дней. Некоторые историки считают, что римское число X (десять) составлено из двух римских пятерок V (одна из них перевернута), а число V в свою очередь возникло из стилизованного изображения человеческой руки. Широкое распространение имела в древности двенадцатеричная система счисления. Происхождение ее тоже связано со счетом на пальцах. А именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимают за единицу следующего разряда. Основное преимущество двенадцатеричной системы состоит в том, что ее основание делится без остатка на 2, 3 и 4. Сторонники двенадцатеричной системы появились еще в XVI веке. В более позднее время к их числу принадлежали столь выдающиеся люди, как Герберт Спенсер, Джон Квинси Адамс и Джордж Бернард Шоу. Существует даже американское двенадцатеричное общество, выпускающее два периодических издания: «Двенадцатеричный бюллетень» и «Руководство по двенадцатеричной системе». Всей «двенадцатеричников» общество снабжает специальной счетной линейкой, в которой в качестве основания используется 12. В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того, чтобы сказать «двенадцать», часть говорят «дюжина». Сохранился обычай считать многие предметы не десятками, а именно дюжинами, например, столовые приборы в сервизе (сервиз на 12 персон) или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе счисления – гросс – встречается теперь редко, но в торговой практике начала XX столетия оно бытовало и, еще сто лет назад, его можно было легко встретить. Например, в написанном в 1928 году стихотворении «Плюшкин» В.В. Маяковский, высмеивая мещан, скупающих подряд все нужное и ненужное, писал: ..Оглядев товаров россыпь, в жадности и в алчи укупил |
Двенадцатеричная система счисления — Википедия
Материал из Википедии — свободной энциклопедии
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Двенадцатеричная система счисления — позиционная система счисления с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а T (от англ. ten, десять) или D (от лат. decem, фр. dix, десять) или X (римское десять), а также E (от англ. eleven, одиннадцать) или O (от фр. onze, одиннадцать). Кроме того, на Западе иногда вместо A используют перевёрнутую двойку ( , U+218A ↊ turned digit two) и вместо B перевёрнутую тройку (
, U+218A ↊ turned digit two) и вместо B перевёрнутую тройку ( , U+218B ↋ turned digit three).
, U+218B ↋ turned digit three).
Число 12 могло бы быть очень удобным основанием системы счисления, так как оно делится нацело на 2, 3, 4 и 6, в то время как число 10 — основание десятичной системы счисления — делится нацело лишь на 2 и 5.
Двенадцатеричная система счисления возникла в древнем Шумере. Предполагается, что такая система возникала, исходя из количества фаланг четырёх пальцев руки (исключая большой) при подсчёте их большим пальцем той же руки.[1][2][3] Фаланги пальцев использовались как простейшие счёты (текущее состояние счёта засекалось большим пальцем), вместо загибания пальцев, принятого в европейской цивилизации. Некоторые народы Нигерии и Тибета используют двенадцатеричную систему счисления в настоящее время.
Также существует гипотеза, что до 12 считали сидя, загибая не только 10 пальцев рук, но и 2 ноги. Хотя, возможно, такое случалось, когда европейцам приходилось сталкиваться с восточным двенадцатеричным счётом.
Двенадцатые доли часто встречались и в европейских системах мер. У римлян стандартной дробью была унция (1/12). 1 английский пенни (пенс) = 1⁄12 шиллинга, 1 дюйм = 1⁄12 фута и т. д.
Переход на двенадцатеричную систему счисления предлагался неоднократно. В XVIII веке её сторонником был знаменитый французский естествоиспытатель Бюффон. Во времена Великой французской революции была учреждена «Революционная комиссия по весам и мерам», которая длительный период рассматривала подобный проект, однако усилиями Лагранжа и других противников реформы дело удалось свернуть. В 1944 году было организовано «Американское двенадцатеричное общество» (англ. The Dozenal Society of America (DSA)), а в 1959 — «Английское двенадцатеричное общество» (англ. The Dozenal Society of Great Britain (DSGB)), объединившие активных сторонников одноимённой системы счисления. Однако главным аргументом против этого всегда служили огромные затраты и неизбежная путаница при переходе. [источник не указан 1504 дня]
 «Счёт дюжинами»
«Счёт дюжинами»Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия:
К удобствам двенадцатеричного счисления можно отнести большее (по сравнению с десятичной системой) количество делителей основания 12 — 2, 3, 4, 6. На практике двенадцатеричная система (в смешанном виде) осталась в часах.
Двенадцатеричная система счисления упоминается и в фантастической литературе:
- ↑ Nishikawa, Yoshiaki (2002), ヒマラヤの満月と十二進法 (The Full Moon in the Himalayas and the Duodecimal System), <http://www.kankyok.co.jp/nue/nue11/nue11_01.html>. Проверено 24 марта 2008. Архивная копия от 29 марта 2008 на Wayback Machine
- ↑ Ifrah, Georges (2000), The Universal History of Numbers: From prehistory to the invention of the computer., John Wiley and Sons, ISBN 0-471-39340-1
- ↑ Macey, Samuel L. The Dynamics of Progress: Time, Method, and Measure (англ.). — Atlanta, Georgia: University of Georgia Press (англ.)русск., 1989. — P. 92. — ISBN 978-0-8203-3796-8.
Шестнадцатеричная система счисления
Использует шестнадцать цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в их обычном смысле, а затем A=10, B=11 , C=12 , D=13 , E=14 , F=15 . Также использует символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа. Внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров. С другой стороны, в некоторых языках сохранились и следы использования этой системы счисления в прошлом.
BIN | OCT | DEC | HEX |
0 | 0 | 0 | 0 |
001 | 1 | 1 | 1 |
010 | 2 | 2 | 2 |
011 | 3 | 3 | 3 |
100 | 4 | 4 | 4 |
101 | 5 | 5 | 5 |
110 | 6 | 6 | 6 |
111 | 7 | 7 | 7 |
1 000 | 10 | 8 | 8 |
1 001 | 11 | 9 | 9 |
1 010 | 12 | 10 | A |
1 011 | 13 | 11 | B |
1 100 | 14 | 12 | C |
1 101 | 15 | 13 | D |
1 110 | 16 | 14 | E |
1 111 | 17 | 15 | F |
10 000 | 20 | 16 | 10 |
Перевод чисел Перевод чисел из двоичной системы в восьмеричную, шестнадцатеричную и обратно
Для перевода чисел из восьмеричной и шестнадцатеричной систем в двоичную существует простой способ: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) — для восьмеричной системы или тетрадой (четверкой цифр) — для шестнадцатеричной системы.
Переведем число 6238 в двоичную систему. Для этого каждую цифру заменим на ее перевод в двоичную систему. Каждое полученное число при необходимости дополним слева нулями до трех цифр. Эти нули называются незначащими.

Полученное число равно 110 010 0112.
Таким образом, 6238 = 110 010 0112.
Аналогично делаем для перевода из шестнадцатеричной системы в двоичную, но дополняя слева нулями до четырех цифр.
Переведем число A01F16 в двоичную систему:

Полученное число равно 1010 0000 0001 11112.
Значит, A01F16 = 1010 0000 0001 11112.
Для перевода двоичного числа в восьмеричное, его надо раз_ бить на группы по три цифры справа налево и заменить каждую группу одной восьмеричной цифрой.
Примеры
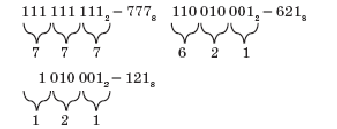
Аналогично, для перевода двоичного числа в шестнадцатеричное, нужно разбить число на группы по четыре цифры справа налево и заменить каждую группу одной шестнадцатеричной цифрой.
Примеры

Заметьте, что максимальное двоичное число, которое можно записать тремя цифрами — 111, и оно равно десятичному (или восьмеричному) числу 7. А максимальное двоичное число, которое можно записать четырьмя цифрами, — 1111, и оно равно десятичному числу 15 или шестнадцатеричному F.
Шестнадцатеричная система счисления — Википедия
Материал из Википедии — свободной энциклопедии
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Применение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика, например Turbo Basic, используют для указания шестнадцатеричных цифр сочетание «&h» или «&H» перед числом. Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 3A5 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
3A516 = 3·162+10·161+5·160== 3·256+10·16+5·1 = 768+160+5 = 93310
При переводе чисел, следует помнить, что в шестнадцатеричной системе счисления: A=10; B=11; C=12; D=13; E=14; F=15.
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведённой таблицы перевода.
Например:
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См. также
Ссылки
Шестнадцатеричная система счисления — это… Что такое Шестнадцатеричная система счисления?
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Применение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
В электронных калькуляторах
Б3-34 и ему подобные используют «-», «L», «C», «Г», «E» « » (space) на их экране.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·160+10·161+5·162= 3·1+10·16+5·256 = 3+160+1280 = 144310
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.
Например:
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См. также
Ссылки
Для чего нужна шестнадцатиричная система счисления
Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная система счисления.
 Системы счисления
Системы счисления
Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют десятичную систему счисления. Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.
 Понятие шестнадцатеричной системы
Понятие шестнадцатеричной системы
Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных – машинное слово – включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки латинского алфавита (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.
 Где применяется
Где применяется
Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности двоичных кодов. Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.
Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.
Шестнадцатиричная система счисления | Практическая электроника
В прошлой статье мы с Вами разбирали двоичную и двоично-десятичную систему счисления. С помощью калькулятора Windows мы переводили числа из двоичной системы в десятичную. Представьте себе, что нам надо перевести число из десятичной в двоичную систему счисления. Такое безобидное число, как 9999 в двоичной системе будет выглядеть уже как 10 0111 0000 1111. Не очень то и удобно, так ведь? С такими числами работает только компьютер и другие цифровые девайсы.
Системы счисления
Если подробнее вдаваться в компьютерные системы, то комп даже на знает, что такое единичка, а что такое ноль. Это для нас понятно, что единичка – это “ДА” , “ИСТИНА”, а ноль это – “НЕТ”, “ЛОЖЬ”. В компьютерах, микропроцессорах, микроконтроллерах да и во всех цифровых микросхемах используются другие понятия единицы и нуля. Напряжение есть и оно соответствует норме – это ЕДИНИЧКА, напряжение маленькое или его нет – это НОЛЬ. Именно так и оперируют цифровые микросхемы и вся сложнейшая цифровая электроника ;-). ЕДИНИЦА И НОЛЬ! 🙂

А вам слабо написать программу на единичках и нулях? Я думаю, это не под силу даже самому наяренному программеру в мире. Люди недолго думали и для удобства написания чисел придумали сначала восьмеричную систему счисления, а потом и шестнадцатеричную. Если помните, в двоичной системе счисления только два знака: 1 и 0. В десятичной – 10 знаков: 0 1 2 3 4 5 6 7 8 9, восьмеричной системе счисления используются только 8 знаков: 0 1 2 3 4 5 6 7. В шестнадцатеричной системе счисления знаков целых 16 штук! Чтобы не мудрить, взяли первые 9 знаков от десятичной системы счисления, а остальные от английского алфавита. Итого – 0 1 2 3 4 5 6 7 8 9 A B C D E F – ровненько 16 знаков.
Почему раньше не использовали десятичную систему вместо восьмеричной? Ведь в десятичной было на два знака больше? Все упиралось в байты. Как вы помните, 8 бит – это один Байт. Именно поэтому было удобно использовать восьмеричную и шестнадцатеричную системы счисления, кратную восьмерке, чем десятеричную. В последнее время самая крутая считается шестнадцатеричная система счисления. Именно она в большинстве используется в микроконтроллерах и в других цифровых микросхемах.
Перевод из одной системы счисления в другую
Как же нам переводить числа из одной системы счисления в другую? Здесь все просто, следуем примеру из второй главы, где написано, как использовать калькулятор Windows для перевода чисел из десятичной системы в двоичную. С помощью этого калькулятора мы также можем переводить числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно. Запускаем наш калькулятор, пишем от балды число “123” в десятичной системе счисления. Для этого ставим маркер на “Dec” и для красоты “1 байт”.

Для того, чтобы перевести это число в двоичную систему счисления, ставим маркер на “Bin” и получаем число “123” в двоичной системе счисления.

Для перевода в восьмеричную систему ставим маркер на “Oct”.

Ну и для перевода в шестнадцатеричную систему ставим маркер на “Hex”.

Все операции взаимозаменяемы. Это значит, что мы можем перевести число из двоичной в шестнадцатеричную, из восьмеричной в двоичную и так далее. Чтобы не спутать системы счисления и знать, какое число записано, после каждого записанного числа снизу ставится его индекс системы счисления. Например:
7ВС16 – значит число записано в шестнадцатеричной системе счисления
10112 – в двоичной системе
4578 – в восьмеричной системе
998510 – в десятеричной системе.



 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.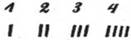 .
.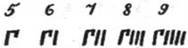
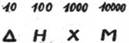
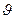 (тэта).
(тэта).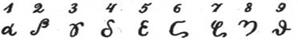
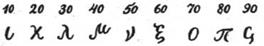
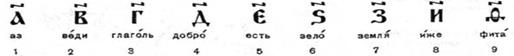
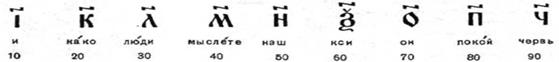







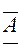 = 100 000 000.
= 100 000 000.