math-public:ravenstvo-vektorov [Президентский ФМЛ №239]
Равенство векторов
Определение
Векторы называются равными, если их длины равны и они сонаправлены.
Теорема
Каждый вектор равен самому себе.
Если вектор $\vec{a}$ равен вектору $\vec{b}$, то вектор $\vec{b}$ равен вектору $\vec{a}$.
Два вектора равные третьему вектору, равны.
Доказательство
Первые два свойства очевидно вытекают из определения равенства векторов.
Докажем третье свойство.
Пусть $\vec{a}=\vec{b}$ и $\vec{c}=\vec{b}$.
Тогда $|\vec{a}|=|\vec{b}|$ и $\vec{a}\upuparrows \vec{b}$, а также $|\vec{c}|=|\vec{b}|$ и $\vec{c}\upuparrows \vec{b}$.
Из равенства модулей следует, что $|\vec{a}|=|\vec{c}|$.
А из теоремы \ref{130} вытекает, что $\vec{a}\upuparrows \vec{c}$.
Поэтому $\vec{a}=\vec{c}$.
Теорема
Если четырехугольник $ABCD$ – параллелограмм, то $\overrightarrow{AB}=\overrightarrow{DC}$.
Доказательство
Из того, что $ABCD$ параллелограмм следует, что $AB=CD$ и $AB\parallel CD$.
Кроме того лучи $AB$ и $DC$ лежат по одну сторону от прямой $AD$, следовательно вектора $\overrightarrow{AB}$ и $\overrightarrow{DC}$ сонаправлены и равны по модулю.
Таким образом $\overrightarrow{AB}=\overrightarrow{DC}$.
Теорема
Если $\overrightarrow{AB}=\overrightarrow{CD}$, то $\overrightarrow{AC}=\overrightarrow{BD}$.
Доказательство
Из равенства векторов $\overrightarrow{AB}$ и $\overrightarrow{CD}$ следует, что $AB=CD$ и либо $AB\parallel CD$, либо точки $A, B, C, D$ лежат на одной прямой.
В первом случае, по признаку, четырехугольник $ABDC$ будет являться параллелограммом.
Следовательно, по теореме $\overrightarrow{AC}=\overrightarrow{BD}$.
Во втором случае введем на прямой $AB$ координату $x$. Пусть числа $x_A, x_B, x_C, x_D$ – координаты точек $A,B,C,D$ соответственно. Тогда условие $\overrightarrow{AB}=\overrightarrow{CD}$ означает, что выполнено равенство $x_B-x_A=x_D-x_C$.
Здесь равенство модулей чисел $x_B-x_A$ и $x_D-x_C$ означает, что $AB=CD$, а совпадение их знаков – что $\overrightarrow{AB}\upuparrows\overrightarrow{CD}$.
Но тогда $x_C-x_A=x_D-x_B$, что и означает $\overrightarrow{AC}\upuparrows\overrightarrow{BD}$.
math-public/ravenstvo-vektorov.txt · Последние изменения: 2016/09/06 18:13 — labreslav
ВЕКТОРЫ
ВЕКТОРЫ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ. СКАЛЯРНОЕ,
ВЕКТОРНОЕ, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
1. ВЕКТОРЫ, ДЕЙСТВИЯ НАД ВЕКТОРАМИ.
Основные определения.
Определение 1. Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
(Перемещение, сила, скорость и т.д.)
Обозначения: 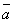 ,
, 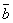 или
или 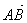 ,
, 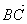 .
.
Геометрический вектор – это направленный отрезок.
Для
вектора 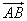 –
точка А –
начало, точка В –
конец вектора.
–
точка А –
начало, точка В –
конец вектора.
Определение 3. Модуль вектора – это длина отрезка AB.
Определение
4. Вектор,
модуль которого равен нулю,
называется нулевым, обозначается 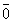 .
.
Определение 5. Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6. Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
1) Сложение векторов.
Опр.
6. Суммой двух
векторов 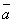 и
и 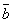 является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
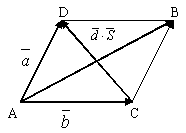
Рис.1.
Опр.
7. Суммой трех
векторов 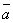 ,
,  ,
,  называется
диагональ параллелепипеда, построенного
на этих векторах (правило
параллелепипеда).
называется
диагональ параллелепипеда, построенного
на этих векторах (правило
параллелепипеда).
Опр. 8. Если А, В, С –
произвольные точки, то 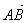 +
+  =
=  (правило
треугольника).
(правило
треугольника).
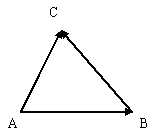
рис.2
Свойства сложения.
1о. 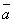 +
+ 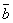 =
= 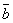 +
+ 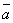 (переместительный
закон).
(переместительный
закон).
2о. 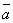 +
(
+
( +
+ 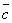 )
= (
)
= (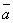 +
+ 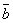 )
+
)
+ 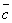 =
(
=
(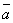 +
+ 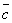 )
+
)
+ 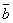 (сочетательный
закон).
(сочетательный
закон).
3о.  +
(–
+
(–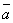 )
+
)
+  .
.
2) Вычитание векторов.
Опр.
9. Под разностью векторов  и
и  понимают
вектор
понимают
вектор 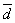 =
= 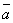 –
– 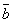 такой,
что
такой,
что 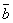 +
+ 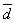 =
= 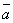 .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
3) Умножение вектора на число.
Опр.
10. Произведением вектора 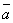 на скаляр k называется
вектор
на скаляр k называется
вектор
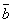 = k
= k =
= 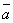 k,
k,
имеющий длину ka, и направление, которого:
1. совпадает
с направлением вектора 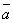 ,
если k >
0;
,
если k >
0;
2. противоположно
направлению вектора 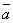 ,
если k <
0;
,
если k <
0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k + l)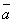 = k
= k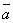 + l
+ l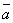 .
.
k(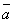 +
+ 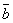 )
= k
)
= k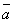 + k
+ k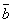 .
.
2o. k(l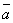 )
= (kl)
)
= (kl)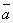 .
.
3o. 1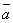 =
= 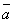 , (–1)
, (–1) 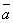 =
–
=
– 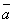 , 0
, 0 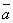 =
= 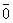 .
.
Свойства векторов.
Опр.
11. Два
вектора 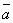 и
и 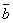 называются коллинеарными,
если они расположены на параллельных
прямых или
на одной
прямой.
называются коллинеарными,
если они расположены на параллельных
прямых или
на одной
прямой.
Нулевой
вектор 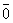 коллинеарен
любому вектору.
коллинеарен
любому вектору.
Теорема
1. Два
ненулевых вектора  и
и 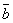 коллинеарны, когда
они пропорциональны т.е.
коллинеарны, когда
они пропорциональны т.е.
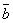 = k
= k , k –
скаляр.
, k –
скаляр.
Опр.
12. Три
вектора 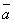 ,
, 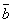 ,
, 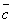 называются компланарными,
если они параллельны некоторой плоскости
или лежат в ней.
называются компланарными,
если они параллельны некоторой плоскости
или лежат в ней.
Теорема
2. Три
ненулевых вектора 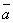 ,
, 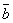 ,
, 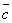 компланарны, когда
один из них является линейной комбинацией
двух других, т.е.
компланарны, когда
один из них является линейной комбинацией
двух других, т.е.
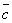 = k
= k + l
+ l , k ,l –
скаляры.
, k ,l –
скаляры.
Проекция вектора на ось.
Теорема
3. Проекция
вектора 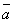 на
ось (направленная прямая) l равна
произведению длины вектора
на
ось (направленная прямая) l равна
произведению длины вектора 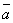 на
косинус угла между направлением вектора
и направлением оси, т.е.
на
косинус угла между направлением вектора
и направлением оси, т.е. 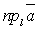 = a cos , = (
= a cos , = (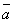 , l).
, l).
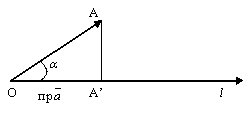
рис.3.
2. КООРДИНАТЫ ВЕКТОРА
Опр.
13. Проекции
вектора 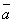 на
координатные оси Ох, Оу, Оz называются координатами
вектора. Обозначение:
на
координатные оси Ох, Оу, Оz называются координатами
вектора. Обозначение: 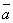 ax,ay, az.
ax,ay, az.
Длина
вектора: 

Пример: Вычислить
длину вектора 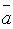
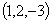 .
.
Решение: 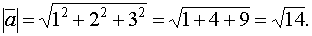
Расстояние
между точками 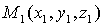 и
и  вычисляется
по формуле:
вычисляется
по формуле:
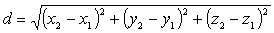 .
.
Пример: Найти расстояние между точками М (2,3,-1) и К (4,5,2).

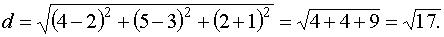
Действия над векторами в координатной форме.
Даны
векторы  =ax, ay, az и
=ax, ay, az и 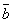 =bx, by, bz.
=bx, by, bz.
1. (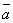
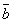 )=ax bx, ay by, az bz.
)=ax bx, ay by, az bz.
2. 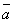 =ax, ay, az,
где –
скаляр.
=ax, ay, az,
где –
скаляр.
Скалярное произведение векторов.
Определение: Под
скалярным произведением двух векторов  и
и 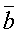
понимается
число, равное произведению длин этих
векторов на косинус угла между ними,
т.е. 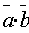 =
=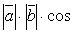
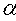 ,
, 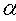 —
угол между векторами
—
угол между векторами 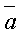 и
и 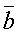 .
.
Свойства скалярного произведения:
1. 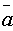
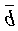 =
=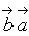

2. ( +
+ 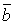 )
) 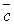 =
=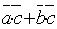
3. 
4. 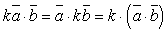
5. 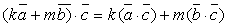 ,
где
,
где 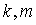 –
скаляры.
–
скаляры.
6. два
вектора перпендикулярны (ортогональны),
если 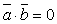 .
.
7. 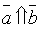 тогда
и только тогда, когда
тогда
и только тогда, когда  .
.
Скалярное
произведение в координатной форме имеет
вид: 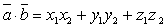 , где
, где 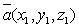 и
и 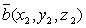 .
.
Пример: Найти
скалярное произведение векторов 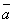
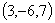 и
и 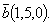
Решение: 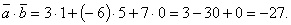
Векторное проведение векторов.
Определение:
Под векторным произведением двух
векторов 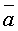 и
и 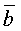 понимается
вектор,
понимается
вектор, 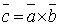 для
которого:
для
которого:
-модуль
равен площади параллелограмма,
построенного на данных векторах, т.е. 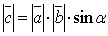 ,
где
,
где 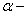 угол
между векторами
угол
между векторами 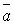 и
и 
-этот
вектор перпендикулярен перемножаемым
векторам, т.е. 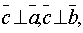
-если
векторы 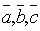 неколлинеарны,
то они образуют правую тройку векторов.
неколлинеарны,
то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При
изменении порядка сомножителей векторное
произведение меняет свой знак на
обратный, сохраняя модуль, т.е. 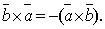
2.Векторный
квадрат равен нуль-вектору, т.е. 
3.Скалярный
множитель можно выносить за знак
векторного произведения, т.е. 
4.Для
любых трех векторов  справедливо
равенство
справедливо
равенство 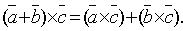
5.Необходимое
и достаточное условие коллинеарности
двух векторов 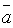 и
и 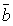 :
: 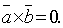
Векторное произведение в координатной форме.
Если
известны координаты векторов 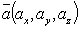 и
и 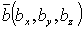 , то
их векторное произведение находится
по формуле:
, то
их векторное произведение находится
по формуле:
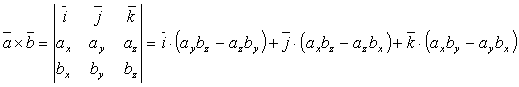 .
.
Тогда
из определения векторного произведения
следует, что площадь параллелограмма,
построенного на векторах  и
и 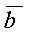 ,
вычисляется по формуле:
,
вычисляется по формуле:
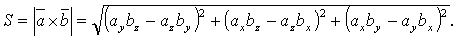
Пример: Вычислить
площадь треугольника с
вершинами 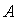 (1;-1;2),
(1;-1;2), 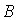 (5;-6;2),
(5;-6;2), 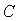 (1;3;-1).
(1;3;-1).
Решение: 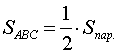 .
.
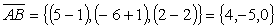 ,
,  ,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
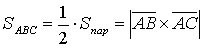 ,
,

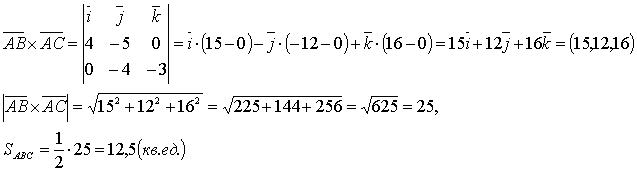
Смешанное произведение векторов.
Определение: Смешанным
(векторно-скалярным) произведением
векторов 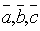 называется
число, определяемое по формуле:
называется
число, определяемое по формуле: 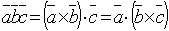 .
.
Свойства смешанного произведения:
1.Смешанное
произведение не меняется при циклической
перестановке его сомножителей, т.е. 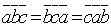 .
.
2.При
перестановке двух соседних сомножителей
смешанное произведение меняет свой
знак на противоположный, т.е. 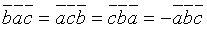 .
.
3.Необходимое
и достаточное условие компланарности
трех векторов 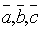 :
: 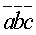 =0.
=0.
4.Смешанное
произведение трех векторов равно объему
параллелепипеда, построенного на этих
векторах, взятому со знаком плюс, если
эти векторы образуют правую тройку, и
со знаком минус, если они образуют левую
тройку, т.е. 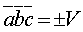 .
.
Если
известны координаты векторов 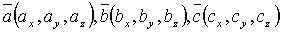 , то
смешанное произведение находится по
формуле:
, то
смешанное произведение находится по
формуле: 
Пример: Вычислить
смешанное произведение векторов 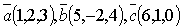 .
.
Решение: 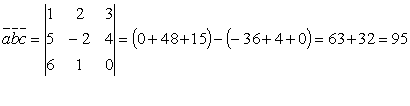
3. Базис системы векторов.
Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространствуR.
Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.
Пример. 
Определение. Любой
вектор вида  =
= называется
линейной комбинацией векторов
называется
линейной комбинацией векторов  .
Числа
.
Числа  — коэффициентами
линейной комбинации.
— коэффициентами
линейной комбинации.
Пример. 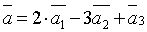 .
.
Определение.
Если вектор 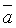 является
линейной комбинацией векторов
является
линейной комбинацией векторов 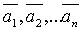 , то
говорят, что вектор
, то
говорят, что вектор  линейно
выражается через векторы
линейно
выражается через векторы  .
.
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.
Пример.
Система векторов 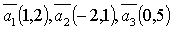 линейно-зависима,
т. к. вектор
линейно-зависима,
т. к. вектор 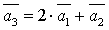 .
.
Определение базиса. Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример
1. Базис
пространства 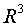 :
: 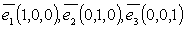 .
.
2. В
системе векторов 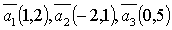 базисом являются векторы:
базисом являются векторы: 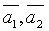 ,
т.к.
,
т.к. 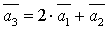 линейно
выражается через векторы
линейно
выражается через векторы 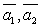 .
.
Замечание. Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Понятие вектора
Существуют величины, которые характеризуются помимо своей величины ещё и направленностью. Это скорость, ускорение, сила, смещение материальной точки и т.п. Можно абстрагироваться от конкретной физической величины и считать, что вектор — это направленный отрезок. Определение: вектор — это направленный отрезок.
Будем обозначать вектор AB . А — начало вектора, В — конец вектора.
 —
означает длина вектора (символ модуля).
—
означает длина вектора (символ модуля).
Вектор называется нулевым, если его начало и конец совпадают.
Важное свойство векторов — коллинеарность. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Теперь сформулируем понятие равенства двух векторов: два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Два нулевых вектора считаются равными.












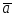

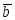 равные
равные 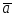
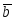 неравные
неравные
Из определения
равенства векторов следует, что мы не
различаем двух равных векторов, имеющих
разные точки приложения. Иными словами,
точка приложения вектора 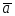 может быть произвольной. В соответствии
с этим векторы в геометрии называются
свободными.
может быть произвольной. В соответствии
с этим векторы в геометрии называются
свободными.
Определим линейные операции над векторами.
Сложение. Суммой 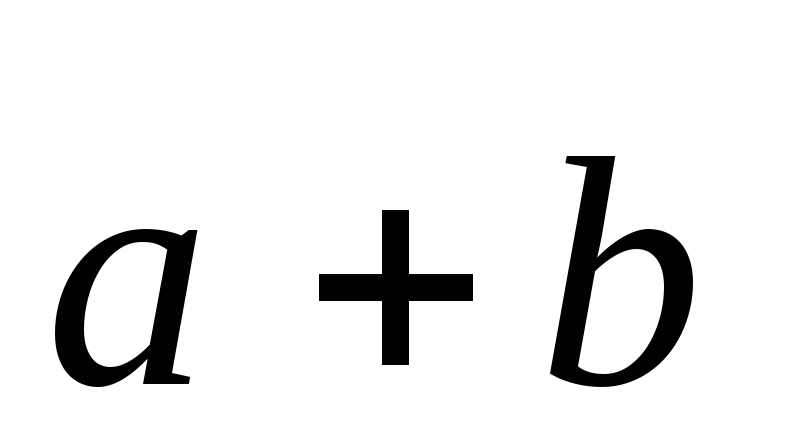 двух векторов
двух векторов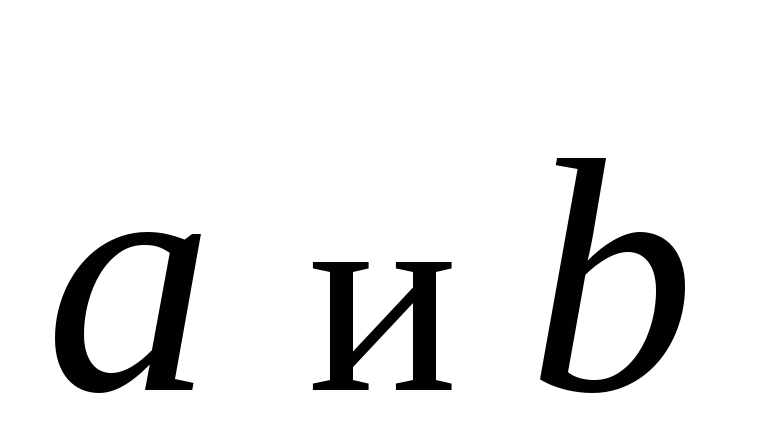 называется
вектор, идущий из начала вектора
называется
вектор, идущий из начала вектора в конец вектора
в конец вектора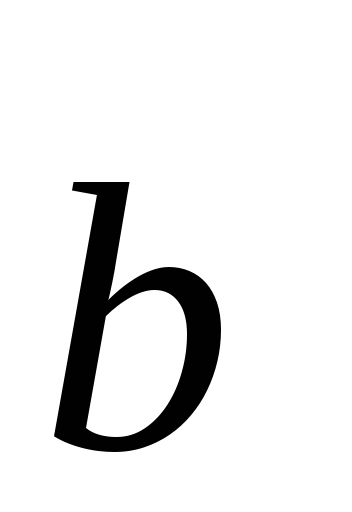 при условии, что начало
при условии, что начало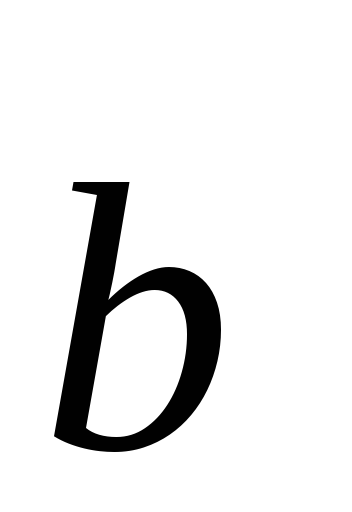 приложено к концу вектора
приложено к концу вектора .
.
Геометрически это можно изобразить правилом треугольника:
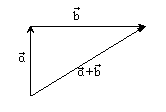
Правило сложения векторов обладает теми же четырьмя свойствами, что и правило сложения вещественных чисел:
1. 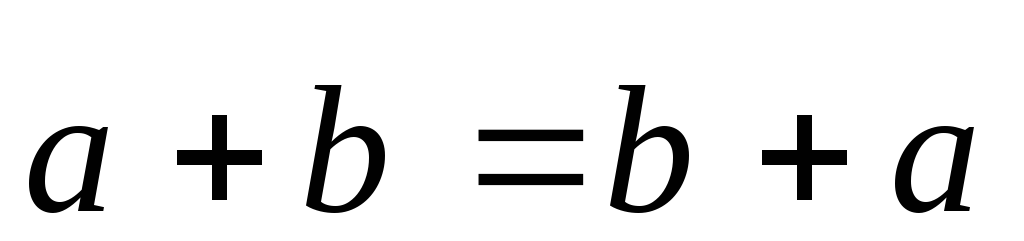 (переместительное свойство).
(переместительное свойство).
2. 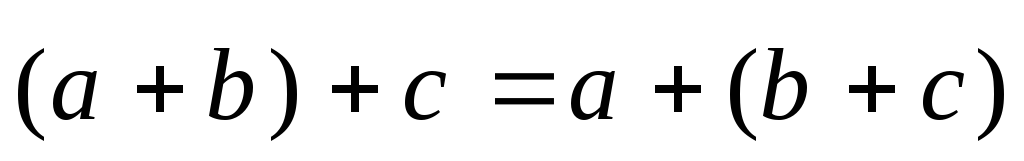 (сочетательное свойство).
(сочетательное свойство).
3. Существует
нулевой вектор, такой, что  .
.
4. Для каждого  существует такой
существует такой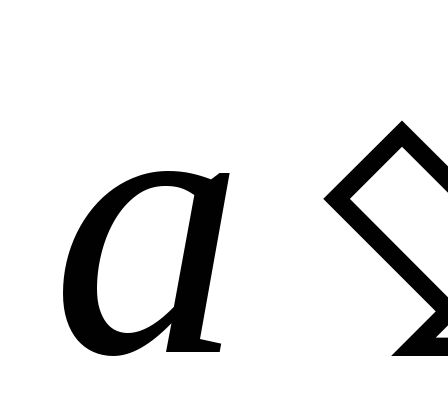 что
что .
.
Эти свойства доказываются геометрическими построениями. К примеру свойство 1:

Эти свойства позволяют оперировать с векторами так же как и с вещественными числами.
О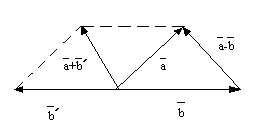 пределим
разность векторовкак сумму
пределим
разность векторовкак сумму где
где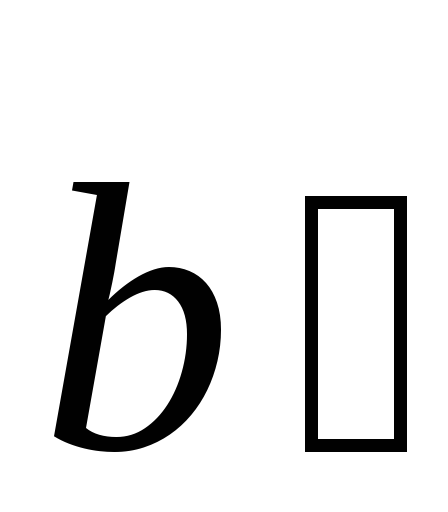 —
противоположный вектор вектору
—
противоположный вектор вектору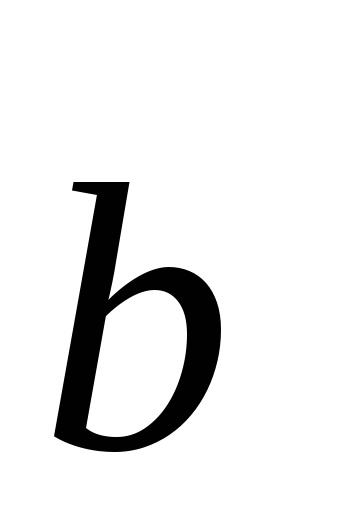 .
.
Определим, наконец, операцию умножения вектора на вещественное число.
Произведением  называется вектор
называется вектор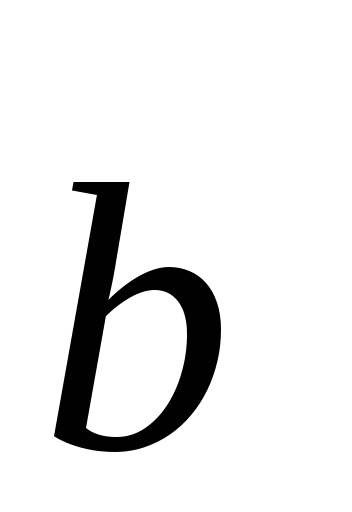 ,
коллинеарный
,
коллинеарный ,
имеющий длину
,
имеющий длину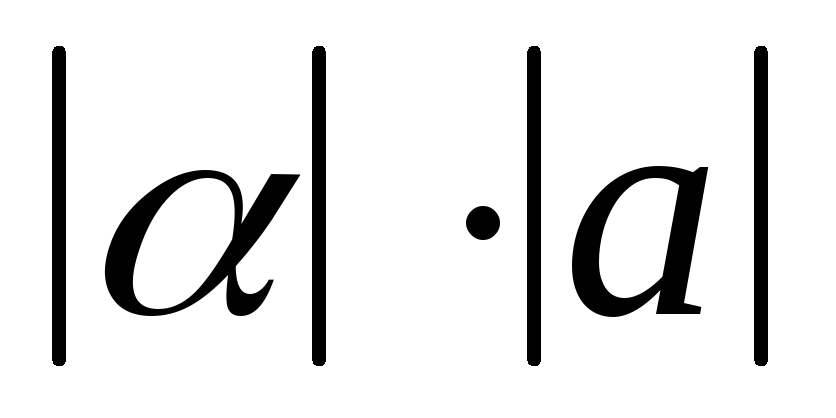 и имеющий направление, совпадающее с
и имеющий направление, совпадающее с если
если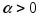 и
противоположное, если
и
противоположное, если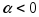 .
.
Геометрический
смысл умножения — вектор  растягивается в
растягивается в раз.
раз.
Операция умножения обладает тремя свойствами:
5. 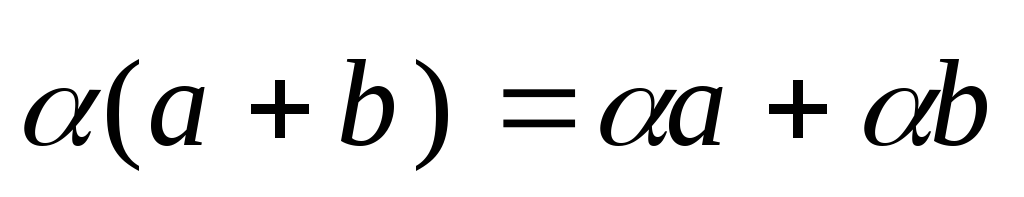 (распределительное свойство относительно
суммы векторов).
(распределительное свойство относительно
суммы векторов).
6. 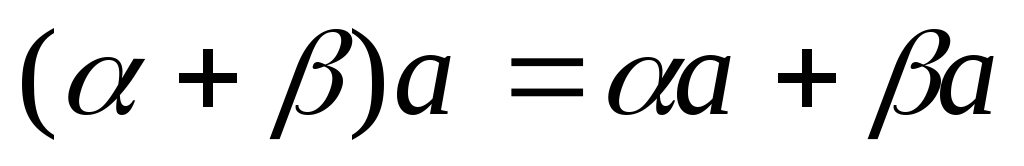 (распределительное свойство относительно
суммы чисел).
(распределительное свойство относительно
суммы чисел).
7. 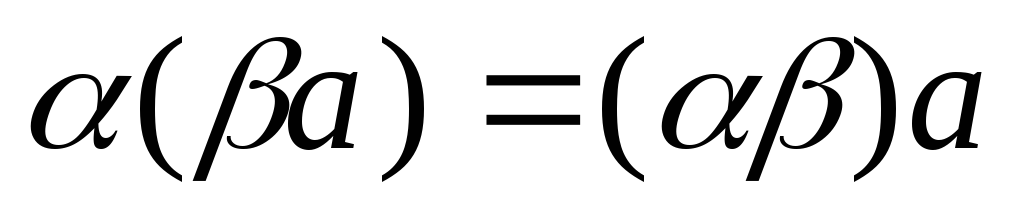 (сочетательное свойство).
(сочетательное свойство).
Доказываются эти свойства тоже графически.
Рассмотрим теорему
1. Если вектор 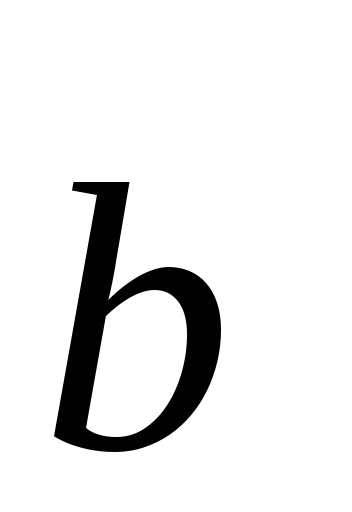 коллинеарен
вектору
коллинеарен
вектору ,
то существует такое вещественное число
,
то существует такое вещественное число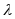 ,
что
,
что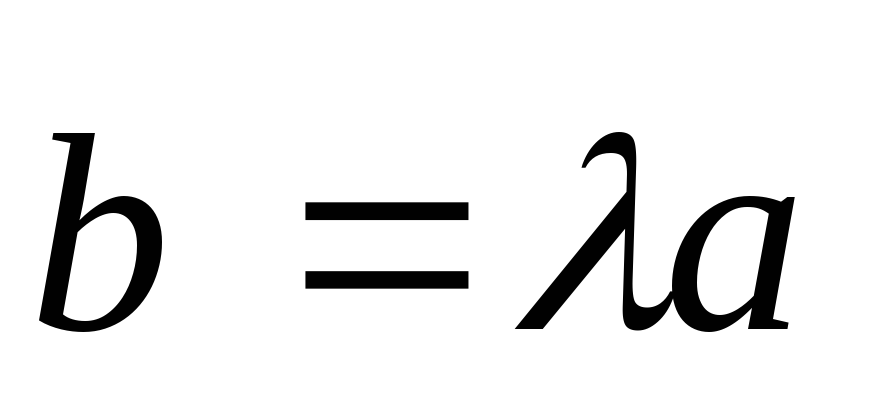 .
.
Совместим  и
и .
В силу коллинеарности они окажутся на
одной прямой. Т. е.
.
В силу коллинеарности они окажутся на
одной прямой. Т. е.




 O
O
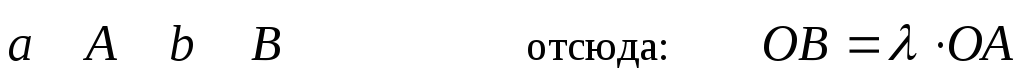 (*)
(*)
Докажем, что 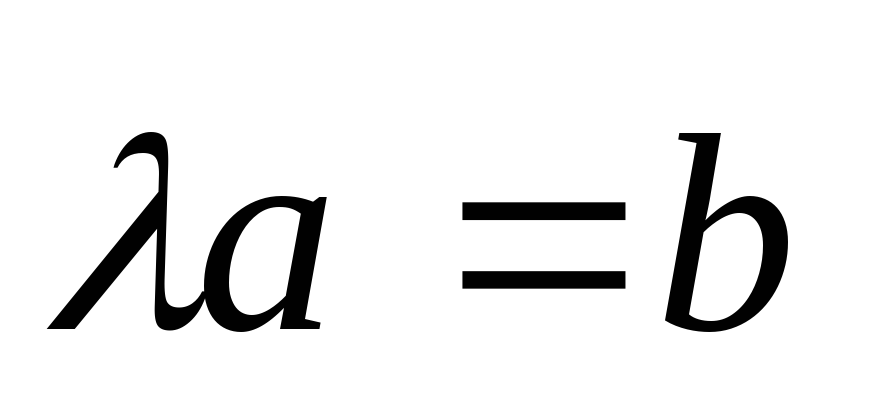 .
Т.е. что длины их равны, направления
совпадают, коллинеарны.
.
Т.е. что длины их равны, направления
совпадают, коллинеарны.
Коллинеарность
вытекает из определения произведения 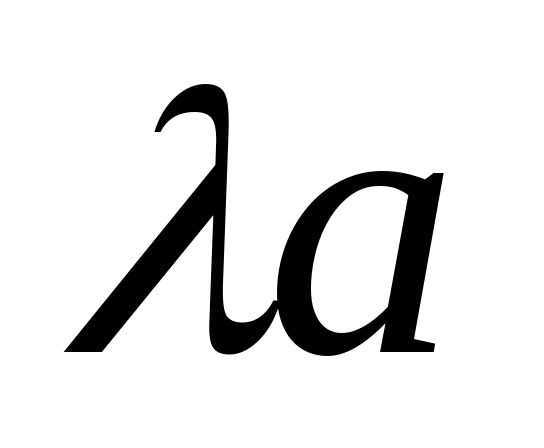 и
коллинеарности
и
коллинеарности и
и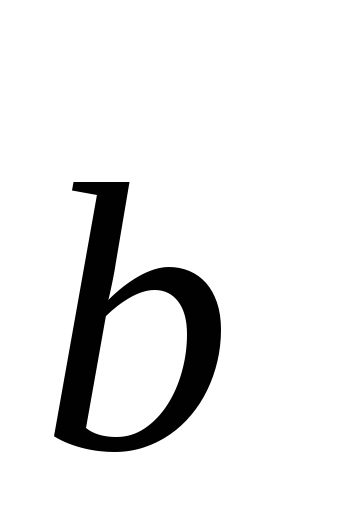 ,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если
,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если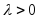 ,
направления совпадают, и если
,
направления совпадают, и если ,
то
,
то и
и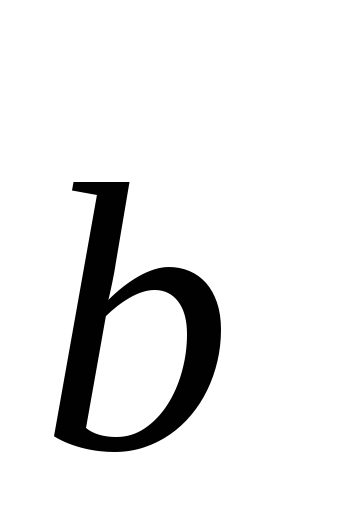 —
противоположно направлены.
—
противоположно направлены.
Определение 1. Линейной комбинацией n векторов мы называем сумму вида
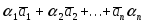
где  —
вещественные числа.
—
вещественные числа.
Определение 2.
Векторы  называются линейно зависимыми, если
существуют такие
называются линейно зависимыми, если
существуют такие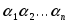 , хотя бы одно из которых отлично от
нуля, что имеет место равенство:
, хотя бы одно из которых отлично от
нуля, что имеет место равенство:
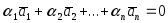
Если все 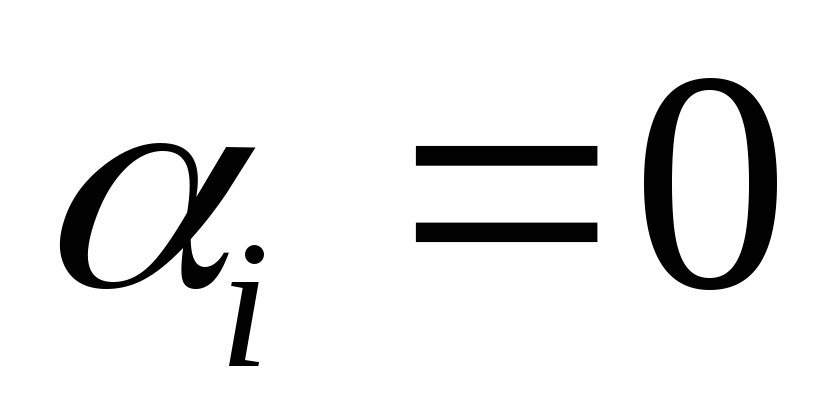 ,
то такие векторы
,
то такие векторы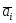 называются линейно независимыми.
называются линейно независимыми.
Докажем теорему
2. Если среди n векторов  хотя бы один нулевой, то эти векторы
являются линейно зависимы. Доказательство:
пусть для определённости
хотя бы один нулевой, то эти векторы
являются линейно зависимы. Доказательство:
пусть для определённости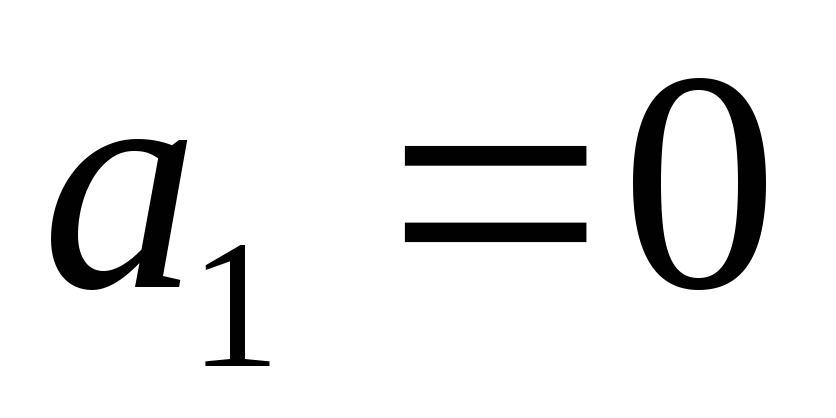 .
Тогда выполняется равенство:
.
Тогда выполняется равенство:
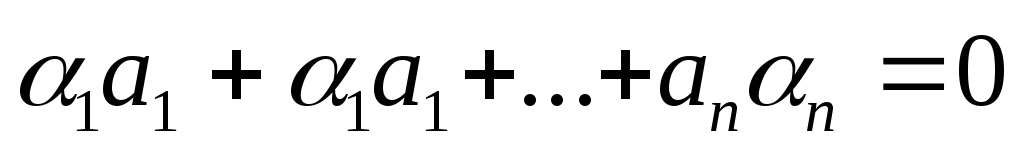
где 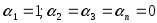 .
.
и по определению линейной зависимости эти векторы линейно зависимы.
Теорема номер
три: если
среди п векторов 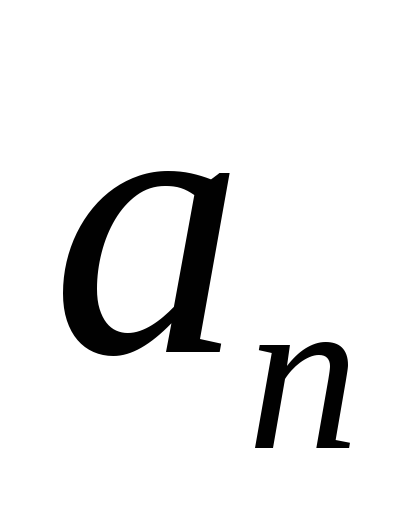 какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.
какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.
Действительно: линейная зависимость (п-1) векторов означает:

Добавим сюда равное
0 слагаемое  и получим
и получим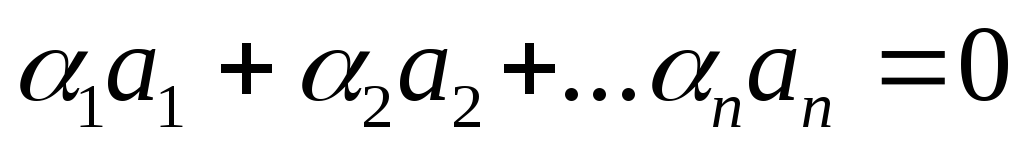 ,
,
где 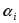 не все равны нулю, т.е. теорема доказана.
не все равны нулю, т.е. теорема доказана.
Линейные комбинации двух векторов.
Теорема 4. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Доказательство
необходимости: предположим, что  и
и линейно зависимы. Т.е.
линейно зависимы. Т.е.
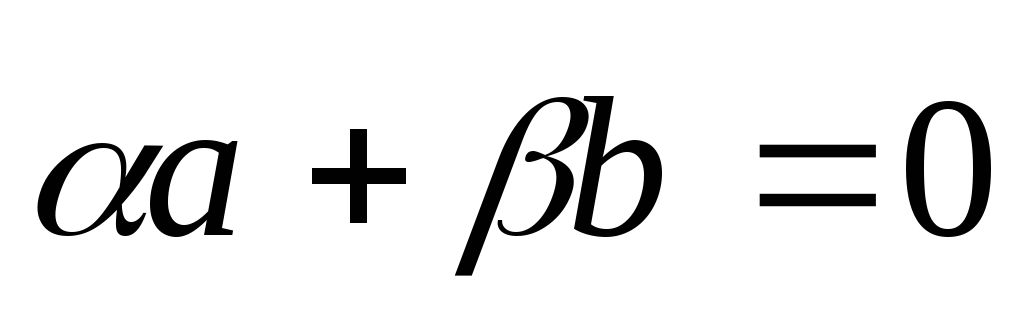
положим, что 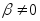 .
Тогда
.
Тогда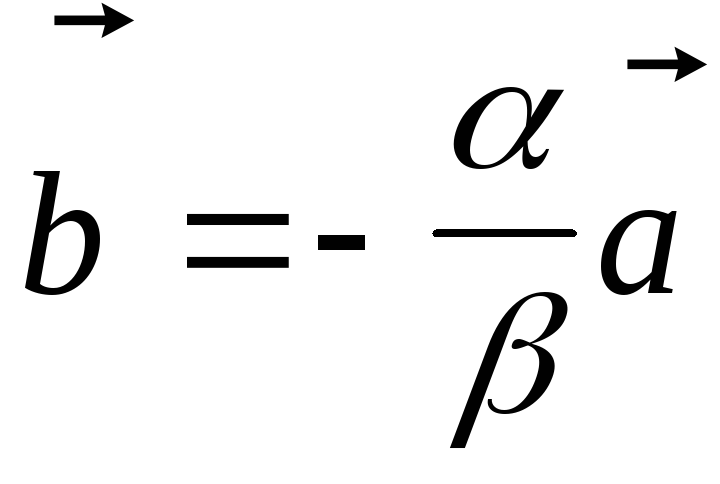 или
или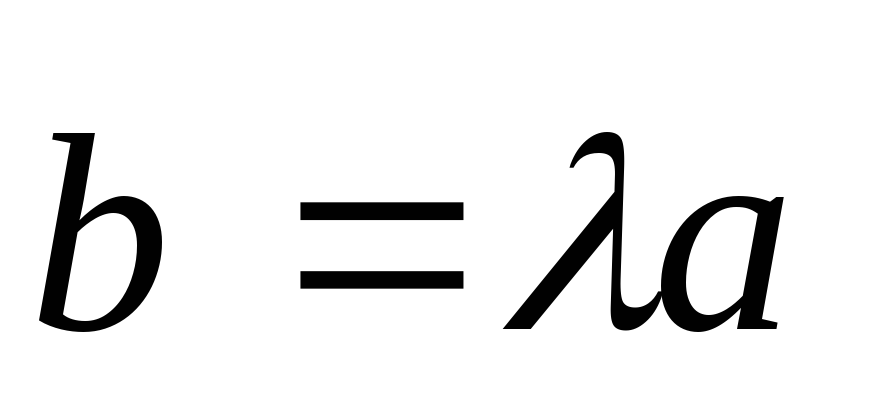 .
По определению произведения
.
По определению произведения и
и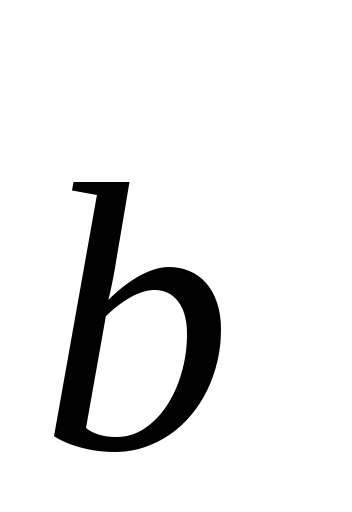 коллинеарны.
коллинеарны.
Достаточность:
предположим,  и
и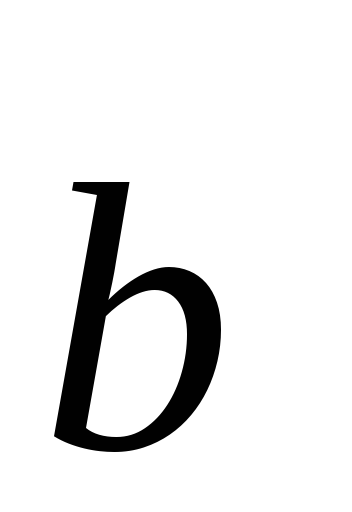 коллинеарны.
Если
коллинеарны.
Если или
или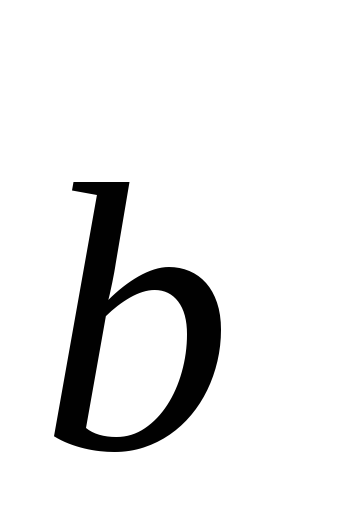 равно
нулю, то они линейно зависимы в силу
теоремы 2. Если
равно
нулю, то они линейно зависимы в силу
теоремы 2. Если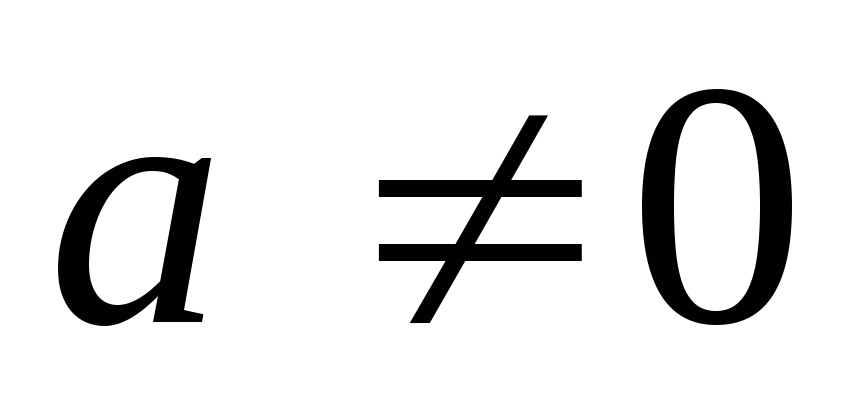 и
и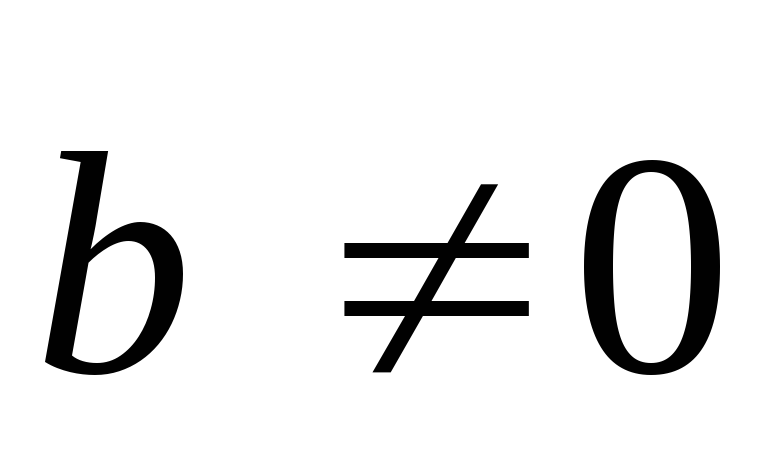 то в силу теоремы 1 имеем:
то в силу теоремы 1 имеем:
 ,
или
,
или 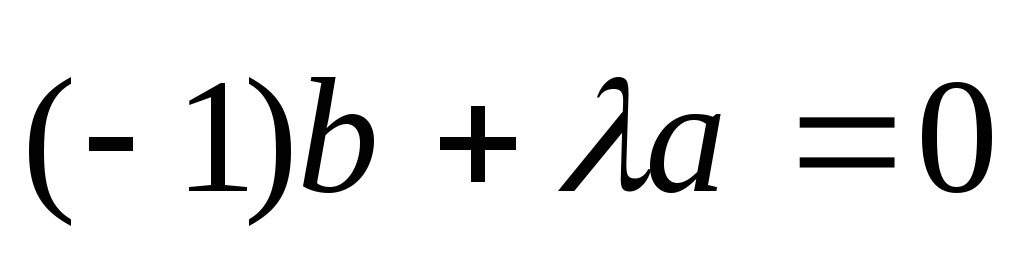 .
.
Т. к. здесь заведомо
(-1) не равно 0, то равенство доказывает
линейную зависимость векторов  и
и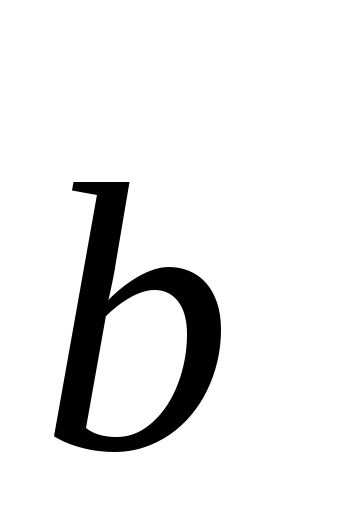 .
.
Следствие 1. Если
векторы  и
и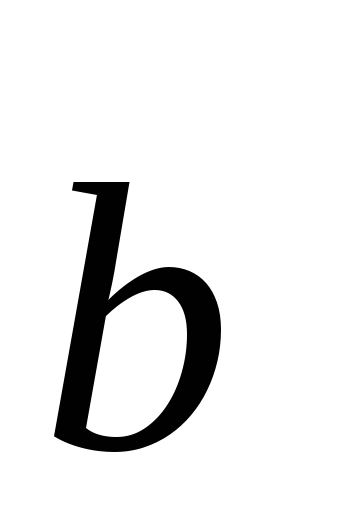 неколлинеарны, то они линейно независимы.
неколлинеарны, то они линейно независимы.
Следствие 2. Среди двух неколлинеарных векторов не может быть нулевых. (Иначе они были бы линейно зависимы).
Линейные комбинации трёх векторов
Определение: векторы называются компланарными, если они лежат в одной плоскости, либо в параллельных плоскостях.
Теорема 5. Необходимым и достаточным условием линейной зависимости трёх векторов является их компланарность.
Необходимость: пусть три вектора линейно зависимы:
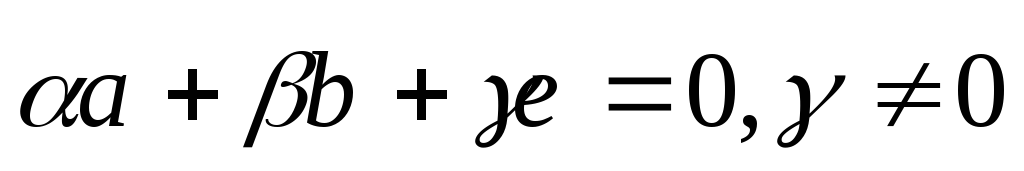 .
.
Тогда 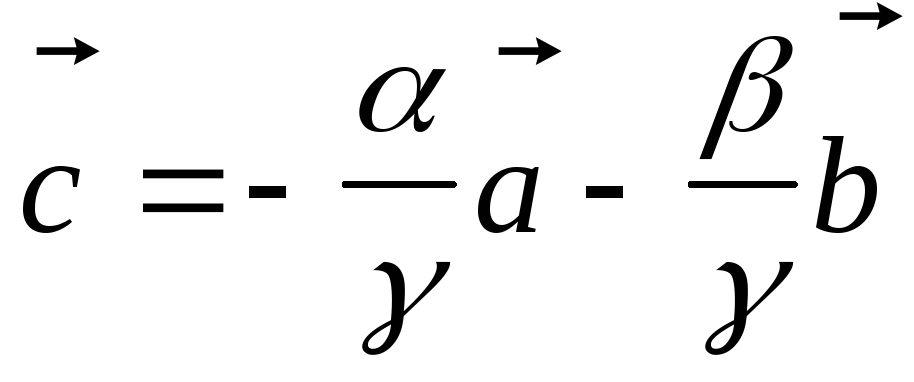 ,
или
,
или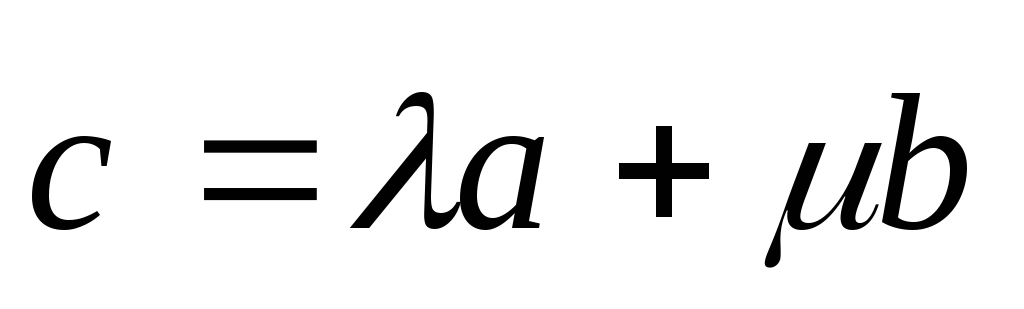
Это равенство означает сложение двух векторов, т.е. все три вектора лежат в одной плоскости.
Достаточность:
пусть 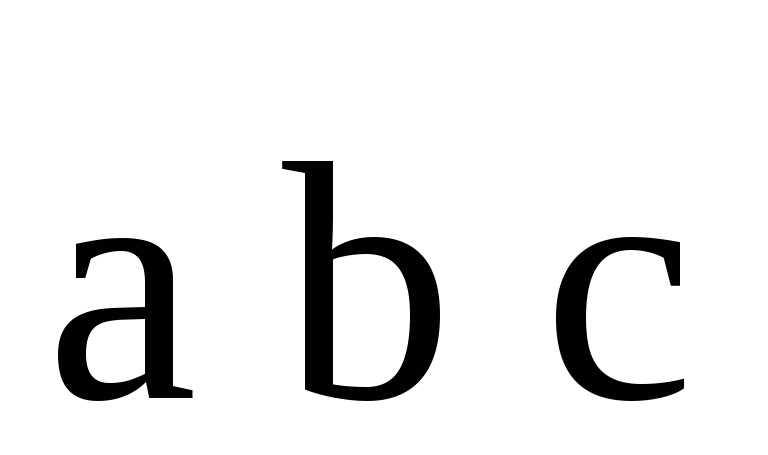 компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.
компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.
Перенесём все векторы в одну плоскость. Поскольку они неколлинеарны, то существует их общая точка пересечения:
В силу теоремы 1,
найдутся такие  и
и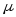 ,
что
,
что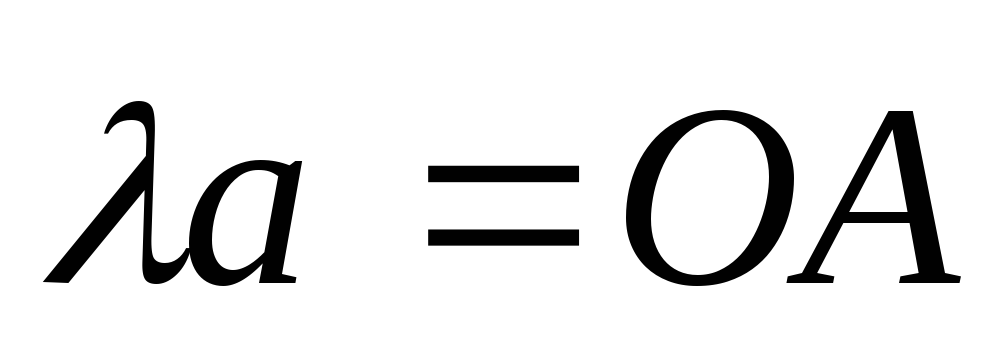
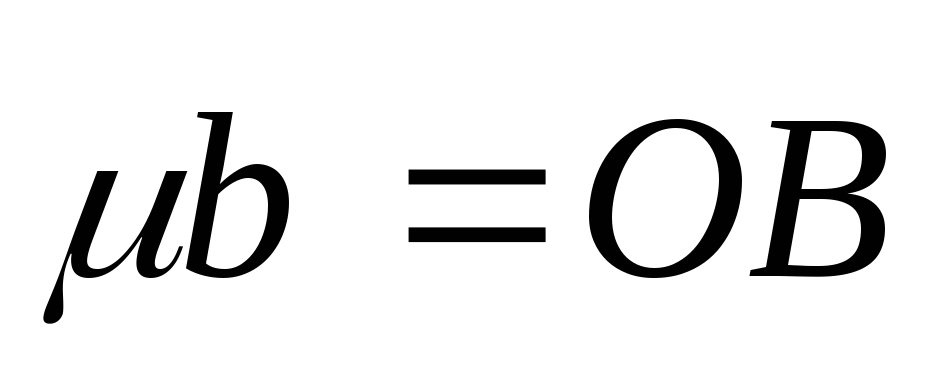
 или
или  .
Теорема доказана.
.
Теорема доказана.
Следствие:
Если векторы и
и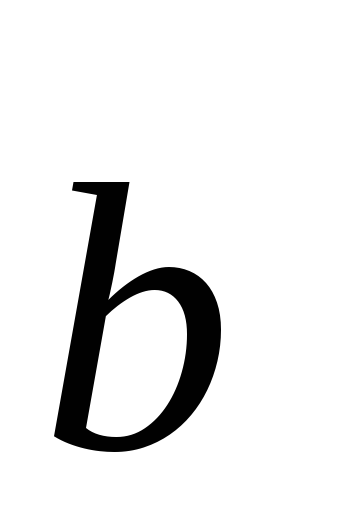 неколлинеарны,
то для любого
неколлинеарны,
то для любого ,
лежащего в одной плоскости с векторами
,
лежащего в одной плоскости с векторами и
и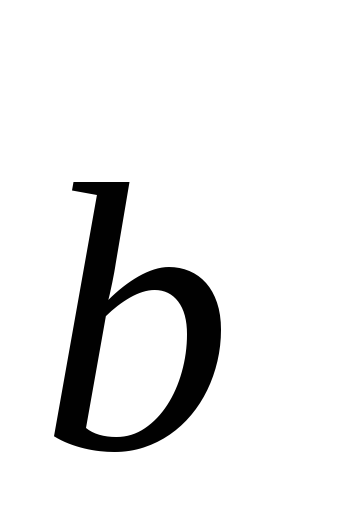 найдутся
такие
найдутся
такие и
и ,
что выполнится равенство:
,
что выполнится равенство:
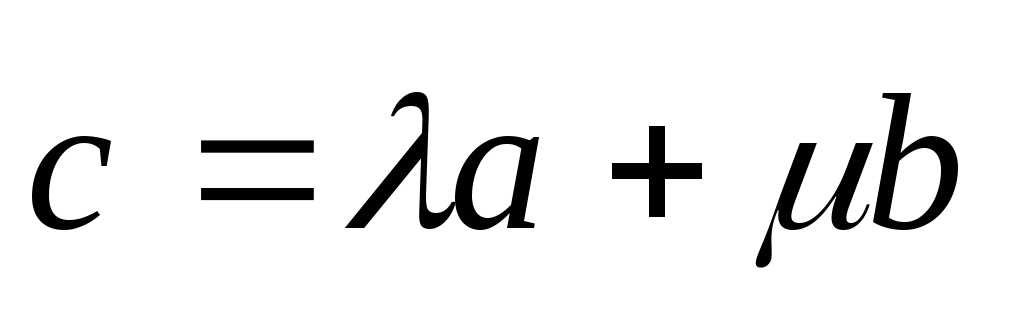
Наконец, линейная зависимость трёх векторов.
Теорема 6. Любые четыре вектора линейно зависимы.
Доказательство. Исключим тривиальные случаи, когда один из векторов ноль или когда какие-либо три компланарны. По предыдущим теоремам будут линейно зависимы все четыре вектора. Т.е. все векторы некомпланарны. Сведём их в одну точку и построим параллелепипед:
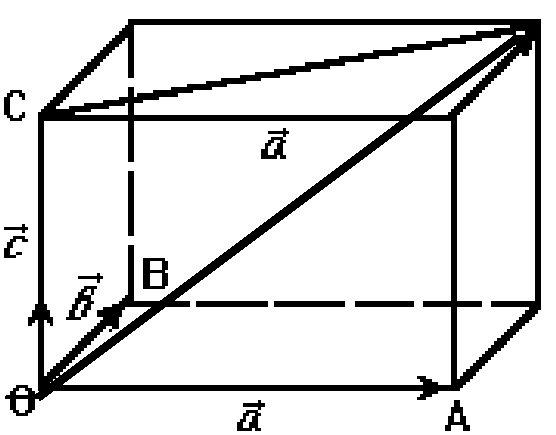
По теореме 1 найдутся такие числа, что:
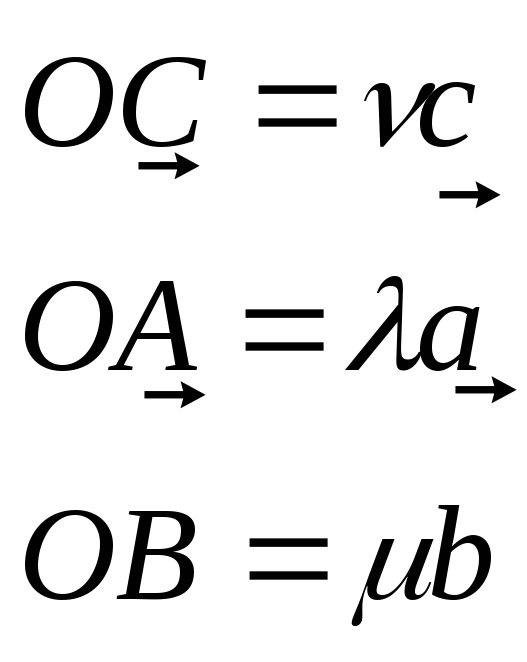
Но вектор  равен
равен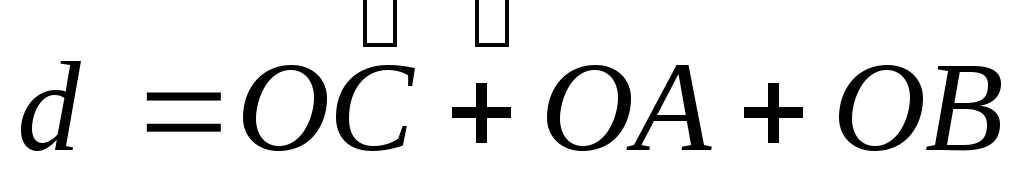 или
или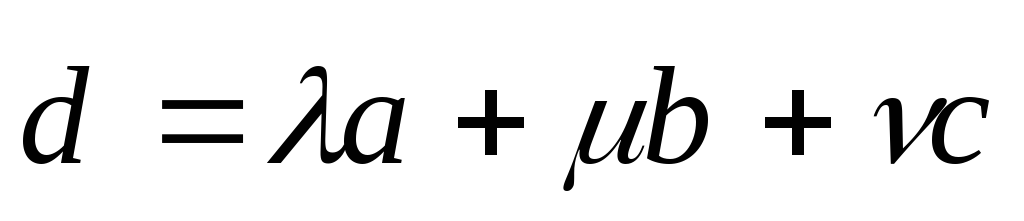 или
или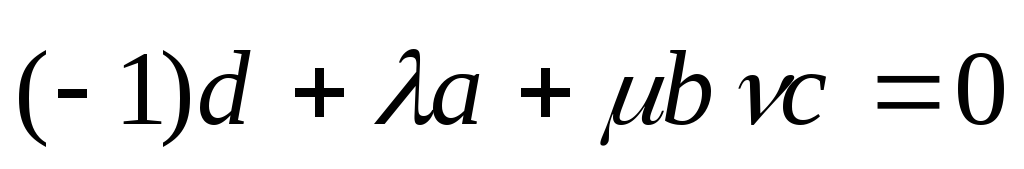 .
.
Теорема доказана.
Попутно мы доказали,
что если 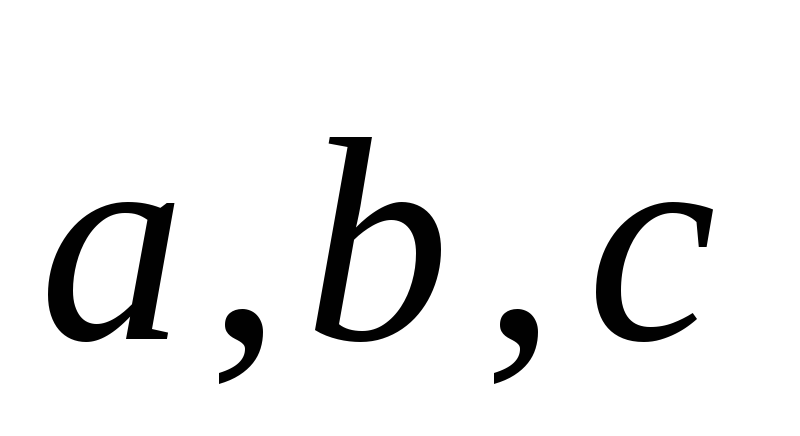 ,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора
,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора можно найти такие числа
можно найти такие числа ,
что
,
что
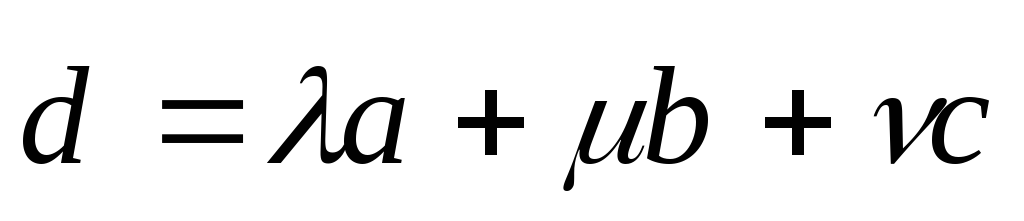 .
.
Понятие базиса.
Говорят, что три
линейно независимых вектора 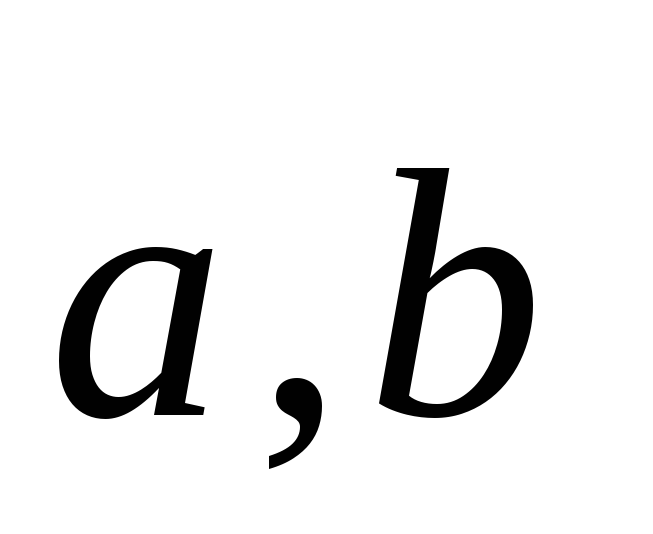 и
и образуют
в пространстве базис, если любой вектор
образуют
в пространстве базис, если любой вектор может
быть представлен в виде линейной
комбинации векторов
может
быть представлен в виде линейной
комбинации векторов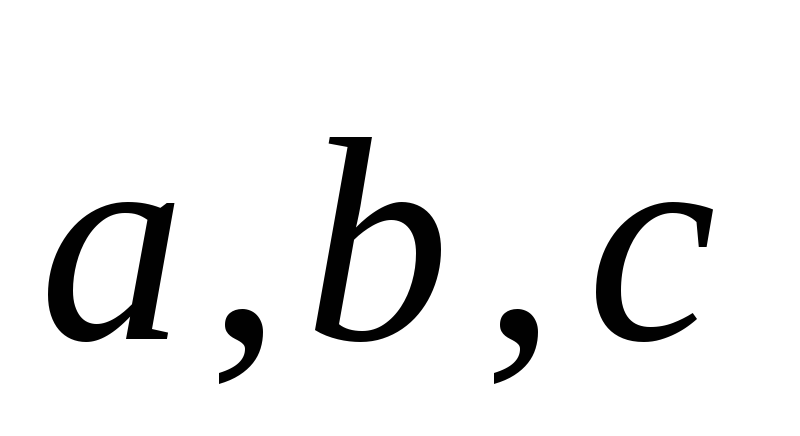
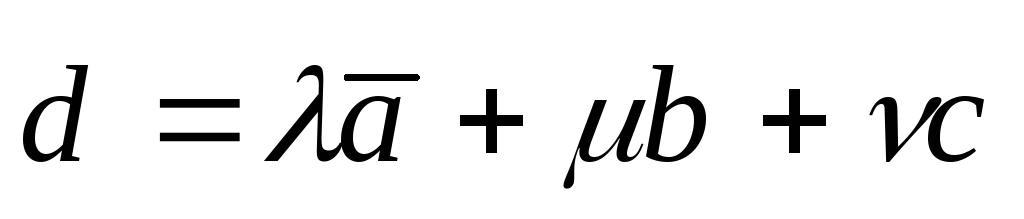 (**)
(**)
Принято называть
(**) разложением вектора d
по базису 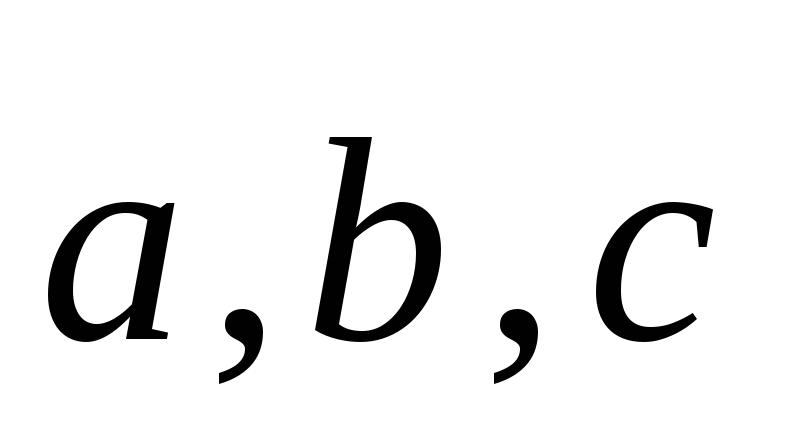 ,
а числа
,
а числа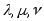 -координатами
вектора
-координатами
вектора относительно
базиса
относительно
базиса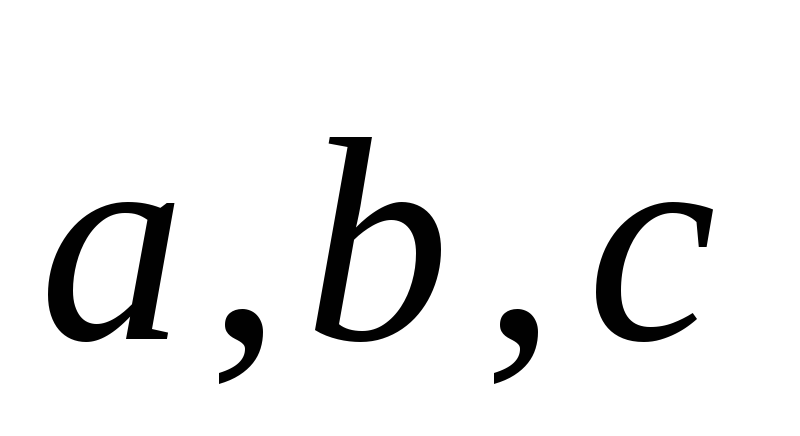 .
Причём можно доказать, что разложение
.
Причём можно доказать, что разложение по
базису
по
базису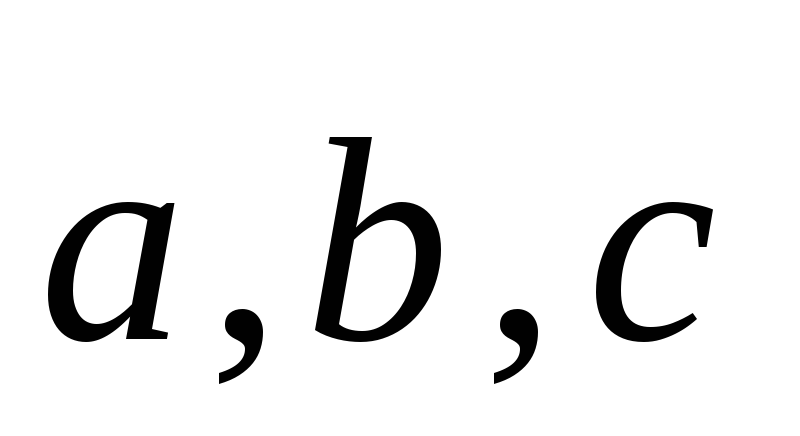 может быть единственным образом
осуществлено.
может быть единственным образом
осуществлено.
Определим так
называемые афинные
координаты.
Афинные координаты в пространстве
определяются заданием базиса 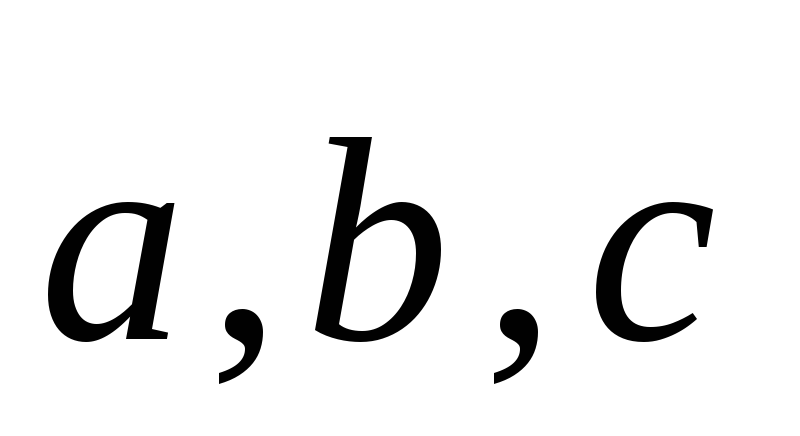 и некоторой точки О, называемой началом
координат.
и некоторой точки О, называемой началом
координат.
Частным случаем
афинных координат являются, очевидно,
прямоугольные декартовы координаты,
Здесь введём три взаимно перпендикулярных
(ортогональных) единичных векторов  .
Для каждого вектора
.
Для каждого вектора найдётся
и при том единственная тройка чисел
найдётся
и при том единственная тройка чисел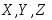 ,
такая, что
,
такая, что
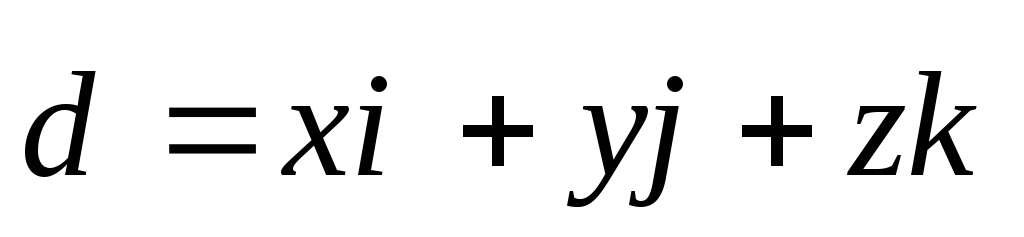
Числа X,Y,Z называют декартовы прямоугольные координаты.
Введём определение
проекции вектора на ось v.
Дан вектор 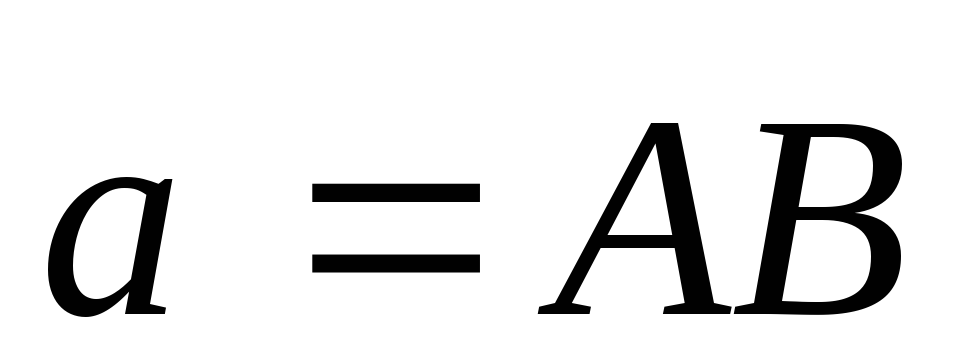 .
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим
.
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим 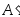 и
и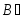 .
.
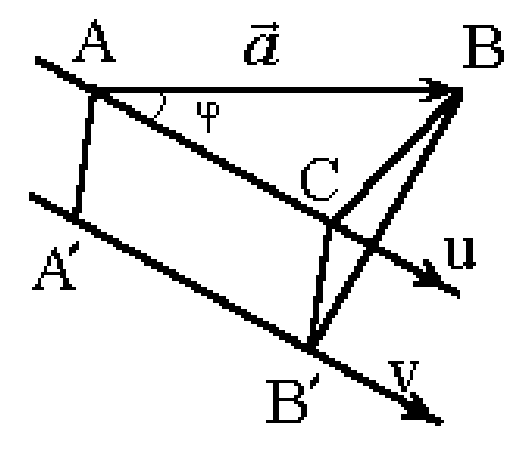
Проекцией вектора  на
осьv назовём величину направленного отрезка
на
осьv назовём величину направленного отрезка 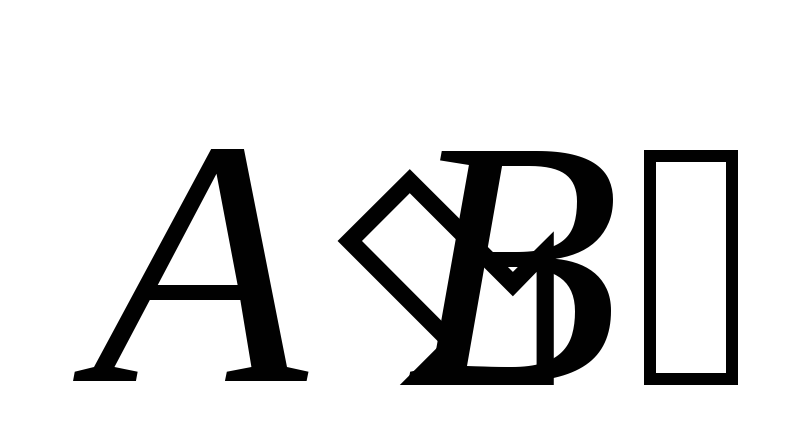 осиv.
осиv.
Углом наклона
вектора  к осиv назовём угол
к осиv назовём угол 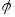 между направлением вектора
между направлением вектора и направлением осиv.
Из рассмотрения треугольника АВС
следует, что
и направлением осиv.
Из рассмотрения треугольника АВС
следует, что 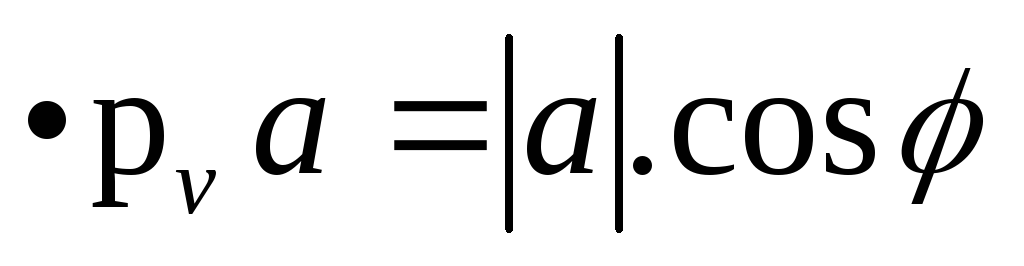 .
.
Можно доказать,
что декартовы координаты X,Y,Z вектора  являются
проекции векторана
оси соответственно ортам:
являются
проекции векторана
оси соответственно ортам:
 -ось
Ох,
-ось
Ох, 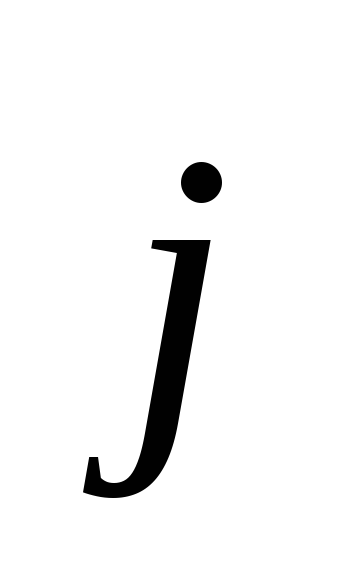 -ось
Oy ,
-ось
Oy ,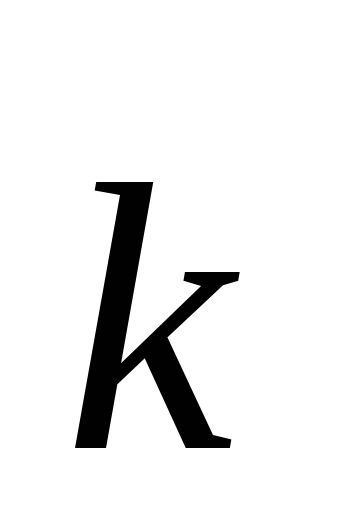 —
ось Oz.
—
ось Oz.
Или можно записать:
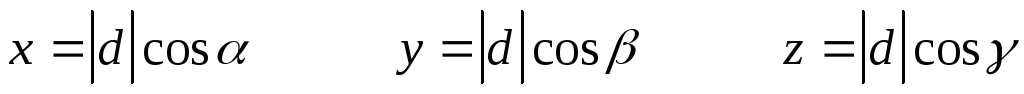 (***)
(***)
Три числа
называются направляющими косинусами
вектора .
.
Длина диагонали
параллелепипеда равна 
Тогда можно записать:
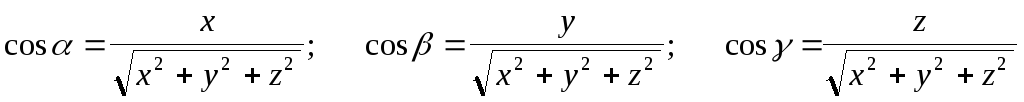
Возведём в квадрат и складывая, получим равенство:
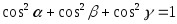 .
.
Лекция 5.
Скалярное произведение векторов — урок. Геометрия, 9 класс.
Скалярным произведением двух векторов a→ и b→ будет скалярная величина (число), равная произведению модулей этих векторов, умноженная на косинус угла между ними:
a→⋅b→=a→⋅b→⋅cosα.

Очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.
Угол между векторами обозначают a→b→ˆ=α.
1. Если векторы сонаправлены, то a→b→ˆ=0°.

Обрати внимание!
Так как косинус угла в \(0\) градусов равен \(1\), то скалярное произведение сонаправленных векторов является произведением их длин.
Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если векторы противоположно направлены, то a→b→ˆ=180°.

Обрати внимание!
Так как косинус угла в \(180\) градусов равен \(-1\), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
3. Векторы называют перпендикулярными, если a→b→ˆ=90°.

Обрати внимание!
Так как косинус прямого угла равен \(0\), то скалярное произведение перпендикулярных векторов равно \(0\).
4. Необходимо внимательно рассмотреть ситуации, когда векторы образуют тупой угол.


Обрати внимание!
Так как косинус тупого угла отрицательный, то скалярное произведение таких векторов, которые образуют тупой угол, является отрицательным.
Скалярное произведение векторов, заданных координатами
Если a→xa;ya и b→xb;yb, то a→⋅b→=xa⋅xb+ya⋅yb.
Так как в координатах a→=xa2+ya2 и b→=xb2+yb2, то можно определить косинус угла между векторами и, следовательно, величину угла.
cosα=a→⋅b→a→⋅b→;cosα=xa⋅xb+ya⋅ybxa2+ya2⋅xb2+yb2.
Свойства скалярного произведения векторов
1. Скалярное произведение вектора самого на себя всегда больше или равно нулю. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору.
a→⋅a→>0;0→⋅0→=0.
2. Скалярное произведение вектора самого на себя равно квадрату его модуля:
a→⋅a→=a→2.
3. Для скалярного произведения в силе переместительный закон:
a→⋅b→=b→⋅a→.
4. Для скалярного произведения в силе распределительный закон:
a→+b→⋅c→=a→⋅c→+b→⋅c→.
5. Для скалярного произведения в силе сочетательный закон:
k⋅a→⋅b→=k⋅a→⋅b→.
6. Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны.


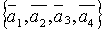
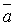 =
=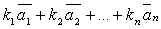 называется
линейной комбинацией векторов
называется
линейной комбинацией векторов  .
Числа
.
Числа 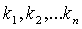 — коэффициентами
линейной комбинации.
— коэффициентами
линейной комбинации.